A new approach to special curved surface families according to modified orthogonal frame

1.   Introduction

Curves and surfaces are one of the most important fundamental topics in differential geometry, and we encounter this topic in almost every differential geometry book ^{[1,2,3,4,5,6,7]}. Recently, there have been studies on the characterization of surfaces, including the characterization of curves defined according to different frame and special surfaces such as ruled and tubular surfaces ^[8,9,10]. In addition, the problem of finding a family of surfaces passing through a given curve and accepting this curve as a special curve is one of the important topics studied recently. In this sense, this problem was first formulated by Wang et al ^[11]. They gave necessary and sufficient conditions for the given curve to be geodesic on the surface. Later, this study was generalized by Kasap and Ayyıldız in ^[12]. Li et al ^[13] studied the problem of finding a family of surfaces that accepts a given curve as a line of curvature. There are also several studies on this topic in three-dimensional Minkowski space; see ^[14,15]. For recent studies on the problem of finding a surface family that contains known special curve pairs and accepts these curves as geodesic, asymptotic, and line of curvature, see ^{[16,17,18,19,20,21,22,23,24]}. As is well-known, there are various frames that can be installed on a curve, and the one that is most frequently studied is the Frenet frame. Although the Frenet frame is a frame that characterizes the curve, one of its disadvantages is that this frame cannot be defined when the curvature of the curve is zero. In 1975, Bishop eliminated this disadvantage and defined a new frame, the Bishop frame ^[25]. In addition, Sasai defined the modified orthogonal frame at points where the curvature is different from zero ^[26]. Bükçü and Karacan expressed Sasai's work in three-dimensional Minkowski space. They also gave a new version of the modified orthogonal frame with torsion in three-dimensional Euclidean and Minkowski space ^[27]. Recently, there have been several studies on special curve pairs and special surfaces based on the modified orthogonal frame ^{[28,29,30,31,32,33,34,35,36]}.

In this study, we defined conditions for the given curve to be both parametric and geodesic, asymptotic, or a line of curvature on the parametric surface by using two types of modified orthogonal frames. Finally, we have given various examples to support the study.

2.   Preliminaries

In this section, we will explain some basic definitions and two types of modified orthogonal frames defined for curves with nonzero curvature and torsion.

Let $\alpha(s)$ be a $C^{3}$ space curve of arc length parameter s in the Euclidean 3-space. Then, the Frenet frame $\{\mathbf{t}(\mathrm{s}), \mathbf{n}(\mathrm{s}), \mathbf{b}(\mathrm{s})\}$ of the curve $\alpha$, where $\mathbf{t}(\mathrm{s}), \mathbf{n}(\mathrm{s}), \mathbf{b}(\mathrm{s})$ are the tangents of the principal normal and binormal vectors of $\alpha$, respectively, is defined by

Derivatives of the Frenet frame are given by the relations

where ${\mathtt{κ}}(\mathrm{s}) = \|\mathtt{α} "(\mathrm{s})\|$ and $\mathtt{τ}(\mathrm{s}) = -\langle\mathrm{b}^{\prime}(\mathrm{s}), \mathrm{n}(\mathrm{s})\rangle$ are called the curvature and torsion of the curve $\alpha$, respectively.

Let $\alpha(s)$ be an analytic curve. Then, this curve can be re-parameterized by its arc length s. For this curve, we assume that the curvature function $\kappa(s)$ is not identically zero or has discrete zero points. Thus, an orthogonal frame $\left\{\mathbf{T}_{\mathtt{κ}}(\mathrm{s}), \mathbf{N}_{\mathtt{κ}}(\mathrm{s}), \mathbf{B}_{\mathtt{κ}}(\mathrm{s})\right\}$ can be defined as follows:

Considering the above equations and the Frenet equations, the obtained relations linking the Frenet frame $\{\mathbf{t}(\mathrm{s}), \mathbf{n}(\mathrm{s}), \mathbf{b}(\mathrm{s})\}$ and a new frame at nonzero points of $\kappa$ are obtained as

In this case, $\mathbf{n}\left(\mathrm{s}_{0}\right) = \mathbf{b}\left(\mathrm{s}_{0}\right) = 0$ when $\kappa\left(s_{0}\right) = 0$ and the squares of the lengths of $\mathbf{n}$ and $\mathbf{b}$ vary analytically in s. Based on these equations, the deriative equations are obtained as

Where $\mathtt{τ}= \frac{\operatorname{det}\left(\mathtt{α}^{\prime}, \mathtt{α}^{\prime \prime}, \mathtt{α}^{\prime \prime \prime}\right)}{\mathtt{κ}^{2}}$ is the torsion of the curve $\mathtt{α}$.

A new frame makes it easier to incorporate the following equations using the Frenet frame:

The orthogonal frame $\left\{\mathbf{T}_{\mathtt{κ}}(\mathrm{s}), \mathbf{N}_{\mathtt{κ}}(\mathrm{s}), \mathbf{B}_{\mathtt{κ}}(\mathrm{s})\right\}$ is therefore called the modified orthogonal frame with nonzero curvature ^[26]. It is easy to see that for $\mathtt{κ}= 1$, the Frenet frame coincides with the modified orthogonal frame.

Let $\alpha(s)$ be an analytic curve. Then, this curve can be re-parameterized by its arc length s. For this curve, we will assume that the torsion function $\tau(s)$ is not identically zero. Thus, an orthogonal frame $\left\{\mathbf{T}_{\mathtt{τ}}(\mathrm{s}), \mathbf{N}_{\mathtt{τ}}(\mathrm{s}), \mathbf{B}_{\mathtt{τ}}(\mathrm{s})\right\}$ can be defined as follows:

Taking into account the above equations and the Frenet equations, we obtain the following relations linking the Frenet frame and a new frame at nonzero points of $\tau$ :

A new frame makes it easier to include the following equations using the Frenet frame:

The derivative equations of the new orthogonal frame $\left\{\mathbf{T}_{\mathtt{τ}}(\mathrm{s}), \mathbf{N}_{\mathtt{τ}}(\mathrm{s}), \mathbf{B}_{\mathtt{τ}}(\mathrm{s})\right\}$ are derived from these fundamental equations:

Where $\mathtt{τ} = \frac{\operatorname{det}\left(\mathtt{α}^{\prime}, \mathtt{α}^{\prime \prime}, \mathtt{α}^{\prime \prime \prime}\right)}{\kappa^{2}}$ is the torsion of the curve $\mathtt{α}$.

Thus, the orthogonal frame $\left\{\mathbf{T}_{\mathtt{τ}}(\mathrm{s}), \mathbf{N}_{\mathtt{τ}}(\mathrm{s}), \mathbf{B}_{\mathtt{τ}}(\mathrm{s})\right\}$ is called the modified orthogonal frame with nonzero torsion ^[27].

An isoparametric curve $\mathtt{α}(s)$ is a curve on a surface $\varphi = \varphi(s, v)$ and has a constant s or v parameter value. In other words, there exists a parameter $s_{0}$ or $v_{0}$ such that $\alpha(s) = \varphi\left(s, v_{0}\right)$ or $\alpha(v) = \varphi\left(s_{0}, v\right)$ ^[4].

A curve $\mathtt{α}$ in $\mathtt{φ} \subset \operatorname{IR}^{3}$ is a geodesic of $\varphi$ provided that its acceleration $\mathtt{α}^{\prime \prime}$ is always normal to $\varphi$ ^[4]. A regular curve $\mathtt{α}$ in $\mathtt{φ} \subset \operatorname{IR}^{3}$ is an asymptotic curve provided that its velocity $\mathtt{α}^{\prime}$ always points in an asymptotic direction, i.e., the direction in which the normal curvature is zero ^[4]. The simplest criterion for a curve in $\varphi$ to be asymptotic is that its acceleration $\mathtt{α}^{\prime \prime}$ is to always be tangent to $\varphi$. A regular curve $\mathtt{α}$ in $\mathtt{φ} \subset \operatorname{IR}^{3}$ is a line of curvature provided that its velocity $\mathtt{α}^{\prime}$ always points in a principal direction ^[4].

Theorem 2.1. A surface curve is a line of curvature if and only if the surface normals along the curve form a developable surface ^[6].

3.   Special curved surface families according to modified orthogonal frame

3.1.   Special curved surface families according to modified orthogonal frame with curvature

Suppose we are given a unit speed parametric curve $\alpha(s)$ with unit velocity, such that $\|\alpha "(s)\| \neq 0$, in three-dimensional space. The surface family that possesses $\mathtt{α}$ as a common curve is given in the parametric form as

where $x(s, v), y(s, v)$, and $z(s, v)$ are $C^{1}$ functions and are called marching scale functions and $\left\{\mathbf{T}_{\mathtt{κ}}(\mathrm{s}), \mathbf{N}_{\mathtt{κ}}(\mathrm{s}), \mathbf{B}_{\mathtt{κ}}(\mathrm{s})\right\}$ is the modified orthogonal frame with nonzero curvature of the curve $\mathtt{α}$.

Remark 3.1. Note that choosing different marching scale functions gives different surfaces which have $\alpha(s)$ as a common curve.

Our goal is to find the conditions for which the given curve $\alpha(s)$ is an isoparametric and geodesic, asymptotic, or line of curvature on the surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$. To begin, as $\alpha(\mathrm{s})$ is an isoparametric curve on the surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$, there exists a parameter $v_{\it 0} \in\left[K_{1}, K_{2}\right]$ such that

The normal vector field of the surface $\mathtt{φ}_{\mathtt{κ}}$ is given by

where "$\times$" is the vector product. We calculate

Along the curve $\alpha(s)$ we have

If the unit normal vector vanishes at any point of a surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$, i.e., at any points, then these points are called the singular points of the surface. So, the following result is obvious.

Corollar 3.2. Since $\kappa \neq 0, \frac{\partial z\left(s, v_{0}\right)}{\partial v}$ or $\frac{\partial y\left(s, v_{0}\right)}{\partial v}$ must be different from zero for the normal to be defined. If $\frac{\partial z\left(s, v_{0}\right)}{\partial v} \neq 0$ and $\frac{\partial y\left(s, v_{0}\right)}{\partial v} \neq 0$, then there is no singular point on the surface $\varphi_{\kappa}(s, v)$.

Theorem 3.3. Let $\mathtt{α}(\mathrm{s})$ be a unit speed curve with nonzero curvature. $\mathtt{α}(\mathrm{s})$ are parametric and geodesic on the surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$ if

Theorem 3.4. Let $\mathtt{α}(\mathrm{s})$ be a unit speed curve with nonzero curvature. $\mathtt{α}(\mathrm{s})$ are parametric and asymptotic on the surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$ if

Corollary 3.5. The curve given according to the modified orthogonal frame with curvature cannot be geodesic and asymptotic at the same time.

Theorem 3.6. Let $\alpha(s)$ be a unit speed curve with nonzero curvature. $\alpha(s)$ are parametric and line of curvature on the surface $\mathtt{φ}_{\mathtt{κ}}(\mathrm{s}, \mathrm{v})$ if

Proof. Let $\mathrm{u}_{\mathtt{κ}}(\mathrm{s})$ be a vector field orthogonal to the curve $\mathtt{α}(\mathrm{s})$. Then, we can write

where $\mathtt{ψ}$ is the angle between $\mathrm{u}_{\mathtt{κ}}(\mathrm{s})$ and is the vector field $\mathrm{N}_{\mathtt{κ}}(\mathrm{s})$ of the curve $\mathtt{α}(\mathrm{s})$. According to Theorem 2.1, a line of curvature on the surface is given by Eq (3.1) if, and only if, $\mathrm{u}_{\mathtt{κ}}(\mathrm{s}) / / \mathrm{U}_{\mathtt{κ}}\left(\mathrm{s}, \mathrm{v}_{0}\right)$ and the ruled surface

is developable. Using (3.3), we have

and $\mathrm{Q}_\mathtt{κ}(\mathrm{s}, \mathrm{v})$ is developable if, and only if, $\operatorname{det}\left(\mathtt{α}^{\prime}(\mathrm{s}), \mathrm{u}_\mathtt{κ}(\mathrm{s}), \mathrm{u}_\mathtt{κ}{ }^{\prime}(\mathrm{s})\right) = 0$. Since

is $\kappa \neq 0$, we get

which completes the proof.

3.2.   Special curved surface families according to modified orthogonal frame with torsion

Suppose we are given a unit speed parametric curve $\alpha(s)$ so that $\|\alpha "(s)\| \neq 0$ and $\tau(s) \neq 0$ in a three-dimensional space. The surface family that possesses $\alpha$ as a common curve is given in the parametric form as

where $x(s, v), y(s, v)$, and $z(s, v)$ are $C^{1}$ functions and are called marching scale functions, and $\left\{\mathbf{T}_{\mathtt{τ}}(\mathrm{s}), \mathbf{N}_{\mathtt{τ}}(\mathrm{s}), \mathbf{B}_{\mathtt{τ}}(\mathrm{s})\right\}$ is the modified orthogonal frame with nonzero torsion of the curve $\mathtt{α}$.

Remark 3.7. Observe that choosing different marching scale functions yields different surfaces possessing $\alpha(s)$ as a common curve.

Our aim is to find the conditions under which the given curve $\alpha(s)$ is isoparametric and geodesic, asymptotic, or line of curvature on the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$. To begin, as $\alpha(\mathrm{s})$ is an isoparametric curve on the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$, there exists a parameter $v_{\mathit{0}} \in\left[K_{1}, K_{2}\right]$ such that

The normal vector field of the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$ is given by

where "$\times$" is the vector product. We calculate

Along the curve $\alpha(s)$, we have

If the unit normal vector vanishes at any point of a surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$, i.e., at any points, then these points are called singular points of the surface. So, the following result is obvious.

Corollary 3.8. Since $\tau \neq 0, \frac{\partial z\left(s, v_{0}\right)}{\partial v}$ or $\frac{\partial y\left(s, v_{0}\right)}{\partial v}$ must be different from zero for the normal to be defined. If $\frac{\partial z\left(s, v_{0}\right)}{\partial v} \neq 0$ and $\frac{\partial y\left(s, v_{0}\right)}{\partial v} \neq 0$, then there is no singular point on the surface $\varphi_{\tau}(s, v)$.

Theorem 3.9. Let $\mathtt{α}(\mathrm{s})$ be a unit speed curve with nonzero torsion. $\mathtt{α}(\mathrm{s})$ are parametric and geodesic on the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$ if

Theorem 3.10. Let $\mathtt{α}(\mathrm{s})$ be a unit speed curve with nonzero torsion. $\mathtt{α}(\mathrm{s})$ are parametric and asymptotic on the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$ if

Corollary 3.11. The curve given according to the modified orthogonal frame with torsion cannot be geodesic and asymptotic at the same time.

Theorem 3.12. Let $\alpha(s)$ be a unit speed curve with nonzero torsion. $\alpha(s)$ are parametric and line of curvature on the surface $\mathtt{φ}_{\mathtt{τ}}(\mathrm{s}, \mathrm{v})$ if

Proof. It is done like the proof of Theorem 3.6.

4.   Examples of generating special curved surfaces according to modified orthogonal frame

Example 4.1. Let $\alpha(s) = \left(\frac{\sqrt{3}}{3} s^{\frac{3}{2}}, \frac{\sqrt{3}}{3}(1-s)^{\frac{3}{2}}, \frac{1}{2} s\right)$ be the unit speed curve. The Frenet apparatus of $\alpha$ is

Curvature and torsion is differentiable for $s \neq 0$ and $s \neq 1$. The modified orthogonal frame with curvature and torsion of the unit speed curve $\alpha(s)$ is the derived elements as follows, respectively:

Choosing $x(s, v) \equiv 0, y(s, v) = v^{2} \sqrt{s(1-s)}, z(s, v) = v \sqrt{s(1-s)}, v_{0} = 0$, we obtain the surface

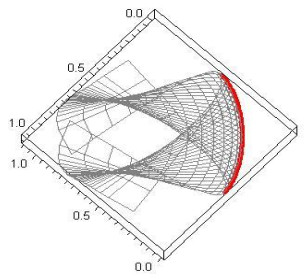
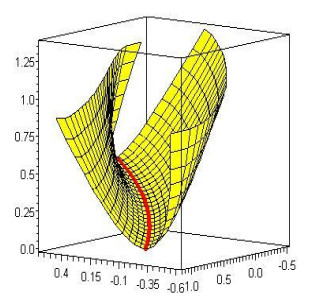
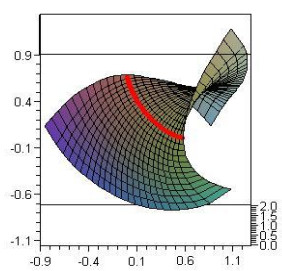
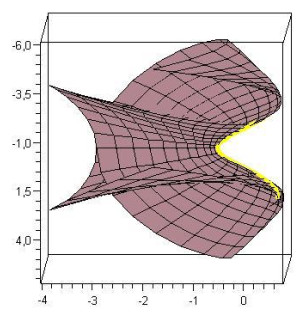
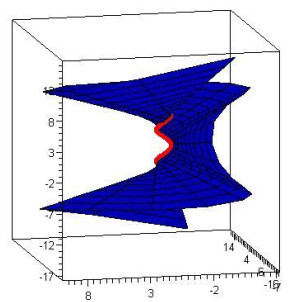
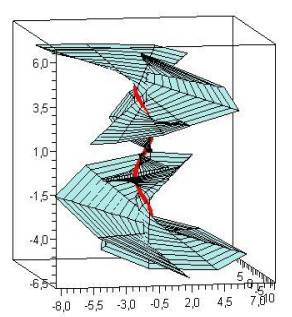
$0 < s < 1, -2 \leq v \leq 2$, satisfying Eq (3.4) and accepting the $\alpha(s)$ as a geodesic curve (Figure 1).

For the same conditions, we obtain the surface

$0 < s < 1, -2 \leq v \leq 2$, satisfying Eq (3.10) and accepting the $\alpha(s)$ as a geodesic curve (Figure 2).

For the same curve, choosing $x(s, v) \equiv 0, y(s, v) = v^{2} \sqrt{s(1-s)}, z(s, v) = v \sqrt{s(1-s)}, v_{0} = 0$, we obtain the surface

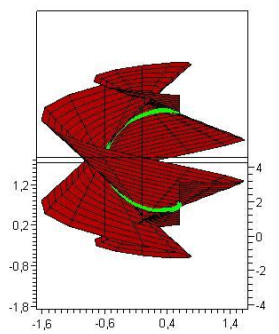
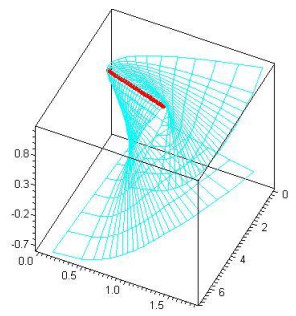
$0 < s < 1, -2 \leq v \leq 2$, satisfying Eq (3.5) and accepting the $\alpha (s)$ as an asymptotic curve (Figure 3). For the same conditions, we obtain the surface

$0 < s < 1, -2 \leq v \leq 2$, satisfying Eq (3.11) and accepting the $\alpha(s)$ as an asymptotic curve (Figure 4).

Example 4.2. Let $\alpha(s) = \left(\frac{3}{5} \sin (s), -\frac{3}{5} \cos (s), \frac{4}{5} s\right)$ be a unit speed curve. The Frenet apparatus of $\alpha$ are

The modified orthogonal frame with curvature and torsion of the unit speed curve $\alpha(s)$ is the derived elements as follows, respectively:

Choosing $x(s, v) = v^{2} \sin (s), y(s, v) = v^{2} \cos (s), z(s, v) = s v, v_{0} = 0$, we obtain the surface

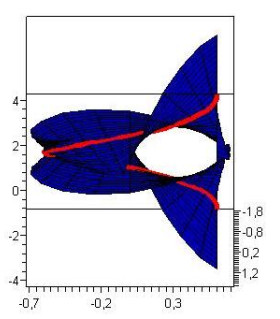
$-\pi \leq s \leq \pi, -2 \leq \nu \leq 2$, satisfying Eq (3.4) and accepting the $\alpha(s)$ as a geodesic curve (Figure 5). For the same conditions, we obtain the surface

$-2 \pi \leq s \leq 2 \pi, -2 \leq v \leq 2$, satisfying Eq. (3.10) and accepting the $\alpha(s)$ as a geodesic curve (Figure 6).

Choosing $x(s, v) = v \cos (s), y(s, v) = -v \sin (s), z(s, v) \equiv 0, v_{0} = 0$, we obtain the surface

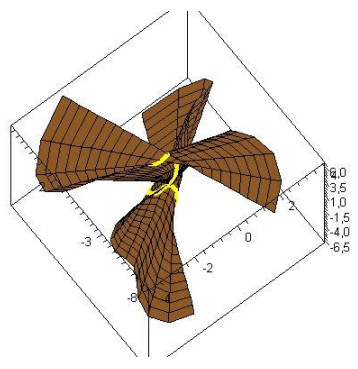
$-\pi \leq s \leq \pi, -2 \leq v \leq 2$, satisfying Eq (3.5) and accepting the $\alpha (s)$ as an asymptotic curve (Figure 7). For the same conditions, we obtain the surface

$-\pi \leq s \leq \pi, -2 \leq v \leq 2$, satisfying Eq. (3.11) and accepting the $\alpha (s)$ as an asymptotic curve (Figure 8).

Choosing $x(s, v) \equiv 0, y(s, v) = s v \sin \left(\frac{4}{5} s\right), z(s, v) = -s v \cos \left(\frac{4}{5} s\right), v_{0} = 0$, we obtain the surface

$-2 \pi \leq s \leq 2 \pi, -2 \leq \nu \leq 2$, satisfying Eq. (3.6) and accepting the $\alpha (s)$ as a line of curvature (Figure 9). For the same conditions, we obtain the surface

$-2 \pi \leq s \leq 2 \pi, -2 \leq \nu \leq 2$, satisfying Eq. (3.12) and accepting the $\alpha(s)$ as a line of curvature (Figure 10).

5.   Conclusions

In this study, the conditions for a geodesic, asymptotic and curvature line on the parametric surface were given according to the modified orthogonal frame defined at the points where the curvature and twist of a curve given in three-dimensional Euclidean space are different from zero. Additionally, the singular points of the surface given by the parametric equation were expressed. Finally, various examples supporting the study and their shapes were given using the Maple 15 program.

Use of AI tools declaration

The author declares that he/she has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We gratefully acknowledge the constructive comments from the editor and the anonymous referees.

Conflict of interest

The author declares no conflict of interest.