Simultaneous characterizations of partner ruled surfaces using Flc frame

1.   Introduction

Surface theory is an attractive research field, as it has applications in many disciplines. Among the surfaces, the ruled surfaces are the most interesting and were first introduced by G. Monge. The ruled surfaces are formed by moving a line along a curve, where this curve is called the base curve, and the straight line is called the generator line. Since it consists of an infinite number of straight lines, it is known as a surface of lines. That is, the ruled surfaces are surfaces created by families of straight lines. The importance of the theory of ruled surfaces in some engineering fields is evident. Especially, in kinematics and computer-aided design problems, these surfaces have widespread use. Cylinder and cone surfaces are the most well-known ruled surfaces. The ruled surfaces also arise in admirable architectural works. For example, the ruled surfaces are seen in many famous structures, such as Ciechanow Water Tower, Kobe Port Tower and Shuckhov Tower. In addition to the visibility of ruled surfaces in real-world applications, theoretical developments for these surfaces continue in depth. After its localization in the scientific literature, researchers started to question the characterizations of these surfaces as well as the isoparametric curves lying on them. For example, the relations between the cylindrical helix and Gaussian curvature and between the Bertrand curve and the mean curvature of a ruled surface were given in ^[1]. The invariants and kinematic/ geometric properties of non-developable ruled surfaces were examined by considering the structural functions of ruled surfaces in ^[2]. The ruled surfaces with directrix of a focal curve of a given curve were studied and characterized in ^[3]. Developable ruled surfaces on Bezier curves were constructed in ^[4]. Normal and binormal ruled surfaces based on W-direction curves were discussed in ^[5].

Motivated by these, in this study, we have introduced partner ruled surfaces based on a polynomial curve and ruled by the vector elements of a Frenet-like frame known as the Flc frame ^[6]. Then, we have simultaneously provided the conditions for each partner ruled surface to be developable or minimal by considering the main curvatures with the Flc frame invariants. Such conditions have also been linked to the characterizations of isoparametric curves such as asymptotic, geodesic or curvature lines. An example has been given at the end of the paper with the corresponding figures of the generated partner ruled surfaces.

2.   Preliminaries

In this section, we present some basic concepts that will be used throughout the paper. Let $\alpha = \alpha (s)$ be a regular space curve satisfying non-degenerate condition ${\alpha }^{'}(s) \wedge {\alpha}^{''}(s) \ne 0.$ Then, the orthonormal vector system called the Frenet frame is defined by

where $T$ is tangent, $N$ is principal normal and $B$ is binormal vector field. The Frenet formulas are given by

where the curvature $\kappa$ and torsion $\tau$ of the curve are^[7],

The $n^{th}$ degree polynomial with parameter $s$ is defined as

where $n \in {\mathbb{N}_0},$ ${a_i} \in \mathbb{R},$ $(0 \le i \le n)$ ^[8].

Now, let us define a curve such that $\alpha :\left[{a, b} \right] \to {E^n}, \, \, \, \, \alpha (s) = \left({{\alpha _1}(s), {\alpha _2}(s), ..., {\alpha _n}(s)} \right)$. If each ${\alpha_i}$s are polynomials for $1 \le i \le n$, then ${a_s} \in \mathbb{R} \left[s \right]$ is defined to be an $n-$dimensional polynomial curve ^[9]. The degree of such a polynomial curve as $\alpha (s)$ is given by

The definition of the Flc frame of a polynomial space curve $\alpha = \alpha(s)$ given by Dede in ^[6] is as follows:

where the prime $'$ indicates the differentiation with respect to $s$ and $^{(n)}$ stands for the $n^{th}$ derivative. The new vectors $D_1$ and $D_2$ are called the binormal-like vector and normal-like vector, respectively. The curvatures of the Flc-frame ${d_1}, {d_2}$and ${d_3}$ are given by

where $\left\| {\alpha '} \right\| = \eta.$ The local rate of change of the Flc-frame called as the Frenet-like formulas can be expressed in the following form:

On the other hand, a ruled surface as a family of straight lines is defined as

where $\alpha (s)$ is the base curve, and the $r(s)$ is the generator. The Gaussian and mean curvatures of the ruled surface $\varphi$ with the normal vector field $N_\varphi$ are given as

Here, the coefficients of first and second fundamental forms are defined as

respectively ^[7].

3.   Simultaneous characterizations of partner ruled surfaces using Flc frame

In this section, we study simultaneously partner ruled surfaces constructed by the tangent, normal-like and binormal-like vectors of the Flc frame along a polynomial space curve.

3.1.   $TD_2$-partner ruled surfaces

Definition 3.1. Let $\alpha$ be a differentiable polynomial space curve and $\left\{ {T, {D_2}, {D_1}} \right\}$ be the Flc frame of the polynomial space curve. The two ruled surfaces defined by

are called $T{D_2}$-partner ruled surfaces with the Flc frame of the polynomial curve.

Theorem 3.1. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces, and then $T{D_2}$-partner ruled surfaces are simultaneously

(i) developable surfaces if and only if $d_1 = 0, \ d_2 \neq 0$ or $d_3 \neq 0$,

(ii) minimal surfaces if and only if ${d_2} = {d_3} = 0$ and $d_1 \neq 0.$

Proof. By differentiating the first equation of (3.1) with respect to $s$ and $u$, respectively and using Flc frame derivative formulas, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _{{D_2}}^T$ given by Eq (3.2) and the cross product of both vectors $(\varphi _{{D_2}}^T)_s$ and $(\varphi _{{D_2}}^T)_u$, the normal vector field of the surface $\varphi _{{D_2}}^T$ is found as

By applying the scalar product for both vectors in (3.2), we find the components of the first fundamental form of the ruled surface $\varphi _{{D_2}}^T$ as follows:

By differentiating Eq (3.2) with respect to $s$ and $u$ and making the scalar product with the normal vector field (3.3), we have the component of the second fundamental form of the ruled surface $\varphi _{{D_2}}^T$ as follows:

Thus, by substituting Eqs (3.4) and (3.5) into Eq (2.8), the Gaussian curvature and the mean curvature of the ruled surface $\varphi _{{D_2}}^T$ are calculated by

On the other hand, by differentiating the second equation of (3.1) with respect to $s$ and $u$, respectively and using the Flc frame derivative formulae, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _T^{{D_2}}$ given by Eq (3.7) and the cross product of both vectors, the normal vector field of the surface $\varphi _T^{{D_2}}$ is found as

By applying the scalar product for both vectors in (3.8), we have the components of the first fundamental form of the ruled surface $\varphi _T^{{D_2}}$ as follows:

By differentiating Eq (3.7) with respect to $s$ and $u$ and making the scalar product with the normal vector field (3.8), we have the component of the second fundamental form of the ruled surface $\varphi _T^{{D_2}}$ as follows:

Thus, by substituting Eqs (3.9) and (3.10) into Eq (2.8), the Gaussian curvature ${K_{{D_2}T}}$ and the mean curvature ${H_{{D_2}T}}$ of the ruled surface $\varphi _T^{{D_2}}$ are calculated by

Consequently, from Eqs (3.6) and (3.11), it can easily be said $T{D_2}$-partner ruled surfaces are simultaneously developable and minimal surfaces under the conditions stated in the hypothesis.

Theorem 3.2. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces, and then $s$-parameter curves of $T{D_2}$-partner ruled surfaces are simultaneously

(i) not geodesic,

(ii) asymptotic if and only if ${d_2} = {d_3} = 0$ and $d_1 \neq 0$.

Proof. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces and the cross products of second partial derivates with the normal vector fields of the $T{D_2}$-partner ruled surfaces being found as

Since $(\varphi _{{D_2}}^T)_{ss} \times U_{{D_2}}^T \ne 0$ and $(\varphi _{T}^{{D_2}})_{ss} \times U_T^{{D_2}} \ne 0$, $s$-parameter curves of the $T{D_2}$-partner ruled surfaces simultaneously are not geodesic. On the other hand, the scalar products of second partial derivates with the normal vector fields of the $T{D_2}$-partner ruled surfaces are calculated as

From here, if ${d_2} = {d_3} = 0$ and $d_1 \neq 0$, then $\langle {(\varphi _{{D_2}}^T)_{ss}, U_{{D_2}}^T} \rangle = 0$ and $\langle {(\varphi _{T}^{{D_2}})_{ss}, U_T^{{D_2}}} \rangle = 0$. So, we can say that $s$-parameter curves of the $T{D_2}$-partner ruled surfaces simultaneously are asymptotic if and only if ${d_2} = {d_3} = 0$ and $d_1 \neq 0$.

Theorem 3.3. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces, and then $u$-parameter curves of $T{D_2}$-partner ruled surfaces are simultaneously

(i) geodesic,

(ii) asymptotic.

Proof. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$- partner ruled surfaces. Since $(\varphi _{{D_2}}^T)_{uu} \times U_{{D_2}}^T = 0$ and $(\varphi _{T}^{{D_2}})_{uu} \times U_T^{{D_2}} = 0$, $u$-parameter curves of the $T{D_2}$-partner ruled surfaces simultaneously are geodesic. On the other hand, since $\langle {(\varphi _{{D_2}}^T)_{uu}, U_{{D_2}}^T} \rangle = 0$ and $\langle {(\varphi _{T}^{{D_2}})_{uu}, U_T^{{D_2}}} \rangle = 0$, $u$-parameter curves of the $T{D_2}$-partner ruled surfaces are simultaneously asymptotic.

Theorem 3.4. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces, and then $s$ and $u$-parameter curves of $T{D_2}$-partner ruled surfaces are simultaneously lines of curvature if and only if $d_1 = 0$.

Proof. Let $\varphi _{{D_2}}^T$ and $\varphi _T^{{D_2}}$ be $T{D_2}$-partner ruled surfaces. For $d_1 = 0$,

and

Thus, we can easily say that $s$ and $u$-parameter curves of $T{D_2}$-partner ruled surfaces are simultaneously lines of curvature if and only if $d_1 = 0$.

3.2.   $TD_1$-partner ruled surfaces

Definition 3.2. Let $\alpha$ be a differentiable polynomial space curve and $\left\{ {T, {D_2}, {D_1}} \right\}$ be the Flc frame of the polynomial space curve. The two ruled surfaces defined by

are called $T{D_1}$-partner ruled surfaces with the Flc frame of the polynomial curve.

Theorem 3.5. Let $\varphi _{{D_1}}^T$ and $\varphi _T^{{D_1}}$ be $T{D_1}$-partner ruled surfaces, and then $T{D_1}$-partner ruled surfaces are simultaneously

(i) developable surfaces if and only if $d_2 = 0$ and $d_1 \neq 0$ or $d_3 \neq 0$,

(ii) minimal surfaces if and only if ${d_1} = {d_3} = 0$ and $d_2 \neq 0$.

Proof. By differentiating the first equation of (3.12) with respect to $s$ and $u$, respectively and using Flc frame derivative formulae, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _{{D_1}}^T$ given by Eq (3.13) and the cross product of both vectors, the normal vector field of the surface $\varphi _{{D_1}}^T$ is found as

By applying the scalar product for both vectors in (3.13), we have the components of the first fundamental form of the ruled surface $\varphi _{{D_1}}^T$ as follows:

By differentiating Eq (3.13) with respect to $s$ and $u$ and making the scalar product with the normal vector field (3.14), we have the component of the second fundamental form of the ruled surface $\varphi _{{D_1}}^T$ as follows:

Thus, by substituting Eqs (3.15) and (3.16) into Eq (2.8), the Gaussian curvature and the mean curvature of the ruled surface $\varphi _{{D_1}}^T$ are found by

On the other hand, by differentiating the second equation of (3.12) with respect to $s$ and $u$, respectively and using Flc frame derivative formulae, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _T^{{D_1}}$ given by Eq (3.18) and the cross product of both vectors, the normal vector field of the surface $\varphi _T^{{D_1}}$ is found as

By applying the scalar product for both vectors in (3.19), we have the components of the first fundamental form of the ruled surface $\varphi _T^{{D_1}}$ as follows:

The scalar products of differentiation of Eq (3.18) with respect to $s$ and $u$ with the normal vector field (3.19) gives us the component of the second fundamental form of the ruled surface $\varphi _T^{{D_1}}$ as follows:

Thus, by substituting Eqs (3.20) and (3.21) into Eq (2.8), the Gaussian curvature ${K_{{D_1}T}}$ and the mean curvature ${H_{{D_1}T}}$ of the ruled surface $\varphi _T^{{D_1}}$ are calculated by

Consequently, from Eqs (3.17) and (3.22), it can easily be said $T{D_1}$-partner ruled surfaces are simultaneously developable and minimal surfaces under the conditions stated in the hypothesis.

Theorem 3.6. Let $\varphi _{{D_1}}^T$ and $\varphi _T^{{D_1}}$ be $T{D_1}$-partner ruled surfaces, and then $s$-parameter curves of $T{D_1}$-partner ruled surfaces are simultaneously

(i) not geodesic,

(ii) asymptotic if and only if ${d_1} = {d_3} = 0$ and $d_2 \neq 0$.

Proof. The proof is done in a similar way to the proof of the theorem given for $T{D_2}$-partner ruled surfaces.

Theorem 3.7. Let $\varphi _{{D_1}}^T$ and $\varphi _T^{{D_1}}$ be $T{D_1}$-partner ruled surfaces, and then $u$-parameter curves of $T{D_1}$-partner ruled surfaces are simultaneously

(i) geodesic,

(ii) asymptotic.

Proof. The proof is done in a similar way to the proof of the theorem given for $T{D_2}$-partner ruled surfaces.

Theorem 3.8. Let $\varphi _{{D_1}}^T$ and $\varphi _T^{{D_1}}$ be $T{D_1}$-partner ruled surfaces, and then $s$ and $u$-parameter curves of $T{D_1}$-partner ruled surfaces are simultaneously lines of curvature if and only if $d_2 = 0$.

Proof. The proof is done in a similar way to the proof of the theorem given for $T{D_2}$-partner ruled surfaces.

3.3.   $D_2D_1$-partner ruled surfaces

Definition 3.3. Let $\alpha$ be a differentiable polynomial space curve and $\left\{ {T, {D_2}, {D_1}} \right\}$ be the Flc frame of the polynomial space curve. The two ruled surfaces defined by

are called ${D_2}{D_1}$-partner ruled surfaces with the Flc frame of the polynomial curve.

Theorem 3.9. Let $\varphi _{{D_1}}^{D_2}$ and $\varphi _{D_2}^{{D_1}}$ be a ${D_2}{D_1}$-partner ruled surfaces, and then ${D_2}{D_1}$-partner ruled surfaces are simultaneously

(i) developable surfaces if and only if $d_3 = 0$ and $d_1 \neq 0$ or $d_2 \neq 0$,

(ii) minimal surfaces if and only if ${d_1} = {d_2} = 0$ and $d_3 \neq 0$.

Proof. By differentiating the first equation of (3.23) with respect to $s$ and $u$, respectively and using Flc frame derivative formulae, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _{D_1}^{{D_2}}$ given by Eq (3.24) and the cross product of both vectors, the normal vector field of the surface $\varphi _{D_1}^{{D_2}}$ is found as

By applying the scalar product for both vectors in (3.24), we have the components of the first fundamental form of the ruled surface $\varphi _{D_1}^{{D_2}}$ as follows:

By differentiating Eq (3.24) with respect to $s$ and $u$ and making the scalar product with the normal vector field (3.25), we have the component of the second fundamental form of the ruled surface $\varphi _{D_1}^{{D_2}}$ as follows:

Thus, by substituting Eqs (3.26) and (3.27) into Eq (2.8), the Gaussian curvature ${K_{{D_2}{D_1}}}$ and the mean curvature ${H_{{D_2}{D_1}}}$ of the ruled surface $\varphi _{D_1}^{{D_2}}$ are calculated by

On the other hand, by differentiating the second equation of (3.23) with respect to $s$ and $u$, respectively and using Flc frame derivative formulae, one can obtain

Then, by considering the partial derivatives of the surface $\varphi _{D_2}^{{D_1}}$ given by Eq (3.29) and the cross product of both vectors, the normal vector field of the surface $\varphi _{D_2}^{{D_1}}$ is found as

By applying the scalar product for both vectors in (3.30), we have the components of the first fundamental form of the ruled surface $\varphi _{D_2}^{{D_1}}$ as follows:

By differentiating Eq (3.29) with respect to $s$ and $u$ and making the scalar product with the normal vector field (3.30), we have the component of the second fundamental form of the ruled surface $\varphi _{D_2}^{{D_1}}$ as follows:

Thus, by substituting Eqs (3.31) and (3.32) into Eq (2.8), the Gaussian curvature ${K_{{D_1}{D_2}}}$ and the mean curvature ${H_{{D_1}{D_2}}}$ of the ruled surface $\varphi _{D_2}^{{D_1}}$ are calculated by

Consequently, from Eqs (3.28) and (3.33), it can easily be said ${D_2}{D_1}$-partner ruled surfaces are simultaneously developable and minimal surfaces under the conditions stated in the hypothesis.

Theorem 3.10. Let $\varphi _{{D_1}}^{D_2}$ and $\varphi _{D_2}^{{D_1}}$ be ${D_2}{D_1}$-partner ruled surfaces, and then $s$-parameter curves of ${D_2}{D_1}$-partner ruled surfaces are simultaneously

(i) not geodesic,

(ii) asymptotic if and only if ${d_1} = {d_2} = 0$ and $d_3 \neq 0$.

Proof. The proof is done in a similar way to the proof of the theorem given for $T{D_2}$-partner ruled surfaces.

Theorem 3.11. Let $\varphi _{{D_1}}^{D_2}$ and $\varphi _{D_2}^{{D_1}}$ be ${D_2}{D_1}$-partner ruled surfaces, and then $s$ and $u$-parameter curves of ${D_2}{D_1}$-partner ruled surfaces are simultaneously line of curvatures if and only if $d_3 = 0$.

Proof. The proof is done in a similar way to the proof of the theorem given for $T{D_2}$-partner ruled surfaces.

Example 3.1. Let us consider a helical polynomial curve parameterized as $\alpha \left(s \right) = \left({6s, 3{s^2}, {s^3}} \right)$. Then, the Flc frame elements of $\alpha$ are given by

and the corresponding curvatures according to the Flc frame are the following:

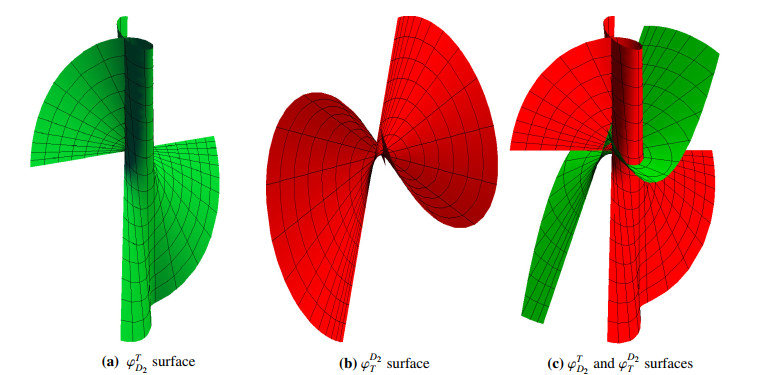
(1) Thus, we have the parametric forms for $T{D_2}$-partner ruled surfaces as follows:

See Figure 1.

(2) Thus, we have the parametric forms for $T{D_1}$-partner ruled surfaces as follows:

See Figure 2.

(3) Thus, we have the parametric forms for ${D_2}{D_1}$-partner ruled surfaces as the following:

See Figure 3.

Example 3.2. Let us consider a helical polynomial curve parameterized as $\beta \left(s \right) = \left({s^3, {s^4}, {s^5}} \right)$.Then the Flc frame elements of $\beta$ are given by

and the corresponding curvatures according to Flc frame are as the following:

(1) Thus, we have the parametric forms for $T{D_2}$-partner ruled surfaces as follows:

See Figure 4.

(2) Thus, we have the parametric forms for $T{D_1}$-partner ruled surfaces as follows:

See Figure 5.

(3) Thus, we have the parametric forms for ${D_2}{D_1}$-partner ruled surfaces as the following:

See Figure 6.

4.   Conclusions

In this paper, the invariants of partner ruled surfaces formed by tangent, normal-like and binormal-like vector fields of a polynomial space curve simultaneously are presented. Also, some characterizations of the parameter curves are examined. Examples of these surfaces are given and their graphics are drawn using the MATLAB R2021b program.

Acknowledgments

We gratefully acknowledge the constructive comments from the editor and the anonymous referees. This work was funded by the National Natural Science Foundation of China (Grant No. 12101168), Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ22A010014).

Conflict of interest

The authors declare no conflict of interest.