On the curve evolution with a new modified orthogonal Saban frame

Atakan Tuğkan Yakut; Alperen Kızılay; Atakan Tuğkan Yakut; Alperen Kızılay

doi:10.3934/math.20241432

AIMS Mathematics

2024, Volume 9, Issue 10: 29573-29586. doi: 10.3934/math.20241432

Previous Article Next Article

Research article

On the curve evolution with a new modified orthogonal Saban frame

Department of Mathematics, Nigde Omer Halisdemir University, Nigde 51240, Turkey

Received: 21 August 2024 Revised: 02 October 2024 Accepted: 11 October 2024 Published: 17 October 2024
MSC : 53C40, 53E10

The flow of a curve is said to be inextensible if the arc length in the first case and the intrinsic curvature in the second case are preserved. In this work, we investigated the inextensible flow of a curve on $S^2$ according to a modified orthogonal Saban frame. Initially, we gave the definition of the modified Saban frame and then established the relations between the Frenet and the modified orthogonal Saban frames. Later, we determined the inextensible curve flow and geodesic curvature of a curve on the unit sphere using the modified orthogonal Saban frame. Also, we gave some theorems and results for special cases of the evolution of a curve on a sphere. Finally, we gave examples and their graphs for the inextensible flow equation of curvatures.

Keywords:

Citation: Atakan Tuğkan Yakut, Alperen Kızılay. On the curve evolution with a new modified orthogonal Saban frame[J]. AIMS Mathematics, 2024, 9(10): 29573-29586. doi: 10.3934/math.20241432

Related Papers:

[1]	Kemal Eren, Hidayet Huda Kosal . Evolution of space curves and the special ruled surfaces with modified orthogonal frame. AIMS Mathematics, 2020, 5(3): 2027-2039. doi: 10.3934/math.2020134
[2]	Gülnur Şaffak Atalay . A new approach to special curved surface families according to modified orthogonal frame. AIMS Mathematics, 2024, 9(8): 20662-20676. doi: 10.3934/math.20241004
[3]	Samah Gaber, Abeer Al Elaiw . Evolution of null Cartan and pseudo null curves via the Bishop frame in Minkowski space $ \mathbb{R}^{2, 1} $. AIMS Mathematics, 2025, 10(2): 3691-3709. doi: 10.3934/math.2025171
[4]	Ayman Elsharkawy, Ahmer Ali, Muhammad Hanif, Fatimah Alghamdi . Exploring quaternionic Bertrand curves: involutes and evolutes in $ \mathbb{E}^{4} $. AIMS Mathematics, 2025, 10(3): 4598-4619. doi: 10.3934/math.2025213
[5]	Sezai Kızıltuǧ, Tülay Erişir, Gökhan Mumcu, Yusuf Yaylı . $ C^* $-partner curves with modified adapted frame and their applications. AIMS Mathematics, 2023, 8(1): 1345-1359. doi: 10.3934/math.2023067
[6]	Emad Solouma, Ibrahim Al-Dayel, Meraj Ali Khan, Youssef A. A. Lazer . Characterization of imbricate-ruled surfaces via rotation-minimizing Darboux frame in Minkowski 3-space $ \mathrm{E}_1^3 $. AIMS Mathematics, 2024, 9(5): 13028-13042. doi: 10.3934/math.2024635
[7]	Ayman Elsharkawy, Clemente Cesarano, Abdelrhman Tawfiq, Abdul Aziz Ismail . The non-linear Schrödinger equation associated with the soliton surfaces in Minkowski 3-space. AIMS Mathematics, 2022, 7(10): 17879-17893. doi: 10.3934/math.2022985
[8]	M. Khalifa Saad, Nural Yüksel, Nurdan Oğraş, Fatemah Alghamdi, A. A. Abdel-Salam . Geometry of tubular surfaces and their focal surfaces in Euclidean 3-space. AIMS Mathematics, 2024, 9(5): 12479-12493. doi: 10.3934/math.2024610
[9]	Yanlin Li, H. S. Abdel-Aziz, H. M. Serry, F. M. El-Adawy, M. Khalifa Saad . Geometric visualization of evolved ruled surfaces via alternative frame in Lorentz-Minkowski 3-space. AIMS Mathematics, 2024, 9(9): 25619-25635. doi: 10.3934/math.20241251
[10]	Samah Gaber, Asmahan Essa Alajyan, Adel H. Sorour . Construction and analysis of the quasi-ruled surfaces based on the quasi-focal curves in $ \mathbb{R}^{3} $. AIMS Mathematics, 2025, 10(3): 5583-5611. doi: 10.3934/math.2025258

Abstract

1. Introduction

It is a very interesting topic to study the evolution of space curves with respect to time. Recently, this topic has attracted a lot of attention and has been investigated by many researchers. The flow of curves has an important place in many areas such as modeling automobile parts, ship hulls, aircraft wings, clothing, etc. The study of the motion of inextensible curves is also found in a number of different engineering applications. It is also used in image processing as well as in the motion of mobile robots ^[1], electroosmotically-driven flow ^[2], acceleration of electrons ^[3], computer vision ^[4], computer animation ^[5], and the health industry ^[6]. In a physical sense, inextensible curve and surface flows are characterized by the absence of any tension energy due to motion ^[7]. The flow of the curve was described by Chirikjian and Burdick ^[8] as the motion of a hyper-redundant (or snake-like) robot moving in a plane. Geometricians have made great progress in the study of time-dependent space curves and have contributed to physicists and engineers. There are many studies in the literature on curve flows in the plane and in different space forms ^[9,10]. To start, Kwon and Park worked on inextensible curve flows and inextensible surfaces in Euclidean 3-space^[11,12]. Then inextensible flows of curves are characterized using different frames such as Frenet, Bishop, Darboux, Saban frames etc. For example, Latifi et al. ^[13] and Gürbüz have examined inextensible flows in non-Euclidean space ^[14] and Yıldız et al. have studied inextensible flows of curves according to the Darboux frame in Euclidean 3-space ^[15]. In ^[16], the modified orthogonal frame was first defined by Sasai in Euclidean space. Many researchers have studied curves and surfaces using this frame. For example, Atalay G. introduced special families of curve surfaces ^[17], the modified orthogonal vector fields with curvature and torsion of a space curve is studied in Minkowski 3-Space by Bükcü et al.^[18]. Smarandache curves and space curves have investigated by Eren et al. ^[19,20]. Kızılay and Yakut have studied inextensible flows of curves according to the modified orthogonal Frenet frame in Euclidean and Minkowskian 3-space ^[21,22]. Throughout this work we use the Saban frame and modified Saban frame. Firstly, the Saban frame was described by Koenderink ^[23] and then, Taşköprü and Ali studied Smarandache curves according to the Saban frame in the Euclidean space ^[24,25]. Also, it was studied in the Minkowski space by Yakut et al. ^[26,27].

This paper aims to investigate the properties of the evolution of a spherical curve with respect to the modified orthogonal Saban frame. The study is organized as follows. We begin with some preliminaries on the modified orthogonal Frenet frame and classic Saban frame. Section 3 presents the relationships betweeen the Saban frame and modified Saban frame. Finally, in Section 4 we consider some basic cases of inextensible curve flows and express the inextensible curve flow as partial differential equations involving geodesic curvature and examples.

2. Preliminaries

Let $\rho$ : $I\subset \mathbb{R}\longrightarrow \mathbb{E}^{3}$ be a regular unit speed curve in $\mathbb{E}^{3}$ , and $\rho_{i}(i = 1, 2, 3)$ coordinates be given in Euclidean space. $\rho$ is a non-singular curve and $\underset{i = 1}{\overset{3}{\sum }}\left(\frac{d\rho_{i}}{ds}\right) ^{2}$ is non-zero. Thus, we can parametrize $\rho(s)$ with arc-length parameter $s$ . After this, we only take $\rho$ as follows:

$\rho = \rho(s) = (\rho_{1}(s), \rho_{2}(s), \rho_{3}(s)), \ \ s\in I,$

where $\rho(s)$ is analytic in $s$ and $I$ is a non-empty open interval.

We supposed that the curvature $\kappa(s)$ of $\rho$ is not identically zero. Thus, the orthogonal frame ${\left\{E_{1}(s), E_{2}(s), E_{3}(s) \right\}}$ is defined as:

$E_{1}(s) = \frac{d\rho}{ds}, \quad E_{2}(s) = \frac{dE_{1}(s)}{ds}, \quad E_{3}(s) = E_{1}(s) x E_{2}(s).$

The correlations between orthogonal frame ${\left\{E_{1}(s), E_{2}(s), E_{3}(s) \right\}}$ and classical Frenet frame ${\left\{e_{1}(s), e_{2}(s), e_{3}(s) \right\}}$ at $\kappa\neq 0$ are

$\begin{equation} \begin{cases} {E_{1}(s)} = {e_{1}(s)}, \\ {E_{2}(s)} = \kappa(s){e_{2}(s)}, \\ {E_{3}(s)} = \kappa(s){e_{3}(s)}. \end{cases} \end{equation}$

(2.1)

Moreover,

$E_{2}({s_{0}}) = E_{3}({s_{0}}) = 0,$

when

$\kappa_{s_{0}} = 0$

and $E_{2}(s)$ and $E_{3}(s)$ vary analytically what squares of the length in $s$ . Differentiating the Eq (2.1), we find

$\begin{bmatrix} {E_{1}} ^{^{\prime }}(s) \\ {E_{2}} ^{^{\prime }}(s) \\ {E_{3}} ^{^{\prime }}(s) \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ -\kappa ^{2}(s) & \frac{\kappa ^{^{\prime }}(s)}{\kappa (s)} & \tau(s) \\ 0 & -\tau(s) & \frac{\kappa ^{^{\prime }}(s)}{\kappa (s)} \end{bmatrix} \begin{bmatrix} {E_{1}(s)} \\ {E_{2}(s)} \\ {E_{3}(s)} \end{bmatrix}$

and

$\tau = \tau (s) = \frac{\det \left( \rho ^{\prime }(s), \; \rho ^{\prime \prime }(s)\; \rho ^{\prime \prime \prime }(s)\right) }{\kappa ^{2}(s)},$

where $\tau$ is the torsion of $\rho$ . Furthermore, ${\left\{E_{1}(s), E_{2}(s), E_{3}(s) \right\}}$ provides that:

$\begin{align*} \langle {E_{1}(s)}, {E_{2}(s)}\rangle & = \langle {E_{1}(s)}, {E_{3}(s)}\rangle = \langle {E_{2}(s)}, {E_{3}(s)}\rangle = 0, \\ \langle {E_{1}(s)}, {E_{1}(s)}\rangle& = 1, \langle {E_{2}(s)}, {E_{2}(s)}\rangle = \langle {E_{3}(s)}, {E_{3}(s)}\rangle = \kappa ^{2}(s), \end{align*}$

where $\langle, \rangle$ denotes the inner product of the Euclidean $3$ -space^[16,18].

Now, let's define a new frame that is different from the Frenet frame in terms of structure. Suppose that $\rho$ : $I\subset \mathbb{R}\longrightarrow S^{2}$ is a regular unit speed curve lying fully on $S^{2}$ in $\mathbb{E}^{3}$ . Then its position vector is $\rho$ , which implies the tangent vector

${ t} = \rho ^{\prime }.$

We now set a vector

$\xi (s) = \rho (s)\wedge t(s)$

along $\rho$ . We have orthonormal Sabban frame $\{\rho (s), t(s), \xi (s)\}$ . This frame is called the Sabban frame of $\rho$ on $S^2$ . The corresponding Frenet formula of $\rho,$ according to the Saban frame, given by

$\begin{eqnarray} \left\{ \begin{array}{lll} \rho^{\prime }(s) = t(s), \\ \; t^{\prime }(s) = \rho(s)+\kappa _{g}(s)\xi(s), \\ \xi^{\prime }(s) = -\kappa _{g}(s)\xi(s), \\ \end{array} \right. \end{eqnarray}$

(2.2)

where

$\kappa _{g}(s) = \det (\rho (s), t(s), t^{\prime }(s))$

is the geodesic curvature of $\rho$ following relations and holds:

$\xi = \rho \wedge t, \; \ \ \rho = t\wedge \xi , \; \ \ t = \xi \wedge \rho.$

The Eq (2.2) is in matrix form ^[23]:

$\begin{equation} \begin{bmatrix} {\rho} ^{^{\prime }}(s) \\ {t} ^{^{\prime }}(s) \\ {\xi} ^{^{\prime }}(s) \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & \kappa_{g}(s)\\ 0 & -\kappa_{g}(s) & 0 \end{bmatrix} \begin{bmatrix} {\rho(s)} \\ {t(s)} \\ {\xi(s)} \end{bmatrix}. \end{equation}$

(2.3)

3. The modified orthogonal Saban frame with curvature on $S^{2}$

Definition 3.1. Let $\rho$ be a spherical curve with unit speed and $s$ is the arc parameter of $\rho(s)$ and

$\rho ^{\prime }(s) = T(s) .$

Assume that $T(s)$ is the unit tangent vector of $\rho(s)$ and

$\Delta(s) = \rho(s) \wedge T(s),$

where $\rho(s) \wedge T(s)$ is vector product of $\rho(s)$ and $T(s)$ . The relations between those and the classical Saban frame $\left\{\rho, t, \xi\right\}$ at nonzero points of $\kappa_{g}$ are

$\begin{eqnarray} \left\{ \begin{array}{lll} \rho(s) = \rho(s, \\ T(s) = \kappa _{g}(s)t(s), \\ \Delta(s) = \kappa _{g}(s)\xi(s). \\ \end{array} \right. \end{eqnarray}$

(3.1)

This frame $\left\{\rho (s), T(s), \Delta(s) \right\}$ is called the modified orthogonal Saban frame of $\rho(s)$ on $S^{2}$ .

Theorem 3.2. Let $\rho$ : $I\subset\ R \rightarrow S ^{2}$ and ${\left\{\rho(s), T(s), \Delta(s)\right\}}$ be a unit speed regular curve on $S^{2}$ and the modified Saban frame, respectively. Thus, the derivative formulas of the modified orthogonal Saban frame are

$\begin{equation} \begin{bmatrix} {\rho} ^{^{\prime }}(s) \\ {T} ^{^{\prime }}(s) \\ {\Delta} ^{^{\prime }}(s) \end{bmatrix} = \begin{bmatrix} 0 & \frac{1}{\kappa_{g}(s)} & 0 \\ -\kappa_{g}(s) & \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g} (s)} & \kappa_{g}(s)\\ 0 & -\kappa_{g}(s) & \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s) } \end{bmatrix} \begin{bmatrix} {\rho(s)} \\ {T(s)} \\ {\Delta}(s) \end{bmatrix}. \end{equation}$

(3.2)

Proof. Differentiating the Eq (3.1) with respect to s and considering (2.2), we obtain

$\begin{align*} \rho ^{^{\prime }}(s) & = t(s), \\ T ^{^{\prime }}(s) & = \left(\kappa_{g}(s) t(s)\right) ^{^{\prime }}\\ & = \kappa_{g} ^{^{\prime }}(s) t(s)+ \kappa_{g}(s) t ^{^{\prime }}(s)\\ & = \kappa_{g} ^{^{\prime }}(s) t(s)+ \kappa_{g}(s) (-\rho(s)+ \kappa_{g}(s) \xi(s)) \\ & = -\kappa_{g}(s) \rho(s)+ \kappa_{g} ^{^{\prime }}(s) t(s)+ \kappa_{g} ^{2}(s) \xi(s) \\ & = -\kappa_{g}(s) \rho(s)+ \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s)} T(s)+ \frac{\kappa_{g} ^{2}(s)}{\kappa_{g}(s)} \Delta(s) \\ & = -\kappa_{g}(s) \rho(s)+ \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s)} T(s)+ \kappa_{g}(s) \Delta(s) \end{align*}$

and

$\begin{align*} \Delta ^{^{\prime }} (s) & = \left(\kappa_{g}(s) \xi(s) \right) ^{^{\prime }}\\ & = \kappa_{g} ^{^{\prime }}(s) \xi(s) +\kappa_{g}(s) \xi ^{^{\prime }}(s)\\ & = \kappa_{g} ^{^{\prime }}(s) \xi(s) +\kappa_{g}(s) \left(-\kappa_{g}(s) t(s)\right) \\ & = \kappa_{g} ^{^{\prime }}(s) \xi(s)-\kappa_{g} ^{2}(s) t(s)\\ & = \kappa_{g} ^{^{\prime }}(s) \frac{\Delta(s)}{\kappa_{g}(s)}- \kappa_{g} ^{2}(s) \frac{T(s)}{\kappa_{g}(s)}\\ & = -\kappa_{g}(s) T(s)+ \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s)} \Delta(s). \end{align*}$

Therefore, from these given expressions, the derivative formulas of the modified orthogonal Saban frame is

$\begin{bmatrix} {\rho} ^{^{\prime }}(s) \\ {T} ^{^{\prime }}(s) \\ {\Delta} ^{^{\prime }}(s) \end{bmatrix} = \begin{bmatrix} 0 & \frac{1}{\kappa_{g}(s)} & 0 \\ -\kappa_{g}(s) & \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s) } & \kappa_{g}(s)\\ 0 & -\kappa_{g}(s) & \frac{\kappa_{g} ^{^{\prime }}(s)}{\kappa_{g}(s) } \end{bmatrix} \begin{bmatrix} {\rho(s)} \\ {T(s)} \\ {\Delta(s)} \end{bmatrix}.$

Thus, the theorem is proved. □

If we take

$\kappa_{g}(s) = 1$

in the modified orthogonal Saban frame, the properties of the curves given relative to the known Saban frame are obtained.

4. The evolution of modified orthogonal Saban framed curves on $S^{2}$

In this section, we briefly review the main results for inextensible flows of curves on $S^{2}$ . The arc length of $l$ of the initial curve is defined as

$\begin{align*} \rho:\left[ 0, l\right] \times \left[ 0, \omega \right) &\rightarrow E^{3}, \\ (u, t)&\rightarrow \rho(u, t). \end{align*}$

Consider a family of differentiable curves with $l$ parameters. Here, $u$ is the variable parameter of the curves and $0 \leq u \leq l$ . Thus, the speed of $\rho$ is given by

$v = \left\Vert \frac{\partial \rho}{\partial u}\right\Vert,$

and from which it follows that the arclength $s$ is

$\begin{equation} s(u) = \int\limits_{0}^{u}\left\Vert \frac{\partial \rho}{\partial u} \right\Vert du = \int\limits_{0}^{u}vdu, \end{equation}$

(4.1)

where " $\left\Vert, \right\Vert$ " denotes the standart norm of $E^3$ . Also,

$\frac{\partial }{\partial s} = \frac{1}{v}\frac{\partial }{\partial u}$

and

$ds = vdu.$

Definition 4.1. The modified orthogonal Saban frame of curve $\rho$ on $S^{2}$ is $\left\{\rho, T, \Delta \right\}$ and the flow of curve $\rho$ is defined as

$\frac{\partial \rho}{\partial t} = f_{1} \rho +f_{2} T +f_{3} \Delta ,$

where $f_{1}, f_{2}, f_{3}$ components are scalar velocity functions ^[11,12].

Definition 4.2. Let $\rho(u, t)$ be a family of curves on $S^{2}$ . If the flow $\frac{\partial \rho}{\partial t}$ of $\rho(u, t)$ satisfies the condition

$\frac{\partial }{\partial t}\left\Vert \frac{\partial \rho}{\partial u}\right\Vert = 0 ,$

then this flow is called inextensible ^[11,12].

Theorem 4.3. Let $\left\{\rho, T, \Delta \right\}$ and

$\frac{\partial \rho}{\partial t} = f_{1} \rho +f_{2} T +f_{3} \Delta$

be modified orthogonal Saban frame and smooth flow of the curve $\rho$ on $S^{2}$ , respectively. The flow is said to be inextensible if

$\frac{\partial f_{2}}{\partial s} = -\frac{1}{ \kappa_{g}}f_{1}- \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}+ \kappa_{g} f_{3}.$

Proof. We have the definition of the initial curve, and Eqs (3.2) and (4.1). Since

$\langle \frac{\partial \rho}{\partial u}, \frac{\partial \rho}{\partial u}\rangle = v^{2},$

and the operators $\frac{\partial }{\partial u}$ and $\frac{\partial }{\partial t}$ are commutative, we hold

$\begin{align*} 2v \frac{\partial v }{\partial t} = & \frac{\partial }{\partial t} \langle \frac{\partial \rho}{\partial u}, \frac{\partial \rho}{\partial u} \rangle \\ = & 2 \langle \frac{\partial \rho}{\partial u}, \frac{\partial }{\partial u}\left(\frac{\partial \rho}{\partial t}\right) \rangle \\ = & 2\langle \frac{\partial \rho}{\partial u}, \frac{\partial }{\partial u}\left( f_{1} \rho + f_{2} T+ f_{3} \Delta\right)\rangle \\ = & 2v\langle \frac{1}{ \kappa_{g}}T, \frac{\partial }{\partial u} f_{1} \rho+ f_{1} v \frac{1}{\kappa_{g}} T+ \frac{\partial }{\partial u} f_{2} T+ f_{2}v \left(-\kappa_{g} \rho+\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}T +\kappa_{g} \Delta \right)\rangle \\ &+ 2v\langle \frac{1}{ \kappa_{g}}T, \frac{\partial }{\partial u} f_{3}+ f_{3} v\left(-\kappa_{g} T +\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}\Delta \right) \rangle \\ = & \frac{2v}{ \kappa_{g}}\left( \frac{\partial f_{2}}{\partial u}+\frac{1}{ \kappa_{g}}f_{1}v+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}v- \kappa_{g} f_{3}v \right). \end{align*}$

Thus, we get

$\begin{equation} \frac{\partial v }{\partial t} = \frac{1}{ \kappa_{g}} \left( \frac{\partial f_{2}}{\partial u}+\frac{1}{ \kappa_{g}}f_{1}v+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}v- \kappa_{g} f_{3}v \right). \end{equation}$

(4.2)

Now suppose that $\frac{\partial \rho }{\partial t}$ is extensible. From the Eqs (4.1) and (4.2), we get

$\frac{\partial }{\partial t}S(u, t) = \int\limits_{0}^{u}\frac{\partial v}{ \partial t}du = \int\limits_{0}^{u}\left( \frac{\partial f_{2}}{\partial u}+\frac{1}{ \kappa_{g}}f_{1}v+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}v- \kappa_{g} f_{3}v \right) du = 0.$

This means that

$\frac{\partial f_{2}}{\partial u} = -\frac{1}{ \kappa_{g}}f_{1}v- \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}v+ \kappa_{g} f_{3}v$

$\frac{\partial f_{2}}{\partial s} = -\frac{1}{ \kappa_{g}}f_{1}- \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}f_{2}+ \kappa_{g} f_{3}.$

The reverse of the proof is done in a similar way. □

Theorem 4.4. Let

$\frac{\partial \rho}{\partial t} = f_{1} \rho +f_{2} T +f_{3} \Delta$

be the smooth flow on $S^{2}$ . The form of derivative formulas is given as follows:

$\begin{equation} \begin{cases} \frac{\partial \rho}{\partial t} = \left( \frac{\partial}{\partial s} f_{1}- \kappa_{g} f_{2}\right) T + \left( \kappa_{g} f_{2}+ \frac{\partial}{\partial s} f_{3}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3}\right) \Delta , \\ \frac{\partial T}{\partial t} = \frac{1}{\kappa_{g}^{2}} \lambda \Delta , \\ \frac{\partial \Delta}{\partial t} = -\kappa_{g}^{2} \left( \kappa_{g} f_{2}+ \frac{\partial}{\partial s} f_{3}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3}\right) \rho -\frac{1}{\kappa_{g}^{2}} \lambda T, \end{cases} \end{equation}$

(4.3)

where

$\lambda = \langle \frac{\partial T}{\partial t}, \Delta \rangle.$

Proof. Using the modified orthogonal Saban frame and Eq (4.3), we obtain

$\begin{align*} \frac{\partial \rho }{\partial t} = & \frac{\partial}{\partial t}\frac{\partial \rho }{\partial s} \\ = & \frac{\partial}{\partial s} \left( f_{1} \rho + f_{2} T+ f_{3} \Delta \right) \\ = & \frac{\partial}{\partial s} f_{1} \rho + \frac{1}{\kappa_{g}} f_{1}T+ \frac{\partial}{\partial s} f_{2} T+ f_{2}\left(-\kappa_{g} \rho+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} T+ \kappa_{g}\Delta \right) + \frac{\partial}{\partial s} f_{3}\Delta + f_{3}\left(-\kappa_{g} T+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}\right) \Delta . \end{align*}$

Thus, we get

$\begin{equation} \frac{\partial \rho }{\partial t} = \left( \frac{\partial}{\partial s} f_{1}- \kappa_{g}f_{2} \right) \rho + \left( \kappa_{g} f_{2} + \frac{\partial}{\partial s} f_{3} +\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3} \right) \Delta. \end{equation}$

(4.4)

Now, using Eq (4.4) and differentiating the modified orthogonal Saban frame with curvature according to t, we get

$\begin{equation} \begin{cases} \frac{\partial}{\partial t} \langle \rho, T \rangle = 0 = \langle \rho, \frac{\partial T}{\partial t} \rangle, \\ \frac{\partial}{\partial t} \langle \rho, \Delta \rangle = 0 = \kappa_{g}^{2} \left( \kappa_{g} f_{2} + \frac{\partial}{\partial s} f_{3} +\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3} \right) + \langle \rho, \frac{\partial \Delta }{\partial t} \rangle , \\ \frac{\partial}{\partial t} \langle T, \Delta \rangle = 0 = \lambda + \langle T, \frac{\partial \Delta}{\partial t}\rangle. \end{cases} \end{equation}$

(4.5)

From Eqs (4.4) and (4.5) we obtain

$\begin{align*} \frac{\partial T}{\partial t} = \frac{1}{\kappa_{g}^{2}} \lambda \Delta \end{align*}$

and

$\begin{align*} \frac{\partial \Delta}{\partial t} = & -\kappa_{g}^{2} \left( \kappa_{g} f_{2}+ \frac{\partial}{\partial s} f_{3}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3}\right) \rho -\frac{1}{\kappa_{g}^{2}} \lambda T. \end{align*}$

This completes the proof. □

Theorem 4.5. Suppose that the modified orthogonal Saban framed curve $\rho$ is inextensible. The evolution of the curvature is given by

$\begin{align*} \frac{\partial \kappa_{g}}{\partial t}& = \kappa_{g}^{2}f_{1}+ \kappa_{g} \frac{\partial }{\partial s} f_{3}+ \kappa_{g}^{^{\prime }}f_{3}+ \lambda \frac{\partial }{\partial s} \frac{1}{\kappa_{g}^{2}}+ \frac{1}{\kappa_{g}^{2}} \frac{\partial }{\partial s} \lambda, \\ \frac{\partial }{\partial t}\left( \frac{1}{\kappa_{g}}\right)& = \frac{1}{\kappa_{g}} \frac{\partial }{\partial s} f_{1}- f_{2}-\kappa_{g}^{2} f_{2}-\kappa_{g}\frac{\partial }{\partial s}f_{3}-\kappa_{g}^{^{\prime }} f_{3} \end{align*}$

and

$\begin{align*} \lambda = & \kappa_{g}^{2} \left( \frac{\partial }{\partial s} (\kappa_{g}f_{2})+ \frac{\partial ^2 }{\partial s^2} (f_{3})+ \frac{\partial }{\partial s} (\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3})+\kappa_{g}^{^{\prime }}f_{2}+\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}\frac{\partial }{\partial s}f_{3}+ \frac{\kappa_{g}^{^{\prime ^2}}}{\kappa_{g}^2} f_{3} \right). \end{align*}$

Proof. Since

$\frac{\partial }{\partial s}\frac{\partial \rho }{\partial t} = \frac{\partial }{\partial t}\frac{\partial \rho }{\partial s},$

$\begin{align*} \frac{\partial }{\partial s}\frac{\partial \rho }{\partial t} = & \frac{\partial }{\partial s}\left[ \left( \frac{\partial}{\partial s} f_{1}- \kappa_{g}f_{2} \right) \rho + \left( \kappa_{g} f_{2} + \frac{\partial}{\partial s} f_{3} +\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3} \right) \Delta \right] \\ = & \left( \frac{\partial }{\partial s^2} f_{1}-\frac{\partial }{\partial s}(\kappa_{g} f_{2}) \right)\rho+ \left( \frac{1}{\kappa_{g}} \frac{\partial }{\partial s} f_{1}- f_{2}\right)T \\ &+ \left(\frac{1}{\kappa_{g}} f_{1}+ \frac{\partial }{\partial s} f_{2}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{2}- \kappa_{g} f_{3} \right) \left( -\kappa_{g} \rho + \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} T+ \kappa_{g} \Delta \right)\\ &+ \left( \frac{\partial }{\partial s} (\kappa_{g} f_{2})+ \frac{\partial ^{2}}{\partial s^{2}} f_{3}+ \frac{\partial }{\partial s} (\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3}) \right) \Delta + \left(\kappa_{g} f_{2}+ \frac{\partial }{\partial s} f_{3}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3} \right) \left( -\kappa_{g} T+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} \Delta \right) \end{align*}$

and

$\begin{align*} \frac{\partial }{\partial t} \frac{\partial \rho }{\partial s} = & \frac{\partial }{\partial t} \left[\frac{1}{\kappa_{g}} T\right]\\ = &\frac{\partial }{\partial t}\left( \frac{1}{\kappa_{g}}\right) + \frac{1}{\kappa_{g}^{2}} \lambda \Delta. \end{align*}$

Then, we get

$\begin{align*} \frac{\partial }{\partial t}\left( \frac{1}{\kappa_{g}}\right) = \frac{1}{\kappa_{g}} \frac{\partial }{\partial s} f_{1}- f_{2}-\kappa_{g}^{2} f_{2}-\kappa_{g}\frac{\partial }{\partial s}f_{3}-\kappa_{g}^{^{\prime }} f_{3} \end{align*}$

and

$\begin{align*} \lambda = & \kappa_{g}^{2} \left( \frac{\partial }{\partial s} (\kappa_{g}f_{2})+ \frac{\partial }{\partial s^2} (f_{3})+ \frac{\partial }{\partial s} (\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3})+\kappa_{g}^{^{\prime }}f_{2}+\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}}\frac{\partial }{\partial s}f_{3}+ \frac{\kappa_{g}^{^{\prime ^2}}}{\kappa_{g}^2} f_{3} \right). \end{align*}$

Considering that the operators

$\frac{\partial }{\partial s}\frac{\partial \Delta }{\partial t} = \frac{\partial }{\partial t}\frac{\partial \Delta }{\partial s}$

are commutative,

$\begin{align*} \frac{\partial }{\partial s}\frac{\partial \Delta }{\partial t} = & \frac{\partial }{\partial s} \left[ -\kappa_{g}^{2} \left( \kappa_{g} f_{2}+ \frac{\partial}{\partial s} f_{3}+ \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3}\right) \rho -\frac{1}{\kappa_{g}^{2}} \lambda T\right] \\ = &- \left(\frac{\partial }{\partial s} (\kappa_{g}^{3} f_{2}) + \frac{\partial }{\partial s} (\kappa_{g}^{2}\frac{\partial }{\partial s} f_{3})+ \frac{\partial }{\partial s} (\kappa_{g}\kappa_{g}^{^{\prime }} f_{3})\right) \rho\\ &- \left(\kappa_{g}^{2} f_{2}+ \kappa_{g}\frac{\partial }{\partial s} f_{3}+ \kappa_{g}^{^{\prime }} f_{3} \right) T - \frac{1}{\kappa_{g}^{2}} \frac{\partial }{\partial s}\left( \lambda \right)T -\lambda \frac{\partial }{\partial s} \left(\frac{1}{\kappa_{g}^{2}}\right) T - \frac{1}{\kappa_{g}^{2}} \lambda \left( -\kappa_{g} \rho + \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} T + \kappa_{g} \Delta \right) \end{align*}$

and

$\begin{align*} \frac{\partial }{\partial t}\frac{\partial \Delta }{\partial s} = & \frac{\partial }{\partial t} \left[ -\kappa_{g} T + \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} \Delta \right] \\ = & -\frac{\partial }{\partial t} \left(\kappa_{g}\right) T - \frac{1}{\kappa_{g}} \lambda \Delta+ \frac{\partial }{\partial t} \left(\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} \right) \Delta - \kappa_{g} \kappa_{g}^{^{\prime }} \left( \kappa_{g} f_{2} +\frac{\partial }{\partial s} f_{3} + \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} f_{3} \right) \rho - \frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}^{3}} \lambda T. \end{align*}$

So, we obtain

$\begin{align*} \frac{\partial \kappa_{g}}{\partial t} = & \kappa_{g}^{2}f_{1}+ \kappa_{g} \frac{\partial }{\partial s} f_{3}+ \kappa_{g}^{^{\prime }}f_{3}+ \lambda \frac{\partial }{\partial s} \frac{1}{\kappa_{g}^{2}}+ \frac{1}{\kappa_{g}^{2}} \frac{\partial }{\partial s} \lambda \end{align*}$

and

$\begin{align*} \frac{\partial }{\partial t}\frac{\kappa_{g}^{^{\prime }}}{\kappa_{g}} = \frac{1}{\kappa_{g}} \lambda - \frac{1}{\kappa_{g}} \lambda = 0. \end{align*}$

This completes the proof. □

In what follows, we compute the curve flow according to the modified Sabban frame for some special spherical curves.

Example 4.6. Let $\rho(s)$ be a unit-speed regular curve of the modified orthogonal Saban frame on $S^{2}$ .

$\begin{align*} \rho :I \subset \mathbb{R} &\rightarrow S^{2}, \\ u&\rightarrow \rho (u) = \left(\frac{cos(u)}{\sqrt{1+u^2}} , \frac{sin(u)}{\sqrt{1+u^2}}, \frac{u}{\sqrt{1+u^2}}\right). \end{align*}$

In this case, the other elements and geodesic curvature of the modified Saban frame are calculated, respectively, as follows:

$\begin{align*} T(s) = & -\frac{1}{\left( u^{2}+1\right) ^{6}}\left( \sin u+u^{2}\sin u+u\cos u\right) \left( u^{7}+3u^{5}+4u^{3}-u^{2}+2u-1\right) \\ &+\frac{1}{\left( u^{2}+1\right) ^{6}}\left( \cos u+u^{2}\cos u-u\sin u\right) \left( u^{7}+3u^{5}+4u^{3}-u^{2}+2u-1\right) \\ &-\frac{1}{\left(u^{2}+1\right) ^{5}}\left( u^{6}+2u^{4}+2u^{2}-u\right), \\ \Delta (s) = & -\frac{1}{\left( u^{2}+1\right) ^{\frac{13}{2}}}\left( u^{3}\cos u-u^{2}\sin u+u\cos u+u\sin u\right) \left( u^{7}+3u^{5}+4u^{3}-u^{2}+2u-1\right)\\ &-\frac{1}{\left(u^{2}+1\right) ^{\frac{13}{2}}}\left( u^{2}\cos u+u^{3}\sin u-u\cos u+u\sin u\right) \left( u^{7}+3u^{5}+4u^{3}-u^{2}+2u-1\right) \\ &+\frac{1}{\left( u^{2}+1\right) ^{\frac{13}{2}}}\left( \cos 2u-u\sin 2u+u^{2}\cos 2u\right) \left( u^{7}+3u^{5}+4u^{3}-u^{2}+2u-1\right), \\ \kappa_{g} (u) = & \frac{1}{({1+u^2})^\frac{9}{2}}\left(u^7 +3u^5 +4u^3- u^2 +2u-1\right). \end{align*}$

If we give

$f_{1} = tanh(u), \ \ f_{2} = cos(u), \ \ f_{3} = sin(u)$

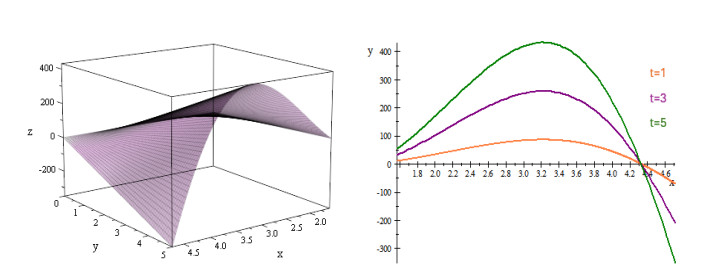
by using Theorem 4.5, the graphs of the evolution equation of $\kappa_{g} (u, t)$ are shown as Figures 1 and 2.

Figure 1. The evolution of

$\kappa_{g} (u, t)$ for

$\dfrac{\pi}{2}\leq u \leq \dfrac{3\pi}{2}, 0 \leq t \leq 5$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The evolution of

$\kappa_{g} (u, t)$ for

$\dfrac{\pi}{3}\leq u \leq \dfrac{4\pi}{3}, 0 \leq t \leq 5$ .

DownLoad: Full-Size Img PowerPoint

Example 4.7. Let $\rho(s)$ be a unit-speed regular curve of the modified orthogonal Saban frame on $S^{2}$ .

$\begin{align*} \rho :I \subset \mathbb{R} &\rightarrow S^{2}, \\ u&\rightarrow \rho (u) = \left(cos(u), sin(u)cos(u), sin^{2}(u)\right). \end{align*}$

In this case, the other elements and geodesic curvature of the modified Saban frame are calculated, respectively, as follows:

$\begin{align*} T(s) = & \frac{1}{8}\sin 4u-\frac{5}{4}\sin 2u, \cos u+\frac{9}{8}\cos 3u-\frac{1 }{8}\cos 5u, \frac{5}{4}\sin u+\frac{9}{8}\sin 3u-\frac{1}{8}\sin 5u, \\ \Delta (s) = & \left( \frac{1}{4}\cos 3u-\frac{9}{4}\cos u\right) \left( \frac{1}{2} \cos 2u-\frac{1}{2}\right) , \left( \frac{1}{4}\cos 3u-\frac{9}{4}\cos u\right) \left( \frac{5}{4}\sin u+\frac{1}{4}\sin 3u\right) \\ &+\frac{27}{16} \cos ^{2}u+\frac{3}{8}\cos u\cos 3u-\frac{1}{16}\cos ^{2}3u, \\ \kappa_{g} (u) = & \left( \frac{9}{4}\cos u-\frac{1}{4}\cos 3u\right). \end{align*}$

For given

$f_{1} = sec(u), \ \ \ f_{2} = cos(u), \ \ \ f_{3} = sin(u)$

by using Theorem 4.5, the graphs of the evolution equation of $\kappa_{g} (u, t)$ are shown as Figures 3 and 4.

Figure 3. The evolution of

$\kappa_{g} (u, t)$ for

$\dfrac{\pi}{2}\leq u \leq \dfrac{3\pi}{2}, 0 \leq t \leq 5$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. The evolution of

$\kappa_{g} (u, t)$ for

$\dfrac{\pi}{3}\leq u \leq \dfrac{4\pi}{3}, 0 \leq t \leq 5$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

Geometrically, the evolution of curves and surfaces means a continuous transformation that transforms one curve or surface into another curve or surface. The aim of studying the evolution of curves and surfaces is to determine the final shape of given curves and surfaces and to find the geometric properties that remain invariant during the evolution process. In this work, inextensible curve flow is studied by using a modified orthogonal Saban frame, which is an orthogonal frame determined by the intrinsic structure of the sphere. Important results were obtained depending on the geodesic curvature. It is obvious that the results obtained here will be used in many areas where the evolutions of curves and surfaces are applied. Computer imaging, computer animation, and image processing are the main examples. Another application of the evolution of curves and surfaces is the modeling of the dynamics of shapes in physics, chemistry, and biology. These models are determined by functions of the intrinsic properties of curves. Since this study uses a frame the modified orthogonal Saban frame based on the intrinsic property of time, it is expected to contribute to further research in these fields.

Author contributions

Atakan Tuğkan Yakut: validation, writing-review and editing, conceptualization, methodology, supervision; Alperen Kızılay: investigation, writing-original draft, writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

[1]	V. Parque, T. Miyashita, Smooth curve fitting of mobile robot trajectories using differential evolution, IEEE Access, 8 (2020), 82855–82866. https://doi.org/10.1109/ACCESS.2020.2991003 doi: 10.1109/ACCESS.2020.2991003
[2]	P. P. Kumar, S. Balakrishnan, A. Magesh, P. Tamizharasi, S. I. Abdelsalam, Numerical treatment of entropy generation and bejan number into an electroosmotically-driven flow of sutterby nanofluid in an asymmetric microchannel, Numer. Heat Transfer., 85 (2024), 1–20. https://doi.org/10.1080/10407790.2024.2329773 doi: 10.1080/10407790.2024.2329773
[3]	F. Lavorenti, P. Henri, F. Califano, S. Aizawa, N. Andre, Electron acceleration driven by the lower-hybrid-drift instability, Astron. Astrophys., 652 (2021), A20. https://doi.org/10.1051/0004-6361/202141049 doi: 10.1051/0004-6361/202141049
[4]	M. Desbrun, M. P. Cani, Active implicit surface for animation, Proceedings of Graphics Interface' 98, 1998. https://doi.org/10.20380/GI1998.18
[5]	F. Precioso, M. Barlaud, T. Blu, M. Unser, Smoothing $B$ -spline active contour for fast and robust image and video segmentation, Proceedings 2003 International Conference on Image Processing, 2003. https://doi.org/10.1109/ICIP.2003.1246917
[6]	O. Nave, Modification of semi-analytical method applied system of ODE, Mod. Appl. Sci., 14 (2020), 75–81. https://doi.org/10.5539/mas.v14n6p75 doi: 10.5539/mas.v14n6p75
[7]	H. Q. Lu, J. S. Todhunter, T. W. Sze, Congruence conditions for nonplanar developable surfaces and their application to surface recognition, CVGIP, 58 (1993), 265–285. https://doi.org/10.1006/ciun.1993.1042 doi: 10.1006/ciun.1993.1042
[8]	G. S. Chirikjian, J. W. Burdick, A modal approach to hyper-redundant manipulator kinematics, IEEE Trans. Rob. Autom., 10 (1994), 343–354. https://doi.org/10.1109/70.294209 doi: 10.1109/70.294209
[9]	Ö. G. Yıldız, M. Tosun, S. Ö. Karakuş, A note on inextensible flows of curves in $E^n$ , Int. Electron. J. Geom., 6 (2013), 118–124.
[10]	A. Kızılay, Ö. G. Yıldız, O. Z. Okuyucu, Evolution of quaternionic curve in the semi-Euclidean space $E^{4}_{2}$ , Math. Methods Appl. Sci., 44 (2021), 7577–7587. https://doi.org/10.1002/mma.6374 doi: 10.1002/mma.6374
[11]	D. Y. Kwon, F. C. Park, Evolution of inelastic plane curves, Appl. Math. Lett., 12 (1999), 115–119. https://doi.org/10.1016/S0893-9659(99)00088-9 doi: 10.1016/S0893-9659(99)00088-9
[12]	D. Y. Kwon, F. C. Park, D. P. Chi, Inextensible flows of curves and developable surfaces, Appl. Math. Lett., 18 (2005), 1156–1162. https://doi.org/10.1016/j.aml.2005.02.004 doi: 10.1016/j.aml.2005.02.004
[13]	D. Latifi, A. Razavi, Inextensible flows of curves in Minkowskian space, Adv. Stud. Theor. Phys., 2 (2008), 761–768.
[14]	N. Gurbuz, Inextensible flows of spacelike, timelike and null curves, Int. J. Contemp. Mtath. Sci., 4 (2009), 1599–1604.
[15]	Ö. G. Yıldız, S. Ersoy, M. Masal, A note on inextensible flows of curves on oriented surface, Cubo (Temuco), 16 (2014), 11–19. http://doi.org/10.4067/S0719-06462014000300002 doi: 10.4067/S0719-06462014000300002
[16]	T. Sasai, The fundamental theorem of analytic space curves and apparent singularities of Fuchsian differential equations, Tohoku Math. J., 36 (1984), 17–24. https://doi.org/10.2748/tmj/1178228899 doi: 10.2748/tmj/1178228899
[17]	G. Ş. Atalay, A new approach to special curved surface families according to modified orthogonal frame, AIMS Math., 9 (2024), 20662–20676. https://doi.org/10.3934/math.20241004 doi: 10.3934/math.20241004
[18]	B. Bükcü, M. K. Karacan, On the modified orthogonal frame with curvature and torsion in 3-space, Math. Sci. Appl. E-Notes, 4 (2016), 184–188. https://doi.org/10.36753/mathenot.421429 doi: 10.36753/mathenot.421429
[19]	K. Eren, A study of the evolution of space curves with modified orthogonal frame in Euclidean 3-space, Appl. Math. E-Notes, 22 (2022), 281–286.
[20]	K. Eren, S. Ersoy, On characterization of Smarandache curves constructed by modified orthogonal frame, Math. Sci. Appl. E-Notes, 12 (2024), 101–112. https://doi.org/10.36753/mathenot.1409228 doi: 10.36753/mathenot.1409228
[21]	A. Kızılay, A. T. Yakut, A work on inextensible flows of space curves with respect to a new orthogonal frame in $E ^3$ , Honam Math. J., 45 (2023), 668–677. https://doi.org/10.5831/HMJ.2023.45.4.668 doi: 10.5831/HMJ.2023.45.4.668
[22]	A. Kızılay, A. T. Yakut, Inextensible flows of space curves according to a new orthogonal frame with curvature in $E^{3}_{1}$ , Int. Electron. J. Geom., 16 (2023), 577–593. https://doi.org/10.36890/iejg.1274663 doi: 10.36890/iejg.1274663
[23]	J. J. Koenderink, Solid shape, MIT Press, 1990.
[24]	K. Taşköprü, Smarandache curves on $S ^2$ , Bol. Soc. Paran. Mat., 32 (2014), 51–59. https://doi.org/10.5269/bspm.v32i1.19242 doi: 10.5269/bspm.v32i1.19242
[25]	A. T. Ali, Special Smarandache curves in the Euclidean space, Int. J. Math. Combin., 2 (2010), 30–36. https://doi.org/10.5281/zenodo.9392 doi: 10.5281/zenodo.9392
[26]	A. T. Yakut, M. Savas, T. Tamirci, The Smarandache curves on $S^{2}_{1}$ and its duality on $H^{2}_{0}$ , J. Appl. Math., 12 (2014), 1–12. https://doi.org/10.1155/2014/193586 doi: 10.1155/2014/193586
[27]	M. Savas, A. T. Yakut, T. Tamirci, The Smarandache curves on $H^{2}_{0}$ , Gazi Univ. J. Sci., 29 (2016), 69–77.

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(730) PDF downloads(52) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(4)

AIMS Mathematics

On the curve evolution with a new modified orthogonal Saban frame

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. The modified orthogonal Saban frame with curvature on $S^{2}$

4. The evolution of modified orthogonal Saban framed curves on $S^{2}$

5. Conclusions

Author contributions

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

On the curve evolution with a new modified orthogonal Saban frame

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. The modified orthogonal Saban frame with curvature on S2 S^{2}

4. The evolution of modified orthogonal Saban framed curves on S2 S^{2}

5. Conclusions

Author contributions

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3. The modified orthogonal Saban frame with curvature on $S^{2}$

4. The evolution of modified orthogonal Saban framed curves on $S^{2}$