Robustness analysis of neutral fuzzy cellular neural networks with stochastic disturbances and time delays

1.   Introduction

In recently years, neural networks have achieved extensive and in-depth applications in many fields such as aerospace ^[1], biomedicine ^[2], and pattern recognition ^[3], which has inspired many scholars to explore them with great interest. With the continuous development of neural network research, many classical network types have been proposed, such as recurrent neural networks^[4], Hopfield neural networks ^[5], cellular neural networks ^[6], and so on. Cellular neural networks were proposed by Chuan and Yang in 1988 ^[6,7], where the neural network connection method derives from neurons that are interconnected only with other neurons in a specific region. This unique connection significantly reduces the complexity of network interconnections, thus showing a great potential and value for applications in many fields such as image encryption ^[8], parallel signal processing ^[9], and so on. As an important branch of cellular neural networks, fuzzy cellular neural networks (FCNNs) were proposed by Yang and Yang in 1996 ^[10,11], who introduced fuzzy logic into cellular neural networks. Fuzzy logic describes and handles uncertainty or ambiguity through fuzzy sets and fuzzy rules, which makes cellular neural networks more accurate and reliable when dealing with complex information in the real world, as well as improves the robustness and fault tolerance of the system, which in turn enhances the practical application of the network ^[12,13].

It is well known that stability is usually the first condition for the successful application of FCNNs. The stability of neural networks not only relies on the configuration of the parameters, but is also inevitably affected by external factors. In practical engineering applications, stochastic disturbances and time delays are common perturbation factors. If the intensity of the perturbation exceeds the perturbation limit, then it will destroy the stability of the network. In recent years, scholars have investigated the stability of FCNNs using Lyapunov's method, the Linear Matrix Inequality (LMI), and other methods, which have produced a series of remarkable research results ^{[14,15,16,17,18,19]}. For example, in the literature ^[14], Long et al. established a new L-operational inequality and used the properties of M-matrices, a p-order moment stability criterion for the exponential stabilisation of FCNNs, and time delays and stochastic perturbations were obtained. In the literature ^[15], Zhang et al. studied fractional order FCNNs with time delays and random perturbations, which produced a new stability criterion.

However, the aforementioned literature solely discusses the stability of FCNNs. The neural network is destabilised when random disturbances and time delays are beyond the specified range. Therefore, it is a fascinating subject to discuss how much an initially stable system can withstand the intensity of perturbations and still remain stable. This type of analysis is often referred to as a robustness analysis of stability. The problem of a robustness analysis has received the attention of many scholars and many excellent outcomes have been published ^{[4,20,21,22,23]}. For example, in the literature ^[4], Shen et al. considered the robustness problem for the stability of recurrent neural networks that contained stochastic perturbations and time delays. In the literature ^[20], Zhu et al. considered the robustness of recurrent neural networks with Markov switching parameters. In the literature ^[21], Yang et al. explored the robustness problem of global exponential stability for nonlinear systems with time-varying delays and nonlinear stochastic perturbations. However, there is less literature on the robustness analysis of the fuzzy neural network stability, which is one of the motivations for writing this paper.

It is worth noting that neutral neural networks belong to a particular class of neural networks whose distinguishing feature is the simultaneous existence of time delays in the system state and state derivatives. This property makes it possible to more accurately describe and portray the changes in the network state, and thus has attracted a great deal of interest from many researchers, and a series of research results were reported ^[24,25]. However, it is also interesting to introduce neutral terms into other neural networks and to consider their robustness. ^{[26,27,28,29]}. For example, in the literature ^[26], Shen et al. explored the robustness of the global exponential stability (GES) for nonlinear systems with time-varying delays and neutral terms as perturbing factors. In the literature ^[29], Si et al. discussed the robustness of the GES of recurrent neural networks with neutral terms and generalized piecewise constant arguments. However, the issue of the robustness of neutral FCNNs with random perturbations and time-varying delays has hardly been considered.

Based on the above discussions and analyses, the main problem investigated for this paper is the robustness of the GES for neutral FCNNs with time delays and stochastic perturbations. The major contents and contributions of this paper include the following:

$(i)$ By using some inequality techniques such as the Gronwall lemma, the Itŏ formula, and the Cauchy inequality, multivariate implicit transcendental equations which incorporate random perturbations, time delays, and contraction coefficients of the neutral terms are obtained. From this, an upper bound on the effect of these perturbations on the stability of the fuzzy system is estimated, which ensures that the initially stable fuzzy system can remain globally exponentially stable when subjected to perturbations.

$(ii)$ Compared with the literature, which is known to contain two kinds of perturbation factors, this paper considers the robustness analysis of the GES of FCNNs with three kinds of perturbation factors: neutral terms, random perturbations and time delays. It not only enriches the theoretical study of FCNNs, but also provides theoretical support for fuzzy system stability analyses and designs.

$(iii)$ Compared with the existing literature ^[4,28,30], the system in this paper contains fuzzy logic, neutral terms, time delays, and random disturbances. Therefore, when solving the transcendental equation, there are more disturbances to be considered, which increases the difficulty of solving and makes the system more applicable.

The rest of the paper is organised as follows: Section 2 provides a model of a neutral FCNN with random disturbances and time delays, as well as the relevant definitions and lemmas to be used in the proof; Section 3 derives the theoretical results for an initially stable fuzzy system that remains GES in spite of multifactorial disturbances; and Section 4 provides some numerical examples to verify the validity of the results.

Notations : Denote $\mathbb{R} = (-\infty, +\infty)$, $\mathbb{R}_{+} = [0, +\infty)$, $\mathbb{N} = \{1, 2, \cdots\}$, and $\mathbb{R}^{m}$ denotes the space which consists of all $m$-dimensional vectors. For a vectors $\eta = (\eta_{1}, \eta_{2}, \cdots, \eta_{m})^{T}$, we denote $\|\eta\Vert = \sum_{i = 1}^{m}|\eta_{i}|$, $i\in \mathbb{N}$, where $\eta_{i}\in \mathbb{R}$. $(\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\geqslant 0}, P)$ is a complete filtered probability space, where $\{\mathcal{F}_{t}\}_{t\geqslant 0}$ is a right-continuous filter and satisfies the usual condition that the space contains all $P$-null sets. $B(t)$ is a scalar brownian motion defined at $(\Omega, \mathcal{F}, \{\mathcal{F}_{t} \}_{t\geqslant 0}, P)$. $E$ represents an operator that computes the mathematical expectation of a given probability measure $P$. Fuzzy AND and fuzzy OR operations are denoted by $\bigwedge$ and $\bigvee$, respectively.

2.   Preliminaries and assumptions

Consider the following mathematical model of FCNNs:

where $i, j\in \mathbb{N}$, and $\bar{P}_{i}(t)$ denotes the state of the $i$ th neuron at time $t$. $d_{ij}$ and $e_{ij}$ are elements of the fuzzy feedback MIN template and the fuzzy feed-forward MAX template, respectively. $g_{j}(\cdot)$ is the activation function. $\bar{P}_{i}(t_{0}) \in \mathbb{R}$ is the initial value of FCNNs (2.1).

Assume $P^{*}$ is the equilibrium point of FCNNs (2.1), where $P^{*} = \{P^{*}_{1}, \cdots, P^{*}_{m}\}^{T}$; then, let $P(t) = \bar{P}(t)-P^{*}(t)$ and $f_{j}(P_{j}(t)) = g_{j}(P_{j}(t)+P^{*}_{j})-g(P^{*})$, $P_{i}(t_{0}) = \varphi(0) = \psi _{i}(0)-\psi ^{*}$. Then, FCNNs (2.1) can be written in the following form:

Next, consider the FCNNs model with neutral terms, random perturbations, and time delays:

where $i, j\in \mathbb{N}$, $Q_{i}(t)$ is the state of the $i$ neuron at time $t$, and $G:\mathbb{R}^{m} \rightarrow \mathbb{R}^{m}$ is the weight matrix of neutral term. $\tau(t)$ is a delay that satisfies $\tau(t)$: [$t_{0}, +\infty$)$\to$ $[0, \bar{\tau}]$, $\tau^{'}(t) \leqslant \zeta < 1$, $\phi = \{\phi_{i}(s):-\bar{\tau}\leqslant s \leqslant 0\}\in([-\bar{\tau}, 0], R^{m})$. $B(t)$ is a scalar brownian motion defined in the probability space $(\Omega, \mathcal{F}, \{\mathcal{F}_{t} \}_{t\geqslant 0}, P)$. $\sigma = (\sigma_{ij})_{m\times m}$ is a matrix of diffusion coefficients.

For the purpose of the proof of this paper, some assumptions and definitions to be used are given below.

Assumption A1. Assume the activation functions $f_{j}(\cdot)$, satisfies the following inequality:

where $L_{j}\in(0, 1)$ are known constants.

Lemma 1. ^[15] If A1 holds, then the solution $P(t) = (P_{1}(t), \cdots, P_{m}(t))^{T}$ of FCNNs (2.2) satisfies the initial unique condition.

Assumption A2. ^[28] There exists the Lipschitz coefficient $\kappa_{i} \in (0, 1)$, $i\in m$, such that $|G_{i}(U_{i}(t))-G_{i}(V_{i}(t))|\leqslant \kappa_{i}|U_{i}(t)-V_{i}(t)|$ holds for any variable component $U_{i}, V_{i}$. Therefore, let $\kappa = \max_{i\in m}\{\kappa_{i}\}$, where the above formula can be expressed as follows:

Definition 1. The state of FCNNs (2.2) is GES, if there exist $\lambda > 0$ and $\theta > 0$ such that

Definition 2. ^[14] FCNNs (2.3) is said to be mean square globally exponentially stable (MSGES), if $t\in R_{+}$, $\phi(0)\in\mathbb{R}^{m}$, exist $\bar{\lambda} > 0$ and $\bar{\theta} > 0$ such that

where the Lyapunov exponent $\limsup_{t\to \infty}\frac{1}{t}\ln E\|Q(t; t_{0}, \phi)\Vert^{2} < 0.$ And $Q(t; t_{0}, \phi)$ is the state of FCNNs (2.3). FCNNs (2.3) is said to be almost surely globally exponentially stable (ASGES), if $t\in R_{+}$, $\phi(0)\in\mathbb{R}^{m}$, and the Lyapunov exponent almost surely $\limsup_{t\to \infty}\frac{1}{t}\ln \|Q(t; t_{0}, \phi)\Vert < 0$.

Remark 1. From the above definitions, it is clear that the ASGES of FCNNs (2.3) implies the MSGES of FCNNs (2.3) ^[31], but not vice versa. Therefore, let Assumption A1 hold. The MSGES of FCNNs (2.3) implies the ASGES of FCNNs (2.3).

Lemma 2.^[11] For FCNNs (2.3),

Lemma 3.^[31] Let $f:\mathbb{R} ^{m}\times \mathbb{R}\times [a, b] \to \mathbb{R}^{m\times m}$, such that the following inequality holds

3.   Results

Theorem 1. If Assumptions A1 and A2, Lemmas 2 and 3 hold, and stystem FCNNs (2.2) is GES, then FCNNs (2.3) is MSGES and ASGES. If $\kappa < \min\{\tilde{\kappa}, \big(\frac{\exp(-2\varDelta M_{1})}{12\big[1+24m_{2}^{2}\varDelta^{2}\big((1-\zeta)^{-1}+(1-2\zeta)^{-1}\big) \big]} \big)^{\frac{1}{2}}\}$, then $|\sigma_{*}| < \bar{\sigma}_{*}$ and $\bar{\tau} < \min\{\varDelta/2, \breve{\tau}\}$, where $\tilde{\kappa}$, $\bar{\sigma}_{*}$, $\breve{\tau}$ are the solutions of following three transcendental equations:

and

and

where

Proof. From the fuzzy systems (2.2) and (2.3),

Let

Based on A1, A2, and Lemma 2, when $t_{0}\leqslant t\leqslant t_{0}+2\varDelta$, we have the following:

Furthermore, by Lemma 3,

For the first term in (3.6), when $t_{0}\leqslant t\leqslant t_{0}+2\varDelta$,

For the time delays term contained in (3.6), when $t_{0}\leqslant t\leqslant t_{0}+\bar{\tau}$, we can obtain the following:

When $t_{0}+\bar{\tau} \leqslant t\leqslant t_{0}+2\varDelta$, we can obtain the following:

Noting that $2\bar{\tau} \leqslant \varDelta$, for the first term in (3.9), when $t_{0}+\bar{\tau} \leqslant t \leqslant t_{0}+2\bar{\tau}$, we have the following:

For the second term in (3.9), exchanging the order of integrations,

Similarly, for the third term in (3.9),

Therefore, from (3.8)–(3.12), when $t_{0}\leqslant t\leqslant t_{0}+2\varDelta$, we have the following:

Substituting (3.7) and (3.13) into (3.6), we further conclude the following:

where

Noting that $2\bar{\tau}\leqslant \varDelta$, by the Gronwall inequality, for $t_{0} \leqslant t \leqslant t_{0}+2\varDelta$, we can obtain the following:

Therefore,

Noting that $\kappa < \big(\frac{\exp(-2\varDelta M_{1})}{12\big[1+24m_{2}^{2}\varDelta^{2}\big((1-\zeta)^{-1}+(1-2\zeta)^{-1}\big) \big]} \big)^{\frac{1}{2}}$, thus $\bar{M}\leqslant \frac{\big[M_{3}+M_{2}\big(1+2\lambda^{2}\exp(-2\theta(\varDelta-\bar{\tau}))\big) \big]\tilde{M}\exp(2\varDelta M_{1})}{1-2M_{2}\exp(2\varDelta M_{1})}.$

Therefore, owing to system (2.2) being GES, when $t_{0}-\bar{\tau}+\varDelta\leqslant t\leqslant t_{0}-\bar{\tau} +2\varDelta$, we have the following:

where, $M(\kappa, \sigma_{*}, \tau) = \frac{2\lambda^{2}\exp(-2\theta(\varDelta-\bar{\tau}))+2(M_{2}+M_{3})\exp(2\varDelta M_{1})}{1-2M_{2}\exp(2\varDelta M_{1})}-1.$ If $\kappa = 0, \sigma_{*} = 0, \bar{\tau} = 0$, then we have $M(0, 0, 0) = 2\lambda^{2}\exp(-2\theta\varDelta)-1 < 0$, and $\varDelta > \ln(2\lambda^{2})/(2\theta)$. Therefore, if $\sigma_{*} = 0, \tau = 0$, then

where $M^{'}_{1} = 12\varDelta(m_{1}+m_{2})^2, \ \ M_{2} = 6\kappa^{2}\big[1+24\varDelta^{2}m_{2}^{2}\big(\frac{1}{1-\zeta}+\frac{1}{1-2\zeta}\big)\big], \ \ M^{'}_{3} = 12\kappa^{2}.$

As $0 < \kappa < \big(\frac{\exp(-2\varDelta M_{1})}{12\big[1+24m_{2}^{2}\varDelta^{2}\big((1-\zeta)^{-1}+(1-2\zeta)^{-1}\big) \big]} \big)^{\frac{1}{2}}$ and $\frac{dM(k, 0, 0)}{dk} > 0$, then $M(\kappa, 0, 0)$ is strictly increasing with respect to $\kappa$. When $\kappa\to \big(\frac{\exp(-2\varDelta M_{1})}{12\big[1+24m_{2}^{2}\varDelta^{2}\big((1-\zeta)^{-1}+(1-2\zeta)^{-1}\big) \big]} \big)^{\frac{1}{2}}$, $M(\kappa, 0, 0)\to +\infty$. Therefore, by the existence theorem for roots, it is known that there exists $\tilde{\kappa}$ such that $M(\tilde{\kappa}, 0, 0) = 0.$ Using the above method, we can get $M(\kappa, \sigma_{*}, 0) = 0$ and $M(\kappa, \sigma_{*}, \bar{\tau}) = 0$.

We can choose $\omega = -\ln(M(\kappa, \sigma_{*}, \bar{\tau})+1)/\varDelta$, where $\omega > 0$, $\varDelta > \ln(2\lambda^{2})/(2\theta)$. For $t_{0}+\varDelta \leq t\leq t_{0}+2\varDelta$, we can obtain the following:

Therefore, for any positvite integer $m = 1, 2, \cdots$, when $t\geqslant t_{0}+(m-1)\varDelta$,

Thus, for $t\geqslant t_{0}+m\varDelta$,

Therefore, when $\forall t > t_{0}+\varDelta$, we have $E\| Q(t)\Vert^{2} \leqslant \exp(-\omega (t-t_{0}))\exp(\omega\varDelta)E\| \phi(t_{0})\Vert ^{2}.$ Obviously, the above formula also holds when $t_{0}\leqslant t\leqslant t_{0}+\varDelta$. Therefore, FCNNs (2.3) is ASGES.

Remark 2. Theorem 1 displays that when system (2.2) is GES, the perturbed system (2.3) can be MSGES; it is also ASGES if the bounds on the neutral terms, the stochastic disturbances, and the time delays are less than the upper bound of the estimation.

4.   Numerical examples

Example 1. We consider the following FCNNs model:

where, $a = (a_{ij})_{2\times 2} = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}, \ \ \ \ b = (b_{ij})_{2\times 2} = \begin{bmatrix} 0.02 & 0.01\\ 0.01 & 0.02\\ \end{bmatrix},$

$c = (c_{ij})_{2\times 2} = \begin{bmatrix} 0.01 & 0.02\\ 0.02 & 0.01\\ \end{bmatrix}, \ \ \ d = (d_{ij})_{2\times 2} = \begin{bmatrix} 0.02 & 0.01\\ 0.01 & 0.02\\ \end{bmatrix}, \ \ \ and\ \ \ e = (e_{ij})_{2\times 2} = \begin{bmatrix} 0.01 & 0.02\\ 0.02 & 0.01\\ \end{bmatrix}.$

Without any disturbance, (4.1) becomes the following:

Based on the principle of comparison, FCNNs (4.2) is GES when $\lambda = 1, \theta = 1.6$. When we select $\Delta = 0.3$ and $f_{j}(\cdot) = tanh(\cdot)$, then $|f_{j}(u)-f_{j}(v)|\leqslant |u-v|$ holds, so $L$ and $l$ are set as $1$. Therefore, if we let $\zeta = 0$, we can obtain $m_{1} = 1.03$ and $m_{2} = 0.09$. From Theorem 1, the following three equations can be obtained:

and

and

Thus, we can obtain $\tilde{\kappa} = 0.0175$, $\bar{\sigma}_{*} = 0.0639$, and $\bar{\tau} = 0.0261$. From Theorem 1, the perturbed FCNNs (4.1) is said to be MSGES if the coefficient of neutrality $\kappa$, the random interferences $\sigma$, and the time delays $\tau(t)$ are lower than the thresholds we deduced above, where, $\kappa \leqslant \tilde{\kappa}$, $\sigma_{*} \leqslant \bar{\sigma}_{*}$ and $\tau(t) \leqslant \min\{ \bar{\tau}, \varDelta/2\}$.

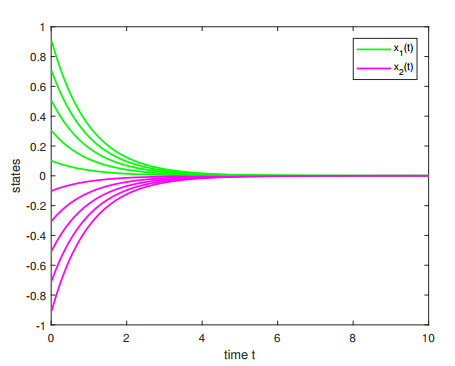
Remark 3. Figure 1 illustrates the state of FCNNs (4.1) at different initial values, where $\kappa = 0.015$, $\sigma = 0.06$, and $\tau = 0.025$. Since the neutrality coefficients, stochastic disturbance intensities, and time delays are all less than the derived bounds, the FCNNs (4.1) can be regarded as MSGES and ASGES.

Remark 4. Figures show that the cases one of the neutrality coefficient, stochastic disturbance intensity, and time delay exceeds the bounds, respectively. In Figure 2, the neutrality coefficient $\kappa = 0.03$ exceeds the given bounds, thus making it unstable. In Figure 3, the stochastic disturbance intensity $\sigma_{*} = 0.15$ clearly exceeds the given bounds; therefore, it is also unstable. In Figure 4, the time delay $\tau(t) = 0.04$, clearly exceeds the threshold; therefore, it is not stable. The parameters of Figures 1– 4 are listed in Table 1.

5.   Conclusions

In this paper, we explored the problem of the robustness analysis of the global exponential stability of FCNNs with the combined interference of three factors, namely neutral items, stochastic disturbances, and time delays. By constructing and solving the transcendental equations relevant to neutral items, random disturbances, and time delays, the upper bound thresholds for each of these disturbances were determined. These thresholds ensure that the initially stable fuzzy system continues to be stable when the perturbation intensity to which the perturbed system is subjected does not exceed these limits. Finally, we used a simulation example to verify the correctness of the derived results, thus enriching the theoretical research system of the FCNNs stabilization problem under multi-factor perturbations. In the future, we will further discuss the effects of other factors on fuzzy neural networks with neutral terms.

Author contributions

Yunlong Ma: Conceptualization, methodology, software, validation, formal analysis, writing—original draft preparation; Tao Xie: Conceptualization, methodology, validation, writing—review and editing, project administration; Yijia Zhang: Conceptualization, software, formal analysis, investigation. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.