Global robust stability of fuzzy cellular neural networks with parameter uncertainties

1.   Introduction

Fuzzy cellular neural network (FCNN) was originally proposed by Yang et al. in ^[1]. Yang et al. pointed out the differences in mathematical morphology between FCNN and CNN in ^[2]. FCNN inherits the properties of CNN well and its structure is based on the uncertainty existing in the modeling of human cognitive process and nervous system. In addition, as a result of the presence of fuzzy logic, FCNN can combine the low-level and high-level information processing capabilities of CNN to obtain better results. Moreover, researches have demonstrated the potential of FCNN for pattern detection and image processing ^[3,4].

The global stability (GS) of FCNN is a prerequisite for these applications mentioned above. However, in the process of signal processing and transmission, due to the limited communication speed of electronic equipment, there will inevitably exist different types of time delays, such as constant delay ^[5], time-varying delay ^[6], and so on, which may destroy the GS of FCNN. Consequently, it is very important to investigate the GS of delayed FCNN (DFCNN). At present, many classical methods have been applied to the GS analysis of FCNN, such as Lyapunov theory ^[7], Razumikhin-type method ^[8], and linear matrix inequality method (LMI) ^[9], etc. In addition, in ^[10], by constructing new fractional-order differential inequalities, Du et al. established numerous adequate criteria to guarantee the stability of fractional FCNN in finite time. In ^[11], Balasubramaniam et al. combined Lyapunov function method with LMI technique to investigate the global exponential stability (GES) of FCNN. In ^[12], fractional inequality techniques are used to analyze the synchronization of fractional-order FCNN in discrete time. Yao et al. used the Laplace transform method, fractional integral method, and complex functional method to propose the GES conditions applicable to fractional-order and integer-order neural networks in ^[13]. Besides, the criteria of GES of FCNN with Caputo-Fabrizio (C-F) operators can be obtained by the methods proposed by Zhang et al. in ^[14,15].

In addition, due to the imprecision of measurement and the influence of environmental factors during system operation, the deviation of parameters will also affect the GS of NNs. Thus, neural networks with parameter uncertainties have been widely studied in recent years ^[16]. An effective way to describe parameter uncertainty is to use the interval matrix principle. Besides, as an internal perturbation of the system, parameter uncertainties will affect the operating state of the system to a certain extent. Therefore, we require the designed system to have a certain robustness, that is, when the system parameters change within a certain deviation range, the system can maintain its dynamic properties. Thus it is necessary to analyze the global robust stability (GRS) of the system. In ^[17], Cao et al. discuss the global asymptotic robust stability (GARS) of a class of delayed recurrent neural networks with interval connection weight matrices by designing appropriate Lyapunov functionals and utilizing matrix norm inequalities. On this basis, new matrix norm inequalities are used in ^{[18,19,20,21]} to improve the results in ^[17], the upper bound of the interval of parameter uncertainties is extended, making it less conservative. Furthermore, Thoiyab and Senan et al. improved the norm inequalities and applied them to the GARS analysis of BAM neural networks in ^[22,23] respectively.

Moreover, it is worth mentioning that the mentioned literature above are all considered the system without fuzzy logic. Fuzziness is also a common inconvenience in modeling. Fuzzy logic is considered to be one of the most powerful tools to solve this problem. Zhang et al. analyzed the existence and uniqueness of the weak solutions of competitive neural networks with C-F operators and fuzzy logics in ^[24]. In ^[25], the GES of discrete-time almost automorphic C-F BAM neural networks with fuzzy logics is explored by the exponential euler technique. The integration of fuzzy logic in the system can describe the problem more accurately and fuzzy systems are also considered a universal approximator; thus, it is necessary to analyze the robust stability of fuzzy neural network models.

On the other hand, in ^{[17,18,19,20,21,22,23]}, only global asymptotic robust stability of the system is discussed. However, in practical application, we always hope the models we design can converge to the stable state as fast as possible. Hence, on the basis of asymptotic stability, exponential stability is proposed. Exponential stability requires that the norm of the system state is always lower than some natural exponential function, and the absolute value of its exponential part is called the decay rate of the system. The greater the attenuation rate, the faster the system stabilizes. Like asymptotic stability, exponential stability is also affected to a certain extent by perturbations within the system. Therefore, robust exponential stability (RES) analysis is essential for the application of the systems. Hence, in ^[26], Niculescu et al. discuss the RES of uncertain systems first. Lan et al. investigated the synchronization and stability of multiple-delayed BAM neural network with interval uncertainties in ^[27] and ^[28]. However, these literatures do not take into account the influence of fuzzy logics.

Therefore, based on the above discussions, the major works and contributions of this paper are as follows:

$(1)$ The model of delayed fuzzy cellular neural networks with parameter uncertainties, which is described by interval matrices, is proposed in this paper.

$(2)$ Using norm inequality method, Lyapunov-Krasovskii method, and mathematical analysis method, the existence and uniqueness of equilibrium solution of the proposed model are analyzed, and sufficient conditions for global robust asymptotic stability of the system are obtained.

$(3)$ In the absence of external control, the sufficient conditions for the existence and uniqueness of the system solutions are obtained, and the global robust asymptotic stability of the system is analyzed. In addition, based on the obtained conditions, the robust exponential stability of the system is further analyzed, and the delay dependent sufficient conditions are obtained.

Finally, we give the organizational structure of this paper. In Section 2, the model we used as well as the assumption and lemmas we needed are given. In Section 3, we obtain the existence and uniqueness (E & U) of UDFCNN equilibrium solutions and the GARS of UDFCNN by constructing Lyapunov functions and using different norm inequalities. In Section 4, on the basis of the works in Section 3, we further study the GERS of UDFCNN, and give some sufficient conditions for the GERS of UDFCNN. Several examples are given in Section 5 to validate the results.

Notations: $|\cdot|$ represents the Euclidean norm. $||W||_2 = \sqrt{\sum_{v = 1}^rw_v^2}$, where $W = \{w_1, \dots, w_r\}^T\in \mathbb{R}^r$. $||A||_2 = \sqrt{\lambda_{\max}(A^TA)}$, where $A = (a_{vw})_{r\times r}\in \mathbb{R}^{r\times r}$ and $A^T$ is the transpose of $A$. Besides, for vector $W\in\mathbb{R}^r$, we denote $|W|_a = \{|w_1|, \dots, |w_r|\}^T\in \mathbb{R}^r$. For matrix $A = (a_{vw})_{r\times r}$, we denote $|A|_a = [|a_{vw}|]_{r\times r}$. $\lambda_{\rm max}(A)$ and $\lambda_{\rm min}(A)$ represent the max and min eigenvalues of $A$ respectively.

2.   Preliminaries

The model of UDFCNN we considered is shown below:

where $q^0_v(t)$ is the initial value function; $c_v > 0$ represents the passive decay rate of $v$th neuron; $a_{vw}$ is the connection weight matrix; $e_{vw}$ and $h_{vw}$ are fuzzy feedback MIN template and fuzzy feedback MAX template respectively; $d_{vw}$ and $m_{vw}$ are the fuzzy feed-forward MIN and MAX template respectively; $\bigwedge$ and $\bigvee$ represent fuzzy AND and fuzzy OR operations respectively; $\rho_w(\cdot)$ is activation function; $q_v(t)$, $u_w$ and $N_v$ are the state, input and bias respectively; $\tau_w$ is a constant delay. Besides, the parameters of UDFCNN (2.1) satisfy the following conditions:

Assume the equilibrium point of UDFCNN (2.1) is $q^\ast$, where $q^\ast = \{q_1^\ast, \dots, q_r^\ast\}$. Let $z_v = q_v-q_v^\ast$, then, the equilibrium point of UDFCNN (2.1) is shifted to origin, and the following model is the altered UDFCNN:

where $\psi_w(z_w(\cdot)) = \rho_w(z_w(\cdot)+q_w^\ast)-\rho_w(q_w^\ast)$, and $\psi_w(0) = 0$.

In order to obtain our main results, we make the following assumption:

Assumption A1. There exist $L_w > 0$ and $\zeta_w > 0(w = 1, \dots, r)$ such that

where $\Omega$ and $\omega$ are the states of UDFCNN (2.3).

Remark 2.1. According to Brouwer's fixed point theorem, if the activation function is limited, the neural network will always have an equilibrium point. Nevertheless, if the activation function is not limited, we cannot always ensure that the equilibrium point of neural network exists ^[18].

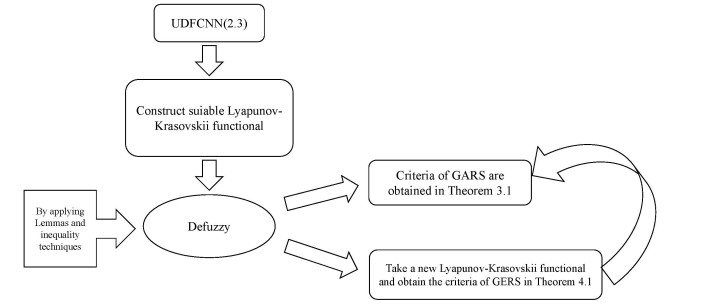
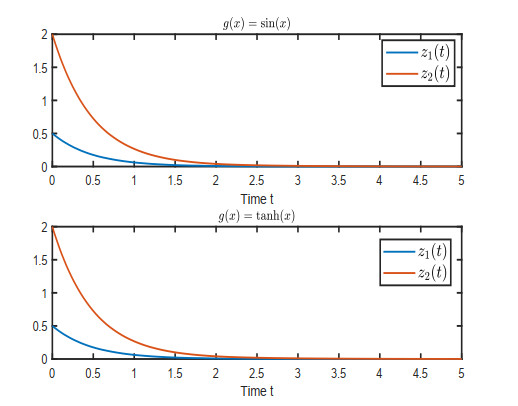
Remark 2.2. Different activation function choices will cause different state responses of the system. For example, consider the following neural network model:

where $A = [-1.0615, -0.6156;2.3504, 0.7480]$, $B = [-0.1924, -0.7648;0.8886, -1.4022]$. We take the activation function $f(\cdot)$ as $sin(\cdot)$ and $\tanh(\cdot)$, respectively. Then, we can find that Assumption A1 is satisfied. However, we can find that the state response of the model is completely different in Figure 1.

Besides, the following Lemmas are needed for getting our main results:

Lemma 2.1. ^[29] Assume $\Omega$ and $\omega$ are the states of UDFCNN (2.1), then

Lemma 2.2. ^[23] For any vectors $u = \{u_1, \dots, u_r\}^T$ and $v = \{v_1, \dots, v_r\}^T$, there must be a positive constant $\sigma > 0$ such that

For any matrix $K\in[\underline{K}, \overline{K}]$, we denote that $K^\ast = \frac{1}{2}(\underline{K}+\overline{K})$ and $K_\ast = \frac{1}{2}(\overline{K}-\underline{K})$, then we have the following lemmas.

Lemma 2.3. ^[22] For any matrix $K\in [\underline{K}, \overline{K}]$, the following inequality holds,

Next, we introduce the definitions of GARS and GERS respectively.

Definition 2.1. ^[17] UDFCNN (2.3) satisfies the conditions (2.2) is GARS, if the unique equilibrium point of UDFCNN (2.3) is globally asymptotically stable (GAS).

Definition 2.2 ^[26] UDFCNN (2.3) is GERS, if there are $\alpha, \beta > 0$ such that

holds, where $\hat{\delta} = \max_{1\le v\le r}\overline{\delta_v}$. That means for any decay rate $\beta$, the equilibrium solution of FCNN is GES for all admissible uncertainties.

3.   Global asymptotic robust stability result

In this part, some criteria for E & U of the solutions of UDFCNN (2.3), and the GARS of UDFCNN (2.3) is explored by choosing suitable LKFs.

Theorem 3.1. Let Assumption A1 hold, and exists $\sigma > 0$ such that

holds, where $||A||_0^2 = \lambda_{\rm max} (|{A^\ast}^TA^\ast|_a+2A_\ast^T|A^\ast|_a+A_\ast^TA_\ast)$. Then, UDFCNN (2.3) is GARS and origin is the unique equilibrium point.

Proof. First and foremost, we demonstrate that the equilibrium point of UDFCNN (2.3) is unique. Let $z^\ast = \{z_1^\ast, \dots, z_r^\ast\}^T\neq 0$ is the equilibrium point of UDFCNN (2.3), then,

We multiply (3.2) by $2z_v^\ast$, we have

Then, from Lemmas 2.1–2.3,

Let $\Delta_{vw} = |e_{vw}|+|h_{vw}|$, then from (2.2), we can get that

where $\overline{\Delta_{vw}} = \max\{|\overline{e_{vw}}|, |\underline{e_{vw}}|\}+\max\{|\overline{h_{vw}}|, |\underline{h_{vw}}|\}$. Thus, we can obtain that $\Delta^\ast = \Delta_\ast = \frac{1}{2}\overline{\Delta}$, and $||\Delta||_2^2\le 4\lambda_{\rm max} ({\Delta^\ast}^T\Delta^\ast) = 4||\Delta^\ast||_2^2 = ||\overline{\Delta}||^2_2$.

Furthermore, let $||A||_0^2 = \lambda_{\rm max} (|{A^\ast}^TA^\ast|_a+2A_\ast^T|A^\ast|_a+A_\ast^TA_\ast)$, where $A^\ast = \frac{1}{2}(\underline{A}+\overline{A})$ and $A_\ast = \frac{1}{2}(\overline{A}-\underline{A})$, we have

And,

Then, we have

Hence, (3.7) is in conflict with (3.1), therefore, UDFCNN (2.1) has no other equilibrium point expect origin.

Next we will prove that UDFCNN (2.3) is GARS. Consider the following LKF:

Take the derivative of $V(z(t))$ with respect to $t$, we can obtain

Similarly,

Therefore,

From (3.1), we can observe that $\dot{V}(z(t)) < 0$, when $z_v(t)\neq 0$. Thus, based on the Lyapunov theory, the origin of UDFCNN (2.3) satisfying condition (2.2) is GAS. Therefore, the UDFCNN (2.3) satisfying the conditions (2.2) is GARS. □

Remark 3.1. Compared with previous results in ^[30,31], the results obtained by us are not affected by time delays. In other words, no matter how big the delays are, the system can always reach GARS as long as the assumptions and sufficient conditions are satisfied. Therefore, the method used in this paper reduces the complexity of the analysis of stability to a certain extent.

4.   Global exponential stability result

Based on the LKFs in Theorem 3.1, the GERS is further discussed. Hence, we further have the following Theorem.

Theorem 4.1. Let Assumption A1 hold, and $\exists\; \sigma > 0$ such that

holds, then, the UDFCNN (2.3) which satisfying the condition (2.2) is GERS.

Proof. Take $W(z(t)) = \exp(2\beta t)V(z(t))$, where $V(z(t))$ is as same as we defined in Theorem 3.1. Thus, we have

Hence, according to the mean value theorem of the integral, there exists a $s\in[t-\overline{\delta_v}, t]$ such that

Then,

where $M = \max\limits_{1\le v\le r}\biggl(1+\frac{\overline{\delta_v}L_v^2}{\sigma}\biggr)$. Therefore, $V(z(t))\le M\exp(-2\beta t)\sup\limits_{s\in[-\hat{\delta}, 0]}||z(s)||^2_2$.

Since $||z(t)||_2^2\le\sum_{v = 1}^r z_v^2(t)\le V(z(t)) = \sum_{v = 1}^r z_v^2(t)+\frac{1}{\sigma}\sum_{v = 1}^r\int_{t-\tau_v}^{t}\psi_v^2(z_v(\eta))d\eta$, hence,

Therefore, UDFCNN (2.3) which satisfying the condition (2.2) is GERS. □

Remark 4.1. It can be seen from Theorem 4.1 that under a certain decay rate, the GERS of the fuzzy neural networks with uncertainty coefficients is related to the size of the delay. In addition, the attenuation coefficient $\alpha$ is also related to the time delay.

Remark 4.2. The steps of analysis of this paper are given in Figure 4.3. From (3.1) and (4.1), we can find that if the system parameters satisfy the conditions of Theorem 4.1, the conditions of Theorem 3.1 must also be satisfied, which reveals the relationship between asymptotic stability and exponential stability.

Remark 4.3 There is a brief comparison between existing literatures and this paper in Table 1. The elements of the comparison are fuzzy logic (F-L), time delays (TDs), GARS, GERS, parameter uncertainties (UP), LMI, and inequality techniques (IT).

5.   Examples

To validate our results, we provide two numerical examples in this part.

Example 5.1. The parameters we considered are as follows:

where $a > 0$.

Hence, we can calculate that

Let $L_v = 1$, $\sigma = 2$, then, from Theorem 3.1, we have

Therefore, we can get $a^2 < \frac{3}{543.8275}$, i.e., $a < 0.0743$. That is, Theorem 3.1 is satisfied when $a < 0.0743$.

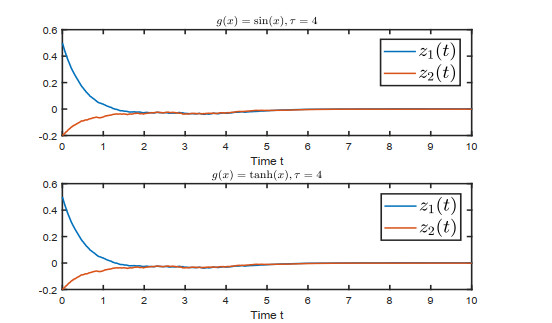
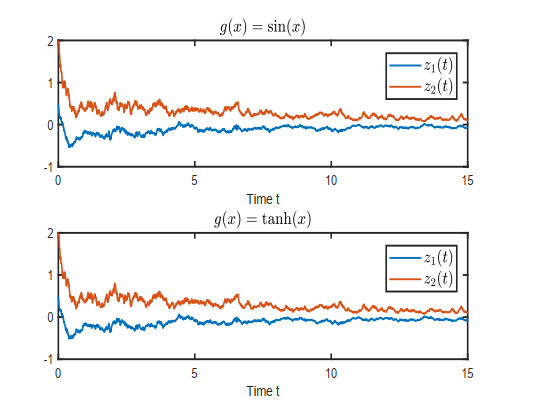
We take $a = 0.06$, and Figures 3 and 4 show the states of UDFCNN (2.3) with different bounded activation functions and parameters satisfy the conditions (5.1). It can be seen that when the parameter uncertainty satisfies the conditions of Theorem 3.1, the system can converge to its equilibrium point and maintain its global asymptotic robust stability. Besides, as can be seen from Figures 3 and 4, as long as the conditions of Theorem 3.1 are satisfied, no matter how big the time delay is, the system maintains global asymptotic robust stability.

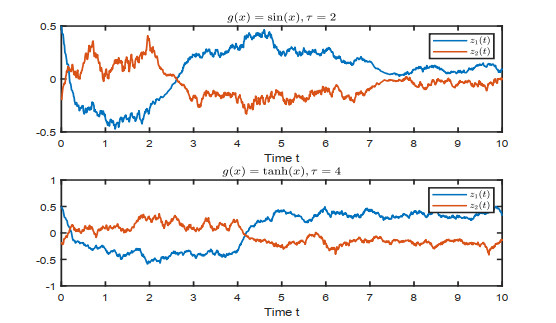
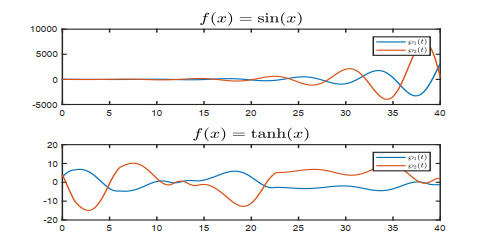
Furthermore, in Figure 5 when $a = 3$, we can observe that the system can not converge to the equilibrium point. This also illustrates the validity of our results.

Example 5.2. In this example, we take the same system parameter values as in Example 5.1. In addition, according to Theorem 4.1, it can be seen that the GERS of the system is related to the delay and the decay rate; thus, in this example we take $\underline{\delta} = a[0, 2]^T$, $\overline{\delta} = a[1, 3]^T$. Let $\alpha = \sqrt{M}$, $\beta = 1.1$. Then, we have,

Calculating by Matlab, we can obtain that $a < 0.0364$. Therefore, if $a < 0.0364$ holds, then the sufficient conditions of Theorems 4.1 is satisfied, i.e., the UDFCNN (2.3) which satisfies the condition (2.2) is GERS.

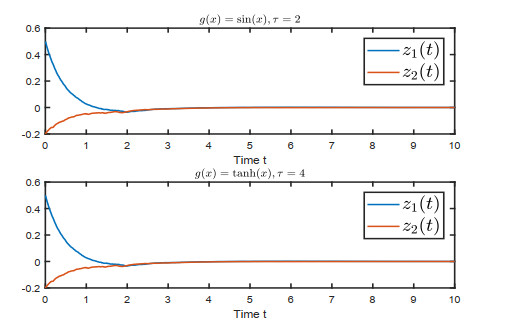
We take $a = 0.02$, then we can obtain that $\tau_1\in[0, 0.02]$, $\tau_2\in [0.04, 0.06]$. Hence, UDFCNN (2.3) with parameter uncertainty is GERS when the variation range of time delay are satisfied. Figure 6 shows the states of UDFCNN (2.3) with uncertain time delay $\tau_w$ and different bounded activation functions, respectively. It can be seen that when the conditions of Theorem 4.1 are satisfied, the equilibrium point of the system is exponentially stable, which means that the system with uncertain parameters is globally exponentially stable.

Figure 7 shows the states of UDFCNN (2.3) with different activation functions under $a = 5$, and we can find that when $a = 5$, the system cannot converge to its equilibrium point, and the system is not exponentially stable, so the system is not globally exponentially robust stable.

Remark 5.1. Compared with the literatures ^{[17,18,19,20,21,22,23]}, this paper considers fuzzy logics in the system. Because of the existence of fuzzy logics, the systems considered in this paper are more widely used. In addition, we further explore the sufficient conditions for the system to maintain robust exponential stability on the basis of robust asymptotic stability, which is different from the known results.

Remark 5.2. In this paper, we use the norm inequality method to obtain sufficient conditions for the robust asymptotic stability of the system. Compared with the LMI method used in ^[27], the results obtained in this paper are easier to verify. Besides, we explore the effect of interval system parameters on the robust exponential stability of the system without adding additional controls, which is different from the literature ^[28].

6.   Conclusions

In this paper, the robust asymptotic and robust exponential stability of delayed fuzzy cellular neural networks are analyzed. We found that the robust asymptotic stability of the system is independent of the time delays and related only to the uncertainties of system parameters, while the robust exponential stability of the system is related to the uncertainties of the time delays. When the uncertainties of time delays of the system are less than the deduced result, the system will not be able to maintain robust asymptotic stability. Finally, we give several examples to verify our results. Future studies can continue to consider the impact of environmental noise on the global robust stability of the system and estimate the maximum disturbance intensity that the system can withstand to maintain stability. Besides, new norm inequalities can be applied to reduce the conservatism of this paper.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported by the Guiding Project for 2023 of Scientific Research Plan of Hubei Provincial Department of Education, the Open Subject for Teacher Education Research of Hubei Normal University (Grant No. 2022TEZ06), Scientific Research and Development Program of Hubei University of Science and Technology (Grant No. 2021-22X20), and the Philosophy and Social Science Research Project of Hubei Provincial Department of Education (Grant No. 23Y122).

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.