Robustness analysis of stability of Takagi-Sugeno type fuzzy neural network

1.   Introduction

Augmented Reality (AR) and Virtual Reality (VR) are emerging technologies with enormous potential for use in the medical field and particularly in novel therapies, diagnostics, and delivery methods ^[1]. Medical AR and VR have the potential to improve the execution of real-time procedures, as well as test results, in a simulated setting ^[2]. Their capacity to remotely transmit conventional and unique knowledge in immersive and realistic ways in a range of clinical scenarios is the key to their potential in diagnosis and therapy.

AR and VR are applied in several medical sectors, such as pediatric diagnostics and treatments, pain management, mental health, neurology, surgery planning, post-operative care, and other rehabilitation therapies. With the objective of achieving real-time guidance, there is substantial need for a fast method for imaging and classification. Recent advances in the field of AR have shown that this technology is a fundamental part of modern interactive systems for the achievement of a dynamic user experience. AR aims to integrate digital information with the user's environment in real time.

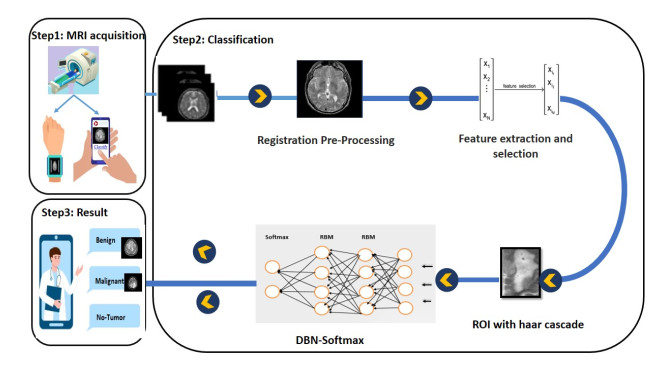
The application of AR to the problem of brain tumors may take place in two stages: the first stage may involve the devices themselves, while the second stage may involve the collection of MRI images directly from patients to see tissue segmentations in real time. The second stage, it refers to the automatic decision-making process. This study discusses the second step after the magnetic resonance imaging (MRI) scan. We use MRI classification to assist doctors in making decisions.

Due to the irregular development of cells inside of the brain, brain tumors have serious effects on their victims. These tumors are dangerous because they can interfere with legitimate mental work. Brain tumors can be classified as either benign or malignant, as noted by the authors of ^[3]. Benign tumors are more stable than malignant tumors; particularly, while malignant tumors are destructive and spread rapidly, benign tumors develop more slowly and are less harmful ^[4,5].

Physicians and radiologists spend much of their time analyzing test results and scanning images, which is very time-consuming. The interpretation of these images depends on the judgment and experience of the individual physician. Medical image processing and analysis in the AR field can solve these problems; therefore, this field offers several different research directions ^[6]. MRI has attracted more attention from medical researchers in recent years. MRI is a medical imaging technique that is mainly used in medicine, especially in radiology, to study internal structures of the human body, such as internal organs, the brain, bones, joints, the heart, blood vessels, etc. MRI technology is considered a type of scan that uses powerful magnets and radio waves to produce detailed images from inside of the body ^[7]. In the brain, MRI can show details of blood flow and fluids around the brain to enable visualization of the tumor and the process of tumor remodeling. The results of an MRI scan can help one to determine abnormalities in the brain.

With the recent adoption of new modern healthcare technologies and the explosion of deep learning applications, many innovative deep learning techniques have been proposed to improve the performance of MRI image processing, particularly with the increasing availability of medical image data ^[8,9]. These techniques have tremendous potential for medical image processing, including medical data analysis and diagnosis. In MRI, deep learning techniques have generally focused on image acquisition, image processing ^[10], segmentation, and classification ^[11]. Several deep learning models are increasingly used in medical image analysis to improve the efficiency of disease diagnosis ^{[12,13,14,15]}, particularly in the detection of brain tumors ^[16]. Convolutional neural network (CNN)-based architectures have been successfully applied to a variety of medical applications, including image recognition ^[17,18], classification ^[19], and segmentation ^[20,21]. The CNN model has shown promising performance on the task of classifying brain tumors into three prominent types: gliomas, meningiomas, and pituitary tumors ^[22,23]. Brain tumors are the most aggressive disease worldwide. Computer-aided diagnosis (CAD) systems are widely used to detect abnormalities of the brain. The aim of this study was to develop an automatic CAD system to classify brain tumors. In this paper, we propose a new classification technique that uses deep belief networks (DBNs) to classify MRI images of brain tumors. Therefore, before classification, we use linear model registration as a preprocessing step to improve our datasets. Registration is an important issue for various medical image analysis applications, such as motion correction, remote sensing, and cartography. As a result, we highlight the transformation that best overlays two images. Thus, the main purpose of our work was to apply a registration method to the input data and then classify the MRI images of brain tumors as malignant or benign while maintaining high classification performance, especially for different types of brain tumors. All of these techniques are based on a hybrid system combining a DBN with softmax (DBN+softmax).

Following is the structure of the remaining parts of this paper: Within the second section, we investigate the most recent classification methods that are pertinent to the diagnosis of brain tumors. In the third section, we will discuss the structure of our brain tumor classification model. Within the fourth section, we will examine the outcomes of the experimental evaluation of our classification model, as well as provide an analysis that corresponds to those results. The final remarks and a discussion of the work that will be done in the future are offered in Section 5.

2.   Related work

Solutions provided by the application of virtual environments and related technologies are explored by medicine and gradually introduced into everyday clinical practice ^[24,25]. The technological revolution of virtual and augmented environments has huge potential in the health care field. In particular, AR/VR technologies have the potential to assist us in the health care field by improving surgical interventions and image-guided therapy ^[26].

Several studies have explored AR/VR in the field of brain tumor surgery by providing clinicians with interactive, three-dimensional visualizations at all stages of treatment ^[24,27,28]. The authors of ^[29] studied the use of AR/VR technologies. They not only proved that these technologies can visualize the tumor structure, they also showed its detailed relationship to anatomical structures.

A growing number of medical systems based on machine learning and deep learning have been proposed for medical imaging tasks, such as medical data classification, segmentation tasks, medical diagnosis, therapy action prediction, and health care in general ^[30]. In particular, the application of machine learning and deep learning techniques have great potential for brain image analysis ^[31]. These techniques have been extensively applied to MRI brain images for the early detection, diagnosis, and automatic classification of brain tumors ^[32,33].

In this section, we review state-of-the-art machine learning and deep learning approaches for the diagnostic classification of brain tumor related diseases.

2.1.   Machine learning-based classification models of brain tumors

A variety of machine learning methods have been applied in MRI image processing, segmentation, and classification. The use of these methods has been shown to be very powerful for tumor diagnosis. Several machine learning classification methods, including k-nearest neighbor ^[34], decision tree algorithms, naïve bayes ^[35], and support vector machines (SVMs) ^[36], were evaluated with the indicated CNN model ^[37].

Using the fuzzy Otsu thresholding morphology methodology, Wisaeng and Sa-Ngiamvibool ^[38] introduced a novel method for segmenting brain tumors. This method was developed by the two researchers. By applying a color normalization preprocessing technique, along with histogram specification, the retrieved values from each histogram in the original MRI image were modified. Images of gliomas, meningiomas, and pituitaries have average accuracy indices of 93.77 percent, 94.32 percent, and 94.37 percent, respectively, according to the findings, which establish, without a doubt, that these are the cases.

In ^[39], the authors proposed a deep generative model for MRI-based classification tasks. They proposed two training methods based on constrained Boltzmann machines, where the first method is fully generative, and the second method is discriminative. They defined an early-late discrimination method to see if the learning approach could detect brain characteristics that discriminated between pre- and post-recovery scans. They found that the generative training-based method produced better results for the early and late processes than the discriminative training-based method.

The authors of ^[7] proposed a technique in which a tumor is classified as one of two types, i.e., "malignant" or "benign". Their model uses the discrete wavelet transform for feature extraction and employs a SVM for classification. The SVM proved to be the best-performing algorithm in terms of accuracy and consistently outperformed the other classification algorithms in this regard. Moreover, the authors of ^[40] proposed a new technique to determine whether a tumor is cancerous or non-cancerous. "Cancerous" means that the tumor is malignant, while "non-cancerous" means that it is benign. Portions of the tumor images were extracted via segmentation. The authors also used a median filter to remove background noise. Their model applies an SVM and a classification and regression tree, acheiving 92.31% accuracy. In the same context, the authors of ^[41] proposed a classification technique with wavelet pooling. They found that wavelet pooling gave better results than other pooling techniques. They obtained good results, but the time cost was high. We cannot determine which pooling method is better because this depends on several parameters, such as the dataset and the number of levels used in the different models. The authors of ^[42] proposed a technique that uses an SVM to classify gliomas into subtypes; they achieved an accuracy of 85% for multi-classification and 88% for binary classification. Also, in ^[43], the authors proposed a model based on an SVM for brain tumor classification and compared two CNN models to determine which would provide the best results.

An improved SVM was proposed by Ansari ^[44] as a novel approach. In order to identify and categorize brain cancers using MRI data, they suggested the following four steps: preprocessing, segmentation of images, extraction of features, and picture categorization. A fuzzy clustering approach was utilized in order to partition the tumors, and GLCM was utilized in order to extract the important features. Improvements to the SVM were finally included during the classification step. There was an accuracy rate of 88% with the strategy that was provided.

The SFCMKA technique was presented in ^[45] to distinguish between stable and defective brain tissue. By combining the spatial equation with the FCM method and applying the k-means algorithm, this strategy reduces the noise in the data. By utilizing an enhanced binomial threshold, the authors of ^[46] made the discovery of multi-feature selection for the purpose of brain tumor segmentation. During the preprocessing stage, a Gaussian filter is utilized, and, during the segmentation stage, an enhanced thresholding system that incorporates morphological processes is utilized. Afterward, a serial method is applied for the purpose of combining derived geometric aspects with Harlick characteristics. During the last stage, the best features from the fused vector are chosen with the help of a GA, and then classification is carried out with the assistance of LSVM.

Through the use of MRI images, Babu et al. ^[47] described an approach that aimed to classify and segment brain tumors. Denoising the image, segmenting the tumor, extracting features, and hybrid classification are the four procedures that make up the technique. After utilizing the thresholding approach to remove malignancies from brain MRI images, they applied a wavelet-based method to extract characteristics from the images. A CNN was utilized in order to carry out the ultimate hybrid categorization. According to the results of the experiment, the method had an accuracy of 95.23 percent when it came to segmentation; however the optimized CNN that was suggested had an accuracy of 99 percent when considering classification.

The authors of ^[48] developed a hybrid technique to effectively identify tumor locations and categorize brain tumors. This technique includes preprocessing with thresholding, morphological methods, and watershed segmentation, as well as postprocessing with watershed segmentation. Segmented MRI images are used to extract GLCM features from the tumor.

2.2.   Deep learning-based classification models of brain tumors

In recent years, complex and quaternion-valued neural networks have gained importance in various applications. Thus, the field of deep learning has evolved and produced more effective methods for neural network formation. Several studies have used deep learning techniques for image reconstruction, magnification, and transformation ^[49]. Other studies have entailed disease detection or diagnosis and medical image segmentation through the use of various neural network architectures ^[50]. In addition, deep learning in MRI has been applied to more complex tasks, including brain tumor identification and disease progression prediction.

The fundamental goal of MRI brain classifiers is to extract relevant and meaningful features. As a result, several methods have been proposed to extract magnetic resonance image features ^[51]. Most of these methods use artificial neural networks for feature selection from medical images ^[52]. The authors of ^[53] proposed a new feature extraction method for classifying different types of brain tumors in DICOM format T2-FLAIR MRI images. The proposed feature extraction method incorporates processing techniques to accurately distinguish benign and malignant tumors. A spatial filtering process is used to remove unwanted information and noise. CNNs are known for their ability to extract complex features and learn meaningful characteristics of medical images ^[54]. Following the success of CNNs a variety of feature extraction methods have been proposed to automatically extract image features. However, these feature extraction methods are not adaptable to segmentation problems ^[55]. The authors of ^[56] proposed a new feature extraction method based on a CNN. As result, the set of extracted features is then combined with the set of handcrafted features. They used the modified gray level co-occurrence matrix method to extract handcrafted textural features. In order to enhance the classification process for MRI brain images, the results of the experiments were used to demonstrate that the greatest yields were obtained by combining the features that were handcrafted with the characteristics that were learned by using deep learning.

An intelligent medical decision-support system was proposed by Hamdaoui and colleagues ^[57] for the purpose of finding and classifying brain cancers by making use of images from the risk of malignancy index. In order to circumvent the limited amount of training data that was necessary for the construction of the CNN model, they utilized the principles of deep transfer learning. In order to accomplish this, they chose seven CNN architectures that had previously been trained on an ImageNet dataset. These designs were then meticulously fitted on MRI data of brain tumors that were obtained from the BRATS resource.

In addition, the authors of ^[58] proposed a DBN-based classification model with an unsupervised preprocessing technique. The proposed preprocessing technique combines the Kolmogorov-Smirnov statistical transform and the wavelet transform to extract the most representative features. The experimental results show that using the proposed preprocessing technique before applying the DBN improves the classification performance. Traditional neural networks that train with deep layers require many training datasets, which leads to poor parameter selection. To solve this problem, DBNs were invented. DBNs are effective because they use a generative model. A DBN is a hierarchy of layers, and like all neural networks, it learns labels that can be used to refine its final layers under supervised training, but only after the initial phase of unsupervised learning. In this context, the authors of ^[59] developed a system whose first stage included a multiscale DBN and a Gaussian mixture model that extracts candidate regions.

In ^[60], the authors developed a DBN as an enhancer, which they constructed from two restricted Boltzmann machines (RBMs). The first RBM had 13 visible nodes, and there were eight nodes in each hidden layer for both RBMs. The enhancer DBN was trained with a backpropagation neural network and predicted lung cancer with an acceptable degree of accuracy, achieving an average F value of 0.96.

In addition, the authors of ^[61] used a probabilistic fuzzy c-means algorithm to identify significant regions in brain images. The segments were processed by using the local directional pattern to extract textural features. The features were then fed into the DBN classifier, which classified the images as either "normal" or "abnormal" to indicate the presence or absence of tumors in each MRI image. The proposed method achieved 95.78% accuracy.

The author of ^[62] submitted a proposal for a completely automated system that would be capable of segmenting and diagnosing brain tumors. To do this, the magnetic resonance image undergoes five preprocessing techniques, followed by a discrete wavelet transform, and, ultimately, six local attributes are extracted from the image. Following this, the photos that have been processed are sent to a neural network, which then proceeds to extract higher-order properties from them. The features are then concatenated with the initial MR image after being weighed by a different deep neural network. The data that have been concatenated ae then loaded into a hybrid U-Net, which is used to segment the brain tumor and classify it.

An enormous step forward in the areas of image identification, segmentation, and classification is represented by the CNN. The main advantage of CNNs is that the preprocessing process and the feature engineering, or feature extraction, do not have to be performed. The authors of ^[63] proposed a model by using a CNN for brain tumor identification. Their model consisted of a total of 16 layers and achieved a maximum accuracy of 96.13%. The first half of their work focused on tumor identification, and, in the second half, they divided tumors into three different subtypes. Their model achieved 100% accuracy for two subtypes and 95% for the third subtype.

A novel CNN architecture for the categorization of brain tumors was presented by the authors of ^[64]. The meningioma, the glioma, and the pituitary tumor were the three types of tumors that were utilized in the classification process. Two 10-fold cross-validation approaches, namely, the record-wise method and the subject-wise method, were utilized in order to evaluate the performance of the suggested network. These methods were applied to two databases called the original picture and the augmented image. In order to achieve the best possible outcome, it is necessary to combine the record-wise procedure with the enhanced dataset.

In addition, the authors of ^[65] proposed a novel DBN-based approach for brain tumor classification. In this approach, all images are segmented by using a segmentation model that combines Bayesian fuzzy clustering and the active contour model. The DBN classifier is trained by using the features obtained during segmentation. The segmentation-based model achieves good brain tumor classification performance. In another study ^[66], the authors proposed a method that is relevant to our topic. Their work was based on brain tumor image segmentation and involved several steps. To improve the performance of DBNs in classification, they used three steps. They used a denoising technique to remove insignificant features in the first step. Then, they used an unsupervised DBN to learn the unlabeled features. The resulting features serve as input to the classifier, which achieved a classification accuracy of 91.6%.

Through the application of an effective hybrid optimization technique, the classification of brain tumors was successfully performed ^[67]. In order to develop a more effective categorization procedure, the CNN characteristics were extracted. The recommended chronological Jaya honey badger algorithm (CJHBA) was applied in order to train the deep residual network (DRN), which was then used to carry out the classification procedure by making use of the retrieved features as input. This took place after the DRN had been trained. Within the framework of the suggested CJHBA, both the Jaya algorithm and the honey badger algorithm have been applied. The chronological concept have also been incorporated into the discussion. Moreover, the authors of ^[68] proposed a new diagnostic system for breast cancer detection based on a DBN that employs an unsupervised pre-training phase, followed by a supervised backpropagation phase. The proposed DBN achieved better classification performance than a classifier using only a supervised phase. The proposed DBNs based on two phases are the closest to our current proposal, although with some limitations. Although the above DBN can provide better results, the initialization of the weights is still time-consuming. We tried to solve this problem by classifying the region of interest (ROI) within each brain tumor rather than the whole image.

A new transfer deep learning model was designed by the author of ^[69] with the purpose of integrating the early diagnosis of brain malignancies into their many classifications, which include meningioma, pituitary, and glioma, among others. This model was designed with the purpose of making it simpler to diagnose brain cancers at an earlier point in their progression. Multiple layers of the models were initially developed from scratch in order to determine whether or not solo CNN models are beneficial when applied to brain MRI images. This was done for the purpose of determining whether or not the models are useful. Following that, the weights of the neurons were modified by employing the transfer learning technique in order to classify brain MRI images into tumor subclasses by utilizing the 22-layer, isolated CNN model. This was done in order to achieve the goal of classifying the images. In order to successfully complete the classification of the photos, this was carried out. As a direct result of this, the transfer-learned model that was developed had an accuracy rate that was determined to be 95.75%.

3.   Proposed classification model for brain tumors

Within the following paragraphs, we will discuss the classification model that we have presented for brain cancers. We also detail the specific selections and hyperparameter settings that lead to its optimal performance. This is done for the sake of transparency.

3.1.   Classification model architecture

Figure 1 illustrates an AR scenario in the medical field. In this paper, we focus on the classification step. We propose a software step-level approach for brain tumor classification, and we validate our approach by using 2D MRI databases. In the first step, we use an abnormal brain tumor as input for the proposed classification model. Then, we proceed to the preprocessing step, where we use a global affine transformation for registration. We pruned the ROI by using the Haar cascade. This required us to (1) know of the existence of the tumor, (2) zoom in on the tumor, and (3) manually label the tumor. Finally, we classify the tumor by using a hybrid system combining a DBN with softmax (DBN+softmax). The architecture of the classification is shown in Figure 1.

3.2.   Preprocessing with registration

Registration is a digital process that consists of transforming the reference image to make it more similar to the target image ^[70]. In image processing, registration is used for image matching to allow researchers to compare or combine their respective data ^[71], as it allows the user to match two sets of images. It is possible for these sets to consist of two examinations of the same patient or one examination and one photograph in the context of the medical field. In the process of deformable template estimation and similarity detection, spatial alignment or registration between two pictures is a fundamental component ^[72].

Because of this, alignment often consists of two stages: a global affine transform and a deformable transform. The affine transformation is the primary emphasis of this work, and we make use of it. In the field of computational neuroanatomical analysis, the linear model and global affine transforms have been utilized extensively due to their inherent properties of topological preservation and invertibility. Linear model approaches use supervised, unsupervised, or semisupervised environments to develop a network that computes the transformation field. These environments can be either supervised or unsupervised (i.e, using classical energy functions). The registration of an image with an existing template has been accomplished with the help of these methods. We differentiate between the linear models that combine rigid and affine transformations, which are among the several models of affine transformation that have been proposed in the existing body of literature.

In affine registration, only parallelism is preserved ^[73]. In addition to the rotations and translations, it allows the addition of an anisotropic scaling factor and takes into account the shear forces:

where Ais the arbitrary matrix of dimension n x n.

Our method of image registration is recalibrated by the cue point, which requires the use of reference markers. Registration of the reference markers ensures registration of the entire image, provided the object remains fixed relative to the markers during scanning. To achieve valid image registration, the images were acquired with reference markers, as shown in Figure 2. The reference markers were used to test the accuracy of the registration. In this algorithm, we performed affine registration with a reference marker. This method is also applicable to the geometric approach, which allows us to align the benchmarks. The affine transformation includes a translation, a rotation, a scale, and the parameters ^[73]. Next, the program selects the number of reference markers to be used for the realignment.

It automatically selects the number of control points and the positions of the corresponding pairs of markers in the target and reference Figure 2(b). The point mapping or control point is used to determine the parameters of the transformation required to match one image with another ^[74]. Point mapping requires that the selected points in an image pair represent the same feature or landmark in both images. This is easily accomplished because the program can place the markers on all centroids in the image. The affine registration steps are shown in Figure 2.

A transformation is called "rigid" if rotation and translation are considered independently. Rigid and refined transformations are used in rigid registration, which is the process of geometrically transforming the source image to match the target image. The deformation in rigid registration is the same throughout the image ^[75]. This is considered as the first step in non-rigid registration.

3.3.   Haar cascading

Concatenating many classifiers and using all of the information gained from the output of a given classifier as extra input for the next classifier within the cascade is the basis for Haar cascading, which is a subtype of ensemble learning. Haar cascading is a special example of ensemble learning. In order to train cascading classifiers, several hundred "positive" sample views of a certain object and any "negative" photos of the same size are introduced into the training process. In our case, the MRI images of the brain contained the optimistic perspectives. After it has been trained, the classifier can be applied to a specific area of an image in order to identify the ROI and crop it to a different size. Moving the search window over the image allows us to check each position for the classifier. This allows us to find the best possible results.

There are four stages that can be used to illustrate the algorithm:

1. Haar features are being calculated.

2. Developing images that are integral.

3. It is using Adaboost.

4. Cascading classifiers are being implemented.

3.3.1.   Calculating Haar features

The first thing that needs to be done is acquire the Haar characteristics. In its most basic form, a Haar feature is a set of calculations that are applied to neighboring rectangular regions at a particular position within a detection window. To complete the calculation, first add up the intensities of the pixels in each region, and then determine the differences between the sums of those intensities. In what follows, you will find several examples of Haar features. When dealing with a huge image, it may be challenging to identify these characteristics. This is where integral images come into play, since they reduce the amount of operations that need to be performed by using the integral image.

3.3.2.   Creating integral images

Without getting into too much detail about the mathematics this behind it ^[76], integral pictures, in essence, speed up the calculation of these Haar features. Instead of computing at each pixel, it generates sub-rectangles and generates array references for each of those sub-rectangles. This ensures that accurate results are obtained. After that, these are computed in order to obtain the Haar characteristics. It is essential to keep in mind that almost all of the Haar characteristics will be irrelevant while doing object detection. This is due to the fact that the only features that are significant are those that pertain to the item itself. On the other hand, how can we choose the Haar features that are most appropriate for representing an object out of the hundreds of thousands of possible Haar features? The influence of Adaboost can be seen in this situation.

3.3.3.   Adaboost algorithm

In essence, Adaboost selects the most advantageous characteristics and instructs the classifiers to make use of them. For the purpose of generating a "strong classifier" that the algorithm can employ in order to identify things, it employs a mixture of "weak classifiers."

Weak learners are produced by moving a window over the input image and computing Haar features for each portion of the image. This process is repeated numerous times. In order to differentiate between non-objects and things, this difference is compared to a threshold that has been learned. In order to build a strong classifier, it is necessary to have a large number of Haar features in order to achieve accuracy. This is because these are "weak classifiers." In the final stage, cascading classifiers are used to integrate these weak learners into a strong learner from the beginning.

3.3.4.   Implementing cascading classifiers

Each stage of the cascading classifier is comprised of a collection of weak learners. The cascading classifier is composed of a succession of stages. A highly accurate classifier can be obtained by training weak learners using boosting, which allows for the mean prediction of all weak learners to be used as the basis for the classification.

This prediction is used by the classifier to determine whether it will signal that an object was identified (i.e., a positive decision), or whether it will go on to the next region (i.e., a negative decision). Because the vast majority of the windows do not contain anything of interest, the stages are designed to discard negative samples as quickly as possible, with the goal of maximizing efficiency.

3.4.   Deep belief networks

DBNs ^[77] constitute a deep learning approach that solves neural network issues. It involve the use of layers of stochastic latent variables in the network. Binary latent variables, or feature detectors and hidden units, are stochastic because they can take any value within a range with some probability. The top two DBN levels have no direction, while the layers above them have directed links to lower layers. DBNs are generative and discriminative, unlike standard neural networks. Image classification requires typical neural network training. DBNs do not employ raw inputs like RBMs or autoencoders. Instead, they start with an input layer with one neuron per input vector and go through several layers to generate outputs by using probabilities from prior layers' activations ^[78].

There is a layered structure in the DBN. The associative memory is located in the upper two layers, whereas the visible units are located in the bottom layer. All of the lower-level relationships are indicated by the arrows that go toward the layer that is closest to the data ^[79].

Associative memory is converted to observable variables by directed acyclic connections in the lower layers. Data input is received by the lowest layer of visible units as actual or binary data. Just like RBMs, DBNs do not have any connections between their layers. The features that embody the data's correlations are represented by the hidden units. Two levels are linked by a weighted matrix W. Each layer's units will be linked to all of the units in the layer above it.

A property layer trained to directly acquire input signals from pixels is the first to be trained. Next, we use the values of this subcaste as pixels to learn the characteristics of the features that were first obtained. With each new subcaste of parcels or feature added to the network, the lower bound on the log-liability of the training data set gets better.

3.5.   The hybrid classification model

Segmentation is performed during the classification phase. Classification of images or examinations is one of the first areas in which deep learning has made an important contribution to medical image analysis. In our case, we focused on classifying abnormal brain tumors as "benign" or "malignant", as shown in Figure 3, in which low-grade brain tumors are labeled "benign" and higher-grade tumors are labeled "malignant." The tumor in this example grows rapidly, has irregular borders, and spreads to nearby brain regions.

A classifier is used to assign a reduced set of features to a class label. The results of the pre-processing of the registration are used as input in the classification phase. The classifier was trained with the extracted and selected features from both classes and categorized the images as either "benign" or "malignant." In the DBNs, the top two layers are undirected and share a symmetric link that forms an associative memory ^[77]. The DBN is competitive for five reasons. Specifically, it can be fine-tuned as a neural network, it is generatively pre-trained, and it can serve as a nonlinear dimensionality reduction tool for the input feature vectors. Moreover, it has many nonlinear hidden layers, and the teacher of the network is another sensory input ^[80]. DBNs also have other advantages, such as the following:

● Feature Learning: DBNs are known for their ability to automatically learn hierarchical and abstract features from data. In medical imaging, where the relevant features might be complex and hierarchical, DBNs can be effective in capturing these representations.

● Unsupervised pre-training: DBNs can be pre-trained in an unsupervised manner layer by layer. This unsupervised pre-training can help the network learn meaningful representations from unlabeled data, which is beneficial when labeled data is scarce, as is often the case in medical imaging.

● Handling Limited Data: If you have a limited amount of labeled data, DBNs might be advantageous, as they can learn from unlabeled data and then fine-tune on the labeled data. This semi-supervised learning approach can be particularly useful when collecting labeled medical data is expensive or challenging.

● Complex Data Distributions: In cases in which the relationships between features in the data are complex and not easily modeled by simpler architectures, DBNs, with their ability to model intricate dependencies, can provide advantages.

● Historical Success in Medical Image Analysis: DBNs have shown success on various medical image analysis tasks. If there is a body of literature supporting the effectiveness of DBNs in similar medical imaging applications, that might influence the choice. However, it is important to note that the choice of a neural network architecture is often empirical and problem-specific. There is no one-size-fits-all solution, and the effectiveness of a particular architecture depends on how well it aligns with the characteristics of your data and the intricacies of the classification task.

● Generative Modeling: DBNs are generative models, meaning that they can generate new samples from the learned data distribution. This property can be advantageous in certain applications, such as data augmentation or synthetic data generation for robust classifiers training.

● Robustness to Noise and Missing Data: DBNs can exhibit robustness against noisy and incomplete data. In medical imaging, where noise and missing information can be common, the ability of DBNs to handle such conditions might be beneficial.

● Transfer Learning: The pre-trained layers of a DBN can be used as feature extractors in other related tasks. If there are similar classification problems or tasks in the medical imaging domain, the pre-trained DBN can potentially be used for transfer learning, providing a head start in the training of a new model.

● Interpretability: The layer-wise structure of DBNs can provide a certain level of interpretability, as each layer can be associated with progressively more abstract features. This interpretability might be valuable in medical applications where understanding the features contributing to a classification decision is crucial.

● Parameter Efficiency: DBNs can be parameter-efficient compared to some deep neural network architectures, especially when dealing with limited data.

In summary, a DBN is a stack of RBMs. Each RBM layer communicates with the previous layer and the next layer. In this study, we investigated the design and overall performance of DBNs by using a series of brain tumor region classification experiments.

An RBM is a type of stochastic neural network that consists of two layers: a visible layer and a hidden layer. The RBM may be trained in an unsupervised manner to produce samples from a complex probability distribution. The RBMs undergo progressive training, starting from the initial layer and progressing to the final layer, through the use of unsupervised learning. The stack of RBMs can be terminated with a softmax layer to form a classifier. Alternatively, it can be utilized to cluster unlabeled data in an unsupervised learning setting, as depicted in Figure 3 ^[81]. The DBN, including the final layer, is trained by using regular error backpropagation in a supervised learning scheme, utilizing a labeled dataset. Figure 3 demonstrates the compatibility of our DBN with the pre-training system. During the process of fine-tuning, the features undergo modest modifications in order to accurately establish the borders of each category. By fine-tuning, we enhance our ability to differentiate between various categories, and, by altering the weights, we achieve an optimal value. This enhances the precision of the model.

Unannotated data assist in the identification of effective features. Conversely, we may obtain characteristics that are not particularly advantageous for task discrimination. Nevertheless, this is not an issue, because we still obtain valuable functionalities from the unprocessed input. Input vectors typically encompass a significantly greater amount of information than labels. The labels facilitate the correlation of patterns and characteristics with the dataset. Hence, DBN training relies on the process of pre-training, followed by fine-tuning.

3.5.1.   The pre-training step

The pre-training step, also called layer-wise unsupervised learning, is a random initialization. There is no correlation between the weight values and the task to be accomplished. Pre-training gives the network a head start. If the network has been previously exposed to the data, the first pre-training task can become the fine-tuning task ^[82]. The datasets used for pre-training may be identical or different from those used for fine-tuning. It is interesting to see how the pre-training for a particular task and dataset can be applied to a new task and dataset that may be slightly different from the first. Using a pre-trained network is generally useful when both tasks and datasets have something in common. In our particular instance, the pre-training was centered on the RBM system, and the layer-wise greedy training algorithm was utilized in order to train the individual RBMs. Data samples for the visible unit were extracted from the input feature vector and placed in the first layer of the image processing pipeline. The conditional probability method was utilized in order to acquire the data samples for the invisible units. When the first RBM had finished learning the weights, they were then applied to each training sample, and the probability of activating the hidden layers could be determined by using the information obtained from this process. It is possible that these could be utilized as visible layers for a different RBM.

3.5.2.   Fine-tuning step

This step is used to greedily learn one layer at a time, and then it is treated as a pre-training step in order to discover a good starting set of weights that can be fine-tuned via a local search technique. The fine-tuning step is responsible for this. In order to get the pre-trained network ready for classification, the fine-tuning process involves refining it through supervised training. A deep neural network's parameters are matched with the parameters of a pre-trained deep neural network (i.e., the DBN) in order to perform fine-tuning ^[83]. In order to carry out a binary classification of benign and malignant brain tumors, a final layer of softmax units is required. Backpropagation can begin only after we have identified reasonable feature detectors that are suitable for classification tasks. The objective of fine-tuning is not to uncover novel characteristics, but rather to enhance the precision of the model by determining the ideal values of the weights connecting the layers.

3.5.3.   Softmax regression function

The softmax regression function was utilized in this stage of the process in order to compute the probability distribution of the event in comparison to other events. Generally speaking, this function gives us the ability to compute the probability of each target class as compared to all of the other potential classes. Subsequently, the estimated probabilities make it easier to identify the target class for the inputs that have been provided. The availability of a wide variety of output probabilities is the primary benefit of utilizing softmax. In this case, the range has a value that falls somewhere between 0 and 1, and the total of all probabilities is equal to one. When the softmax function is used for a multi-classification model, the probabilities of each class are returned, and the one with the highest probability is regarded as the target class. The softmax regression technique is a generalization of the logistic regression method that can be applied to the classification of several classes. As a result of its ease of execution, it is frequently utilized in practical applications, such as the categorization of brain cancers using MRI, as seen in Figure 3. As shown in the figure, softmax and DBNs can be seamlessly combined in a soft hybrid system, which can fully utilize the labeled samples and achieve higher accuracy through global optimization.

4.   Experimental results and discussion

This section provides a description of the brain image dataset, outlines our methodology for training neural networks, and presents the details of our studies. We provide a detailed account of the images in the brain tumor dataset, including an explanation of the original dataset image and the augmentation techniques employed to expand the image count and acquire additional training data. Lastly, we will analyze the outcomes of our model.

4.1.   Dataset and evaluation metrics description

We utilized the T1-weighted image dataset from Harvard Medical School for our experiment. The dataset consists of 250 photos, with 150 categorized as "malignant" (high-grade gliomas) and the remaining 100 categorized as "benign" (low-grade gliomas). The fundamental objective of the annual BraTS challenge serves as a valuable framework that has directed and strengthened our work. To be more precise, the network was trained by using the BraTS 2013 and BraTS 2015 training sets, both of which may be accessed online. The group comprises four modalities: T1, T1-Contrasted, T2, and Flair. The BraTS 2013 study consists of 30 training photos, with 20 containing high-grade cancers and 10 containing low-grade tumors. Additionally, there are 10 brains with high-grade tumors specifically for testing purposes. The 2013 dataset contains two additional data subsets: the leaderboard data and the challenge data. There is a combined total of 65 magnetic resonance images in these two groupings. BraTS 2015 comprises a total of 274 photos, of which 220 were classed as high-grade gliomas and the other 54 as low-grade gliomas. There were no images displaying healthy brains included in the study.

We utilized conventional measures that are utilized in large image sets to estimate classification tasks, such as accuracy, sensitivity, and specificity, in order to evaluate the performance of the proposed model, in addition to other learning methods. Also, in order to determine the importance of the improvement brought about by our model, we computed the p-value that exists between the result that our model has produced and the accuracy rate that the SVM model has produced.

In this context, TP stands for true positive, FP for false positive, TN for true negative and, FN for false negative.

4.2.   Data preprocessing and augmentation

The MRI images from the database varied in size. Since these images represented the input layer of the network, they were normalized and resized to a standard size of 256 × 256 pixels based on 2D slices. The performance of tumor segmentation and classification was improved and the dataset was expanded through the utilization of a number of different MRI techniques for data augmentation. These techniques included translation, noise addition, rotation, and shearing. Khan et al. ^[84] utilized the noise addition and shearing procedures to increase the dataset. This was done with the intention of enhancing the accuracy of the classification and tumor segmentation processes. A number of other techniques, including blurring, translation, rotation, random cropping, and noise addition, were utilized by Dufumier et al. ^[85] in order to improve the size of the dataset and the effectiveness of the prediction algorithms for age and gender classification. Various studies simultaneously improved tumor segmentation and accuracy by using elastic deformation, rotation, and scaling ^[86,87]. These methods are widely used since they are effective and easy to understand. Researchers used these methods in addition to creating synthetic images for a particular purpose. The mix-up, which involves combining the patches from two arbitrary photos to create a new image, is the most popular method of image production. Different datasets and image counts were employed by the researchers in each of these applications. Also, every single one of them employed a unique network topology. Researchers reported their findings according to the methods they used. The prevalent methods are employed in this essay following a thorough assessment of the relevant literature.

To improve the capability and performance of our model, we extended the dataset by transforming the images. We first rotated the images by 45 degrees and then flipped them horizontally. The method was derived from several data augmentation techniques.

4.3.   Training process

Our training process was divided into three phases, i.e., training, validation, and testing, for each of the processed datasets, which contained 150, 50, and 50 images, respectively. Note that, in the training set, there must be no observations of individuals in the test set. The network was trained with the stochastic gradient descent (SGD) optimizer to minimize the loss function, with a mini-batch size of 32, data shuffling at each iteration, and 200 epochs. Using SGD, we iteratively updated our weighting parameters in the direction of the gradient until we reached a minimum loss function. The validation set was separate from the training set we used to validate our model during training. With each epoch, the model was trained on the data from the training set. The regularization factor was set to 0.01 and the initial learning rate was set to 0.001. Once our model was trained and verified using the training and validation data, we assessed the ability of the neural networks to classify cancers from the fresh images by using the test data.

4.4.   Comparison at registration results level

In this section, we compare the registration results of the different algorithms by using a common 3D histogram that looks for the combination of gray levels between the two images. The following Figure 4 gives this combination.

The joint histogram technique ignores the neighborhood information around each pixel to increase the contrast. This makes the output image more unstable. A particular pixel in an image has intensity levels (0 to L-1), and the average intensity levels in its neighborhood are (0 to L-1). The common histogram contains (L x L) entries. Each value corresponds to a particular pixel intensity value and the corresponding average intensity value in the neighborhood at the same location.

Horizontal axis-1 (f(x, y) = i) represents the gray levels of the original image, while horizontal axis-2 (g(x, y) = j) represents the gray levels of the average image in the 3D representation. The number of occurrences of the pixel pair (i, j) is represented by the vertical axis of the 3D plot. We found that the greater the distance between two images (its graph is a plane), the more uniform the joint histogram. Affine registration shows that the gray value of each point on one image is the same as on the other image at the same coordinates, and it determines the best neighborhood size for a given input image. In contrast, when we used the rigid transform, we saw that the two resampled images produced a very similar joint histogram in which the comb shape was lower than the affine joint histogram. Thus, we found that the affine registration gave a better result than the rigid transformation.

4.5.   Comparison of different network architectures

To validate the performance of the proposed model, we experimented with the number of RBMs. The model with four RBMs was found to be the best-performing. The DBN was a multi-RBM layer, so the output of each RBM was the input of the next RBM, as shown in Table 1.

In Table 1, the network starts with 3200 units in the visible layer. This represents one-quarter of the original data size, as determined by preprocessing the global affine registration data. A total of 500,400,250, and 150 units are considered in the hidden layers of the RBMs. The 150 units in the last layer force the DBN to select the 150 most relevant features to represent each image. These deeply structured features are the input to the softmax classifier. During DBN training, the learning rate controls the pace of learning. A high learning rate leads to an unstable training outcome. In contrast, an excessively low learning rate leads to a longer training process. Therefore, a suitable learning rate can speed up the training process while maintaining satisfactory performance. When the maximum epoch reaches 200, our proposed method can achieve the best classification performance.

Now, we will compare the results of the proposed method with those of the classical SVM and KNN algorithms. The accuracy per image was a metric to evaluate the classification models. It was calculated by dividing the total number of observations in the dataset by the number of correct predictions. This was the metric used to measure prediction quality. To evaluate test performance, the accuracy per image was applied to uncropped images (whole image) and cropped images (i.e., the ROI). Table 2 contains complete model details, as well as the test results.

The obtained results on the three datasets used to train our hybrid DBN softmax model (DBN+softmax) showed a significant improvement in accuracy. As can be seen in Table 2, we deduce that preprocessing the affine registration and training our hybrid DBN softmax model with cropped images (i.e., the ROIs) from the Harvard Medical School dataset gave us the highest accuracy, 97.2%. Thus, we can say that training our hybrid DBN softmax model with the Brats 2013 dataset achieved a very high improvement in accuracy, at 96.7%. Furthermore, the results of the DBN+softmax combination trained on the Harvard Medical School dataset outperformed all other models, achieving the highest accuracy of 97.2%.

Ultimately, a conclusion has been drawn based on these findings. Our research indicates that utilizing DBN+softmax, in conjunction with affine registration preprocessing, yields superior classification accuracy compared to other models like those based on the KNN and SVM. Furthermore, due to its utilization of an indirect approach to optimize the weights, SGD is better suited for fine-tuning. This can substantially enhance the accuracy of the system and expedite its convergence.

The training and testing accuracy and loss of our MRI brain tumor classification model are depicted in Figure 5. This plot demonstrates our attainment of a high level of accuracy while minimizing loss. The model demonstrates neither overfitting nor underfitting.

4.6.   Comparison of improvement level

For the purpose of statistically validating our findings, we utilized the signed-rank test of the Wilcoxon test ^[88], which is the non-parametric equivalent of the paired sample test. The purpose of this test is to determine the significance of a value p (0, 1), which is an estimate of the probability that the difference between the two approaches is the result of random chance. The conclusion that we may reach is that the two techniques are statistically distinct when the value of p is less than or equal to $\alpha$, where $\alpha$ is often set at 0.05 ^[89]. To be more specific, the purported difference between the two procedures increases in proportion to the degree to which p approaches zero. We consider the difference between two approaches to be significant when the p-value is less than or equal to 0.1, as presented in Table 3 by "^*", and we consider it to be highly significant when the p-value is less than or equal to 0.05, which is presented by "^**".

Table 3 shows the improvement of our model compared to other models.

As compared to the use of any other classifier model with both uncropped and cropped images, the first observation that can be found in Table 3 is the positive effect that is produced by the DBN+softmax method. For instance, as compared to the SVM model, our methods dramatically enhance results by at least 7%, and as compared to the KNN model, they improve the results by 14 percent. The results that were obtained demonstrate that the utilization of a DBN+softmax method following the ROI extraction produced positive results.

5.   Conclusions

In this work, we focus on the software part of the AR model. We classified abnormal MRI brain tumors as either "malignant" or "benign." We presented a hybrid model by using a DBN and softmax regression, preceded by global affine registration preprocessing to achieve better results. Our method relied on registration preprocessing to evaluate the dataset. We then integrated the unsupervising (DBN) and supervising (softmax regression) networks. We utilized DBN to perform feature learning, specifically addressing the challenges posed by high-dimensional and sparse matrix problems. Additionally, we employed softmax regression to accurately categorize the regions affected by brain tumors. The two algorithms will function as a unified model through the process of fine-tuning. The accuracy of our suggested method surpassed that of standard machine learning algorithms, such as SVM and KNN, when trained on datasets. The results of our tests indicate that our approach is robust. With an accuracy of 97.2%, we expect our proposed method to be used as input for the segmentation phase.

In the future, we plan to use other deep learning algorithms with larger datasets to improve the accuracy of MRI brain tumor classification while reducing the time cost. In particular, we plan to explore other powerful deep neural network architectures based on optimization methods. Also, we plan to implement our method in a real AR model and implement it in an Android app.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

This work was funded by the Deanship of Scientific Research at Jouf University through the Fast-track Research Funding Program.

Conflict of interest

All authors declare that there are no competing interests.