Numerical investigation for the fractional model of pollution for a system of lakes using the SCM based on the Appell type Changhee polynomials

Mohamed Adel; Mohamed M. Khader; Mohammed M. Babatin; Maged Z. Youssef; Mohamed Adel; Mohamed M. Khader; Mohammed M. Babatin; Maged Z. Youssef

doi:10.3934/math.20231592

AIMS Mathematics

2023, Volume 8, Issue 12: 31104-31117. doi: 10.3934/math.20231592

Previous Article Next Article

Research article Special Issues

Numerical investigation for the fractional model of pollution for a system of lakes using the SCM based on the Appell type Changhee polynomials

1.
Department of Mathematics, Faculty of Science, Islamic University of Madinah, Medina 42210, Saudi Arabia
2.
Department of Mathematics and Statistics, College of Science, Imam Mohammad, Ibn Saud Islamic University (IMSIU), Riyadh, 11566, Saudi Arabia
3.
Department of Mathematics, Faculty of Science, Benha University, Benha 13518, Egypt
4.
Department of Mathematics, Faculty of Science, Ain Shams University, Cairo 11566, Egypt

Received: 29 August 2023 Revised: 13 November 2023 Accepted: 15 November 2023 Published: 22 November 2023
MSC : 34A12, 41A30, 47H10, 65N20

This article proposed a useful simulation to investigate the Liouville-Caputo fractional order pollution model's solution behavior for a network of three lakes connected by channels. A supposedly new approximation technique using the Appell type Changhee polynomials (ACPs) was used to treat the periodic and linear input models. This work employs the spectral collocation method based on the properties of the ACPs. The given technique creates a system of algebraic equations from the studied model. We verified the efficiency of the suggested technique by computing the residual error function. We compared the results to those obtained by the fourth-order Runge-Kutta method (RK4). Our findings confirmed that the technique used provides a straightforward and efficient tool to solve such problems. The key benefit of the suggested method is that it only requires a few easy steps, doesn't produce secular terms and doesn't rely on a perturbation parameter.

Keywords:

Citation: Mohamed Adel, Mohamed M. Khader, Mohammed M. Babatin, Maged Z. Youssef. Numerical investigation for the fractional model of pollution for a system of lakes using the SCM based on the Appell type Changhee polynomials[J]. AIMS Mathematics, 2023, 8(12): 31104-31117. doi: 10.3934/math.20231592

Related Papers:

[1]	Khalid K. Ali, Mohamed A. Abd El Salam, Mohamed S. Mohamed . Chebyshev fifth-kind series approximation for generalized space fractional partial differential equations. AIMS Mathematics, 2022, 7(5): 7759-7780. doi: 10.3934/math.2022436
[2]	K. Ali Khalid, Aiman Mukheimer, A. Younis Jihad, Mohamed A. Abd El Salam, Hassen Aydi . Spectral collocation approach with shifted Chebyshev sixth-kind series approximation for generalized space fractional partial differential equations. AIMS Mathematics, 2022, 7(5): 8622-8644. doi: 10.3934/math.2022482
[3]	Imran Talib, Md. Nur Alam, Dumitru Baleanu, Danish Zaidi, Ammarah Marriyam . A new integral operational matrix with applications to multi-order fractional differential equations. AIMS Mathematics, 2021, 6(8): 8742-8771. doi: 10.3934/math.2021508
[4]	Xiaojun Zhou, Yue Dai . A spectral collocation method for the coupled system of nonlinear fractional differential equations. AIMS Mathematics, 2022, 7(4): 5670-5689. doi: 10.3934/math.2022314
[5]	Younes Talaei, Sanda Micula, Hasan Hosseinzadeh, Samad Noeiaghdam . A novel algorithm to solve nonlinear fractional quadratic integral equations. AIMS Mathematics, 2022, 7(7): 13237-13257. doi: 10.3934/math.2022730
[6]	Yumei Chen, Jiajie Zhang, Chao Pan . Numerical approximation of a variable-order time fractional advection-reaction-diffusion model via shifted Gegenbauer polynomials. AIMS Mathematics, 2022, 7(8): 15612-15632. doi: 10.3934/math.2022855
[7]	Jagdev Singh, Jitendra Kumar, Devendra Kumar, Dumitru Baleanu . A reliable numerical algorithm for fractional Lienard equation arising in oscillating circuits. AIMS Mathematics, 2024, 9(7): 19557-19568. doi: 10.3934/math.2024954
[8]	Nurain Zulaikha Husin, Muhammad Zaini Ahmad . Hybridization of the shooting and Runge-Kutta Cash-Karp methods for solving Fuzzy Boundary Value Problems. AIMS Mathematics, 2024, 9(11): 31806-31847. doi: 10.3934/math.20241529
[9]	Eman A. A. Ziada, Salwa El-Morsy, Osama Moaaz, Sameh S. Askar, Ahmad M. Alshamrani, Monica Botros . Solution of the SIR epidemic model of arbitrary orders containing Caputo-Fabrizio, Atangana-Baleanu and Caputo derivatives. AIMS Mathematics, 2024, 9(7): 18324-18355. doi: 10.3934/math.2024894
[10]	Anwar Ahmad, Dumitru Baleanu . On two backward problems with Dzherbashian-Nersesian operator. AIMS Mathematics, 2023, 8(1): 887-904. doi: 10.3934/math.2023043

Abstract

Table . Nomenclature.

$I^{\nu}$	Riemann-Liouville fractional integral of order $\nu$
$\Gamma(\textbf{.})$	Gamma function
$\mathbb{R}^{+}$	Positive real numbers
$^{\mathrm{RL}}D^\nu$	Riemann-Liouville fractional derivative
$\mathbb{N}$	The natural numbers
$^{\mathrm{LC}}D^\nu$	Liouville-Caputo fractional derivative of order $\nu$
$C$	Constant number
$Ch_m(t)$	Changhee polynomials
$Ch_m$	Changhee numbers
$Ch_m^*(t)$	Appell type Changhee polynomials
$\lceil\nu\rceil$	The smallest integer number bigger than or equal to $\nu$
$V_k$	The water volume of the lake $k$
$\psi_{k}(t)$	The pollutant count in the lake $k$
$r_{ik}(t)$	The pollutant rate in the lake $k$ flows into the lake $i$ at time $t$
$\alpha$	The average pollutant input concentration
$\beta$	The size of fluctuations
$\omega$	The fluctuations's frequency.

| Show Table

DownLoad: CSV

1. Introduction

The model's purpose is to explain the contaminant levels in a system that consists of three lakes ^[1,2], as shown in Figure 1. With interconnected channels acting as pipelines with specific flow directions between the compartments, each lake is thought of as a sizable compartment. The first lake receives a pollutant at a specific rate that may be changed or constant over time. We want to know how polluted each lake is at any given time. The water volume in any of the three lakes is assumed to be constant and each lake's contaminant is evenly distributed across the lake by some sort of mixing procedure, as we assumed. Additionally, the pollution is constant and does not change into other forms.

Figure 1. System with three lakes and waterways that connect them.

DownLoad: Full-Size Img PowerPoint

We shall take into account the periodic and linear input models for the pollution source. The input model with periodic has not, as far as the authors are aware, been mentioned in any published works as possible behaviors for the pollution source.

A field of mathematics known as fractional analyzers have the ability to represent and analyze a wide range of real-world situations ^[3,4]. Fractional-order analysis has drawn increasing interest in the study of biological models, where such complex systems are regularly explained empirically by the scaling power law of fractional order. The system's three connected lakes' pollution model by waterways uses one of these mathematical equations. There are many research papers that studied this important model ^[5,6,7].

For recent developments based on the collocation approach, this article presents the first use of the Appell type Changhee polynomials (ACPs) based spectral collocation approach to solve fractional-order pollution models for a system of three lakes connected by waterways. When the approach is applied, the set of differential equations is converted into a system of algebraic equations. The approximate solution for the original equation is found by solving this system, which produces the unknown coefficients of the series solution. The spectral collocation method (SCM) has some advantages for handling this class of problems in which the Appell-type Changhee coefficients for the solution can exist very easily after using the numerical programs. For this reason, this method is much faster than the other methods ^[8,9]. They are widely used because of their good properties in the approximation of functions. Also, this method is a numerical technique with high accuracy and fast convergence and it is easy to use in finite and infinite domains for different problems. In addition, the domain discretization and approximation of the nonlinear terms are not necessary for this method, which is an important advantage.

The reader may find it helpful to understand the mathematical modeling process by reading through many significant studies, such as the one on the mathematical model of internal atmospheric waves, also referred to as gravity waves, which occur inside a fluid rather than on the surface ^[10]; time-fractional (2+1)-dimensional Wu-Zhang nonlinear system of partial differential equations describing a long dispersive wave ^[11]; how nonlinear time-fractional diffusion equations are thought to describe oil pollution in the water ^[12] and nine-dimensional chaos for the fractional (Caputo-sense) Lorenz system ^[13].

In this study, we will use the ACPs for the first time to develop an approximation of the fractional derivative formula and use it to solve the fractional pollution model of three lakes by using the SCM.

The rest of the paper is organized as follows: In section two, we present some definitions and concepts concerning fractional derivatives, the Appell-type Changhee polynomials and other related ideas. In section three, we give an approximate formula for the fractional derivatives by using the ACPs. Section four is devoted to presenting an explanation of the pollution model of three lakes and its formulation. Through section five, we give the implementation of the proposed method. In section six, we present a numerical simulation of the proposed model under study. Finally, the conclusions are in section seven.

2. Preliminaries

2.1. Integral and derivative of fractional order

Fractional-order operators have numerous definitions in the literature ^[14,15]. The two most important fractional derivatives used in the development of fractional calculus theory are defined below.

Definition 2.1. The Riemann-Liouville fractional integral $I^\nu$ of order $\nu$ , for the function $\psi(t)$ is defined as follows ^[14,15]:

$\begin{equation} I^{\nu} \psi(t) = \frac{1}{\Gamma(\nu)} \int_0^{t}(t-\tau)^{\nu-1} \psi(\tau)\, d\tau, \quad t > 0; \quad \nu \in \mathbb{R}^{+}, \end{equation}$

(2.1)

where $\Gamma(t) = \int_{0}^{\infty}\, z^{t-1}\, e^{-z}dz$ is the Gamma function.

Definition 2.2. The Riemann-Liouville fractional derivative $^{\mathrm{RL}}D^{\nu}$ of order $\nu$ , of the function $\psi(t)$ is defined as follows ^[14,15]:

$\begin{equation} \;^{\mathrm{RL}}D^\nu \psi(t) = \frac{d^m}{d t^m}\left(I^{m-\nu} \psi(t)\right), \quad m-1 < \nu \leqq m; \quad m \in \mathbb{N}. \end{equation}$

(2.2)

These formulations have several limitations when simulating some real-world problems ^[14,15]. The Liouville-Caputo formulation, however, was designed to address these problems. As stated in the definition that follows, we use it.

Definition 2.3. The fractional derivative in the Liouville-Caputo sense $D^\nu$ of $\psi(t)$ is given as

$\begin{equation} D^\nu \psi(t) = \frac{1}{\Gamma(n-\nu)}\int_{0}^{t} \frac{\psi^{(n)}(\tau)}{(t-\tau)^{\nu-n+1}} d \tau, \quad n-1 < \nu < n; \quad n \in \mathbb{N}. \end{equation}$

(2.3)

The Liouville-Caputo fractional derivative $D^\nu$ possesses that

$D^\nu C = 0, \quad \hbox{C is a constant},$

and

$\begin{equation} D^\nu t^\theta = \frac{\Gamma(\theta+1)}{\Gamma(\theta+1-\nu)} t^{\theta-\nu}, \quad \theta \in \mathbb{N} \cup\{0\};\quad \theta \geqq\lceil\nu\rceil, \end{equation}$

(2.4)

where $\lceil\nu\rceil$ is the ceil function. Also,

$\begin{equation} D^\nu(c_{1}\, f_{1}(t)+c_{2}\, f_{2}(t)) = c_{1}D^\nu\, f_{1}(t)+c_{2}D^\nu\, f_{2}(t), \quad c_{1}, \, c_{2} \in \mathbb{R}. \end{equation}$

(2.5)

2.2. The Changhee polynomials and other related ideas

Changhee polynomials $Ch_m(t)$ and Changhee numbers $Ch_m$ are defined by ^[16,17]:

$\begin{equation} \frac{2}{z+2}(1-z)^t = \sum\limits_{m = 0}^{\infty} Ch_m(t) \frac{z^m}{m !}, \end{equation}$

(2.6)

where $Ch_m = Ch_m(0)$ are the Changhee numbers ^[16]. The ACPs of degree $m$ are defined by

$\begin{equation} Ch_m^*(t) = \sum\limits_{j = 0}^m\left(\begin{array}{l} m \\ j \end{array}\right) Ch_{m-j}^*\, t^{j}. \end{equation}$

(2.7)

From (2.7), we get

$\begin{equation} \frac{d}{dt} Ch_m^*(t) = m\, Ch_{m-1}^*(t). \end{equation}$

(2.8)

From (2.8), we have

$\begin{equation} Ch_m^*(t) = \int_0^t\, m\, Ch_{m-1}^*(y) dy+Ch_m^*, \end{equation}$

(2.9)

and $Ch_0^* = 1$ and $2 Ch_m^*+m \, Ch_{m-1}^* = 0, \, \forall\, m \geq 1$ .

Any function $u(t)\in\mathrm{L}^2[0, 1]$ can be approximated (and denoted by $u^*(t)$ ) as a finite series sum of the form

$\begin{equation} u(t) \approx u^*(t) = \sum\limits_{i = 0}^m\, c_i\, Ch_i^*(t). \end{equation}$

(2.10)

3. Approximation formula of $D^{\nu}$ using ACPs

Now, we give the following theorem to derive an approximate formula of the fractional derivative $D^{\nu}$ for the function $u^{*}(t)$ given in (2.10).

Theorem 3.1. For $u^{*}(t)$ given in (2.10), the Caputo derivative of order $\nu > 0$ can be approximated by

$\begin{equation} D^\nu\, u^{*}(t) = \sum\limits_{i = \lceil\nu\rceil}^{m}\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{i}\, \kappa_{i, j, \nu}\, t^{j-\nu}, \end{equation}$

(3.1)

where $Ch_{i-j}^*$ is the Changhee number and $\kappa_{i, j, \nu}$ is given by

$\begin{equation*} \kappa_{i, j, \nu} = \frac{(i)!\, Ch_{i-j}^*}{(i-j)!\, \Gamma(j+1-\nu)}. \end{equation*}$

Proof. By taking $\mathrm{Ch}_{\mathrm{i}}^*(\mathrm{t})$ of degree $i$ , where $i = 0, 1, \ldots, m$ , from (2.4) and (2.10) we have

$\begin{equation} \begin{split} D^\nu u^*(t)& = \sum\limits_{i = 0}^{m}c_{i}\, D^{\nu}\, Ch_{i}^{*}(t) = \sum\limits_{i = \lceil\nu\rceil}^{m}\sum\limits_{j = \lceil\nu\rceil}^{i} \, c_{i}\, \frac{(i!)Ch_{i-j}^{*}}{(j!)(i-j)!}\, D^{\nu}t^{j}\\& = \sum\limits_{i = \lceil\nu\rceil}^{m}\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{i}\, \frac{(i!)\, Ch_{i-j}^{*}}{(i-j)!\, \Gamma(j+1-\nu)}\, t^{j-\nu} \\& = \sum\limits_{i = \lceil\nu\rceil}^{m}\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{i}\, \kappa_{i, j, \nu}\, t^{j-\nu}, \end{split} \end{equation}$

(3.2)

where $\kappa_{i, j, \nu}$ is given in (3.1), and the proof is finished. □

4. Some concepts about the pollution problem

4.1. An explanation of the pollution model

A group of lakes connected by channels is referred to as a system of lakes. Models of these lakes consist of sizable segments connected by pipelines ^[18]. Three lakes are shown in a system in . A pollutant is delivered into only one of the lakes (in this case, lake one) with rate b at time $t = 0$ ; for instance, from a factory $b(t)$ , then as shown by the arrows, the contaminated water enters the other lakes via the pipes or channels ^[19]. We also assume that the pollution is distributed equally throughout all of the lakes and that in each lake the volume of water stays constant. Predicting the amount of contamination in each lake is our goal for $t \geq 0$ using these assumptions.

Let $V_k$ and $\psi_{k}(t), k = 1, 2, 3$ symbolize the water volume and pollutant count in lake $k$ , respectively, to describe the dynamic behavior of the system. The concentration of the pollutant in the lake $k$ at time $t$ is then given by

$\begin{equation} c_k(t) = \frac{\psi_{k}(t)}{V_k}. \end{equation}$

(4.1)

The following equation describes the pollution flux $r_{ik}(t)$ flowing from the lake $k$ into $i$ during time t. When we further assume that the flow rate $F_{ik}$ between lakes $k$ and $i$ is constant, the following results follow:

$\begin{equation} r_{ik}(t) = F_{ik}\, c_{k}(t) = \frac{F_{ik}\psi_{k}(t)}{V_k}. \end{equation}$

(4.2)

As a result, the pollutant rate in lake $k$ flows into lake $i$ at time $t$ and is represented by the expression $r_{ik}(t)$ .

By applying the subsequent idea to every lake $(i = 1, 2, 3)$ :

$\begin{equation} \frac{d \psi_i}{d t} = \hbox{Input rates- Output rates, } \end{equation}$

(4.3)

we obtain that

$\begin{equation} \begin{split} \frac{d \psi_1}{d t} & = \frac{F_{13}}{V_3} \psi_3(t)-\frac{F_{31}}{V_1} \psi_1(t)-\frac{F_{21}}{V_1} \psi_1(t)+b(t), \\ \frac{d \psi_2}{d t} & = \frac{F_{21}}{V_1} \psi_1(t)-\frac{F_{32}}{V_2} \psi_2(t), \\ \frac{d \psi_3}{d t} & = \frac{F_{31}}{V_1} \psi_1(t)+\frac{F_{32}}{V_2} \psi_2(t)-\frac{F_{13}}{V_3} \psi_3(t). \end{split} \end{equation}$

(4.4)

The initial conditions for (4.4) are

$\begin{equation} \psi_1(0) = \psi_2(0) = \psi_3(0) = 0. \end{equation}$

(4.5)

The rate of entering flow is equal to the rate of outgoing flow for each lake because the amount of water in each lake remains constant for time $t \geq 0$ . As a result, the following flow rate circumstances arise:

$\begin{equation} \begin{split} \hbox{Lake 1}:\, \, \, & F_{13} = F_{21}+F_{31}, \\ \hbox{Lake 2}:\, \, \, & F_{21} = F_{32}, \\ \hbox{Lake 3}:\, \, \, & F_{31}+F_{32} = F_{13}. \end{split} \end{equation}$

(4.6)

4.2. Fractional case of the pollution model

In this part, we provide a revised version of the pollution model in the sense that the Liouville-Caputo fractional derivative is taken into consideration in the current study to better understand both the qualitative analysis and the numerical iterative analysis of the proposed model. It is described as follows ^[20]:

$\begin{equation} D^{\nu}\psi_{1}(t) = \frac{F_{13}}{V_3} \psi_3(t)-\frac{F_{31}}{V_1} \psi_1(t)-\frac{F_{21}}{V_1} \psi_1(t)+b(t), \end{equation}$

(4.7)

$\begin{equation} D^{\nu}\psi_{2}(t) = \frac{F_{21}}{V_1} \psi_1(t)-\frac{F_{32}}{V_2} \psi_2(t), \end{equation}$

(4.8)

$\begin{equation} D^{\nu}\psi_{3}(t) = \frac{F_{31}}{V_1} \psi_1(t)+\frac{F_{32}}{V_2} \psi_2(t)-\frac{F_{13}}{V_3} \psi_3(t), \end{equation}$

(4.9)

with

$\begin{equation} \psi_{k}(0) = 0, \quad k = 1, 2, 3. \end{equation}$

(4.10)

Using this model (4.7)–(4.10) in its fractional version ^[21], we may more clearly assess the water volume and pollutant count in each lake of the system in the future and the past, thanks to the memory effect of fractional derivatives. While mathematical models with integer derivatives are crucial for understanding the dynamics of such systems, they have certain limits because these systems lack memory or nonlocal effects and, hence, these models in their current state are not always appropriate. As a result, to effectively examine various natural phenomena, it is important to convert several pollution models into fractional differential equations (FDEs). FDEs are extensively used in the study of unusual events in nature and the theory of complex systems in general, and they take into account the curves characteristics to a large extent. Finally, it can explain temporal delays, fractal features, and other phenomena. In addition, we can control the rate of pollutant transmission between the three lakes.

5. Numerical implementation

In this part, we lay out how the suggested strategy that would be applied to simulate the fractional-order form of the model (4.7)–(4.10). This aim will be achieved through the following steps.

(1) Let us express and approximate the solution $\psi_{\gamma}(t), \, \gamma = 1, 2, 3$ as a finite series form in terms of the ACPs and denoted by $\Psi_{\gamma, m}(t), \, \, \gamma = 1, 2, 3$ as follows:

$\begin{equation} \Psi_{\gamma, m}(t) = \sum\limits_{i = 0}^{m}\, c_{\gamma, i}\, Ch_{i}^{*}(t). \end{equation}$

(5.1)

(2) Upon substituting from (5.1) into the system (4.7)–(4.9), we get

$\begin{equation} \begin{split} \sum\limits_{i = \lceil\nu\rceil}^{m}&\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{1, i}\, \kappa_{i, j, \nu}\, t^{j-\nu} = \frac{F_{13}}{V_3}\, \left(\sum\limits_{i = 0}^{m}\, c_{3, i}\, Ch_{i}^{*}(t)\right)-\frac{F_{31}-F_{21}}{V_1}\, \left(\sum\limits_{i = 0}^{m}\, c_{1, i}\, Ch_{i}^{*}(t)\right)+b(t), \end{split} \end{equation}$

(5.2)

$\begin{equation} \begin{split} \sum\limits_{i = \lceil\nu\rceil}^{m}&\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{2, i}\, \kappa_{i, j, \nu}\, t^{j-\nu} = \frac{F_{21}}{V_1}\, \left(\sum\limits_{i = 0}^{m}\, c_{1, i}\, Ch_{i}^{*}(t)\right)-\frac{F_{32}}{V_2}\, \left(\sum\limits_{i = 0}^{m}\, c_{2, i}\, Ch_{i}^{*}(t)\right), \end{split} \end{equation}$

(5.3)

$\begin{equation} \begin{split} \sum\limits_{i = \lceil\nu\rceil}^{m}&\sum\limits_{j = \lceil\nu\rceil}^{i}\, c_{3, i}\, \kappa_{i, j, \nu}\, t^{j-\nu} = \sum\limits_{i = 0}^{m}\, \left(\frac{F_{31}}{V_1}\, c_{1, i}+\frac{F_{32}}{V_2}\, c_{2, i}-\frac{F_{13}}{V_3}\, c_{3, i}\right)\, Ch_{i}^{*}(t). \end{split} \end{equation}$

(5.4)

(3) By collocation the above system (5.2)–(5.4) at $m-1$ of points $t_{r} = \frac{r}{m-1}+1, \; r = 1, 2, \cdots, m-1$ , this reduces them to a linear system of algebraic equations in the coefficients $c_{\gamma, i}, \, \gamma = 1, 2, 3, \, i = 0, 1, ..., m.$

(4) Also, by substituting from Eq (5.1) into the initial conditions (4.10), then (4.10) will be reduced also to algebraic equations in the coefficients $c_{\gamma, i}$ :

$\begin{equation} \sum\limits_{i = 0}^{m}\, c_{\gamma, i}\, Ch_{i}^{*}(0) = 0, \quad\quad\quad \gamma = 1, 2, 3. \end{equation}$

(5.5)

(5) We now use the successive over-relaxation algorithm to solve numerically the linear system (5.2)–(5.5) for the unknowns $c_{\gamma, i}, \, \gamma = 1, 2, 3, \, \, \, i = 0, 1, \cdots, m.$ This, in turn, will lead us to compute the approximate solution by substitution in the form (5.1).

6. Numerical experimentations

Now, we proceed to check the quality of the scheme by checking some numerical simulations on two examples in the interval $[0, 25]$ for the system (4.7)–(4.10) for different two pollution models. Howevwer, in all figures, we take the same values of the following parameters ^[22]:

$\begin{equation} \begin{split} F_{21} = 18 \, \mathrm{mi.}^3/\hbox{year, }\, & \quad\, \, F_{32} = 18 \, \mathrm{mi.}^3/\hbox{year, }\, \quad\, \, F_{31} = 20 \, \mathrm{mi.}^3/\hbox{year, }\, \quad\, \, F_{13} = 38 \, \mathrm{mi.}^3/\hbox{year}, \\& V_1 = 2900 \, \mathrm{mi.}^3, \quad\quad V_2 = 850\, \mathrm{mi.}^3, \quad\quad V_3 = 1180 \, \mathrm{mi.}^3. \end{split} \end{equation}$

(6.1)

Now, we are going to study the following two input models ^[20]. In each case, we will compare the obtained solutions with the fourth-order Runge-Kutta method (RK4). We also evaluate the residual error function (REF) ^[23] to check the accuracy and quality of the proposed scheme.

Case 1: Periodic input model

When the pollutant is intermittently delivered into lake one, this input model is employed. Here's an illustration:

$b(t) = \alpha+\beta\, \hbox{sin}(\omega\, t),$

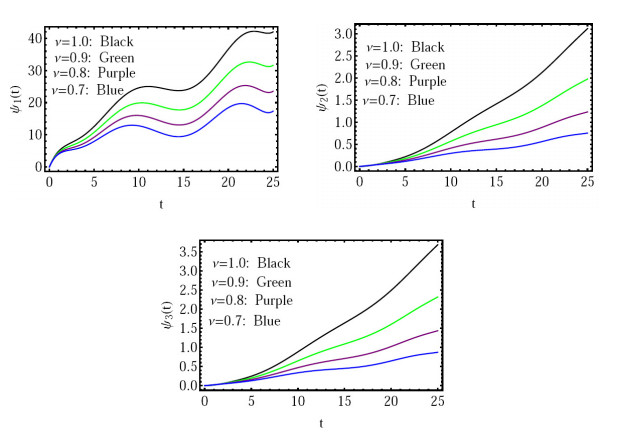
where $\alpha$ represents the average pollutant input concentration, $\beta$ is the size of fluctuations and $\omega$ is the fluctuations's frequency. Let $\alpha = \beta = 2, \, \omega = 1$ , with the same values of the parameters given in (6.1) and the initial conditions. Figures 2–4 represent the results for this studied case.

Figure 2. The solution for case 1,

$\psi_{i}(t), \, i = 1, 2, 3$ with some values of

$\nu$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The solution for case 1,

$\psi_{i}(t), \, i = 1, 2, 3$ by ACPs and RK4 solutions

$\nu = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. The REF of

$\psi_{i}(t), \, i = 1, 2, 3$ for case 1.

DownLoad: Full-Size Img PowerPoint

(1) In : The solution for $\nu = 1.0, \, 0.9, \, 0.8, \, 0.7$ , for $m = 4$ .

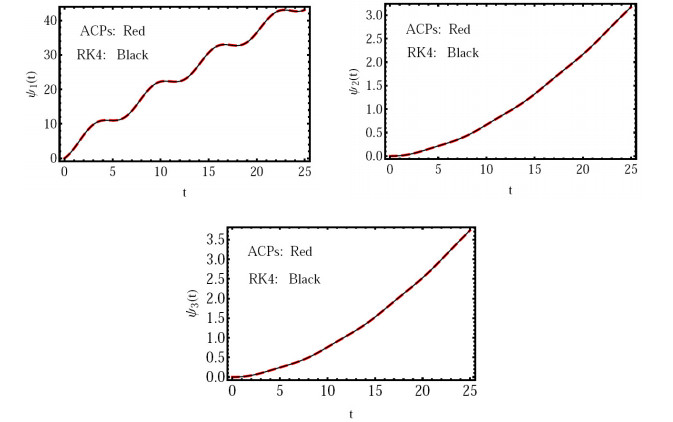
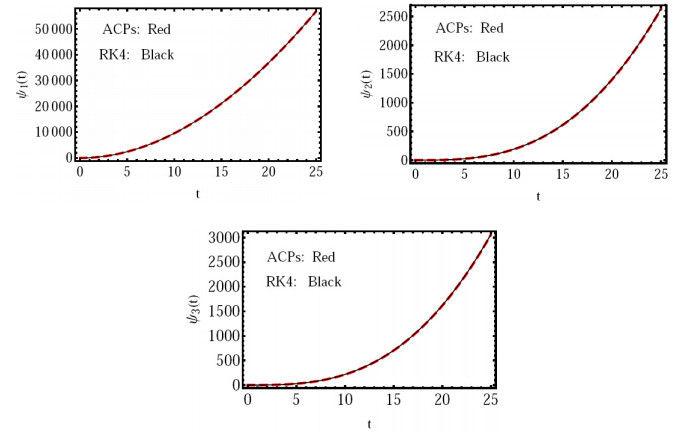
(2) In : Analysis of the solution in comparison to the RK4 solutions at ( $\nu = 1$ ) for $m = 5$ .

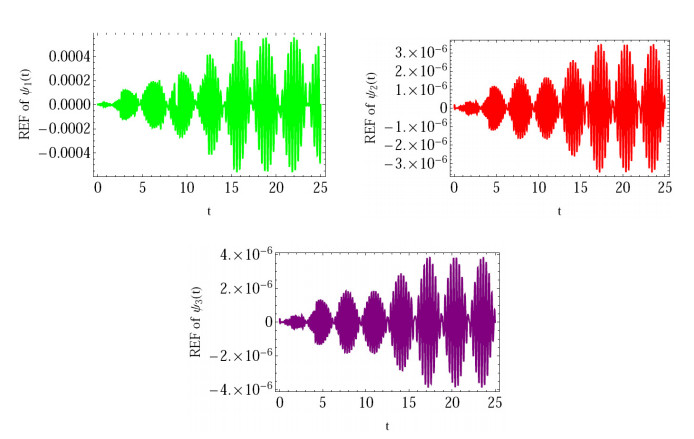
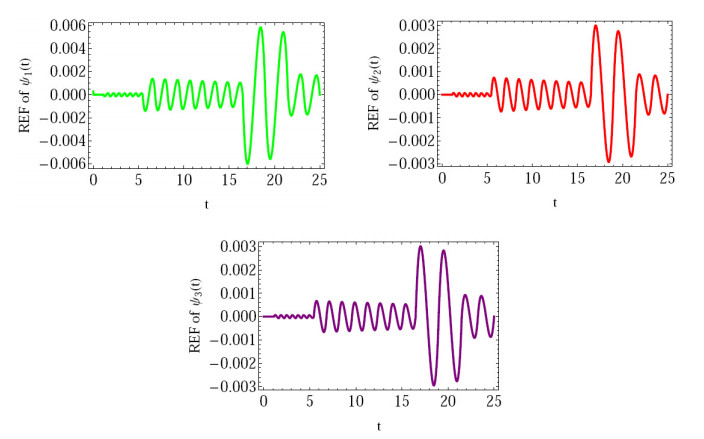
(3) In : We compute and plot the REF at $\nu = 0.96$ .

Case 2: Linear input model

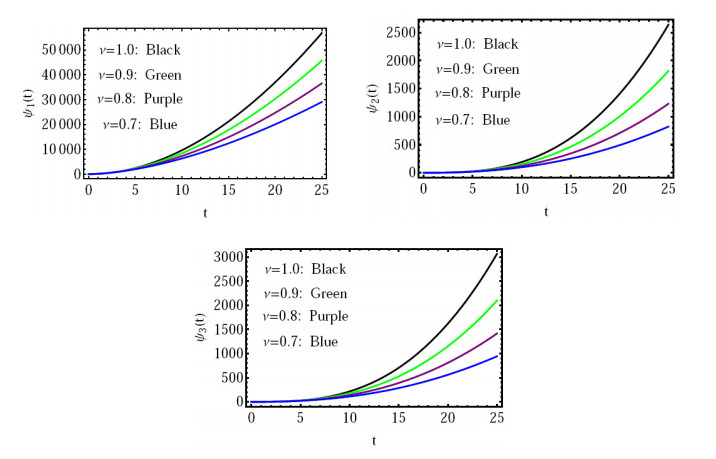
When a linear concentration of the pollutant is injected into the first lake, this input model is utilized. As an example, we take $b(t) = \lambda\, t,$ where the positive constant $\lambda = 200$ , take the zero initial conditions and the values of the parameters given in (6.1). Figures 5–7 represent the results for this studied case.

Figure 5. The solution for case 2,

$\psi_{i}(t), \, i = 1, 2, 3$ with some values of

$\nu$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. The solution for case 2,

$\psi_{i}(t), \, i = 1, 2, 3$ by ACPs and RK4 solutions

$\nu = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The REF of

$\psi_{i}(t), \, i = 1, 2, 3$ for case 2.

DownLoad: Full-Size Img PowerPoint

(1) In : The solution for $\nu = 1.0, \, 0.9, \, 0.8, \, 0.7$ , for $m = 4$ .

(2) In : Analysis of the solution in comparison to the RK4 solutions at ( $\nu = 1$ ) for $m = 5$ .

(3) In : We compute and plot the REF at $\nu = 0.96$ .

These results show that the suggested method is suitable for the fractional-order Liouville-Caputo fractional derivative solution for the given model. The values of $\nu, m$ determine how the numerical solution produced using the suggested approach behaves. The suggested approach also considerably improves the method's efficacy and outcomes.

Through the results that we obtained, especially in Figures 2 and 5 as well as in light of the geometric diagram for the placement of these three lakes, and based on the direction of the arrows that show the path of movement and transfer of pollution among the three lakes, we find that these results are consistent with the natural behavior of pollution in the lakes. This indicates that these solutions are closer to the actual and real solutions and, therefore, we confirm the efficiency of the method proposed here.

In addition through , we provide a comparison between the obtained approximate solution by the current method ( $\psi_{i-ACPs}(t)$ , $i = 1, 2, 3$ ) with the variational iteration method (VIM) ^[1] ( $\psi_{i-VIM}(t)$ ) where we computed the REF at $\nu = 0.97$ with different values of the approximation-order $m$ to estimate the effectiveness and precision of the provided approach. We take the same initial conditions and the same values of the parameters mentioned above. The given results of the errors in this table provide more confirmation of the efficiency and effectiveness of the proposed method than other methods.

Table 1. A comparison of the REF between the current method and VIM via different values of

$m$ .

$\mathrm{t}$	$\mathrm{m}$	$\psi_{1-ACPs}$	$\psi_{1-VIM}$	$\psi_{2-ACPs}$	$\psi_{2-VIM}$	$\psi_{3-ACPs}$	$\psi_{3-VIM}$
	3	2.65E-08	1.09E-05	1.85E-09	2.25E-05	5.58E-08	7.35E-05
0.0	6	1.02E-08	8.25E-06	7.58E-10	8.10E-07	8.25E-09	3.57E-06
	9	5.24E-10	5.22E-07	1.09E-10	5.91E-07	1.47E-10	9.51E-07
	3	0.10E-08	0.52E-05	4.25E-08	9.88E-06	6.54E-08	1.75E-05
0.2	6	9.08E-09	7.29E-06	6.92E-09	1.24E-07	7.35E-09	9.36E-06
	9	5.24E-10	0.05E-07	7.53E-10	6.54E-07	9.51E-10	2.58E-07
	3	8.11E-08	9.11E-06	3.55E-08	1.23E-05	1.54E-09	7.14E-06
0.4	6	5.34E-09	5.20E-06	4.22E-09	6.75E-07	2.55E-10	6.45E-07
	9	2.85E-10	7.28E-07	5.81E-10	7.53E-07	7.50E-10	1.23E-07
	3	9.00E-09	0.55E-06	3.07E-09	1.59E-05	7.06E-08	8.46E-05
0.6	6	7.04E-10	7.54E-07	9.21E-10	0.25E-06	3.88E-09	1.05E-06
	9	3.25E-10	6.96E-07	7.01E-10	8.52E-07	1.00E-10	9.58E-07
	3	5.09E-08	7.55E-05	9.52E-08	7.98E-06	9.85E-08	1.25E-05
0.8	6	7.15E-09	3.57E-06	3.28E-09	5.46E-06	6.75E-09	3.50E-06
	9	9.01E-10	1.45E-07	7.55E-10	8.64E-07	4.19E-10	7.85E-07
	3	8.22E-09	9.21E-06	9.10E-09	0.20E-05	7.59E-09	9.87E-05
1.0	6	9.99E-10	4.57E-06	1.00E-09	8.25E-06	6.41E-10	9.65E-07
	9	7.58E-10	4.05E-07	9.05E-10	3.34E-07	8.83E-10	6.38E-07

| Show Table

DownLoad: CSV

7. Conclusions

The target of this work was to analyze the dynamical behavior of the system of lakes pollution model utilizing the Liouville-Caputo fractional derivative operator and fractional calculus tools and methods. The mathematical model under inquiry was solved with various values of $\nu$ and $m$ , as well as by computing the REF. We have established that the suggested method is surprisingly successful in studying this mathematical model. Additionally, by adding more terms from the approximation solution series, or by raising $m$ , we can regulate the precision of the error and lower it. Also, we concluded that the mathematical model under consideration in this research is better suited for numerical simulations using the Liouville-Caputo fractional derivative operator. The findings obtained graphically and those acquired by utilizing the RK4 approach are comparable. Our findings also demonstrate the proposed method's accuracy and computational effectiveness. In addition, we compared the solution obtained by the proposed method with the variational iteration method where we computed the REF with different values of the approximation-order $m$ to estimate the effectiveness and precision of the provided approach. These results show that the present method is very effective and thorough. As a generalization of the current work, we intend to use the same model in future research but with different types of polynomials or fractional derivatives. In addition, we will study this model as an optimization problem to help us in controlling it. Finally, we must point out that the Mathematica software program was used to carry out the numerical simulation work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah for the support provided to the Post-Publishing Program.

Conflict of interest

There are no competing interests declared by the authors.

References

[1]	J. Biazar, M. Shahbala, H. Ebrahimi, VIM for solving the pollution problem of a system of lakes, J. Control Sci. Eng., 2010 (2010), 1–6. https://doi.org/10.1155/2010/829152 doi: 10.1155/2010/829152
[2]	J. Biazar, L. Farrokhi, M. R. Islam, Modeling the pollution of a system of lakes, Appl. Math. Comput., 178 (2006), 423–430. https://doi.org/10.1016/j.amc.2005.11.056 doi: 10.1016/j.amc.2005.11.056
[3]	M. Adel, M. M. Khader, S. Algelany, High-dimensional chaotic Lorenz system: Numerical treatment using Changhee polynomials of the Appell type, Fractal Fract., 7 (2023), 1–16. https://doi.org/10.3390/fractalfract7050398 doi: 10.3390/fractalfract7050398
[4]	Y. F. Ibrahim, S. E. Abd El-Bar, M. M. Khader, M. Adel, Studying and simulating the fractional COVID-19 model using an efficient spectral collocation approach, Fractal Fract., 7 (2023), 1–18. https://doi.org/10.3390/fractalfract7040307 doi: 10.3390/fractalfract7040307
[5]	M. Merdan, Homotopy perturbation method for solving modelling the pollution of a system of lakes, SDU J. Sci., 4 (2009), 99–111.
[6]	M. Merdan, A new application of modified differential transformation method for modelling the pollution of a system of lakes, Selcuk J. Appl. Math., 11 (2010), 27–40.
[7]	M. Merdan, He's variational iteration method for solving modelling the pollution of a system of lakes, Fen Bilimleri Dergisi, 18 (2009), 59–70.
[8]	Y. H. Youssri, W. M. Abd-Elhameed, Numerical spectral Legendre-Galerkin algorithm for solving time fractional telegraph equation, Rom. J. Phys., 63 (2018), 1–16.
[9]	M. M. Khader, K. M. Saad, A numerical study by using the Chebyshev collocation method for a problem of biological invasion: Fractional Fisher equation, Int. J. Biomath., 11 (2018), 1850099. https://doi.org/10.1142/S1793524518500997 doi: 10.1142/S1793524518500997
[10]	T. Patel, H. Patel, R. Meher, Analytical study of atmospheric internal waves model with fractional approach, J. Ocean Eng. Sci., 2022, In press. https://doi.org/10.1016/j.joes.2022.02.004
[11]	T. Patel, H. Patel, An analytical approach to solve the fractional-order (2+1)-dimensional Wu-Zhang equation, Math. Methods Appl. Sci., 46 (2023), 479–489. https://doi.org/10.1002/mma.8522 doi: 10.1002/mma.8522
[12]	H. Patel, T. Patel, D. Pandit, An efficient technique for solving fractional-order diffusion equations arising in oil pollution, J. Ocean Eng. Sci., 8 (2023), 217–225. https://doi.org/10.1016/j.joes.2022.01.004 doi: 10.1016/j.joes.2022.01.004
[13]	M. Alqhtani, M. M. Khader, K. M. Saad, Numerical simulation for a high-dimensional chaotic Lorenz system based on Gegenbauer wavelet polynomials, Mathematics, 11 (2023), 1–12. https://doi.org/10.3390/math11020472 doi: 10.3390/math11020472
[14]	A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier, 2006.
[15]	H. M. Srivastava, An introductory overview of fractional-calculus operators based upon the Fox-Wright and related higher transcendental functions, J. Adv. Eng. Comput., 5 (2021), 135–166. http://dx.doi.org/10.55579/jaec.202153.340 doi: 10.55579/jaec.202153.340
[16]	D. S. Kim, T. Kim, J. J. Seo, A note on Changhee polynomials and numbers, Adv. Stud. Theor. Phys., 7 (2013), 993–1003.
[17]	J. G. Lee, L. C. Jang, J. J. Seo, S. K. Choi, H. I. Kwon, On Appell-type Changhee polynomials and numbers, Adv. Differ. Equ., 2016 (2016), 1–10. https://doi.org/10.1186/s13662-016-0866-7 doi: 10.1186/s13662-016-0866-7
[18]	S. Yuzbasi, N. Sahin, M. Sezer, A collocation approach to solving the model of pollution for a system of lakes, Math. Comput. Model., 55 (2012), 330–341. https://doi.org/10.1016/j.mcm.2011.08.007 doi: 10.1016/j.mcm.2011.08.007
[19]	J. C. Varekamp, Lake-pollution modelling, J. Geol. Educ., 36 (1988), 4–8. https://doi.org/10.5408/0022-1368-36.1.4 doi: 10.5408/0022-1368-36.1.4
[20]	B. Benhammouda, H. Vazquez-Leal, L. Hernandez-Martinez, Modified differential transform method for solving the model of pollution for a system of lakes, Discrete Dyn. Nat. Soc., 2014 (2014), 1–12. https://doi.org/10.1155/2014/645726 doi: 10.1155/2014/645726
[21]	E. U. Haq, Analytical solution of fractional model of pollution for a system lakes, Comput. Res. Prog. Appl. Sci. Eng., 6 (2020), 302–308.
[22]	M. Adel, M. M. Khader, Theoretical and numerical treatment for the fractal-fractional model of pollution for a system of lakes using an efficient numerical technique, Alex. Eng. J., 82 (2023), 415–425. https://doi.org/10.1016/j.aej.2023.10.003 doi: 10.1016/j.aej.2023.10.003
[23]	H. M. El-Hawary, M. S. Salim, H. S. Hussien, Ultraspherical integral method for optimal control problems governed by ordinary differential equations, J. Global Optim., 25 (2003), 283–303. https://doi.org/10.1023/A:1022463810376 doi: 10.1023/A:1022463810376

This article has been cited by:

1.	Rashad A. Al-Jawfi, Abdulghani Muhyi, Wadia Faid Hassan Al-shameri, A New Family of Appell-Type Changhee Polynomials with Geometric Applications, 2024, 13, 2075-1680, 93, 10.3390/axioms13020093
2.	Miao Feng, Haoran Si, Yang Li, Junrui Zhang, Mohamed Rafik N. Qureshi, Evaluating the drivers of B2B performance: An empirical analysis based on Alibaba, 2024, 19, 1932-6203, e0306919, 10.1371/journal.pone.0306919
3.	Ashish Rayal, Shailendra Giri, Prerak A. Patel, Meenu Prajapati, Dynamical analysis and numerical treatment of pond pollution model endowed with Caputo fractional derivative using effective wavelets technique, 2024, 12, 2195-268X, 4218, 10.1007/s40435-024-01494-5
4.	Nasreen Kausar, Harish Garg, Contra-hormonic generalized fuzzy numerical scheme for solving mechanical engineering problems, 2024, 70, 1598-5865, 4629, 10.1007/s12190-024-02148-7
5.	M. Rakshana, P. Balasubramaniam, Dynamical analysis of non-electric guitar-like instruments with single saddle via Hopf bifurcation, 2024, 1951-6355, 10.1140/epjs/s11734-024-01406-w

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1031) PDF downloads(74) Cited by(5)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(7) / Tables(1)

AIMS Mathematics

Numerical investigation for the fractional model of pollution for a system of lakes using the SCM based on the Appell type Changhee polynomials

Related Papers:

Abstract

1. Introduction

2. Preliminaries

2.1. Integral and derivative of fractional order

2.2. The Changhee polynomials and other related ideas

3. Approximation formula of Dν D^{\nu} using ACPs

4. Some concepts about the pollution problem

4.1. An explanation of the pollution model

4.2. Fractional case of the pollution model

5. Numerical implementation

6. Numerical experimentations

7. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Preliminaries

2.1. Integral and derivative of fractional order

2.2. The Changhee polynomials and other related ideas

3. Approximation formula of Dν D^{\nu} using ACPs

4. Some concepts about the pollution problem

4.1. An explanation of the pollution model

4.2. Fractional case of the pollution model

5. Numerical implementation

6. Numerical experimentations

7. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

3. Approximation formula of $D^{\nu}$ using ACPs

3. Approximation formula of $D^{\nu}$ using ACPs