1.
Introduction
Developing ideas and relations in numerous science topics has been significantly influenced by the development of fuzzy sets and fuzzy logic [1]. The Fuzzy Differential Equations (FDEs) theory has received much attention since it offers a natural framework for simulating dynamical systems with uncertainty [2]. The concept of a fuzzy derivative was first proposed by Chang and Zadeh in 1972 [3]. It was then developed further by Dubois and Prade [4], who incorporated the extension concept into their strategy. The derivative for fuzzy valued mappings was initially created by Puri and Ralescu [5], who generalized and expanded on the idea of Hukuhara differentiability (H-derivative) for the class of fuzzy mappings. Consequently, the theory for FDE was further developed by Kaleva [6] using the idea of H-derivative.
The FDE is used to solve fuzzy initial or boundary conditions, which is employed to model several science and engineering-related problems [7]. Furthermore, the solution of FDE, which involves a Fuzzy Initial Value Problem (FIVP) or Fuzzy Boundary Value Problem (FBVP), can be solved for almost all practical problems. However, not all FIVP or FBVP can be solved precisely due to the difficulty of finding their analytical solution [8]. Therefore, reliable and effective numerical techniques may be required for the corresponding FDE. In handling the FBVP, it can be approached by two types [9]. The first approach assumes that the boundary values are fuzzy and the solution is a fuzzy function. Correspondingly, the derivative of the differential equation can be considered as the derivative of a fuzzy function. Moreover, the second approach is generating a fuzzy solution from a crisp one.
Most scientific and engineering problems require FDE solutions, which are satisfied by fuzzy boundary values. Using generalized differentiability, Khastan and Nieto [10] explain a two-point Boundary Value Problem (BVP) for a second-order FDE. Jamshidi and Avazpour [2] suggested a shooting method to solve Fuzzy Boundary Value Differential Equations (FBVDEs) under generalized differentiability. The FBVDE is divided into two Fuzzy Initial Value Differential Equations (FIVDEs), and the Adomian approach is used to solve the differential equation system. Subsequently, Rabiei, Ismail, Ahmadian, and Salahshour [11] proposed a Fuzzy Improved Runge-Kutta Nystrom method (FIRKN), which was an extension of the Fuzzy Runge-Kutta Nystrom method (FRKN). By analyzing the outcomes of FIRKN and FRKN, a numerical example of second-order FDE has been conducted. The findings demonstrate that the FIRKN requires fewer function evaluations and has a lower computational cost than the FRKN. In 2016, the chasing method to solve the FBVP was introduced by Can, Bayrak, and Hicdurmaz [12]. In order to demonstrate the effectiveness of the proposed method, the heat transfer problems are resolved by comparing the analytical and approximate solutions of (1, 1) and (1,2)-systems.
In 2016, Saadeh, Al-Smadi, Gumah, Khalil, and Khan [13] implemented the Iterative Reproducing Kernel Method (IRKM) to solve the fuzzy two-point BVP based on generalized differentiability. Bayrak [14] developed the Adomian Decomposition Method (ADM) with Green's function to solve second-order FBVP under generalized H-differentiability. The examples were created by splitting the domain into two subdomains, and the results demonstrate how effective this approach is at resolving numerical problems. Moreover, Gumah, Naser, Al-Smadi, and Al-Omari [15] presented the reproducing kernel Hilbert space method to solve the second-order Fuzzy Volterra Integro-Differential Equation (FVIDE) with the assumption of strongly generalized differentiability. It has been demonstrated that this method is more accurate than analytical solutions and that examples employing the (1, 1) and (1,2)-systems have been provided to indicate their robustness.
Liu and Lou [16] converted the second-order system of partial differential equations into a first-order system by applying variable substitution. Sufficient conditions for global exponential stability and the existence of periodic solutions in fuzzy wave equations have been obtained by creating a suitable Lyapunov functional and utilizing various analytical techniques. An and Guo [17] solved a second-order fuzzy linear differential equation through decentralization. Using the Hukuhara difference, a given problem is solved, and an approximation of the solution is obtained by resolving a crisp function extended system of linear equations. The Random Fixed Point (RFP) theorem was introduced in fuzzy metric space by Srivastava, Chaharpashlou, Saadati and Li [18]. To demonstrate the presence of a unique random solution, the authors studied the nonlinear BVP for a system of random differential equations using an iterative method from the RFP. Furthermore, Hashim, Anakira, Jameel, Alomari, Zureigat, Alomari, and Ying [19] proposed the Fuzzy Fractional Homotopy Analysis Method (FFHAM) to address the linear and nonlinear Fuzzy Fractional Two-Point Boundary Value Problems (FFTBVPs) in the context of the application. Accordingly, the FFTBVP solution suggests that FFHAM is more straightforward and produces accurate results than other methods.
Therefore, we propose Fuzzy Runge-Kutta Cash-Karp of the fourth-order method (FRKCK4) to solve the second-order FBVP, and the approximate solutions are compared with Fuzzy Runge-Kutta of the fourth-order method (FRK4). Thus, the process involved throughout this paper is divided into a few sections: In Section 2, we recall some basic concepts on fuzzy numbers and generalized differentiability. In Section 3, the concept of the shooting method for BVP is explained. In Section 4, we discuss the shooting method for FBVPs where the general equation is split into four types of systems, namely the (1, 1), (1,2), (2,1), and (2,2)-system. Using the first-order FDE, which is obtained in Section 4, the FRKCK4 is proposed in Section 5. In Section 6, we present the numerical example, and the solutions of the proposed method are compared with the solutions of the analytical and FRK4 methods. The tables and graphs are presented to summarize our findings. Correspondingly, the overall conclusion and future work are written in Section 7.
2.
Preliminaries
Throughout this section, the basic ideas of fuzzy numbers are introduced. The set of all real numbers and fuzzy numbers are indicated as R and RF.
Definition 2.1. [2] A fuzzy number is mapping u:R→[0,1] with the following properties:
(1) u is upper semi-continuous,
(2) u is fuzzy convex, i.e., u(λx+(1−λ)y)≥min{u(x),u(y)} for all x,y∈R,λ∈[0,1],
(3) u is normal, i.e., ∃x0∈R for which u(x0)=1,
(4) supp u={x∈R|u(x)>0} is the support of the u and its closure cl(suppu) is compact.
Definition 2.2. [20] A fuzzy number (or interval) u is completely determined by any pair u=(u_,¯u) of functions [u_,¯u]:[0,1]→R, defining the end-points of α− cuts, satisfying the three conditions:
(1) u_:α→u_α∈R is bounded monotonic increasing (nondecreasing) left–continuous function ∀α∈]0,1] and right–continuous for α=0;
(2) ¯u:α→¯uα∈R is bounded monotonic decreasing (nonincreasing) left–continuous ∀α∈]0,1] and right–continuous for α=0;
(3) u_α≤¯uα∀α∈[0,1].
Definition 2.3 [21] If A and B are two fuzzy intervals, then the distance D between A and B is defined as
where
Definition 2.4. [22] Let x,y∈RF. If there exits z∈RF such that x=y+z then z is called the H-difference of x,y and it is denoted xΘy.
Definition 2.5. [23] Let x0∈S. A fuzzy mapping f:S→F is said to be continuous at x0 if for each ϵ>0 there exists a δ>0 such that D(f(x),f(x0))<δ, whenever x∈S∩Bδ(x0). f:S→F is said to be continuous if it is continuous at each x∈S.
Next, the fuzzy derivative of the fuzzy function is recalled.
Definition 2.6. [22] Let F:I→RF and fix x0∈I. We say F is (1)-differentiable at x0, if there exists an element F′(x0)∈RF such that for all h>0 sufficiently near to 0, exist
and the limits (in the metric D)
In this case we denote F′(x0) by D11F(x0).
And F is (2)-differentiable if for all h>0 sufficiently near to 0, exist
and the limits (in the metric D)
In this case, the derivative is denoted by D12F(x0).
Theorem 2.1. [22] Let F:I→RF be a fuzzy function, where [F(x,α)]=[f_(x,α),¯f(x,α)] for each α∈[0,1].
(1) If F is (1)-differentiable, then f_′(x,α) and ¯f(x,α) are differentiable functions and
(2) If F is (2)-differentiable, then f_′(x,α) and ¯f(x,α) are differentiable functions and
Definition 2.7. [22] Let F:I→RF and n,m=1,2. We say F is (n,m)− differentiable at x0∈I, if D1nF exists on a neighborhood of x0 as a fuzzy function and it is (m)− differentiable at x0. The second derivative of F is denoted by D2n,mF(x0) for n,m=1,2.
Theorem 2.2. [22] Let D11F:I→RF or D12F:I→RF be a fuzzy function, where [F(x,α)]=[f_(x,α),¯f(x,α)]. Then:
(1) If D11F is (1)-differentiable, f_′(x,α) and ˉf′(x,α) are differentiable functions and
(2) If D11F is (2)-differentiable, f_′(x,α) and ˉf′(x,α) are differentiable functions and
(3) If D12F is (1)-differentiable, f_′(x,α) and ˉf′(x,α) are differentiable functions and
(4) If D12F is (2)-differentiable, f_′(x,α) and ¯f′(x,α) are differentiable functions and
3.
The shooting method for Boundary Value Problem
This section discusses the concept of BVP using the shooting method. Let the second-order BVP be in the form:
By implementing the shooting method [2], two Initial Value Problems (IVPs) are considered: Non-homogeneous and homogeneous equations.
(1) Non-homogeneous equation
The non-homogeneous equation occurred when u(x)≠0 and let h"=w",h′=w′ and h=w.
(2) Homogeneous equation
The homogeneous equation occurred when u(x)=0 and let j"=w",j′=w′ and j=w.
By referring to Eqs (3.2) and (3.3), we define m1=h,m2=h′,m3=jandm4=j′. Both equations are converted into first-order Ordinary Differential Equations (ODEs) as follows:
subject to initial conditions h(p)=β,h′(p)=0,j(p)=0andj′(p)=1. Eq (3.4) is solved by any numerical method and the solution of Eq (3.1) is calculated based on the following equation.
Theorem 3.1. [2] Let us consider FIVP (see Eq (3.2)), where F:[x0,x0+a]×RF×RF→RF is such that:
(1) [F(x,y(x),y′(x))(α)]=[f(x,y,y′)_(α),¯f(x,y,y′)(α)] for each α∈[0,1],
(2) The functions f(x,y,y′)_(α) and ¯f(x,y,y′)(α) are equi-continuous, i.e., for any ϵ>0 there exists δ>0 such that for any (x,u,v),(x1,u1,v1)∈[x0,x0+a,x0+b]×R2, we have |f(x,u,v)_(α)−f(x1,u1,v1)_(α)|<ϵ and |¯f(x,u,v)(α)−¯f(x1,u1,v1)(α)|<ϵ whenever ‖(x1,u1,v1)−(x,u,v)‖<δ.
(3) [F(x,y(x),y′(x))(α)] is named uniformly bounded on any bounded set, if exists L>0 such that
and also
Then, for (n,m) - differentiability, the FIVP (Eq (3.2)) and the corresponding (n, m)-system are equivalent.
The concept of the shooting method for FBVP is discussed in the following section.
4.
The shooting method for Fuzzy Boundary Value Problem
This section introduces the concept of FBVP under fuzzy generalized differentiability. Suppose the second order of FBVP is as follows:
where W(p),W(q)∈F(R), S(x),T(x),U(x)>0, and x∈[p,q]. Based on Theorem 2.2, Eq (4.1) is split into four types of systems as follows:
(1) (1, 1)-system
Using Theorem 2.2 (1), the (1, 1)-system of Eq (4.1) is presented as:
The fuzzy non-homogeneous equation for Eq (4.2) is written as:
The fuzzy homogeneous equation for Eq (4.2) is:
To solve Eqs (4.3) and (4.4) simultaneously, we define
Consequently, the system of first-order FDEs is obtained.
with fuzzy initial conditions
(2) (1,2)-system
Using Theorem 2.2 (2), the (1,2)-system of Eq (4.1) is presented as:
The fuzzy non-homogeneous equation for Eq (4.6) is written as:
The fuzzy homogeneous equation for Eq (4.6) is:
To solve Eqs (4.7) and (4.8) simultaneously, let define
Correspondingly, the system of first-order FDEs is obtained.
with fuzzy initial conditions
(3) (2,1)-system
Using Theorem 2.2 (3), the (2,1)-system of Eq (4.1) is presented as:
The fuzzy non-homogeneous equation for Eq (4.10) is written as:
The fuzzy homogeneous equation for Eq (4.10) is:
To solve Eqs (4.11) and (4.12) simultaneously, we define
Consequently, the system of first-order FDEs is obtained.
with fuzzy initial conditions given by
(4) (2,2)-system
Using Theorem 2.2 (4), the (2,2)-system of Eq. (4.1) is presented as:
The fuzzy non-homogeneous equation for Eq. (4.14) is written as:
The fuzzy homogeneous equation for Eq (4.14) is:
To solve Eqs (4.15) and (4.16) simultaneously, we define
Subsequently, the system of first-order FDEs is obtained.
with fuzzy initial conditions given by
5.
Fuzzy Runge-Kutta Cash-Karp of the Fourth-Order method for the systems
In this section, we discuss how to solve the system of first-order FDE using FRKCK4. The idea of FRKCK4 is obtained from [24]. Based on the four types of systems presented in the previous section, the procedures to obtain the approximate solution for (1, 1), (1,2), (2,1), and (2,2)-systems using the FRKCK4 are detailed below.
(1) (1, 1)-system
Using the FRKCK4, the approximate solution for the (1, 1)-system is suggested as follows:
where
(2) (1,2)-system
Using the FRKCK4, the approximate solution for the (1,2)-system is suggested as follows:
where
(3) (2,1)-system
Using the FRKCK4, the approximate solution for the (2,1)-system is suggested as follows:
Where
(4) (2,2)-system
Using the FRKCK4, the approximate solution for the (2,2)-system is suggested as follows:
where
By implementing the system of first-order FDEs with FRKCK4, the solution to the problem of Eqs (4.2), (4.6), (4.10) and (4.14) are derived as
where m_1(xi,α),¯m1(xi,α),m_3(xi,α)and¯m3(xi,α) are unique solutions for fuzzy non-homogeneous and fuzzy homogeneous equations. Hence, the analytical and approximate solution for Eq (4.1) are denoted as Wanalytical(x,α)=[w_analytical(x,α),¯wanalytical(x,α)] and W(x,α)=[w_(x,α), ¯w(x,α)], respectively.
6.
Numerical example
This section presents a numerical example to express the ability of the proposed method. For the (1,1)-system, the solution of the proposed method is compared with the analytical solution and FRK4. The errors between FRKCK4 and FRK4 are determined by deducting the absolute values of analytical and approximative solutions. Since the analytical solutions for the (1,2), (2,1) and (2,2)-systems could not be determined analytically, we now analyze the approximations provided by FRKCK4 and FRK4. This section discusses the example of FBVP, where the idea was obtained from Example 5.1 in [2].
Let the FBVP as follows:
where [0]α=[α−1,1−α] and [1]α=[α,2−α]. Based on Sections 4 and 5, the procedure to solve Eq (6.1) using the (1,1)-system is discussed below:
(1) (1,1)-system
With reference to Eq. (6.1), it is expressed as follows in (1,1)-system:
The fuzzy non-homogeneous equation for Eq (6.2) is translated as:
The fuzzy homogeneous equation for Eq (6.2) is:
Equations (6.3) and (6.4) are solved simultaneously and defined as:
The system of first-order FDE is:
with fuzzy initial conditions
To solve the (1,1)-system, the following is proposed:
The analytical solution for Eq (6.2) is
The numerical example is evaluated using step size Δx=0.01, N=100, and the solutions are corrected to 13 significant figures. Table 1 compares the analytical and approximate solutions of FRKCK4 and FRK4, while Table 2 provides the errors (Err(x,α)=[err_(x,α),¯err(x,α)]) for (1,1)-system at x=0.5.
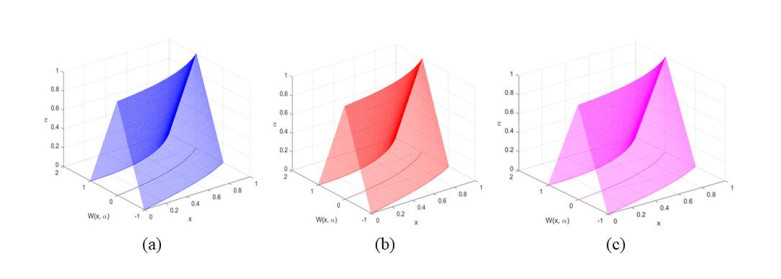
A comparison of the analytical and numerical solutions, FRKCK4 and FRK4, is provided in Table 1. The error analysis is computed and displayed in Table 2 to demonstrate the efficacy of the proposed method. According to the findings, FRKCK4's error is less than FRK4's, and all three fuzzy solutions are displayed in Figure 1.
Apart from error analysis, we can measure the area under the curve at a certain x using the following formula:
For instance, when applying Eq (6.5), the area under the curve for the analytical solution at x = 0.5 is 0.501882736424, while the areas under the curve for FRKCK4 and FRK4 are 0.501882736418 and 0.501882736677, respectively. As a result, the area under the curve of FRKCK4 is closer to the area under the curve of the analytical solution. However, the difference in area under the curve between FRK4 and the analytical solution is quite significant. Figure 1 below illustrates the analytical and approximate solutions of FRKCK4 and FRK4 for the (1,1)-system.
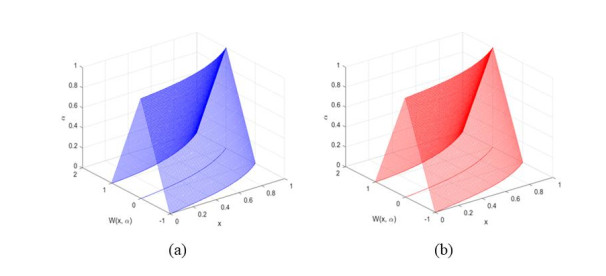
Next, we discuss the steps to solve Eq (6.1) using the (1,2)-system, and the results are summarized in Table 3 and Figure 2.
(2) (1,2)-system
The fuzzy non-homogeneous equation for Eq. (6.6) is expressed as:
The fuzzy homogeneous equation for Eq (6.6) is:
Equations (6.7) and (6.8) are solved simultaneously and defined as:
The system of first-order FDE is:
with fuzzy initial conditions
To solve the (1,2)-system, the following is proposed:
The numerical example is evaluated using step size \varDelta x = 0.01, N = 100, and the solution is corrected to 13 significant figures using the proposed method. Table 3 compares the approximate solutions of FRKCK4 and FRK4 for the (1,2)-system. As there is no analytical solution for the (1,2)-system, this can be demonstrated by calculating the area under the curve using Eq. (6.5). Based on Table 3, the areas under the curve at x = 0.5 for FRKCK4 and FRK4 are 0.510199655305 and 0.510199655592, respectively. According to the findings, the area under the curve for FRKCK4 is smaller than the area under the curve for FRK4. This indicates that FRKCK4 offers a better approximation than FRK4.
Figure 2 below displays how the approximate solutions of FRKCK4 and FRK4 behaved in the time domain x.
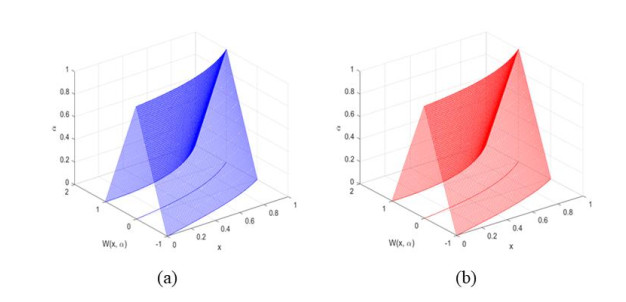
Next, we discuss the steps to solve Eq (6.1) using the (2,1)-system, and the results are summarized in Table 4 and Figure 3.
(3) (2,1)-system
The fuzzy non-homogeneous equation for Eq (6.9) is translated as:
The fuzzy homogeneous equation for Eq (6.9) is:
Equations (6.10) and (6.11) are solved simultaneously and defined as:
The system of first-order FDE is:
with fuzzy initial conditions
To solve the (2,1)-system, the following is proposed:
The numerical example is evaluated using step size \varDelta x = 0.01, N = 100, and the solution is corrected to 13 significant figures using the proposed method. Table 4 compares the approximate solutions of FRKCK4 and FRK4 for the (2,1)-system. Based on Table 4, we quantify the area under the curve to demonstrate the efficacy of the proposed method. Using Eq (6.5), the areas under the curve for FRKCK4 and FRK4 are 0.501882736418 and 0.501882736677, respectively. The results suggest that the area under the curve for FRKCK4 is smaller than the area under the curve for FRK4. This indicates that FRKCK4 offers a better approximation than FRK4.
Figure 3 displays how the approximate solutions of FRKCK4 and FRK4 behave in the time domain x for the (2,1)-system.
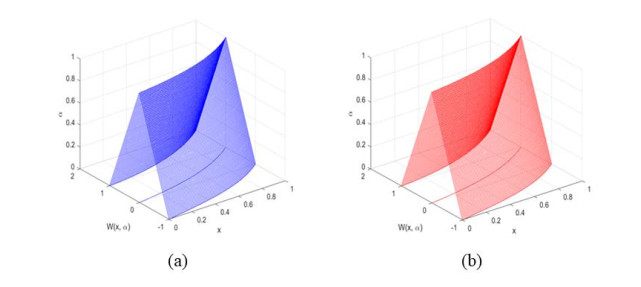
Next, we discuss the steps to solve Eq (6.1) using the (2,2)-system, and the results are summarized in Table 5 and Figure 4.
(4) (2,2)-system
The fuzzy non-homogeneous equation for Eq (6.12) is translated as:
The fuzzy homogeneous equation for Eq. (6.12) is:
Equations (6.13) and (6.14) are solved simultaneously and defined as:
The system of first-order FDE is:
with fuzzy initial conditions
To solve the (2,2)-system, the following is proposed:
The numerical example is evaluated using step size \varDelta x = 0.01, N = 100, and the solution is corrected to 13 significant figures using the proposed method. Table 5 displays the comparisons between the approximate solutions of FRKCK4 and FRK4 for the (2,2)-system. Table 5 indicates that the approximation of FRKCK4 is better than FRK4. To support the statement, we applied Eq (6.5) and obtained the areas under the curve for FRKCK4 and FRK4 at x = 0.5 are 0.510199655305 and 0.510199655592, respectively. It suggests that FRKCK4's area under the curve is smaller than FRK4's.
Figure 4 portrays how the approximate solutions of FRKCK4 and FRK4 for the (2,2)-system behave in the time domain x.
The approximate solutions for FRKCK4 and FRK4 are provided in Table 1 and Tables 3–5. Although the (1,2), (2,1) and (2,2)-systems do not have analytical solutions, we may compute the area under the curve, and the findings demonstrate that FRKCK4's area under the curve is less than FRK4's. In general, we are able to conclude that for all of the tested systems, the FRKCK4 solution is superior to the FRK4 solution. Based on [2], there is a semi-analytical solution that can be sampled. However, when the errors of FRKCK4 and FRK4 are compared, FRK4's errors are superior to FRKCK4's. This semi-analytical solution is considered only inappropriate as an example in this study. With the help of the MATLAB program, the above problem was solved, and we discovered that the solutions for the (1,1) and (2,1)-systems, as well as the (1,2) and (2,2)-systems are comparable.
7.
Conclusions
In conclusion, the RKCK4 method can be modified for time-delay systems by effectively managing past state information and applying interpolation as needed. This approach helps to accurately simulate complex systems where current behavior depends on delayed inputs. Whereas delay fuzzy system models a situation where the system's behavior is uncertain and influenced by both current and past conditions. These models are used to handle real-world problems where both uncertainty and time delays are factors.
In this paper, the idea of FBVP has been presented and explained in terms of fuzzy generalized differentiability. This FBVP is used to address the issues for the (1, 1), (1,2), (2,1), and (2,2)-systems, and a detailed procedure is provided to obtain the first-order FDE system. The FRKCK4 numerical approach is used to solve each of these FDE systems.
Numerical simulations of FBVP are discussed to illustrate the effectiveness of FRKCK4. The results from FRKCK4 for the (1, 1)-system were compared to those from FRK4 and analytical solutions. According to error analysis, FRKCK4 generates answers that are more precise than FRK4. This is true since when compared to the analytical solution, FRKCK4's error is smaller than FRK4's error. Since the analytical solution cannot be solved analytically for (1,2), (2,1) and (2,2)-systems, we compute the area under the curve, and it was discovered that the area of FRKCK4 is less than the area of FRK4. In light of this, it may be considered that FRKCK4 generates a better solution than FRK4.
Note that the findings from the research have also been represented graphically to demonstrate the behavior of all four systems at the time interval x. It was discovered that when x increases, the graphs for the (1, 1) and (2,1)-systems as well as the (1,2) and (2,2)-system produced the same graph.
Basically, the FRKCK4 can be used to solve FBVP with a good agreement where this FRKCK4 can handle the six time-steps while FRK4 can handle only four time-steps. This will make the solution of FRKCK4 better than FRK4. Since FRKCK4 has more numbers and notations than FRK4, managing it can be more challenging than FRK4. For future studies, this FBVP can be improved using higher-order derivatives for a better approximation.
Author contributions
N. Z. Husin and M. Z. Ahmad: Writing-original draft. These authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Acknowledgements
This research was funded by the Ministry of Higher Education of Malaysia under the Fundamental Research Grant Scheme (FRGS): FRGS/1/2020/STG06/UNIMAP/02/2.
Conflict of interest
The authors declare no conflict of interest.
Appendix







 DownLoad:
DownLoad: