1.
Introduction
Due to the development of numerous effective learning methods and network structures in the late 1980s, neural networks have become a popular topic in the fields of machine learning and artificial intelligence [1]. Innovative methods include multilayer perceptron networks trained using backpropagation type algorithms, self-organizing maps and radial basis function networks. While neural networks are successfully used in a variety of applications, interest in this field has waned in recent years. Hinton et al. [2] presented deep learning in 2006, which is based on the notion of artificial neural networks (ANNs). Deep learning became a popular topic after that, leading to a renaissance in neural network research, which is sometimes referred to as new generation neural networks. This is because deep networks, when correctly trained, have demonstrated great success in a range of classification and regression difficulties [1]. Due to its ability to learn from supplied data, deep learning technology is currently regarded as one of the hottest subjects in the fields of machine learning, artificial intelligence, data science, and analytics. According to historical data obtained from Google trends [3], the international popularity of deep learning is increasing day by day [4]. Deep learning differs from traditional machine learning in that, as the volume of data increases, deep learning technology employs more layers to represent data abstractions in order to develop computational models. While deep learning takes a long time to train a model because of the enormous number of parameters, it runs relatively quickly during testing when compared to other machine learning methods [5]. Although deep learning models are effectively employed in the aforementioned application domains, developing an adequate deep learning model is a difficult undertaking due to the dynamic nature and variability of real-world problems and data. Convolutional neural networks (CNNs or, alternatively, ConvNets) [6] have a prevalent discriminative deep learning architecture that learns directly from input without requiring human feature extraction. CNNs are widely used in image and video recognition, medical image analysis, recommender systems, image classification, image segmentation, natural language processing, financial time series, and many other applications. Recurrent neural networks (RNNs) constitute another prominent neural network that uses sequential or time-series data and feeds the result from the previous phase as input to the current stage [7,8]. Recurrent networks, like feed-forward networks and CNNs, learn from training input but differ in that they have "memory" which allows them to influence the current input and output by utilizing information from prior inputs. Long short-term memory networks (LSTMNs) were first proposed in [9] to address RNN concerns with vanishing/exploding gradients. These challenges can arise during the backpropagation over time as the algorithm trains on extended temporal sequences. Deep learning models, which include the autoencoder (AE), generative adversarial networks (GANs) and their derivatives, have been classified as generative models. GAN deployment is generally intended for unsupervised learning tasks, but it has also proven to be a better solution for semi-supervised and reinforcement learning activities, depending on the task [10].
Multi-criteria group decision making (MCGDM) [11,12,13] is a consistent decision-making approach that aims to determine the best alternative based on a number of criteria. The MCGDM approach has grown more popular among experts due to its wide range of applications in fields such as operations research, engineering technology and management science. Due to the expanding ambiguities and uncertainties in the data, the decision experts found it difficult to apply crisp values [14,15].
Zadeh first introduced the idea of a fuzzy set in 1965 [16] which took into account an element's degree of membership (DM) in a set. It has been widely applied in a variety of multi-criteria decision-making problems. Later researchers examined that membership in fuzzy sets did not cover an object's uncertainty. Because the fuzzy set failed to describe the uncertainty with only the DM of an element, Atanassov [17] established the generalized notion when he added the degree of non- membership (DNM) to a fuzzy set and created the so called intuitionstic fuzzy set (IFS). The basic features of the IFS were developed and researched in 1986. In the case of the IFS there are some constraints on DM and DNM. Due to IFS constraints in some circumstances, the IFS is unable to explain the uncertainty of real-world data. Huang [18] established some generalized operations for IFSs, such as the Hamacher sum, the Hamacher product, Hamacher exponentiation, etc., and further developed some generalized Hamacher aggregation operators, such as the intuitionistic fuzzy Hamacher weighted averaging operator, the intuitionistic fuzzy Hamacher ordered weighted averaging operator and the intuitionistic fuzzy Hamacher hybrid averaging operator. Zhou and Chang [19] extended the concept of an IFS and developed fuzzy number intuitionistic fuzzy Hamacher aggregation operators. Because the total of the values of the DM and DNM is more than one, IFS theory has its own limitations in transmitting information regarding the DM and DNM of an object; thus, IFS theory has failed to describe the uncertainty in daily life applications.
Pawlak [20] developed a new, important rough set theory approach for dealing with ambiguous and uncertain information in the decision-making process in 1982. In recent years, there has been significant progress in both theoretical and practical investigation into rough sets, and many scholars have contributed to this research in different ways. Dubois and Prade [21] described the mathematical structure of fuzzy rough sets (FRSs). Khan et al.[22] extended the concept of a rough set to a probabilistic hesitant FRS and then explained and applied it to decision-making problems. Further, Zhou and Wu. [23] defined generalized approximation operators for intuitionistic FRSs. To solve multi-attribute group decision making problems, Huang et al. [24] proposed an evaluation based on the distance from the average solution technique.
Gundogdu and Kahraman [25,26] worked on the multi-criteria decision-making problem to propose a decision-making system based on the multi-criteria decision-making model. In their hospital location selection, Kahraman et al. [27] utilized TOPSIS method in Spherical fuzzy environment. In [28] Mahmood et al. introduced the concept of spherical fuzzy sets and T-spherical fuzzy sets, as well as their basic operators laws and aggregation operators. To solve a decision-making problem, Ashraf et al. [29,30] used spherical fuzzy set aggregation operators. Gundogdu et al.[31,32] applied the VIKOR method to site selection and waste management problems in the spherical fuzzy environment. Sharaf [33] proposed a spherical fuzzy-VIKOR method based on spherical weighted average mean/geometric mean operators. The spherical fuzzy graph was proposed by Akram et al.[34], and these spherical fuzzy graphs were used by Akram [35] to propose a decision-making method.
Although all of these traditional fuzzy set theory models excel at carrying fuzzy information, their ability to deal with one-dimensional information is limited. Many complex multi-criteria decision-making problems have two-dimensional information that cannot be handled by existing multi-criteria decision-making strategies. To counteract this trend, Ramot et al.[36,37] created complex fuzzy sets (CFSs), which incorporate fuzzy set theory by introducing complex amplitude and phase terms. The phase term is a key component of complex fuzzy sets making it the only tool capable of capturing two-dimensional information. Alkouri and Salleh [38] proposed complex intuitionistic fuzzy sets (CIFSs) and terms for the DM and NDM, including amplitude and phase terms, that can be applied to decision-making problems with two-dimensional information.
Akram et al. [39] established the generalized the complex intuitionistic fuzzy Hamacher weighted averaging/geometric operator and complex intuitionistic fuzzy Hamacher ordered weighted averaging/geometric operator. The disadvantage of CIFSs is that the restrictions on the amplitude and phase terms are relatively strict, which illustrates the inadequacy of a CIFS when one or both conditions are not satisfied. Due to this fact, Ullah et al. [40] developed distance measure for the complex Pythagorean fuzzy sets (CPyFSs), making MCGDM more accurate. Due to the fully tunable requirement of the CPyFSs model, it is more efficient and predominant than other two-dimensional imprecise knowledge techniques. Ma et al. [41] proposed a CPyFS-VIKOR method for MCGDM problems based on linguistic information. Akram et al. [42] extended the of ELECTRE-I and TOPSIS methods for MCGDM problems under CPyFSs. Akram and Naz [43] presented a novel decision-making approach by implementing a CPyFSs environment. Garg et al. [44] discussed the CPyFSs for MCGDM problems. Further Akram et al. [45] extended the complex spherical fuzzy to VIKOR method for solving the MCGDM problems. Morever Akram et al. [46] also defined a series of prioritized weighted aggregation operators for a complex spherical fuzzy. Hence in this paper, we present some Hamacher operational laws and some new aggregation operators for the hybrid study of complex spherical fuzzy rough sets (CSFRSs) to accommodate more uncertainty during decision-making problems.
1.1. Contribution of study
In this work, we have created various types of complex spherical fuzzy rough Hamacher weighted averaging/geometric aggregation operators in the CSFRSs environment. The CSFRSs can undoubtedly explain the uncertain subjective data in the most ideal manner and complex spherical fuzzy rough Hamacher weighted averaging/geometric aggregation operators give more versatility in the data aggregation process. The main contributions of the article are given as follows.
(a) First, we define CSFRSs with the help of spherical fuzzy sets and complex spherical fuzzy sets (CSFSs).
(b) We introduce a new score and accuracy functions for CSFRSs.
(c) We developed various types of complex spherical fuzzy rough Hamacher weighted averaging/geometric aggregation operators for CSFRSs, such as the WA(H)CSFR aggregation operator, the OWA(H)CSFR aggregation operator, the WG(H)CSFR aggregation operator and the OWG(H)CSFR aggregation operator to deal with group decision making problems in which the attributes have interrelationships.
1.2. Motivation of the study
According to a review of complex fuzzy sets, CIFS, CPyFS and CSFS. CSFRSs constitute an effective tool for decision making in a complex and ambiguous setting, and it overcomes the shortcomings of the previous concepts of a CIFS, CPyFS and CSFS under the condition of two dimensional information. Some extensions have been attempted since its inception, as have several techniques for aggregation operators under the complex spherical fuzzy rough Hamacher t-norm and t-conorm. The following is a description of the motivation for the proposed theory:
(a) CSFRSs have a highly competent structure to better represent vague human opinions in DM, DNeM(degree of neutral membership) and NDM, which is another common and powerful feature of receiving two-dimensional information.
(b) We aimed to construct a new notion of CSFRSs based on Hamacher norms, and also to construct their operational laws.
(c) We aimed to create a list of aggregation operators based on Hamacher norms, as well as to explain the associated properties.
(d) We aimed to develop a decision-making methodology using the proposed aggregation operators to aggregate the uncertain information in real-world decision-making problems.
(e) We aimed to validate the suggested methodology through a numerical example related to deep learning technique selection is given.
The rest of the paper is summarized as follows. In Section 2, we discuss the properties of the fundamental ideas. In Section 3, we first define complex spherical fuzzy rough relations, CSFRSs and operational laws for CSFRSs under the conditions of the Hamacher t-norm and t-conorm. In Section 4, we develop complex spherical fuzzy rough Hamacher weighted averaging/geometric aggregation operators and complex spherical fuzzy rough Hamacher ordered weighted averaging/geometric aggregation operators their properties are discussed. In Section 5, we define the algorithm based on the CSFRS proposed operators. In Section 6, presents a numerical example and a case study regarding to the selection of best alternative for deep learning technique is explained. In Section 7, we present a comparison analysis. In Section 8, we present the conclusion of the article.
2.
Preliminaries
We will introduce some basic literature on CFS, CIFS, CPyFS, CSFSs, rough set relations and complex spherical rough sets (CSRSs) in the section, which will be useful in a later section.
Definition 1. [37] Consider ˆS to be a non-empty universe; the CFS is mathematically defined as
where i=√−1. μΥ∈[0,1] and ℓμΥ ∈[0,2π], The DM is represented as μΥ and the amplitude term of degrees is represented by ℓμΥ.
Definition 2. [48] Consider ˆS to be a non-empty universe; the CIFS is mathematically defined as
where i=√−1. μΥ, νΥ∈[0,1] and ℓμΥ, ℓνΥ∈[0,2π], such that 0≤μΥ(ˊs)+νΥ(ˊs)≤1 and 0≤ℓμΥ(ˊs)+ℓνΥ(ˊs)≤2π. The two dimensional information in term of represent by μΥ(ˊs)ei2π(ℓμΥ(ˊs)),νΥ(ˊs)ei2π(ℓνΥ(ˊs)).
Definition 3. [47] Consider ˆS to be a non-empty universe; CPyFS is mathematically defined as
where i=√−1, μΥ, νΥ∈[0,1] and ℓμΥ, ℓνΥ∈[0,2π], such that 0≤μΥ(ˊs)2+νΥ(ˊs)2≤1 and 0≤ℓμΥ(ˊs)2+ℓνΥ(ˊs)2≤2π. The two dimensional information represent by μΥ(ˊs)ei2π(ℓμΥ(ˊs)), νΥ(ˊs)ei2π(ℓνΥ(ˊs)).
Definition 4. [45] Consider ˆS to be a non-empty universe; the CSFS is mathematically defined as
where i=√−1, μΥ, ρΥ, νΥ∈[0,1] and ℓμΥ, ℓρΥ, ℓνΥ∈[0,2π]. Such that 0≤μΥ(ˊs)2+ρΥ(ˊs)2+νΥ(ˊs)2≤1 and 0≤ℓμΥ(ˊs)2+ℓρΥ(ˊs)2+ℓνΥ(ˊs)2≤2π. The two dimensional information is represented by μΥ(ˊs)ei2π(ℓμΥ(ˊs)), ρΥ(ˊs)ei2π(ℓρΥ(ˊs)) and νΥ(ˊs)ei2π(ℓνΥ(ˊs)).
Definition 5. [45] Suppose that Υ(ϱg)=(μgei2π(ℓμg),ρgei2π(ℓρg),νgei2π(ℓνg)) ∈ CSFS(ˆS) (g∈N). The operational laws for CSFSs is given as follows:
(1)
(2)
(3)
(4)
Definition 6. [24] Consider ˊZ to be a non-empty universe and Υ∈SFS(ˆS׈S) as any spherical fuzzy relation on a set ˆS. Then the following holds:
(1) Υ is reflexive if (μΥ(ˊs,ˊs))=1 , (ρΥ(ˊs,ˊs))=0 and νΥ(ˊs,ˊs) =0,∀ ˊs∈ˆS.
(2) Υ is symmetric if (ˊs,∂)∈ˆS׈S, μΥ(ˊs,∂) = μΥ(∂,ˊs), ρΥ(ˊs,∂) = (ρΥ(∂,ˊs)) and νΥ(ˊs,∂)=(νΥ(∂,ˊs)).
(3) Υ is transitive if (ˊs,d)∈ˆS׈S, μΥ(ˊs,d)≥⋀∂∈ˆS[μΥ(ˊs,∂)∨μΥ(∂,d)], ρΥ(ˊs,d)=⋁∂∈ˆS[ρΥ(ˊs,∂)∧ρΥ(∂,d)] and νΥ(ˊs,d)=⋁∂∈ˆS[νΥ(ˊs,∂)∧νΥ(∂,d)].
Alternatively, the relation Υ is transitive if the following holds for all ˊs,∂∈ˆS and κ1,κ2,κ3∈[0.1]
(a) ∀ d∈ˆS, μΥ(∂,ˊs)≥κ1, and μΥ(ˊs,d)≥κ1⟹μΥ(∂,d)≥κ1,
(b) ∀ d∈ˆS, ρΥ(∂,ˊs)≤κ2, and ρΥ(ˊs,d)≤κ2⟹ρΥ(∂,d)≤κ2,
(c) ∀ d∈ˆS, νΥ(∂,ˊs)≤κ3, and νΥ(ˊs,d)≤κ3⟹νΥ(∂,d)≤κ3.
Definition 7. [24] Consider ˆS to be a non-empty universe and for any subset Υ∈SRS(ˆS׈S) is any arbitrary spherical rough set (SRS) relation on a set ˆS. The pair (ˆS,Υ) denotes the approximation space of the SRS. Now for any ϱ⊆ SFS(ˆS) the lower and upper approximations of ϱ with respect to (ˆS,Υ) are spherical fuzzy sets which are defined follows:
where
and
They are defined such that 0≤(μΥ_(ϱ)(ˊs))2+(ρΥ_(ϱ)(ˊs))2+(νΥ_(ϱ)(ˊs))2≤1 and 0≤(μ¯Υ(ϱ)(ˊs))2+(ρ¯Υ(ϱ)(ˊs))2+(ν¯Υ(ϱ)(ˊs))2≤1.
Υ_(ϱ) and ¯Υ(ϱ) are spherical fuzzy sets so Υ_(ϱ),¯Υ(ϱ):SRS(ˆS)→SRS(ˆS) are upper and lower approximation operators.
Then, the pair Υ(ϱ)=(Υ_(ϱ),¯Υ(ϱ))={⟨ˊs,(μΥ_(ϱ)(ˊs),ρΥ_(ϱ)(ˊs),νΥ_(ϱ)(ˊs)),(μ¯Υ(ϱ)(ˊs),ρ¯Υ(ϱ)(ˊs),ν¯Υ(ϱ)(ˊs))⟩:ˊs∈ˆS} is called a SFRS.
3.
CSFRS
The CSRFS is the most important modification of the CIFS, CPyFS and CSFS because it allows for greater space for experts to provide values for the DM, NeDM and NDM which consist of amplitude and phase terms for the processing of imprecise two-dimensional information. We will combine the concepts of CSFSs and rough sets to introduce the new concept of CSFRSs. For the created models, new operational laws, scores and accuracy mappings are designed and studied.
Definition 8. Consider ˊZ to be a non-empty universe and Υ∈CSFS(ˆS׈S) as any complex spherical fuzzy relation on a set ˆS. Then the following holds.
(1) Υ is reflexive if μΥ(ˊs,ˊs)ei2π(ℓμΥ(ˊs,ˊs))=1 , ρΥ(ˊs,ˊs)ei2π(ℓρΥ(ˊs,ˊs))=0,
and νΥ(ˊs,ˊs)ei2π(ℓνΥ(ˊs,ˊs)) =0,∀ ˊs∈ˆS.
(2) Υ is symmetric if (ˊs,∂)∈ˆS׈S, μΥ(ˊs,∂)ei2π(ℓμΥ(ˊs,∂)) = μΥ(∂,ˊs)ei2π(ℓμΥ(∂,ˊs)),
ρΥ(ˊs,∂)ei2π(ℓρΥ(ˊs,∂)) = ρΥ(∂,ˊs)ei2π(ℓρΥ(∂,ˊs)) and νΥ(ˊs,∂)ei2π(ℓνΥ(ˊs,∂)=νΥ(∂,ˊs)ei2π(ℓνΥ(∂,ˊs).
(3) Υ is transitive if (ˊs,d)∈ˆS׈S,
μΥ(ˊs,d)ei2π(ℓμΥ(ˊs,d))≥⋀∂∈ˆS[μΥ(ˊs,∂)∨μΥ(∂,d)]ei2π(⋀∂∈ˆS[ℓμΥ(ˊs,∂)∨ℓμΥ(∂,d)]),
ρΥ(ˊs,d)ei2π(ℓρΥ(ˊs,d))=⋁∂∈ˆS[ρΥ(ˊs,∂)∧ρΥ(∂,d)]ei2π(⋁∂∈ˆS[ℓρΥ(ˊs,∂)∧ℓρΥ(∂,d)]), and νΥ(ˊs,d)ei2π(ℓνΥ(ˊs,d))=⋁∂∈ˆS[νΥ(ˊs,∂)∧νΥ(∂,d)]ei2π(⋁∂∈ˆS[ℓνΥ(ˊs,∂)∧ℓνΥ(∂,d)]).
Alternatively, the relation Υ is transitive if the following holds for all ˊs,∂∈ˆS and κ1,κ2,κ3∈[0.1].
(a) ∀ d∈ˆS, μΥ(∂,ˊs)ei2π(ℓμΥ(∂,ˊs))≥κ1, and
μΥ(ˊs,d)ei2π(ℓμΥ(ˊs,d))≥κ1⟹μΥ(∂,d)ei2π(ℓμΥ(∂,d))≥κ1,
(b) ∀ d∈ˆS, ρΥ(∂,ˊs)ei2π(ℓρΥ(∂,ˊs))≤κ2, and
ρΥ(ˊs,d)ei2π(ℓρΥ(ˊs,d))≤κ2⟹ρΥ(∂,d)ei2π(ℓρΥ(∂,d))≤κ2,
(c) ∀ d∈ˆS, νΥ(∂,ˊs)ei2π(ℓνΥ(∂,ˊs))≤κ3, and
νΥ(ˊs,d)ei2π(ℓνΥ(ˊs,d))≤κ3⟹νΥ(∂,d)ei2π(ℓνΥ(∂,d))≤κ3.
Definition 9. Consider ˆS to be a non-empty universe and for any subset Υ∈CSRS(ˆS׈S) is any arbitrary CSRS relation on a set ˆS. The pair (ˆS,Υ) denotes the approximation space of the CSRS. Now for any ϱ⊆ CSFS(ˆS) the lower and upper approximations of ϱ with respect to (ˆS,Υ) are CSFSs, which are defined as follows
where
and
Such that
and
Υ_(ϱ) and ¯Υ(ϱ) are CSRSs, so Υ_(ϱ),¯Υ(ϱ):CSRS(ˆS)→CSRS(ˆS) are upper and lower approximation operators. The combination
is called a CSRS.
The complex spherical fuzzy rough values are denoted by Υ(ϱ)=((μg_ei2π(ℓμg_),ρg_ei2π(ℓρg_),νg_ei2π(ℓνg_)),(¯μgei2π(ℓ¯μg),¯ρgei2π(ℓ¯ρg),¯νgei2π(ℓ¯νg))).
Definition 10. [18] Suppose that x,y are two real numbers and α≥0; then, the Hamacher t-norm and t-conorm are respectively defined as follows
where α≥1 and (x,y)∈[0,1]×[0,1].
3.1. Complex spherical fuzzy Hamacher aggregation operators
In this section, we used the Hamacher operators to define complex spherical fuzzy rough operational laws for complex spherical fuzzy rough values (CSFRVs) using the Hamacher t-norm and t-conorm. We are working to develop some aggregation operators for CSFRVs.
Definition 11. Suppose that Υ(ϱ1)=(Υ_(ϱ1),¯Υ(ϱ1))=((μ1_ei2π(ℓμ1_),ρ1_ei2π(ℓρ1_),ν1_ei2π(ℓν1_)),(¯μ1ei2π(ℓ¯μ1),¯ρ1ei2π(ℓ¯ρ1),¯ν1ei2π(ℓ¯ν1))) and Υ(ϱ2)=(Υ_(ϱ2),¯Υ(ϱ2))=((μ2_ei2π(ℓμ2_),ρ2_ei2π(ℓρ2_),ν2_ei2π(ℓν2_)),(¯μ2ei2π(ℓ¯μ2),¯ρ2ei2π(ℓ¯ρ2),¯ν2ei2π(ℓ¯ν2))) are two CSFRVs, where κ>0. Then, the Hamacher t-norm and t-conorm operations for CSFRSs are given by
(1)
(2)
(3)
(4)
We use the score function to compare two or more CSFRVs.
Definition 12. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg))=((μg_ei2π(ℓμg_),ρg_ei2π(ℓρg_),νg_ei2π(ℓνg_)),(¯μgei2π(ℓ¯μg),¯ρgei2π(ℓ¯ρg),¯νgei2π(ℓ¯νg))) ∈ CSRS(ˆS) (g∈N). The score (ˆSˆc) and accuracy (Ac) functions are respectively defined as follows:
and
where ˆSˆc(Υ(ϱg)) ∈[−2,2] and Ac(Υ(ϱg))∈[0,2].
Definition 13. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg))=((μg_ei2π(ℓμg_),ρg_ei2π(ℓρg_),νg_ei2π(ℓνg_)),(¯μgei2π(ℓ¯μg),¯ρgei2π(ℓ¯ρg),¯νgei2π(ℓ¯νg))) ∈ CSRS(ˆS) (g∈N). Then, the following holds:
(1) If ˆSˆc(Υ(ϱ1))>ˆSˆc(Υ(ϱ2)), then Υ(ϱ1)>Υ(ϱ2);
(2) If ˆSˆc(Υ(ϱ1))=ˆSˆc(Υ(ϱ2)), thenΥ(ϱ1)=Υ(ϱ2);
(a) If Aˆc(Υ(ϱ1))>Aˆc(Υ(ϱ2)), then Υ(ϱ1)>Υ(ϱ2);
(b) If Aˆc(Υ(ϱ1))=Aˆc(Υ(ϱ2)), then Υ(ϱ1)=Υ(ϱ2).
4.
Complex spherical fuzzy rough Hamacher aggregation operators
We use the Hamacher operators of CSFRs to define the weighted averaging and geometric aggregation operations described.
4.1. Complex spherical fuzzy rough Hamacher averaging aggregation operators
Definition 14. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg))∈ CSRS(ˆS) (g∈N). Then the WA(H)CSFR aggregation operator can be defined as
where (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1.
Theorem 1. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1. Then the WA(H)CSFR aggregation operator is a mapping Dn→D such that
In Theorem 2, some important properties of the WA(H)CSFR aggregation operators are listed.
Theorem 2. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1. Then the important properties of the WA(H)CSFR aggregation operator are described as follows
(1) (Idempotency): If Υ(ϱg)=Υ(ϱ)=(Υ_(ϱ),¯Υ(ϱ)) ∀ g∈N, then
(2) (Boundedness): Let (Υ(ϱ))−=(mingΥ_(ϱg),maxg¯Υ(ϱg)) and (Υ(ϱ))+=(maxgΥ_(ϱg),ming¯Υ(ϱg)). Then
(3) (Monotonicity): Let P(ϱg)=(P_(ϱg),¯P(ϱg)) ∈ CSFRS(ˆS) (g∈N) such that P_(ϱg)≤ Υ_(ϱg) and ¯P(ϱg)≤¯Υ(ϱg). Then
4.2. Complex spherical fuzzy rough Hamacher ordered averaging aggregation operators
Definition 15. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg))∈ CSRS(ˆS) (g∈N). Then the OWA(H)CSFR aggregation operator can be defined as
where (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1. Thus, Υ(ϱg) is a family of the greatest values.
Theorem 3. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then the OWA(H)CSFR aggregation operator is a mapping Dn→D such that
In Theorem 4, some important properties of the WA(H)CSFR aggregation operators are listed.
Theorem 4. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then, the important properties of OWA(H)CSFR operator are described as follows
(1) (Idempotency): If Υ(ϱg)=Υ(ϱ)=(Υ_(ϱ),¯Υ(ϱ)) ∀ g∈N, then
(2) (Boundedness): Let (Υ(ϱ))−=(mingΥ_(ϱg),maxg¯Υ(ϱg)) and (Υ(ϱ))+=(maxgΥ_(ϱg),ming¯Υ(ϱg)). Then
(3) (Monotonicity): Let P(ϱg)=(P_(ϱg),¯P(ϱg)) ∈ CSFRS(ˆS) (g∈N) such that P_(ϱg)≤ Υ_(ϱg) and ¯P(ϱg)≤¯Υ(ϱg). Then
4.3. Complex spherical fuzzy rough Hamacher geometric aggregation operators
Definition 16. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N). Then, the WG(H)CSFR aggregation operator can be defined as
where (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1.
Theorem 5. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then the WG(H)CSFR aggregation operator is a mapping Dn→D such that
In Theorem 6, some important properties of the WG(H)CSFR aggregation operators are listed.
Theorem 6. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then, the important properties of the WG(H)CSFR operator are described as follows
(1) (Idempotency): If Υ(ϱg)=Υ(ϱ)=(Υ_(ϱ),¯Υ(ϱ)) ∀ g∈N, then
(2) (Boundedness): Let (Υ(ϱ))−=(mingΥ_(ϱg),maxg¯Υ(ϱg)) and (Υ(ϱ))+=(maxgΥ_(ϱg),ming¯Υ(ϱg)). Then
(3) (Monotonicity): Let P(ϱg)=(P_(ϱg),¯P(ϱg)) ∈ CSFRS(ˆS) (g∈N) such that P_(ϱg)≤Υ_(ϱg) and ¯P(ϱg)≤¯Υ(ϱg). Then
4.4. Complex spherical fuzzy rough Hamacher ordered geometric aggregation operators
Definition 17. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N). Then the OWG(H)CSFR aggregation operator can be defined as:
where (κ1,κ2,...κn)T is the weight vector of Υ(ϱg) with κg≥0; ∑ng=1κg=1. Thus, Υ(ϱg) is a family of the greatest values.
Theorem 7. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then the OWG(H)CSFR operator is a mapping Dn→D such that
In Theorem 8, some important properties of the OWG(H)CSFR aggregation operators are listed.
Theorem 8. Suppose that Υ(ϱg)=(Υ_(ϱg),¯Υ(ϱg)) ∈ CSRS(ˆS) (g∈N) and (κ1,κ2,...κn)T is the weight vector of (Υ(ϱ1),Υ(ϱ2),...,Υ(ϱn)) with κg≥0; ∑ng=1κg=1. Then, some important properties of the OWG(H)CSFR operator are described as follow
(1) (Idempotency): If Υ(ϱg)=Υ(ϱ)=(Υ_(ϱ),¯Υ(ϱ)) ∀ g∈N, then
(2) (Boundedness): Let (Υ(ϱ))−=(mingΥ_(ϱg),maxg¯Υ(ϱg)) and (Υ(ϱ))+=(maxgΥ_(ϱg),ming¯Υ(ϱg)). Then
(3) (Monotonicity): Let P(ϱg)=(P_(ϱg),¯P(ϱg)) ∈ CSFRS(ˆS) (g∈N) such that P_(ϱg)≤Υ(ϱg) and ¯P(ϱg)≤¯Υ(ϱg). Then
5.
Algorithm for decision making problems with complex spherical fuzzy rough information
In this section we analyze a decision-making problem in an uncertain environment using the idea of CSFRS aggregation operators. It is essential to take decision-makers' deep learning technique into account when evaluating the deep learning model upon which decisions will be made in various real life situations. We take into consideration a real-time decision problem that applies deep learning methodology using the proposed aggregation operators with CSFRSs.
Decision-making steps.We will construct an algorithm based on the proposed method with CSFRSs in this part. Following are the main steps.
Step 1: Identify the n attributes represented by ℵ={ℵ1,...,ℵn}.
Step 2:Identify the m alternatives represented by ℑ={ℑ1,...,ℑm}.
Step 3: Identify the d experts (E1,...,Ed) that are responsible for selecting the best alternative from a collection of m alternatives for every n attribute.
Step 4: Use the CSFRS information and the decision matrix (E)(k)=Υ(k)ij to evaluate the values for each alternatives.
Step 5: Construct the normalized expert matrices denoted by(N)ˆȷ, as follows.
i=1,2,..,g, j=1,2,..,g, and ˆȷ=1,2,...d.
Step 6a: Aggregate the different preferences Υ(ˆȷ)ij,ˆȷ=1,...,d into Υ(k)ij=(Υ_ij,¯Υij)=((μij_ei2π(ℓμij_),ρij_ei2π(ℓρij_),νij_ei2π(ℓνij_)),(¯μijei2π(ℓ¯μij),¯ρijei2π(ℓ¯ρij),¯νijei2π(ℓ¯νij))) using the WA(H)CSFR aggregation operators.
Step 6b: Aggregate the different preferences Υ(k)ij,k=1,...,d into Υ(k)ij=(Υ_ij,¯Υij)=((μij_ei2π(ℓμij_),ρij_ei2π(ℓρij_),νij_ei2π(ℓνij_)),(¯μijei2π(ℓ¯μij),¯ρijei2π(ℓ¯ρij),¯νijei2π(ℓ¯νij))) using the WG(H)CSFR aggregation operators.
Step 7a:Determine the overall values Υi for each alternative ℑi by using the weight vector η and the OWA(H)CSFR aggregation operators.
Step 7b:Determine the overall values Υi for each alternative ℑi by using the weight vector η and the OWG(H)CSFR aggregation operators.
Step 8: Using Eq (12), calculate the Υi score values.
Step 9: Rank and arrange the alternatives ℑi (i=1,2,....,g) in ascending order based on its Definition 13. The alternative with the highest score value is our best value.
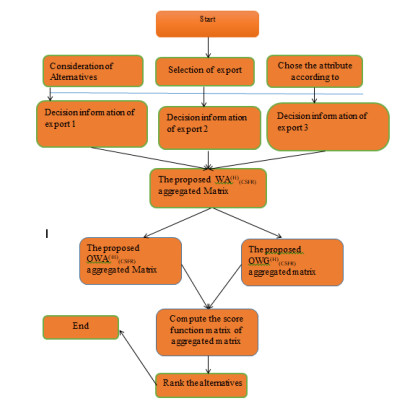
The proposed method is graphically represented in Figure 1.
6.
Case study
This section discusses a applications of the proposed approach for the evaluation of deep learning. Today's Fourth Industrial Revolution (Industry 4.0) is often defined by technology-driven automation and smart and intelligent systems in a variety of application areas such as smart healthcare, business intelligence, smart cities, cybersecurity intelligence and many others [49]. Deep learning algorithms have evolved considerably in terms of performance in a wide range of applications, particularly in security technologies, as an ideal option for discovering complicated architecture in high-dimensional data. As a result of their outstanding ability to learn on historical data, deep learning approaches can play a critical role in developing intelligent data-driven systems that meet todays needs. As a result, deep learning has the potential to revolutionize the planet as well as humans' daily lives through its ability to automate and learn from experience. Deep learning technology is thus applicable to well-known areas of computer science, such as artificial intelligence [50], machine learning [51] and data science with advanced analytics [49]. Although deep learing models have been successfully deployed in a variety of applications, picking an effective deep learning model is a difficult issue. For this, four possible deep learning techniques to consider as alternatives are presented as follows in Step 1.
Step 1.
CNNs (ℑ1): CNNs [6] have a prevalent discriminative deep learning architecture that learns directly from input without requiring human feature extraction. As a result, the CNN improves the design of classic ANNs such as regularized multilayer perceptron networks. Each layer in a CNN considers the optimal parameters for meaningful output while also reducing model complexity. CNNs also employs a 'dropout' [52] to address the issue of overfitting that may arise in a conventional network. CNNs are designed particularly to cope with a broad range of two-dimensional forms and are therefore widely used in visual identification, medical image analysis, image segmentation, natural language processing and many other applications [6,53]. The capacity to automatically uncover crucial properties from input without the need for human interaction makes it more powerful than a typical network.
RNNs(ℑ2): The RNN is another prominent neural network that uses sequential or time-series data and feeds the result from the previous phase as input to the current stage [7,8]. Recurrent networks, like the feed-forward network and CNN, learn from training input but differ in that they have "memory" which allows them to influence current input and output by utilizing information from prior inputs. As a traditional deep neural networks which posits that inputs and outputs are independent of one another, RNN output is dependent on earlier items in the sequence. However, conventional recurrent networks suffer from diminishing gradients, which makes learning large data sequences difficult. Another early paper [54] described a new learning process called backpropagation, which modifies the weights of connections in recurrent networks using internal hidden units. RNNs are frequently employed to process data in the temporal domain (sequential information) due to the presence of an "internal memory" [55].
LSTM(ℑ3): LSTM networks were first proposed in [9] to address RNN concerns with vanishing/exploding gradients. These challenges can arise during the backpropagation over time during the algorithm's training on extended temporal sequences. In this respect, gradients can exponentially attain very low values near zero (vanishing) or very high values (exploding) after repeated operations of compound functions with weight matrices. LSTM introduced the use of "gates", i.e., nonlinear devices that control memory cells using sigmoidal and hyperbolic tangent functions [56]. Despite having the same inputs and outputs as a standard RNN, an LSTM cell has internal recurrence (self-loop) to transmit information flow through a long sequence.
GANs(ℑ4): Deep learning models, which include the AE, GANs and their derivatives, have been classified as generative models. GAN deployment is generally intended for unsupervised learning tasks, but it has also proven to be a better solution for semi-supervised and reinforcement learning activities, depending on the task[10]. GANs are also employed in cutting-edge transfer learning research to enforce the alignment of the latent feature space [57].
Step 2. Description of the criteria for deep learning
There are four different criteria to evaluate the four alternatives as follows.
Data Availability (DA)(ℵ1): Deep learning models often require a substantial amount of labeled data for training. Sufficient and high-quality data are critical for obtaining good performance. The availability and quality of data are important factors in evaluating whether deep learning is a good approach [58].
Model Complexity (MC) (ℵ2): Deep learning models are made up of numerous layers of interconnected artificial neurons that allow them to learn complicated representations from data. The intricacy of the problem at hand may influence the decision to use deep learning. Deep learning may be a useful solution if the task involves the capture of complicated patterns or characteristics.
Computational Resources (CR) (ℵ3) : Deep learning models are computationally intensive and require substantial computational resources, especially when training large-scale models [59]. GPUs, or specialized hardware accelerators are commonly used to speed up training and inference. Availability of such resources and infrastructure is an important consideration.
Interpretability (I)(ℵ4): Deep learning models are frequently referred to as black boxes due to their complicated nature, which makes interpreting their internal workings and decision-making process difficult [60]. If interpretability is critical for a certain application (e.g., healthcare or legal domains), alternate approaches that provide more transparency, such as decision trees or rule-based systems, may be selected.
Step 3. A group of three experts {E1,E2,E3} were formed by CSFRVs.
Step 4. Describe the CSFRVs of the three expert matrices as in Tables 1–3.
Step 5. All criteria are benefits, so it is not necessary to find the normalization, All expert matrices are considered as normalized matrices.
Step 6a. As shown in Tables 1–3, the overall CSFRV matrices were derived with the WA_{CSFR}^{(H)} aggregation operators. Suppose that the weight of the experts is \kappa = \left(0.33, 0.37, 0.3\right) ^{T} and a = 1; the results are shown in Table 4.
Step 7a. As shown in Table 4, the overall CSFRV matrices were derived with the OWA_{CSFR}^{(H)} aggregation operators. Suppose that the weight of the experts is \eta = (0.23, 0.32, 0.25, 0.20)^{T} and a = 1; the results are shown in Table 5.
Step 8.Based on the information in Table 5 and the Definition 12 are shown in Table 6.
Step 9.The ranking of all alternatives \Im _{i} (i = 1, ..., 4) according to the above score values is given in Table 7.
So CNNs (\Im _{1}) is the best alternative.
Influence of the parameter on the final result.
Using the proposed aggregation operators in the overall ranking was the same in terms of the values of the alternatives, as shown in Step 3a above. The ranking of the alternatives shows that \Im _{1} is the best alternative. In order to show the effects of changing the parameter, i.e., 1\leq a\leq 30 in the OWA_{CSFR}^{(H)} operators on the ranking results, all results are shown in Table 8.
Table 9 represents the ranking of the OWA_{CSFR}^{(H)} operators.
Step 6b. Next, we analyze the WG_{CSFR}^{(H)} aggregation operator. Considers that the weight of the experts is \kappa = \left(0.33, 0.37, 0.3\right) ^{T} . After which, for a given decision matrix, we applied the WG_{CSFR}^{(H)} aggregation operators to produce new aggregated values, as shown in Table 10.
Step 7b. We used the OWG_{CSFR}^{(H)} aggregation operator to compute all of the performance values for the alternatives \Im _{i} (i = 1, ..., 4) and the given weight vector \eta = (0.23, 0.32, 0.25, 0.20)^{T} , as shown in Table 11.
Step 8.We used Definition 12 to find the values of the score function, \Upsilon _{i} (i = 1, 2, ...., g) for each CSFRS is given in Table 12.
Step 9.The ranking of all alternatives \Im _{i} (i = 1, ..., 4), according to the above score values is given in Table 13.
So CNNs (\Im _{1}) is the best alternative.
Influence of the parameter on the final result.
Using the proposed aggregation operators in the overall ranking was the same in terms of the values of the alternatives, as shown in Step 3a above. The ranking of the alternatives shows that \Im _{1} is the best alternative. In addition, we used different values of a and the \Im _{i} (i = 1, ..., 4) alternatives in the range of 1\leq a\leq 30 for the OWG_{CSFR}^{(H)} aggregation operators, as shown in Table 14.
Table 15 represents the ranking parameter values for OWG_{CSFR}^{(H)} operator.
7.
Comparative analysis
This part compares the achievement and advantages of the proposed complex spherical fuzzy rough Hamacher aggregations operators and several other existing aggregation operators. Previous research includes different aggregation operators such as the intuitionstic fuzzy weighted averaging and geometric aggregation operators [17] and the intuitionstic fuzzy Hamacher weighted averaging and geometric aggregation operators [18] taking into consideration the phase term to zero. To compare the proposed CSFRSs with IFSs first we convert the CSFRSs to IFSs. Similarly, by comparing the proposed method with different spherical fuzzy aggregation operators such as Dombi averaging/geometric aggregation operators for SFSs [24,30] averaging/geometric aggregation operators for SFRSs, we apply some condition to transform the data into spherical fuzzy set so that the comparison is easy. By evaluating the information with some previous operators and coming to the same optimal decision, the authors were able to use the take different information given above and apply the proposed aggregation operators in the results are same as that of the existing approaches as shown in Table 16.
From Table 16, we can see that the rankings of the alternatives obtained from the proposed operators and existing operators are the same and that the alternative \Im _{1} is the best option.
8.
Conclusions
In this article, we have presented a structured and comprehensive view of deep learning technology and decision making methodologies for selecting deep learning technology, which is considered a core part of artificial intelligence as well as data science. This paper began with a history of ANNs and moved to recent deep learning techniques and breakthroughs in different applications. CSFRS theory has been defined as a complementary extension of CSFS and rough set theories, which helps to solve uncertainty in decision making problems. Aggregating data from different sources into a single data is a very critical issue in the decision-making process, so we have proposed different types of CSFRS aggregation operators, such as the WA_{CSFR}^{(H)} , WG_{CSFR}^{(H)} , OWA_{CSFR}^{(H)} and OWG_{CSFR}^{(H)} aggregation operators based on Hamacher t norms. Also fundamental aspects of these operators have been discussed in depth. Stepwise algorithms to solve real world problems are included. In addition, we address multi-attribtue decision-making issues in the selection of deep learning technology to demonstrate the scope of applicability of the operators proposed in this paper. Finally, to show applicability, we have compared our results with existing decision-making methods.
In the future, the research directions include the aspects below:
(1) Our existing techniques may be extended to include heterogeneous information, as different forms of information are closer to actual scenarios and can accept different criteria.
(2) We can use Frank, Yager and Einstein norms to develop generalized aggregation operators to handle uncertain information.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 748-611-1443). The authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflict of interest
The authors declared that there is no conflict of interest regarding the publication of this paper.









 DownLoad:
DownLoad:



