A successive midpoint method for nonlinear differential equations with classical and Caputo-Fabrizio derivatives

1.   Introduction

A legally accepted relationship or settlement agreement involving two people establishes duties and responsibilities amongst them, their respective in-laws, and the community as a whole. When an intimate physical engagement is genetically accepted, it is regularly alluded to as marriage or consensual incest ^[1]. Marriage was intended to be a non-acrimonious partnership from the beginning. Nevertheless, unpleasant situations have surfaced, with the divorce process being the most common. When the proportion of unfavorable to desirable deeds is equal to or larger than unity, the latter phenomenon is more probable to occur. Divorce is defined as the dissolution of a two-person union ^[2], and it has a negative impact on domestic organizations in today's society. This vexing pattern persists unabated throughout Asia and the civilized world. Forced marriage, illiteracy, poverty, extramarital intimacy and pregnancy, betrayal, and a dearth of religious commitment are just a few of the causative factors of a breakup ^[3].

Divorce is an alarming trend that, like any sickness, has an influence on the psychological and cultural formation of modern civilization. About half of all early marriages in the system end in divorce ^[4], with subsequent unions having significantly higher divorce rates ^[5]. Separation frequently leads to divorce, with 75 percent of separations ending in divorce ^[6]. Separation conditions have been linked to a higher prevalence of juvenile adversity and unemployment ^[7]. It is critical to eradicating this lethal sociological plague from our civilization.

In recent years, the numerical formulation has been utilized as a powerful strategy in the prevention of outbreaks, and one might apply it to the prevention of separation in matrimonial organizations. The impact of economic growth ^[8] and cultural propagation ^[9] on separation patterns has been a source of worry in the past. In particular, ^[2] has suggested a framework for the rise of separation in Ghana, dividing incidents into three categories: marital, divorced, and separated. Similarly, ^[2] expanded their research to encompass individuals who had not taken particular steps to avoid separation. Several researchers have investigated various mathematical models in this area, which can be found in references ^[10,11,12].

Fractional calculus (FC) is defined as the advancement or modification of conventional derivatives and integrals to non-integer order instances, has received considerable scholarly emphasis in recent times ^{[13,14,15,16]}. According to the research, numerous scientific and other physical processes involve fractional derivatives, including ideological, aquifer, electrostatics, financing, and hydrodynamics, to highlight a few ^[17,18].

Several researchers have explored the simulated predictions owing to the availability and distinctiveness of fractional differential equation systems in diverse configurations, for example, ^{[19,20,21,22]}. In FC, there are three types of fractional derivative/integral formulations: the Riemann-Liouville and Caputo derivatives, which are a concatenation of power law (PL) functions ^[17], including the first derivative; the Caputo-Fabrizio fractional derivative, which is a combination of the first derivative and the exponential decay (ED) law ^[23], including the Delta-Dirac feature; and the Atangana-Baleanu fractional derivative ^[24], which has a generalized Mittag-Leffler (GML) as a kernel ^{[25,26,27,28]}. The majority of the relevant and purposeful formulations in the various configuration domains of such fractional-order derivative formulations in the scope of FC, which includes numerical simulations modeled with formulae utilizing these three types of kernels, can be found in significant relevant scholarly studies in ^{[29,30,31,32,33,34]} and the references cited therein.

Except for the previously mentioned continuous advancement that originated from the interaction of ideologies between L'Hopital and his advisor Leibniz, researchers in ^{[35,36,37,38]} proposed some other revolutionary notion in which conventional differentiation is lengthened to the core principle of fractal differentiation derivative, with the result that unless the fractal-order approaches 1, the conventional derivative is recovered. Furthermore, the fractal derivative is equivalent to $\alpha \zeta^{\alpha-1}$ if the mapping is differentiable. Although this differential formulation has been employed in a number of cases, the concept has yet to be recognized and implemented in the domains of mathematics, physics, and bio-sciences. However, this fractal derivative concept emerges in several natural phenomena; for example, favorable aquifer circulation pathways can be recorded by applying such a novel concept. Certain individuals assume there's nothing really novel or revolutionary, but it is evident, or at least can be claimed, that combining two existent materials can result in a creative and inventive notion, or at the very best, a customized rendition of the key construct. This additional feature will be much more effective and convenient than the previous versions.

In 2017, Atangana ^[39], proposed a novel notion of differentiation, which is termed "fractal-fractional" (FF), in which the researcher recommended the fractal derivative of the combination of a specified function utilizing three previous notions, notably the PL kernel, the ED kernel, and the GML function. The concept is novel, and it appears to have offered up significant avenues of exploration into a wide range of scientific domains, encompassing economics, hydrodynamics, life science, randomness, hydrology, acoustic emission, physiology, biomechanics, and plenty of others ^[40,41]. The researcher ^[39] suggested that the fractional formulation can only represent a handful of complicated situations, whereas the fractal derivative can catch various forms of intricacies, and that integrating theories can allow us to effectively comprehend the challenges of precise existence ^[42,43]. Atangana and Qureshi ^[44] recently introduced the modeling of chaotic dynamic system attractors using FF operators, and Goméz-Aguilar ^[45] proposed chaos and multiple attarctors in a FF model. Shinriki's oscillator system and Rashid et al. ^[46] presented a revolutionary FF model for comprehending the oscillatory and challenging behavior of the human liver with a GML kernel. Etemad et al. ^[41] contemplated a novel mathematical analysis on the FF model of the AH1N1/09 virus and its generalized Caputo-type version. Khan et al. ^[26] expounded a case study of FF tuberculosis model in China. Rezapour et al. ^[27] defined a theoretical and numerical analysis of a FF two-strain model of meningitis.

Owing to the aforementioned proclivity, we proposed a numerical framework for the propagation of the breakup outbreak, similar to other researchers ^[9,47] via the Atangana-Baleanu fractional derivative in the Caputo perspective and the FF operator in the Atangana-Baleanu fractional derivative context. Meanwhile, the existence and uniqueness results are derived via the aforesaid model. Besides that, we add a category of reconstituted marital instances involving anti-divorce counseling and reconciliation to the system of ^[47], in which the cohesive societal disturbance is propagated by divorced and separated people over partnered people, applying the conventional incidence functional as the cause of spousal disharmony. This is a key element that has been lacking in earlier research. A system for qualitative analysis of the divorce epidemic has been developed via the FF Atangana-Baleanu operator. Graphical illustrations are demonstrated by incorporating the fractional-order and fractal-dimension with varying values. A simulation scheme is presented for with and without counseling control via the Atangana-Baleanu fractional derivative in the Caputo perspective, respectively. Our contribution to this new approach is to design this mathematical structure via the newly-defined hybrid Mittag-Leffler kernel. Also, for the first time, in this paper, we derive numerical schemes for the FF divorce epidemic model with the help of the Newton polynomials and by comparing our results with the Adams-Bashforth simulations. In this direction, we can see some dynamical behaviors of the solutions in our simulations.

To follow this study, the Section "Preliminaries" is devoted to recalling some definitions. The main structure of the FF divorce epidemic model is presented in Section 3. The existence analysis and positivity of the proposed model are conducted with the qualitative aspects, such as disease-free equilibrium and stability analysis, presented using appropriate Lyapunov's candidates. Section 4 investigates the unique solutions using the Banach contraction principle. Fractal-fractional divorce epidemic model analysis is also presented in the sense of the Cauchy problem. To simulate the suggested model numerically, we use a new type of two-step Lagrange polynomials in the context of the Adams–Bashforth method to derive some algorithms in Section 5. In Section 5, by using Matlab, we analyze the behaviors of solutions during a finite time period and try to investigate the role of some parameters in controlling the epidemic by varying the values of dimensions and orders. The conclusions are presented in the Section "Conclusions".

2.   Preliminaries

It is vital to investigate some basic FF operator theories before continuing on to the mathematical formulation. Consider the function $\mathbf{w}(\zeta)$, which is continuous and fractal differentiable on $[c, d]$ with fractal-dimension $\eta_{2}$ and fractional-order $\eta_{1}$, as well as the specifications available in ^[39].

Definition 2.1. (^[39]) The fractal-fractional operator of $\mathbf{w}(\zeta)$ containing the power-law kernel in the context of Riemann-Liouville can be stated as follows for $\eta_{1}\in[0, 1]$:

where

and $\mathbf{u}-1 < \eta_{1}, \eta_{2}\leq \mathbf{u}\in\mathbb{N}.$ Also, $\Gamma(\zeta) = \int_{0}^{\infty}e^{-u}u^{\zeta-1}d\zeta$ signifies the Gamma function.

Definition 2.2. (^[39]) The fractal-fractional operator of $\mathbf{w}(\zeta)$ containing the exponential decay kernel in the context of Riemann-Liouville can be stated as follows for $\eta_{1}\in[0, 1]$:

such that $\mathbf{s}(0) = \mathbf{s}(1) = 1$ having $\eta_{1} < 1, \; \eta_{2}\leq \mathbf{u}\in\mathbb{N}.$

Definition 2.3. (^[39]) The fractal-fractional operator of $\mathbf{w}(\zeta)$ containing the generalized Mittag-Leffler kernel in the context of Riemann-Liouville can be stated as follows for $\eta_{1}\in[0, 1]$:

such that $\mathbb{ABC}(\eta_{1}) = 1-\eta_{1}+\frac{\eta_{1}}{\Gamma(\eta_{1})}$ having $\eta_{1} < 1, \; \eta_{2}\leq 1\in\mathbb{N}.$

Definition 2.4. (^[39]) The corresponding fractal-fractional integral formulation of (2.1) is defined as:

Definition 2.5. (^[39]) The corresponding fractal-fractional integral formulation of (2.2) is defined as:

Definition 2.6. (^[39]) The corresponding fractal-fractional integral formulation of (2.3) is defined as:

Definition 2.7. (^[24]) Let $\mathbf{w}\in H^{1}(\upsilon, \lambda), \; \; \upsilon < \lambda$ and the Atangana-Baleanu fractional derivative operator is defined as:

where $\mathbb{ABC}(\eta_{1})$ denotes the normalization function.

3.   Model description

The observed system was inspired by the research of ^[47], and the fundamental framework can be described as follows:

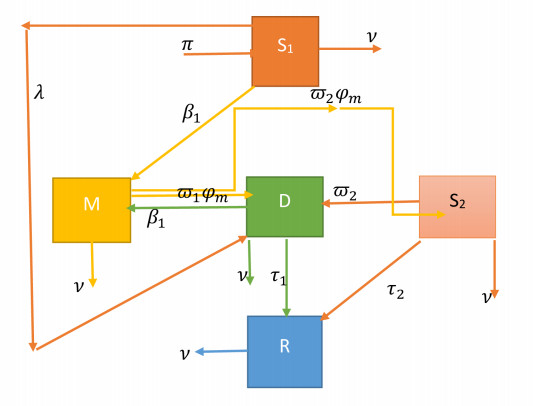
subject to the ICs $\mathcal{S}_{1}(0) = {\mathcal{S}_{1}}_{0}, \; \mathcal{M}(0) = {\mathcal{M}}_{0}, \; \mathcal{D}(0) = {\mathcal{D}}_{0}, \; \mathcal{S}_{2}(0) = {\mathcal{S}_{2}}_{0}, \; \mathcal{R}(0) = {\mathcal{R}}_{0}.$ According to the hypothesis provided and the schematic representation in Figure 1, a relatively comprehensive concept of the divorce outbreak (3.1) with anti-divorce counseling. People who are unmarried or who are eager to marry but have not actually committed. The population of bachelors who intend to marry at time $\zeta$ is represented by $\mathcal{S}_{1}(\zeta)$. Certain isolated situations may result in separation but not the other way around, whereas $\mathcal{M}(\zeta)$ refers to the proportion of coupled cases at time $\zeta.$ Unbreakable marriages or separated situations can be reconciled. The proportion of separated individuals at time $\zeta$ is indicated by $\mathcal{D}(\zeta)$. Those who have been divorced and are unable to remarry are now represented by $\mathcal{S}_2(\zeta)$, which is denoted as separated cases at time $\zeta.$ Divorced individuals have the option of remarrying or remaining single. Furthermore, $\mathcal{M}(\zeta)$ represents the proportion of restored marital cases at $\zeta.$ It can be seen that the approximated parameters by the proposed model (3.1) are close to the curve of real data which validates the accuracy of the presented model in this study. (see; Table 1). The anti-divorce setting is changed when $0\leq\alpha\leq1.$ The model (3.1) is obtained using the following flow diagram of the divorce pandemic as follows:

3.1.   Positivity and boundedness of the divorce model

To show that the (3.1) divorce framework is significant, we must show that the system's corresponding parameters are non-negative at all times $\zeta$. This is addressed more simply by noting that the divorce model with non-negative starting circumstances remains non-negative for all $\zeta > 0$. The preceding is a lemma.

Lemma 3.1. Assume that the initial data $\mathcal{G}(0)\geq0,$ where $\mathcal{G}(\zeta) = \big(\mathcal{S}_{1}(\zeta), \mathcal{M}(\zeta), \mathcal{D}(\zeta), \mathcal{S}_{2}(\zeta), \mathcal{R}(\zeta)\big).$ Thus, the model solution's described by (3.1) are non-negative for $\zeta > 0.$ Also, $\lim\limits_{\zeta\mapsto\infty}\leq\frac{\pi}{\upsilon}$ having $\mathcal{N}(\zeta) = \mathcal{S}_{1}(\zeta)+\mathcal{M}(\zeta)+\mathcal{D}(\zeta)+\mathcal{S}_{2}(\zeta)+\mathcal{R}(\zeta).$

Proof. Suppose $t_{*} = \sup\big\{\zeta > 0:\mathcal{G}(\zeta) > 0\in[0, \zeta]\big\}.$ Therefore, $t_{*} > 0.$ For (3.1), we find the corresponding outcomes as

(3.2) can be written as:

Thus,

Observe that

Repetition of the earlier procedures for the remaining system elements $(3.1),$ we can obtain $\mathcal{G}(\zeta) > 0$ for any $\zeta > 0$.

Now, summing up all cohorts of the model (3.1) leads to the following

with $\mathcal{N} = \mathcal{S}_{1}+\mathcal{M}+\mathcal{D}+\mathcal{S}_{2}+\mathcal{R}.$

Consequently, we have

which is the desired result.

Furthermore, we present the feasible region for the divorce epidemic model (3.1). Assume that the invariant domain

Now, the underlying findings are presented for the viable region.

Lemma 3.2. Assume that the domain presented by $\nabla$ is positively invariant for the divorce epidemic model (3.1) with $\mathcal{S}_{1}(0) = {\mathcal{S}_{1}}_{0}, \; \mathcal{M}(0) = {\mathcal{M}}_{0}, \; \mathcal{D}(0) = {\mathcal{D}}_{0}, \; \mathcal{S}_{2}(0) = {\mathcal{S}_{2}}_{0}, \; \mathcal{R}(0) = {\mathcal{R}}_{0}.$

Proof. By using hypothesis (3.3), then the divorce epidemic model leads to

So that $\frac{d\mathcal{N}}{d\zeta}\leq0,$ if $\mathcal{N}(0)\geq\frac{\pi}{\upsilon}.$ Hence, $\mathcal{N}(\zeta)\leq\mathcal{N}(0)\exp(-\upsilon \zeta)+\frac{\pi}{\upsilon}(1-\exp(-\upsilon \zeta)).$ Ultimately, the region presented by $\nabla$ is positively invariant. Also, $\mathcal{N}(0)\geq\frac{\pi}{\upsilon},$ then $\mathcal{N}(\zeta)$ approaches to $\frac{\pi}{\upsilon}$ asymptotically. Therefore, the domain presented by $\nabla$ contain all solutions in $\mathbb{R}_{+}^{5}.$

3.2.   Divorce epidemic model for FF operator

Divorce is the dissolution of two parties' marriage. As a result of the prevalence of divorce, there have been attacks on the family and attempts to redefine marriage in modern society. To deal with this social disaster, we create a fractional model of the fractal-fractional operators type, with the fractional order $\eta_{1}$ and fractal dimension $\eta_{2}.$ Fractal-fractional differential equations transfer the order and dimension of every dynamical system into a rational one. To upgrade and improve the approximate results, inspired by the standard model (3.1), we present a mathematical FF model on the dynamics of divorce epidemics under the effect of restored marital cases via the generalized Mittag-Leffler-type kernel as

where $\eta_{1}$ signifies the fractional-order and $\eta_{2}$ denotes the fractal-dimension, respectively.

3.3.   Existence and positivity of the divorce epidemic model

Here, we investigate the model's (3.4) validity and usefulness.

Theorem 3.3. Assume that there is a unique positive solution for the system (3.4) and stays in $\mathbb{R}_{+}^{5}.$

Proof. First, we present the following outcomes to identify that the solution of the model (3.4) is positive:

For all $\zeta\geq0,$ we conclude that the system solution remains in $\mathbb{R}_{+}^{5}.$

Observe that

Finally, the realm of biological viability for the system (3.4) can be demonstrated by

Furthermore, the concept of divorce epidemic provided before (3.4) in the FF operators' Atangana-Baleanu is applied to obtain the steady state of the aforesaid model.

3.4.   Disease free equilibrium (DFE)

The system (3.4) comprises the following configuration in its steady state as

we have the following

The basic reproductive number $\bar{\mathbb{R}}$, which may be determined by applying the next-generation matrix ^[48] for the system (3.4), can be used to investigate the efficacy of DFE at $\mathcal{E}_{0}.$ The divorce regulated reproductive number, denoted by $\bar{\mathbb{R}}_{c}$ herein, is determined using the conventional notation presented as

where

In the nonappearance of anti–divorce counseling and reunion, we get the breakup reproduction number by setting $\alpha = 0, \; \tau_{1} = 0, \; \tau_{2} = 0,$ we have

Furthermore, we only have reproductive data for individual interventions in regards of anti–divorce counseling and unification:

The divorce epidemic model (3.4) is locally asymptotically stable at the DFE $\mathcal{E}_{0}$, as shown in the presented model. Predicated on ^[48], we arrive at the following conclusions:

Theorem 3.4. The divorce epidemic model (3.4) at the DFE $\mathcal{E}_{0}$ is locally asymptotically stable if $\bar{\mathbb{R}}_{c} < 1$ which admits

Proof. The presence of endemic divorce equilibrium comes directly from the following

when $\varphi_{m}^{\ast}\neq0$. Therefore, the divorce-endemic steady state can be obtained by utilizing (3.11), is denoted by $\mathcal{E}_{1} = \big(\bar{\mathcal{S}_{1}}, \bar{\mathcal{M}}, \bar{\mathcal{D}}, \bar{\mathcal{S}_{2}}, \bar{\mathcal{R}}\big).$

Notice from (3.11), $\varphi_{m}^{\ast} > 0$ if and only if $\bar{\mathbb{R}}_{0} > 1$ and $\beta_{2} < \beta_{1}$, which are the essential prerequisites for divorce to prevail in the marriage contract.

The accompanying is the consequence of the linearization procedure of the system (3.1) at divorce endemic obtained by the Jacobian matrix:

From the aforesaid system (3.12), we can write

with the corresponding characteristic polynomial is

where

According to the Routh-Hurwitz stability condition ^[49], which admits that for the assumption reported $b_{1}b_{2}b_{3} > b_{3}^{2}+b_{1}^{2}b_{0},$ where $b_{\ell} > 0$ for all $\ell = 1, 2, ..., 4.$ Ultimately, the Rough-Hurtwiz assumptions assure the local asymptotic stability of the divorce model (3.4) at DFE $\mathcal{E}_{0}.$ As can be seen, all of the coefficients in (3.13) are non-negative. This demonstrates that $\bar{\mathbb{R}}_{c} > 1$ and ${\bar{\mathcal{M}}} < {\mathcal{N}}.$ It is clear that the endemic equilibrium of divorce if $\bar{\mathbb{R}}_{c} > 1$ and ${\bar{\mathcal{M}}} < {\mathcal{N}}$ is localized asymptotically.

3.5.   Stability analysis

Here, employing the noted stability technique of the Lyapunov candidate ^[50], this report outlines the global behavior of framework (3.4) at the divorce-free steady state.

Theorem 3.5. Suppose that the system (3.4) satisfies a global asymptotic divorce-free steady state if and only if $\bar{\mathbb{R}}_{c} < 1.$

Proof. Applying a matrix theoretic technique, as shown in ^[50], that generates the corresponding Lyapunov candidate

whose $\, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}$ yields

Simple computations yield

Observe that in divorce-free steady state, $\frac{\mathcal{M}}{\mathcal{N}} = \frac{\mathcal{M}^{0}}{\mathcal{N}^{0}} = \frac{\beta_{1}}{\upsilon+\beta_{1}}.$ Thus, we have

Hence, $\, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}(\mathcal{U}(\zeta)) = (\xi_{1}\mathcal{D}+\xi_{2}\mathcal{S}_{2})(\bar{\mathbb{R}_{c}}-1), \; \, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}(\mathcal{U}(\zeta))\leq0$ and $\mathcal{D} = \mathcal{S}_{2} = 0.$ According to Lyapunov's stability criterion ^[49], $\mathcal{E}_{0}$ is a globally asymptotically steady state point.

Theorem 3.6. For $\beta_{2} = 0,$ then the divorce-endemic steady state of model (3.4) is globally stable if $\bar{\mathbb{R}}_{c} > 1.$

Proof. Considering the Lyapunov candidate $\mathcal{X}(\zeta)$ ^[51] presented as follow

are positive constants $\psi_{1}, \psi{2}, ..., \psi_{5}$ must be specifically selected.

Applying $\, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}$ on (3.14) and in view of (3.4) with the substitution $\beta_{2} = 0$ produces

At $\mathcal{E}_{1} = (\bar{\mathcal{S}_{1}}, \bar{\mathcal{M}}, \bar{\mathcal{D}}, \bar{\mathcal{S}_{2}}, \bar{\mathcal{R}}),$ we have

Thus, we have

As $(\mathcal{S}_{1}, \mathcal{M}, \mathcal{D}, \mathcal{S}_{2}, \mathcal{R})\neq(\bar{\mathcal{S}_{1}}, \bar{\mathcal{M}}, \bar{\mathcal{D}}, \bar{\mathcal{S}_{2}}, \bar{\mathcal{R}}), \; \, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}(\mathcal{X}(\zeta)) < 0, \; \, ^{\mathbf{FF}}\mathbb{D}_{0, \zeta}^{\eta_{1}, \eta_{2}}(\mathcal{X}(\zeta)) = 0$ if $\mathcal{S}_{1} = \bar{\mathcal{S}_{1}}, \; \mathcal{M} = \bar{\mathcal{M}}, \; \mathcal{D} = \bar{\mathcal{D}}, \mathcal{S}_{2} = \bar{\mathcal{S}_{2}}, \mathcal{D} = \bar{\mathcal{D}}.$ According to Lyapunov's stability criterion ^[49], divorce endemic is globally stable.

4.   Existence and uniqueness results for divorce epidemic model

Here, we intend to replace the first-order derivatives using innovative Atangana-Baleanu fractional derivative in Caputo sense to strengthen the system (3.1), as demonstrated in

Employing the fixed point hypothesis, we evaluate the existence of a unique solution for the problem (4.1). To apply it, we convert the (4.1) divorce epidemic model into an integral formulation that includes the fractional order integral operator (2.7). The mechanism (4.1) can be written as follows:

The vector $\Phi(\zeta) = (\mathcal{S}_{1}, \mathcal{M}, \mathcal{D}, \mathcal{S}_{2}, \mathcal{R})$ reflects the initial configuration of parameters $\Phi_{0} = \big(\mathcal{S}_{1}(0), \mathcal{M}(0), \mathcal{D}(0), \mathcal{S}_{2}(0), \mathcal{R}(0)\big)$ illustrates the basic requirements that were described in (4.2). Additionally, $\mho$ denotes a continuous vector function as shown in:

Furthermore, the function $\mho$ admits the Lipschitz hypothesis stated as as:

Hence, $\Phi$ is a contraction from (4.3). Thus, (4.2) has a unique solution and so does the system (4.1) has a unique solution.

Now, we use the underlying argument to arrive at the desired result.

Theorem 4.1. The system (4.2) admits a unique solution if

Proof. By means of Definition 2.7 and considering (4.2), then the scheme is transformed to a Volterra integral equation as follows:

Considering $\intercal = (0, \mathbf{T})$ and the functional $\mathbf{g}:\mathbb{C}(\intercal, \mathbb{R}^{5})\mapsto\mathbb{C}(\intercal, \mathbb{R}^{5})$ stated as

Ultimately, (4.5) can be simplified as

Applying the supremum norm $\intercal$ indicated by $\|.\|_{ \intercal}$ is written as:

Clearly, the Banach space $\mathbb{C}(\intercal, \mathbb{R}^{3})$ have the norm $\|.\|_{ \intercal}.$ Furthermore, the ensuing variant is easily verified:

such that

In view of (4.7), one can find

Additionally, considering (4.3), (4.9), and triangular variant, (4.11) gives:

Consequently, this leads to the subsequent conclusion:

where

So that the expression $\mathbf{g}$ holds the (4.4) criterion, it can be a contraction mapping. As a result, the scheme suggested by (4.2) has a unique solution.

In this part, we utilize Definition 2.3 to reconstruct the conventional integer-order divorce epidemic framework using the revolutionary FF operator. The divorce epidemic framework that develops when the FF operator is analyzed can be described in (3.3). Furthermore, the existence and uniqueness of the divorce epidemic framework developed in the FF operator are discussed clearly. To provide it, we shall use the following expression to produce the generic Cauchy problem containing a FF derivative:

In view of Definition (2.3), the right hand side of (4.12) gives the foregoing expression:

By making the use of integral operator, the conclusions are as follows:

Employing the Picard-Lindelöf method, we were able to

where $\overline{\mathfrak{I}_{\mathbf{u}}({\zeta}_{\mathbf{u}})} = \big[{\zeta}_{\mathbf{u}-\upsilon_{1}}, {\zeta}_{\mathbf{u}+\upsilon_{1}}\big], \; \overline{\mathfrak{P}_{0}(\Delta_{0})} = \big[{\zeta}_{0}-\nu_{1}, {\zeta}_{0}+\nu_{1}\big].$

Assume the following:

In particular, the norm is written as follows:

and introduce the functional

defined as

The essential objective is to demonstrate that the above function can convert a completely empty metric space onto itself. We also intend to illustrate that it has the competence to identify contractions. Therefore, we reveal that

Putting $\mathbf{x} = \zeta\mathbf{w},$ then it produces the following

Consequently,

Therefore, considering $\Delta_{1}, \Delta_{2}\in\complement[\mathfrak{I}_{\mathbf{u}}({\zeta}_{\mathbf{u}}), \mathfrak{P}_{\mathfrak{b}}({\zeta}_{\mathbf{u}})].$ To find at the following modifications, apply the Banach fixed point theorem:

where $\mathfrak{L}_{\Phi} < 1.$

Using the fact of contraction mapping $\Psi,$ so that

Therefore, we have

As a result, assuming the underpinning supposition is valid:

then the contraction supposition is fulfilled, thus, we have

Finally, the above process state that (3.3) has a unique solution. This completes the proof. In the next subsection, we explain the numerical methods for the proposed divorce epidemic system.

5.   Numerical approximations for the divorce epidemic model

Firstly, we established the numerical outcomes with the aid of the modified Adams-Bashforth method via the ABC fractional derivative operator, and then we found the numerical results using the Newton polynomial approach via the FF operator technique.

5.1.   Modified Adams-Bashforth method

To begin, we employ the modified fractional Adams–Bashforth approach introduced by ^[52] to assess the fractional system (4.1).

The foremost mechanisms in the construction strategy of the fractional divorce epidemic system (4.1) are effectively described using a modified Adams-Bashforth technique. Following implementing the ABC integral to construct (2.7), we currently get the following integral equation:

Also, plugging $\zeta = {\zeta}_{ \mathbf{s}+1},$ where $\mathbf{s} = 0, 1, 2, ...,$ yields

Here, we compute the functional by attempting to use the interpolation polynomial technique $\Lambda(\tau, \Phi(\tau))$ on $[{\zeta}_{\ell}, {\zeta}_{\ell+1}]$:

(5.1) diminishes to

As a consequence of merging the integrals in (5.2), we obtained the following results:

5.2.   Newton polynomial approach

Now, we perform a detailed evaluation of the mathematical system (3.4), which is based on a promising means developed using the Newton polynomial strategy. This methodology, which was initially envisioned in ^[53], seems to be more effective than the alternative methods available in the investigation. To continue ahead, utilizing the plan, we employ the formula.

Integrating (5.3) with respect to $\mathbf{x}$ over $0$ to $\zeta$, we find

Taking $\mathcal{W}(\zeta, \Delta(\zeta)) = \eta_{2}\zeta^{\eta_{2}-1}\Psi(\zeta, \Delta(\zeta)),$ then (5.4) reduces to

At ${\zeta}_{\mathbf{u}+1} = (n+1)\Delta \zeta,$ we have

Also, we get

Using the fact of the Newton polynomial to find the function $\mathcal{W}(\zeta, \Delta(\zeta))$, we have

Substituting (5.8) into (5.5), gives

Simple computations yield, we have

Note that

After simplifying, we have

It follows that

Thus, the general approximate divorce epidemic model:

5.3.   Results and discussion

In what follows, we numerically simulated the suggested systems (3.3) and (4.1) employing the MATLAB programming and the system parameters listed in Table 1 to facilitate comprehension of the examined outcomes via the FF operator in the Atangana-Baleanu context.

Figures 2–4 show that couples who attend marital information sessions and have a sense of reconciling in addressing respective conflicts have a better chance of progressing or enduring in their relationship for a longer period of time. However, if the aforesaid rules are disregarded, the relationship can simply disintegrate. Figures 2–4 depict the influence of anti-divorce regulation on separated individuals via the FF derivative operator. While rapprochement and anti-divorce counseling are lacking, and incidences of marital dissolution (divorce) continue consistently in the parental network. Additionally, the findings show that by using regulations, separated instances in marital establishments may be eradicated, and married couples who stay married for up to 3 decades can have a compassionate domestic framework and no more separate their mates when there is decrease in fractional-order and a significant boost in the fractal-dimension, respectively.

Figures 5–7 show how increasing the incidence of unification benefits fractured communities by reconnecting them and thus increasing the proportion of incidents healed via the FF derivative operator in the Atangana-Baleanu context. Lacking a proper rapprochement procedure, estranged or emancipated couples will stay dysfunctional. Furthermore, Figures 5–7 show the effect of $\beta_{2}$ on divorcees. The significant variability in $\beta_{2}$ diminishes the number of marriages that end in disaster. As a result, it is reasonable to conclude that re-marriage between the divorcing aids in the reunification of fractured communities when the fractional-order increases and there is a significant decrease in fractal-dimension.

The delimited instances in Figures 8–10 expand rapidly in comparison to the marital situations via the FF derivative in the context of the Atanagan-Baleanu operator. This suggests that as long as couples remain united, domestic dysfunction in the form of relationship breakdown is likely to occur. Alternatively, divorce cannot occur in the absence of a marital relationship, and the greater the number of incidents of people getting married, the greater the number of divorced couples. We noticed the system's reproductive quantities' behavioral tendencies in relation to the variant $\bar{\mathbb{R}}_{c} < \bar{\mathbb{R}}_{b} < \bar{\mathbb{R}}_{ad} < \bar{\mathbb{R}}_{u}.$ This represents the fact that using an amalgamation of rapprochement and anti-divorced procedures is more effective in preserving relationships than using a solitary therapy incorporating the decrease in fractional-order and keeping fractal-dimension fixed, respectively.

In Figures 11–13, the estimate grows in the situation where the individuals have not received adequate preconception counseling and also don't resolve their disagreements on a regular basis with the FF derivative operator in the Atangana-Baleanu perspective. Furthermore, the findings suggest that matrimonial individuals who have been together for more than 1.5 decades without separating are less predisposed to breakup when fractal-dimension is increased and fractional-order is assumed to be $1,$ respectively.

Figures 14–16 show that using the Atanagan-Baleanu fractional derivative in the Caputo context and the scheme developed in subsection 5.1 reduces breakup significantly in the early stages. This rise in difficulty encourages individuals to seek counseling; that increases in the first few weeks but then falls and stabilizes after several months, implying that it drives the wider community to marry, but as counseling declines, remarriage declines as well. Figures 17–19 show the numerical and graphical results, which show that these two numerical algorithms produce the same results with minor differences. Also, we investigated the effect of fractal dimensions and fractional orders on these simulations. Also, the effect of different values for the average number of separated people and the restored cases was simulated in some graphs under the Adams-Bashforth method. This study showed that we can predict the next behavior of the FF divorce epidemic model via the two mentioned numerical methods and their results are more accurate and identical.

Additionally, it is critical to note that, as indicated in ^[2], peace in family reunification is preferable to marital seminars/courses.

6.   Conclusions

The evolution of the divorce pandemic combined with anti-divorce counseling has been established and investigated by considering two novel fractional derivative operator techniques depending on the generalized Mittag-Leffler function. At both equilibria, the structures were shown to be locally and globally asymptotically robust. At a divorce-free steady state, four basic reproduction number $\bar{\mathbb{R}}$ have been estimated, indicating that separation will never be an outbreak in the population if counseling is provided. The Picard-Lendelöf mechanism is performed to prove its existence and uniqueness. In the following experiments, the proposed divorce epidemic system is reconstructed using a novel fractional-fractal operator in the Atangana-Baleanu perspective. The existence and uniqueness of the fractional-fractal divorce epidemic framework are shown. Additionally, powerful and robust methods were used to examine both the aforesaid fractional frameworks. We conclude that the fractal-fractional model provides a solid understanding of epidemic dynamics and may be implemented as a trustworthy modeling approach based on the graphical outcomes. The investigation's numerical findings imply that the existence of corrective measures, including marital seminars/courses and rapprochement attempts, can assure protracted successful marriages and avoid or restore social dynamics breaches (detachment or separation).

Conflict of interest

The authors declare no conflicts of interest.