In this article, the generalized (N+1)-dimensional nonlinear Boussinesq equation is analyzed via Lie symmetry method. Lie point symmetries of the considered equation and accompanying invariant groups are computed. After transforming the equation into a nonlinear ordinary differential equation (ODE), analytical solutions of various types are obtained using the (G′/G,1/G) expansion method. The concept of nonlinear self-adjointness is used in order to determine nonlocal conservation laws of the equation in lower dimensions. By selecting the appropriate parameter values, the study provides a graph of the solutions to the equation under study.
Citation: Amjad Hussain, Muhammad Khubaib Zia, Kottakkaran Sooppy Nisar, Velusamy Vijayakumar, Ilyas Khan. Lie analysis, conserved vectors, nonlinear self-adjoint classification and exact solutions of generalized (N+1)-dimensional nonlinear Boussinesq equation[J]. AIMS Mathematics, 2022, 7(7): 13139-13168. doi: 10.3934/math.2022725
| [1] | Chaudry Masood Khalique, Oke Davies Adeyemo, Kentse Maefo . Symmetry solutions and conservation laws of a new generalized 2D Bogoyavlensky-Konopelchenko equation of plasma physics. AIMS Mathematics, 2022, 7(6): 9767-9788. doi: 10.3934/math.2022544 |
| [2] | Ziying Qi, Lianzhong Li . Lie symmetry analysis, conservation laws and diverse solutions of a new extended (2+1)-dimensional Ito equation. AIMS Mathematics, 2023, 8(12): 29797-29816. doi: 10.3934/math.20231524 |
| [3] | M. TarikulIslam, M. AliAkbar, M. Abul Kalam Azad . Traveling wave solutions in closed form for some nonlinear fractional evolution equations related to conformable fractional derivative. AIMS Mathematics, 2018, 3(4): 625-646. doi: 10.3934/Math.2018.4.625 |
| [4] | Harivan R. Nabi, Hajar F. Ismael, Nehad Ali Shah, Wajaree Weera . W-shaped soliton solutions to the modified Zakharov-Kuznetsov equation of ion-acoustic waves in (3+1)-dimensions arise in a magnetized plasma. AIMS Mathematics, 2023, 8(2): 4467-4486. doi: 10.3934/math.2023222 |
| [5] | Imran Siddique, Khush Bukht Mehdi, Sayed M Eldin, Asim Zafar . Diverse optical solitons solutions of the fractional complex Ginzburg-Landau equation via two altered methods. AIMS Mathematics, 2023, 8(5): 11480-11497. doi: 10.3934/math.2023581 |
| [6] | Qaiser Khan, Muhammad Arif, Bakhtiar Ahmad, Huo Tang . On analytic multivalent functions associated with lemniscate of Bernoulli. AIMS Mathematics, 2020, 5(3): 2261-2271. doi: 10.3934/math.2020149 |
| [7] | Sharief Deshmukh, Mohammed Guediri . Some new characterizations of spheres and Euclidean spaces using conformal vector fields. AIMS Mathematics, 2024, 9(10): 28765-28777. doi: 10.3934/math.20241395 |
| [8] | Ziyu Dong, Zhengjun Zhao . An application of $ p $-adic Baker method to a special case of Jeśmanowicz' conjecture. AIMS Mathematics, 2023, 8(5): 11617-11628. doi: 10.3934/math.2023588 |
| [9] | Huizhang Yang, Wei Liu, Yunmei Zhao . Lie symmetry reductions and exact solutions to a generalized two-component Hunter-Saxton system. AIMS Mathematics, 2021, 6(2): 1087-1100. doi: 10.3934/math.2021065 |
| [10] | W. Y. Chan . Simultaneous and non-simultaneous quenching for a coupled semilinear parabolic system in a $ n $-dimensional ball with singular localized sources. AIMS Mathematics, 2021, 6(7): 7704-7718. doi: 10.3934/math.2021447 |
In this article, the generalized (N+1)-dimensional nonlinear Boussinesq equation is analyzed via Lie symmetry method. Lie point symmetries of the considered equation and accompanying invariant groups are computed. After transforming the equation into a nonlinear ordinary differential equation (ODE), analytical solutions of various types are obtained using the (G′/G,1/G) expansion method. The concept of nonlinear self-adjointness is used in order to determine nonlocal conservation laws of the equation in lower dimensions. By selecting the appropriate parameter values, the study provides a graph of the solutions to the equation under study.
The Boussinesq equation received a lot of attention in recent years. Originally, it was used to describe long waves in shallow water [1] in 1871. The peculiar behavior of the Boussinesq equation's soliton solutions explains our newfound interest in the equation. Solitons in integrable systems are commonly thought to be stable objects that interact trivially with altering only phase as a result of the interaction. Some recent studies on solitons solution to different partial differential equations (PDEs) can be found in [2,3,4,5,6]. The behavior of solitons in the Boussinesq equation, on the other hand, defies this stereotype. The Boussinesq equation aroused the interest of academics in both mathematics and physics [7,8,9,10,11,12,13,14] due to its profound importance and enticing mathematical properties, despite the fact that its solitons may decay under perturbations and cause a singularity in finite time [15].
Nonlinear evolution equations [16] play an important role in nonlinear science, particularly in plasma physics, ferromagnetic chains, water wave tanks, meta-materials, nonlinear wave propagation [17,18,19,20], Bose-Einstein condensates, and nonlinear optical fibers. In this article, we look at the extension of generalized Boussinesq equation [21] to (N+1) dimensions. Thus, we can write the (N+1)-dimensional Boussinesq equation as:
| utt=auxx+b(u2)xx+cuxxxx+N−1∑j=1djuyjyj,b≠0, | (1.1) |
where the scalars dj denote the coefficients of dissipation terms in yj directions and u(t,x,y1,⋯,yN−1) is a field function of spatial and temporal components. Equation (1.1) is similar to the (N+1)-dimensional Boussinesq equation [22] for n=2 and dj=1∀j=1,⋯,N−1.
For N=1, Eq (1.1) reduces to generalized (1+1)-dimensional Boussinesq equation [23]
| utt=auxx+b(u2)xx+cuxxxx, | (1.2) |
while for N=2, Eq (1.1) exhibits generalized (2+1)-dimensional Boussinesq equation [24]
| utt=auxx+b(u2)xx+cuxxxx+duyy. | (1.3) |
In addition, the (3+1)-dimensional Boussinesq equation considered in [21,25], is
| utt=auxx+b(u2)xx+cuxxxx+d1uyy+d2uzz. | (1.4) |
For arbitrary parameter values, many special instances of Eq (1.1) for different dimensions are investigated [26,27,28,29,30,31,32].
Differential equations are unavoidable when dealing with numerous abnormalities in applied math, physical research, and design. A detailed grasp of the dynamic cycles portrayed in these scenarios is required in many branches of study. In financial, monetary, and sociological concerns, these conditions are utilized to mimic a wide range of nonlinear cycles. We can look at a variety of actual properties connected with these nonlinear circumstances thanks to their arrangements. An overall hypothesis clarifying the viability of numerous circumstances linked with them is utterly impracticable. As a result, a lot of focus has recently been paid to establishing various organizational techniques for these nonlinear situations. Researchers have devised many strategies for solving nonlinear partial differential equations.
In any nonlinear media, detailing with nonlinear PDEs and their exact solutions is an essential job. These solutions might help with a superior comprehension of intricate cycles and give knowledge into the actual attributes of the nonlinear models viable. This is mainly because they can supply a lot of physical information and help us understand how these physical models work. Many researchers focused on nonlinear elements, creating and applying an assortment of mathematical techniques for producing new exact analytical solutions for nonlinear differential equations. These methods include the Simplest equation method [33], the extended Trial equation method [34], the extended (1/G′) method [35], the direct extended algebraic method [36,37,38], the Hirota bilinear method [39], the extended sinh-Gordon equation expansion method [40], the meshless radial basis function method [41], the exp(−ϕ(ξ)) expansion method [42], the Painlevé-expansion method [43], modified Khater method [44], Jacobi elliptic function expansion method [45], etc. These analytical techniques proved significantly more trustworthy and efficient for obtaining solutions to many PDEs.
Numerous speculations meaning to distinguish procedures for getting explicit exact solutions went to the Lie group of transformation method of differential equations [46,47]. The Lie group strategy is a standard methodology for deciding a nonlinear complex system's Lie symmetries. The method, specifically, permits us to reduce the dimension of the equation by one after only one application. Hence, the Lie symmetry technique is a typical, compelling, and exceptionally strong strategy with a variety of applications [48,49,50,51,52,53,54].
Any physical system's conservation laws play a critical role in characterizing its dynamics. These laws provide insight into the system's physical meaning. Conserved quantities such as energy, mass, and momentum are special cases of these laws. These are used to investigate integrability and linearization of mappings [55]. Many scholars contributed to the advancement of various method to construct conservation law for PDEs [56], making them a prominent research topic for mathematicians and physicists [57,58,59,60].
The rest of the manuscript is organized as follows. In Section 2, there is a brief review of some basic concepts and definitions used in this study. Lie point symmetries and group invariant solutions of considered Eq (1.1) are presented in Section 3. Section 5 contains the symmetry reduction and various exact solutions of Eq (1.1) along with their graphical portrays. In Section 6, nonlinear self-adjoint classification of Eq (1.1) is accomplished. Section 4 is devoted to the computation of nonlocal conserved vectors for lower dimensional Boussinesq equation. The study comes to an end with concluding remarks in Section 7.
In this portion, we'll look at N. H. Ibragimov's method for constructing a conserved vector for a system of partial differential equations.
Consider a system containing ˜m partial differential equations:
| U˜ρ(˜x,˜u,˜u(1),˜u(2),⋯,˜u(r))=0,(˜ρ=1,⋯,˜m), | (2.1) |
where U˜ρ∈V, V being the vector space of all differential functions of finite order.
In Eq (2.1), ˜x=(x1,x2,⋯,x˜n) denotes the ˜n independent variables and ˜u=(u1,u2,⋯,u˜m) are the ˜m dependent variables, while ˜ui represents the partial derivative of ˜u w.r.t. the ith component of ˜x.
Definition 1. The conservation law for the system of PDEs (2.1) is defined as:
| [Dj(Tj)]U˜ρ=0=0, | (2.2) |
where Dj represents the total derivative operators w.r.t. xj (1≤j≤˜n), given by:
| Dj=∂∂xj+u˜ρj∂∂u˜ρ+u˜ρjk∂∂u˜ρk+u˜ρjkℓ∂∂u˜ρkℓ+⋯,˜ρ=1,⋯,˜m. | (2.3) |
The repeated indices in Eq (2.2) denotes the standard summation convention.
Theorem 1. If the system (2.1) is invariant due to an infinitesimal generator
| X=ξj(˜x,˜u)∂∂xj+η˜ρ(˜x,˜u)∂∂u˜ρ, | (2.4) |
then the components of the conserved vector T=(T1,T2,⋯,T˜n) for the system (2.1) satisfying the conservation law (2.2) are determined as follows:
| Tj=ξjL+W˜ρ[∂L∂uj−Dk(∂L∂ujk)+DkDℓ(∂L∂ujkℓ)−⋯]+Dk(W˜ρ)[∂L∂ujk−Dℓ(∂L∂ ujkℓ)+⋯]+DkDℓ(W˜ρ)[∂L∂ujkℓ−⋯]+⋯, | (2.5) |
where W˜ρ=η˜ρ−ξiu˜ρi(˜ρ=1,2,⋯,˜m),andL=P˜ρU˜ρ represents the formal Lagrangian.
Remark: Since the components of a conserved vector of system (2.1) depend on the nonlocal variables P˜ρ,˜ρ=1,⋯,˜m, therefore (2.2) is also refered as the nonlocal conservation law for the system (2.1).
The choice of nonlocal variables P˜ρ for the construction of formal lagrangian leads to a concept of nonlinear selfadjointness.
In this portion, we present some basic definitions related to the concept of nonlinear self-adjointness [61].
Definition 2. The adjoint system of equations corresponding to the Eq (2.1) is determined by taking the variational derivatives as:
| U∗˜ρ(˜x,˜u,˜P,˜u(1),˜P(1),˜u(2),˜P(2),⋯,˜u(r),˜P(r))=δLδu˜ρ=0,(˜ρ=1,⋯,˜m), | (2.6) |
where ˜P=(P1,P2,⋯,P˜m) are the new dependent variables termed as nonlocal variables, and the subscripts of ˜P denotes the order of partial derivatives w.r.t. independent variables in ˜x. Moreover, L=PϱUϱ is the formal Lagrangian while δ/δu˜ρ is the Euler-Lagrange operator given by:
| δδu˜ρ=∂∂u˜ρ+∞∑i=1(−1)i Dj1⋯Dji ∂∂u˜ρj1⋯ji | (2.7) |
The total differentiation (2.3) is now extended to new variables (P1,⋯,P˜m) as:
| Dj=∂∂xj+u˜ρj∂∂u˜ρ+P˜ρj∂∂P˜ρ+u˜ρjk∂∂u˜ρk+P˜ρjk∂∂P˜ρk+u˜ρjkℓ∂∂u˜ρkℓ+P˜ρjkℓ∂∂P˜ρkℓ+⋯,˜ρ=1,⋯,˜m. | (2.8) |
Definition 3. The system of PDEs (2.1) is said to be nonlinearly self-adjoint, if for some ˜ρ=1,⋯,˜m, the substitution P˜ρ=Ψ˜ρ(˜x,˜u)≠0, to the adjoint system yields:
| U∗ρ(˜x,˜u,˜Ψ(˜x,˜u),⋯,u(r),˜Ψ(r))=λϱρUϱ(˜x,˜u,⋯,˜u(r)),ρ=1,⋯,m, | (2.9) |
where λϱρ∈V are the undetermined coefficients and, P and Ψ are ˜m dimensional vectors.
Note that, if ˜m>m, then system (2.1) is over-determined, while the corresponding adjoint system is sub-definite. Similarly, if m>˜m, then the system (2.1) is sub-definite, while its corresponding adjoint system is over-determined.
Definition 4. The system of PDEs (2.1) is said to be quasi self-adjoint, if the substitution to the adjoint system defined by a continuously differentiable mapping P˜ρ=Ψ˜ρ(˜u) from ˜m-dimensional space of variables ˜u into ˜m-dimensional space of variables ˜P, satisfies
| U∗˜ρ(˜x,˜u,˜Ψ,⋯,u(r),˜Ψ(r))=λϱ˜ρUϱ(˜x,˜u,⋯,˜u(r)),˜ρ=1,⋯,˜m, | (2.10) |
where the coefficients λϱ˜ρ∈V are undetermined while the components Ψ˜ρ(˜u) of ˜Ψ are not all equals to zero simultaneously.
Definition 5. The system (2.1) of partial differential equations is called strictly self-adjoint, if the substitution ˜P=˜u to its adjoint system fulfills:
| U∗˜ρ(˜x,˜u,˜Ψ,⋯,u(r),˜Ψ(r))=λϱ˜ρUϱ(˜x,˜u,⋯,˜u(r)),˜ρ=1,⋯,˜m,λϱ˜ρ∈V. | (2.11) |
However, the substitution ˜P=˜u is not uniquely determined in the case of more than one dependent variables. For example in case of ˜m dependent variables it is possible that (P1,P2,⋯,P˜m)=(u˜m,u˜m−1,⋯,u1) yields Eq (2.11). Thus, in this case there is one out of ˜m! possible arrangements of the components of ˜u, which satisfies Eq (2.11) upon substitution. In the situation of a single dependent variable, this definition is ideal.
Similarly, M. L. introduced the concept of weak selfadjointness [62]. However, it is important to note that Definitions 3 is the most generic, as it encompasses all of the other definitions related to the concept of self-adjointness. It's worth noting that all of the preceding Definitions 1–5 are applicable to the case of a single partial differential equation having only one dependent variable.
Remark: After determining the non-local variables by utilizing the knowledge of nonlinear self-adjointness, one will able to construct a formal Lagrangian and hence the components of the conserved vector for the system (2.1) by using Eq (2.5).
Consider a nonlinear partial differential equation for u(t,x,y1,y2,⋯,yN−1) having general form:
| U(u,ut,ux,uy1,uy2,⋯)=0. | (2.12) |
Assuming that upon using the similarity transformation u(t,x,y1,y2,⋯,yN−1)=g(ω), the nonlinear PDE (2.12) is reduced into a nonlinear ODE:
| U(Θ,Θ′,Θ′′,⋯)=0, | (2.13) |
where prime (′) denotes the ordinary derivative w.r.t. ω. Integrating Eq (2.13) can reduce its complexity.
According to the scheme of (G′/G,1/G)-expansion method, Eq (2.13) possesses the solution of the form:
| Θ(ω)=m∑i=0piΔi(ω)+m∑i=1qiΔi−1(ω)φ(ω), | (2.14) |
where m is the positive integer obtained by taking the homogeneous balance between highest order nonlinear term and highest order linear term of ODE (2.13), p0,pi,qi (1≤i≤m) are coefficients while Δ(ω) and φ(ω) defined by:
| Δ=G′G,φ=1G, | (2.15) |
in which G(ω) is a solution of second order ODE:
| G′′(ω)+sG(ω)=υ, | (2.16) |
where s and υ are arbitrary constants.
From Eqs (2.15) and (2.16), we have
| Δ′=−Δ2+υφ−s,φ′=−Δφ. | (2.17) |
Depending on the sign of the parameter s, the solution of Eq (2.16) is categorized into three cases:
Case 1. When s<0:
The general solution of Eq (2.16) is:
| G(ω)=γ1sinh(√−sω)+γ2cosh(√−sω)+υs, | (2.18) |
where γ1 and γ2 are the integration constants. Substituting Eq (2.18) into Eq (2.15) and using Eq (2.17), we get:
| φ2=−s(Δ2−2υφ+s)s2σ+υ2,σ=γ21−γ22. | (2.19) |
Case 2. When s>0:
The general solution of Eq (2.16) is:
| G(ω)=γ1sin(√sω)+γ2cos(√sω)+υs, | (2.20) |
where γ1 and γ2 are the integration constants. Substituting Eq (2.20) into Eq (2.15) and using Eq (2.17), we get:
| φ2=s(Δ2−2υφ+s)s2σ−υ2,σ=γ21+γ22. | (2.21) |
Case 3. When s=0:
In this case Eq (2.16) gives the solution of the form:
| G(ω)=υ2ω2+γ1ω+γ2, | (2.22) |
where γ1 and γ2 are the integration constants. Thus Eq (2.15) by the use of Eqs (2.22) and (2.17), gives us:
| φ2=Δ2−2υφγ21−2υγ2. | (2.23) |
The following steps are used to obtain the solution of nonlinear PDE (2.12) corresponding to each case (say Case 1):
Step 1. After determining the value of positive integer m, Eq (2.14) is substituted into Eq (2.13) and, by the aid of Eqs (2.17) and (2.19), Eq (2.13) is changed into a polynomial of Δi, φj where 0≤i≤n, j≤1 (n is any integer).
Step 2. Equating the coefficients of Δi(ω) and Δi−1φ(ω) to zero, yields the system of algebraic equations involving pi, qi, s, σ, υ (and possibly the parameters of ODE (2.13)). After solving the system of algebraic equations and using Eq (2.15), Eq (2.14) gives the solution of ODE (2.13) (corresponding to Case 1).
Step 3. The above process is repeated for the evaluation of parameters for the remaining two cases and in a similar way solutions for ODE (2.13) are obtained.
Step 4. The solutions of nonlinear PDE (2.12) corresponding to the three cases are obtained by substituting the similarity variable (ω).
In this section, we shall find the Lie algebra admitted by Eq (1.1) using Lie theory. After the computation of the Lie point symmetries, we shall present the group invariant solutions, which are new types of solutions of Eq (1.1).
Consider a one parameter (ε) Lie group of point transformation on the space of "N+2" variables, which preserves the invariance of Eq (1.1).
| t†=t+εξ0(t,x,y1,⋯,yN−1,u)+O(ε2),x†=x+εξ1(t,x,y1,⋯,yN−1,u)+O(ε2),y†j=yj+εηj(t,x,y1,⋯,yN−1,u)+O(ε2),j=1,⋯,N−1u†=u+εζ(t,x,y1,⋯,yN−1,u)+O(ε2), | (3.1) |
where ξ0,ξ1,ηj and ζ are known as infinitesimals of point transformation (3.1) while ε is the small parameter.
The infinitesimal generator corresponding to the above Lie group (3.1) is given by:
| X=ξ0(t,x,y1,⋯,yN−1,u)∂∂t+ξ1(t,x,y1,⋯,yN−1,u)∂∂x+N−1∑j=1ηj(t,x,y1,⋯,yN−1,u)∂∂yj+ζ(t,x,y1,⋯,yN−1,u)∂∂u. | (3.2) |
The Lie invariance condition [47] for Eq (1.1) reads:
| pr(4)X(Ω)|Ω=0=0,Ω=utt−auxx−b(u2)xx−cuxxxx−N−1∑j=1djuyjyj, | (3.3) |
where pr(4)X is the fourth prolongation of the infinitesimal generator (3.2) given by:
| pr(3)X=X+ζtt∂∂utt+ζx∂∂ux+ζxx∂∂uxx+ζxxxx∂∂uxxxx+N−1∑j=1ζyjyj∂∂uyjyj, | (3.4) |
in which ζtt,ζx,ζxx,ζxxxx and ζyjyj are the extended infinitesimals [46].
Using Eqs (3.3) and (3.4), we obtain an overdetermined system of PDEs about the infinitesimals of point transformation (3.1), which upon solving yields a finite dimensional Lie algebra of (N+1) dimensional Boussinesq equation (1.1).
Theorem 2. The (N+1) dimensional Boussinesq equation (1.1) admits a finite dimensional Lie algebra spanned by exactly N2+N+42 Lie point symmetries given by:
| X1=∂∂t,X2=∂∂x,Xj+2=∂∂yj,j=1,⋯,N−1.XN+j+1=yjdj∂∂t+t∂∂yj,j=1,⋯,N−1X2N+α+β−1=yα+1∂∂yβ−dα+1dβyβ∂∂yα+1,α=1,⋯,N−2,β=1,⋯,α.XN2+N+42=−2bt∂∂t−bx∂∂x−2bN−1∑j=1yj∂∂yj+(a+2bu)∂∂u. | (3.5) |
It is evident from Eq (3.5) that Eq (1.1) admits infinitesimal generators XN+j+1 and X2N+α+β−1 only when N>1 and N>2, respectively.
● Lie point symmetries of Eq (1.2)
Equation (1.2) constitutes three dimensional Lie algebra \left(\because(1^2+1+4)/2 = 3\right) , given by (3.5) as follows
| \begin{equation} X_1 = \; \frac{\partial}{\partial t},\; \; X_2 = \; \frac{\partial}{\partial x},\; \; X_3 = \; -2bt\frac{\partial}{\partial t}-bx\frac{\partial}{\partial x}+\left(a+2bu\right)\frac{\partial}{\partial u}. \end{equation} | (3.6) |
● Lie point symmetries of Eq (1.3)
Equation (1.3) possesses five dimensional Lie algebra \left(\because(2^2+2+4)/2 = 5\right) , given by (3.5) as follows:
| \begin{eqnarray} \begin{aligned} X_1 = &\; \frac{\partial}{\partial t},\; \; X_2 = \; \frac{\partial}{\partial x},\; \; X_3 = \; \frac{\partial}{\partial x},\; \; X_4 = \frac{y}{d}\frac{\partial}{\partial t}+t\frac{\partial}{\partial y},\\ X_5 = &\; -2bt\frac{\partial}{\partial t}-bx\frac{\partial}{\partial x}-2by\frac{\partial}{\partial y}+\left(a+2bu\right)\frac{\partial}{\partial u}. \end{aligned} \end{eqnarray} | (3.7) |
● Lie point symmetries of Eq (1.4)
Equation (1.4) possesses eight dimensional Lie algebra \left(\because(3^2+3+4)/2 = 8\right) , given by (3.5) as follows:
| \begin{eqnarray} \begin{aligned} X_1 = &\; \frac{\partial}{\partial t},\; \; X_2 = \; \frac{\partial}{\partial x},\; \; X_3 = \; \frac{\partial}{\partial y},\; \; X_4 = \; \frac{\partial}{\partial z},\\ X_5 = &\frac{y}{d_1}\frac{\partial}{\partial t}+t\frac{\partial}{\partial y},\; \; X_6 = \frac{z}{d_2}\frac{\partial}{\partial t}+t\frac{\partial}{\partial z},\\ X_7 = &z\frac{\partial}{\partial y}-\frac{d_2}{d_1}y\frac{\partial}{\partial z},\\ X_8 = &\; -2bt\frac{\partial}{\partial t}-bx\frac{\partial}{\partial x}-2by\frac{\partial}{\partial y}-2bz\frac{\partial}{\partial z}+\left(a+2bu\right)\frac{\partial}{\partial u}. \end{aligned} \end{eqnarray} | (3.8) |
Suppose the one parameter Lie group of transformations corresponding to the infinitesimal generators in (3.5) has the following form:
| \begin{eqnarray} \begin{aligned} t^{\dagger} = &T\left(t,x,y_{1},\cdots,y_{N-1},u;\varepsilon\right)\ ,\\ x^{\dagger} = &\chi\left(t,x,y_{1},\cdots,y_{N-1},u;\varepsilon\right) ,\\ y_{j}^{\dagger} = &Y_{j}\left(t,x,y_{1},\cdots,y_{N-1},u;\varepsilon\right) ,\\ u^{\dagger} = &U\left(t,x,y_{1},\cdots,y_{N-1},u;\varepsilon\right). \end{aligned} \end{eqnarray} | (3.9) |
To determine the group of point transformations (3.9) from the infinitesimal generators (3.5), we consider the following initial value problem:
| \begin{eqnarray} \begin{aligned} \frac{dt^{\dagger}}{d\varepsilon} = &\xi^{0}\left(t^{\dagger},x^{\dagger},y_{1}^{\dagger},\cdots,y_{N-1}^{\dagger},u^{\dagger}\right)\ ,\\ \frac{dx^{\dagger}}{d\varepsilon} = &\xi^{1}\left(t^{\dagger},x^{\dagger},y_{1}^{\dagger},\cdots,y_{N-1}^{\dagger},u^{\dagger}\right)\ ,\\ \frac{dy_{j}^{\dagger}}{d\varepsilon} = &\eta^{j}\left(t^{\dagger},x^{\dagger},y_{1}^{\dagger},\cdots,y_{N-1}^{\dagger},u^{\dagger}\right),\ j = 1,\cdots,N-1,\\ \frac{du^{\dagger}}{d\varepsilon} = &\zeta\left(t^{\dagger},x^{\dagger},y_{1}^{\dagger},\cdots,y_{N-1}^{\dagger},u^{\dagger}\right), \end{aligned} \end{eqnarray} | (3.10) |
with the initial condition (t^{\dagger}, x^{\dagger}, y_{1}^{\dagger}, \cdots, y_{N-1}^{\dagger}, u^{\dagger})|_{\varepsilon = 0} = \left(t, x, y_{1}, \cdots, y_{N-1}, u\right).
After providing the infinitesimals of each Lie point symmetry in (3.5), the solutions of the initial value problem (3.10) yield the following Lie groups.
| \begin{equation*} G_1: \begin{cases} t^{\dagger} = t+\varepsilon,\\ x^{\dagger} = x,\\ y_{j}^{\dagger} = y_{j},\; j = 1,\cdots,N-1.\\ u^{\dagger} = u. \end{cases}\; \; \; G_2: \begin{cases} t^{\dagger} = t,\\ x^{\dagger} = x+\varepsilon,\\ y_{j}^{\dagger} = y_{j},\; j = 1,\cdots,N-1.\\ u^{\dagger} = u. \end{cases} \end{equation*} |
| \begin{equation*} G_{j+2}:\begin{cases} t^{\dagger} = t,\\ x^{\dagger} = x,\\ y_{j}^{\dagger} = y_{j}+\varepsilon,\; j = 1,\cdots,N-1.\\ u^{\dagger} = u. \end{cases} \end{equation*} |
| \begin{equation*} G_{N+j+1}:\begin{cases} t^{\dagger} = t\cosh{\left(\frac{\varepsilon}{\sqrt{d_{j}}}\right)}+\frac{y_{j}}{\sqrt{d_{j}}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{j}}}\right)},\\ x^{\dagger} = x,\\ y_{j}^{\dagger} = t\sqrt{d_{j}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{j}}}\right)}+y_{j}\cosh{\left(\frac{\varepsilon}{\sqrt{d_{j}}}\right)},\\ u^{\dagger} = u. \end{cases}\; j = 1,\cdots,N-1. \end{equation*} |
| \begin{equation*} G_{2N+\alpha+\beta-1}:\begin{cases} t^{\dagger} = t,\\ x^{\dagger} = x,\\ \begin{cases} y_{\beta}^{\dagger} = y_{\beta}\cos{\left(\sqrt{\frac{d_{\alpha+1}}{d_{\beta}}}\varepsilon\right)}+y_{\alpha+1}\sqrt{\frac{d_{\beta}}{d_{\alpha+1}}}\sin{\left(\sqrt{\frac{d_{\alpha+1}}{d_{\beta}}}\varepsilon\right)},\\ y_{\alpha+1}^{\dagger} = y_{\alpha+1}\cos{\left(\sqrt{\frac{d_{\alpha+1}}{d_{\beta}}}\varepsilon\right)}-y_{\beta}\sqrt{\frac{d_{\alpha+1}}{d_{\beta}}}\sin{\left(\sqrt{\frac{d_{\alpha+1}}{d_{\beta}}}\varepsilon\right)},\\ y_{k}^{\dagger} = y_{k},\; \left(k\neq \alpha+1,\beta\right),\; \alpha = 1,\cdots,N-2,\; \beta = 1,\cdots,\alpha. \end{cases}\\ u^{\dagger} = u. \end{cases} \end{equation*} |
| \begin{equation*} G_{\frac{N^2+N+4}{2}}:\begin{cases} t^{\dagger} = te^{-2b\varepsilon},\\ x^{\dagger} = xe^{-b\varepsilon},\\ y_{j}^{\dagger} = y_{j}e^{-2b\varepsilon},\; j = 1,\cdots,N-1.\\ u^{\dagger} = ue^{2b\varepsilon}+\frac{a}{2b}\left(e^{2b\varepsilon}-1\right). \end{cases} \end{equation*} |
Theorem: If u\left(t, x, y_1, \cdots, y_{N-1}\right) is a solution of \left(N+1\right) -dimensional generalized Boussinesq equation (1.1), then new solutions u^{\ell} = u^{\ell}\left(t, x, y_1, \cdots, y_{N-1}\right), \; \; \left(\ell = 1, \cdots, \frac{N^2+N+4}{2}\right) of Eq (1.1) corresponding to each group are given by:
For G_1:
| u^{1} = u\left(t-\varepsilon,x,y_1,\cdots,y_{N-1}\right). |
For G_2:
| u^{2} = u\left(t,x-\varepsilon,y_1,\cdots,y_{N-1}\right). |
For G_{j+2}\; \left(j = 1, \cdots, N-1\right):
| \begin{array}{c} u^{3} = u\left(t,x,y_1-\varepsilon,\cdots,y_{N-1}\right), \\ \cdots\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \cdots \\ u^{N+1} = u\left(t,x,y_1,\cdots,y_{N-1}-\varepsilon\right). \end{array} |
For G_{N+j+1}\; \left(j = 1, \cdots, N-1\right):
| u^{N+2} = u\left(t\cosh{\left(\frac{\varepsilon}{\sqrt{d_{1}}}\right)}-\frac{y_1}{\sqrt{d_1}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{1}}}\right)},x,-t\sqrt{d_1}\sinh{\left(\frac{\varepsilon}{\sqrt{d_1}}\right)}+\\ y_1\cosh{\left(\frac{\varepsilon}{\sqrt{d_1}}\right)},y_2,\cdots,y_{N-1}\right),\\ |
| u^{N+3} = u\left(t\cosh{\left(\frac{\varepsilon}{\sqrt{d_{2}}}\right)}-\frac{y_2}{\sqrt{d_2}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{2}}}\right)},x,y_1,-t\sqrt{d_2}\sinh{\left(\frac{\varepsilon}{\sqrt{d_2}}\right)}+\\ y_2\cosh{\left(\frac{\varepsilon}{\sqrt{d_2}}\right)},\cdots,y_{N-1}\right), |
| \cdots\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \cdots |
| u^{2N} = u\left(t\cosh{\left(\frac{\varepsilon}{\sqrt{d_{N-1}}}\right)}-\frac{y_{N-1}}{\sqrt{d_{N-1}}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{N-1}}}\right)},x,y_1,\cdots,-t\sqrt{d_{N-1}}\sinh{\left(\frac{\varepsilon}{\sqrt{d_{N-1}}}\right)}+ \\ y_{N-1}\cosh{\left(\frac{\varepsilon}{\sqrt{d_{N-1}}}\right)}\right) . |
For G_{2N+\alpha+\beta-1}\; \left(\alpha = 1, \cdots, N-2, \; \; \beta = 1, \cdots, \alpha\right):
| \begin{equation*} { u^{2N+1} = u\left(t,x,y_{1}\cos{\left(\sqrt{\frac{d_{2}}{d_{1}}}\varepsilon\right)}-y_2\sqrt{\frac{d_{1}}{d_{2}}}\sin{\left(\sqrt{\frac{d_{2}}{d_{1}}}\varepsilon\right)},y_{2}\cos{\left(\sqrt{\frac{d_{2}}{d_{1}}}\varepsilon\right)}+\\ y_1\sqrt{\frac{d_{2}}{d_{1}}}\sin{\left(\sqrt{\frac{d_{2}}{d_{1}}}\varepsilon\right)},y_3,\cdots,y_{N-1}\right) ,}\\ \end{equation*} |
| u^{2N+2} = u\left(t,x,y_{1}\cos{\left(\sqrt{\frac{d_{3}}{d_{1}}}\varepsilon\right)}-y_3\sqrt{\frac{d_{1}}{d_{3}}}\sin{\left(\sqrt{\frac{d_{3}}{d_{1}}}\varepsilon\right)},y_{2},y_{3}\cos{\left(\sqrt{\frac{d_{3}}{d_{1}}}\varepsilon\right)}+\\ y_1\sqrt{\frac{d_{3}}{d_{1}}}\sin{\left(\sqrt{\frac{d_{3}}{d_{1}}}\varepsilon\right)},\cdots,y_{N-1}\right) , |
| \cdots\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \cdots |
| u^{(N^2+N+2)/2} = u\left(t,x,y_{1},\cdots,y_{N-2}\cos{\left(\sqrt{\frac{d_{N-1}}{d_{N-2}}}\varepsilon\right)}-y_{N-1}\sqrt{\frac{d_{N-2}}{d_{N-1}}}\sin{\left(\sqrt{\frac{d_{N-1}}{d_{N-2}}}\varepsilon\right)},\\ y_{N-1}\cos{\left(\sqrt{\frac{d_{N-1}}{d_{N-2}}}\varepsilon\right)}+ y_{N-2}\sqrt{\frac{d_{N-1}}{d_{N-2}}}\sin{\left(\sqrt{\frac{d_{N-1}}{d_{N-2}}}\varepsilon\right)}\right) . |
For G_{(N^2+N+4)/2}:
| \begin{equation*} u^{(N^2+N+4)/2} = \frac{a}{2b}\left(e^{-2b\varepsilon}-1\right)+e^{-2b\varepsilon}u\left(t e^{2b\varepsilon},x e^{b\varepsilon},y_{1} e^{2b\varepsilon},\cdots,y_{N-1} e^{2b\varepsilon}\right). \end{equation*} |
In this section, we shall find the closed form solutions of Eq (1.1). To accomplish this, we'll first conduct symmetry reduction in such a way that Eq (1.1) becomes a nonlinear ODE.
After computing the commutation relations [46] for Eq (1.1), it is found that the Lie algebra (3.5) is closed w.r.t. the Lie bracket for every N . As the Lie bracket is commutative for all the translational Lie point symmetries in (3.5). i.e., \left[X_i, X_j\right] = 0, \; \forall\; i, j = 1, \cdots, N+1. Therefore, these translational symmetries create an abelian subalgebra, and the associated one dimensional optimal system of Eq (1.1) comprises conjugacy classes [46] that are formed by these symmetries. One of them is the conjugacy class, that makes advantage of all translational symmetries is < X_1+\mathscr{H}X_2+\sum_{j = 1}^{N-1}{{\rm{ \mathsf{ θ}}}_jX_{j+2}} > , corresponding to which the similarity solution is obtained by solving the characteristic equation:
| \frac{dt}{1} = \frac{dx}{\mathscr{H}} = \frac{dy_1}{{\rm{ \mathsf{ θ}}}_1} = \cdots = \frac{dy_{N-1}}{{\rm{ \mathsf{ θ}}}_{N-1}}, |
which yields the similarity variables
| \begin{equation} \omega = t-\mathscr{H} x-\sum\limits_{j = 1}^{N-1}{{\rm{ \mathsf{ θ}}}_jy_j},\; \; u = \Theta\left(\omega\right). \end{equation} | (4.1) |
Using Eq (4.1) in Eq (1.1) we obtain the nonlinear ODE:
| \begin{equation} \mathscr{H}^4 c\Theta^{\left(4\right)}+\mathscr{H}^2 b\left(2\Theta \Theta^{\prime \prime}+2\Theta^{\prime 2}\right)+\left(\mathscr{H}^2a-1+\sum\limits_{j = 1}^{N-1}{d_j{\rm{ \mathsf{ θ}}}_j^2}\right)\Theta^{\prime \prime} = 0. \end{equation} | (4.2) |
For convenience, we take
| \begin{equation} \mu = \mathscr{H}^2a-1+\sum\limits_{j = 1}^{N-1}{d_j{\rm{ \mathsf{ θ}}}_j^2}. \end{equation} | (4.3) |
Thus, Eq (4.2) takes the form
| \begin{equation} \mathscr{H}^4 c\Theta^{\left(4\right)}+\mathscr{H}^2 b\left(2\Theta \Theta^{\prime \prime}+2\Theta^{\prime 2}\right)+\mu\Theta^{\prime \prime} = 0,\; \; \left(\prime = \frac{d}{d\omega}\right). \end{equation} | (4.4) |
Integrating twice and neglecting the constants of integration each time, we obtain a second order nonlinear ODE:
| \begin{equation} \mathscr{H}^4c\Theta^{\prime \prime}+\mathscr{H}^{2}b\Theta^2+\mu \Theta = 0. \end{equation} | (4.5) |
By taking homogeneous balance between highest order linear term \left(\Theta^{\prime \prime}\right) and the highest order nonlinear term \left(\Theta^2\right) of Eq (4.5), we find the value of the positive integer m = 2 , thus from Eq (2.14), we assume the solution of the form:
| \begin{equation} \Theta\left(\omega\right) = p_{0}+p_{1}\Delta\left(\omega\right)+p_{2}\Delta^2\left(\omega\right)+q_1\varphi\left(\omega\right)+q_2\Delta\left(\omega\right)\varphi\left(\omega\right). \end{equation} | (4.6) |
We get a system of algebraic equations by substituting Eq (4.6) into Eq (4.5) and comparing the coefficients of like powers of \Delta\left(\omega\right) and \varphi\left(\omega\right) using the approach outlined in Section 2.2. Solving that algebraic system using Maple software, yields the values of parameters \mu, \; \upsilon, \; p_0, \; p_1, \; p_2, \; q_1, and q_2 .
For s < 0 , the following two sets of parameters yields the hyperbolic solutions for Eq (1.1).
● Set 1:
| \begin{equation} p_0 = -\frac{6\mathscr{H}^2cs}{b},\; p_1 = 0,\; p_2 = -\frac{6\mathscr{H}^2c}{b},\; q_1 = q_2 = 0,\; \mu = 4s\mathscr{H}^4c,\; \upsilon = 0. \end{equation} | (4.7) |
● Set 2:
| \begin{equation} p_0 = -\frac{2\mathscr{H}^2cs}{b},\; p_1 = 0,\; p_2 = -\frac{6\mathscr{H}^2c}{b},\; q_1 = q_2 = 0,\; \mu = -4s\mathscr{H}^4c,\; \upsilon = 0. \end{equation} | (4.8) |
By substituting these values of the parameters in Eq (4.6), we get solutions for Eq (4.5), which, when combined with the similarity variables (4.1), produces the solutions for Eq (1.1).
For Set 1 :
We get the following solution for Eq (1.1) by plugging Eq (4.7) into Eq (4.6) and considering Eq (4.1).
| \begin{equation} u_1\left(t,x,y_1,y_2,\cdots,y_{N-1}\right) = \frac{6\mathscr{H}^2\sigma sc}{b\left(\gamma_1\sinh{\left(\sqrt{-s}\omega\right)}+\gamma_2\cosh{\left(\sqrt{-s}\omega\right)}\right)^2}\; , \end{equation} | (4.9) |
where \sigma = \gamma_1^2-\gamma_2^2 and \omega = t-\mathscr{H}x-{\rm{ \mathsf{ θ}}}_1y_1-\cdots-{\rm{ \mathsf{ θ}}}_1y_{N-1} .
For Set 2 :
We get the following solution for Eq (1.1) by plugging Eq (4.8) into Eq (4.6) and considering Eq (4.1).
| \begin{equation} u_2\left(t,x,y_1,y_2,\cdots,y_{N-1}\right) = \frac{6\mathscr{H}^2sc}{b}\left[\left(\frac{\gamma_1\cosh{\left(\sqrt{-s}\omega\right)}+\gamma_2\sinh{\left(\sqrt{-s}\omega\right)}}{\gamma_1\sinh{\left(\sqrt{-s}\omega\right)}+\gamma_2\cosh{\left(\sqrt{-s}\omega\right)}}\right)^2-\frac{1}{3}\right], \end{equation} | (4.10) |
where \omega = t-\mathscr{H}x-{\rm{ \mathsf{ θ}}}_1y_1-\cdots-{\rm{ \mathsf{ θ}}}_{N-1}y_{N-1} .
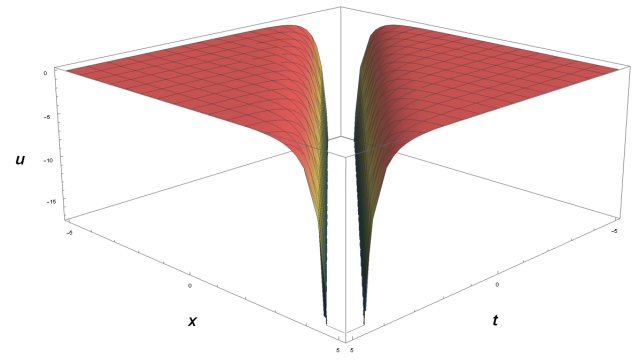
The hyperbolic exact solutions u_1 and u_2 represented by Eqs (4.9) and (4.10) are portrayed in Figures 1 and 2, respectively.
Graph of u_1 by choosing a = -1, \; b = -1, \; c = -1, \; s = -1, \; \mathscr{H} = 1, \; \gamma_1 = 1, \; \gamma_2 = 0 , y_1 = y_2 = \cdots = y_{N-1} = 0.
Graph of u_2 by choosing a = -1, \; b = -1, \; c = -1, \; s = -1, \; \mathscr{H} = 1, \; \gamma_1 = 1, \; \gamma_2 = 0 , y_1 = y_2 = \cdots = y_{N-1} = 0.
For s > 0 , the following two sets of parameters yields the hyperbolic solutions for Eq (1.1).
● Set 1:
| \begin{equation} p_0 = -\frac{6\mathscr{H}^2cs}{b},\; p_1 = 0,\; p_2 = -\frac{6\mathscr{H}^2c}{b},\; q_1 = q_2 = 0,\; \mu = 4s\mathscr{H}^4c,\; \upsilon = 0. \end{equation} | (4.11) |
● Set 2:
| \begin{equation} p_0 = -\frac{2\mathscr{H}^2cs}{b},\; p_1 = 0,\; p_2 = -\frac{6\mathscr{H}^2c}{b},\; q_1 = q_2 = 0,\; \mu = -4s\mathscr{H}^4c,\; \upsilon = 0. \end{equation} | (4.12) |
By substituting these values of the parameters in Eq (4.6), we get solutions for Eq (4.5), which, when combined with the similarity variables (4.1), produces the solutions for Eq (1.1).
For Set 1 :
We get the following solution for Eq (1.1) by plugging Eq (4.11) into Eq (4.6) and considering Eq (4.1).
| \begin{equation} u_3\left(t,x,y_1,y_2,\cdots,y_{N-1}\right) = -\frac{6\mathscr{H}^2\sigma sc}{b\left(\gamma_1\sin{\left(\sqrt{s}\omega\right)}+\gamma_2\cos{\left(\sqrt{s}\omega\right)}\right)^2}\; , \end{equation} | (4.13) |
where \sigma = \gamma_1^2+\gamma_2^2 and \omega = t-\mathscr{H}x-{\rm{ \mathsf{ θ}}}_1y_1-\cdots-{\rm{ \mathsf{ θ}}}_1y_{N-1} .
For Set 2 :
We get the following solution for Eq (1.1) by plugging Eq (4.12) into Eq (4.6) and considering Eq (4.1).
| \begin{equation} u_4\left(t,x,y_1,y_2,\cdots,y_{N-1}\right) = -\frac{6\mathscr{H}^2sc}{b}\left[\left(\frac{\gamma_1\cos{\left(\sqrt{s}\omega\right)}-\gamma_2\sin{\left(\sqrt{s}\omega\right)}}{\gamma_1\sin{\left(\sqrt{s}\omega\right)}+\gamma_2\cosh{\left(\sqrt{s}\omega\right)}}\right)^2+\frac{1}{3}\right], \end{equation} | (4.14) |
where \omega = t-\mathscr{H}x-{\rm{ \mathsf{ θ}}}_1y_1-\cdots-{\rm{ \mathsf{ θ}}}_{N-1}y_{N-1} .
The trigonometric exact solutions u_3 and u_4 represented by Eqs (4.13) and (4.14) are portrayed in Figures 3 and 4 respectively.
Graph of u_3 by choosing a = -1, \; b = -1, \; c = -1, \; s = 1, \; \mathscr{H} = 1, \; \gamma_1 = 1, \; \gamma_2 = 0 , y_1 = y_2 = \cdots = y_{N-1} = 0.
Graph of u_4 by choosing a = -1, \; b = -1, \; c = -1, \; s = 1, \; \mathscr{H} = 1, \; \gamma_1 = 1, \; \gamma_2 = 0 , y_1 = y_2 = \cdots = y_{N-1} = 0.
When s = 0 , We get a trivial solution
| \begin{equation} u_5\left(t,x,y_1,y_2,\cdots,y_{N-1}\right) = p_0, \end{equation} | (4.15) |
for the set of parameters:
| \begin{equation} p_0 = p_0,\; p_1 = 0,\; p_2 = 0,\; q_1 = q_2 = 0,\; \mu = -\mathscr{H}^2bp_0,\; \upsilon = 0. \end{equation} | (4.16) |
Thus, Eq (1.1) does not have any nontrivial rational function solutions.
Suppose,
| \begin{equation} \mathfrak{U}\left(t,x,u,u_t,u_x,u_{xx},u_{y_{1}y_{1}},u_{y_{2}y_{2}},\cdots,u_{y_{N-1}y_{N-1}}\right) = 0 \end{equation} | (5.1) |
represents Eq (1.1) where
| \begin{equation} \mathfrak{U} = u_{tt}-a u_{xx}-b\left(u^2\right)_{xx}-c u_{xxxx}-\sum\limits_{j = 1}^{N-1}{d_{j} u_{y_{j}y_{j}}}\; . \end{equation} | (5.2) |
Considering the nonlocal variable \mathscr{P}\left(t, x, y_1, y_2, \cdots, y_{N-1}\right) , the formal Lagrangian for Eq (1.1) is of the form:
| \begin{equation} \mathscr{L} = \mathscr{P}\left(t,x,y_1,y_2,\cdots,y_{N-1}\right)\left(u_{tt}-a u_{xx}-b\left(u^2\right)_{xx}-c u_{xxxx}-\sum\limits_{j = 1}^{N-1}{d_{j} u_{y_{j}y_{j}}}\right). \end{equation} | (5.3) |
The corresponding adjoint equation of Eq (1.1) is:
| \begin{equation} \mathfrak{U}^* = \frac{\delta}{\delta u}\left[\mathscr{P}\left(u_{tt}-a u_{xx}-b\left(u^2\right)_{xx}-c u_{xxxx}-\sum\limits_{j = 1}^{N-1}{d_{j} u_{y_{j}y_{j}}}\right)\right] = 0, \end{equation} | (5.4) |
where the Euler Lagrange operator \delta/\delta u has the following form for Eq (1.1):
| \begin{equation} \frac{\delta}{\delta u} = \frac{\partial}{\partial u}-\mathscr{D}_{x}\frac{\partial}{\partial u_{x}}-\mathscr{D}_{t}^2\frac{\partial}{\partial u_{tt}}-\mathscr{D}_{x}^2\frac{\partial}{\partial u_{xx}}-\sum\limits_{j = 1}^{N-1}{\mathscr{D}_{y_{j}}^2\frac{\partial}{\partial u_{y_{j}y_{j}}}}-\mathscr{D}_{x}^4\frac{\partial}{\partial u_{xxxx}}, \end{equation} | (5.5) |
in which the total derivatives are as follows:
| \begin{eqnarray} \begin{aligned} \mathscr{D}_x = &\frac{\partial}{\partial x}+u_{x}\frac{\partial}{\partial u}+u_{xx}\frac{\partial}{\partial u_{x}}+u_{xxx}\frac{\partial}{\partial u_{xx}}+u_{xxxx}\frac{\partial}{\partial u_{xxx}}+u_{xxxxx}\frac{\partial}{\partial u_{xxxx}},\\ \mathscr{D}_t = &\frac{\partial}{\partial t}+u_{t}\frac{\partial}{\partial u}+u_{tt}\frac{\partial}{\partial u_{t}}+u_{ttt}\frac{\partial}{\partial u_{tt}},\\ \mathscr{D}_{y_{j}} = &\frac{\partial}{\partial y_{j}}+u_{y_{j}}\frac{\partial}{\partial u}+u_{y_{j}y_{j}}\frac{\partial}{\partial u_{y_{j}}}+u_{y_{j}y_{j}y_{j}}\frac{\partial}{\partial u_{y_{j}y_{j}}}\; \left(j = 1,\cdots,N-1\right). \end{aligned} \end{eqnarray} | (5.6) |
Using Eqs (5.5) and (5.6), Eq (5.4) becomes:
| \begin{equation} \mathfrak{U}^* = \mathscr{P}_{tt}-\left(a+2bu\right)\mathscr{P}_{xx}-c\; \mathscr{P}_{xxxx}-\sum\limits_{j = 1}^{N-1}{d_{j}\mathscr{P}_{y_{j}y_{j}}} = 0. \end{equation} | (5.7) |
Invoking the Definitions 3–5 for the pair of Eqs (5.1) and (5.7), we state the following theorem after reckoning.
Theorem: Equation (1.1) is not strictly, quasi or weak self-adjoint, rather it is nonlinear self-adjoint (i.e., \mathfrak{U} = \lambda\mathfrak{U}, \; \lambda = \Psi_u ), with the nonlocal variable \mathscr{P} = \Psi determined from the following system of PDEs:
| \begin{equation} \Psi_{xx} = 0,\; \; \; \Psi_{tt} = \sum\limits_{j = 1}^{N-1}{d_{j}\Psi_{y_{j}y_{j}}},\; \; \; \Psi_{u} = 0. \end{equation} | (5.8) |
Remark: From above system of PDEs (5.8), it is clear that the nonlocal variable \mathscr{P} = \Psi is independent of variable u , i.e., \mathscr{P} = \Psi\left(t, x, y_1, \cdots, y_{N-1}\right) .
Consider the scenario when Eq (1.1) reflects the \left(1+1\right) and \left(2+1\right) dimensional Boussinesq equations (1.2) and (1.3).
● Nonlocal variable for N = 1 :
For N = 1 , the system of PDEs (5.8) takes the form:
| \begin{equation} \Psi_{xx} = 0,\; \; \; \Psi_{tt} = 0,\; \; \; \Psi_{u} = 0, \end{equation} | (5.9) |
which upon solving yields
| \begin{equation} \mathscr{P} = \Psi\left(t,x,u\right) = C_1xt+C_2x+C_3t+C_4. \end{equation} | (5.10) |
● Nonlocal variable for N = 2 :
For N = 2 , the system of PDEs (5.8) takes the form:
| \begin{equation} \Psi_{xx} = 0,\; \; \; \Psi_{tt} = d_1\Psi_{y_{1}y_{1}},\; \; \; \Psi_{u} = 0, \end{equation} | (5.11) |
For sake of convenience, we remove the indices in Eq (5.11) (i.e., taking d_1 = d and y_1 = y ). Thus solving
| \begin{equation*} \Psi_{xx} = 0,\; \; \; \Psi_{tt} = d\Psi_{yy},\; \; \; \Psi_{u} = 0, \end{equation*} |
yields
| \begin{equation} \mathscr{P} = \Psi\left(t,x,y,u\right) = \left(x+1\right)\left[f\left(t+\frac{y}{\sqrt{d}}\right)+g\left(t-\frac{y}{\sqrt{d}}\right)\right]. \end{equation} | (5.12) |
where f and g are arbitrary functions of its arguments.
Components of conserved vector for Eq (1.1) corresponding to Lie symmetries (3.5) can be determined using Ibragimov's Theorem (2.1) using Eq (2.5).
If \mathscr{T} = \left(\mathscr{T}^t, \mathscr{T}^x, \mathscr{T}^{y_1}, \cdots, \mathscr{T}^{y_{N-1}}\right) is a conserved vector for Eq (1.1), then it must satisfy the conservation law:
| \begin{equation} \left[\mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y_{1}}\left(\mathscr{T}^{y_{1}}\right)+\cdots+\mathscr{D}_{y_{N-1}}\left(\mathscr{T}^{y_{N-1}}\right)\right]_{\left(1.1\right)} = 0. \end{equation} | (6.1) |
Equation (2.5) yields the following components of conserved vector \mathscr{T} for Eq (1.1):
| \begin{eqnarray} \begin{aligned} \mathscr{T}^t = &\; \xi_{\ell}^{0}\mathscr{L}-\mathcal{W}_{\ell}\mathscr{D}_{t}\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right)+\mathscr{D}_{t}\left(\mathcal{W}_{\ell}\right)\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right),\\ \mathscr{T}^x = &\; \xi_{\ell}^{1}\mathscr{L}+\mathcal{W}_{\ell}\left[\frac{\partial\mathscr{L}}{\partial u_{x}}-\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xx}}\right)-\mathscr{D}_{x}^{3}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]+\mathscr{D}_{x}^{3}\left(\mathcal{W_{\ell}}\right)\left(\frac{\partial ]\mathscr{L}}{\partial u_{xxxx}}\right)\\ &+\mathscr{D}_{x}\left(\mathcal{W}_{\ell}\right)\left[\frac{\partial \mathscr{L}}{\partial u_{xx}}+\mathscr{D}_{x}^{2}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]-\mathscr{D}_{x}^{2}\left(\mathcal{W}_{\ell}\right)\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right),\\ \mathscr{T}^{y_{j}} = &\; \eta_{\ell}^{y_{j}}\mathscr{L}-\mathcal{W}_{\ell}\mathscr{D}_{y_{j}}\left(\frac{\partial \mathscr{L}}{\partial u_{y_{j}y_{j}}}\right)+\mathscr{D}_{y_{j}}\left(\mathcal{W}_{\ell}\right)\left(\frac{\partial \mathscr{L}}{\partial u_{y_{j}y_{j}}}\right),\; \; \; \begin{array}{cc} j = 1,\cdots,N-1 & \\ \ell = 1,\cdots,\frac{N^2+N+4}{2}&, \end{array} \end{aligned} \end{eqnarray} | (6.2) |
where
| \begin{equation} \mathcal{W}_{\ell} = \zeta_{\ell}-\xi_{\ell}^{0}\frac{\partial u}{\partial t}-\xi_{\ell}^{1}\frac{\partial u}{\partial x}-\sum\limits_{j = 1}^{N-1}{\eta_{\ell}^{y_{j}}\frac{\partial^2 u}{\partial y_j^2}}\; \; \; (\ell = 1,\cdots,\frac{N^2+N+4}{2}), \end{equation} | (6.3) |
denotes the Lie characteristic function corresponding to Lie point symmetries X_{\ell} (3.5) and \mathscr{L} = \mathscr{P} \mathfrak{U} represents the formal Lagrangian in which the nonlocal variable \mathscr{P} satisfies the PDE system (5.8).
Conservation laws of generalized fourth order Boussinesq equation [63] have been computed using multiplier approach. Moreover, infinite conservation laws for Eq (1.3) have also computed using Bell polynomials [64].
In the following subsections, we shall compute the components of conserved vectors for Eqs (1.2) and (1.3) corresponding to the classical Lie point symmetries (3.6) and (3.7), respectively by using the nonlocal conservation laws.
The nonlocal conservation law for Eq (1.2) is given by:
| \begin{equation} \left[\mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)\right]_{\left(1.2\right)} = 0, \end{equation} | (6.4) |
where \mathscr{T} = \left(\mathscr{T}^t, \mathscr{T}^x\right) represents the conserved vector for Eq (1.2).
The components of conserved vector \mathscr{T}^t and \mathscr{T}^x are followed by Eq (6.2) as:
| \begin{eqnarray} \begin{aligned} \mathscr{T}^t = &\; \xi_{\ell}^{0}\mathscr{L}-\mathcal{W}_{\ell}\mathscr{D}_{t}\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right)+\mathscr{D}_{t}\left(\mathcal{W}_{\ell}\right)\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right),\\ \mathscr{T}^x = &\; \xi_{\ell}^{1}\mathscr{L}+\mathcal{W}_{\ell}\left[\frac{\partial\mathscr{L}}{\partial u_{x}}-\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xx}}\right)-\mathscr{D}_{x}^{3}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]+\mathscr{D}_{x}^{3}\left(\mathcal{W_{\ell}}\right)\left(\frac{\partial ]\mathscr{L}}{\partial u_{xxxx}}\right)\\ &+\mathscr{D}_{x}\left(\mathcal{W}_{\ell}\right)\left[\frac{\partial \mathscr{L}}{\partial u_{xx}}+\mathscr{D}_{x}^{2}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]-\mathscr{D}_{x}^{2}\left(\mathcal{W}_{\ell}\right)\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right), \end{aligned} \end{eqnarray} | (6.5) |
where \mathcal{W}_{\ell} = \zeta_{\ell}-\xi_{\ell}^{0}u_{t}-\xi_{\ell}^{1}u_{x}, \; \left(\ell = 1, 2, 3\right) are the Lie characteristic functions corresponding to Lie point symmetries X_{\ell} (3.6), given by:
| \begin{equation} \mathcal{W}_{1} = -u_{t},\; \; \mathcal{W}_2 = -u_{x},\; \; \mathcal{W}_3 = a+2bu+2btu_t+bxu_x, \end{equation} | (6.6) |
and \mathscr{L} is the the formal Lagrangian
| \begin{equation} \mathscr{L} = \mathscr{P}\mathfrak{U},\; \; \mathfrak{U} = u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}, \end{equation} | (6.7) |
with nonlocal variable \mathscr{P} given by Eq (5.11).
Case 1. For X_1 = \frac{\partial}{\partial t}
Substituting \xi_{1}^{0} = 1, \; \xi_{1}^{1} = \zeta_{1} = 0 , \mathcal{W}_{1} = -u_{t} and \mathscr{L} from Eq (6.7), in the pair of Eq (6.5), yields
| \begin{eqnarray} \begin{aligned} \mathscr{T}^{t} = &\left(C_1x+C_3\right)u_t-\left(C_1xt+C_2x+C_3t+C_4\right)\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right),\\ \mathscr{T}^{x} = &\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)\left(C_1xt+C_2x+C_3t+C_4\right)-\left(cu_{txx}-\left(a+2bu\right)u_{t}\right)\left(C_1t+C_2\right). \end{aligned} \end{eqnarray} | (6.8) |
Surely, the conservation law (6.4) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right) = \left(C_1x+C_3\right)\mathfrak{U}. \label{NS4.1.3a.6} \end{equation*} |
Four pairs of components of conserved vectors of Eq (1.2) can be obtained from Eq (6.8), w.r.t. set of arbitrary constants \{C_1, C_2, C_3, C_4\} .
● For C_1 = 1, C_2 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = xu_t-xt\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right), \\ \mathscr{T}^{x} = xt\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)-t\left(cu_{txx}-\left(a+2bu\right)u_{t}\right). \end{cases}
● For C_2 = 1, C_1 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = -x\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right), \\ \mathscr{T}^{x} = x\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)+\left(a+2bu\right)u_t-cu_{txx}. \end{cases}
● For C_3 = 1, C_1 = C_2 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = u_t-t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right), \\ \mathscr{T}^{x} = t\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right). \end{cases}
● For C_4 = 1, C_1 = C_2 = C_3 = 0
\begin{cases} \mathscr{T}^{t} = -au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}, \\ \mathscr{T}^{x} = au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}. \end{cases}
Case 2. For X_2 = \frac{\partial}{\partial x} Substituting \xi_{2}^{1} = 1, \; \xi_{2}^{0} = \zeta_{2} = 0 , \mathcal{W}_{2} = -u_{x} and \mathscr{L} from Eq (6.7), in the pair of Eq (6.5), yields
| \begin{eqnarray} \begin{aligned} \mathscr{T}^{t} = &\left(C_1x+C_3\right)u_x-\left(C_1xt+C_2x+C_3t+C_4\right)u_{tx},\\ \mathscr{T}^{x} = &\left(C_1xt+C_2x+C_3t+C_4\right)u_{tt}-\left(cu_{xxx}+\left(a+2bu\right)u_{x}\right)\left(C_1t+C_2\right). \end{aligned} \end{eqnarray} | (6.9) |
Clearly, these components satisfy conservation law (6.4), since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right) = \left(C_1t+C_2\right)\mathfrak{U}. \label{NS4.1.3a.8} \end{equation*} |
Four pairs of components of conserved vectors of Eq (1.2) can be obtained from Eq (6.9), w.r.t. set of arbitrary constants \{C_1, C_2, C_3, C_4\} .
● For C_1 = 1, C_2 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = xu_{x}-xtu_{tx}, \\ \mathscr{T}^{x} = xtu_{tt}-t\left(cu_{xxx}+\left(a+2bu\right)u_x\right). \end{cases}
● For C_2 = 1, C_1 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = -xtu_{tx}, \\ \mathscr{T}^{x} = xu_{tt}-cu_{xxx}-\left(a+2bu\right)u_x. \end{cases}
● For C_3 = 1, C_1 = C_2 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = u_x-tu_{tx}, \\ \mathscr{T}^{x} = tu_{tt}. \end{cases}
● For C_4 = 1, C_1 = C_2 = C_3 = 0
\begin{cases} \mathscr{T}^{t} = -u_{tx}, \\ \mathscr{T}^{x} = u_{tt}. \end{cases}
Case 3. For X_3 = -2bt\frac{\partial}{\partial t}-bx\frac{\partial}{\partial x}+\left(a+2bu\right)\frac{\partial}{\partial u}
Substituting \xi_{3}^{0} = -2bt, \; \xi_{3}^{1} = -bx, \; \zeta_{3} = a+2bu , \mathcal{W}_{3} = a+2bu+2btu_{t}+bxu_{x} and \mathscr{L} from Eq (6.7), in the pair of Eq (6.5), yields
| \begin{array}{l} \mathscr{T}^{t} = b\left(xu_{tx}+2t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right)+4u_{t}\right)\left(C_1xt+C_2x+C_3t+C_4\right)\\ \qquad \;-\left(a+2bu+2btu_t+bxu_x\right)\left(C_1x+C_3\right),\\ \mathscr{T}^{x} = \left[\left(a+2bu\right)\left(a+2bu+bxu_x+2btu_t\right)+bc\left(xu_{xxx}+2tu_{txx}+4u_{xx}\right)\right]\left(C_1t+C_2\right)\\ \qquad \;-b\left[xu_{tt}+\left(a+2bu\right)\left(5u_{x}+2tu_{tx}\right)+4btu_{t}u_{x}+c\left(5u_{xxx}+2tu_{txxx}\right)\right] \\ \qquad\; \left(C_1xt+C_2x+C_3t+C_4\right). \end{array} | (6.10) |
Evidently, these components satisfy conservation law (6.4), since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right) = \left(2C_2bx+C_3bt+3C_4b\right)\mathfrak{U}. \label{NS4.1.3a.10} \end{equation*} |
Four pairs of components of conserved vectors of Eq (1.2) can be obtained from Eq (6.10), w.r.t. set of arbitrary constants \{C_1, C_2, C_3, C_4\} .
● For C_1 = 1, C_2 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = bxt\left(xu_{tx}+2t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right)+2u_{t}\right)-x\left(a+2bu+bxu_{x}\right), \\ \begin{array}{cc} \mathscr{T}^{x} = &t\left[\left(a+2bu\right)\left(a+2bu-2b\left(2xu_x-tu_t\right)\right)+bc\left(2tu_{txx}+4u_{xx}\right)\right]\\ & -bxt\left[xu_{tt}+2t\left(a+2bu\right)u_{tx}+4btu_{t}u_{x}+2c\left(2cu_{xxx}+tu_{txxx}\right)\right]. \end{array} \end{cases}
● For C_2 = 1, C_1 = C_3 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = bx\left(xu_{tx}+2t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right)+4u_{t}\right), \\ \begin{array}{cc} \mathscr{T}^{x} = &t\left(a+2bu\right)\left(a+2bu-2b\left(2xu_x-tu_t\right)\right)+bc\left(2tu_{txx}+4u_{xx}\right)\\ & -bx\left[xu_{tt}+2t\left(a+2bu\right)u_{tx}+4btu_{t}u_{x}+2c\left(2cu_{xxx}+tu_{txxx}\right)\right]. \end{array} \end{cases}
● For C_3 = 1, C_1 = C_2 = C_4 = 0
\begin{cases} \mathscr{T}^{t} = bt\left(xu_{tx}+2t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right)+2u_{t}\right)-\left(a+2bu+bxu_x\right), \\ \mathscr{T}^{x} = -bt\left(xu_{tt}+\left(a+2bu\right)\left(5u_{x}+2tu_{tx}\right)+c\left(5u_{xxx}+2tu_{txxx}\right)+4btu_{t}u_{x}\right). \end{cases}
● For C_4 = 1, C_1 = C_2 = C_3 = 0
\begin{cases} \mathscr{T}^{t} = bt\left(xu_{tx}+2t\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}\right)+2u_{t}\right)-\left(a+2bu+bxu_x\right), \\ \mathscr{T}^{x} = -b\left(xu_{tt}+\left(a+2bu\right)\left(5u_{x}+2tu_{tx}\right)+c\left(5u_{xxx}+2tu_{txxx}\right)+4btu_{t}u_{x}\right). \end{cases}
The nonlocal conservation law for Eq (1.3) is given by:
| \begin{equation} \left[\mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right)\right]_{\left(1.3\right)} = 0, \end{equation} | (6.11) |
where \mathscr{T} = \left(\mathscr{T}^t, \mathscr{T}^x, \mathscr{T}^y\right) represents the conserved vector for Eq (1.3).
The components of conserved vector \mathscr{T}^t, \; \mathscr{T}^x and \mathscr{T}^y are followed by Eq (6.2) as:
| \begin{eqnarray} \begin{aligned} \mathscr{T}^t = &\; \xi_{\ell}^{0}\mathscr{L}-\mathcal{W}_{\ell}\mathscr{D}_{t}\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right)+\mathscr{D}_{t}\left(\mathcal{W}_{\ell}\right)\left(\frac{\partial \mathscr{L}}{\partial u_{tt}}\right),\\ \mathscr{T}^x = &\; \xi_{\ell}^{1}\mathscr{L}+\mathcal{W}_{\ell}\left[\frac{\partial\mathscr{L}}{\partial u_{x}}-\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xx}}\right)-\mathscr{D}_{x}^{3}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]+\mathscr{D}_{x}^{3}\left(\mathcal{W_{\ell}}\right)\left(\frac{\partial ]\mathscr{L}}{\partial u_{xxxx}}\right)\\ &+\mathscr{D}_{x}\left(\mathcal{W}_{\ell}\right)\left[\frac{\partial \mathscr{L}}{\partial u_{xx}}+\mathscr{D}_{x}^{2}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right)\right]-\mathscr{D}_{x}^{2}\left(\mathcal{W}_{\ell}\right)\mathscr{D}_{x}\left(\frac{\partial \mathscr{L}}{\partial u_{xxxx}}\right),\\ \mathscr{T}^y = &\; \eta_{\ell}\mathscr{L}-\mathcal{W}_{\ell}\mathscr{D}_{y}\left(\frac{\partial \mathscr{L}}{\partial u_{yy}}\right)+\mathscr{D}_{y}\left(\mathcal{W}_{\ell}\right)\left(\frac{\partial \mathscr{L}}{\partial u_{yy}}\right), \end{aligned} \end{eqnarray} | (6.12) |
where \mathcal{W}_{\ell} = \zeta_{\ell}-\xi_{\ell}^{0}u_{t}-\xi_{\ell}^{1}u_{x}-\eta_{\ell}u_{y}, \; \left(\ell = 1, 2, 3, 4, 5\right) are the Lie characteristic functions corresponding to Lie point symmetries X_{\ell} (3.7), given by:
| \begin{equation} \mathcal{W}_{1} = -u_{t},\; \mathcal{W}_2 = -u_{x},\; \mathcal{W}_3 = -u_{y},\; \mathcal{W}_4 = -\frac{y}{d}u_{t}-tu_{y},\; \mathcal{W}_5 = a+2bu+2btu_t+ \\ bxu_x+2byu_y, \end{equation} | (6.13) |
and \mathscr{L} is the the formal Lagrangian
| \begin{equation} \mathscr{L} = \mathscr{P}\mathfrak{U},\; \; \mathfrak{U} = u_{tt}-a u_{xx}-b\left(u^2\right)_{xx}-c u_{xxxx}-d u_{yy}, \end{equation} | (6.14) |
with nonlocal variable \mathscr{P} given by Eq (5.12).
Case 1. For X_1 = \frac{\partial}{\partial t}
Substituting \xi_{1}^{0} = 1, \; \xi_{1}^{1} = \eta_{1} = \zeta_{1} = 0 , \mathcal{W}_{1} = -u_{t} and \mathscr{L} from Eq (6.14), in the pair of Eq (6.12), yields
| \begin{eqnarray} \begin{aligned} \mathscr{T}^{t} = &\left(x+1\right)\left[\left(f^{\prime}+g^{\prime}\right)u_{t}-\left(f+g\right)\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right],\\ \mathscr{T}^{x} = &\left(f+g\right)\left[\left(x+1\right)\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)-\left(au_t+b\left(u^2\right)_t+cu_{txx}\right)\right],\\ \mathscr{T}^{y} = &\left(x+1\right)\left[d\left(f+g\right)u_{ty}-\sqrt{d}\left(f^{\prime}-g^{\prime}\right)u_{t}\right], \end{aligned} \end{eqnarray} | (6.15) |
where f = f\left(t+\frac{y}{\sqrt{d}}\right) and g = g\left(t-\frac{y}{\sqrt{d}}\right) are the arbitrary functions and, f^\prime and g^\prime denote their first order explicit derivatives.
Surely, the conservation law (6.11) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right) = \left(x+1\right)\left(f^{\prime}+g^{\prime}\right)\mathfrak{U}. \end{equation*} |
The components of conserved vectors of Eq (1.3), w.r.t the arbitrary functions f and g are followed by Eq (6.15) as:
● For f\neq0, and g = 0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(f^\prime u_{t}-f\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right), \\ \mathscr{T}^{x} = f\left(x+1\right)\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)-f\left(au_t+b\left(u^2\right)_t+cu_{txx}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left(f\; du_{ty}-f^\prime\; \sqrt{d}u_{t}\right). \end{cases}
● For f = 0, and g\neq0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(g^\prime u_{t}-g\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right), \\ \mathscr{T}^{x} = g\left(x+1\right)\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)-g\left(au_t+b\left(u^2\right)_t+cu_{txx}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left(g\; du_{ty}+g^\prime\; \sqrt{d}u_{t}\right). \end{cases}
Case 2. For X_2 = \frac{\partial}{\partial x}
Substituting \xi_{2}^{1} = 1, \; \xi_{2}^{0} = \eta_{2} = \zeta_{2} = 0 , \mathcal{W}_{2} = -u_{x} and \mathscr{L} from Eq (6.14), in the pair of Eq (6.12), yields
| \begin{eqnarray} \begin{aligned} \mathscr{T}^{t} = &\left(x+1\right)\left[\left(f^{\prime}+g^{\prime}\right)u_{x}-\left(f+g\right)u_{tx}\right],\\ \mathscr{T}^{x} = &\left(f+g\right)\left[\left(x+1\right)\left(u_{tt}-du_{yy}\right)-\left(au_x+b\left(u^2\right)_x+cu_{xxx}\right)\right],\\ \mathscr{T}^{y} = &\left(x+1\right)\left[d\left(f+g\right)u_{xy}-\sqrt{d}\left(f^{\prime}-g^{\prime}\right)u_{x}\right], \end{aligned} \end{eqnarray} | (6.16) |
where f = f\left(t+\frac{y}{\sqrt{d}}\right) and g = g\left(t-\frac{y}{\sqrt{d}}\right) are the arbitrary functions and, f^\prime and g^\prime represent their first order explicit derivatives.
Clearly, the conservation law (6.11) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right) = \left(f+g\right)\mathfrak{U}. \label{NS4.1.3b.8} \end{equation*} |
The components of conserved vectors of Eq (1.3), w.r.t the arbitrary functions f and g are followed by Eq (6.16) as:
● For f\neq0, and g = 0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(f^\prime u_{x}-fu_{tx}\right), \\ \mathscr{T}^{x} = f\left(x+1\right)\left(u_{tt}-du_{yy}\right)-f\left(au_x+b\left(u^2\right)_x+cu_{xxx}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left(f\; du_{xy}-f^\prime\; \sqrt{d}u_{x}\right). \end{cases}
● For f = 0, and g\neq0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(g^\prime u_{x}-gu_{tx}\right), \\ \mathscr{T}^{x} = g\left(x+1\right)\left(u_{tt}-du_{yy}\right)-g\left(au_x+b\left(u^2\right)_x+cu_{xxx}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left(g\; du_{xy}+g^\prime\; \sqrt{d}u_{x}\right). \end{cases}
Case 3. For X_3 = \frac{\partial}{\partial y}
Substituting \eta_{3} = 1, \; \xi_{3}^{0} = \xi_{3}^{1} = \zeta_{3} = 0 , \mathcal{W}_{3} = -u_{y} and \mathscr{L} from Eq (6.14), in the pair of Eq (6.12), yields
| \begin{eqnarray} \begin{aligned} \mathscr{T}^{t} = &\left(x+1\right)\left[\left(f^{\prime}+g^{\prime}\right)u_{y}-\left(f+g\right)u_{ty}\right],\\ \mathscr{T}^{x} = &\left(f+g\right)\left[\left(x+1\right)\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)-\left(au_y+b\left(u^2\right)_y+cu_{xxy}\right)\right],\\ \mathscr{T}^{y} = &\left(x+1\right)\left[\left(f+g\right)\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)-\sqrt{d}\left(f^{\prime}-g^{\prime}\right)u_{y}\right], \end{aligned} \end{eqnarray} | (6.17) |
where f = f\left(t+\frac{y}{\sqrt{d}}\right) and g = g\left(t-\frac{y}{\sqrt{d}}\right) are the arbitrary functions and, f^\prime and g^\prime denote their first order explicit derivatives.
Clearly, the conservation law (6.11) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right) = -\left(x+1\right)\left(\frac{f^\prime -g^\prime}{\sqrt{d}}\right)\mathfrak{U}. \label{NS4.1.3b.10} \end{equation*} |
The components of conserved vectors of Eq (1.3), w.r.t the arbitrary functions f and g are followed by Eq (6.17) as:
● For f\neq0, and g = 0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(f^\prime u_{y}-fu_{ty}\right), \\ \mathscr{T}^{x} = f\left(x+1\right)\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)-f\left(au_y+b\left(u^2\right)_y+cu_{xxy}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left[f\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)-f^\prime\; \sqrt{d}u_{y}\right]. \end{cases}
● For f = 0, and g\neq0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left(g^\prime u_{y}-gu_{ty}\right), \\ \mathscr{T}^{x} = g\left(x+1\right)\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)-g\left(au_y+b\left(u^2\right)_y+cu_{xxy}\right), \\ \mathscr{T}^{y} = \left(x+1\right)\left[g\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)+g^\prime\; \sqrt{d}u_{y}\right]. \end{cases}
Case 4. For X_4 = \frac{\partial}{\partial y}
Substituting \xi_4^{0} = \frac{y}{d}, \; \eta_4 = t, \; \xi_{4}^{1} = \zeta_{4} = 0 , \mathcal{W}_{4} = -\frac{y}{d}u_{t}-tu_{y} and \mathscr{L} from Eq (6.14), in the pair of Eq (6.12), yields
| \begin{array} {l} \mathscr{T}^{t} = \left(x+1\right)\left(f^{\prime}+g^{\prime}\right)\left(\frac{y}{d}u_{t}+tu_{y}\right)-\left(x+1\right)\left(f+g\right) \\ \left(\left(tu_y\right)_t+\frac{y}{d}\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right),\\ \mathscr{T}^{x} = \left(f+g\right)\left(x+1\right)\left[\frac{y}{d}\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)+t\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)\right]\\ \qquad \;\; -\left(f+g\right)\left[\frac{y}{d}\left(au_t+b\left(u^2\right)_{t}+cu_{txx}\right)+t\left(au_{y}+b\left(u^2\right)_{y}+cu_{xxy}\right)\right],\\ \mathscr{T}^{y} = \left(x+1\right)\left(f+g\right)\left(\left(yu_{t}\right)_{y}+t\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)\right)-\left(x+1\right)\left(f^{\prime}-g^{\prime}\right) \\ \left(t\sqrt{d}u_{y}+\frac{y}{\sqrt{d}}u_{t}\right), \end{array} | (6.18) |
where f = f\left(t+\frac{y}{\sqrt{d}}\right) and g = g\left(t-\frac{y}{\sqrt{d}}\right) are the arbitrary functions and, f^\prime and g^\prime represent their first order explicit derivatives.
Evidently, the conservation law (6.11) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right) = \left(x+1\right)\left(\frac{y}{d}\left(f^{\prime}+g^{\prime}\right)+\frac{t}{\sqrt{d}}\left(f^{\prime}-g^{\prime}\right)\right)\mathfrak{U}. \label{NS4.1.3b.12} \end{equation*} |
The components of conserved vectors of Eq (1.3), w.r.t the arbitrary functions f and g are followed by Eq (6.18) as:
● For f\neq0, and g = 0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left[f^{\prime}\left(\frac{y}{d}u_{t}+tu_{y}\right)-f\left(\left(tu_y\right)_t+\frac{y}{d}\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right)\right], \\ \begin{array}{cc} \mathscr{T}^{x} = &f\left(x+1\right)\left[\frac{y}{d}\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)+t\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)\right]\\ & -f\left[\frac{y}{d}\left(au_t+b\left(u^2\right)_{t}+cu_{txx}\right)+t\left(au_{y}+b\left(u^2\right)_{y}+cu_{xxy}\right)\right], \end{array}\\ \mathscr{T}^{y} = \left(x+1\right)\left[f\left(\left(yu_{t}\right)_{y}+t\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)\right)-f^{\prime}\left(t\sqrt{d}u_{y}+\frac{y}{\sqrt{d}}u_{t}\right)\right]. \end{cases}
● For f = 0, and g\neq0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left[g^{\prime}\left(\frac{y}{d}u_{t}+tu_{y}\right)-g\left(\left(tu_y\right)_t+\frac{y}{d}\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right)\right)\right], \\ \begin{array}{cc} \mathscr{T}^{x} = &g\left(x+1\right)\left[\frac{y}{d}\left(au_{tx}+b\left(u^2\right)_{tx}+cu_{txxx}\right)+t\left(au_{xy}+b\left(u^2\right)_{xy}+cu_{xxxy}\right)\right]\\ & -g\left[\frac{y}{d}\left(au_t+b\left(u^2\right)_{t}+cu_{txx}\right)+t\left(au_{y}+b\left(u^2\right)_{y}+cu_{xxy}\right)\right], \end{array}\\ \mathscr{T}^{y} = \left(x+1\right)\left[g\left(\left(yu_{t}\right)_{y}+t\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)\right)+g^{\prime}\left(t\sqrt{d}u_{y}+\frac{y}{\sqrt{d}}u_{t}\right)\right]. \end{cases}
Case 5. For X_5 = -2bt\frac{\partial}{\partial t}-bx\frac{\partial}{\partial x}-2by\frac{\partial}{\partial y}+\left(a+2bu\right)\frac{\partial}{\partial u}
Substituting \xi_5^{0} = -2bt, \; \xi_{5}^{1} = -bx, \; \eta_4 = -2by, \; \zeta_{4} = a+2bu , \mathcal{W}_{5} = a+2 b u+2 b t u_{t}+b x u_{x}+2 b y u_{y} and \mathscr{L} from Eq (6.14), in the pair of Eq (6.12), yields
| \begin{array}{l} \mathscr{T}^{t} = b\left(x+1\right)\left(f+g\right)\left(4u_{t}+xu_{tx}+2yu_{ty}\right)-\left(x+1\right)\left(f^{\prime}+g^{\prime}\right)\left(a+bxu_{x}+2b\left(u+tu_t+yu_y\right)\right)\\ \qquad\;\; +2bt\left(x+1\right)\left(f+g\right)\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right),\\ \mathscr{T}^{x} = \left(a+2bu\right)\left(f+g\right)\left(a+2bu+bxu_x+2b\left(tu_t+yu_y\right)\right)+bc\left(f+g\right) \\ \qquad\;\; \left(xu_{xxx}+2\left(tu_{txx}+yu_{xxy}\right)+4u_{xx}\right)\\ \qquad\;\; -b\left(f+g\right)\left(x+1\right)\left[xu_{tt}-dxu_{yy}+\left(a+2bu\right)\left(5u_x+2tu_{tx}+2yu_{xy}\right)\right]\\ \qquad\;\; -b\left(f+g\right)\left(x+1\right)\left[4b\left(tu_t+yu_y\right)u_x+c\left(5u_{xxx}+2tu_{txxx}+2yu_{xxxy}\right)\right],\\ \mathscr{T}^{y} = -\left(f+g\right)\left(x+1\right)\left[2by\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)-d\left(bxu_{xy}+4bu_{y}+2btu_{ty}\right)\right]\\ \qquad\;\; +\sqrt{d}\left(a+2bu+2b\left(tu_t+yu_y\right)+bxu_x\right)\left(f^{\prime}-g^{\prime}\right)\left(x+1\right). \end{array} | (6.19) |
where f = f\left(t+\frac{y}{\sqrt{d}}\right) and g = g\left(t-\frac{y}{\sqrt{d}}\right) are the arbitrary functions and, f^\prime and g^\prime represent their first order explicit derivatives.
Surely, the conservation law (6.11) is satisfied, since
| \begin{equation*} \mathscr{D}_{t}\left(\mathscr{T}^{t}\right)+\mathscr{D}_{x}\left(\mathscr{T}^{x}\right)+\mathscr{D}_{y}\left(\mathscr{T}^{y}\right) = b\left[f+g-2\left(x+1\right)\left(t\left(f^{\prime}+g^{\prime}\right)+\frac{y}{\sqrt{d}}\left(f^{\prime}-g^{\prime}\right)\right)\right]\mathfrak{U}. \label{NS4.1.3b.14} \end{equation*} |
The components of conserved vectors of Eq (1.3), w.r.t the arbitrary functions f and g are followed by Eq (6.19) as:
● For f\neq0, and g = 0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left[bf\left(4u_{t}+xu_{tx}+2yu_{ty}\right)-f^{\prime}\left(a+bxu_{x}+2b\left(u+tu_t+yu_y\right)\right)\right]\\ \; \; \; \; \; \; \; \; +2btf\left(x+1\right)\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right), \\ \mathscr{T}^{x} = f\left(a+2bu\right)\left(a+2bu+bxu_x+2b\left(tu_t+yu_y\right)\right)+bcf\left(xu_{xxx}+2\left(tu_{txx}+yu_{xxy}\right)+4u_{xx}\right)\\ \; \; \; \; \; \; \; \; -bf\left(x+1\right)\left[xu_{tt}-dxu_{yy}+\left(a+2bu\right)\left(5u_x+2tu_{tx}+2yu_{xy}\right)\right]\\ \; \; \; \; \; \; \; \; -bf\left(x+1\right)\left[4b\left(tu_t+yu_y\right)u_x+c\left(5u_{xxx}+2tu_{txxx}+2yu_{xxxy}\right)\right], \\ \mathscr{T}^{y} = f^{\prime}\sqrt{d}\left(x+1\right)\left(a+2bu+2b\left(tu_t+yu_y\right)+bxu_x\right)\\ \; \; \; \; \; \; \; \; -f\left(x+1\right)\left[2by\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)-d\left(bxu_{xy}+4bu_{y}+2btu_{ty}\right)\right]. \end{cases}
● For f = 0, and g\neq0 :
\begin{cases} \mathscr{T}^{t} = \left(x+1\right)\left[bg\left(4u_{t}+xu_{tx}+2yu_{ty}\right)-g^{\prime}\left(a+bxu_{x}+2b\left(u+tu_t+yu_y\right)\right)\right]\\ \; \; \; \; \; \; \; \; +2btg\left(x+1\right)\left(au_{xx}+b\left(u^2\right)_{xx}+cu_{xxxx}+du_{yy}\right), \\ \mathscr{T}^{x} = g\left(a+2bu\right)\left(a+2bu+bxu_x+2b\left(tu_t+yu_y\right)\right)+bcg\left(xu_{xxx}+2\left(tu_{txx}+yu_{xxy}\right)+4u_{xx}\right)\\ \; \; \; \; \; \; \; \; -bfg\left(x+1\right)\left[xu_{tt}-dxu_{yy}+\left(a+2bu\right)\left(5u_x+2tu_{tx}+2yu_{xy}\right)\right]\\ \; \; \; \; \; \; \; \; -bg\left(x+1\right)\left[4b\left(tu_t+yu_y\right)u_x+c\left(5u_{xxx}+2tu_{txxx}+2yu_{xxxy}\right)\right], \\ \mathscr{T}^{y} = -g^{\prime}\sqrt{d}\left(x+1\right)\left(a+2bu+2b\left(tu_t+yu_y\right)+bxu_x\right)\\ \; \; \; \; \; \; \; \; -g\left(x+1\right)\left[2by\left(u_{tt}-au_{xx}-b\left(u^2\right)_{xx}-cu_{xxxx}\right)-d\left(bxu_{xy}+4bu_{y}+2btu_{ty}\right)\right]. \end{cases}
In this article, the \left(N+1\right) -dimensional generalized Boissinesq equation was studied using the classical Lie theory of differential equations. Lie point symmetries and the corresponding group invariant solutions of the equation were obtained with the help of which new form of solutions were detected. Using the appropriate similarity variables, the considered equation was transformed into nonlinear ordinary differential equation, whose solutions were constructed by the aid of \left(G^\prime/G, 1/G\right) expansion method. Some of the significant solutions were graphically depicted. The concept of nonlinear self-adjointness was employed with the help of which the nonlocal conservation laws were obtained. This article's research findings are novel, more generic, and physically applicable.
The authors declare no conflict of interest.
| [1] | J. Boussinesq, Théorie des ondes et des remous qui se propagent le long d'un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond, J. Math. Pure. Appl., 1872, 55–108. |
| [2] |
Y. L. Ma, A. M. Wazwaz, B. Q. Li, Novel bifurcation solitons for an extended Kadomtsev-Petviashvili equation in fluids, Phys. Lett. A, 413 (2021), 127585. https://doi.org/10.1016/j.physleta.2021.127585 doi: 10.1016/j.physleta.2021.127585

|
| [3] |
B. Q. Li, New breather and multiple-wave soliton dynamics for generalized Vakhnenko-Parkes equation with variable coefficients, J. Comput. Nonlinear Dyn., 16 (2021), 091006. https://doi.org/10.1115/1.4051624 doi: 10.1115/1.4051624

|
| [4] |
Y. L. Ma, A. M. Wazwaz, B. Q. Li, A new (3+1)-dimensional Kadomtsev-Petviashvili equation and its integrability, multiple-solitons, breathers and lump waves, Math. Comput. Simul., 187 (2021), 505–519. https://doi.org/10.1016/j.matcom.2021.03.012 doi: 10.1016/j.matcom.2021.03.012

|
| [5] |
B. Q. Li, Loop-like kink breather and its transition phenomena for the Vakhnenko equation arising from high-frequency wave propagation in electromagnetic physics, Appl. Math. Lett., 112 (2021), 106822. https://doi.org/10.1016/j.aml.2020.106822 doi: 10.1016/j.aml.2020.106822

|
| [6] |
Y. L. Ma, A. M. Wazwaz, B. Q. Li, New extended Kadomtsev-Petviashvili equation: Multiple soliton solutions, breather, lump and interaction solutions, Nonlinear Dynam., 104 (2021), 1581–1594. https://doi.org/10.1007/s11071-021-06357-8 doi: 10.1007/s11071-021-06357-8

|
| [7] | M. N. Alam, M. A. Akbar, S. T. Mohyud-Din, A novel G^{\prime}/G-expansion method and its application to the Boussinesq equation, Chinese Phys. B, 23 (2013). |
| [8] |
X. Lü, J. P. Wang, F. H. Lin, X. W. Zhou, Lump dynamics of a generalized two-dimensional Boussinesq equation in shallow water, Nonlinear Dynam., 91 (2018), 1249–1259. https://doi.org/10.1007/s11071-017-3942-y doi: 10.1007/s11071-017-3942-y

|
| [9] |
A. M. Jawad, M. Petković, P. Laketa, A. Biswas, Dynamics of shallow water waves with Boussinesq equation, Sci. Iran., 20 (2013), 179–184. https://doi.org/10.1016/j.scient.2012.12.011 doi: 10.1016/j.scient.2012.12.011

|
| [10] |
S. Rashid, K. T. Kubra, H. Jafari, S. U. Lehre, A semi-analytical approach for fractional order Boussinesq equation in a gradient unconfined aquifers, Math. Method. Appl. Sci., 45 (2021), 1033–1062. https://doi.org/10.1002/mma.7833 doi: 10.1002/mma.7833

|
| [11] |
M. A. Akbar, N. H. M. Ali, T. Tanjim, Adequate soliton solutions to the perturbed Boussinesq equation and the KdV-Caudrey-Dodd-Gibbon equation, J. King Saud Univ. Sci., 32 (2020), 2777–2785. https://doi.org/10.1016/j.jksus.2020.06.014 doi: 10.1016/j.jksus.2020.06.014

|
| [12] |
Y. L. Ma, B. Q. Li, Analytic rogue wave solutions for a generalized fourth-order Boussinesq equation in fluid mechanics, Math. Method. Appl. Sci., 42 (2019), 39–48. https://doi.org/10.1002/mma.5320 doi: 10.1002/mma.5320

|
| [13] |
Y. L. Ma, N-solitons, breathers and rogue waves for a generalized Boussinesq equation, Int. J. Comput. Math., 97 (2020), 648–1661. https://doi.org/10.1080/00207160.2019.1639678 doi: 10.1080/00207160.2019.1639678

|
| [14] |
Y. L. Ma, B. Q. Li, Bifurcation solitons and breathers for the nonlocal Boussinesq equations, Appl. Math. Lett., 124 (2020), 107677. https://doi.org/10.1016/j.aml.2021.107677 doi: 10.1016/j.aml.2021.107677

|
| [15] |
G. Fal'kovich, M. Spector, S. Turitsyn, Destruction of stationary solutions and collapse in the nonlinear string equation, Phys. Lett. A, 99 (1983), 271–274. https://doi.org/10.1016/0375-9601(83)90882-4 doi: 10.1016/0375-9601(83)90882-4

|
| [16] | G. Morosanu, Nonlinear evolution equations and applications, Springer Science & Business Media, 26 (1988). |
| [17] |
Q. Liu, R. Zhang, L. Yang, J. Song, A new model equation for nonlinear Rossby waves and some of its solutions, Phys. Lett. A, 383 (2019), 514–525. https://doi.org/10.1016/j.physleta.2018.10.052 doi: 10.1016/j.physleta.2018.10.052

|
| [18] |
J. Zhang, R. Zhang, L. Yang, Q. Liu, L. Chen, Coherent structures of nonlinear barotropic-baroclinic interaction in unequal depth two-layer model, Appl. Math. Comput., 408 (2021), 126347. https://doi.org/10.1016/j.amc.2021.126347 doi: 10.1016/j.amc.2021.126347

|
| [19] |
X. Zhang, H. Zhang, Y. Yang, J. Song, Effect of quadric shear basic zonal flows and topography on baroclinic instability, Tellus A, 72 (2020), 1–9. https://doi.org/10.1080/16000870.2020.1843330 doi: 10.1080/16000870.2020.1843330

|
| [20] |
Y. Yang, J. Song, On the generalized eigenvalue problem of Rossby waves vertical velocity under the condition of zonal mean flow and topography, Appl. Math. Lett., 121 (2021), 107485. https://doi.org/10.1016/j.aml.2021.107485 doi: 10.1016/j.aml.2021.107485

|
| [21] |
X. L. Gai, Y. T. Gao, X. Yu, Z. Y. Sun, Soliton interactions for the generalized (3+1)-dimensional Boussinesq equation, Int. J. Mod. Phys. B, 26 (2012), 125006. https://doi.org/10.1142/S0217979212500622 doi: 10.1142/S0217979212500622

|
| [22] |
Z. Yan, Similarity transformations and exact solutions for a family of higher-dimensional generalized Boussinesq equations, Phys. Lett. A, 361 (2007), 223–230. https://doi.org/10.1016/j.physleta.2006.07.047 doi: 10.1016/j.physleta.2006.07.047

|
| [23] |
P. A. Clarkson, M. D. Kruskal, New similarity reductions of the Boussinesq equation, J. Math. Phys., 30 (1989), 2201–2213. https://doi.org/10.1063/1.528613 doi: 10.1063/1.528613

|
| [24] |
M. El-Sabbagh, A. Ali, New exact solutions for (3+1)-dimensional Kadomtsev-Petviashvili equation and generalized (2+1)-dimensional Boussinesq equation, Int. J. Nonlinear Sci. Numer. Simul., 6 (2005), 151–162. https://doi.org/10.1515/IJNSNS.2005.6.2.151 doi: 10.1515/IJNSNS.2005.6.2.151

|
| [25] |
X. W. Yan, Generalized (3+1)-dimensional Boussinesq equation: Breathers, rogue waves and their dynamics, Mod. Phys. Lett. B, 34 (2020), 2050003. https://doi.org/10.1142/S0217984920500037 doi: 10.1142/S0217984920500037

|
| [26] |
W. X. Ma, C. X. Li, J. He, A second Wronskian formulation of the Boussinesq equation, Nonlinear Anal.-Theor., 70 (2009), 4245–4258. https://doi.org/10.1016/j.na.2008.09.010 doi: 10.1016/j.na.2008.09.010

|
| [27] | H. Zhang, B. Tian, H. Q. Zhang, T. Geng, X. H. Meng, W. J. Liu, et al., Periodic wave solutions for (2+1)-dimensional Boussinesq equation and (3+1)-dimensional Kadomtsev-Petviashvili equation, Commun. Theor. Phys., 50 (2008), 1169. |
| [28] |
W. Y. Sun, Y. Y. Sun, The degenerate breather solutions for the Boussinesq equation, Appl. Math. Lett., 128 (2022), 107884. https://doi.org/10.1016/j.aml.2021.107884 doi: 10.1016/j.aml.2021.107884

|
| [29] |
M. Parvizi, A. Khodadadian, M. Eslahchi, Analysis of Ciarlet-Raviart mixed finite element methods for solving damped Boussinesq equation, J. Comput. Appl. Math., 379 (2020), 112818. https://doi.org/10.1016/j.cam.2020.112818 doi: 10.1016/j.cam.2020.112818

|
| [30] |
Y. Liu, B. Li, A. M. Wazwaz, Novel high-order breathers and rogue waves in the Boussinesq equation via determinants, Math. Method. Appl. Sci., 43 (2020), 3701–3715. https://doi.org/10.1002/mma.6148 doi: 10.1002/mma.6148

|
| [31] |
D. J. Ratliff, Double degeneracy in multiphase modulation and the emergence of the Boussinesq equation, Stud. Appl. Math., 140 (2018), 48–77. https://doi.org/10.1111/sapm.12189 doi: 10.1111/sapm.12189

|
| [32] | M. T. Darvishi, M. Najafi, A. M. Wazwaz, Traveling wave solutions for Boussinesq-like equations with spatial and spatial-temporal dispersion, Rom. Rep. Phys., 70 (2018), 108. |
| [33] | A. Zafar, H. Rezazadeh, W. Reazzaq, A. Bekir, The simplest equation approach for solving non-linear Tzitzéica type equations in non-linear optics, Mod. Phys. Lett. B, 35 (2021). https://doi.org/10.1142/S0217984921501323 |
| [34] |
M. Ekici, M. Mirzazadeh, A. Sonmezoglu, M. Z. Ullah, Q. Zhou, H. Triki, et al., Optical solitons with anti-cubic nonlinearity by extended trial equation method, Optik, 136 (2017), 368–373. https://doi.org/10.1016/j.ijleo.2017.02.004 doi: 10.1016/j.ijleo.2017.02.004

|
| [35] |
H. Durur, E. Ilhan, H. Bulut, Novel complex wave solutions of the (2+1)-dimensional hyperbolic nonlinear Schrödinger equation, Fractal Fract., 4 (2020), 41. https://doi.org/10.3390/fractalfract4030041 doi: 10.3390/fractalfract4030041

|
| [36] | A. Hussain, A. Jhangeer, S. Tahir, Y. M. Chu, I. Khan, K. S. Nisar, Dynamical behavior of fractional Chen-Lee-Liu equation in optical fibers with beta derivatives, Results Phys., 18 (2020). https://doi.org/10.1016/j.rinp.2020.103208 |
| [37] | A. Jhangeer, A. Hussain, S. Tahir, S. Sharif, Solitonic, super nonlinear, periodic, quasiperiodic, chaotic waves and conservation laws of modified Zakharov-Kuznetsov equation in transmission line, Commun. Nonlinear Sci. Numer. Simul., 86 (2020). https://doi.org/10.1016/j.cnsns.2020.105254 |
| [38] | A. Hussain, M. Junaid-U-Rehman, F. Jabeen, I. Khan, Optical solitons of NLS-type differential equations by extended direct algebraic method, Int. J. Geom. Methods Mod. Phys., 19 (2022). https://doi.org/10.1142/S021988782250075X |
| [39] | M. A. H. Khaled, M. A. Shukri, Y. A. U. Hager, Dust acoustic multi-soliton collisions in a dusty plasma using Hirota bilinear method, J. Amr. Uni., 1 (2021), 129. |
| [40] |
A. S. Bezgabadi, M. Bolorizadeh, Analytic combined bright-dark, bright and dark solitons solutions of generalized nonlinear Schrödinger equation using extended Sinh-Gordon equation expansion method, Results Phys., 30 (2021), 104852. https://doi.org/10.1016/j.rinp.2021.104852 doi: 10.1016/j.rinp.2021.104852

|
| [41] | Y. Bi, Z. Zhang, Q. Liu, T. Liu, Research on nonlinear waves of blood flow in arterial vessels, Commun. Nonlinear Sci. Numer. Simul., 102 (2021). https://doi.org/10.1016/j.cnsns.2021.105918 |
| [42] | B. Elma, E. Mısırlı, Applications of the extended exp (- \phi (\xi))-expansion method to some non-linear fractional evolution equations, In 9th (Online) International Conference on Applied Analysis and Mathematical Modeling (ICAAMM21), Istanbul-Turkey, 2021, 17. |
| [43] | Y. L. Zhao, Y. P. Liu, Z. B. Li, A connection between the (G^{\prime}/G)-expansion method and the truncated Painlevé expansion method and its application to the mKdV equation, Chinese Phys. B, 19 (2010). |
| [44] |
J. Li, Y. Qiu, D. Lu, R. A. Attia, M. Khater, Study on the solitary wave solutions of the ionic currents on microtubules equation by using the modified Khater method, Therm. Sci., 23 (2019), 2053–2062. https://doi.org/10.2298/TSCI190722370L doi: 10.2298/TSCI190722370L

|
| [45] |
H. M. Ahmed, W. B. Rabie, M. A. Ragusa, Optical solitons and other solutions to Kaup-Newell equation with Jacobi elliptic function expansion method, Anal. Math. Phys., 11 (2021), 1–16. https://doi.org/10.1007/s13324-020-00464-2 doi: 10.1007/s13324-020-00464-2

|
| [46] | P. E. Hydon, P. E. Hydon, Symmetry methods for differential equations: A beginner's guide, Cambridge University Press, 2000. |
| [47] | D. J. Arrigo, Symmetry analysis of differential equations: An introduction, John Wiley & Sons, 2015. |
| [48] |
A. Hussain, A. Jhangeer, N. Abbas, I. Khan, K. S. Nisar, Solitary wave patterns and conservation laws of fourth-order nonlinear symmetric regularized long-wave equation arising in plasma, Ain Shams Eng. J., 12 (2021), 3919–3930. https://doi.org/10.1016/j.asej.2020.11.029 doi: 10.1016/j.asej.2020.11.029

|
| [49] | S. Kumar, M. Niwas, A. M. Wazwaz, Lie symmetry analysis, exact analytical solutions and dynamics of solitons for (2+1)-dimensional NNV equations, Phys. Scripta, 95 (2020). |
| [50] | A. Hussain, A. Jhangeer, N. Abbas, Symmetries, conservation laws and dust acoustic solitons of two-temperature ion in inhomogeneous plasma, Int. J. Geom. Methods Mod. Phys., 18 (2021). https://doi.org/10.1142/S0219887821500717 |
| [51] | M. R. Ali, W. X. Ma, R. Sadat, Lie symmetry analysis and invariant solutions for (2+1)-dimensional Bogoyavlensky-Konopelchenko equation with variable-coefficient in wave propagation, J. Ocean Eng. Sci., 2021. https://doi.org/10.1016/j.joes.2021.08.006 |
| [52] |
A. Hussain, S. Bano, I. Khan, D. Baleanu, K. Sooppy Nisar, Lie symmetry analysis, explicit solutions and conservation laws of a spatially two-dimensional Burgers-Huxley equation, Symmetry, 12 (2020), 170. https://doi.org/10.3390/sym12010170 doi: 10.3390/sym12010170

|
| [53] |
K. Sethukumarasamy, P. Vijayaraju, P. Prakash, On Lie symmetry analysis of certain coupled fractional ordinary differential equations, J. Nonlinear Math. Phys., 28 (2021), 219–241. https://doi.org/10.2991/jnmp.k.210315.001 doi: 10.2991/jnmp.k.210315.001

|
| [54] | A. Jhangeer, A. Hussain, M. Junaid-U-Rehman, I. Khan, D. Baleanu, K. S. Nisar, Lie analysis, conservation laws and travelling wave structures of nonlinear Bogoyavlenskii-Kadomtsev-Petviashvili equation, Results Phys., 19 (2020). https://doi.org/10.1016/j.rinp.2020.103492 |
| [55] | D. Yu, Z. G. Zhang, H. H. Dong, H. W. Yang, Bäcklund transformation, infinite number of conservation laws and fission properties of an integro-differential model for ocean internal solitary waves, Commun. Theor. Phys., 73 (2021). https://doi.org/10.1088/1572-9494/abda1e |
| [56] |
R. Naz, F. M. Mahomed, D. P. Mason, Comparison of different approaches to conservation laws for some partial differential equations in fluid mechanics, Appl. Math. Comput., 205 (2008), 212–230. https://doi.org/10.1016/j.amc.2008.06.042 doi: 10.1016/j.amc.2008.06.042

|
| [57] |
M. B. Riaz, D. Baleanu, A. Jhangeer, N. Abbas, Nonlinear self-adjointness, conserved vectors, and traveling wave structures for the kinetics of phase separation dependent on ternary alloys in iron (Fe-Cr-Y (Y = Mo, Cu)), Results Phys., 25 (2021), 104151. https://doi.org/10.1016/j.rinp.2021.104151 doi: 10.1016/j.rinp.2021.104151

|
| [58] |
M. Inc, A. I. Aliyu, A. Yusuf, D. Baleanu, Combined optical solitary waves and conservation laws for nonlinear Chen-Lee-Liu equation in optical fibers, Optik, 158 (2018), 297–304. https://doi.org/10.1016/j.ijleo.2017.12.075 doi: 10.1016/j.ijleo.2017.12.075

|
| [59] | C. M. Khalique, O. D. Adeyemo, A study of (3+1)-dimensional generalized Korteweg-de Vries-Zakharov-Kuznetsov equation via Lie symmetry approach, Results Phys., 18 (2020). https://doi.org/10.1016/j.rinp.2020.103197 |
| [60] |
C. Fu, C. N. Lu, H. W. Yang, Timespace fractional (2+1)-dimensional nonlinear Schrödinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions, Adv. Diff. Equ., 2018 (2018), 1–20. https://doi.org/10.1186/s13662-018-1512-3 doi: 10.1186/s13662-018-1512-3

|
| [61] | N. H. Ibragimov, Nonlinear self-adjointness and conservation laws, J. Phys. A, 44 (2021). https://doi.org/10.1088/1751-8113/44/43/432002 |
| [62] | M. Gandarias, Weak self-adjoint differential equations, J. Phys. A, 44 (2011). https://doi.org/10.1088/1751-8113/44/26/262001 |
| [63] | S. F. Tian, Lie symmetry analysis, conservation laws and solitary wave solutions to a fourth-order nonlinear generalized Boussinesq water wave equation, Appl. Math. Lett., 100 (2020). https://doi.org/10.1016/j.aml.2019.106056 |
| [64] |
M. J. Xu, S. F. Tian, J. M. Tu, T. T. Zhang, Bäcklund transformation, infinite conservation laws and periodic wave solutions to a generalized (2+1)-dimensional Boussinesq equation, Nonlinear Anal.-Real, 31 (2016), 388–408. https://doi.org/10.1016/j.nonrwa.2016.01.019 doi: 10.1016/j.nonrwa.2016.01.019

|
| 1. | Naseem Abbas, Amjad Hussain, Aziz Khan, Thabet Abdeljawad, Bifurcation analysis, quasi-periodic and chaotic behavior of generalized Pochhammer-Chree equation, 2024, 15, 20904479, 102827, 10.1016/j.asej.2024.102827 | |
| 2. | Saurabh Kumar, Vikas Gupta, An Efficient Numerical Approach to Solve Fractional Coupled Boussinesq Equations, 2024, 19, 1555-1415, 10.1115/1.4066389 | |
| 3. | Mengmeng Wu, Lili Xia, Yudan Lan, Lie symmetry analysis and conservation laws of axially uniform strings, 2024, 12, 2195-268X, 1259, 10.1007/s40435-023-01289-0 | |
| 4. | A. Tomar, H. Kumar, M. Ali, H. Gandhi, D. Singh, G. Pathak, Application of symmetry analysis and conservation laws to a fractional-order nonlinear conduction-diffusion model, 2024, 9, 2473-6988, 17154, 10.3934/math.2024833 | |
| 5. | AMJAD HUSSAIN, ADIL JHANGEER, MUHAMMAD KHUBAIB ZIA, ILYAS KHAN, ABDUL HAMID GANIE, SAYED M. ELDIN, ANALYSIS OF (1 + n)-DIMENSIONAL GENERALIZED CAMASSA–HOLM KADOMTSEV–PETVIASHVILI EQUATION THROUGH LIE SYMMETRIES, NONLINEAR SELF-ADJOINT CLASSIFICATION AND TRAVELLING WAVE SOLUTIONS, 2023, 31, 0218-348X, 10.1142/S0218348X23400789 |