Symmetry solutions and conservation laws of a new generalized 2D Bogoyavlensky-Konopelchenko equation of plasma physics

1.   Introduction

A molecular graph in chemical graph theory is the graphical representation of the structural formula of a chemical compound in which the vertices represent atoms and edges represent chemical bond between those atoms. A topological index of a molecular graph $G$ is a real number which characterizes the topology of $G$. Also it is invariant under graph automorphism. Topological indices have been widely used in Quantitative Structure-Activity Relationship (QSAR) and Quantitative Structure-Property Relationship (QSPR) studies. It has application in many folds, to name a few areas, biochemistry, nanotechnology, pharmacology. Bond energy is a measure of bond strength of a chemical compound. The distance between two atoms is considered as the bond length between them. The higher the bond energy, the smaller is the bond length between those atoms. The recently introduced 2-degree based topological invariants, analogous to novel graph invariants (Zagreb indices), namely leap Zagreb indices, may be applied in studying such bond energy between atoms in a molecular graph of a chemical compound.

Throughout this paper, $G = (V, E)$ represents a connected molecular graph with the vertex set $V(G)$ and the edge set $E(G)$. Let the number of vertices and edges of $G$ be $n$ and $m$ respectively. The degree of a vertex $v$ in $G$ is the number of vertices adjacent to $v$ in $G$ and denoted by $deg(v:G)$. The $2$-degree (or the second-degree) of a vertex $v$ in $G$ is the number of vertices which are at distance two from $v$ in $G$ and denoted by $d_2(v:G)$. The Zagreb indices, namely, the first and second Zagreb indices, are the most important and oldest molecular structure descriptors. These indices have been studied extensively in the field of Mathematical Chemistry ^[3,4,5]. Recently, the concept of Forgotten topological index also known as F-index have attracted many researchers which results in over 100 research articles related to F-index. A.M.Naji et al. ^[13] have recently introduced and studied some properties of a new topological invariant called Leap Zagreb indices. They are defined as follows:

Definition 1. (ⅰ) The first leap Zagreb index $LM_1(G)$ of a graph $G$ is equal to the sum of squares of the second degrees of the vertices, $LM_1(G) = \sum\limits_{u\in V(G)} d_2(u)^2$.

(ⅱ) The second leap Zagreb index $LM_2(G)$ of a graph $G$ is equal to the sum of the products of the second degrees of pairs of adjacent vertices, $LM_2(G) = \sum\limits_{uv\in E(G)} d_2(u)d_2(v)$.

(ⅲ) The third leap Zagreb index $LM_3(G)$ of a graph $G$ is equal to the sum of the products of the degree with the second degree of every vertex in $G$, $LM_3(G) = \sum\limits_{u\in V(G)} deg(u)d_2(u)$

Subsequently, Z. Shao et al. ^[18] generalized the results of Naji et al.^[13] for trees and unicyclic graphs and determined upper and lower bounds on leap Zagreb indices and characterized extremal graphs. Basavanagoud et al.^[2] computed exact values for first and second leap hyper Zagreb indices of some nano structures. V. R. Kulli ^[7,8,9] introduced and studied various leap indices. Shiladhar et al.^[17] computed leap Zagreb indices of wind mill graphs. Most recently, Naji et al.^[14] have studied some properties of leap graphs.

Azari et al.^[1] found formulae for first and second Zagreb indices of bridge and chain graphs. Nilanjan De ^[15,16] computed F-index and hyper Zagreb index of bridge and chain graphs. Jerline et al. ^[6] obtained exact values for harmonic index of bridge and chain graphs. E. Litta et al. ^[10] worked on modified Zagreb indices of bridge graphs. Mohanad Ali et al. ^[11] computed F-leap index of some special classes of bridge and chain graphs. Zhang et al.^[12] worked on Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of generalized bridge molecular graphs. Motivated by their results, we compute exact values for the first and third leap Zagreb indices of bridges and chain graphs. Also we discuss some applications related to these indices in the last section of this paper. First, we recall the definitions of bridge and chain graphs from ^[1] as follows:

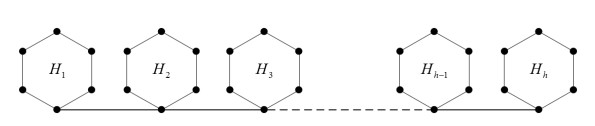
Definition 2. Let ${\{G_i\}}_{i = 1}^d$ be a set of finite pairwise disjoint graphs with distinct vertices $v_i\in V(G_i)$. The bridge graph $\mathcal{B}_1 = \mathcal{B}_1(G_1, G_2, \dots, G_d; v_1, v_2, v_3, \dots, v_d)$ of ${\{G_i\}}_{i = 1}^d$ with respect to the vertices ${\{v_i\}}_{i = 1}^d$ as shown in Figure 1, is the graph obtained from the graphs $G_1, G_2, \dots, G_d$ by connecting the vertices $v_i$ and $v_{i+1}$ by an edge for all $i = 1, 2, \dots, d-1$.

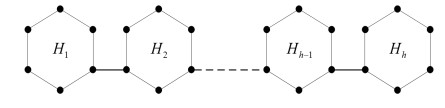
Definition 3. The bridge graph $\mathcal{B}_2 = \mathcal{B}_2(G_1, G_2, \dots, G_d; v_1, w_1, v_2, w_2, \dots, v_d, w_d)$ of ${\{G_i\}}_{i = 1}^d$ with respect to the vertices ${\{v_i, w_i\}}_{i = 1}^d$ as shown in Figure 2, is the graph obtained from the graphs $G_1, G_2, G_3, \dots, G_d$ by connecting the vertices $w_i$ and $v_{i+1}$ by an edge for all $i = 1, 2, \dots, d-1$.

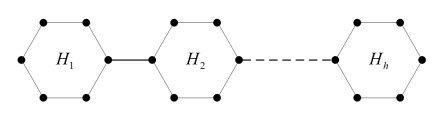
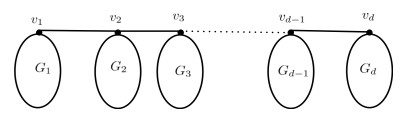
Definition 4. The chain graph $\mathcal{C} = \mathcal{C}(G_1, G_2, \dots, G_d; v_1, w_1, v_2, w_2, \dots, v_d, w_d)$ of $\{G_i\}_{i = 1}^{d}$ with respect to the vertices $\{v_i, w_i\}_{i = 1}^{d}$ as shown in Figure 3, is the graph obtained from the graphs $G_1, G_2, \dots, G_d$ by identifying the vertices $w_i$ and $v_{i+1}$ for all $i = 1, 2, \dots, d-1$.

2.   First and third leap Zagreb indices of bridge and chain graphs

2.1.   The bridge graph $\mathcal{B}_1$

The following lemma gives the $2$-degree of any arbitrary vertex in the bridge graph $\mathcal{B}_1$.

Lemma 5. Let $G_1, G_2, \cdots, G_d$ be $d\geq 5$ connected graphs. Then the $2$-degree of any arbitrary vertex $u$ in the bridge graph $\mathcal{B}_1$ formed by these graphs is as follows:

where $\nu_{i} = d_2(v_i:G_i)$ and $\mu_i = deg(v_i:G_i), \; 1\le i \le d$.

Next, we compute the first leap Zagreb index of the type-Ⅰ bridge graph $\mathcal{B}_1$.

Let $S_i = \sum\limits_{u \in N_{G_i}(v_i)}d_2(u:G_i)$, $1\le i \le d$.

Theorem 6. $LM_1(\mathcal{B}_1) = \sum\limits_{i = 1}^{d}LM_1(G_i)+\sum\limits_{i = 2}^{d-1}\left[ (\mu_{i-1}+\mu_{i+1}+1)^2+2\nu_i(\mu_{i-1}+\mu_{i+1}+1)+4S_i+8\mu_i\right]+2\sum\limits_{i = 3}^{d-2}\nu_i\\+2(S_1+S_d)+(\mu_1+\mu_d-2\mu_3-2\mu_{d-2})+(\mu_2+1)(\mu_2+2\nu_1+1) +(\mu_{d-1}+1)(\mu_{d-1}+2\nu_d+1)+3d-12$.

Proof. By virtue of Lemma 5

Thus the result follows.

Corollary 7. If $G_1 = G_2 = \cdots = G_d = G$ in a bridge graph $\mathcal{B}_1$, then $LM_1(\mathcal{B}_1) = dLM_1(G)+(4d-6)\mu^2+(4d-8)\nu+(12d-26)\mu+(4d-4)(\nu\mu+S)+4d-12$, where $S = \sum\limits_{u\in N_{G}(v)}d_2(u:G)$.

Lemma 8. ^[1] The degree of an arbitrary vertex $u$ of the bridge graph $B_1, \:\:d\geq5$ is given by:

where $\mu_i = deg(v_i:G_i), \; 1\le i \le d$.

Next, we compute the third leap Zagreb index of the type-Ⅰ bridge graph $\mathcal{B}_1$ Let us denote $s_i = \sum\limits_{u\in N_{G_i}(v_i)}deg(u:G_i)$, $1 \le i \le d$.

Theorem 9. $LM_3(\mathcal{B}_1) = \sum\limits_{i = 1}^{d}LM_3(G_i)+(s_1+s_d)+2\sum\limits_{i = 2}^{d-1}s_i+\sum\limits_{i = 1}^{d}(2\nu_i+ 6\mu_i)+2\sum\limits_{i = 2}^{d}(\mu_{i-1}\mu_{i})-2(\mu_2+\mu_{d-1})-(\nu_1+\nu_d)-3(\mu_1+\mu_d)+4d-10$.

Proof. By virtue of Lemma 5 and 8

Thus the result follows.

Corollary 10. If $G_1 = G_2 = \cdots = G_d = G$ in a bridge graph $\mathcal{B}_1$, then $LM_3(\mathcal{B}_1) = dLM_3(G)+ 2(d-1)(s+\nu+\mu^2)+2\mu(3d-5)+4d-10$, where $s = \sum\limits_{u \in N_G(v)}deg(u:G)$.

2.2.   The bridge graph $\mathcal{B}_2$

For any two nonempty sets $A$ and $B$, $A \Delta B$ denotes the symmetric difference of $A$ and $B$ and defined as $A \Delta B = (A\setminus B)\cup (B \setminus A) = (A\cup B)\setminus (A \cap B)$. First, we obtain the $2$-degree of any arbitrary vertex in the type-Ⅱ bridge graph $\mathcal{B}_2$ as follows:

Lemma 11. Let $G_1, G_2, \cdots, G_d$ be $d\geq 5$ triangle free connected graphs. Then $2$-degree of any arbitrary vertex $u$ in the bridge graph $\mathcal{B}_2$ formed by these graphs is as follows:

where $\nu_i = d_2(v_i:G_i), \; \mu_i = deg(v_i:G_i)\; ; 2\le i \le d, \; \delta_i = d_2(w_i:G_i), \; \lambda_i = deg(w_i:G_i); \; 1 \le i \le d-1$.

Next, we compute the first leap Zagreb index of type-Ⅱ bridge graph $\mathcal{B}_2$.

Let us denote $S_1^{'} = \sum\limits_{u\in N_{G_1}(w_1)}d_2(u:G_1)$ and $S_d = \sum\limits_{u\in N_{G_d}(v_d)}d_2(u:G_d)$

Theorem 12. $LM_1(\mathcal{B}_2) = \sum\limits_{i = 1}^{d}LM_1(G_i)+2(S_{1}^{'}+S_{d})+(\lambda_1+\mu_d)+\\ \sum\limits_{i = 2}^{d-1}\sum\limits_{u\in N_{G_i}(v_i)\Delta N_{G_i}(w_i)}[2d_2(u:G_i)+1]+4\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(v_i)\cap N_{G_i}(w_i)}[d_2(u:G_i)+1]+\sum\limits_{i = 1}^{d-1}(\mu_{i+1}^{2}+2\delta_i\mu_{i+1})+\sum\limits_{i = 2}^{d}(\lambda_{i-1}^{2}+2\nu_i\lambda_{i-1}).$

Proof.

Thus,

Corollary 13. If $G_1 = G_2 = \cdots, G_d = G$, in a bridge graph $\mathcal{B}_2$, then $LM_1(\mathcal{B}_2) = dLM_1(G)+\lambda+\mu+2(S+S') + (d-2)\sum\limits_{u \in N_{G}(v)\Delta N_{G}(w)}(2d_2(u:G)+1)+4(d-2)\sum\limits_{u \in N_{G}(v)\cap N_{G}(w)}(d_2(u:G)+1)+(d-1)[\mu^2+\lambda^2] +2(d-1)[\delta\mu+\nu\lambda]$, where $S = \sum\limits_{u\in N_{G}(w)}d_2(u:G)$ and $S' = \sum\limits_{u \in N_{G}(v)}d_2(u:G).$

In what follows next, we compute the third leap Zagreb index of $\mathcal{B}_2$.

Lemma 14. The degree of an arbitrary vertex $u$ of the bridge graph $B_2$, $d\geq5$ is given by:

where $\mu_i = deg(v_i:G_i)\; ; 2\le i \le d, \; \lambda_i = deg(w_i:G_i); \; 1 \le i \le d-1$.

Theorem 15. $LM_3(\mathcal{B}_2) = \sum\limits_{i = 1}^{d}LM_3(G_i)+\sum\limits_{u \in N_{G_1}(w_1)}deg(u:G_1)+\sum\limits_{u \in N_{G_d}(v_d)}deg(u:$$G_d)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(w_i)\setminus N_{G_i}(v_i)}deg(u:G_i)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(v_i)\setminus N_{G_i}(w_i)}deg(u:$$G_i)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(v_i)\cap N_{G_i}(w_i)}2deg(u:G_i)+\sum\limits_{i = 1}^{d-1}2\mu_{i+1}\lambda_{i}+\sum\limits_{i = 1}^{d-1}\mu_{i+1}+\sum\limits_{i = 2}^{d}\lambda_{i-1}+\sum\limits_{i = 1}^{d}(\delta_i+\nu_i)-\nu_1-\delta_d.$

Proof. By virtue of Lemma 2.7 and 2.10

Thus the result follows.

Corollary 16. If $G_1 = G_2 = \cdots = G_d = G$ in a bridge graph $\mathcal{B}_2$, then $LM_3(\mathcal{B}_2) = dLM_3(G)+\sum\limits_{u \in N_{G}(w)}deg(u:G)+\sum\limits_{u \in N_{G}(v)}deg(u:G)+(d-2)(\sum\limits_{u \in N_{G}(w)\setminus N_{G}(v) }deg(u:G)+$$\sum\limits_{u \in N_{G}(v)\setminus N_{G}(w)}deg(u:G)+\sum\limits_{u \in N_{G}(v)\cap N_{G}(w)}2deg(u:G))+(d-1)(2\mu\lambda+\mu+\lambda)+d(\delta+\nu)-(\nu+\delta).$

2.3.   The chain graph $\mathcal{C}$

In the following lemma, we obtain the $2$-degree of any vertex in the chain graph $\mathcal{C}$.

Lemma 17. Let $G_1\; ,\; G_2\; ,\cdots, G_d$, $d\geq 5$ be $C_3$-free connected graphs and let $\mathcal{C} = \mathcal{C}(G_1, G_2, \cdots, G_d; w_1, v_2, w_2, v_3, \cdots, w_{d-1}, v_{d})$ be the chain graph formed using these graphs. Then the $2$-degree of any vertex $u$ in $\mathcal{C}$ is given as follows:

where $\nu_{i} = d_2(v_i:G_i), \; \mu_i = deg(v_i:G_i), \; \lambda_i = deg(w_i:G_i)$ and $\delta_i = d_2(w_i:G_i)$ for all $1\le i \le d$.

Now, we compute the first leap Zagreb index of the chain graph $\mathcal{C}$ by applying Lemma 17.

Theorem 18. For the chain graph $\mathcal{C}$,

Proof. By Lemma 17, we have

Corollary 19. In a chain graph $\mathcal{C}$, if $G_1 = G_2 = \cdots = G_d = G$, then $LM_1(\mathcal{C}) = dLM_1(G)+\sum\limits_{u \in N_{G}(w)}[2 \mu d_2(u:G)+\mu^{2}] +\sum\limits_{u\in N_G(v)}[2\lambda d_2(u:G)+\lambda^{2}]+ (d-2)\sum\limits_{u \in N_{G}(w)\setminus N_{G}(v)}[2 \mu d_2(u:G)+\mu^{2}] +(d-2)\sum\limits_{u \in N_{G}(v)\setminus N_{G}(w)}[2\lambda d_{2}(u:G)+\lambda^{2}]\\ + 2(d-2)\sum\limits_{u \in N_{G}(v)\cap N_{G}(w)}[\lambda d_2(u:G)+\mu d_2(u:G)+\lambda \mu] \\ + (d-2)\sum\limits_{u \in N_{G}(v)\cap N_{G}(w)}(\lambda^{2}+\mu^{2})+2(d-1)\delta \nu$.

Lemma 20. Let $G_1\; ,\; G_2\; ,\cdots, G_d$, $d\geq 5$ be $C_3$-free connected graphs and let $\mathcal{C} = \mathcal{C}(G_1, G_2, \cdots, G_d; w_1, v_2, w_2, v_3, \cdots, w_{d-1}, v_{d})$ be the chain graph formed using these graphs. Then the degree of any vertex $u$ in $\mathcal{C}$ is given as follows:

where $\mu_i = deg(v_i:G_i), \; \lambda_i = deg(w_i:G_i)$ for all $1\le i \le d$

Finally, we compute the third leap Zagreb index of the chain graph $\mathcal{C}$ by applying Lemma 17 and 2.16.

Theorem 21. $LM_3(\mathcal{C}) = \sum\limits_{i = 1}^{d}LM_3(G_i)+\sum\limits_{u \in N_{G_1}(w_1)}\mu_2 deg(u:G_1)+\sum\limits_{u \in N_{G_d}(v_d)}\lambda_{d-1}deg(u:G_d)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(w_i)\setminus N_{G_i}(v_i)}\mu_{i+1}deg(u:G_i)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(v_i)\setminus N_{G_i}(w_i)}\lambda_{i-1}deg(u:G_i)+\sum\limits_{i = 2}^{d-1}\sum\limits_{u \in N_{G_i}(v_i)\cap N_{G_i}(w_i)}(\lambda_{i-1}deg(u:G_i)+\mu_{i+1}deg(u:G_i))+\sum\limits_{i = 1}^{d-1}(\delta_i\mu_{i+1}+\nu_{i+1}\lambda_i).$

Proof. By virtue of Lemma 17 and 20

Thus the result follows.

Corollary 22. In a chain graph $\mathcal{C}$, if $G_1 = G_2 = \cdots = G_d = G$, then $LM_3(\mathcal{C}) = dLM_3(G)+\sum\limits_{u \in N_{G}(w)}\mu deg(u:G)+\sum\limits_{u \in N_{G}(v)}\lambda deg(u:G)+(d-2)(\sum\limits_{u \in N_{G}(w)\setminus N_{G}(v)}\mu deg(u:G)+\sum\limits_{u \in N_{G}(v)\setminus N_{G}(w)}\lambda deg(u:G)+\sum\limits_{u \in N_{G}(v) \cap N_{G}(w)} (\lambda+\mu)deg(u:G))+(d-1)(\delta\mu+\nu\lambda).$

3.   Examples

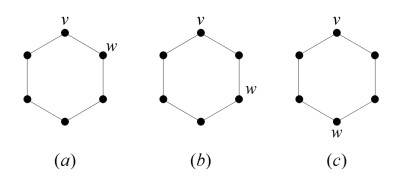
In this section, we determine the first and third leap Zagreb indices of some molecular graph structures. Two vertices $v$ and $w$ of a hexagon $H$ ($C_6$) (please refer Figure 4) are said to be in

(ⅰ) ortho-position, if they are adjacent in $H$

(ⅱ) meta-position, if they are distance two in $H$

(ⅲ) para-position, if they are distance three in $H$.

We connect $h\geq 5$ ortho-hexagons to form a polyphenyl chain denoted by $\mathcal{O}_h$ as follows:

One can observe that the Polyphenyl chain $\mathcal{O}_h$ shown in Figure 5 is a $\mathcal{B}_1$ type bridge graph. Therefore, from Corollary 7, we get

Similarly,

From Corollary 10, we get

The polyphenyl chain $\mathcal{M}_h$ is formed by connecting $h \ge 5$ meta-hexagons as shown in Figure 6.

The polyphenyl chain $\mathcal{P}_h$ is formed by connecting $h \ge 5$ para-hexagons as shown in the following Figure 7.

It is clear that the Polyphenyl chains $\mathcal{M}_h$ and $\mathcal{P}_h$ are type-Ⅱ bridge graphs $\mathcal{B}_2$.

Using Corollary 2.9, we get

Thus $LM_1(\mathcal{M}_h) = 70h-48.$

Similarly, by Corollary 13, we have

Therefore, $LM_1(\mathcal{P}_h) = 68h-44$.

Using Corollary 2.12, we get

Next, we shall see an application related to the chain graph $\mathcal{C}$. The spiro-chain $SPC_4(d, 3)$ is a chain graph formed using $d\ge 5$ copies of the cycle $C_4$.

Here the number $3$ in the construction denotes the position of the vertices $v$ and $w$ in the spiro-chain (refer Figure 8).

The spiro-chain $SPC_6(d, 4)$ is a chain graph formed using $d\ge 5$ copies of the cycle $C_6$ or hexagon where the vertices $v$ and $w$ are connected in the $4^{th}$ position (refer Figure 9).

By applying Corollary 19, we get

Similarly, from Corollary 19, we have $LM_1(SPC_6(d, 4)) = 80d-56$.

By applying Corollary 22, we get

Similarly, from Corollary 22, we have $LM_3(SPC_6(d, 4)) = 48d-24$.

4.   Conclusions

We have computed exact values of one of the recent topological invariants namely first and third leap Zagreb indices for bridge and chain graphs. It is worth mentioning that computing second leap Zagreb index of bridges and chain graphs has not yet addressed and interested researchers may work on it. Also these indices need to be explored for several other interesting graph structures arising from mathematical chemistry and other branches of science.

Acknowledgments

The authors wish to thank the referees for their careful reading of the manuscript and valuable suggestions. This work was supported in part by the National Key Technologies R & D Program of China under Grant 2017YFB0802300, 2018YFB0904205, in part by the Key Laboratory of Pattern Recognition and Intelligent Information Processing, Institutions of Higher Education of Sichuan Province under Grant MSSB-2020-12.

Conflict of interest

The authors declare that no competing interests exist.