Diverse optical solitons solutions of the fractional complex Ginzburg-Landau equation via two altered methods

1.   Introduction

Solitons are currently being examined in a very efficient manner. They occur by the elimination of dispersive effects when they propagate. Soliton is a solution to the weak massive dispersive nonlinear partial differential equation (NLPDE) that can be found in mathematics, physics, biology, engineering finance as well as fractional dynamics. There are several models that are under consideration today for the exploration of soliton solutions ^[1–7]. One such model that has been taken into account for many years is the complex Ginzburg-Landau (CGL) model. Complex Ginzburg-Landau equation (CGLE) is one of the most important models to describe optical phenomena ^[8–10]. In order to better analyze the complex optical phenomena and study their essence, the best ways are to find exact traveling solutions to the CGLE describing the nonlinear optical phenomena. In recent years, a variety of powerful mathematical approaches have been applied to derive the exact soliton solutions of CGLE. Liu et al. ^[11] obtained the kink and periodic wave solutions by using the Hirota bilinear method. Inc et al. ^[12] obtained the bright and singular soliton solutions for the non-linearity term of the CGL model by utilizing the Sine-Gordon method. Arnous et al. ^[13] observed the optical soliton solution by using the modified simple equation method. The quadratic and multiple solitons of n-dimension CGLE were gained by Khater et al. ^[14] using the Sine-Gordon expansion method. Das et al. ^[15] used the $F -$ expansion method to get bright and dark solitons of CGLE.

Recently, the study of physical models with fractional derivatives has attracted a great deal of attention since some materials are well-described as fractal media. To investigate such models, several definitions of fractional derivatives such as Caputo ^[16], Caputo-Fabrizio ^[17], Riemann Liouville ^[18], conformable fractional derivative ^[19], Beta derivative ^[20] and Grunwald-Letnikov ^[21] have been introduced. It is found that fractional derivatives do not satisfy some basic properties of derivatives, such as the product rule and chain rule. Recently, Sousa and Oliveira ^[22] developed a local derivative called a new truncated M-fractional derivative where this fractional calculus satisfies all the properties of derivatives like the chain rule. Also, this derivative has some appealing consequences in diverse areas including fluid mechanics, optical physics, chaos theory, biological models, disease analysis, circuit analysis and others.

The present study sheds light on the space-time fractional CGLE ^[23,24]. The space-time fractional CGL model addressed here is described by

where $\alpha$ and $\beta$ are the fractional parameters, $x$ denotes distance along the fiber, $t$ denotes time in dimensionless form, $a, \, \, c$ and $P$ are valued constants, the symbol $*$ indicates the complex conjugate of the function $u\left({x, t} \right)$ and $H$ is a real-valued algebraic function and its smoothness is possessed by a complex function $H\left({{{\left| u \right|}^2}} \right)u:C \to C.$ Now, taking $C$ as a complex plane to be a two dimensional linear space ${R^2},$ $H\left({{{\left| u \right|}^2}} \right)u$ is $k$ times continuously differentiable real-valued function ^[25]:

where $\delta = 2N,$ then Eq (1) reduces to

Equation (2) is one of the extremely many models that govern pulse propagation dynamics through optical fibers for transcontinental and transoceanic distances. In ^[26], Sulaiman et al. studied the conformable time-space fractional complex Ginzburg-Landau equation via the extended Sine-Gordon equation expansion method. In ^[27], Abdou et al. considered the fractional complex Ginzburg- Landau equation by employing the extended Jacobi elliptic function expansion method. In ^[28], Arshed constructed the soliton solutions to the fractional complex Ginzburg-Landau equation by utilizing the exp $\left({ - \phi \left(\xi \right)} \right) -$expansion method. In ^[29], Ghanbari and Gomez-Aguilar employed the generalized exponential rational functional method to study the periodic and hyperbolic soliton solutions conformable Ginzburg-Landau equation. In ^[30], Lu et al. studied the (2+1)- dimensional fractional complex Ginzburg-Landau equation via the fractional Riccati method and fractional bifunction method. In ^[31], Hussain and Jhangeer obtained the optical solitons of fractional complex Ginzburg-Landau equation with conformable, beta, and M-truncated derivatives. In ^[32] Akram et al. studied the optical solitons for the fractional CGLE with Kerr law nonlinearity using different fractional differential operators. In ^[33], Sadaf et al. obtained the dark, bright, complexion, singular and periodic optical solitons of fractional order complex Ginzburg–Landau equation with Kerr law nonlinearity implementing conformable, beta and M-truncated derivatives. Zafar et al. in ^[34] acquired the kink, bright, W-shaped bright and dark solitons of fractional CGL model using the modified Exp-function and Kudryshov methods. The model is examined with quadratic-cubic law, Kerr law, and parabolic laws non-linear fibers.

The major concern of this existing study is to utilize the novel meanings of fractional-order derivative, named truncated M-fractional derivative ^[35,36], for space-time fractional CGLE, and to find the novel soliton solutions and other solutions in the appearance of a detuning factor in non-linear optics by employ two modified methods, the $\left({1/G'} \right) -$expansion method ^[37] and the modified $\left({G'/{G^2}} \right) -$expansion method ^[38–40]. According to the best authors' knowledge, such type of investigation has not been done before ^[31–34] for the considered fractional CGL model and thus it is interesting to report here. Further, under the given constraint conditions, we obtained the dynamic behavior of solitary wave solutions. Such solutions are important for further studies of this model due to their significant applications in nonlinear optics.

The rest of the paper is structured as follows. In Section 2, the truncated M-fractional derivative and its properties are presented. In Section 3, a truncated M- fractional derivative is applied on the fractional CGLE. In Sections 4 and 5, exact solutions of fractional CGLE are obtained with the Kerr law, quadratic-cubic law and parabolic law nonlinearity. The graphical representation of our obtained solutions in given in Section 6. In the end, conclusions are announced in Section 7.

2.   M-Truncated fractional derivatives and its properties ^[22]

Definition 2.1: The truncated Mittag-Leffler function ^[22,39] with one parameter is defined as follows:

in which $\beta > 0$ and $z \in \, C.$ It is defined in the sense of non-fuzzy concept as given below.

Definition 2.2: Suppose that $g:\left[{0, \infty } \right) \to R$ and $\alpha \in \left({0, 1} \right),$ the truncated derivative $g$ of order $\alpha$ is defined by

Properties 2.1: Suppose that $f$ is a differentiable function of $\alpha$ order at ${t_0} > 0$ with $\alpha \in \left({0, 1} \right]$ and $\, \beta > 0.$ Then $f$ is continuous at ${t_0}.$

Properties 2.2: If $\alpha \in \left({0, 1} \right],$$\, \beta > 0, \, \, g, \, \, h$ are differentiable up to $\alpha$ order at ${t_0} > 0,$ then:

(1) $iT_M^{\alpha, \beta }\left({pg + qh} \right) = {p_i}T_M^{\alpha, \beta }\left(g \right) + {q_i}T_M^{\alpha, \beta }\left(h \right),$ where $p, \, q$ are real constants;

(2) $iT_M^{\alpha, \beta }\left({{t^v}} \right) = v{t^{v - \alpha }}, \, v \in R;$

(3) $iT_M^{\alpha, \beta }\left({gh} \right) = {g_i}T_M^{\alpha, \beta }\left(h \right) + {h_i}T_M^{\alpha, \beta }\left(g \right);$

(4) $iT_M^{\alpha, \beta }\left({\frac{g}{h}} \right) = \frac{{{g_i}T_M^{\alpha, \beta }\left(h \right) - {h_i}T_M^{\alpha, \beta }\left(g \right)}}{{{h^2}}};$

(5) $iT_M^{\alpha, \beta }\left(g \right)\left(t \right) = \frac{{{t^{1 - \alpha }}}}{{\Gamma \left({\beta + 1} \right)}}\frac{{dg}}{{dt}};$

(6) $iT_M^{\alpha, \beta }\left({goh} \right)\left(t \right) = f'{\left({h\left(t \right)} \right)_i}T_M^{\alpha, \beta }h\left(t \right).$

3.   The space time-fractional CGLE and its soliton solutions

To solve Eq (3), we consider the following traveling wave transformation

where $u\left({x, t} \right)$, $w, \, \, k, \, \, v, \, \, \Theta \left({x, t} \right)\,$ and $\varepsilon$ represents the pulse shape, wave number, frequency, speed, phase component and phase function of soliton respectively.

Substituting Eq (6) into Eq (3), an ordinary differential equation is obtained, whose real and imaginary parts respectively are:

and

Now, the focus of the study is to consider Eq (7) with three shapes of non-linear fibers, namely, the Kerr law, the quadratic-cubic law and the parabolic law nonlinearity.

4.   Representation of the modified $\left({{{G'} / {{G^2}}}} \right)$- expansion method and its applications

Let us consider the nonlinear partial differential equation (NLPDE) is given by

where $u = u\left({x, \, t} \right)$ is an unknown function, $Q$ is a polynomial depending on $u\left({x, t} \right)$ and its various partial derivatives.

Step 1: By suitable wave transformation

Here, $v$ is the wave speed. The wave variable allows us to reduce Eq (10) into a nonlinear ordinary differential equation (ODE) for $U = U\left(\eta \right):$

Step 2: Extend the solution of Eq (11) in the following form. Let the modified $\left({{{G'} / {{G^2}}}} \right)$-equation is

where ${a_i}\left({i = 0, 1, 2, 3, ..., m} \right)$ are constants and find to be later. It is important that ${a_i} \ne 0.$

The function $G = G(\eta)$ satisfies the following Riccati equation,

where ${\lambda _0}$ and ${\lambda _1}$ are constants. We gain the below solutions to Eq (13) due to different conditions of ${\lambda _0}$:

When ${\lambda _0}{\lambda _1} < 0,$

When ${\lambda _0}{\lambda _1} > 0,$

When ${\lambda _0} = 0$ and ${\lambda _1} \ne 0,$

where ${C_1}$ and ${C_2}$ are arbitrary constant.

Substituting Eq (12) into Eq (11) along with Eq (13) and apply symbolic computations results in an algebraic system whose solution leads to optical solitons of the nonlinear partial differential Eq (9).

4.1.   Kerr law

In this case, when we take

This appears in water waves and in nonlinear fiber optics Biswas et al. ^[41]. Then Eq (3) becomes:

Thus; Eq (18) changes to

According to the balance principle, we obtain $m = 1.$ Putting $m = 1$ to Eq (12), then we get

Here, ${a_0}$ and ${a_1}$ are unknown parameters. By substituting Eq (19) with Eq (13) into Eq (19) and summing up all coefficients of same order of $\left({{{G'} / {{G^2}}}} \right),$ we get the algebraic expressions involving ${a_0}, \, \, {a_1}$ and other parameters as follows:

Solving the system of algebraic equations in (21) with the help of software MATHEMATICA, we attain the following solutions:

Now we use Eqs (14)–(16), (20) and (22) into Eq (6) and set to the below cases. $\text{If}{\lambda }_{0}{\lambda }_{1}\text{ < 0, then}$

If ${\lambda _0}{\lambda _1} > 0, \, \, {\text{then}}$

4.2.   Quadratic-Cubic law

This type of nonlinearity was studied in ^[42]. In this case, we take

Then Eq (3) becomes:

Thus; Eq (26) changes to

According to the balance principle, we obtain $m = 1.$ Putting $m = 1$ into Eq (12), we get Eq (20).By putting Eq (20) with Eq (13) into Eq (27) and summing up all coefficients of same order of $\left({{{G'} / {{G^2}}}} \right),$ we get the algebraic expressions involving ${a_0}, \, \, {a_1}$ and other parameters as:

Now with the use of MATHEMATICA, we get the below solution:

Now we use Eqs (14)–(16), (20) and (29) into Eq (6) and set to the below cases. $\text{If}{\lambda }_{0}{\lambda }_{1}\text{ < 0, }$ then

If ${\lambda _0}{\lambda _1} > 0,$ then

4.3.   Parabolic law

This type of nonlinearity can be found in ^[43]. In this case, we take

Then Eq (3) becomes:

Thus; Eq (33) changes to

Substituting

Then Eq (34) converts to

According to the balance principle, we obtain $m = 1.$ Putting $m = 1$ into Eq (12), we get Eq (20). By putting Eq (20) with Eq (13) into Eq (36) and summing up all coefficients of same order of $\left({{{G'} / {{G^2}}}} \right),$ we get the algebraic expressions involving ${a_0}, \, \, {a_1}$ and other parameters as:

Now with the use of MATHEMATICA, we get the below solution:

Now we use Eqs (20), (38) and (14)–(16) into Eq (6) and set to the below cases. I$\text{f}{\lambda }_{0}{\lambda }_{1}\text{ < 0, }$ then

If ${\lambda _0}{\lambda _1} > 0,$ then

5.   Representation of $\left({{1 / {G'}}} \right)$- expansion method and its applications

Here, we will describe the basic steps of $\left({{1 / {G'}}} \right) -$expansion method ^[37].

Step 1: Consider Eqs (9)–(11).

Step 2: Extend the solution of Eq (11) in the following form

where $G = G(\eta)$ and satisfies the following linear ordinary differential equation which is

where ${a_i}\left({i = 1, ...., m} \right), \, \, \lambda {\text{ }}\, {\text{and}}\, {\text{ }}\mu$ are constants to be determined. The positive integer $m$ can be obtained by using the homogenous balance between the highest order derivatives and the nonlinear term appearing in Eq. (11). Additionally, the solution of the differential equation given in Eq (42) is

where ${C_1}$ and ${C_2}$ are arbitrary integration constants.$\left({{1 / {G'}}} \right)$ can be expressed as

Step 3: Substituting Eq (41) into Eq (11) along with Eq (42) and apply symbolic computations results in an algebraic system whose solution leads to optical solitons of the nonlinear partial differential Eq (9).

5.1.   Kerr law

Consider Eqs (17)–(19). By applying balance principle on Eq (19), we obtain $m = 1.$ Putting $m = 1$ in Eq (41), then we get

Here ${a_0}$ and ${a_1}$ are unknown parameters. By putting Eq (45) with Eq (42) into Eq (19) and summing up all the coefficients of same order of $\left({{1 / {G'}}} \right),$ we get the algebraic expression involving ${a_0}, \, \, {a_1}$ and other parameters.

Now with the use of MATHEMATICA Aid, we get:

Following the above solutions, we get the hyperbolic solution:

5.2.   Quadratic-Cubic law

Consider Eqs (25)–(27). By applying balance principle on Eq (27), we obtain $m = 1.$ Putting $m = 1$ in Eq (41), and then we get Eq (45). By putting Eq (45) with Eq (42) into Eq (27) and summing up all the coefficients of same order of $\left({{1 / {G'}}} \right),$ we get the algebraic expression involving ${a_0}, \, \, {a_1}$ and other parameters as:

Now, with the use of MATHEMATICA Aid, we get the below solution:

Following the above solutions, we get the hyperbolic solution:

5.3.   Parabolic law

Consider Eqs (32), (33) and (36). By applying the balance principle on Eq (36), we obtain $m = 1.$ Putting $m = 1$ to Eq (41), and then we get Eq (45).By putting Eq (45) with Eq (42) into Eq (36) and summing up all the coefficients of same order of $\left({{1 / {G'}}} \right),$ we get the algebraic expression involving ${a_0}, \, \, {a_1}$ and other parameters as:

Now with the use of MATHEMATICA Aid, we get the below solution:

Following the above solutions, we get the hyperbolic solution:

6.   Results and discussion

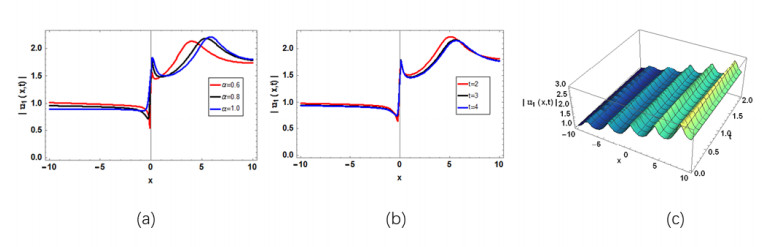
This section deals with a graphical demonstration of the obtained results and provides a brief discussion on the effect of fractional parameter $\alpha.$ Figure 1c depicts the physical appearance of the multiple soliton solutions of Eq (23) and Figures 1(a, b)demonstrates the effect of fractional parameter $\alpha$ and time $t$ along fixed space parameter. A graphical illustration of the periodic soliton solution of Eq (24)can be viewed in Figure 2(c), and its 2D fractional and time parameters effects are depicted in Figure 2(a, b). Figures 3(c), 4(c), 5(c), 6(c), 7(c) and 8(c) highlight the physical appearance of the bright soliton solution of Eq (31), singular soliton solution of Eq (39), bright-dark soliton solution of Eq (40), bright singular soliton solution of Eq (48), smooth antiking soliton solution of Eq (51) and steep antiking soliton solution of Eq (54) respectively, and their respective 2D fractional and time parameter effects are given in Figues 3(a, b), 4(a, b), 5(a, b), 6(a, b), 7(a, b) and 8(a, b).

7.   Conclusions

In this study, we have used a truncated M-fractional derivative to find the optical solutions of the fractional CGLE. We carried out this objective by adopting a specific wave transformation to change the fractional CGLE to a nonlinear ODE of second order such that the resultant ODE could be solved by employing the modified $\left({{{G'} / {{G^2}}}} \right)$ and $\left({{1 / {G'}}} \right)$ expansion methods. These methods restored the bright, multiple and bright-dark solitons for Kerr law, quadratic-cubic law and parabolic law nonlinearities. To describe the physical phenomena of the space-time fractional CGLE, some solutions are plotted in the form of (3D surface graphs and 2D line plots) by assigning the specific value to the parameters under the constrained conditions. Compared with other work ^[31–34], our solutions have not been reported in the former literature. Moreover, these methods are very efficient and powerful in finding the soliton solutions for the nonlinear fractional differential equations, and the obtained solutions can help us to more deeply explain the nonlinear dynamics of optical soliton propagations. Also, these methods can be applied to many NLPDEs in mathematical physics. Finally, our solutions have been checked using the software MATHEMATICA by putting them back into the original equation.

Acknowledgement

This work was partially funded by the research center of the Future University in Egypt, 2022.

Conflict of interest

The authors declare there is no conflict of interest.