Numerical simulation for the fractional-in-space Ginzburg-Landau equation using Fourier spectral method

1.   Introduction

In the 1950s, Vitaly Lazarevich Ginzburg and Lev Davidovich Landau combined the electrokinetic, quantum mechanical and thermodynamic properties of superconductors on the basis of Landau's second-order phase transition theory. The Ginzburg-Landau equation ^[1] was proposed, and has been widely used to describe the phenomena of superconductivity, Bose-Einstein condensation, superfluidity, liquid crystals and strings. Since the 1880s, with the development of cryogenic superconductivity and other fields, the equation has attracted many scholars to study it.

In the past few decades, the theory and applications of fractional calculus ^{[2,3,4,5,6,7]} have been widely studied and developed rapidly. The fractional generalization of the Ginzburg-Landau equation was suggested in ^[8,9] from the variational Euler-Lagrange equation for fractal media. Since then, the fractional Ginzburg-Landau equation (FGLE) by Tarasov and Zaslavsky ^[8,9] has been exploited to describe various physical phenomena. The FGLE has been widely studied in diverse aspects, and these studies include but are not limited to ^{[10,11,12,13,14,15,16]}. The FGLE has singularity, non-locality, and it sometimes even involves space-time coupling, which bringing many difficulties and challenges to analysis and numerical methods.

The numerical solution of the FGLE has received some attention and made some progress in recent decades. In ^{[11,12,13,14,15]}, some numerical methods have been studied for the FGLE. In ^[11], the authors studied a two-dimensional nonlinear spatial FGLE by using a centered finite difference method. In ^[12], the authors proposed a splitting iteration method for solving the space FGLE. In ^[13], the authors proposed a three-level linearized finite difference scheme for the high-dimensional nonlinear FGLE. The fractional Laplacian is discretized by the fractional centered difference scheme, and the Crank-Nicolson scheme is used for time discretization. In ^[14], the author proposed a fast and efficient spectral-Galerkin method for the nonlinear complex FGLE involving the fractional Laplacian operator. By employing the Fourier-like bi-orthogonal mapped Chebyshev function as basis functions, and an exponential time difference scheme is proposed for the temporal discretization. In ^[15], the authors proposed Galerkin finite element method of the FGLE, an implicit midpoint difference method was employed for the temporal discretization, and a Galerkin finite element method was used for the spatial discretization.

This paper introduces the Fourier spectral method for the FGLE with Riesz fractional derivative. The Fourier spectral method can effectively avoid singularity, non-locality, and space-time coupling of the FGLE. So, we can effectively capture the propagation and interaction behavior of the FGLE in different parameters and different fractional derivatives by using the Fourier spectral method. Comparisons are made between the numerical and the exact solution, and it is found that the Fourier spectral method is a satisfactory and efficient algorithm for capturing the propagation of the FGLE.

2.   Description of Fourier spectral method

In recent years, the Fourier spectral method has been widely used in space fractional nonlinear equations. It$^{, }$s main idea is the Fourier transform for spatial discretization. We have used a Fourier spectral method to investigate a class of fractional KdV-modified KdV equations ^[17] and fractional Gray-Scott model ^[18]. This paper introduces a Fourier spectral method for the FGLE.

We consider the following fractional-in-space Ginzburg-Landau equation with the Riesz fractional derivative

with the initial condition $u(\mathbf{x}, 0) = u_0(\mathbf{x})$ and periodic boundary condition or homogeneous Dirichlet boundary condition.

$i = \sqrt{-1},$ parameters $\nu > 0,$ $\kappa > 0,$ $\eta,$ $\zeta,$ $\kappa$ are given real constants, and $u_0(\mathbf{x})$ is a given smooth function. $-(-{\Delta }^{\frac{\alpha}{2}}) u(\mathbf{x}, t)$ is the fractional Laplacian operators of $\alpha$-order with the Riesz fractional derivative. $(\mathbf{x}, t) = (x, y, z, t)\in\Omega \times [0, T] = [-L/2, L/2]\times[-L/2, L/2]\times[-L/2, L/2]\times [0, T].$ $u(\mathbf{x}, t)$ is a unknown complex-valued function.

The Laplacian is an important operator in engineering and physics. However, the standard definition cannot deal with domains that are neither homogeneous nor isotropic. In ^[7], the Riesz implicitly suggested several possible definitions of a fractional Laplacian. The Riesz fractional Laplacian is implemented by the inverse of the Riesz potential. At present, finding a definition of a fractional Laplacian for both isotropic and anisotropic media is a hot topic in applied science. In ^[6], the authors generalized the fractional Laplacian.

Definition 2.1. The Laplacian operator of $\alpha$-order with Riesz fractional derivative is defined as follows: ^[8,9]

where ${}_x\!D_L^{\alpha}$, ${}_x\!D_R^{\alpha}$, ${}_y\!D_L^{\alpha}$, ${}_y\!D_R^{\alpha}$ and ${}_z\!D_L^{\alpha}$, ${}_z\!D_R^{\alpha}$ are the Riemann-Liouville fractional derivative.

The corresponding Fourier transform of the Laplacian operator of $\alpha$-order with Riesz fractional derivative is

Definition 2.2. The continuous Fourier transform and inverse Fourier transform of function $u(\mathbf{x}, t)$ about $\mathbf{x}$ are defined as

The corresponding Fast Fourier transform (FFT) and the inverse Fast Fourier transform (IFFT) are defined as

and $\mathcal{F}^{-1}_\mathbf{x}(\hat{u})$ is the inverse Fast Fourier transform (IFFT) for $\hat{u}(k_x, k_y, k_z)$.

By using the Fast Fourier transform (FFT) for Eq (2.1) in the space domain, Eq (2.1) can be transformed into the following ODEs about $t$.

In the actual calculation, we generate grids as follows in Matlab. Input $L; N;$ $x = L/N*[-N/2:N/2-1];y = x; z = x;$ $kX = 2*pi./L.*[0:N/2-1-N/2:-1];kY = kX; kZ = kX;$ $[X, Y, Z] = meshgrid(x, y, z);$ $[kx, ky, kz] = meshgrid(kX, kY, kZ);$ Noting $k_\alpha = |k_x|^{\alpha}+|k_y|^{\alpha}+|k_z|^{\alpha}$.

Equation (2.5) can be transformed into the following form:

where

Equation (2.6) can be rewritten as

where $g(t, \hat{u}_N) = -\Big ((\nu+i\eta)k_\alpha\Big)\hat{u}_N-(\kappa+i\zeta)\mathcal{F}_\mathbf{x}\Big(|\mathcal{F}^{-1}_\mathbf{x}(\hat{u}_N)|^{2}\mathcal{F}^{-1}_\mathbf{x}(\hat{u}_N)\Big).$

Then, we use the fourth-order Runge-Kutta method to solve the ordinary differential equation (2.7) as follows:

where $\tau$ is step-size, and incremental function $\psi(\hat{u}_{N, n}, t_n, \tau) = \frac{1}{6}(\tilde{k}_1+2\tilde{k}_2+2\tilde{k}_3+\tilde{k}_4)$.

Theorem 2.3. ^[17] If $\psi(\hat{u}_N, t, \tau)$ satisfies the Lipschitz condition in $\hat{u}_N$, then the fourth-order Runge-Kutta method is stable.

Theorem 2.4. ^[17] Let $\hat{u}_{N}(t_{n})$ be the exact solution of problem (2.7), and $\hat{u}_{N, n}$ is the numerical solution. If $\psi(\hat{u}_{N}, t, h)$ satisfies the Lipschitz condition on $0\leq t\leq T$, then there holds the following error estimate:

where $\epsilon_i = \hat{u}_{N}(t_{n})-\hat{u}_{N, n}$, $M_0 = max(\left|\epsilon_0 \right|, \left|\epsilon_1 \right|, \cdots, \left|\epsilon_{n-1} \right|)$, $L$ is a Lipschitz constant, and $c$ is a constant.

Finally, we find the numerical solution $u_N$ using the inverse discrete Fourier transform.

The error norms, $E_{2}$, $E_{\infty}$ and global relative error $\rm GRE$ are used to determine the accuracy of the method:

3.   Numerical simulation

Experiment 1. Subject to the initial condition in Eq (2.1),

and the exact solution for $\alpha = 2, \eta = \frac{1}{2}, \zeta = -1$ is ^[15]

where

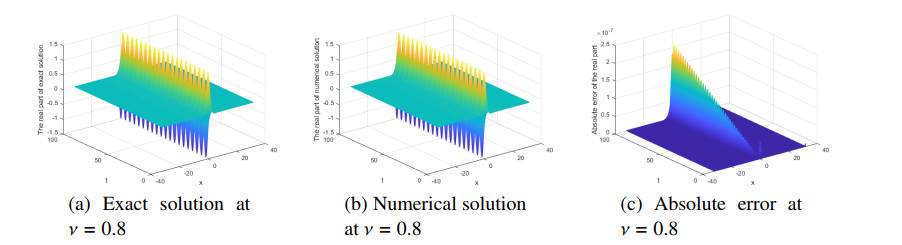
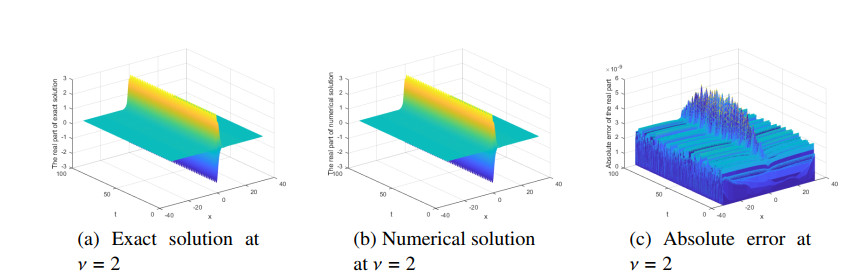
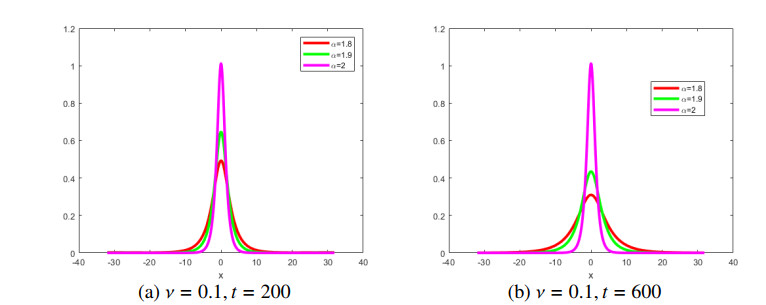
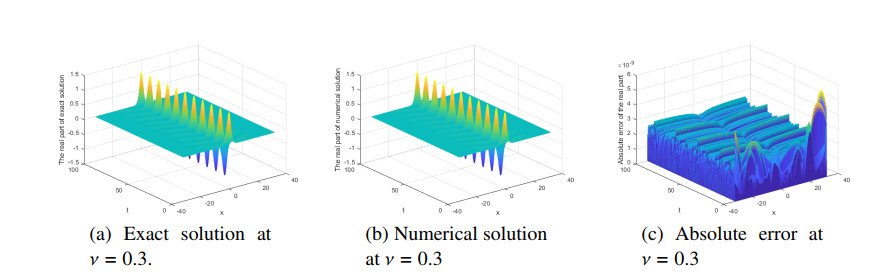
First, the numerical and exact solutions are compared to confirm the validity of the present method. We set $\kappa = -\frac{\nu(3\sqrt{1+4\nu^{2}}-1)}{2(2+9\nu^{2})}, T = 100, \tau = 0.01, L = 64, N = 512$. Numerical results at different values of $\nu = 0.3, 0.8, 2$ are shown in Figures 1–3.

In Figures 1–3, we observe the relationship between the parameter $\nu$ and the soliton. We find that if the parameter $\nu$ is big, the more soliton waves are seen, and if the time $t$ is long, the more soliton waves are seen. The absolute error has little relation to the parameter $\nu$. When the parameter $\nu$ changes, the shape of the soliton does not change. Figures 1–3 confirm the validity of the present method and capture the propagation and interaction behavior of the parameter $\nu$. In Figures 1–3, one can see that the energy norm of the numerical solution seems to be conservative, which coincides with the exact solution.

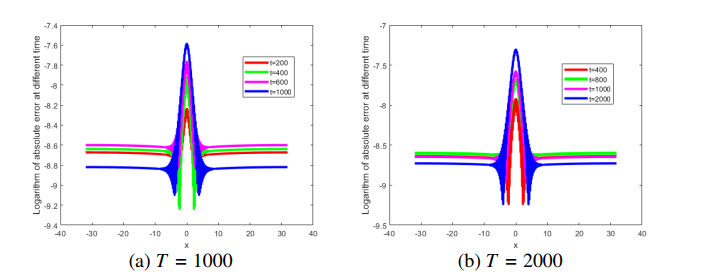
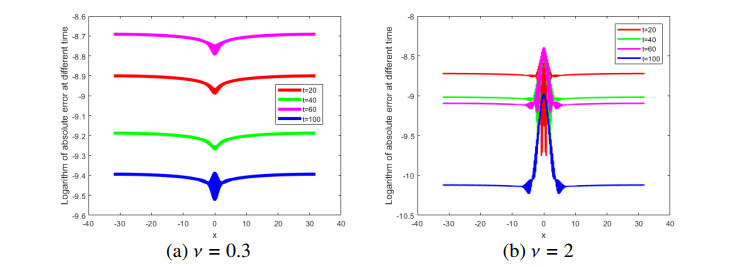
In order to show the present method has higher precision for large interval lengths and long time, we set different parameters. The logarithm of absolute error at different times $t$ are plotted in Figures 4 and 5.

$E_{2}, E_{\infty}, {\rm GRE}$ and the order of convergence in space are shown Tables 1–3. From Tables 1–3, errors $E_{2}, E_{\infty}, {\rm GRE}$ do not change much. From the numerical simulation results, it can be seen that the time step $\tau$ has little influence on the absolute error of the numerical solution with $L = 32, N = 512$, and it is found that the Fourier spectral method is a satisfactory and efficient algorithm. From Tables 1–3 and in Figures 1–5, the present method has higher precision for large interval lengths and long time.

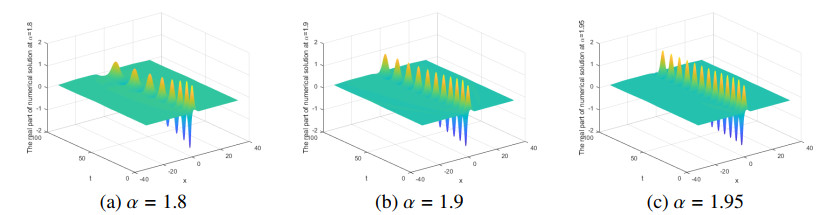
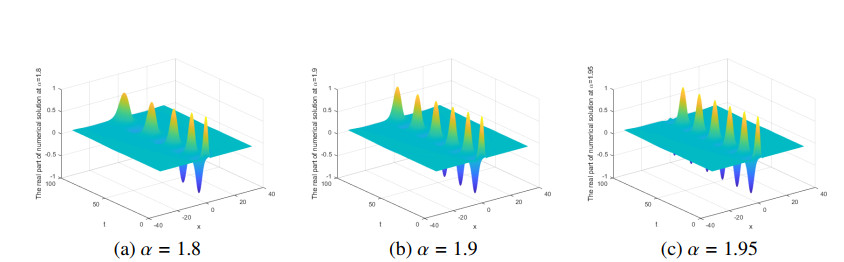
Next, we pay our attention to the impact on the dissipative mechanism of the fractional Laplacian. We set different values of $\alpha$. Numerical results are shown in Figures 6–8. When the fractional $\alpha$ changes, the shape of the soliton and the number of solitons change accordingly, which can be easily seen in the spectrogram.

The numerical solutions are shown in Figures 7 and 8. In Figures 6–8, it can be seen that the wave-shape changes with the fractional parameter $\alpha$, and when $\alpha$ tends to 2, the numerical solutions of the FGLE are convergent to the solutions of the usual classical integer one, concurring with the results of ^[11].

In Figures 1–7, we set the initial condition $u(x, 0) = a(x)\exp(id\ln[a(x)])$. In Figure 8, the initial condition is $u(x, 0) = \sin(a(x))\sec(x-3/4\sin(x))$. In Figures 1–8 and Tables 1–3, we set $\eta = \frac{1}{2}, \kappa = -\frac{\nu(3\sqrt{1+4\nu^{2}}-1)}{2(2+9\nu^{2})}, \zeta = -1.$

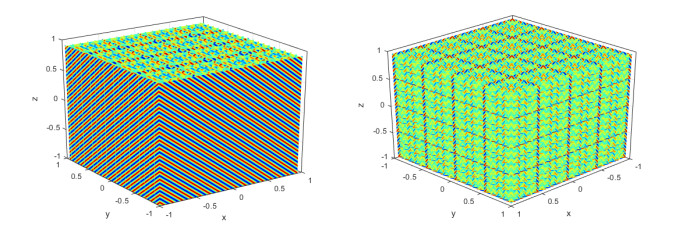
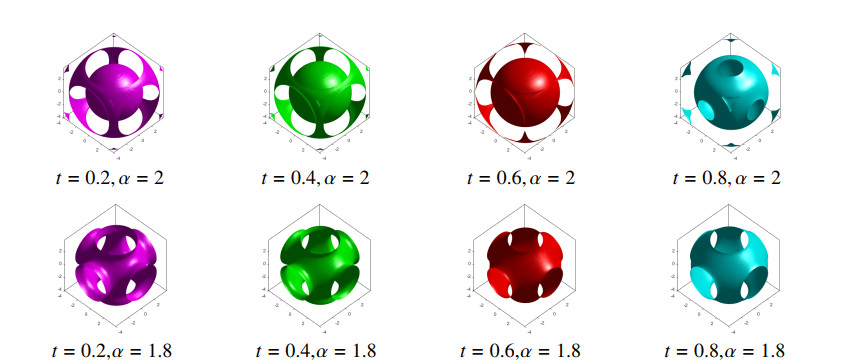
Experiment 2. For (3+1)-dimensional model (2.1), we set differently the initial conditions. Fractal propagations of waves are shown in Figures 9 and 10.

Figure 9 shows the numerical solution. Figure 10 shows the isosurface plot for the real part of the numerical solution at different fractional derivative values $\alpha$, and $\nu = 0.5, \; \eta = 0.5, \; \kappa = 1, \; \zeta = -1, \; \tau = 0.01, \; N = 64, \; L = 8, \; T = 1, \; u(\mathbf{x}, 0) = \sec(\mathbf{r})\tanh(\mathbf{r})$, where $\mathbf{r} = x^2+y^2+x^2$. The spatio-temporal symmetry group illustrated in Figures 9, and 10 shows the fractal properties of quantum space-time. Some unusual features of the isosurface plot (Figure 10) are found by using the present method.

4.   Conclusions

This paper effectively observes some attractive behaviors of fractal propagation and fractal interaction of particles' waves, which are modeled by FGLE. The Fourier spectral method is used to reveal the solution properties numerically, and the fractal properties are illustrated graphically by choosing different coefficients and different fractional orders. The influence of the fractional Laplacian operator on GLE is observed. In Experiment 1, we observe the relationship between the parameter $\nu$ and the soliton. We find that if the parameter $\nu$ is big, the more soliton waves are seen, and if the time $t$ is long, the more soliton waves are seen. In Figures 6–8, it can be seen that the wave-shape change with the fractional parameter $\alpha$, and when $\alpha$ tends to 2, the numerical solutions of the FGLE are convergent to the solutions of the usual classical integer one, concurring with the results of ^[15]. When the fractional parameter $\alpha$ changes, the shape of the soliton and the number of solitons change accordingly. In Experiment 2, we observe the propagation behaviors of 3D FGLE, which are unlike any that have been previously obtained in numerical studies. The fractal propagation of solitary waves reveals a totally new physical law for particles motion in a fractal space, that is the particle wave in a fractal space has a spatiotemporal symmetry group. It is worth noting that the Fourier spectral method can also be used to study other attractive behaviors of fractal propagation and fractal interaction of particles' waves. In further work, we will be devoted to studying fractional-order fractal propagation of high dimensional particle waves.

All computations were performed by the MatlabR2017b software.

Acknowledgments

The work was supported by the Natural Science Foundation of Inner Mongolia [2021MS01009].

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this article.