Pseudo almost periodic solutions for quaternion-valued high-order Hopfield neural networks with time-varying delays and leakage delays on time scales

1.   Introduction

Because high-order Hopfield neural networks have more extensive applications than Hopfield neural networks, various dynamical behaviours of high-order Hopfield neural networks such as the existence and stability of equilibrium points ^[1,2], anti-periodic solutions ^[3], almost periodic solutions ^[4,5,6] and pseudo almost periodic solutions ^[7] have been studied by many scholars.

On the one hand, due to the limited switching speed of neurons and amplifiers, time delays are inevitably introduced into neural network models ^{[8,9,10,11,12]}. Among all kinds of time delays, the leakage delay, that is, the time delay in the leakage term, has been proved to have a great influence on the dynamics of the system. Therefore, it is significant to consider neural networks with time delays in leakage terms ^{[13,14,15,16]}.

On the other hand, both continuous-time and discrete-time neural networks have equally importance in various applications. Therefore, it is necessary to consider both continuous time neural networks and discrete time neural networks. Fortunately, the theory of time scale calculus ^[17] can unify the study of continuous analysis and discrete analysis, so the study of neural network models on time scale can unify the study of continuous-time and discrete-time neural networks ^{[18,19,20,21]}.

In addition, quaternion-valued neural networks, as an extension of real-valued neural networks and complex-valued neural networks, have been extensively applied in many fields such as robotics, satellite attitude control, computer graphics, ensemble control and so on ^[22,23,24]. Currently, the study quaternion-valued neural networks have received much attention of many scholars.

Moreover, although non-autonomous neural networks are more general and practical than autonomous neural networks, so far, there are still few results about the dynamic behavior of non-autonomous quaternion-valued neural networks ^{[25,26,27,28,29]}. It is well known that periodicity, almost periodicity and pseudo almost periodicity are very important dynamic behaviors of non-autonomous systems. Besides, almost periodicity is more reasonable than periodicity. Also, pseudo almost periodicity is more complex than almost periodicity ^[30,31]. Therefore, for non-autonomous neural networks, pseudo almost periodic oscillation is a very important dynamics ^{[32,33,34,35,36,37]}.

However, up to now, there has been no paper published on the pseudo almost periodic oscillation of quaternion-valued high-order Hopfield neural networks. Besides, the pseudo almost periodic oscillation of quaternion-valued neural networks with quaternion leakage coefficients on time scales has not been reported. Consequently, it is necessary to study the pseudo almost periodic solutions of quaternion-valued high-order Hopfield neural networks on time scales whose leakage coefficients are also quaternions.

Motivated by the above statement, in this paper, we consider the following quaternion-valued high-order Hopfield neural network with time-varying delays and leakage delays on time scales:

where $p\in\{1, 2, \ldots, n\} = :\mathcal{S}$, $n$ is the number of neurons in layers; $x_{p}(t)$ denotes the activation of the $p$th neuron at time $t$; $a_{p}(t)\in\mathbb{Q}$ represents the rate with the $p$th unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at time $t$; $b_{pq}(t), c_{pq}(t)\in\mathbb{Q}$ are the delay connection weights from neuron $q$ to neuron $p$ at time $t$, respectively; $T_{pql}(t)\in\mathbb{Q}$ denotes the second-order connection weights of the neural network; $f_{q}, g_{q}, h_{q}:\mathbb{Q}\rightarrow \mathbb{Q}$ are the activation functions of signal transmission; $u_{p}(t)\in\mathbb{Q}$ is the external input on the $p$th unit at time $t$; $\eta_{p}$ denotes the leakage delay at time $t$ and satisfies $t-\eta_{p}(t)\in \mathbb{T}$; $\tau_{pq}$, $\delta_{pql}$ and $\vartheta_{pql}$ are transmission delays at time $t$ and satisfy $t-\tau_{pq}(t)\in \mathbb{T}$, $t-\delta_{pql}(t)\in \mathbb{T}$ and $t-\vartheta_{pql}(t)\in \mathbb{T}$ for $t\in \mathbb{T}$.

The skew field of quaternions is denoted by

where $q^{R}$, $q^{I}$, $q^{J}$, $q^{K}$ are real numbers, the three imaginary units $i$, $j$ and $k$ obey the Hamilton's multiplication rules:

Throughout this paper, for $x = x^{R}+ix^{I}+jx^{J}+kx^{K}\in\mathbb{Q}$, we denote $\hat{x} = x^{R}-x$, $\|x\|_{\mathbb{Q}} = \max\big\{|x^{R}|, |x^{I}|, |x^{J}|, |x^{K}|\big\}$, and for $x = (x_{1}, x_{2}, \ldots, x_{n})^{T}\in\mathbb{Q}^{n}$, we denote $\|x\|_{\mathbb{Q}^n} = \max\limits_{p\in\mathcal{S}}\{\|x_{p}\|_{\mathbb{Q}}\}$. Also, for convenience, we introduce the following notation:

The initial condition of system (1.1) is of the form

where $\phi_{p}, \psi_p^\Delta\in C\big([t_{0}-\theta, t_{0}]_{\mathbb{T}}, \mathbb{Q}\big)$, $p\in\mathcal{S}$.

Our main aim of this paper is to study the existence and stability of pseudo almost periodic solutions of $(1.1)$. The main contributions of this paper are listed as follows. Firstly, this is the first time to consider quaternion-valued neural networks on time scales with all the coefficients are quaternions except time delays. Secondly, this is the first paper to study the pseudo almost periodic solutions for quaternion-valued high-order Hopfield neural networks with time-varying delays and leakage delays on time scales. Finally, our method of this paper can be used to study pseudo almost periodic solutions for other types of quaternion-valued neural networks on time scales.

This paper is organized as follows: In Section 2, we introduce some definitions, preliminary lemmas. In Section 3, we establish some sufficient conditions for the existence and global exponential stability of pseodo almost periodic solutions of system (1.1). In Section 4, we give an example to demonstrate the feasibility of our results. This paper ends with a brief conclusion in Section 5.

2.   Preliminaries

Definition 2.1. ^[38,39] A time scale $\mathbb{T}$ is an arbitrary nonempty closed subset of the real set $\mathbb{R}$ with the topology and ordering inherited from $\mathbb{R}$. The forward and backward jump operators $\sigma, \rho:\mathbb{T}\rightarrow \mathbb{T}$, and the forward graininess $\mu: \mathbb{T}\rightarrow [0, \infty)$ are defined, respectively, by

The point $t\in \mathbb{T}$ is called left-dense, left-scattered, right-dense or right-scattered if $\rho(t) = t$, $\rho(t) < t, \sigma(t) = t$ or $\sigma(t) > t$, respectively. Points that are right-dense and left-dense at the same time are called dense. If $\mathbb{T}$ has a left-scattered maximum m, define $\mathbb{T}^{\kappa} = \mathbb{T}-\{m\}$; otherwise, set $\mathbb{T}^{\kappa} = \mathbb{T}$. If $\mathbb{T}$ has a right-scattered maximum m, define $\mathbb{T}_{\kappa} = \mathbb{T}-\{m\}$; otherwise, set $\mathbb{T}_{\kappa} = \mathbb{T}$.

Definition 2.2. ^[38,39] Assume that $f:\mathbb{T} \rightarrow \mathbb{R}$ is a function and let $t\in \mathbb{T}^{k}$. Then we define $f^{\Delta}(t)$ to be the number (provided it exists) with the property that given any $\varepsilon > 0$, there is a neighborhood U of t (i.e, $U = (t-\delta, t+\delta)\cap \mathbb{T}$ for some $\delta > 0$) such that

for all $s\in U$. We call $f^{\Delta}(t)$ the delta (or Hilger) derivative of f at t. Moreover, we say that $f$ is delta (or Hilger) differentiable (or in short: differentiable) on $\mathbb{T}^{k}$ provided $f^{\Delta}(t)$ exists for all $t\in \mathbb{T}^{k}$. The function $f^{\Delta}:\mathbb{T}^{k} \rightarrow \mathbb{R}$ is then called the (delta) derivative of $f$ on $\mathbb{T}^{k}$.

The derivative of function $f(t) = f^{R}(t)+if^{I}(t)+jf^{J}(t)+kf^{K}(t):\mathbb{T}\rightarrow \mathbb{Q}$ is given by

where $f^{R}, f^{I}, f^{J}, f^{K}:\mathbb{T}\rightarrow \mathbb{R}$.

Definition 2.3. ^[38,39] A function $p: \mathbb{T}\rightarrow \mathbb{R}$ is said to be regressive provided

The set of all positive regressive and rd-continuous functions $p:\mathbb{T}\rightarrow \mathbb{R}$ are denoted by

Definition 2.4. ^[38,39] If $p \in \mathcal {R}^{+}$, then we define the exponential function by

with the cylinder transformation

Definition 2.5. ^[38,39] Let $p, q:\mathbb{T} \rightarrow \mathbb{R}$ be two regressive functions, define

Lemma 2.1. ^[38,39] Let $p\in\mathcal {R}$, and $t, s, r\in\mathbb{T}$. Then

$(i)$ $e_{0}(t, s)\equiv 1$ and $e_{p}(t, t)\equiv 1$;

$(ii)$ $e_{p}(t, s) = \frac{1}{e_{p}(s, t)} = e_{\ominus p}(s, t)$;

$(iii)$ $e_{p}(t, s)e_{p}(s, r) = e_{p}(t, r)$;

$(iv)$ $(e_{\ominus p}(t, s))^{\Delta} = (\ominus p)(t)e_{\ominus p}(t, s)$.

Definition 2.6. ^[18] A time scale $\mathbb{T}$ is called an almost periodic time scale if

We denote by $BC(\mathbb{T}, \mathbb{Q}^{n})$ the set of all bounded continuous functions from $\mathbb{T}$ to $\mathbb{Q}^{n}$. Similar to Definition in ^[18], we give the following definition.

Definition 2.7. Let $\mathbb{T}$ be an almost periodic time scale. A function $f \in BC(\mathbb{T}, \mathbb{Q}^{n})$ is called an almost periodic on $\mathbb{T}$ if the $\varepsilon$-translation set of

is a relatively dense set in $\mathbb{R}$ for all $\varepsilon > 0$; that is, for any given $\varepsilon > 0$, there exists a constant $l(\varepsilon) > 0$ such that each interval of length $l(\varepsilon)$ contains at least one $\tau(\varepsilon)\in T(\varepsilon, f)$ such that

We denote by $AP(\mathbb{T}, \mathbb{Q}^{n})$ the set of all almost periodic functions defined on $\mathbb{T}$.

Define the class of functions $PAP_{0}(\mathbb{T}, \mathbb{Q}^{n})$ as follows:

Similar to Definition in ^[35], we give the following definition.

Definition 2.8. A function $f\in BC(\mathbb{T}, \mathbb{Q}^{n})$ is called pseudo almost periodic if $f = g+h$, where $g\in AP(\mathbb{T}, \mathbb{Q}^{n})$ and $h\in PAP_{0}(\mathbb{T}, \mathbb{Q}^{n})$.

We denote by $PAP(\mathbb{T}, \mathbb{Q}^{n})$ the set of all pseudo almost periodic functions from $\mathbb{T}$ to $\mathbb{Q}^{n}$.

Similar to the proofs in ^[21], it is not difficult to prove the following lemmas.

Lemma 2.2. If $f, g\in PAP(\mathbb{T}, \mathbb{Q}^{n})$, then $f+g, fg\in PAP(\mathbb{T}, \mathbb{Q}^{n})$; if $f\in PAP(\mathbb{T}, \mathbb{Q}^{n})$, $g\in AP(\mathbb{T}, \mathbb{Q}^{n})$, then $fg\in PAP(\mathbb{T}, \mathbb{Q}^{n})$.

Lemma 2.3. If $f\in C(\mathbb{Q}, \mathbb{Q})$ satisfies the Lipschitcz condition, $\varphi\in PAP(\mathbb{T}, \mathbb{Q})$ and $\tau\in C^{1}(\mathbb{T}, \Pi)\cap AP(\mathbb{T}, \mathbb{R}^{+})$ with $\inf\limits_{t\in\mathbb{T}}\big\{1-\tau^{\Delta}(t)\big\} > 0$, then $f(\varphi(\cdot-\tau(\cdot)))\in PAP(\mathbb{T}, \mathbb{Q})$.

Throughout this paper, we assume that the following conditions hold:

$(H_{1})$ $a_{p}^{R}\in AP(\mathbb{T}, \mathbb{R}^{+})$ with $-a_{p}^{R}\in\mathcal{R}^{+}$, $a_{p}\in AP(\mathbb{T}, \mathbb{Q})$, $b_{pq}, c_{pq}, T_{pql}, u_{p}\in PAP(\mathbb{T}, \mathbb{Q})$, $\eta_{p}, \tau_{pq}, \delta_{pql}, \vartheta_{pql}\in C^{1}(\mathbb{T}, \Pi)\cap AP(\mathbb{T}, \mathbb{R}^{+})$ with $\inf\limits_{t\in \mathbb{T}}\big\{1-\eta_{p}^{\Delta}(t)\big\} > 0$, $\inf\limits_{t\in \mathbb{T}}\big\{1-\tau_{pq}^{\Delta}(t)\big\} > 0$, $\inf\limits_{t\in \mathbb{T}}\big\{1-\delta_{pql}^{\Delta}(t)\big\} > 0$, $\inf\limits_{t\in \mathbb{T}}\big\{1-\vartheta_{pql}^{\Delta}(t)\big\} > 0$, where $p, q, l\in \mathcal{S}$.

$(H_{2})$ There exist positive constants $L_{q}^{f}, L_{q}^{g}, L_{q}^{h}, M_{q}^{h}$ such that for any $x, \, y\in\mathbb{Q}$,

and $f_{q}(0) = g_{q}(0) = h_{q}(0) = 0$, where $q\in \mathcal{S}$.

$(H_{3})$ $\max\limits_{p\in \mathcal{S}}\bigg\{\frac{\Xi_{p}}{a_{p}^{-}}, \Big(1+\frac{a_{p}^{+}}{a_{p}^{-}}\Big)\Xi_{p}\bigg\} = :\rho < 1$, where

3.   Main results

Let $\mathbb{E} = \big\{\phi = (\phi_1, \phi_2, \ldots, \phi_n)^T\big|\phi, \phi^{\Delta}\in PAP\big(\mathbb{T}, \mathbb{Q}^{n}\big)\big\}$ with the norm

where $\big\|\phi\big\|_{0} = \sup\limits_{t\in\mathbb{T}}\max\limits_{p\in \mathcal{S}}\Big\{\big\|\phi_p\big\|_{\infty}\Big\}$ and $\big\|\phi_p\big\|_{\infty} = \sup\limits_{t\in\mathbb{T}}\big\|\phi_p(t)\big\|_{\mathbb{Q}}$, then $\mathbb{E}$ is a Banach space.

Set $\phi^{0} = \big(\phi^{0}_{1}, \phi^{0}_{2}, \ldots, \phi^{0}_{n}\big)^{T}$, where

and $\kappa$ is a constant satisfying $\kappa\geq \big\|\phi^{0}\big\|_{\mathbb{E}}$.

Lemma 3.1. Let $(H_{1})$ hold, then every bounded solution $x = (x_1, x_2, \ldots, x_{n})^{T}$ of system $(1.1)$ is a solution of the following system:

where $p\in \mathcal{S}$, $t\in\mathbb{T}$, and vice versa.

Proof. On the one hand, if $x = (x_1, x_2, \ldots, x_{n})^{T}$ is a solution of (3.1), then by $\Delta$-differentiate both sides of (3.1), we see that $x = (x_1, x_2, \ldots, x_{n})^{T}$ is also a solution of (1.1).

On the other hand, let $x$ be a bounded solution of (1.1), then for $p\in \mathcal{S}$,

Multiply both sides of (3.2) by $e_{-a_{p}^{R}}(t_{0}, \sigma(t))$, we can get

where $t\geq t_{0}$, $t_{0}\in\mathbb{T}$. Integrating both sides of (3.3) from $t_{0}$ to $t$, we obtain

Letting $t_{0}\rightarrow -\infty$, then we obtain that (1.1) holds. The proof is complete.

Theorem 3.1. Let $(H_{1})$-$(H_{3})$ hold. Then system $(1.1)$ has a unique pseudo almost periodic solution in $\mathbb{E}^{\ast} = \big\{\phi\mid\phi\in\mathbb{E}\big|\|\phi-\phi^{0}\|_{\mathbb{E}}\leq \frac{\kappa \rho}{1-\rho}\big\}$.

Proof. For any $\phi\in \mathbb{E}$, we define a mapping $\Phi: \mathbb{E}\rightarrow PAP\big(\mathbb{T}, \mathbb{Q}^{n}\big)$ by setting

where

First, we will prove that $\Phi$ maps $\mathbb{E}$ into itself. To this end, let

Then, by Lemmas 2.2 and 2.3, we find that $\mathcal{F}_{p}(s)\in PAP(\mathbb{T}, \mathbb{Q})$. So, for all $p\in\mathcal{S}$, we can set $\mathcal{F}_{p}(s) = \mathcal{F}_{p}^{1}(s)+\mathcal{F}_{p}^{0}(s)$, where $\mathcal{F}_{p}^{1}\in AP(\mathbb{T}, \mathbb{Q})$ and $\mathcal{F}_{p}^{0}\in PAP_{0}(\mathbb{T}, \mathbb{Q})$. We shall show that $x_{p}^{\phi}\in PAP(\mathbb{T}, \mathbb{Q})$, that is, $x_{p}^{\phi}$ can be expressed as

where $\Omega^{1}_{p}\in AP(\mathbb{T}, \mathbb{Q})$ and $\Omega^{0}_{p}\in PAP_{0}(\mathbb{T}, \mathbb{Q})$.

In fact, since $a_{p}^{R}\in AP(\mathbb{T}, \mathbb{R}^{+})$ and $\mathcal{F}_{p}^{1}\in AP(\mathbb{T}, \mathbb{Q})$, for every $\varepsilon > 0$, there exists $l > 0$ such that every interval of length $l$ contains a number $\tau\in\Pi$ satisfying

Consequently, we have

which implies that $\Omega^{1}_{p}\in AP(\mathbb{T}, \mathbb{Q})$. Then, we will prove that $\Omega^{0}_{p}\in PAP_{0}(\mathbb{T}, \mathbb{Q})$. In addition, from $\mathcal{F}_{p}^{0}\in PAP_{0}(\mathbb{T}, \mathbb{Q})$, $r\in \mathbb{T}$, we have

which implies that $\Omega^{0}_{p}\in PAP_{0}(\mathbb{T}, \mathbb{Q})$. Therefore, $x_{p}^{\phi}\in PAP(\mathbb{T}, \mathbb{Q})$, that is, $\Phi$ maps $\mathbb{E}$ into $PAP\big(\mathbb{T}, \mathbb{Q}^{n}\big)$.

Next, we will show that $\Phi$ is a self-mapping from $\mathbb{E}^{\ast}$ to $\mathbb{E}^{\ast}$. In fact, for each $\phi\in\mathbb{E}^{\ast}$, we have

Thus, we have

On the other hand, we have

Noting the fact that for $\phi\in\mathbb{E}^{\ast}$, we have

It follows from (3.4)-(3.5), and $(H_{3})$ that

thus, we have $\Phi\phi\in \mathbb{E}^{\ast}$.

Finally, we will show that $\Phi$ is a contraction mapping in $\mathbb{E}^{\ast}$. For any $\phi, \psi\in \mathbb{E}^{\ast}$, we can get

It follows from (3.6) that

On the other hand, we can derive that

By (3.7), (3.8) and $(H_{3})$, we have

in view of the definition of $\rho$, which implies that $\Phi$ is a contraction mapping. Therefore, $\Phi$ has a unique fixed point in $\mathbb{E}^{\ast}$, that is, (1.1) has a unique pseudo almost periodic solution in $\mathbb{E}^{\ast}$. The proof is complete.

Definition 3.1. Let $x = (x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a solution of $(1.1)$ with the initial value $\phi = (\phi_{1}, \phi_{2}, \ldots, \phi_{n})^{T}$. If there exist positive constants $\lambda > 0$ and $M > 0$ such that every solution $y = (y_{1}, y_{2}, \ldots, y_{n})^{T}$ of $(1.1)$ with initial value $\psi = (\psi_{1}, \psi_{2}, \ldots, \psi_{n})^{T}$ satisfies

where

then the solution $x$ is said to be globally exponentially stable.

Theorem 3.2. Assume that $(H_{1})$-$(H_{3})$ hold, then system $(1.1)$ has a unique pseudo almost periodic solution that is globally exponentially stable.

Proof. From Theorem 3.1, we see that system (1.1) has a pseudo almost periodic solution $x(t) = (x_{1}(t), x_{2}(t), \ldots, x_{n}(t))^{T}$ with initial value $\phi(s) = (\phi_{1}(s), \phi_{2}(s), \ldots, \phi_{n}(s))^{T}$. Suppose that $y(t) = (y_{1}(t), y_{2}(t), \ldots, y_{n}(t))^{T}$ is an arbitrary solution of system (1.1) with initial value $\psi(s) = (\psi_{1}(s), \psi_{2}(s), \ldots, \psi_{n}(s))^{T}$ and let $z(t) = y(t)-x(t)$, then we have

For $p\in\mathcal{S}$, let $\Theta_{p}$ and $\Psi_{p}$ be defined as follows:

and

By $(H_{3})$, we have

and

Based on the continuities of functions $\Theta_{p}$ and $\Psi_{p}$ on $[0, +\infty)$, and the fact that $\Theta_{p}(\omega), \Psi_{p}(\omega) \rightarrow -\infty$, as $\omega\rightarrow +\infty$, there exist $\zeta_{p}, \xi_{p} > 0$ such that $\Theta_{p}(\zeta_{p}) = \Psi_{p}(\xi_{p}) = 0$ and $\Theta_{p}(\omega) > 0$ for $\omega\in(0, \zeta_{p})$, $\Psi_{p}(\omega) > 0$ for $\omega\in(0, \xi_{p})$. Take $\gamma = \min\limits_{p\in\mathcal{S}}\big\{\zeta_{p}, \xi_{p}\big\}$, we have $\Theta_{p}(\gamma)\geq 0$, $\Psi_{p}(\gamma)\geq 0$. So, we can choose a positive constant $0 < \lambda < \min\big\{\gamma, \min\limits_{p\in\mathcal{S}}\{a_{p}^{-}\}\big\}$ with $\lambda\in \mathcal {R}^{+}$ such that

which implies that

and

Let $M = \max\limits_{p\in\mathcal{S}}\Big\{\frac{a_{p}^{-}}{\Xi_{p}}\Big\}$, then by $(H_{3})$, we have $M > 1$. Thus,

Since $e_{\ominus\lambda}(t, t_{0}) > 1$ for $t\in[t_{0}-\theta, t_{0}]_{\mathbb{T}}$, it is obvious that, for any $\varepsilon > 0$,

and

We claim that

If (3.10) is not true, then there must be some $t_{1}\in(t_{0}, +\infty)_{\mathbb{T}}$ such that

Hence, there must exist a constant $\mathcal{P}\geq1$ such that

Multiplying both sides of (3.9) by $e_{-a_{p}^{R}}(t_{0}, \sigma(t))$ and integrating over $[t_{0}, t]_{\mathbb{T}}$, we get

In view of (3.12) and $M > 1$, we have

and

The above two inequalities imply that

which contradicts the first equation of (3.11). Therefore, (3.10) holds. Letting $\varepsilon\rightarrow0^{+}$ leads to

Hence, the pseudo almost periodic solution of system (1.1) is globally exponentially stable. The proof is complete.

4.   Illustrative example

Example 4.1. In system $(1.1)$, let $n = 2, t_0 = 0$ and take

If $\mathbb{T} = \mathbb{R}$, we take

If $\mathbb{T} = \mathbb{Z}$, we take

By a simple calculation, we have

When $\mathbb{T} = \mathbb{R}$, we have

and

When $\mathbb{T} = \mathbb{Z}$, we have

and

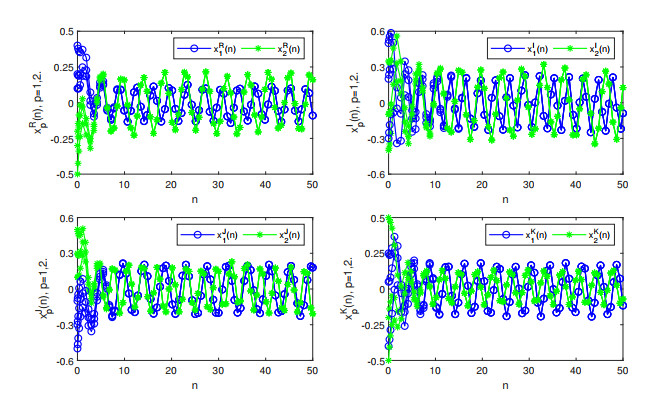
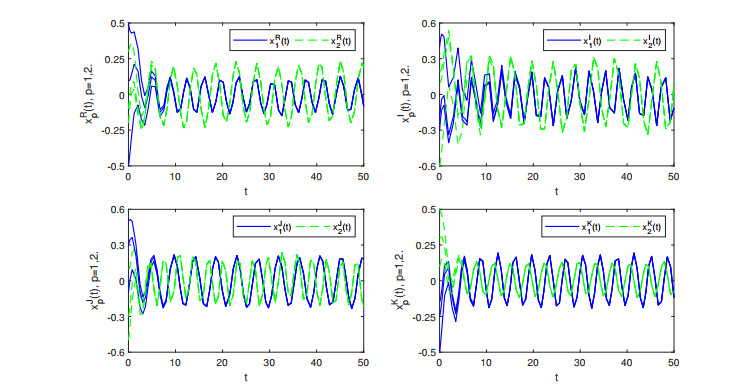
Hence, whether $\mathbb{T} = \mathbb{R}$ or $\mathbb{T} = \mathbb{Z}$, all the conditions of Theorems 3.1 and 3.2 are satisfied. Consequently, we know that system $(1.1)$ has a pseudo almost periodic solution, which is globally exponentially stable. Simulated by Matlab, when $\mathbb{T} = \mathbb{R}$ and $\mathbb{T} = \mathbb{Z}$, Figures 1 and 2 show the time responses of the variables of system $(1.1)$. Figure 1 has initial values

Figure 2 has initial values

5.   Conclusions

In this paper, we have established the existence and global exponential stability of pseudo almost periodic solutions for quaternion-valued high-order Hopfield neural networks with time-varying delays and leakage delays on time scales. The results of this paper are essentially new. In addition, we expect to extend this work to study other types of quaternion-valued neural networks on time scales.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant No. 11861072.

Conflict of interest

Both authors declare no conflicts of interest in this paper.