Construction of the spacelike constant angle surface family in Minkowski 3-space

1.   Introduction

A Helix, as we all know, is an interesting curve in science and nature. It is defined by its tangent lines making a constant angle with a fixed vector. A closely concept is the constant angle surface which tangent planes make a constant angle with a fixed constant vector in the ambient space. For the interests from theory of mathematics and physics and real applications, in recent years, more and more researchers studied on constant angle surfaces. The main applications of constant angle surfaces are for light such as liquid, crystal, shape from shading problem. Cermelli ^[1] focused on examples motivated by the physics of interfaces in liquid crystals and of layered fluids. As described by Munteanu and Nistor in ^[2], Cernelli ^[1] studied how constant angle surfaces may be used to describe interfaces which occur in special equilibrium configurations of nematic and smectic C liquid crystals and to determine the shape of disclination cores in nematics. Dillen etc. ^[3,4] studied surfaces whose unit normal makes a constant angle with the $\mathbb{R}$-direction in product spaces $\mathbb{S}^2\times \mathbb{R}$ and $\mathbb{H}^2\times \mathbb{R}$. $\mathbb{S}^2$ is unit 2 sphere and $\mathbb{H}^2$ is hyperbolic plane. Munteanu and Nistor ^[2] studied constant angle surfaces in Euclidean 3-space. They gave an approach to classify all surfaces whose unit normal vector makes a constant angle with a fixed direction. In view of the property of the constant angle, $\ddot{O}$zkaldi and Yayli ^[5] gave a classification of special developable surfaces and some conical surfaces.

As well known, comparing with Euclidean 3-space ($E^3$), Minkowski 3-space ($E_1^3$) is more complicated. There are many papers focused on the properties of surface in Minkowski 3-space ^[6,7,8,9]. L$\acute{o}$pez and Munteanu ^[10] studied the classification for the spacelike surfaces whose the normals make a constant angle with a timelike constant direction. Subsequently, Şaffak, G$\ddot{u}$ler and Kasap ^[11] discussed the classifications for the spacelike surfaces by choosing the constant direction spacelike. They also showed that the minimal spacelike constant angle surfaces are planes. A closely related concept is the constant slope surfaces whose normal makes a constant angle with the position vector. Recently, constant slope surfaces have been widely discussed, we can refer to ^{[12,13,14,15]}. Minkowski space has many different properties with Euclidean space mainly because of the metric in $E_1^3$ is not positive definite metric. The distance function in $E_1^3$ can be positive, negative or zero. Therefore, the vectors in $E_1^3$ can be classified into three types: spacelike vectors, timelike vectors and lightlike vectors according to the sign of the distance function. Different with Euclidean space, there doesn't exist a natural concept angle between two arbitrary vectors because of the causal character of the vector in $E^3_1$. Only when the two vectors are not lightlike vectors, it is possible to define the angle between them. By using the Frenet trihedron frame, Wang etc. ^[16] gave an expression of parametric surface. In Minkowski 3-space, we can express the surface pencil in the same way. Therefore, we consider the construction of the spacelike surface in $E^3_1$ based on this expression. We give the concrete expression of the constant angle spacelike surface family through an isoparametric curve. This is different from the methods in ^[10] and ^[11]. The construction of proposed method is easy and we can see the conclusion from the Theorems 3.2, 3.4, 3.6, 3.8 and the Examples. We not only distinguish the cases according to the fixed unit vector lying in the spacelike cone and in the timelike cone, but also in any cases we consider the principal normal vectors of the given curve are spacelike and timelike respectively. We assume that the fixed unit vector possesses more general expressions. The coefficients of the fixed unit vector can help us to control the shape of the surface more conveniently.

We organize the structure of the paper as follows. In Section 2, we simply introduce the relevant concepts and results of differential geometry of curve and surface in $E_1^3$. In Section 3, for a given non-null parametric curve $\boldsymbol{r}(s)$, where $s$ is arc-length parameter, by using Frenet frame, we construct a family of spacelike surfaces which make constant angle with the fixed vector which lying in the spacelike cone and in the timelike cone respectively. Under this expression, the normal vector and fixed unit vector can be expressed by the tangent vector $\boldsymbol{T}(s)$, normal vector $\boldsymbol{N}(s)$ and binormal vector $\boldsymbol{B}(s)$ of the curve $\boldsymbol{r}(s)$. This expression provides a new method to study the constant surface in Minkowski 3-space. At the same time, the spacelike surface family possess $\boldsymbol{r}(s)$ as isoparametric curve. Moreover, we give some representative examples. Finally, we conclude the whole paper in Section 4.

2.   Preliminaries

In the Lorentz-Minkowski space $E_1^3 = (\mathbb{R}^3, < , > )$, the metric $< , >$ can be defined by

where $\boldsymbol{x} = (x_1, x_2, x_3), \boldsymbol{y} = (y_1, y_2, y_3).$ We call this metric $< , >$ as Lorentzian metric.

Since the metric is not positive, there exist three different vectors in $E^3_1$. A vector $\boldsymbol{x}\in E_1^3$ is called spacelike if $< \boldsymbol{x}, \boldsymbol{x} > > 0$ or $\boldsymbol{x} = 0$. It is timelike when $< \boldsymbol{x}, \boldsymbol{x} > < 0$ and lightlike if $< \boldsymbol{x}, \boldsymbol{x} > = 0$ and $\boldsymbol{x}\neq 0$. Similarly, an arbitrary curve $\boldsymbol{R} = \boldsymbol{R}(s), s\in I$ in $E^3_1$ is called spacelike, timelike or lightlike if all of its velocity vectors $\boldsymbol{R}^{'}(s)$ are spacelike, timelike or lightlike for all $s\in I$.

Moreover, the Lorentzian vector product of x and y is a vector denoted by $\boldsymbol{x}\times \boldsymbol{y} = (x_2y_3-x_3y_2, x_3y_1-x_1y_3, -(x_1y_2-x_2y_1))$, where $\boldsymbol{x} = (x_1, x_2, x_3)$ and $\boldsymbol{y} = (y_1, y_2, y_3)$.

The angle between two vectors in $E_1^3$ is defined by the following definitions. We can refer to ^[12,13]. In Definitions 1–4, $g(, )$ represents the Lorentz metric.

Definition 1. In $E_1^3$, given two spacelike vectors $\boldsymbol{x}$ and $\boldsymbol{y}$ which span a spacelike vector subspace, then $|g(\boldsymbol{x}, \boldsymbol{y})|\leq \|\boldsymbol{x}\|\|\boldsymbol{y}\|$. Then there exists a unique real number $\alpha$, such that

we call $\alpha$ the Lorentzian spacelike angle between $\boldsymbol{x}$ and $\boldsymbol{y}$.

Definition 2. In $E_1^3$, given two spacelike vectors $\boldsymbol{x}$ and $\boldsymbol{y}$ which span a timelike vector subspace, then $|g(\boldsymbol{x}, \boldsymbol{y})| > \|\boldsymbol{x}\|\|\boldsymbol{y}\|$. Then there exists a unique real number $\alpha$, such that

we call $\alpha$ the Lorentzian timelike angle between $\boldsymbol{x}$ and $\boldsymbol{y}$.

Definition 3. Let $\boldsymbol{\boldsymbol{x}}$ and $\boldsymbol{y}$ be positive or negtive timelike vectors in $E_1^3$. Then there exists $\alpha$ satisfies

where $\alpha$ is a unique non-negative real number, we called it the Lorentzian timelike angle between $\boldsymbol{x}$ and $\boldsymbol{y}$.

Definition 4. Suppose $\boldsymbol{x}$ and $\boldsymbol{y}$ be a spacelike vector and a positive timelike vector in $E_1^3$ respectively. Then there exists $\alpha$ satisfies

The $\alpha$ is a unique non-negative real number, we called it the Lorentzian timelike angle between $\boldsymbol{x}$ and $\boldsymbol{y}$.

We call a parametric surface $\boldsymbol{X}(s, t)$ a spacelike or timelike surface when the unit normal vector

of the surface is timelike of spacelike on each point of the surface.

In this paper, we will study the construction of a family of spacelike surfaces which form a constant angle with a fixed vector lying in the spacelike cone and in the timelike cone respectively.

3.   Spacelike constant angle surface family

Let $\boldsymbol{R}(s), s\in [0, L]$ be a parametric curve in $E_1^3$, where $s$ is the arc-length parameter. Assume $\boldsymbol{R}^{''}(s)\neq0$ for all $s\in [0, L]$. When $\boldsymbol{R}^{'}(s)$ is a spacelike (resp. timelike, lightlike) vector, $\boldsymbol{R}(s)$ is called spacelike (resp. timelike, lightlike) at $s$. In the following section, we assume $\boldsymbol{R}(s)$ be a spacelike curve. We consider the spacelike surfaces which form a constant angle $\alpha$ with a fixed unit constant vector $\boldsymbol{L}$. When the surface is spacelike, its normal vector is timelike. Denote $\|\boldsymbol{L}\| = 1$, since there doesn't exist the angle concept between any vector with a lightlike vector, then we always assume $\boldsymbol{L}$ does not lie in the light cone. We discuss the constant spacelike surface from two different cases.

3.1.   The constant vector $\boldsymbol{L}$ lying in the timelike cone

In this case, we assume the fixed unit constant vector lies in timelike cone, i.e., $< \boldsymbol{L}, \boldsymbol{L} > = -1$. Since the given curve $\boldsymbol{R}(s)$ is spacelike, there are two cases according to the causal characters of $\boldsymbol{e}^{'}(s)$ and $\boldsymbol{e}(s) = \boldsymbol{R}^{'}(s)$.

(a) $\boldsymbol{e}^{'}(s)$ is a spacelike vector

In this case, $k(s) = |\boldsymbol{e}^{'}(s)|$ is the curvature of $\boldsymbol{R}(s)$. $\boldsymbol{n}(s) = \boldsymbol{e}^{'}(s)/k(s)$ and $\boldsymbol{b}(s) = \boldsymbol{e}(s)\times \boldsymbol{n}(s)$ are the normal vector and binormal vector respectively. The corresponding Frenet equations are given by

and $\tau(s) = - < \boldsymbol{n}^{'}, \boldsymbol{b} >$ is the torsion of $\boldsymbol{r}(s)$. Moreover

The parametric surface through the given curve $\boldsymbol{R}(s)$ can be expressed by

Because $\boldsymbol{R}(s)$ is the isoparametric curve, then there exists $t_0\in [0, T]$, such that

The unit normal vector $\boldsymbol{N}(s, t)$ can be defined as

After simple computation, we have

where

Substitute $t = t_0$ in Eqs (3.3)–(3.5), we can get

Let $\boldsymbol{X}(s, t)$ be a constant angle surface. Since the angle between the unit normal vector and a fixed timelike vector is constant, according to the Theorem $3.4$ of paper ^[10], the unit normal must depend on only one parameter. Thus the following relation holds.

Substitute $t = t_0$ into the above equation, we have

That is

Then

Moreover, the fixed unit vector $\boldsymbol{L}$ can be expressed

where $u(s), v(s), w(s)$ are continuous functions. Since $\boldsymbol{L}$ is a timelike vector, then $u^2(s)+v^2(s)-w^2(s) = -1$. Computing the first derivative of $\boldsymbol{L}$, we have

Since $\boldsymbol{L}$ is a constant vector, there are the following relations:

Let $\alpha$ be a hyperbolic constant angle between $\boldsymbol{N}(s)$ which is the timelike normal vector and the fixed unit timelike vector $\boldsymbol{L}$, then we have

According to the above analysis, we can get the following theorem.

Theorem 1. The necessary and sufficient conditions of a spacelike surface $\boldsymbol{X}(s, t)$ through the isoparametric curve $\boldsymbol{R}(s)$ whose spacelike $\boldsymbol{e}^{'}(s)$ forms a constant angle with a fixed constant timelike vector are it satisfies $(3.8), (3.9), (3.10)$ and $(3.14)$.

Next, we give another condition of spacelike constant angle surface. Since $\lambda_1(s, t) = 0$, suppose $\frac{\partial g(s, t)}{\partial t}\neq 0, \frac{\partial h(s, t)}{\partial t}\neq 0$, we have

Substituting it in Eq $(3.4), (3.5)$, we can get

where $F(s, t) = -\frac{\partial f(s, t)}{\partial t}(f(s, t)k(s)+\frac{\partial g(s, t)}{\partial s}+h(s, t)\tau(s))/ \frac{\partial g(s, t)}{\partial t}+(1+\frac{\partial f(s, t)}{\partial s}-g(s, t)k(s))$. That is

According to Eq $(3.6)$, we have $g(s, t) = p(s)h(s, t)$ or $h(s, t) = q(s)g(s, t)$, then we have Theorem $2$.

Theorem 2. Given the spacelike curve $\boldsymbol{R}(s)$ with spacelike $\boldsymbol{e}^{'}(s)$, the surface $\boldsymbol{X}(s, t)$ possessing $\boldsymbol{R}(s)$ as isoparametric curve forms a constant angle with a fixed constant timelike vector if and only if the following conditions hold.

$(1) \; w(s)^2-\cosh^2{\alpha}\neq 0$,

$(2)$

Proof. We only prove condition $(1)$ here, and the condition $(2)$ can be proved in the same way.

Substituting Eq $(3.15)$ in $\lambda_1(s, t) = 0$, we can get Eqs $(3.16)$. Then according to

we can derive the condition $(3.17)$.

Conversely, if the surface $\boldsymbol{X}(s, t)$ satisfies the condition $(1)$ or $(2)$, then $< \boldsymbol{N}(s, t), \boldsymbol{L} > = -\cosh{\alpha}$ holds.

Example 1. A parametric spacelike Helix is given by

with spacelike normal vector and timelike binormal vector.

By computing, we can get

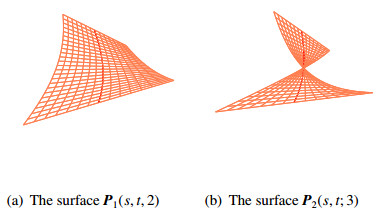
By using Eqs $(3.12)$ and $(3.13)$, we can get the coefficients $u(s) = -1, v(s) = 0, w(s) = \sqrt{2}$. Let $\alpha = 2, t_0 = 0$ and we choose $g(s, t) = t$. According to Theorem $3.2$, we obtain a spacelike constant angle surface $\boldsymbol{X}_1(s, t;\alpha)$ which passes through the given curve $\boldsymbol{R}(s)$ (see Figure ${1(a)}$). For $\alpha = 3, t_0 = 0$, if we choose $g(s, t) = st$, we can obtain another spacelike constant angle surface $\boldsymbol{X}_2(s, t;3)$ which is shown in Figure $1(b)$.

(b) The vector $\boldsymbol{T}^{'}(s)$ is timelike

In this case, $k(s) = \sqrt{- < \boldsymbol{T}^{'}(s), \boldsymbol{T}^{'}(s) > }, \boldsymbol{N}(s) = \boldsymbol{T}^{'}(s)/k(s)$ and $\boldsymbol{B}(s) = \boldsymbol{T}(s)\times \boldsymbol{N}(s)$. The corresponding Frenet equations are given by

and $\tau(s) = < \boldsymbol{N}^{'}, \boldsymbol{B} >$. Moreover

The parametric surface through the given curve $\boldsymbol{r}(s)$ can be expressed by

The unit normal vector of the surface $\boldsymbol{P}(s, t)$ is given by

where

Similar to section $(a)$, we have the following theorems.

Theorem 3. The spacelike surface $\boldsymbol{P}(s, t)$ through the isoparametric curve $\boldsymbol{r}(s)$ with timelike $\boldsymbol{T}^{'}(s)$ makes a constant angle with a fixed constant timelike vector if and only if it satisfies the following conditions,

Theorem 4. Given the spacelike curve $\boldsymbol{r}(s)$ with timelike $\boldsymbol{T}^{'}(s)$, the surface $\boldsymbol{P}(s, t)$ possessing $\boldsymbol{r}(s)$ as isoparametric curve makes a constant angle with a fixed constant timelike vector if and only if the following conditions hold.

$(1)$

$(2) \; y^2(s)-\cosh^2(\theta)\neq 0$

Example 2. Let $\boldsymbol{r}(s) = (\sinh{(\frac{s}{\sqrt{2}})}, \frac{s}{\sqrt{2}}, \cosh{(\frac{s}{\sqrt{2}})})$ be a spacelike Helix with timelike normal vector and spacelike binormal vector. After computation, we have

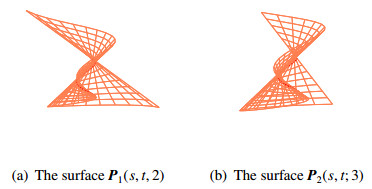
and $x(s) = -\frac{\sqrt{2}}{2}\sinh{(\frac{\sqrt{2}}{2}s)}, y(s) = \cosh{(\frac{\sqrt{2}}{2}s)}, z(s) = -\frac{\sqrt{2}}{2}\sinh{(\frac{\sqrt{2}}{2}s)}$. Let $\theta = 2, t_0 = 0$. By choosing $w(s, t) = t$, we can obtain a spacelike constant angle surface $\boldsymbol{P}_1(s, t;2)$ which passes through the given curve $\boldsymbol{r}(s) \; ($see Figure ${2(a)}$$)$. For $\theta = 3, t_0 = 0, w(s, t) = st$, we can obtain another spacelike constant angle surface $\boldsymbol{P}_2(s, t;3)$ which is shown in Figure $2(b)$.

3.2.   The constant vector $\boldsymbol{A}$ lying in the spacelike cone

In this case, the fixed unit constant vector lies in spacelike cone, i.e., $< \boldsymbol{A}, \boldsymbol{A} > = 1$. Similar to Section $3.1$, we can get the corresponding conclusions.

(a) The vector $\boldsymbol{T}^{'}(s)$ is spacelike

Let $\theta$ be the constant angle between the timelike normal vector $\boldsymbol{n}(s, t)$ and the fixed unit spacelike vector $\boldsymbol{A}$, then we have

The corresponding theorems are as follows.

Theorem 5. The spacelike surface $\boldsymbol{P}(s, t)$ through the isoparametric curve $\boldsymbol{r}(s)$ with spacelike $\boldsymbol{T}^{'}(s)$ makes a constant angle with a fixed constant spacelike vector if and only if it satisfies $(3.8), (3.9), (3.10)$ and $(3.26)$.

Theorem 6. Given the spacelike curve $\boldsymbol{r}(s)$ with spacelike $\boldsymbol{T}^{'}(s)$, the surface $\boldsymbol{P}(s, t)$ possessing $\boldsymbol{r}(s)$ as isoparametric curve makes a constant angle with a fixed constant spacelike vector if and only if the following conditions hold.

$(1) \; z(s)^2-\sinh^2{\theta}\neq 0$,

$(2)$

Example 3. In this example, we consider a spacelike circle

where $\theta$ is the constant angle. After computation, we have

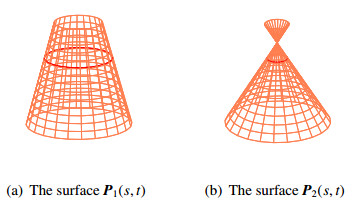
and $x(s) = -\sin{s}, y(s) = -\cos{s}, z(s) = 0$. We show two spacelike constant angle surfaces $\boldsymbol{P}(s, t)$ from the surface family in Figure $3(a)$ and $3(b)$.

(b) The vector $\boldsymbol{T}^{'}(s)$ is timelike

Theorem 7. The spacelike surface $\boldsymbol{P}(s, t)$ through the isoparametric curve $\boldsymbol{r}(s)$ with timelike $\boldsymbol{T}^{'}(s)$ makes a constant angle with a fixed constant spacelike vector if and only if it satisfies the following conditions,

where $\varphi_1(s, t), \varphi_2(s, t), \varphi_3(s, t)$ are given by Eqs (3.25)–(3.27).

Theorem 8. Given the spacelike curve $\boldsymbol{r}(s)$ with timelike $\boldsymbol{T}^{'}(s)$, the surface $\boldsymbol{P}(s, t)$ passing through the isoparametric curve $\boldsymbol{r}(s)$ is a spacelike constant angle surface if and only if the following conditions hold,

$(1)$

$(2) \; y^2(s)-\sinh^2(\theta)\neq 0$

Example 4. In this example, given a spacelike circle

with timelike normal vector. Then we have

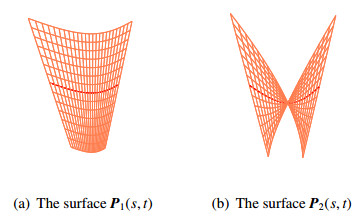
and $x(s) = \cosh{s}, y(s) = -\sinh{s}, z(s) = 0$. Figure $4(a)$ and $4(b)$ show the two constant surfaces from the surface family.

4.   Conclusions

In this paper, we present an approach for constructing a spacelike constant angle surface family which passes through the given isoparametric curve in Minkowski 3-space. We consider the fixed vector lies in the spacelike cone and in the timelike cone respectively. Each of the family makes a constant angle with a fixed unit vector and we derive the necessary and sufficient condition of the constant spacelike surface through the isoparametric curve. It will very be interesting to implement our method for real life applications although the motivation of the paper is from mathematics. We will study it in future.

Acknowledgements

This work is partly supported by the National Natural Science Foundation of China (Nos. 11401077, 11671068, 11271060)and Fundamental Funds for the Central Universities (DUT20LK13).

Conflict of interest

The author declare no conflicts of interest in this paper.