Geometric invariants and focal surfaces of spacelike curves in de Sitter space from a caustic viewpoint

1.   Introduction

The geometry of submainfolds immersed in de Sitter space is an important subject that has fascinated many mathematicians and physicists ^{[1,2,3,4,5,6,7]}. Up to now, different types of surfaces and curves in de Sitter space such as spacelike curves, timelike curves and null curves have been studied. For instance, in ^[1], Wang and Pei considered null Cartan curves in de Sitter $3$-space and classified the singularities of ruled null surfaces generated by these curves. In ^[2], the authors investigate the singularities of normal hypersurfaces of de Sitter timelike curves. In ^[3,4], the authors classified Weingarten rotation surfaces and Hyperbolic rotation surfaces in de Sitter $3$-space. There are also some important works on hypersurfaces immersed in hyperbolic space and lightcone ^[8,9,10]. Because there are two kinds of spacelike curves in $S^3_1$, one is the spacelike curve with spacelike normal vector ${\bf{n}}$ and the other is the spacelike curve with timelike normal vector ${\bf{n}},$ the case of spacelike curve that is immersed in a three-dimensional de Sitter space is more sophisticated and interesting than timelike curves in de Sitter space ^[5].

The focal surface of a space curve in Euclidean space is the analogue of the evolute of a plane curve which is well defined and is a smooth curve away from the inflection points of the plane curve. It is local bifurcation set of the family of distance squared functions on plane curve and is the critical value of a Lagrangian map, i.e. it is a caustic. As a consequence, it has only Lagrangian singularities. We can conclude that the evolute of a plane curve has an ordinary cusp singularity at points corresponding to ordinary vertices of the plane curve. However, it is very hard to know is there focal surface for spacelike curve in de Sitter space and what does the focal surface look like from the classical differential geometry view point. The classical method has several limitations. For instance, it does not define focal surface in a natural way, explain which singularities could appear in focal surface and how these bifurcate as the original curve is deformed. It is also misses to capture the deep concepts such as caustic which involved. But, it is very powerful to use singularity theory to find new focal surface and describe their singularities more finer. For a spacelike curve $\gamma: I \rightarrow S^3_1\subset \mathbb{R}^4_1$ with spacelike normal vector ${\bf{n}}$ and nowhere vanishing curvature, we find its associated first de Sitter focal surface and for a spacelike curve $\gamma: I \rightarrow S^3_1\subset \mathbb{R}^4_1$ with timelike normal vector ${\bf{n}}$ and nowhere vanishing curvature, we find its associated second de Sitter focal surface. It is shown that de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities. In order to characterize the types of singularities of de Sitter focal surfaces via differential calculations, we find a de Sitter invariant of $\gamma$ which is defined to be

For detail, the caustic is a regular surface at an $A_2$-singularity of $h_{v}^S(s).$ It is a cuspidal edge at an $A_3$-singularity of $h_{v}^S(s)$ and has swallowtail singularity at an $A_4$-singularity of $h_{v}^S(s)$. Moreover, we use Legendrian duality to investigate the spacelike curve and de Sitter focal surfaces related by duality. We find that the spacelike curve $\gamma(s)$ and de Sitter focal surfaces are $\Delta_5$-dual to each other (cf., Proposition 5.1). Meanwhile, we summarize the results in Table 1.

In Section $2$, two classes of focal surfaces of spacelike curves in de Sitter $3$-space, where the ones are generated by the spacelike curve with spacelike normal vector ${\bf{n}}$ and the other ones are related to the spacelike curve with timelike normal vector ${\bf{n}},$ and the the main theorems (cf., Theorem 2.1 and Theorem 2.2) are presented. In Section $3$, we present de Sitter height function on spacelike curve $\gamma$ and establish the equivalent relations between $A_k$-singularities of the height function and geometric invariant $\rho(s)$ (cf., Proposition 3.1 and Proposition 3.2). Moreover, we discuss in detail the geometric meanings of the invariant $\rho(s)$ (cf., Corollary 3.3 and Proposition 3.4). In Section $4$, by applying some general results of the singularity theory to de Sitter focal surfaces, we give the proof of the main theorems (cf., Theorem 2.1 and Theorem 2.2) so as to complete the classifications of singularities of the de Sitter focal surfaces. In Section $5$, we investigate the relationships between the de Sitter focal surfaces and the spacelike curves by Legendrian dualities ^[11]. To better illustrate our results, we give three examples in Section $6$.

All maps considered here are of class $C^\infty$ unless otherwise stated.

2.   Preliminaries

In this section, we give the basic notions on Minkowski $4$-space and de Sitter $3$-space. Let $\mathbb{R}^4$ be a $4$-dimensional vector space. For any two vectors ${\bf{x}} = (x_0, x_1, \cdots, x_3), \; {\bf{y}} = (y_0, y_1, \cdots, y_3)$ in $\mathbb{R}^4,$ their pseudo scalar product is defined by $\langle {\bf{x}}, {\bf{y}} \rangle = -x_0y_0+x_1y_1 +x_2y_2 +x_3y_3. \; (\mathbb{R}^4, \langle, \rangle)$ is called $4$-dimensional Minkowski space. We denote it as $\mathbb{R}^4_1.$ Pseudo vector product of ${\bf{x}}, {\bf{y}}, {\bf{z}}$ is defined by

where ${\bf{x}} = (x_0, x_1, x_2, x_3), \; {\bf{y}} = (y_0, y_1, y_2, y_3),$ ${\bf{z}} = (z_0, z_1, z_2, z_3)$ are in $\mathbb{R}^4_1,$ $({\bf{e}}_0, {\bf{e}}_1, {\bf{e}}_2, {\bf{e}}_3)$ is the canonical basis of $\mathbb{R}_1^4.$ We remark that $\langle {\bf{x}}\wedge {\bf{y}}\wedge {\bf{z}}, {\bf{w}}\rangle = det({\bf{x}}, {\bf{y}}, {\bf{z}}, {\bf{w}}).$ A non-zero vector ${\bf{x}}$ in $\mathbb{R}^4_1$ is called spacelike, lightlike or timelike if $\langle {\bf{x}}, {\bf{x}} \rangle > 0,$ $\langle {\bf{x}}, {\bf{x}}\rangle = 0,$ $\langle {\bf{x}}, {\bf{x}} \rangle < 0,$ respectively. The norm of a nonzero vector ${\bf{x}}\in \mathbb{R}^4_1$ is defined by $\parallel {\bf{x}} \parallel = \sqrt{\mid \langle {\bf{x}}, {\bf{x}} \rangle \mid }.$ We define de Sitter three-space by

Let $\gamma: I \rightarrow S^3_1\subset \mathbb{R}^4_1$ be a smooth spacelike curve parameterized by arc-length parameter $s,$ so we have the unit spacelike tangent vector ${\bf{t}}(s) = \gamma^\prime(s).$ Under the assumption that $\langle{\bf{t}}^{'}(s), {\bf{t}}^{'}(s)\rangle \neq 1,$ one can construct a unit vector ${\bf{n}}(s) = \frac{{\bf{t}}^{'}(s)+ \gamma(s)}{\parallel{\bf{t}}^{'}(s)+ \gamma(s)\parallel}.$ Moreover, define ${\bf{e}}(s) = \gamma(s) \wedge {\bf{t}}(s) \wedge {\bf{n}}(s),$ then we can define a pseudo orthonormal frame $\{ \gamma(s), {\bf{t}}(s), {\bf{n}}(s), {\bf{e}}(s)\}$ of $\mathbb{R}_1^4$ along $\gamma(s).$ We have the following Frenet-Serret type formula:

where $\delta(s) = -\langle{\bf{n}}(s), {\bf{n}}(s)\rangle, \; \kappa_g(s) = \parallel {\bf{t}}^{'}(s)+ \gamma(s)\parallel$ and $\tau_g(s) = \frac{1}{\kappa_g^2(s)}det(\gamma (s), \gamma ^{'}(s), \gamma^{''}(s), \gamma^{'''}(s)).$

For a vector ${\bf{v}}\in \mathbb{R}_1^{4}$ and a real number $c,$ we define the hyperplane with pseudo-normal vector ${\bf{v}}$ by $HP({\bf{v}}, c) = \{{\bf{x}} \in \mathbb{R}_1^{4} \mid \langle {\bf{x}}, {\bf{v}} \rangle = c\}.$ The $HP({\bf{v}}, c)$ is called a spacelike hyperplane, a timelike hyperplane or a lightlike hyperplane if ${\bf{v}}$ is timelike, spacelike or lightlike respectively. Typical surfaces in de Sitter $3$-space are given by the intersection of $S_1^3$ with a hyperplane in $\mathbb{R}_1^{4}.$ A surface $S_1^3 \cap HP({\bf{v}}, c)$ is elliptic, hyperbolic or parabolic if ${\bf{v}}$ is timelike, spacelike or lightlike respectively. For any $r\in \mathbb{R}$ and ${\bf{v}}_0\in S_1^3,$ we denote $HPS^1 ({\bf{v}}_0, r) = \{{\bf{v}}\in S_1^3\mid\langle {\bf{v}}, {\bf{v}}_0 \rangle = r\}.$ We call $HPS^1 ({\bf{v}}_0, r)$ a hyperbolic pseudo-sphere in $S_1^3$ with the center ${\bf{v}}_0.$ If $\delta(s) = -1,$ we define the first de Sitter focal surface of spacelike curve by

If $\delta(s) = 1,$ we define a map as follow:

where $\kappa_g(s) > 1$ and $J\in [0, 2\pi),$ and

where $0 < \kappa_g(s) < 1$ and $J$ is an open interval in $\mathbb{R}.$ We call $\ SDF_{ \gamma}(s, \theta)$ the second de Sitter focal surface of $\gamma.$ By some calculations, we can get that

$\frac{\partial {FDF}_\gamma}{\partial s}(s, \theta)$ and $\frac{\partial {FDF}_\gamma}{\partial \theta}(s, \theta)$ are linearly dependent if and only if there exists an nonzero $\lambda \in \mathbb{R},$ such that $\frac{\partial {FDF}_\gamma}{\partial s}(s, \theta) = \lambda \frac{\partial {FDF}_\gamma}{\partial \theta}(s, \theta),$ i.e.

This is equivalent to $\lambda = \frac{\tau_g}{(1+\kappa_g^{2})^{\frac{1}{2}}}$ and $\kappa_g(s)\tau_g \sinh\theta-\frac{\kappa_g' cosh\theta}{(1+\kappa_g^{2})^{\frac{1}{2}}} = 0.$ This means that the first de Sitter focal surface $FDF_\gamma(s, \theta)$ is singular at a point $(s_0, \theta_0)$ if and only if

By similar calculations, when $\delta(s) = 1$ and $\kappa_g(s) > 1,$ we can get that

$\frac{\partial {SDF}_\gamma}{\partial s}(s, \theta)$ and $\frac{\partial {SDF}_\gamma}{\partial \theta}(s, \theta)$ are linearly dependent if and only if there exists an nonzero $\lambda \in \mathbb{R},$ such that $\frac{\partial {SDF}_\gamma}{\partial s}(s, \theta) = \lambda \frac{\partial {SDF}_\gamma}{\partial \theta}(s, \theta),$ i.e.

We get $\lambda = \frac{\tau_g}{(\kappa_g^{2}-1)^{\frac{1}{2}}}$ and $\kappa_g(s)\tau_g \sin\theta-\frac{\kappa_g' cos\theta}{(\kappa_g^{2}-1)^{\frac{1}{2}}} = 0.$ This is equivalent that

When $0 < \kappa_g(s) < 1,$ we get

This means that the second de Sitter focal surface $SDF_\gamma(s, \theta)$ is singular at a point $(s_0, \theta_0)$ if and only if $\kappa_g(s_0)\tau_g(s_0)\sqrt{\kappa_g^2(s_0)-1}sin\theta_0-\kappa_g^{'}(s_0)cos\theta_0 = 0,$ or $\kappa_g(s_0)\tau_g(s_0)\sqrt{1-\kappa_g^2(s_0)}cosh\theta_0-\kappa_g^{'}(s_0)sinh\theta_0 = 0.$ Thus, we obtain geometric information about focal surfaces of de Sitter spacelike curves. This method has several limitations. For instance, it does not explain which singularities could appear in the focal surfaces and how these bifurcate as the original curve is deformed. It also misses to capture the deep concepts involved. To describe the generic singularities of focal surfaces, we should suppose that $cos\theta\neq0$ or $sinh\theta\neq0$ for the case $\delta(s) = 1$ unless otherwise stated. Continuing with notation, we give a brief review on Lagrangian singularity theory mainly due to Arnold ^[12]. The main tool of Lagrangian singularities theory is the notion of generating families and caustic. Let $G : (\mathbb{R}\times \mathbb{R}^n, {\bf{0}})\longrightarrow(\mathbb{R}, 0)$ be a function germ. We say that $G$ is a Morse family if the mapping

is non-singular, where $(s, {\bf{v}}) = (s, v_1, \ldots, v_n)\in(\mathbb{R}\times \mathbb{R}^n, {\bf{0}}).$ In this case we have a smooth $n$-dimensional submanifold,

and the map germ $\Phi_G:(\mathcal{C}_{G}, {\bf{0}})\longrightarrow T^*\mathbb{R}^n$ defined by

is a Lagrangian immersion germ. We call $G$ a generating family of $\Phi_G(\mathcal{C}_{G}).$ Let $\pi_2:(\mathbb{R}^k\times\mathbb{R}^n, {\bf{0}})\longrightarrow(\mathbb{R}^n, {\bf{0}})$ denote the canonical projection and consider the map-germ $\pi_{\mathcal{C}_{G}}$ which is given by the restriction of the projection $\pi_2$ to $(\mathcal{C}_{G}, {\bf{0}}).$ Thus $\pi_{\mathcal{C}_{G}}:(\mathcal{C}_{G}, {\bf{0}})\longrightarrow(\mathbb{R}^n, {\bf{0}})$ with $\pi_{\mathcal{C}_{G}}(s, {\bf{v}}) = {\bf{v}}$ for any $(s, {\bf{v}}) \in (\mathcal{C}_{G}, {\bf{0}}).$ The map $\pi_{\mathcal{C}_{G}}$ is the catastrophe map of $G$ and it is a Lagrangian map. A caustic is the set of critical values of a Lagrangian map. Therefore the corresponding caustic is

We sometimes denote $\mathcal{B}_G = C(\Phi_G)$ and call it the bifurcation set of $G$. Now, we can apply the above arguments to our situation, we find that de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities. In order to characterize the types of singularities of de Sitter focal surfaces via differential calculations, we find a de Sitter invariant of $\gamma$ which is defined to be

To state the main results, we respectively call $C \times \mathbb{R} = \{(x_1, x_2)\mid x_1^2 = x_2^3\}\times\mathbb{R}$ a cuspidal edge,

a swallowtail, $C(2, 3, 4) = \{(t^2, t^3, t^4)\in \mathbb{R}^3\mid t\in \mathbb{R}\}$ a $(2, 3, 4)$-cusp (cf., Figure 1). The main results in this paper are given as follows:

Theorem 2.1. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s) \neq 0,$ then de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities. For details, if $\delta(s) = -1,$ then we have the following:

$\rm(1)$ The first de Sitter focal surface $FDF_\gamma(s, \theta)$ is singular at a point $(s_0, \theta_0)$ if and only if

$\rm(2)$ The first de Sitter focal surface $FDF_\gamma(s, \theta)$ is locally diffeomorphic to cuspidal edge $C \times \mathbb{R}$ at $(s_0, \theta_0)$ if

$\rho(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $4$ for $s_0$ and $FDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the line.

$\rm(3)$ The first de Sitter focal surface $FDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is locally diffeomorphic to the $SW$ at $(s_0, \theta_0)$ if

$\rho(s_0) = 0$ and $\rho'(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $5$ for $s_0$ and $FDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the $(2, 3, 4)$-cusp.

Theorem 2.2. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s) \neq 0,$ then de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities. For details:

$\rm(A)$ Suppose that $\delta(s) = 1$ and $\kappa_g(s) > 1,$ then we have the following:

$\rm(1)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is singular at a point $(s_0, \theta_0)$ if and only if $\kappa_g(s_0)\tau_g(s_0)\sqrt{\kappa_g^2(s_0)-1}sin\theta_0-\kappa_g^{'}(s_0)cos\theta_0 = 0.$

$\rm(2)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is locally diffeomorphic to cuspidal edge $C \times \mathbb{R}$ at $(s_0, \theta_0)$ if

$\rho(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $4$ for $s_0$ and $SDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the line.

$\rm(3)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is locally diffeomorphic to the $SW$ at $(s_0, \theta_0)$ if

$\rho(s_0) = 0$ and $\rho'(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $5$ for $s_0$ and $SDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the $(2, 3, 4)$-cusp.

$\rm(B)$ Suppose that $\delta(s) = 1$ and $0 < \kappa_g(s) < 1,$ then we have the following:

$\rm(1)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is singular at a point $(s_0, \theta_0)$ if and only if $\kappa_g(s_0)\tau_g(s_0)\sqrt{1-\kappa_g^2(s_0)}cosh\theta_0-\kappa_g^{'}(s_0)sinh\theta_0 = 0.$

$\rm(2)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is locally diffeomorphic to cuspidal edge $C \times \mathbb{R}$ at $(s_0, \theta_0)$ if

and $\rho(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $4$ for $s_0$ and $SDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the line.

$\rm(3)$ The second de Sitter focal surface $SDF_\gamma(s, \theta)$ of spacelike curve $\gamma$ is locally diffeomorphic to the $SW$ at $(s_0, \theta_0)$ if

$\rho(s_0) = 0$ and $\rho'(s_0)\neq 0.$ Under this condition, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $5$ for $s_0$ and $SDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the $(2, 3, 4)$-cusp.

3.   De Sitter height functions and geometric invariant

In order to study the singularities of the first de Sitter focal surface and the second de Sitter focal surface of spacelike curve in $S_1^3,$ we introduce a very useful family of function on spacelike curve in de Sitter $3$-space. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve, we now define a function $H^{S}: I \times S^3_1 \longrightarrow \mathbb{R}$ by $H^{S}(s, {\bf{v}}) = \langle \gamma(s), {\bf{v}} \rangle$. For any fixed ${\bf{v}}\in S^3_1,$ we denote $h^S_v (s) = H^{S}(s, {\bf{v}}).$ We call $H^{S}$ the de Sitter height function on the curve $\gamma.$ We will consider the contact of a spacelike curve $\gamma : I \rightarrow S^3_1$ with hyperbolic pseudo-sphere. By definition, a hyperbolic pseudo-sphere in $S_1^3$ with the centre ${\bf{v}}_0$ and radius $r$ is the level set $h_v^S(s) = r.$ We stress that the contact of $\gamma$ with the level sets of $h_v^S$ can be measured by the vanishing of successive derivatives of the function $g(s) = h^S_{v}(\gamma(s)) = \langle \gamma(s), {\bf{v}}\rangle.$ In particular, a point $\gamma(s_0)$ is on a hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ of centre ${\bf{v}}_0$ and radius $r$ if and only if $g(s_0) = r.$ Furthermore, the curve $\gamma$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ have an ordinary tangency at $\gamma(s_0)$ if and only if $g(s_0) = r, g'(s_0) = 0$ and $g''(s_0)\neq 0.$ Higher orders of tangency between $\gamma$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ are captured by the vanishing of successive derivatives of the function $g$ at $s_0.$ We say that $\gamma$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ have $(k+1)$-point contact at $s_0$ if $g^{'}(s_0) = g^{''}(s_0) = \cdots = g^{(k)}(s_0) = 0$ but $g^{(k+1)}(s_0)\neq 0.$ Then $s_0$ is said to be a singularity of $g$ of type $A_k.$ We say that $\gamma$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ have at least $k$-point contact at $s = s_0$ if $g^{'}(s_0) = g^{''}(s_0) = \cdots = g^{(k)}(s_0) = 0$ and call $s_0$ a singularity of $g$ of type $A_{\geq k}.$ If the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ and a de Sitter spacelike curve have contact of at least order $3$ for a points $s_0,$ we call $HPS^1 ({\bf{v}}_0, r)$ the osculating hyperbolic pseudo-sphere of $\gamma(s)$ at $s_0.$ Then we have the following proposition which contains a geometric invariant $\rho(s).$

Proposition 3.1. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s)\neq 0$ and $\delta(s) = -1, \; HPS^1 ({\bf{v}}, r)$ be a hyperbolic pseudo-sphere of centre ${\bf{v}}_0$ and radius $r.$ Suppose that $g(s_0) = r$ for some $s_0.$ Then $g$ has a singularity of type $A_1, A_2, A_3$ or $A_4$ at $s_0$ if and only if the geometric conditions in Table 2 are satisfied.

Proof. By definition and the Frenet-Serret type formulae, we have

(a) $(h^S_ {\bf{v}})^\prime(s) = \langle{{\bf{t}}}(s), {\bf{v}}\rangle$

(b) $(h^S_ {\bf{v}})^{\prime\prime}(s) = \langle - \gamma(s)+\kappa_g(s){{\bf{n}}}(s), {\bf{v}}\rangle.$

(c) $(h^S_ {\bf{v}})^{(3)}(s) = \langle(\delta(s)\kappa_g^2(s)-1){{\bf{t}}}(s)+\kappa_g^\prime(s){\bf{n}}(s)+\kappa_g(s)\tau_g(s){\bf{e}}(s), {\bf{v}}\rangle,$

(d) $(h^S_ {\bf{v}})^{(4)}(s) = \langle 3\delta(s)\kappa_g(s)\kappa_g^\prime(s){{\bf{t}}}(s)+(\delta(s)\kappa_g^3(s)-\kappa_g(s)+ \kappa_g^{\prime\prime}(s)+\kappa_g(s)\tau_g^2(s)){{\bf{n}}}(s)+(2\kappa_g^{'}(s)\tau_g(s)+\kappa_g(s)\tau_g^{'}(s)){{\bf{e}}}(s)-(\delta(s)\kappa_g^2(s)-1) \gamma(s), {\bf{v}}\rangle,$

(e) $(h^S_ {\bf{v}})^{(5)}(s) = \langle -5\delta(s)\kappa_g(s)\kappa_g^{'}(s) \gamma(s)+ (3\delta(s)(\kappa_g^\prime(s))^2+4\delta(s)\kappa_g(s)\kappa_g^{''}(s)+\kappa_g^4(s)-2\delta(s)\kappa_g^2(s)+\delta(s)\kappa_g^2(s)\tau_g^2(s)+1){{\bf{t}}}(s) +(6\delta(s)\kappa_g^2(s)\kappa_g^{'}(s)-\kappa_g^{'}(s)+\kappa_g^{'''}(s)+3\kappa_g^{'}(s)\tau_g^2(s)+3\kappa_g(s)\tau_g(s)\tau_g^{'}(s)){\bf {n}}(s)+(\delta(s)\kappa_g^{3}(s)\tau_g(s)-\kappa_g(s)\tau_g(s)+3\kappa_g^{''}(s)\tau_g(s)+\kappa_g(s)\tau_g^{3}(s)+3\kappa_g^{'}(s)\tau_g^{'}(s)+\kappa_g(s)\tau_g^{''}(s)){\bf{e}}(s), {\bf{v}}\rangle.$

By the conditions that$(h^S_ {\bf{v}})^\prime(s) = 0$, ${\bf{v}}\in S^3_1$ and $\delta(s) = -1,$ we have that there are real numbers $\lambda, \mu, \nu$ such that ${\bf{v}} = \lambda\gamma(s)+\mu {\bf{n}}(s)+\nu{{\bf{e}}}(s)$ and $\lambda^2+\mu^2-\nu^2 = 1.$ The converse direction also holds. This is equivalent that $g$ has a singularity of type $A_1,$ which is also equivalent that the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ and the de Sitter spacelike curve have contact of at least order $2.$ Meanwhile, it is equivalent that the centre of the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ lies on the normal space to $\gamma$ at $s_0$ but is not on the focal surface of $\gamma.$ By the above formula (b), we have $(h^S_ {\bf{v}})^{\prime}(s) = (h^S_ {\bf{v}})^{\prime\prime}(s) = 0$ if and only if $\lambda = \mu \kappa_g(s).$ By the fact that $\lambda^2+\mu^2-\nu^2 = 1,$ we have $\mu^2(\kappa_g^2(s)+1)-\nu^2 = 1.$ Let $\mu = \frac{cosh\theta}{\sqrt{1+\kappa_g^2(s)}}, \nu = sinh\theta.$ Thus, we have

This is equivalent that $g$ has a singularity of type $A_2,$ which is also equivalent that the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ and the de Sitter spacelike curve have contact of at least order $3.$ And it is also equivalent that the centre of the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ lies on the regular part of the focal surface of $\gamma$ at $s_0.$ By the similar arguments to above and formula (c), we have $(h^S_ {\bf{v}})^\prime(s) = (h^S_ {\bf{v}})^{\prime\prime}(s) = (h^S_ {\bf{v}})^{(3)}(s) = 0$ if and only if $\frac{cosh\theta}{\sqrt{\kappa_g^2(s)+1}}(\kappa_g^\prime(s))-\kappa_g(s)\tau_g(s)sinh\theta = 0.$ This is equivalent to the condition $tanh\theta = \frac{\kappa_g^\prime(s)}{\kappa_g(s)\tau_g(s)\sqrt{1+\kappa_g^2(s)}}.$ Combining with the condition that ${\bf{v}} = \frac{cosh \theta}{\sqrt{ \kappa_g^2(s)+1}}(\kappa_g(s) \gamma(s)+{\bf{n}}(s))+sinh\theta{\bf{e}}(s).$ Therefore, we have

and

In the meanwhile, this is equivalent that $g$ has a singularity of type $A_3,$ which is also equivalent that the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ and the de Sitter spacelike curve have contact of at least order $4.$ In addition, it is equivalent that the centre of the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ lies on the non-degenerate singular part of the focal surface of $\gamma$ at $s_0.$ Subsequently, by the above formula (d), $(h^S_ {\bf{v}})^\prime(s) = (h^S_ {\bf{v}})^{\prime\prime}(s) = (h^S_ {\bf{v}})^{(3)}(s) = (h^S_ {\bf{v}})^{(4)}(s) = 0$ if and only if

Substituting

in the above condition, we get

Therefore, we have the conditions

and $\rho(s) = 0$ which indicate $g$ has a singularity of type $A_4.$ Under these conditions, the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ and the de Sitter spacelike curve have contact of at least order $5$ and the centre of the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r)$ lies on the degenerate singular part of the focal surface of $\gamma$ at $s_0.$ Finally, by the similar arguments to the above cases we can show that $(h^S_ {\bf{v}})^\prime(s) = (h^S_ {\bf{v}})^{\prime\prime}(s) = (h^S_ {\bf{v}})^{(3)}(s) = (h^S_ {\bf{v}})^{(4)}(s) = (h^S_ {\bf{v}})^{(5)}(s) = 0$ if and only if $\frac{cosh\theta}{\sqrt{1+\kappa_g^2(s)}}(-\kappa_g^2(s)\kappa_g^{'}(s)-\kappa_g^{'}(s)+\kappa_g^{'''}(s)+3\kappa_g^{'}(s)\tau_g^2(s)+3\kappa_g(s)\tau_g(s)\tau_g^{'}(s))-sinh\theta(-\kappa_g^3(s)\tau_g(s)-\kappa_g(s)\tau_g(s)+3\kappa_g^{''}(s)\tau_g(s)+\kappa_g(s)\tau_g^{3}(s)+3\kappa_g^{'}(s)\tau_g^{'}(s)+\kappa_g(s)\tau_g^{''}(s)) = 0.$ This is equivalent that $\kappa_g(s)\kappa_g^{'''}(s)\tau_g(s)+2\kappa_g(s)\kappa_g^{'}(s)(\tau_g(s))^3+3\kappa_g^{2}(s)\tau_g^2(s)\tau_g^{'}(s)-3\kappa_g^{'}(s)\kappa_g^{''}(s)\tau_g(s)-3(\kappa_g^{'}(s))^2\tau_g^{'}(s)-\kappa_g(s)\kappa_g^{'}(s)\tau_g^{''}(s) = 0.$ In particular, we get

and $\rho(s) = \rho^{'}(s) = 0.$ This completes the proof.

By the similar arguments to the above cases we can show that the following proposition holds.

Proposition 3.2. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s)\neq 0,$ $\kappa_g(s) \neq 1$ and $\delta(s) = 1. \; HPS^1 ({\bf{v}}, r)$ be a hyperbolic pseudo-sphere of centre ${\bf{v}}_0$ and radius $r.$ Suppose that $g(s_0) = r$ for some $s_0.$ Then $g$ has a singularity of type $A_1, A_2, A_3$ or $A_4$ at $s_0$ if and only if the geometric conditions in Table 3 are satisfied.

Proof. (1) From $(h^S_ { {\bf{v}}})^\prime(s) = \langle {{\bf{t}}}(s), {{\bf{v}}}\rangle = 0, \; {\bf{v}}\in S^3_1$ and $\delta(s) = 1,$ we get that there are real numbers $\lambda, \mu, \nu$ such that ${\bf{v}} = \lambda\gamma(s)+\mu{\bf{n}}(s)+\nu{\bf{e}}(s)$ and $\lambda^2-\mu^2+\nu^2 = 1.$ Furthermore, we calculate that $(h^S_ {{\bf{v}}})^{\prime\prime}(s) = \langle -\gamma(s)+k_g(s){\bf{n}}(s), {\bf{v}}\rangle = 0,$ which indicates that $\lambda = -\mu k_g(s),$ hence $\mu^2(k_g^2(s)-1)+\nu^2 = 1.$ When $k_g(s) > 1,$ let $\mu = \frac{cos\theta}{\sqrt{k_g^2(s)-1}}, \nu = sin\theta.$ Thus, we have

When $0 < k_g(s) < 1,$ let $\mu = \frac{\sinh\theta}{\sqrt{1-k_g^2(s)}}, \nu = \cosh\theta.$ It follows that

Subsequently, it can be examined that $(h^S_ { {\bf{v}}})^{(3)}(s) = \langle(\delta(s)k_g^2(s)-1){\bf{t}}(s)+k_g^\prime(s){\bf{n}}(s)+k_g(s)\tau_g(s){\bf{e}}(s), {\bf{v}}\rangle = 0,$ which implies $\frac{cos\theta}{\sqrt{k_g^2(s)-1}}(-k_g^\prime(s))+k_g(s)\tau_g(s)sin\theta = 0$ or $\frac{\sinh\theta}{\sqrt{1-k_g^2(s)}}(-k_g^\prime(s))+k_g(s)\tau_g(s)\cosh\theta = 0.$ This is equivalent to the condition $tan\theta = \frac{k_g^\prime(s)}{k_g(s)\tau_g(s)\sqrt{k_g^2(s)-1}}$ or $coth\theta = \frac{k_g^\prime(s)}{k_g(s)\tau_g(s)\sqrt{1-k_g^2(s)}}.$ Moreover, calculating the 4th derivative of $h^S_ {{\bf{v}}}, \; (h^S_ {{\bf{v}}})^{(4)}(s) = \langle 3\delta(s)k_g(s)k_g^\prime(s){{\bf{t}}}(s)+(\delta(s)k_g^3(s)-k_g(s)+k_g^{\prime\prime}(s)+k_g(s)\tau_g^2(s)) {\bf{n}}(s)+(2k_g^{'}(s)\tau_g(s)+k_g(s)\tau_g^{'}(s)) {\bf{e}}(s)-(\delta(s)k_g^2(s)-1)\gamma(s), {\bf{v}}\rangle,$ we can state that $(h^S_ { {\bf{v}}})^\prime(s) = (h^S_ {{\bf{v}}})^{\prime\prime}(s) = (h^S_ {{\bf{v}}})^{(3)}(s) = (h^S_ {{\bf{v}}})^{(4)}(s) = 0$ if and only if there exists $\theta$ such that $tan\theta = \frac{k_g^\prime(s)}{k_g(s)\tau_g(s)\sqrt{k_g^2(s)-1}}$ and $\rho(s) = 0$ or $coth\theta = \frac{k_g^\prime(s)}{k_g(s)\tau_g(s)\sqrt{1-k_g^2(s)}}$ and $\rho(s) = 0.$ Finally, we calculate $(h^S_ {{\bf{v}}})^{(5)}(s) = \langle -5\delta(s)k_g(s)k_g^{'}(s)\gamma(s)+ (3\delta(s)(k_g^\prime(s))^2+4\delta(s)k_g(s)k_g^{''}(s)+k_g^4(s)-2\delta(s)k_g^2(s)$ +$\delta(s)k_g^2(s)\tau_g^2(s)+1){\bf{t}}(s) +(6\delta(s)k_g^2(s)k_g^{'}(s)-k_g^{'}(s)+k_g^{'''}(s)$ +$3k_g^{'}(s)\tau_g^2(s)+3k_g(s)\tau_g(s)\tau_g^{'}(s)){\bf{n}}(s)+(\delta(s)k_g^{3}(s)\tau_g(s)-k_g(s)\tau_g(s)+3k_g^{''}(s)\tau_g(s)$ +k$_g(s)\tau_g^{3}(s)+3k_g^{'}(s)\tau_g^{'}(s)+k_g(s)\tau_g^{''}(s)){\bf{e}}(s), {\bf{v}}\rangle.$ From $(h^S_ {{\bf{v}}})^\prime(s) = (h^S_ { {\bf{v}}})^{\prime\prime}(s) = (h^S_ {{\bf{v}}})^{(3)}(s) = (h^S_ {{\bf{v}}})^{(4)}(s) = (h^S_ {{\bf{v}}})^{(5)}(s) = 0,$ when $k_g(s) > 1,$ we have -$\frac{cos(\theta)}{\sqrt{1+k_g^2(s)}}(-k_g^2(s)k_g^{'}(s)-k_g^{'}(s)+k_g^{'''}(s)+3k_g^{'}(s)\tau_g^2(s)+3k_g(s)\tau_g(s)\tau_g^{'}(s))+sin(\theta)(-k_g^3(s)\tau_g(s)-k_g(s)\tau_g(s)+3k_g^{''}(s)\tau_g(s)+k_g(s)\tau_g^{3}(s)+3k_g^{'}(s)\tau_g^{'}(s)+k_g(s)\tau_g^{''}(s)) = 0.$ Combining with the condition that

This is equivalent that $k_g(s)k_g^{'''}(s)\tau_g(s)+2k_g(s)k_g^{'}(s)(\tau_g(s))^3+3k_g^{2}(s)\tau_g^2(s)\tau_g^{'}(s)-3k_g^{'}(s)k_g^{''}(s)\tau_g(s)-3(k_g^{'}(s))^2\tau_g^{'}(s)-k_g(s)k_g^{'}(s)\tau_g^{''}(s) = 0,$ which means $\rho^{'}(s) = 0.$ Therefore, we get the condition

and $\rho(s) = \rho^{'}(s) = 0.$ When $0 < k_g(s) < 1,$ by the similar arguments to above, we can get

and $\rho(s) = \rho^{'}(s) = 0.$ By the similar arguments to above proposition, these assertions hold.

Corollary 3.3. Let $\gamma: I \rightarrow S^3_1$ be a unit speed space curve with $\kappa_g(s)\tau_g(s) \neq 0.$

$\rm(A)$ Suppose that $\delta(s) = -1,$ then we have the following:

$\rm(1)$ There exists an osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ of $\gamma(s)$ at a point $s_0.$

$\rm(2)$ Under the above notations, $\gamma(s)$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ have at least a $4$-point (respectively, $5$-point) contact at $\gamma(s_0)$ if and only if $\rho(s_0)\neq 0$ (respectively, $\rho(s_0) = 0$ and $\rho^{\prime}(s_0)\neq 0$).

$\rm(B)$ Suppose that $\delta(s) = 1,$ then we have the following:

$\rm(1)$ There exists an osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ of $\gamma(s)$ at a point $s_0$ if and only if $\kappa_g(s_0)\neq 1.$

$\rm(2)$ Suppose that $\kappa_g(s_0)\neq 1.$ Then $\gamma(s)$ and the hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ have at least a $4$-point (respectively, $5$-point) contact at $\gamma(s_0)$ if and only if $\rho(s_0)\neq 0$ (respectively, $\rho(s_0) = 0$ and $\rho^{\prime}(s_0)\neq 0$).

Proof. (A) Under the condition that $\delta(s) = -1.$ Let $\mathcal {H}^S :S^3_1\times S^3_1\rightarrow \mathbb{R}$ be a function defined by $\mathcal {H}^S({\bf u}, {\bf{v}}) = \langle{\bf u}, {\bf{v}} \rangle.$ We claim that $\mathcal{H}_{\bf{v}}^S$ is a submersion and $(\mathfrak{h}^S)^{-1}_{v_0}(c)$ is a hyperbolic pseudo-sphere for any ${\bf{v}}\in S^3_1$, where $\mathfrak{h}_{ v}^S({\bf u}) = \mathcal {H}^S({\bf u, v}).$ We have that $\mathfrak{h}_{ v}^S\circ \gamma(s) = h^S_{v_0}(s),$ here $h^S_{v_0}(s) = H^S(s, {\bf{v}}_0).$ Therefore we have $(h^S_{{\bf v_0}})^{-1}(r_0)$ is an osculating hyperbolic pseudo-sphere if and only if $h^S_{v_0}(s) = r_0$ and $(h^S_ {\bf{v}})^\prime(s) = (h^S_ {\bf{v}})^{\prime\prime}(s) = 0.$ By Proposition 3.1, this condition is equivalent to the condition that

where

and $r_0 = H^S(s_0, {\bf{v}}_0).$ It is clearly that there exist such ${\bf{v}}_0$ and $\theta(s)$ for any $\kappa_g(s).$ The assertion (2) follows from the rest assertions of Proposition 3.1.

(B) Under the condition that $\delta(s) = 1.$ The assertion follows from exactly the same arguments as those of the previous case.

By some calculations, we can get the following proposition which contains the geometric meanings of the important invariant $\rho(s).$

Proposition 3.4. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s)\neq 0.$

$\rm(A)$ Suppose that $\delta(s) = -1.$ Let $\theta(s)$ be a function defined by $tanh(\theta(s)) = \frac{\kappa_g^{'}(s)}{\kappa_g(s)\tau_g(s)\sqrt{1+\kappa_g^2(s)}}.$ Then the following conditions are equivalent:

$\rm(1) \; FDF_\gamma(s, \theta(s))$ is a constant vector,

$\rm(2) \; \rho(s) = 0,$

$\rm(3) \; Im(\gamma(s))\subset HPS^1 ({\bf{v}}_0, r).$

$\rm(B)$ Suppose that $\delta(s) = 1$ and $\kappa_g(s)\neq1.$ Let $\theta(s)$ be a function defined by $tan(\theta(s)) = \frac{\kappa_g^{'}(s)}{\kappa_g(s)\tau_g(s)\sqrt{\kappa_g^2(s)-1}}$ or $coth(\theta(s)) = \frac{k_g^\prime(s)}{k_g(s)\tau_g(s)\sqrt{1-k_g^2(s)}}.$ Then the following conditions are equivalent:

$\rm(1) \; SDF_\gamma(s, \theta(s))$ is a constant vector,

$\rm(2) \; \rho(s) = 0,$

$\rm(3) \; Im(\gamma(s))\subset HPS^1 ({\bf{v}}_0, r).$

Proof. First, we consider the assertion (A). Let $\theta = \theta(s),$ by some calculations, we have

Differentiating both sides of the equation

on the variable $s$, we get

This is equivalent to

Therefore,

Substituting $tanh(\theta(s))$ and $\theta'(s)$ into the left of the following equations, we get

and

Furthermore, substituting Eqs (3.2), (3.3) and (3.4) into (3.1), we get

Therefore, $FDF_\gamma^\prime(s, \theta(s))\equiv 0$ if and only if $\rho(s)\equiv 0.$ This means that the conditions (1) and (2) are equivalent. Assume that the condition (1) holds. Then we have $\langle \gamma(s), FDF_\gamma(s, \theta(s))\rangle = \frac{\kappa_g cosh(\theta(s))}{\sqrt{1+\kappa_g^2}},$ which is constant. Under this condition, we put $r = \frac{\kappa_gcosh(\theta(s))}{\sqrt{1+\kappa_g^2}}$ and ${\bf{v}}_0 = \frac{cosh (\theta(s))}{\kappa_g(s)\tau_g(s)\sqrt{ \kappa_g^2(s)+1}}(\kappa_g^2(s)\tau_g(s) \gamma(s)+\kappa_g(s)\tau_g(s){\bf{n}}(s)+\kappa_g^{'}(s){\bf{e}}(s)).$ Then it is easy to show that $\gamma(s)$ is a part of the pseudo-sphere $HPS^1 ({\bf v}_0, r).$ The condition (3) holds. For the converse, we assume that $\langle \gamma(s), {\bf{v}}\rangle = c$ for a constant vector ${\bf{v}}$ and a real number $c.$ Since $h_v^{S}(s) = c,$ we have ${\bf{v}} = \frac{cosh (\theta(s))}{\kappa_g(s)\tau_g(s)\sqrt{ \kappa_g^2(s)+1}}(\kappa_g^2(s)\tau_g(s) \gamma(s)+\kappa_g(s)\tau_g(s){\bf{n}}(s)+\kappa_g^{'}(s){\bf{e}}(s)),$ by Proposition 3.1, so that the condition (1) holds.

For the proof of the assertion (B), when $\kappa_g > 1$, since $tan\theta(s) = \frac{\kappa_g'}{\kappa_g\tau_g\sqrt{\kappa_g^2-1}},$ locally, we get $\theta(s) = arctan\frac{\kappa_g'}{\kappa_g\tau_g\sqrt{\kappa_g^2-1}}.$ A direct computation shows that

and

Therefore, $SDF_\gamma^\prime(s, \theta(s))\equiv 0$ if and only if $\rho(s)\equiv 0.$ This means that the conditions (1) and (2) are equivalent. Assume that the condition (1) holds. Then we have $\langle \gamma(s), SDF_\gamma(s, \theta(s))\rangle = -\frac{\kappa_g cos(\theta(s))}{\sqrt{\kappa_g^2-1}},$ which is constant. Under this condition, we put $r = -\frac{\kappa_gcos(\theta(s))}{\sqrt{\kappa_g^2-1}}$ and ${\bf{v}}_0 = \frac{cos (\theta(s))}{\kappa_g(s)\tau_g(s)\sqrt{ \kappa_g^2(s)-1}}(-\kappa_g^2(s)\tau_g(s) \gamma(s)+\kappa_g(s)\tau_g(s){\bf{n}}(s)+\kappa_g^{'}(s){\bf{e}}(s)).$ Then it is easy to show that $\gamma(s)$ is a part of the pseudo-sphere $HPS^1 ({\bf v}_0, r).$ The condition (3) holds. For the converse, we assume that $\langle \gamma(s), {\bf{v}}\rangle = c$ for a constant vector ${\bf{v}}$ and a real number $c.$ Since $h_v^{S}(s) = c,$ we have ${\bf{v}} = \frac{cos (\theta(s))}{\kappa_g(s)\tau_g(s)\sqrt{ \kappa_g^2(s)-1}}(-\kappa_g^2(s)\tau_g(s) \gamma(s)+\kappa_g(s)\tau_g(s){\bf{n}}(s)+\kappa_g^{'}(s){\bf{e}}(s)),$ by Proposition 3.2, so that the condition (1) holds. When $0 < \kappa_g(s) < 1,$ the proof is similar to those of (A). This completes the proof.

4.   Proof of the main results

Let function germ $F :(\mathbb{R}\times \mathbb{R}^r, (s_0, x_0))\rightarrow \mathbb{R}$ be an $r$-parameter unfolding of $f(s)$ which has $A_k$- singularity $(k \geq 1)$ at $s_0,$ where $f(s) = F(s, x_0).$ We denote the $(k - 1)$-jet of the partial derivative $\frac{\partial F }{\partial x_i}$ at $s_0$ by

Then $F$ is called a $\mathcal{R}^+$-versal unfolding if the $(k-1)\times r$ matrix of coefficients $(a_{ji})$ has rank $k-1$, $(k-1 \leq r)$. The bifurcation set of order $l$ concerning the unfolding $F$ is defined by

Then $\mathfrak{B}_F^1 = \mathfrak{B}_F$ is the bifurcation set and $\mathfrak{B}_F^2$ is the set of singular points of $\mathfrak{B}_F.$ We have the following classification result (cf., ^[13]).

Theorem 4.1. Let $F : (\mathbb{R} \times \mathbb{R}^r, (s_0, {\bf{x}}_0)) \longrightarrow \mathbb{R}$ be an $r$-parameter unfolding of $f(s)$ which has the $A_k$ singularity at $s_0$. Suppose that $F(s, {\bf{x}})$ is an $\mathcal{R}^+$-versal unfolding, then we have the following claims.

$\rm(a)$ If $k = 2$, then $\mathfrak{B}_F$ is locally diffeomorphic to $\{ 0 \}\times \mathbb{R}^{r-1}$ and $\mathfrak{B}_F^2 = \varnothing.$

$\rm(b)$ If $k = 3$, then $\mathfrak{B}_F$ is locally diffeomorphic to $C (2, 3)\times \mathbb{R}^{r-2 }, \; \mathfrak{B}_F^2$ is diffeomorphic to $\{ 0 \}\times \mathbb{R}^{r-2 }$ and $\mathfrak{B}_F^3 = \varnothing.$

$\rm(c)$ If $k = 4$, then $\mathfrak{B}_F$ is locally diffeomorphic to $SW \times \mathbb{R}^{r-3}, \; \mathfrak{B}_F^2$ is diffeomorphic to $C(2, 3, 4) \times \mathbb{R}^{r-3}, \; \mathfrak{B}_F^3$ is diffeomorphic to $\{ 0 \} \times \mathbb{R}^{r-3 }$ and $\mathfrak{B}_F^4 = \varnothing.$

We consider that $H^S (s, {\bf{v}})$ is an unfolding of $h^S_{ {\bf{v}}_0}(s)$. Then we have the following proposition:

Proposition 4.2. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s)\neq 0, \; H^{S}: I \times S^3_1 \longrightarrow \mathbb{R}$ be the de Sitter height function on $\gamma(s).$ If $h^S_{ {\bf{v}}_0}(s)$ has an $A_k$-singularity $(k = 3, 4)$ at $s_0$, then $H^S(s, {\bf{v}})$ is a $\mathcal{R}^+$-versal unfolding of $h^S_{ {\bf{v}}_0}(s).$

Proof. Suppose that $\delta(s) = -1.$ We consider the pseudo orthonormal basis

instead of the canonical basis of $\mathbb{R}_1^4.$ Let $\gamma(s) = (x_1(s), x_2(s), x_3(s), x_4(s))$ and ${\bf{v}} = (v_1, \cdots, v_{4})\in S_{1}^3.$ Because ${\bf{v}} \in S_{1}^3$ is a nonzero vector, we have $-v_1^2+v_{2}^2+\cdots+v_{4}^2 = 1.$ Without loss of the generality, we might assume that $v_1 > 0,$ hence $v_1 = \sqrt{-1 + v_{2}^2 + \cdots + v_{4}^2}.$ By a straightforward calculation,

Therefore the $3$-jet of $\frac{\partial H^S}{\partial v_i}(s, {\bf{v}})(i = 2, 3, 4)$ at $s_0$ is given by

When $h^S_{v_0}$ has $A_3$-singularity at $s_0$, we require the $2\times 3$ matrix

to be nonsingular at $s_0$. It is enough to show that the rank of the matrix $A$ at $s_0$ is $3,$ where

When $h^S_{v_0}$ has $A_4$-singularity at $s_0$, we require the rank of the $3\times 3$ matrix $A$ at $s_0$ is $3$. Denote that

then we obtain

Because

and

therefore

Because $\kappa_g(s)\tau_g(s)\neq 0, sech\theta(s)\neq0$ for any $s,$ therefore, $\kappa_g(s_0)\tau_g(s_0)\neq 0, sech\theta(s_0)\neq0.$ Hence, $det A\neq 0$ at $s_0,$ the rank of the matrix $A$ is three. In conclution, $H^S(s, {\bf{v}})$ is a $\mathcal{R}^+$-versal unfolding of $h^S_{ {\bf{v}}_0}(s).$

For the case of $\delta(s) = 1,$ when $\kappa_g(s) > 1,$

Under the assumption that $\kappa_g(s)\tau_g(s)\neq 0, cos\theta(s)\neq0$ for any $s,$ therefore, $\kappa_g(s_0)\tau_g(s_0)\neq 0, sec\theta(s_0)\neq0.$ Hence, $det A\neq 0$ at $s_0,$ the rank of the matrix $A$ is also three. When $0 < \kappa_g(s) < 1,$ we get

In conclusion, if $h^S_{ {\bf{v}}_0}(s)$ has an $A_k$-singularity $(k = 3, 4)$ at $s_0,$ then $H^S(s, {\bf{v}})$ is a $\mathcal{R}^+$-versal unfolding of $h^S_{ {\bf{v}}_0}(s).$ This completes the proof.

By Proposition 4.2 and the definition of caustic, we can prove the following Proposition 4.3.

Proposition 4.3. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g(s)\tau_g(s)\neq 0,$ then de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities. For detail, the caustic is a regular surface at an $A_2$-singularity of $h_{v}^S(s).$ It is a cuspidal edge at an $A_3$-singularity of $h_{v}^S(s)$ and has swallowtail singularity at an $A_4$-singularity of $h_{v}^S(s)$.

Proof. Taking

in Proposition 4.2 for example. We get the Jacobi matrix of $\Delta^*H^{S} = (\frac{\partial H^{S}}{\partial s})$ is

Since the rank of the matrix $A$ in the proof of the Proposition 4.2 is $3$, the rank of the matrix $J\Delta^*H^{S}$ is $1$. This means that $H^{S}(s, {\bf{v}})$ is a Morse family. Suppose that $\delta(s) = -1,$ we have a smooth $3$-dimensional submanifold,

We denote $\pi_{\mathcal{C}_{H^{S}}}$ and the map germ $\Phi_H^{S}:\mathcal{C}_{H^{S}}\longrightarrow T^*S_1^3$ defined by

is a Lagrangian immersion germ. Therefore $H^{S}$ is a generating family of $\Phi_H^{S}(\mathcal{C}_{H^{S}}).$ Let $\pi_2:\mathbb{R}\times S_1^3\longrightarrow S_1^3$ denote the canonical projection and consider the map-germ $\pi_{\mathcal{C}_{H^{S}}}$ which is given by the the restriction of the projection $\pi_2$ to ${\mathcal{C}_{H^{S}}}.$ Thus $\pi_{\mathcal{C}_{H^{S}}}:\mathcal{C}_{H^{S}}\longrightarrow S_1^3$ with $\pi_{\mathcal{C}_{H^{S}}}(s, {\bf{v}}) = {\bf{v}}$ for any $(s, {\bf{v}}) \in \mathcal{C}_{H^{S}}.$ The map $\pi_{\mathcal{C}_{H^{S}}}$ is the catastrophe map of $H^{S}$ and it is a Lagrangian map. Therefore, the corresponding caustic is

and is precisely the bifurcation set of $H^{S},$ i.e. $\mathcal{B}_H^{S} = C(\Phi_H^{S}).$ It follows that for a generic curve, the caustic $C(\Phi_H^{S})$ of $\gamma(s)$ is locally either a regular surface, or has cuspidal edge singularity, or swallowtail. The local models of the caustic at ${\bf{v}}$ corresponding to $s \in I$ depend on the $\mathcal{R}^+$-singularity type of $h_{v}^{S}(s)$ at $s$. For a generic $\gamma(s), \; h_{v}^S(s)$ has local singularities of types $A_1$, $A_2, \; A_3$ or $A_4$. The caustic is a regular surface at an $A_2$-singularity of $h_{v}^S(s).$ It is a cuspidal edge at an $A_3$-singularity of $h_{v}^S(s)$ and has swallowtail singularity at an $A_4$-singularity of $h_{v}^S(s)$. For the case of $\delta(s) = 1,$ we have the similar arguments to the above proof, so that we omit it.

Proof of Theorem 2.1. Proposition 4.3 states that de Sitter focal surfaces are two dimensional caustics which have Lagrangian singularities and the bifurcation set of $H^S (s, {\bf{v}})$ is

This means that the bifurcation set of the de Sitter height function is the image of the first de Sitter focal surface of $\gamma(s).$ It follows from Proposition 3.1 that $h_{v_0}^S$ has the $A_3$ -type singularity (respectively, the $A_4$ -type singularity) at $s_0$ if and only if

$\rho(s_0)\neq 0.$ (respectively,

$\rho(s_0) = 0, \; \rho'(s_0)\neq 0$) By Theorem 4.1 and Proposition 4.2, we have the assertions (2) (respectively, (3)). By Corollary 3.3, this means that the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $4$ for $s = s_0.$ (respectively, the osculating hyperbolic pseudo-sphere $HPS^1 ({\bf{v}}_0, r_0)$ and $\gamma(s)$ have contact of order $5$ for $s = s_0.$) Since the locus of the singularities of $CE$ is locally diffeomorphic to the line, $FDF_\gamma(s, \theta(s))$ is locally diffeomorphic to the line holds (respectively, since the locus of singularities of $SW$ is $C(2, 3, 4),$ $FDF_\gamma(s, \theta(s))$ is locally diffeomorphic to $C(2, 3, 4)$ holds).

For the proof of the Theorem 2.2, we apply Proposition 3.2, Theorem 4.1, Proposition 4.2 similar to the Theorem 2.1. This completes the proof.

5.   Legendrian dualities between focal surfaces and spacelike curves

In this section, we investigate the relationships between de Sitter focal surfaces and spacelike curve by Legendrian dualities ^[11]. Firstly, we introduce the Legendrian dualities between pseudo-spheres in Minkowski space-time which have been proved to be a basic tool for the study of surfaces in pseudo-spheres in Minkowski space. One-forms on $\mathbb{R}_1^4\times \mathbb{R}_1^4$ are defined by $\langle d{\bf{v}}, {\bf{w}} \rangle = -w_0dv_0+\sum_{i = 1}^{3}w_idv_i$ and $\langle {\bf{v}}, d{\bf{w}}\rangle = -v_0dw_0+\sum_{i = 1}^{3}v_idw_i.$ We consider the following three double fibrations.

$(1)\ (a) \ S_{1}^3\times S_{1}^3 \supset \Delta_5 = \{({\bf{v}}, {\bf{w}})\ | \ \langle {\bf{v}}, {\bf{w}}\rangle = 0\},$

$\qquad(b)\ \pi_{11}:\Delta_5\longrightarrow S_{1}^3, \pi_{12}:\Delta_5\longrightarrow S_{1}^3,$

$\qquad (c) \ \theta_{11} = \langle d{\bf{v}}, {\bf{w}}\rangle|_{\Delta_5}, \theta_{12} = \langle {\bf{v}}, d{\bf{w}}\rangle|_{\Delta_5}.$

Here $\pi_{11}({\bf{v}}, {\bf{w}}) = {\bf{v}}, \pi_{12}({\bf{v}}, {\bf{w}}) = {\bf{w}}.$ We remark that $\theta_{11}^{-1}(0)$ and $\theta_{12}^{-1}(0)$ define the same tangent hyperplane field over $\Delta_5$ which is denoted by $K_5.$ The basic duality theorem is that $(\Delta_5, K_5)$ is a contact manifold and both of $\pi_{1j}(j = 1, 2)$ are Legendrian fibrations. If there exists an isotropic mapping $i:L\longrightarrow \Delta_5,$ which means that $i^*\theta_{11} = 0,$ we say that $\pi_{11}(i(L))$ and $\pi_{12}(i(L))$ are $\Delta_5$-dual to each other. It is easy to see that the condition $i^*\theta_{11} = 0$ is equivalent to $i^*\theta_{12} = 0.$ Then we have the following proposition on the relationships among the first de Sitter focal surface, the second de Sitter focal surface, and the spacelike curve with the help of the above Legendrian dualities.

Proposition 5.1. Let $\gamma: I \rightarrow S^3_1$ be a unit speed spacelike curve with $\kappa_g\tau_g(s)\neq 0,$ then we have the following claims.

$\rm(1)$ For the case that $\delta(s) = -1,$ $\gamma(s)$ and $FDF_{ \gamma}(s, \theta)$ are $\Delta_5$-dual to each other, ${\bf{t}}(s)$ and $FDF_{ \gamma}(s, \theta)$ are $\Delta_5$-dual to each other.

$\rm(2)$ For the case that $\delta(s) = 1$ and $\kappa_g(s)\neq 1,$ $\gamma(s)$ and $SDF_{ \gamma}(s, \theta)$ are $\Delta_5$-dual to each other, ${\bf{t}}(s)$ and $SDF_{ \gamma}(s, \theta)$ are $\Delta_5$-dual to each other.

Proof. (1) Consider the mapping $\mathfrak{L}_{11}(s, \theta) = (FDF_{ \gamma}(s, \theta), \gamma(s))$ and $\mathfrak{L}_{12}(s, \theta) = (FDF_{ \gamma}(s, \theta), {\bf{t}}(s)).$ Then we have $\langle FDF_{ \gamma}(s, \theta), \gamma(s)\rangle = 0, \; \langle FDF_{ \gamma}(s, \theta), {\bf{t}}(s)\rangle = 0$ and

The assertion (1) holds.

(2) Using the same computation as the proof of (A), we consider the mapping $\mathfrak{L}_{21}(s, \theta) = (SDF_{ \gamma}(s, \theta), \gamma(s))$ and $\mathfrak{L}_{22}(s, \theta) = (SDF_{ \gamma}(s, \theta), {\bf{t}}(s)).$ Then we have $\langle SDF_{ \gamma}(s, \theta), \gamma(s)\rangle = 0, \; \langle SDF_{ \gamma}(s, \theta), {\bf{t}}(s)\rangle = 0.$ When $\kappa_g(s) > 1,$

When $0 < \kappa_g(s) < 1,$

In conclusion, the assertion (2) holds.

6.   Examples

In order to better illustrate the main results, we give three examples that consist of de Sitter focal surfaces.

Example 6.1 Let $\gamma(s)$ be a unit speed spacelike curve on $S_1^3$ defined by

with respect to an arclength parameter $s,$ where $s\in (0.5, 1.4)$.

We get that $\langle{\bf{t}}'(s), {\bf{t}}'(s)\rangle = \frac{8}{9}(\cos({\frac{\sqrt{3}}{3}}s))^2+\frac{1}{9}\neq 1,$ $\kappa_g(s) = \frac{2}{3}\sqrt{8(\cos({\frac{\sqrt{3}}{3}}s))^2-2},$

and ${\bf{n}}(s) = (n_1(s), n_2(s), n_3(s), n_4(s)),$ where

Thus, we can get $\delta(s) = -1,$ the first de Sitter focal surface $FDF_\gamma(s, \theta)$ and the singular locus of the first de Sitter focal surface $SFDF_\gamma(s).$ We see that $\rho(s) = 0$ for $s = 1.360349523, \; \rho'(s) = 0$ for $s = 0.5113872103.$ Hence, we have that the first de Sitter focal surface $FDF_\gamma(s, \theta)$ is locally diffeomorphic to cuspidal edge at its singular points and the singular locus of the first de Sitter focal surface $SFDF_\gamma(s)$ is locally diffeomorphic to a line for $s\neq 1.360349523.$ The first de Sitter focal surface of spacelike curve $FDF_\gamma(s, \theta)$ is locally diffeomorphic to the $SW$ at its singular points and the singular locus of the first de Sitter focal surface $SFDF_\gamma(s)$ is locally diffeomorphic to the $(2, 3, 4)-$cusp for $s\neq 0.5113872103.$

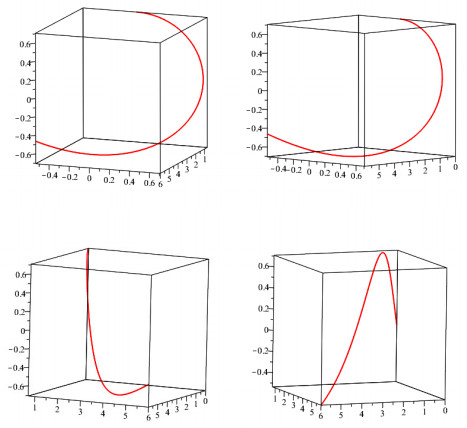
Example 6.2. Let $\gamma(s)$ be a unit speed spacelike curve on $S_1^3$ defined by

with respect to an arclength parameter $s$. We draw the pictures of the spacelike curve $\gamma$, by projecting them into three-dimensional spaces, see Figure 2. Then we get that $\langle{\bf{t}}'(s), {\bf{t}}'(s)\rangle = 10\neq 1,$ $\kappa_g(s) = 3$ and $\tau_g(s) = 2\sqrt{2}.$ Thus, we can get $\rho(s) = 144\sqrt{2}.$ We obtain one of normal vector ${\bf{n}}(s)$ which is given by

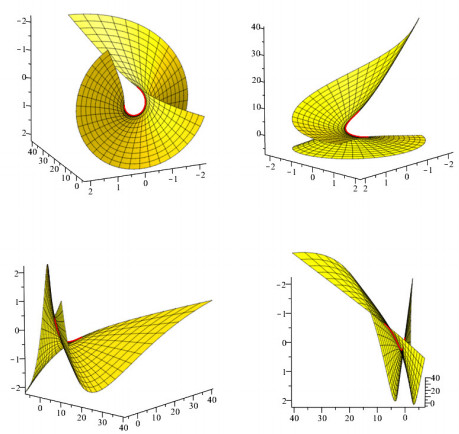
It is easy to get $\delta(s) = -1.$ Let $\sinh(\theta) = u, \ \cosh(\theta) = \sqrt{1+u^2}.$ Thus, the first de Sitter focal surface is given by

and we obtain the vector parametric equations of the singular locus of the first de Sitter focal surface as follow:

where

We see that $\rho(s) = 144\sqrt{2}\neq 0$ for arbitrary real numbers $s > 0.$ Hence, we have that the first de Sitter focal surface $FDF_\gamma(u, s)$ is locally diffeomorphic to cuspidal edge at its singular points and the singular locus of the first de Sitter focal surface $SFDF_\gamma(s)$ is locally difeomorphic to a line. The structure of the spacelike curve $\gamma$ and the focal surface is not easily imagined but it is possible to project them into three-dimensional spaces. We draw the pictures of the spacelike curve $\gamma$, the focal surface and its singular locus by projecting them into three-dimensional spaces, see Figure 2 and Figure 3.

Example 6.3. Let $\gamma(s)$ be a unit speed spacelike curve on $S_1^3$ defined by

where the arclength parameter $s \in (0, 2).$ Furthermore, the tangent vector

Then we get that $\langle{\bf{t}}'(s), {\bf{t}}'(s)\rangle = -\frac{1}{8}\neq 1,$ $\kappa_g(s) = \frac{3}{4}\sqrt{2}$ and $\tau_g(s) = -\frac{\sqrt{2}}{4}.$ Subsequently, it can be examined that $\rho(s) = -\frac{9\sqrt{2}}{256}.$ It is calculated that the timelike normal vector ${\bf{n}}(s)$ which is given by

So, we can get $\delta(s) = 1,$ we calculate the other normal vector

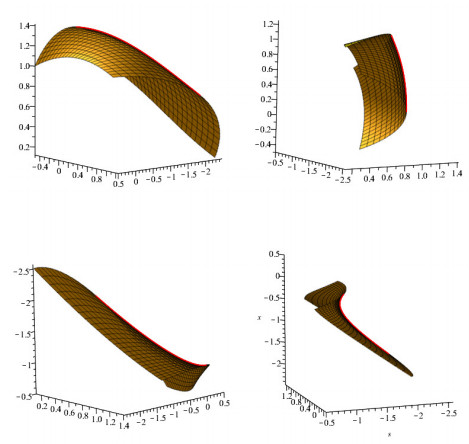
Moreover, the second de Sitter focal surface is formulated as

where

In addition, we obtain the vector parametric equations of the singular locus of the second de Sitter focal surface as follow:

Noticing that $\rho(s) = -\frac{9\sqrt{2}}{256}\neq 0$ for arbitrary real numbers $s > 0.$ Hence, we have that the second de Sitter focal surface $SDF_\gamma(s, \theta)$ is locally difeomorphic to cuspidal edge at its singular points and the singular locus of the second de Sitter focal surface $SSDF_\gamma(s)$ is locally difeomorphic to a line. We draw the projection of the image of the second de Sitter focal surface $SDF_\gamma(s, \theta)$ (in orange) and its critical value set $SSDF_\gamma(s)$ (in red) to three-dimensional spaces (see Figure 4).

Acknowledgments

The authors would like to appreciate the reviewers for their comments and suggestions, which are very helpful to improve the manuscript.

This research was funded by the Reform and Development Foundation for Local Colleges and Universities of the Central Government, (Excellent Young Talents project of Heilongjiang Province, Grant No. ZYQN2019071) and the Project of Science and Technology of Heilongjiang Provincial Education Department (Grant No. 1354ZD008).

Conflict of interest

The authors declare that there is no conflicts of interests in this work.