The developable surfaces with pointwise 1-type Gauss map of Frenet type framed base curves in Euclidean 3-space

1.   Introduction

In the late 1970s, the concept of finite-type submanifold was developed by Chen in Euclidean and semi-Euclidean spaces and this finite-type concept was later extended to differentiable maps defined on submanifolds. Thus, the finite-type Gauss map concept, which is very useful in classifying surfaces, was developed ^[1,2,3]. Chen and Piccinni presented a general study on the submanifolds of Euclidean spaces with finite-type Gauss map and formed the basis of the theory of submanifolds with finite-type Gauss map and classified compact surfaces with a 1-type Gauss map ^[4]. The ruled surfaces with a finite-type Gauss map have been studied by many researchers in Euclidean space ^[5,6,7,8]. In addition, pointwise 1-type Gauss maps of Darboux ruled surfaces, which are one of the special ruled surfaces, were examined and classified in the study ^[9].

Although the moving frame of a regular space curve has been generally taken into consideration in these studies on surfaces, it is known that an arbitrary curve can also have singular points. However, the moving frame of a space curve cannot be defined at points where the first derivative of the curve is zero. In other words, the Frenet frame cannot be defined at any singular point of a space curve. Due to this reason, our study considers curves that may have some singular points to make a difference from the previous research and present a wider perspective for new research.

Framed curves were introduced to generalize regular curves with the linear independent condition and Legendre curves in the unit tangent bundle in ^[10]. The basic concepts related to the framed curves and the existence and uniqueness conditions of the framed curve have been explored extensively in studies ^[11,12,13]. Moreover, the framed surfaces were investigated using curves with singular points. A framed surface in Euclidean space is a smooth surface with a moving frame. It is also a generalization of not only regular surfaces but also frontals at least locally. So, the framed surfaces may have singularities ^[14,15]. In recent years, some of the latest connected studies can be seen in ^{[16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]}. The Gauss maps of the ruled developable surfaces have been investigated in previous studies, but the Gauss map of ruled developable surfaces with singular points has not been studied. For this reason, unlike the above studies, we want to contribute to the scientific world by investigating the Gauss map of ruled developable surfaces with singular points in our study and to form a basis for new research.

In this study, we investigate the tangent developable surface, the focal developable surface, and the rectifying developable surface with a pointwise 1- type Gauss map of the Frenet-type framed base (Ftfb) curve. Also, the graphs of some of these types of sample surfaces are drawn.

2.   Geometric concepts associated with Gauss map and framed curve in Euclidean 3-space

Let $\sigma: I \to {{{\mathbb{R}}^{3}}}$ be a smooth space curve with singular points in Euclidean 3-space and ${\Delta _2}$ be a 3-dimensional smooth manifold, then ${\Delta _2}$ is denoted by

Let $\mu = \left({{\mu _{1, }}{\mu _2}} \right) \in {\Delta _2}$, then the unit vector $\upsilon$ is defined as $\upsilon = {\mu _1} \wedge {\mu _2}$ ^[10].

Definition 2.1. $\left({\sigma, \mu } \right):I \to {{{\mathbb{R}}^{3}}} \times {\Delta _2}$ is called framed curve if $\langle {\sigma '\left(y \right), {\mu _1}\left(y \right)} \rangle = \langle {\sigma '\left(y \right), {\mu _2}\left(y \right)} \rangle = 0$ for each $y \in I$. Also, $\sigma :I \to {{{\mathbb{R}}^{3}}}$ is a framed base curve if there exists $\mu :I \to {\Delta _2}$ such that $\left({\sigma, \mu } \right)$ is a framed curve ^[10].

Let $\left({\sigma, {\mu _1}, {\mu _2}} \right):I \to {{{\mathbb{R}}^{3}}} \times {\Delta _2}$ be a framed curve and $\upsilon = {\mu _1} \wedge {\mu _2}$. Then we can write the Frenet-Serret type formula of the framed curve as follows:

where $l\left(y \right) = \langle {{{\mu '}_1}\left(y \right), {\mu _2}\left(y \right)} \rangle$, $m\left(y \right) = \langle {{{\mu '}_1}\left(y \right), \upsilon \left(y \right)} \rangle$ and $n\left(y \right) = \langle {{{\mu '}_2}\left(y \right), \upsilon \left(y \right)} \rangle$ ^[10]. Also, there exists a smooth mapping $\alpha: I \to {\mathbb{R}}$ such that

and $\alpha \left({{y_0}} \right) = 0$ if and only if ${y_0}$ is a singular point of the curve $\sigma$. In addition, the functions $\left\{ {l\left(y \right), m\left(y \right), n\left(y \right), \alpha \left(y \right)} \right\}$ are called the curvatures of the framed curve $\sigma$. If $m\left(y \right) = n\left(y \right) = 0$, then $\upsilon '\left(y \right) = 0$. The case $\upsilon '\left(y \right) \ne 0$ is assumed in this article. If the curve $\sigma$ has a singular point, then the Frenet frame cannot be constructed along the curve $\sigma$. But under a certain condition, one can define Frenet type frame along $\sigma$.

Definition 2.2. $\sigma :I \to {{{\mathbb{R}}^{3}}}$ is called Frenet type framed base (Ftfb) curve, if there exists a regular curve $T:I \to {S^2}$ and a smooth function $\alpha :I \to {\mathbb{R}}$ such that $\sigma '\left(y \right) = \alpha \left(y \right)T\left(y \right)$ for each $y \in I$. Then, we call $T\left(y \right)$ as the unit tangent vector and $\alpha \left(y \right)$ as a speed function of $\sigma \left(y \right)$ ^[18].

$T\left(y \right)$, $N\left(y \right) = \frac{{T'\left(y \right)}}{{\left\| {T'\left(y \right)} \right\|}}$ and $B\left(y \right) = T\left(y \right) \wedge N\left(y \right)$ are unit tangent vector, unit principal normal vector and unit binormal vector of the curve $\sigma \left(y \right)$ with singular point, respectively. Then there exists an orthonormal frame $\left\{ {T\left(y \right), N\left(y \right), B\left(y \right)} \right\}$. This frame is called the Frenet type frame along $\sigma$ and we can give the Frenet type framed formula as follows:

where $\kappa \left(y \right) = \left\| {T'\left(y \right)} \right\|$ and $\tau \left(y \right) = \frac{{\det \left({T\left(y \right), T'\left(y \right), T''\left(y \right)} \right)}}{{{{\left\| {T'\left(y \right)} \right\|}^2}}}$ are the curvature and the torsion of the Ftfb curve $\sigma$, respectively. From here, we can say that $\sigma$ is a framed base curve. Moreover, $\left\{ {\sigma, N, B} \right\}$ is a framed curve with the curvature $\left\{ {\tau \left(y \right), - \kappa \left(y \right), 0, \alpha \left(y \right)} \right\}$.

Let $M:X = X\left({y, u} \right)$ be a surface in Euclidean 3-space. It is well-known that, the Gauss map of a surface $M$ carries the unit normal vector at any point $p$ on the surface $M$ to the center of ${S^2}$ which denotes the unit sphere centered at the origin. Denoting the Gauss map of a surface $M$ with $\Omega$, then it is defined as

where "$\wedge$" denotes the cross product of two vectors, ${X_y} = \frac{{\partial X}}{{\partial y}}$ and ${X_u} = \frac{{\partial X}}{{\partial u}}$ are the first order partial derivatives according to the parameters of $X$.

Let ${g_{ij}} = \langle {\frac{{\partial X}}{{\partial {x_i}}}, \frac{{\partial X}}{{\partial {x_j}}}} \rangle, \left({1 \le i, j \le 2} \right)$ be an induced metric on the surface $M$. Then the Laplacian operator $\Delta$ with respect to the induced metric on $M$ is defined as

where ${x_{i}}$ $\left({1 \le i \le 2} \right)$ are the local coordinates on $M$. Moreover, the matrices $\left({{g_{ij}}} \right)$ and the inverse matrix $\left({{g^{ij}}} \right)$ of $\left({{g_{ij}}} \right)$ are defined as ${g_{ij}} = \left({\begin{array}{*{20}{c}} {{g_{11}}} & {{g_{12}}}\\ {{g_{21}}} & {{g_{22}}} \end{array}} \right)$ and ${g^{ij}} = \frac{1}{{\det \left({{g_{ij}}} \right)}}\left({\begin{array}{*{20}{c}} {{g_{22}}} & { - {g_{12}}}\\ { - {g_{21}}} & {{g_{11}}} \end{array}} \right)$, respectively. Also, $g = \det \left({{g_{ij}}} \right)$ denotes the determinant of the matrix $\left({{g_{ij}}} \right)$.

Let $M$ be a surface in Euclidean 3-space. The Gauss map $\Omega$ of $M$ is 1–type Gauss map if and only if the Gauss map $\Omega$ is to satisfy the equation $\Delta \Omega = \lambda \left({\Omega + C} \right)$ for a non-zero real constant $\lambda$ and constant vector $C$ ^[11]. With the studies carried out over time, it has been observed that the Gauss maps of some surfaces such as helicoids and catenoids in $E^3$ provide this equality for a regular function $f$, not for a constant $\lambda$. This situation led to the emergence of the concept called the Gauss map, which is a pointwise 1-type. If the Gauss map $\Omega$ of a surface $M$ in $E^3$ satisfies the equation $\Delta \Omega = f\left({\Omega + C} \right)$ for a regular function $f$ and a constant vector $C$. Then, this map is called the pointwise 1-type Gauss map ^[7,11]. If the constant vector $C = 0$, the pointwise 1-type Gauss map is called the first kind, otherwise, the second kind. On the other hand, if $\Delta \Omega = 0$ it is called that the surface $M$ has a harmonic Gauss map, see details in ^[8].

3.   The developable surfaces with pointwise 1-type Gauss map of Frenet type framed base curves

In this section, we study the tangent developable surface, focal developable surface, and rectifying developable surface with the Ftfb curve. These surfaces are classified via their pointwise 1-type Gauss maps and the examples of these surfaces are also illustrated.

Note that, the curvature of the Ftfb curve has to be non-zero, otherwise, at the construction of the Frenet type frame along the Ftfb curve, the normal, accordingly, binormal vectors are undefined.

3.1.   The tangent developable surface with pointwise 1- type Gauss map of Frenet type framed base curves

Let ${M_1}$ be a tangent developable surface associated with the Ftfb curve $\sigma :I \to {{{\mathbb{R}}^{3}}}$ and $\left\{ {T, N, B} \right\}$ be the Frenet type frame of $\sigma$ such that $\sigma '\left(y \right) = \alpha \left(y \right)T\left(y \right)$ and $\alpha \left(y \right)$ be the speed function of $\sigma \left(y \right)$ for all $y \in I$, then the parametric equation of the tangent developable surface associated with the Ftfb curve can be written as follows:

Here, the curve $\sigma \left(y \right)$ and the vector field $T\left(y \right)$ are called the base curve and the director curve or director vector of the surface, respectively ^[14]. The first order partial derivatives with respect to parameters $y$ and $u$ of the surface defined by (3.1) are found as

The Gauss map of the tangent developable surface ${M_1}$ parameterized by (3.1) is given by

For the matrix $\left({{g_{ij}}} \right)$ consisting of the components of the metric on the tangent developable surface ${M_1}$, we denote by $g$ and $\left({{g^{ij}}} \right)$ the determinant and the inverse matrix of the matrix $\left({{g_{ij}}} \right)$, respectively. In this case, we can easily find that

Therefore, the formula of the Laplacian $\Delta$ on the surface ${M_1}$ is given in terms of $y$ and $u$ by

Now, let's apply the Laplace operator $\Delta$ to the Gauss map $\Omega$. If the derivatives of the Gauss map ${\Omega _y}$, ${\Omega _{yy}}$, ${\Omega _u}$, ${\Omega _{uu}}$ and ${\Omega _{yu}}$ are calculated and the derivatives of the Gauss map are substituted in Eq (3.2), then we get

From this last equation, we have $\tau = 0$ if and only if $\Delta \Omega = 0$. In this case, we can give the following Theorem.

Theorem 3.1. Let ${M_1}$ be a tangent developable surface associated with the Ftfb curve, then the surface ${M_1}$ has a harmonic Gauss map if and only if the Ftfb curve $\sigma$ is a plane curve.

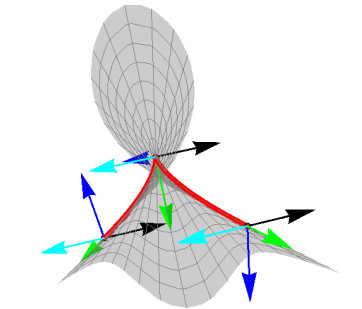
Example 3.1. Let ${M_1}$ be a tangent developable surface associated with the Ftfb curve $\sigma: R \to {{{\mathbb{R}}^{3}}}$ defined by the parametric equation

The curve $\sigma$ has a singular point at $y = 0$, so this curve is not a Frenet curve. The curve $\sigma$ is a Ftfb curve with the mapping $\left({T, \alpha } \right):R \to {S^2} \times R$. Then

and

are the unit tangent vector and the speed function of $\sigma$, respectively. By making the necessary calculations, the normal, the binormal vectors, the curvature, and the torsion of the curve $\sigma$ are found as follows, respectively

Consequently, the tangent developable surface associated with the Ftfb curve is parametric by

Hence,

As the fact that, the tangent developable surface $X\left({y, u} \right)$ has harmonic Gauss map, see Figure 1.

3.2.   The focal developable surface with pointwise 1-type Gauss map of the Frenet type framed base curves

Let ${M_2}$ be a focal developable surface associated with the Ftfb curve and $\sigma :I \to {{{\mathbb{R}}^{3}}}$ be a Ftfb curve with Frenet type frame $\left\{ {T, N, B} \right\}$ such that $\sigma '\left(y \right) = \alpha \left(y \right)T\left(y \right)$ and $\alpha \left(y \right)$ is the speed function of $\sigma \left(y \right)$ for all $y \in I$, then the parametric equation of the focal developable surface can be written as following:

where $N$ and $B$ are the principal normal vector and binormal vector of the curve $\sigma$, respectively ^[14]. The first order partial derivatives with respect to parameters $y$ and $u$ of the surface $M_2$ are found as

where $\eta \left(y \right) = \frac{{\alpha \left(y \right)}}{{\kappa \left(y \right)}}$. The Gauss map of the focal developable surface $M_2$ parameterized by (3.3) is given by

at the points satisfying $\eta ' - u\tau \ne 0$. Considering the matrix $\left({{g_{ij}}} \right)$ consisting of the components of the metric on the surface $M_2$, we can express the matrix $\left({{g_{ij}}} \right)$, the determinant $g$ and the inverse matrix $\left({{g^{ij}}} \right)$ of the matrix $\left({{g_{ij}}} \right)$ as

and

respectively. Therefore, the formula of the Laplacian $\Delta$ on the surface ${M_2}$ is found as

Now, let's apply the Laplace operator $\Delta$ to the Gauss map $\Omega$. If the partial derivatives of the Gauss map ${\Omega _y}$, ${\Omega _{yy}}$, ${\Omega _u}$, ${\Omega _{uu}}$ and ${\Omega _{yu}}$ are found and these are substituted in Eq (3.4), then we get

Theorem 3.2. Let ${M_2}$ be a focal developable surface associated with the Ftfb curve, then the surface ${M_2}$ has pointwise 1-type Gauss map of the first kind if and only if $\kappa \eta '$ is constant and Ftfb curve is planar.

Proof. Let ${M_2}$ have pointwise 1-type Gauss map of the first kind, the following conditions are satisfied:

and

The first condition is always true. For the second one, by considering $N$ and $B$ are linearly independent, we obtain

and

Solving these equations, we get that $\kappa \eta '$ is constant and $\tau = 0$.

The sufficiency is obviously proven by substituting $\kappa \eta '$ is constant and $\tau = 0$ in Eq (3.5).

As a result, we can give the following corollary.

Corollary 3.1. Let ${M_2}$ be a focal developable surface with pointwise 1-type Gauss map of the first kind, then the following equality is satisfied:

Example 3.2. Let $M_2$ be a focal developable surface associated with the Ftfb curve $\sigma: {\mathbb{R}} \to {{{\mathbb{R}}^{3}}}$ defined by the parametric equation

The curve $\sigma$ has a singular point at $y = -1$, so this curve is not a Frenet curve. The curve $\sigma$ is a Ftfb curve with the mapping $\left({T, \alpha } \right):{\mathbb{R}} \to {S^2} \times {\mathbb{R}};$

The normal and binormal vector of the curve $\sigma$ are obtained as

Also, the curvature and torsion of the curve $\sigma$ are

Consequently, the focal developable surface associated with the Ftfb curve is parameterized as

Hence,

Therefore, the Gauss map $\Omega$ has pointwise 1-type of the first kind, see Figure 2.

3.3.   The rectifying developable surface with pointwise 1- type Gauss map of Frenet type framed base curves

Let ${M_3}$ be a rectifying developable surface associated with the Ftfb curve and $\sigma :I \to {{{\mathbb{R}}^{3}}}$ be a Ftfb curve with Frenet type frame $\left\{ {T, N, B} \right\}$ such that $\sigma '\left(y \right) = \alpha \left(y \right)T\left(y \right)$ and $\alpha \left(y \right)$ is a speed function of $\sigma \left(y \right)$ for all $y \in I$, then the parametric equation of the rectifying developable surface ${M_3}$ can be written as following:

where $T$ and $B$ are unit tangent vector and binormal vector of the Ftfb curve $\sigma$, respectively ^[14,18]. The first order partial derivatives with respect to parameters $y$ and $u$ of the surface $M_3$ are found as

where ${\delta ^2} = {\kappa ^2} + {\tau ^2}$ and $\rho = \tau \kappa ' - \kappa \tau '$.

At the points satisfying $\frac{{\alpha \kappa }}{\delta } + u\frac{\rho }{{{\delta ^2}}} \ne 0$, the Gauss map of the rectifying developable surface $M_3$ parameterized by (3.6) is given by

Considering the matrix $\left({{g_{ij}}} \right)$ consisting of the components of the metric on the surface $M_3$, we can easily find the matrix $\left({{g_{ij}}} \right)$, the determinant $g$ and the inverse matrix $\left({{g^{ij}}} \right)$ of the matrix $\left({{g_{ij}}} \right)$ as

and

where $h = {\left({\alpha - \frac{{u\kappa \rho }}{{{\delta ^3}}}} \right)^2} + \frac{{{u^2}{\rho ^2}{\tau ^2}}}{{{\delta ^6}}}$. Therefore, the formula of the Laplacian $\Delta$ on the surface ${M_3}$ is calculated as

where ${h_y} = \frac{{\partial h}}{{\partial y}}$ and ${h_u} = \frac{{\partial h}}{{\partial u}}$ are given by

and

respectively. Now, let's apply the Laplace operator $\Delta$ to the Gauss map of the surface $M_3$. If the partial derivatives of the Gauss map ${\Omega _y}$, ${\Omega _{yy}}$, ${\Omega _u}$, ${\Omega _{uu}}$ and ${\Omega _{yu}}$ are calculated and these are substituted in Eq (3.7), then we get

Theorem 3.3. Let $M_3$ be a rectifying developable surface of the Ftfb curve with the Frenet type frame $\left\{ {T, N, B} \right\}$, then the surface $M_3$ has pointwise 1-type Gauss map of the first kind if and only if the Ftfb curve is a helix.

Proof. Let the Gauss map be pointwise 1-type map of the first kind, it requires the following conditions:

which is obviously satisfied, and

Since $T$ and $B$ are linearly independent, we obtain

and

If the first and second equations are multiplied by $\tau$ and $\kappa$, respectively, and then they are added, it is found

Since $\delta \ne 0$ and $\left({h{\delta ^2} - {\alpha ^2}{\tau ^2}} \right) \ne 0$, we get $\frac{\kappa }{\tau }$ is constant which means that the curve is framed helix.

For the sufficient condition, if the Ftfb curve is a framed helix, then $\frac{\kappa }{\tau }$ is constant. Thus, $\kappa '\tau - \kappa \tau ' = 0$ requires $\rho$ to vanish, that is, $h = \alpha$. From (3.8), we see that the Gauss map is pointwise 1-type map of the first kind.

Equation (3.8) gives us the following corollary.

Corollary 3.2. Let ${M_3}$ be a rectifying developable surface with pointwise 1-type Gauss map of the first kind, then the following equality

is satisfied at non-singular points where $\alpha \ne 0$.

Example 3.3. Let's investigate the Gauss map the rectifying developable surface associated with the Ftfb curve $\sigma :\left[{0, 2\pi } \right) \to {{{\mathbb{R}}^{3}}}$ defined by the parametric equation

The curve $\sigma$ has singular points at $y = 0, \frac{\pi }{2}, \pi, \frac{{3\pi }}{2}$, so this curve is not a Frenet curve. The curve $\sigma$ is a Ftfb curve with the mapping $\left({T, \alpha } \right):{\mathbb{R}} \to {S^2} \times {\mathbb{R}};$

By calculations, we get the normal, binormal vectors, the curvature and the torsion of the curve $\sigma$ are, respectively, obtained as

Consequently, the rectifying developable surface associated with the Ftfb curve is parametric by

Hence, the Gauss map is found as

where $y \ne 0, \frac{\pi }{2}, \pi, \frac{{3\pi }}{2}$. Obviously, it is seen that the pointwise 1-type Gauss map is first kind, see Figure 3.

4.   Conclusions

In this study, unlike other studies, we have examined developable surfaces with pointwise 1-type Gauss map constructed by curves with singular points in Euclidean 3-space. The tangent, focal, and rectifying developable surfaces of the Ftfb curve were studied in ^[14,16,18]. As a contribution to them, we have studied these surfaces with a pointwise 1-type Gauss map. In addition, we have obtained their characterizations to be the first kind or harmonic. The examples of obtained results have been illustrated in detail for each type of surface.

Acknowledgments

We gratefully acknowledge the constructive comments from the editor and the anonymous referees. This work was funded by National Natural Science Foundation of China (Grant No. 12101168), Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ22A010014).

Conflict of interest

The authors declare no conflict of interest.