Spacelike ruled surfaces with stationary Disteli-axis

1.   Introduction

A ruled surface is a surface which can be generated by the movement of an oriented line along a space curve. The significance of the ruled surface lies in the fact that it is utilized in numerous areas of manufacturing and engineering, including the modeling of apparel, automobile components and ship hulls (see e.g., ^[1,2,3,4]). One of the most convenient methods to consider the movement of line space seems to establish a relationship among this space and dual numbers. According to the E. Study map in screw and dual number algebra, the set of all oriented lines in Euclidean 3-space $\mathbb{E}^{3}$ is immediately connected to the set of points on the dual unit sphere in the dual 3-space $\mathbb{D}^{3}$ ^[1,2,3]. More specifics on the necessary fundamental definitions of the dual elements and the relationship among ruled surfaces and one-parameter dual spherical movements can be found in ^[3,4,5,6,7].

In Minkowski 3-space $\mathbb{E}_{1}^{3}$ the research of ruled surfaces is more motivating than the Euclidean situation, as Lorentzian distance can be negative, positive or zero whereas the Euclidean distance can only be positive. Then, if we take the Minkowski 3-space $\mathbb{E}_{1}^{3}$ as an alternative of the Euclidean 3-space $\mathbb{E}^{3}$ the E. Study map can be given as The timelike (spacelike) oriented lines with the timelike (spacelike) dual points on a hyperbolic (Lorentzian) dual unit sphere in the Lorentzian Dual 3-space $\mathbb{D}_{1}^{3}$. It means that a regular curve on $\mathbb{H}_{+}^{2}$ appears as a timelike ruled surface at $\mathbb{E}_{1}^{3}$. Similarly the spacelike (timelike) curve on $\mathbb{S}_{1}^{2}$ appears as a timelike (spacelike) ruled surface at $\mathbb{E}_{1}^{3}$. In view of its relationships with engineering, and those with physical sciences in Minkowski space, many geometers and engineers have studied and gained many ownerships of the ruled surfaces (see ^{[8,9,10,11,12,13,14]}).

This work is an approach for constructing spacelike ruled surfaces with a stationary spacelike Disteli-axis by using the E. Study map. Then, we define and study the kinematic geometry of a spacelike Plücker conoid generated by the spacelike Disteli-axis. In addition, we give some necessary and sufficient conditions to have constant spacelike dual angles with respect to a constant spacelike Disteli-axis and we discuss some special cases which lead to some special spacelike ruled surfaces such as the general spacelike surface, the spacelike helicoidal surface and the spacelike cone.

2.   Preliminaries

In this section, we give a short summary of the theory of dual numbers and dual Lorentzian vectors. (see ^{[1,2,3,4,5,6,7,9,10,11,12,13,14,15,16,17]}). If $x\;$and $x^{\ast }$ are real numbers, the number $\widehat{x} = x+\varepsilon x^{\ast }$ is named a dual number. Here $\varepsilon$ is a dual unit subject to $\varepsilon \neq 0, \; \varepsilon ^{2} = 0, \, \varepsilon.1 = 1.\varepsilon = \varepsilon.$ The set of dual numbers, $\mathbb{D}$, creates a commutative ring that have the numbers $\varepsilon x^{\ast }(x^{\ast }\in \mathbb{R}$) as divisors of zero, not a field. No number $\varepsilon x^{\ast }$ has an inverse in the algebra. But, the other lows of the algebra of dual numbers are the same as those of the complex numbers. Then, the set

together with the Lorentzian scalar product

forms the dual Lorentzian 3-space $\mathbb{D}_{1}^{3}$. This yields

where $\widehat{{\bf f}}_{1}$, $\widehat{{\bf f}}_{2}$ and $\widehat{ {\bf f}}_{3}$ the dual base at the origin point $\widehat{{\bf 0}} \left(0, 0, 0\right)$ of the dual Lorentzian 3-space $\mathbb{D}_{1}^{3}$. Then, a dual point $\widehat{x} = (\widehat{x}_{1}, \widehat{x}_{2}, \widehat{x} _{3})^{t}$ has the coordinates $\widehat{x}_{i} = (x_{i}+\varepsilon x_{i}^{\ast })\in \mathbb{D}$. If ${\bf x}\neq {\bf 0}$ the norm $\left\Vert \widehat{{\bf x}}\right\Vert$ of $\widehat{{\bf x}}$ is defined by

then, the vector $\widehat{{\bf x}}$ is named a spacelike (timelike) dual unit vector if $\left\Vert \widehat{{\bf x}}\right\Vert ^{2}{\bf = }1$ ($\left\Vert \widehat{{\bf x}}\right\Vert ^{2}{\bf = -}1$). It is evident that

The six components $x_{i}, x_{i}^{\ast }\, (i = 1, 2, 3)$ of ${\bf x}\;$and ${\bf x}^{\ast }$ are named the normed Plücker coordinates of the line. The hyperbolic and Lorentzian (de Sitter space) dual unit spheres are

and

respectively. Hence, the E. Study's map can be stated as follows: The dual unit spheres are shaped as a pair of conjugate hyperboloids. The common asymptotic cone represents the set of null lines, the ring shaped hyperboloid represents the set of spacelike lines and the oval shaped hyperboloid forms the set of timelike lines opposite points of each hyperboloid represent the pair of opposite vectors on a line (see Figure 1). Consequently, a timelike ruled surface is then a regular curve on $\mathbb{H} _{+}^{2}$, and a timelike (or spacelike) ruled surface is a regular curve on $\mathbb{S}_{1}^{2}$.

Definition 1. For any two non-null dual vectors $\widehat{ {\bf x}}$ and $\widehat{{\bf y}}$ in $\mathbb{D}_{1}^{3}$, we have the following basic relations ^{[9,10,11,12,13]}:

i) Let $\widehat{{\bf x}}$ and $\widehat{{\bf y}}$ two spacelike dual vectors

● If they span a spacelike dual plane, there is a unique dual number $\widehat{\varphi } = \varphi +\varepsilon \varphi ^{\ast }$; $0\leq \varphi \leq \pi$ and $\varphi ^{\ast }\in \mathbb{R}$ such that $< \widehat{{\bf x}}, \widehat{{\bf y}} > = \left\Vert \widehat{ {\bf x}}\right\Vert \left\Vert \widehat{{\bf y}}\right\Vert \cos \widehat{\varphi }$. This number is named the spacelike dual angle between $\widehat{{\bf x}}$ and $\widehat{{\bf y}}$.

● If they span a timelike dual plane, there is a unique dual number $\widehat{\varphi } = \varphi +\varepsilon \varphi ^{\ast }\geq 0$ such that $< \widehat{{\bf x}}, \widehat{{\bf y}} > = \epsilon \left\Vert \widehat{ {\bf x}}\right\Vert \left\Vert \widehat{{\bf y}}\right\Vert \cosh \widehat{\varphi }$, where $\epsilon = +1$ or $\epsilon = -1$ via $sign(\widehat{x}_{2}) = sign(\widehat{y}_{2})$ or $sign(\widehat{x}_{2})\neq sign(\widehat{y}_{2})$, respectively. This number is named the central dual angle between $\widehat{x}$ and $\widehat{{\bf y}}$.

ii) Let $\widehat{{\bf x}}$ and $\widehat{{\bf y}}$ two timelike dual vectors, there is a unique dual number $\widehat{\varphi } = \varphi +\varepsilon \varphi ^{\ast }\geq 0$ such that $< \widehat{{\bf x}}, \widehat{{\bf y}} > = \epsilon \left\Vert \widehat{{\bf x}}\right\Vert \left\Vert \widehat{{\bf y}}\right\Vert \cosh \widehat{\varphi }$, where $\epsilon = +1$ or $\epsilon = -1$ via $\widehat{x}$ and $\widehat{{\bf y}}$ have different or the same time orientation, respectively. This dual number is named the Lorentzian timelike dual angle between $\widehat{x}$ and $\widehat{{\bf y}}$.

iii) If $\widehat{{\bf x}}$ is spacelike dual and $\widehat{{\bf y}}$ is timelike dual, then there is a unique dual number $\widehat{\varphi } = \varphi +\varepsilon \varphi ^{\ast }\geq$ 0 such that $< \widehat{{\bf x }}, \widehat{{\bf y}} > = \epsilon \left\Vert \widehat{{\bf x}}\right\Vert \left\Vert \widehat{{\bf y}}\right\Vert \sinh \widehat{\varphi }$, where $\epsilon = +1$ or $\epsilon = -1$ via $sign(\widehat{x}_{2}) = sign(\widehat{y} _{1})$ or $sign(\widehat{x}_{2})\neq sign(\widehat{y}_{1})$. This number is named the Lorentzian timelike dual angle between $\widehat{x}$ and $\widehat{ {\bf y}}$.

Definition 2. A set of non-null oriented lines $\widehat{ {\bf a}} = ({\bf a, a}^{\ast })\in \mathbb{E}_{1}^{3}$ satisfying

where $\left\Vert \widehat{{\bf x}}\right\Vert ^{2}{\bf = }1\, (\left\Vert \widehat{{\bf x}}\right\Vert ^{2}{\bf = -}1$) is referred to as a spacelike (timelike) line complex when $< {\bf x}, {\bf x}^{\ast } > \neq 0$ is a spacelike (timelike) singular line complex when ${\bf < x}^{\ast }{\bf, x > = }0$$\;$and ${\bf \left\Vert \widehat{x}\right\Vert ^{2} = \pm }1$.

Geometrically, a non-null singular line complex is a set of all non-null lines $\widehat{{\bf a}} = ({\bf a, a}^{\ast })$ intersecting the non-null line $\widehat{{\bf x}} = ({\bf x, x}^{\ast })$. Then, we can define a non-null line congruence by intersecting any two non-null line complexes. The intersection of two non-null line congruences forms a differentiable set of non-null lines in $\mathbb{E}_{1}^{3}$ defined as a non-null ruled surface. Non-null ruled surfaces (such as cones and cylinders) include non-null lines in which the tangent plane touches the surface over the non-null generator. Such non-null lines are mentioned as non-null torsal lines.

2.1.   One-parameter Lorentzian dual spherical movements

Let $\mathbb{S}_{1m}^{2}$ and $\mathbb{S}_{1f}^{2}$ be two Lorentzian dual unit spheres with a mutual center $\widehat{{\bf o}}$ in $\mathbb{D}_{1}^{3}$. We choose $\{\widehat{{\bf e}}\} = \{\widehat{{\bf o }}$; $\ \widehat{{\bf e}}_{1}, \; \widehat{{\bf e}}_{2}$(timelike)$, \; \widehat{{\bf e}}_{3} \}$ and $\{\widehat{{\bf f}}\} = \{\widehat{ {\bf o}}$; $\; \widehat{{\bf f}}_{1}$, $\; \widehat{{\bf f}}_{2}$ (timelike), $\; \widehat{{\bf f}}_{3} \}$ as two orthonormal dual frames associated with $\mathbb{S}_{1m}^{2}$ and $\mathbb{S}_{1f}^{2}$, respectively. Set $\{\widehat{{\bf f}}\}$ is stationary, whereas the elements of the set $\{\widehat{{\bf e}}\}$ are functions of a real parameter $t\in \mathbb{R}$ (say the time). Then, we say that $\mathbb{S}_{1m}^{2}$ moves with respect to $\mathbb{S}_{1f}^{2}.$ Such movement is named a one-parameter Lorentzian dual spherical movement and indicated by $\mathbb{S}_{1m}^{2}/\mathbb{S} _{1f}^{2}$. If $\mathbb{S}_{1m}^{2}$ and $\mathbb{S}_{1f}^{2}$ correspond to the Lorentzian line spaces $\mathbb{L}_{m}$ and $\mathbb{L}_{f}$, respectively, then $\mathbb{S}_{1m}^{2}/\mathbb{S}_{1f}^{2}$ represents the one-parameter Lorentzian spatial movements $\mathbb{L}_{m}/\mathbb{L}_{f}.$ Therefore, $\mathbb{L}_{m}$ is the movable Lorentzian space with respect to the stationary Lorentzian space $\mathbb{L}_{f}$ in $\mathbb{E}_{1}^{3}$.

By putting $< \widehat{{\bf f}}_{i}, \widehat{{\bf e}}_{j} > = \widehat{l} _{ij}$ and introducing the dual matrix $\widehat{l} = (l_{ij})+\varepsilon (l_{ij}^{\ast })$, we can express the E. Study map in the matrix form as follows:

From Eq (2.6), the signature matrix $\epsilon$ characterizing the inner product in $\mathbb{D}_{1}^{3}$ is given by

The dual matrix $\widehat{l}$ has the possession that $\widehat{l} ^{T} = \epsilon \widehat{l}^{-1}\epsilon$, $\widehat{l}^{-1} = \epsilon \widehat{l}^{T}\epsilon \widehat{l}$. So, we get

where $I$ is the $3\times 3$ unit matrix. Therefore, when a one-parameter Lorentzian spatial movement is given in $\mathbb{E}_{1}^{3}$, we can find a Lorentzian dual orthogonal $3\times 3$ matrix $\widehat{l}(t) = (\widehat{l} _{ij})$, where $(\widehat{l}_{ij})$ dual functions of one variable $t\in \mathbb{R}$. As the set of real Lorentzian orthogonal matrices, the set of Lorentzian dual orthogonal $3\times 3$ matrices, indicated by $\mathbb{O(D} _{1}^{3\times 3})$, define a group with matrix multiplication as the group operation (real Lorentzian orthogonal matrices are a subgroup of Lorentzian dual orthogonal matrices). The identity element of $\mathbb{O}(\mathbb{D} _{1}^{3\times 3})$ is the $3\times 3$ unit matrix. Since the center of the Lorentzian dual unit sphere in $\mathbb{D}_{1}^{3}$ have to stay stationary, the transformation group in $\mathbb{D}_{1}^{3}$ (the representation of Lorentzian movements in the Minkowski 3-space $\mathbb{E}_{1}^{3})$ does not consist of any translations.

The Lie algebra $\mathbb{L}(\mathbb{O}_{\mathbb{D}_{1}^{3\times 3}})$ of the group $\mathbb{GL}$ of $3\times 3$ positive orthogonal dual matrices $\widehat{l}$ is the algebra of skew-adjoint $3\times 3$ dual matrices

Here, "dash" indicates the derivative with respect to $t\in \mathbb{R}$. Then, the movement $\mathbb{S}_{1m}^{2}/\mathbb{S}_{1f}^{2}$ is

where $\widehat{\boldsymbol{\omega }}(t)\boldsymbol{ = \omega (}t{\bf)+}\varepsilon \boldsymbol{\omega }^{\ast }(t) = (\widehat{\omega }_{1}, \widehat{\omega }_{2}, - \widehat{\omega }_{3})$ is named the instantaneous dual rotation vector of $\mathbb{S}_{1m}^{2}/\mathbb{S}_{1f}^{2}$. $\boldsymbol{\omega }$ and $\boldsymbol{ \omega }^{\ast }$, respectively, are the instantaneous rotational differential velocity vector and the instantaneous translational differential velocity vector of the movement $\mathbb{L}_{m}/ \mathbb{L}_{f}$.

3.   Spacelike ruled surfaces with stationary Disteli-axis

In general, any stationary point $\widehat{{\bf x}}\in \mathbb{S}_{1m}^{2}$ at the movement $\mathbb{S}_{1m}^{2}/\mathbb{S}_{1f}^{2}$ traces a dual curve $\widehat{{\bf x}}(t)$ on $\mathbb{S}_{1f}^{2}$ corresponds to a spacelike or timelike ruled surface in $\mathbb{L}_{f}$. Assume a spacelike ruled surface in our study, and let us indicate it by ($\widehat{x}$). Therefore, ($\widehat{x}$) is parametrized by a timelike dual curve $\widehat{{\bf x}}(t)\in \mathbb{S}_{1}^{2}$. Then, the Blaschke frame can be set up:

where

The dual unit vectors $\widehat{{\bf x}}$, $\widehat{{\bf t}}$ and $\widehat{{\bf g}}$ correspond to three concurrent mutually orthogonal oriented lines in $\mathbb{L}_{f}$. Their point of intersection is the central point ${\bf c}$ on the ruling $\widehat{{\bf x}}$. $\widehat{ {\bf g}}$ is the limit position of the mutual perpendicular to $\widehat{ {\bf x}}(t)$ and $\widehat{{\bf x}}(t+dt)$, and it is named the central tangent of the ruled surface at the central point. The locus of the central points is named the striction curve. $\widehat{{\bf t}}$ is named the central normal of $\widehat{{\bf x}}$ at the central point. The Blaschke formula of $\widehat{{\bf x}}(t)$ is

where $\widehat{\boldsymbol{\omega }}(t){\bf = }(\widehat{q}, 0, -\widehat{p})$ and

$\widehat{p}(t)$ and $\widehat{q}(t)$ are the Blaschke invariants of the timelike dual curve $\widehat{{\bf x}}(t)\in \mathbb{S}_{1f}^{2}$. It can be shown that the tangent of the striction curve is given by

Under the assumption that $p(t)\neq 0$, we have the functions

The geometric clarifications of these functions are as follows:$\ \gamma$ is the geodesic curvature of the spherical image curve ${\bf x} = {\bf x(}t)$; $\Gamma$ characterizes the angle of the tangent to the striction curve and the ruling of ($\widehat{x}$); $\mu$ is its distribution parameter at the ruling. These functions define spacelike ruled surfaces with a given striction spacelike curve via the equation

3.1.   Spacelike Disteli-axis

In view of Eq (2.8), the spacelike Disteli-axis of ($\widehat{x}$) in $\mathbb{L}_{f}$ is

As per the above illustrations, Eq (3.2) can be written as

Then, at any instant $t\in \mathbb{R}$, we get

$\omega ^{\ast }$ and $\omega$ are the translational angular speed and the rotational angular speed of the movement $\mathbb{L}_{m}/\mathbb{L}_{f}$ along $\widehat{{\bf b}}$, respectively. So, the spacelike Disteli-axis is the instantaneous screw axis of the movement $\mathbb{L}_{m}/\mathbb{L }_{f}.$

Proposition 1. At any instant $t\in \mathbb{R}$, the pitch of the one-parameter spatial movement $\mathbb{L}_{m}/\mathbb{L}_{f}$ is given by

However, the Disteli-axis $\widehat{{\bf b}}(t)$ can be determined by Eq (3.1), and one has the following:

(1) The dual angular speed can be specified as $\left\Vert \widehat{\boldsymbol{\omega }}(t)\right\Vert = \omega (t)(1+\varepsilon h(t))$.

(2) If ${\bf r}$ is a point on the spacelike Disteli-axis $\widehat{ {\bf b}}(t)$, then we get

This parametrization defines a non-developable spacelike ruled surface $(\widehat{b})$.

In the case the movement $\mathbb{L}_{m}/\mathbb{L}_{f}$ is pure rotation ($h(u) = 0$), then

whereas if $h(t) = 0$ and $\left\Vert \boldsymbol{\omega }(t)\right\Vert ^{2} = 1$, then $\widehat{\boldsymbol{\omega }}(t)$ is a spacelike line. However, if $\widehat{\boldsymbol{\omega }}(t){ = }$ $0$ ${ +}\varepsilon \boldsymbol{\omega }^{\ast }(t)$, that is the movement $\mathbb{L}_{m}/\mathbb{L }_{f}\ $is pure translational, we let $\omega ^{\ast }(t) = \left\Vert \boldsymbol{ \omega }^{\ast }(t)\right\Vert;$ $\omega ^{\ast }{\bf b}(t{) = } \boldsymbol{\omega }^{\ast }$ for arbitrary ${\bf b}^{\ast }(t)$ such that $\omega ^{\ast }(t)\neq 0$, ${\bf b}(t)$ can be arbitrarily, too.

According to Eq (3.1), the spacelike Disteli-axis is perpendicular to the timelike central normal $\widehat{{\bf t}}$ and parallel to the tangent plane of the spacelike ruled surface ($\widehat{x}$). Let $\widehat{\psi }(t) = \psi (t)+\varepsilon \psi ^{\ast }(t)$ be the spacelike dual angle (dual radius of curvature) between $\widehat{{\bf b}}$ and $\widehat{{\bf x}}$. Then, we define the spacelike Disteli axis of ($\widehat{x}$) as

where

Consequently, from the real and dual parts, we have

where $\psi ^{\ast }$ is measured along the timelike central normal $\widehat{{\bf t}}$ (see Figure 2). From Eqs (3.4), (3.8) and (3.9), we obtain

These formulae are Lorentzian versions of the Hamilton and Mannhiem formulae of surface theory in Euclidean 3-space $\mathbb{E}^{3}$, respectively^[1,2,3,4].

3.2.   Spacelike Plücker's conoid

In this subsection we examine and study the geometrical explanations of the Hamilton and Mannhiem formulae as follows. The surface defined by $\psi ^{\ast }$ is the spacelike version of the well-known Plücker's conoid or cylindroid as follows: let $\widehat{{\bf t}}$ and the $y$ axis of a fixed Lorentzian frame $(oxyz)$ be coincident and the location of the spacelike dual unit vector $\widehat{{\bf b}}$ be defined by the angle $\psi$ and distance $\psi ^{\ast }$ on the positive orientation of the $y$ axis. The spacelike dual unit vectors $\widehat{{\bf x}}$ and $\widehat{{\bf g}}$ can be taken in along the $x$ and $z$ axes, respectively. This leads to $\widehat{{\bf x}}$ and $\widehat{{\bf g}}$ together with $\widehat{ {\bf t}}$ constitute the coordinate system of the spacelike Plücker's conoid (Figure 2).

Let ${\bf r}(x, y, z)$ be a point on $(\widehat{b})$, we have

Consequently, we get

By an easy calculation, we obtain

which is the Cartesian equation for $(\widehat{b})$. The Eq (3.13) based only on the variation of its two integral invariants of the first order; $\mu -\Gamma = -2, \ 0\leq \psi \leq 2\pi, \, 0\leq \upsilon \leq 2$ (Figure 3). Further, one can get a second-order equation in $x/z$ in which its solutions are given by

By equating the discriminant of Eq (3.14) to zero, we define the limits of $(\widehat{b})$. Then, the two limits of $(\widehat{b})$ are given by

Equation (3.14) shows the locations of the two torsal spacelike planes, each of which contains one torsal spacelike line $L$.

On the other hand, the function $h(u)$ in Eq (3.10) is a periodic function with at most two extreme values, the curvature functions $\mu$ and $\Gamma$. However, the spacelike dual unit vectors $\widehat{{\bf x}}$ and $\widehat{ {\bf g}}$ are principal axes of $(\widehat{b})$. Also, the geometric aspects of $(\widehat{b})$ are as follows:

(ⅰ). If $h(t)\neq 0$, then we have two rulings that are movable through the point $(0, y, 0)$ if $y < \left(\Gamma -\mu \right) /2$; and for the two limit points $y = \pm \left(\Gamma -\mu \right) /2$, the rulings and the spacelike principal axes $\widehat{{\bf x}}$ and $\widehat{{\bf g}}$ are coincident.

(ⅱ). If $h(t) = 0,$ then we have two torsal lines $L_{1}$ and $L_{2}$ given by

Equation (3.16) shows that the two torsal lines $L_{1}$ and$\ L_{2}$ are orthogonal to each other. So, if $\mu$ and $\Gamma$ are equal, then the spacelike Plücker's conoid degenerates to a pencil of spacelike lines through the origin "${\bf o}$" in the spacelike torsal plane $y = 0$. In this case $L_{1}$ and $L_{2}$ are the principal axes of an elliptic spacelike line congruence. However, if $\mu$ and $\Gamma$ have opposite signs, then $L_{1}$ and $L_{2}$ are real and coincident with the principal axes of a spacelike hyperbolic line congruence. If either $\mu$ or $\Gamma$ is zero, then the lines $L_{1}$ and $L_{2}$ both coincide with the timelike $y$ axis; for $\mu \neq 0, \Gamma = 0$ or $\Gamma \neq 0, \, \mu = 0$, they coincide with the spacelike $z$ axis.

Furthermore, to convert from polar coordinates to Cartesian, we use

at Hamilton's formula to obtain

of a conic section. This conic section is a Minkowski version of the Dupin indicatrix of the surface theory in Euclidean 3-space $\mathbb{E} ^{3}$ ^[1,2,3].

3.2.1.   Serret-Frenet motion

In Eq (2.9): (a) If $p^{\ast } = 0$, then $(\widehat{x})$ is a spacelike tangential developable ruled surface, that is, ${\bf c}^{^{^{\prime }}} = {\bf x}$. In this case, the Blaschke frame $\{{\bf x},$ ${\bf t}$, ${\bf g}\}$ coincides with the classical Serret-Frenet frame and then the striction curve ${\bf c}$ becomes the edge of regression of $(\widehat{x})$. Hence, $p$ and $q$ are the curvature $\kappa$ and the torsion $\tau$ of ${\bf c}$, respectively. Moreover, $q^{\ast } = 1$ and $\Gamma = 1/\tau$. Thus, $\Gamma$ is the radius of torsion of ${\bf c}$. In this case, we get

Also, the corresponding spacelike Plücker conoid is

Based on ^[17], we have the following:

Theorem 1. Any spacelike ruled surface ($\widehat{x}$) with the curvature function

with real constants $(a, b)\neq (0, 0)$ is a spacelike tangential surface of a spacelike curve that lies on a Lorentzian sphere of radius $\sqrt{b^{2}-a^{2}}$.

Corollary 1. The curvature function $\kappa (t)$ and torsion function $\tau (t)$ of the spherical curve in Theorem 1, respectively, are

(b) If $\Gamma (t) = 0$, then the striction curve is tangent to ${\bf g}$; it is normal to the ruling through ${\bf c}\mathbb{(}t\mathbb{)}$. In this case ($\widehat{x}$) is a spacelike binormal ruled surface and

Therefore, the curvature function $\mu (t)$ is the radius of torsion of the spacelike striction curve ${\bf c}(t)$ of the binormal surface. Similarly, we get

where $\cot \psi = \frac{\tau }{\kappa }$ and

By similar arguments, we summarize this result :

Theorem 2. Any spacelike ruled surface ($\widehat{x}$) with the curvature function

with real constants $(a, b)\neq (0, 0)$ is a spacelike binormal surface of a spacelike curve that lies on a Lorentzian sphere of radius $\sqrt{b^{2}-a^{2}}$.

Corollary 2. The curvature function $\kappa (t)$ and torsion function $\tau (t)$ of the spherical curve in Theorem 2, respectively, are

3.3.   Special spacelike ruled surfaces

We give some characterizations and equations of special spacelike ruled surfaces undergoing one-parameter Lorentzian screw movement.

Let $d\widehat{s} = ds+\varepsilon ds^{\ast }$ indicate the dual arc length of $\widehat{{\bf x}}(t)$ Then, we have

In fact, it is significant to research the dual curvature $\widehat{\kappa }(\widehat{s})$ and the dual torsion $\widehat{\tau }(\widehat{s})$. Then, the Serret-Frenet frame can be set up:

In fact, the relative orientation is given by

Then, by differentiating with respect to $s$ and using the Blaschke frame derivative formulae, one can obtain

where

The functions found in Eq (3.20) are analogous to their equivalents in 3-dimensional Euclidean spherical geometry.

Proposition 2. If the dual geodesic curvature function $\widehat{ \gamma }(\widehat{s})$ = constant, $\widehat{{\bf x}}(\widehat{s})$ is a timelike dual circle on $\mathbb{S}_{1}^{2}$.

Proof. From Eq (3.20), we can find that $\widehat{\gamma }(\widehat{s })$ = constant yields that $\widehat{\tau }(\widehat{s}) = 0$ ($\widehat{\psi }$ = constant) and $\widehat{\kappa }(\widehat{s})$ = constant, which implies that $\widehat{{\bf x}}(\widehat{s})$ is a timelike dual circle on $\mathbb{S} _{1}^{2}$.

Definition 3. A non-developable spacelike ruled surface $(\widehat{ x})$ is a stationary Disteli-axis spacelike ruled surface if $\widehat{\gamma }(\widehat{s})$ = constant.

In view of the E. Study map, the spacelike ruled surfaces with the stationary Disteli-axis ($\widehat{x}$) is created by a one-parameter Lorentzian screw motion with the stationary pitch $h$ along its Disteli-axis $\widehat{{\bf b}}$ by using the spacelike line $\widehat{{\bf x}}$ determined at a spacelike fixed distance $\psi ^{\ast }$ and spacelike fixed angle $\psi$ with respect to the spacelike Disteli-axis $\widehat{{\bf b}}$. In the special case, if $\widehat{\gamma }(\widehat{s}) = 0$, then $\widehat{{\bf x}}(\widehat{s})$ is a timelike great dual circle on $\mathbb{S}_{1}^{2}$, that is,

In this case, all rulings of ($\widehat{x}$) intersected orthogonally with the spacelike Disteli-axis $\widehat{{\bf b}}$, that is, $\psi = \frac{\pi }{2}$ and $\psi ^{\ast } = 0$. Thus, we have that $\widehat{\gamma }(\widehat{s}) = 0\Leftrightarrow$($\widehat{x}$) is a spacelike helicoidal surface. The ruled surfaces with a stationary Disteli-axis and the helicoidal surface are essential to the curvature theory of ruled surfaces. We will therefore inspect them in some detail.

Example. We attain the spacelike ruled surfaces with a stationary Disteli-axis. Since $\widehat{\gamma }(\widehat{s})$ is constant, from Eq (3.19), we have the ODE $\widehat{{\bf t}}^{^{^{\prime \prime }}}-\widehat{\kappa }^{2}\widehat{{\bf t}} = {\bf 0}$. Without loss of generalization, we may let $\widehat{{\bf t}}(0) = (0, 1, 0)$ the general solution of the ODE becomes

where $\widehat{a}_{1}$, $\widehat{a}_{2}$ and $\widehat{a}_{3}$ are dual constants. Since$\left\Vert \widehat{{\bf t}}\right\Vert ^{2} = -1$, we get $\widehat{a}_{2} = 0$ and $\widehat{a}_{1}^{2}+\widehat{a}_{3}^{2} = 1$. It follows that $\widehat{{\bf x}}(\widehat{s})$ is given by

where $\widehat{b}_{2}$ and $\widehat{b}_{3}$ are dual constants satisfying $\widehat{a}_{1}\widehat{b}_{1}+\widehat{a}_{3}\widehat{b}_{3} = 0$ and $\widehat{b}_{1}^{2}+\widehat{b}_{3}^{2} = 1-\widehat{\rho }^{2}$. We now replace the coordinates by

Then, $\widehat{{\bf x}}(\widehat{s})$ becomes

for a dual constant $\widehat{b} = \widehat{a}_{1}\widehat{b}_{3}-\widehat{a} _{3}\widehat{b}_{1}$, with $\widehat{b} = \pm \cos \widehat{\psi }$. Notice that $\widehat{{\bf x}}(\widehat{s})$ is not based on the choice of the lower sign or upper sign of $\pm$. Therefore, we may choose upper sign, that is,

where $\widehat{\varphi } = \widehat{\kappa }\widehat{s}$. It is a timelike dual spherical curve with the dual curvature $\widehat{\kappa } = \sqrt{ \widehat{\gamma }^{2}+1}$ on the Lorentzian dual unit sphere $\mathbb{S} _{1}^{2}$. Let $\widehat{\varphi } = \varphi (1+\varepsilon h)$, $h$ be the stationary pitch of the helical motion and $\varphi$ the motion parameter. Then, Eq (3.23) is a spacelike ruled surface. In this case, the Blaschke frame is as follows:

It is readily seen that

From the real and dual parts of Eq (3.25), we find

Consequently, from Eqs (3.11) and (3.28), we have

This shows that the axis of the Lorentzian screw motion is the stationary spacelike Disteli-axis $\widehat{{\bf b}}$.

The equation of $(\widehat{x})$ in terms of the point coordinates can be obtained as follows: If we separate $\widehat{{\bf x}}(\varphi)$ into real and dual parts we reach

and

Let $\boldsymbol{\beta }(\beta _{1}, \beta _{2}, \beta _{3})$ be a point on $\widehat{{\bf x}}$. Since $\beta$${\bf \times x} = {\bf x} ^{\ast }$ we have the system of linear equations in $\beta _{1},$ $\beta _{2}$ and $\beta _{3}$:

The matrix of coefficients unknowns $\beta _{1},$ $\beta _{2}$ and $\beta _{3}$ is

its rank is 2 with $s\neq 0$, and $\vartheta \neq p\pi$ (p is an integer). In addition, the rank of the augmented matrix

is 2. Then, this system has infinitely many solutions represented with

Since $\beta _{3}$ is taken at random, we may take $\varphi ^{\ast }+\beta _{3} = 0$. In this case, Eq (3.26) becomes

Then, we get

It is clear that $< \boldsymbol{\beta }^{^{\prime }}, {\bf x}^{^{\prime }} > = 0$; ($^{\prime } = \frac{d}{d\varphi }$), so the base curve of ($\widehat{x}$) is its striction curve. Then, the spacelike ruled surface with a stationary Disteli-axis is

The constants $h$, $\psi$ and $\psi ^{\ast }$ can control the shape of $(\widehat{x})$. Via Eq (3.32), we have

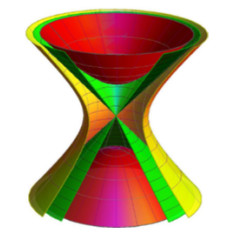
(1) General helicoidal spacelike surface: for $h = -2$, $\psi ^{\ast } = -0.5$, $\psi = \frac{\pi }{4}$, $-3\leq \varphi \leq 3$ and $-1.5\leq v\leq 1.5$ (see Figure 4),

(2) Spacelike helicoidal surface: for $h = -2$, $\psi ^{\ast } = 0$, $\psi = \frac{\pi }{2}$, $-3\leq \varphi \leq 3$ and $-1.5\leq v\leq 1.5$ (see Figure 5),

(3) Spacelike helicoidal surface: for $h = 0$, $\psi ^{\ast } = -0.5$, $\psi = \frac{\pi }{4}$, and $-1.5\leq \varphi$, $v\leq 1.5$ (see Figure 6),

(4) Spacelike cone: for $h = \psi ^{\ast } = 0$, $\psi = \frac{\pi }{4}$, $-1\leq \varphi \leq 1$ and $-1\leq v\leq 1$ (see Figure 7).

4.   Conclusions

This paper develops the kinematic geometry for spacelike ruled surfaces with a stationary Disteli-axis by using the analogy with Lorentzian dual spherical kinematics. This provides the ability to compute a set of curvature functions which define the local shape of spacelike ruled surfaces. Hence, the Lorentzian version of the well known equation of the Plücker's conoid has been derived and its kinematic geometry is examined in detail. Finally, a characterization for a spacelike line trajectory to be a constant Disteli-axis derived and investigated. The study of spatial kinematics in Minkowski 3-space $\mathbb{E}_{1}^{3}$ via the geometry of lines may be used to solve some problems and conclude new applications.

For future research, we will design of spacelike ruled surfaces as tooth flanks for gears with skew spacelike axes such that, at any instant, the contact points located on a spacelike line, and so forth, as offered in ^[18,19,20].

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R27), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.