Caliberating length scale parameter and micropolarity on transference of Love-type waves in composite of CoFe₂O₄ and Aluminium-Epoxy laden with Newtonian liquid

Nomenclature

$S_{kl}^\dagger: \text{Strain tensor}$; $\sigma_{ij}^\dagger: \text{Stress tensor}$; $C_{ijkl}: \text{Elastic coefficient}$; $h_{kij}: \text{Piezomagnetic constants}$; $m_{ij}: \text{Magnetic permeability}$; $H_{i}^\dagger: \text{Magnetic field}$; $B_i^\dagger: \text{Magnetic induction}$; $\phi^\dagger: \text{Magnetic potential}$; $\epsilon_{ijk}: \text{Permutation tensor}$; $\delta_{ij}: \text{Kronecker delta}$

1.   Introduction

In the present scenario, there are laudable applications of magnetic materials in piezo-composites due to their potential for multi-functional device applications, including magnetic sensors, energy harvesters, tunable microwave devices, magnetoelectric (ME) random access memory and logic devices, and ME antenna. These composites have undoubtedly made their presence felt in this cutting edge technology and has many future perspectives and engineering applications ^[1,2]. From physical consideration, the magnetostriction phenomenon is associated with a strong coupling between the magnetic and mechanical properties of materials. In a PM material, a spontaneous magnetic moment is induced by applying a physical stress, or a physical deformation by applying a magnetic field. This can be ascribed by the dependence of the stress tensor $\sigma$ and the magnetic field $H$ towards the magnetic induction $B$ and the strain tensor $S$. The PM effect depends on various parameters of the material such as density, elastic constant, permeability, piezomagnetic coefficients etc. Some common examples of piezomagnetic materials are uranium dioxide, terfenol-D, ferromagnetic materials etc. Among magnetostrictive phases, $CoFe_2O_4$ stands out because of its very high magnetostriction which is due to high magneto-crystalline anisotropy and coercive field. PM materials are smart materials also called as responsive or intelligent materials. Smart materials are designed materials which have one or more properties that can be changed accordingly with the change in external stimuli such as magnetic field, electric field, stress, chemical composition etc. In the recent past, surface wave propagation in smart structures has been explored by various researchers. Alshits et al. ^[3] investigated the existence of surface waves in semi-infinite anisotropic elastic media with piezoelectric and PM properties. Wei et al. ^[4] examined SH-waves in a piezoelectric-piezomagnetic coupled layered half-space. SH-wave propagation in imperfect interface of piezoelectric-piezomagnetic bilayer system was examined by Nie et al. ^[5]. Theoretical study of SH-wave propagation in periodically-layered PM structure is done by Liu et al. ^[6]. Scattering phenomena of shear waves by a two-phase multiferroic sensor embedded in a piezoelectric/piezomagnetic medium is explored by Hashemi ^[7]. Sahu et al. ^[8,9] analyzed surface wave behavior in PM layer. Modelling of Love-type wave propagation in a PM layer of Terfenol-D over a lossy viscoelastic substrate was consummated by Suman et al. ^[10]. Ray et al. ^[11] used Green's function technique to model Love type wave propagation due to an impulsive point source in a PM layered structure. Pang et al. ^{[12,13,14,15]} discussed surface wave propagation in various layered structures comprising of PM layer. Love wave in a corrugated isotropic layer over a homogeneous isotropic half-space has been analyzed by Singh ^[16]. Li et al. ^[17] theoretically investigated the propagation characteristics of SH wave in piezomagnetic-piezoeletric structures.

The Love-type wave based devices were designed by employing classical model of elasticity for the substrate but the classical model is incompetent to expound the behavior of motion of inner structure of contemporary engineering materials like crystalline materials and materials with fibrous or coarse grain. The granular structure or microstructure is a very minute form of a material. These can vigorously influence hardness, toughness, corrosion resistance, high/low temperature behavior, ductility, or wear resistance. These properties consecutively govern the applications of these materials in chemical engineering and industrial practices. Hence, it is very important to scrutinize the microstructural behavior of materials that remarkably influences the wave propagation in the considered structures. Voigt ^[18] was the first who introduced the idea of couple stresses in addition to force stresses to overcome the shortcomings of the classical theory of elasticity. He interpreted that each element or grain of microstructure rotates about its center of gravity in addition to translation assumed in classical theory of elasticity. Cosserat and Cosserat brothers ^[19] gave the mathematical model to analyze materials with couple stresses, by considering that the deformation of the medium is described by displacement vector and an independent rotation vector. Further, Eringen ^[20] established the generalized interpretation of this theory which illuminates the deformation of elastic media with oriented particles. In view of significant influence by microstructures on the material, considerable attention must be given to the substrate exhibiting microstructural properties ^[21,22]. Many researchers have employed micropolar theory of elasticity to capture the microstructural characteristics of the material. This study will aid researchers to delve out the relationship between the engineering properties of the materials and their microstructural characteristics ^[23,24]. Gauthier ^[25] performed experimental investigations on micropolar media. Love waves in homogeneous micropolar elastic media were analyzed by Midya ^[26]. Eremeyev ^[27] applied micropolar theory to strength analysis of bioceramic materials for bone reconstruction. Kaur et al. ^[28] analyzed the influence of imperfect bond of micropolar elastic half-space with non-homogeneous viscoelastic layer on SH-wave propagation. Examination of Love wave propagation in PM layered structures was conducted by Ezzin et al. ^[29,30]. Rayleigh-type waves in nonlocal micropolar solid half-space were examined by Khurana and Tomar ^[31]. Kundu et al. ^[32] investigated Love wave propagation in heterogeneous micropolar media. Goyal et al. ^[33] investigated Love wave propagation in micropolar-piezoelectric structure.

To explore more applications of the sensors, occasionally they are laden with viscous liquid (Newtonian) layer ^[34]. Consequently, energy loss through the liquid and attenuation of SAW modes requires attention for enhancement in designing of devices. In liquid media, Love-type wave sensors are mostly preferred due to their high sensitivity. The acoustic energy is concentrated within a few wavelengths near the surface. Such devices have immense applications like evaluation of mass density, viscosity, and the acoustic-electric phenomenon of liquids ^{[35,36,37,38,39,40,41,42]}. These kind of sensors comprises of layered structure in which a thin stratum is coated on a substrate and the wave propagates slower in the layer than that in the substrate. The significance of viscous liquid loading on the wave propagation phenomenon has been explored by numerous researchers. Zaitsev et al. ^[43] studied acoustic waves in piezoelectric plates bordered with viscous and conductive liquid. Du et al. ^[44,45] investigated Love wave propagation in various layered structures loaded with viscous liquid. Guo and Sun ^[46] examined the propagation of B-G wave in 6 mm piezoelectric materials loaded with viscous liquid. Kielczynski et al. ^[47] studied the effect of viscous liquid loading on Love wave propagation. Nie et al. ^[48] investigated SH-wave propagation in piezoelectric layered structures under viscous loading. The above illustrated details insist the present study to confer the viscous liquid loading and microstructural effects on the Love-type wave propagation in PM layer overlying semi-infinite micropolar elastic substrate. Dispersion relations for magnetically open and short conditions are obtained. The obtained findings may significantly contribute to enhance the performance of Love-type wave based SAW devices functioning in liquid environment.

2.   Formulation of the problem

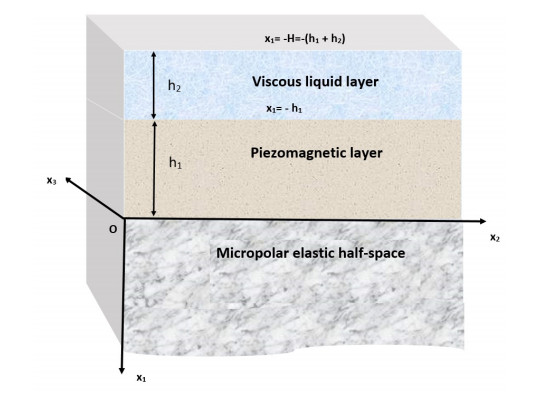
Consider a piezomagnetic (PM) layer of thickness $h_1$ loaded with viscous liquid (VL) layer of thickness $h_2$. PM layer is overlying a micropolar (MP) half-space substrate as shown in Figure 1. Both materials PM and MP are transversely isotropic in nature. The interface at $x_1 = 0$ is bonded perfectly with magnetic and elastic properties simultaneously. Considering Cartesian coordinate system in such a way that $x_2$-axis is along the direction of propagation of Love-type wave and $x_1$-axis is positive in vertically downward direction.

The mechanical displacement components in the PM layer and MP half-space substrate obtained due to the propagation of Love-type wave are given by $\overrightarrow{u^{\dagger}} = (u^{\dagger}_1, u^{\dagger}_2, u^{\dagger}_3)$ and $\overrightarrow{u^{\diamond}} = (u^{\diamond}_1, u^{\diamond}_2, u^{\diamond}_3)$, respectively. By virtue of propagation of Love-type wave in $x_2-$ direction and inducing displacement in $x_3-$ direction, it may be assumed that

2.1.   Formulation and solution of viscous liquid (VL) layer

In a viscous liquid (VL) the velocity $v_l$ of liquid particle in $x_3-$ direction is administered by the Navier-Stokes equation (Guo and Sun ^[46]):

where $\mu_l$ and $\rho_l$ represents coefficient of viscosity and liquid mass density of VL, respectively.

Assuming the solution of equation (2.3) in the form

where $k$ is the wave number and $c$ is the phase velocity of the wave.

On substituting (2.4) into (2.3) we get:

where $p = \sqrt {k^2-\frac{ikc \rho_l}{\mu_l}}$ and $Re(p) > 0.$

On solving equation (2.5) we get

where $\wp_1$ and $\wp_2$ are arbitrary constants.

The velocity component in VL is given by

The only non-vanishing shear stress component $\sigma^l_{31}$ in VL is given by

2.2.   Formulation and solution of piezomagnetic (PM) layer

The governing equation for the PM layer in the absence of body forces (Goyal et al. ^[10]) is given by:

where $\rho'$ denotes the mass density of the PM layer. The dot denotes time differentiation.

For a PM layer the constitutive relations are given as:

where $i, j, k = 1, 2, 3$. Here superscript $'\dagger'$ indicates the quantities in PM layer. $\sigma^{\dagger}_{ij}$ and $S^{\dagger}_{kl}$, respectively are the stress and strain tensors in PM layer. $C_{ijkl}$, $h_{kij}$, $m_{ij}$, $H^{\dagger}_i$, and $B^{\dagger}_i$ are the stiffness, PM constants, magnetic permeability, magnetic field, and magnetic inductions, respectively.

The constitutive relations can be written as

where $C_{66} = \frac{1}{2}(C_{11}- C_{12}).$

The strain components are defined as

To determine the relation between magnetic field and the magnetic potential function following formula is used:

where $\phi^{\dagger}$ represents the magnetic potential.

Inserting equation (2.1) in equations (2.12) and (2.13) we get

Inserting equations (2.14)-(2.16) in equations (2.11) and then substituting in equation (2.9), the governing equation for the PM layer is obtained as

On reducing equations (2.17) and (2.18) we get

where $\alpha_1 = \sqrt{\frac{C_{44}^0}{\rho'}}$, $C_{44}^0 = C_{44}+\frac{h^2_{15}}{m_{11}}$, $\nabla^2 = \frac{\partial ^2}{\partial x_1^2}+\frac{\partial ^2}{\partial x_2^2}$. $\alpha_1$ is the shear wave velocity in the PM layer.

Assuming the following solutions of the mechanical displacement component and magnetic potential function of the Love wave in the PM layer:

Conjuring equation (2.21) in equation (2.19), we get

where $\alpha_2^2 = \left(\frac{c^2}{\alpha_1^2}-1\right).$

On solving differential equation (2.23) under the assumption that $c > \alpha_1,$ we get the displacement component as

Now, invoking equation (2.22) in equation (2.20), we get the differential equation as:

On solving differential equation (2.25), magnetic potential function can be expressed as

where $\wp_3$, $\wp_4$, $\wp_5$, and $\wp_6$ are arbitrary constants.

2.3.   Semi-infinite micropolar (MP) elastic substrate

In a homogeneous MP isotropic elastic media $(x_1 > 0)$, the propagation of Love-type wave in $x_2-$direction induces displacement components and microrotation as

respectively. Here, superscript as index $'\diamond'$ is used for quantities in semi-infinite MP elastic substrate. Following are the equation of motion and constitutive relations as suggested by Eringen ^[20] for MP elastic space in the absence of body forces in vector form

where i, j, k = 1, 2, 3; $\lambda$ and $\mu$ are Lame's constants. $\rho$ is density of MP elastic material, $\sigma_{ij}^{\diamond}$ and $m_{ij}^{\diamond}$ are the force stress tensors and the couple stress tensors, respectively of the semi-infinite MP elastic substrate. $\alpha$, $\beta$, $\gamma$, $\kappa$ are the additional MP elastic constants. $\jmath$ is the micro inertia. $\delta_{ij}$ is kronecker delta. $\epsilon_{ijk}$ is permutation tensor.

In the MP model, the parametric relations (Fatemi et al. ^[49]) are characterized as

where $N$ $(0\le N < 1)$ is a coupling constant. It regulates the degree of micropolarity produced by the materials. Here, $N = 0$ coincides to the classical theory of elasticity.

Moreover, the length scale parameter is estimated by the characteristic length $l$ which is of the order of the average cell size of the considered material.

Using the Helmholtz decomposition of vectors by assuming the potential functions $\Im$ and $\xi$, we can write

where $\vec{\xi} = (0, 0, -\xi)$. $\Im$ is scalar potential and $\xi$ is vector potential function.\\ The microrotation vector components can be written as

With the help of equations (2.27) and (2.34), the system of equations (2.29) and (2.30) becomes,

where values of $\Re_1$, $\Re_2$, $\Re_3,$ $\Re_4$, and $\Re_5$ are provided in the appendix.

Let us assume the solutions of above equations (2.35)-(2.37) as

where $k$ is the wave number and $c$ is the phase velocity.

Solving equations (2.35)-(2.37) with the help of equations (2.38)-(2.40) and using the radiation conditions $W(x_1)$, $Q(x_1)$ and $\Xi(x_1) \to 0$ as $x_1 \to \infty$ on the general solutions of differential equations (2.35) to (2.37), we get the following solutions of potential functions and displacement component in semi-infinite MP elastic substrate

where $\wp_7$, $\wp_8$ and $\wp_9$ are arbitrary constants. Values of $A_1$, $A_2$, $r_1$, $r_2$, and $\alpha_3$ are provided in the appendix.

The microrotation components obtained from equations (2.34), (2.41), and (2.42) are as follows:

3.   Boundary conditions

To derive the dispersion equation, the admissible boundary conditions at the upper free surface and at the common interfaces of the viscous liquid layer and piezomagnetic layer (VL-PM interface) and piezomagnetic layer and micropolar substrate (PM-MP interface) are stated below:

(ⅰ) The zero traction condition at $x_1 = -H$ is

(ⅱ) The magnetically open condition at $x_1 = -h_1$ is given as

(ⅲ) The magnetically short condition at $x_1 = -h_1$ is given as

(ⅳ) At the interface $x_1 = -h_1$, the velocity and stress components are continuous

(ⅴ) Magnetic potential function must vanish at the common interface $x_1 = 0$

(ⅵ) At the interface $x_1 = 0$, the displacement and stress components are continuous

4.   Dispersion relations

Using specified boundary conditions (3.1) to (3.6), the following equations in terms of nine unknown coefficients $\wp_1, \; \wp_2, \; \wp_3, \; \wp_4, \; \wp_5, \; \wp_6, \; \wp_7, \; \wp_8,$ and $\wp_9$ are procured.

Values of $A_4$, $A_5$, $A_6$, $A_7$, $A_8$, $A_9$, $A_{10}$, and $A_{11}$ are provided in the appendix.

For non-trivial solutions, the determinant of the coefficient matrix must vanish. This condition leads to a complex dispersion equation. Real part is responsible for free propagation of the wave while the imaginary part is responsible for attenuation/absorption. Here, for further investigation we have considered free propagation of the wave.

4.1.   For magnetically open case

After eliminating the unknown constants $\wp_1, \; \wp_2, \; \wp_3, \; \wp_4, \; \wp_5, \; \wp_6, \; \wp_7, \; \wp_8$ and $\; \wp_9$ from equations (4.1)-(4.2) and (4.4)-(4.10), we get the following dispersion equation for Love-type wave propagation in PM layer loaded with VL, overlying semi-infinite MP substrate.

4.2.   For magnetically short case

After eliminating the unknown constants $\wp_1, \; \wp_2, \; \wp_3, \; \wp_4, \; \wp_5, \; \wp_6, \; \wp_7, \; \wp_8$ and $\; \wp_9$ from equations (4.1) and (4.3)-(4.10), we get the following dispersion equation for Love-type wave propagation in PM layer loaded with VL, overlying semi-infinite MP substrate.

Values of $A_{12}$, $A_{13}$, $A_{14}$, $A_{15}$, $A_{16}$, $A_{17}$, $A_{18}$, $A_{19}$ and $A_{20}$ are provided in the appendix.

Equations (4.11) and (4.12) are dispersion equations for the Love-type wave propagation in PM layer loaded with VL layer, overlying semi-infinite MP substrate for magnetically open and short cases, respectively.

5.   Particular cases and validation of results

Case-Ⅰ

In the absence of VL layer i.e. $\mu_l = 0$, $h_2 = 0$ which will lead to $A_{14} = 0$. The dispersion equations (4.11) and (4.12) will become,

respectively. Equations (5.1) and (5.2) portrays the dispersion equations of Love-type wave in PM layer overlying semi-infinite MP substrate, for magnetically open and short cases, respectively.

Case-Ⅱ

Contemplating the previous case-Ⅰ in the absence of MP constants $\alpha, \beta, \gamma,$ and $\kappa \to 0$, we get the changed values of $\Re_2$ and $\frac{A_{13}}{A_{12}}$ as $\Re_2 = \sqrt{\frac{\mu+\kappa}{\rho}}\to \sqrt{\frac{\mu}{\rho}} = \beta_1$ and $\frac{A_{13}}{A_{12}} \to -\mu k \sqrt{1-\frac{c^2}{\beta_1^2}}$. Putting these values in above equations we get

respectively. Equations (5.3) and (5.4) describes the dispersion equations of Love-type wave propagating in PM layer overlying isotropic elastic half-space for magnetically open and short cases, respectively.

Case-Ⅲ

Without consideration of piezomagneticity in the PM layer, i.e. $h_{15} = 0$ will lead to $C^0_{44} = C_{44}$ and hence $\alpha_1^2$ will become $\frac{C_{44}}{\rho'} = \beta_2^2$. Therefore, dispersion equation is reduced to

where $c$ is the phase velocity of Love-type wave. Equation (5.5) matches with the well-known classical Love wave equation (Love ^[50]) which validates the outcomes of the present problem.

6.   Numerical results

This section intends to explore the dispersion curves, i.e. curves elucidating variation of $c/\alpha_1$ against $kh_1$, to examine the influence of magnetic boundary conditions, the viscosity, the liquid mass density, the length scale parameter, the thickness of VL layer, and the PM parameters, viz. PM constant, elastic constant, magnetic permeability as well as thickness on the velocity of the propagating wave. Figures 2(a)-10(a) are plotted for the magnetically open case and Figures 2(b)-10(b) are plotted for the magnetically short case. Cobalt Ferrite ($CoFe_2O_4$) is chosen as PM layer and aluminium-epoxy admitting microstructural properties is chosen as MP substrate. The material constants of materials are listed below (Tables 1 and 2).

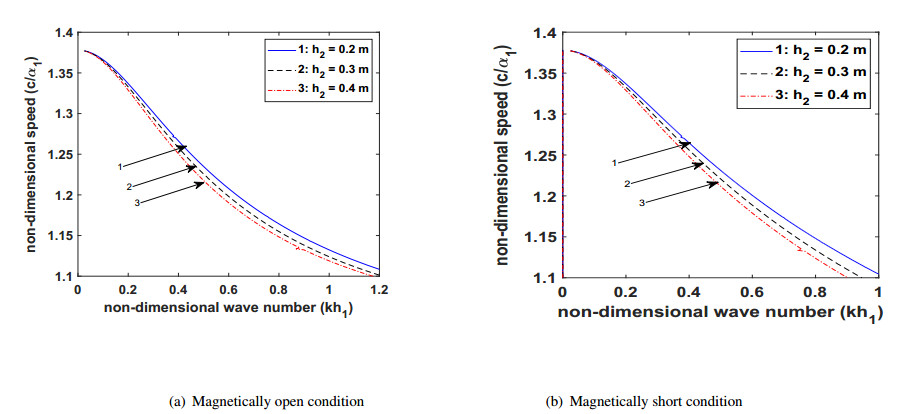
For viscous liquid layer: (Kielczynski et al. ^[47]): $\mu_l = 50$ $Pa.s$, $\rho_l = 10^3$ $kg/m^3$. The thickness of the VL layer and PM layer is assumed to be 0.2 m and 0.3 m, respectively.

6.1.   Effect of PM parameters

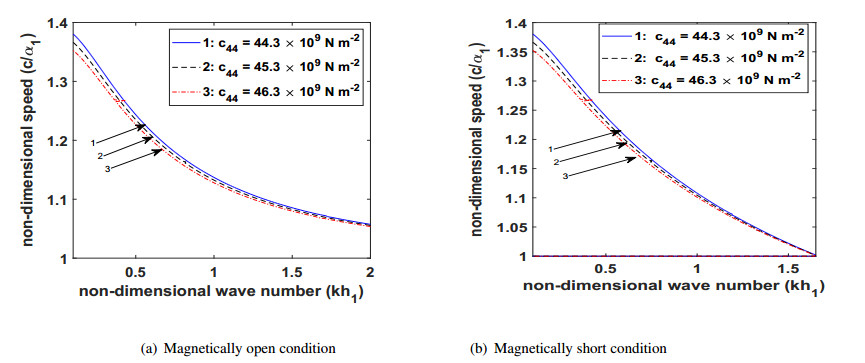
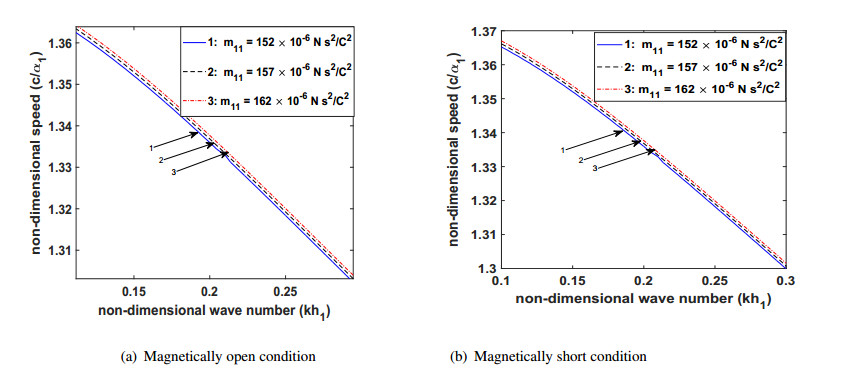
In order to check the impact of the material properties of the PM layer $CoFe_2O_4$ on the dispersion equations, Figures 2(a)-5(a) are plotted for magnetically open condition and Figures 2(b)-5(b) are plotted for magnetically short condition. Figures 2(a) and 2(b) depict the effect of the thickness of PM layer on the phase velocity of the wave for magnetically open and short conditions, respectively. The thickness of the PM layer has an unfavorable effect on the phase velocity of the wave. As the thickness of the PM layer increases, the phase velocity of the wave decreases. The effect of PM constant on the phase velocity of the wave is depicted by Figures 3(a) and 3(b) for magnetically open and short conditions, respectively. PM constant has a discouraging effect on the phase velocity of the wave. This may be ascribed to the fact that with the increase in the magnitude of the said parameter, the force due to magnetism gets remarkably strengthened, thus offering more resistance and causing loss of energy of the wave particles, resulting in lowering of the velocity of the wave. On examining Figures 4(a) and 4(b), it is reported that the elastic constant has adverse effects on the phase velocity of the wave. An increase in the values of elastic constant leads to a decrease in the phase velocity of the propagating wave.

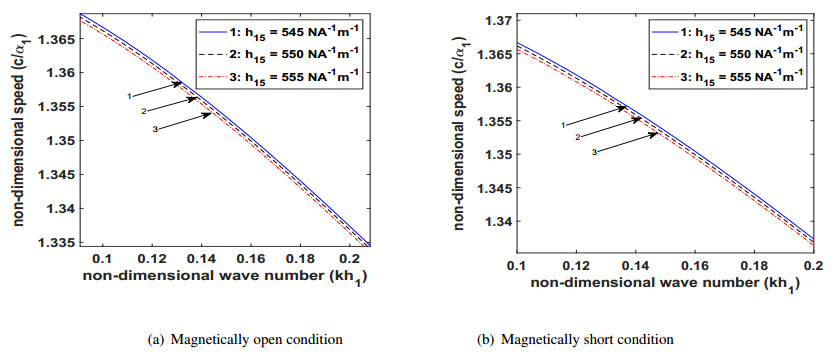
It can be observed from Figures 5(a) and 5(b) that magnetic permeability has an encouraging effect on the phase velocity of the wave under magnetically open and short conditions, respectively. With the increasing values of magnetic permeability, the phase velocity of the wave also increases. This may be due to the fact that an increase in the said parameter leads to a decrease in the magnetic field. Therefore, it may be possible that a weak magnetic field offers less resistance to the flow of wave particles thereby, increasing the phase velocity of the transferring wave.

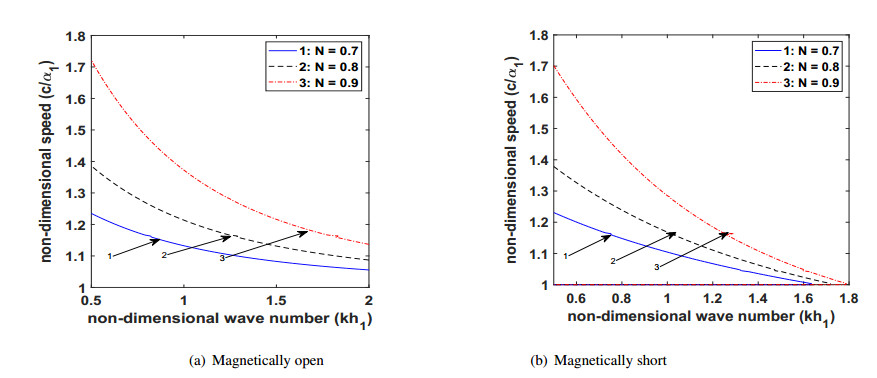
6.2.   Effect of microstructures

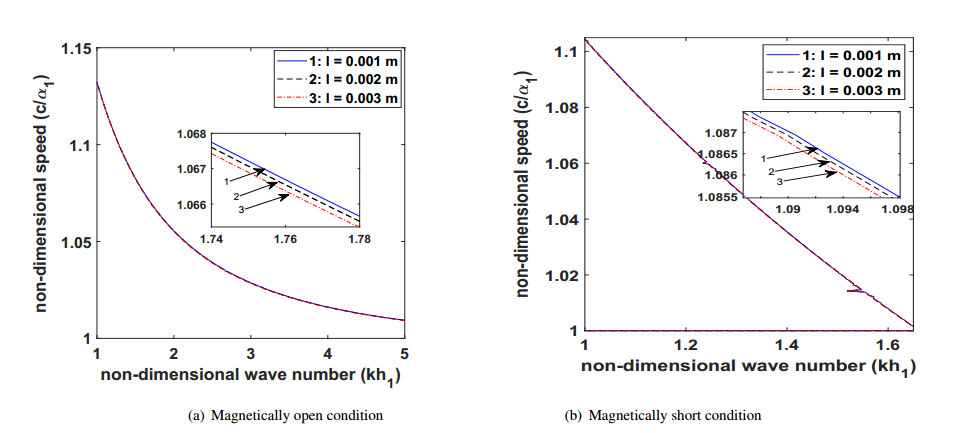
To grab the influence of microstructural dependence on the dispersion equations, Figures 6(a) and 7(a) are presented for magnetically open condition and Figures 6(b) and 7(b) are presented for magnetically short condition. Figures 6(a) and 6(b) adduces the effect of the micropolarity constant on the phase velocity of the wave for magnetically open and short conditions, respectively. These figures establish that the phase velocity of the wave increases with an increase in the values of the micropolarity constant. This is ascribed due to the additional couple stress and rotation of the particles at the microscale level. The curves in Figures 7(a) and 7(b) delve out the effect of characteristic length on the phase velocity of the propagating wave for magnetically open and short conditions, respectively. It has been remarked by many researchers that it is very difficult to identify the exact value of the characteristic length. Its value is of the order of the internal cell size of the material bearing microstructures. Hence, the value of the characteristic length is varied as 0.001 m, 0.002 m, 0.003 m. As the values of the characteristic length increases, the phase velocity of the wave decreases. Thus, characteristic length has a suppressing effect on the phase velocity of the wave.

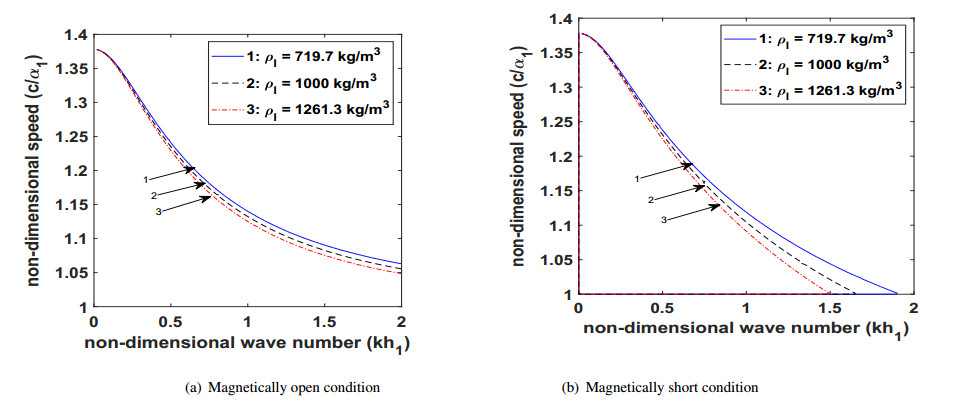
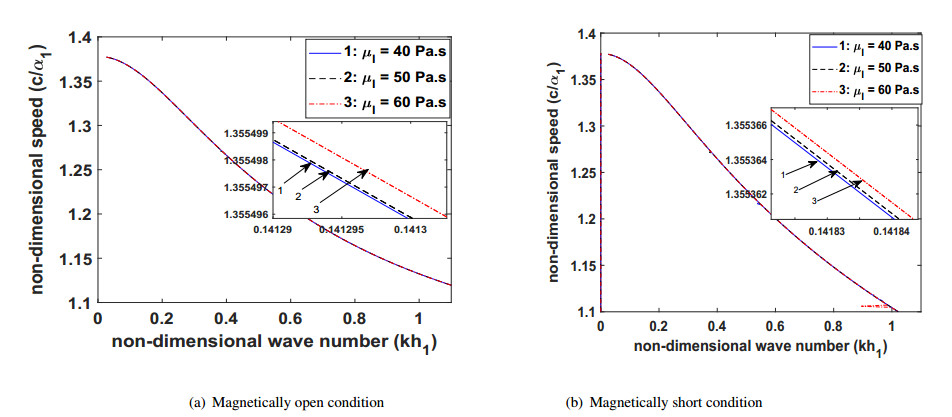
6.3.   Effect of VL loading

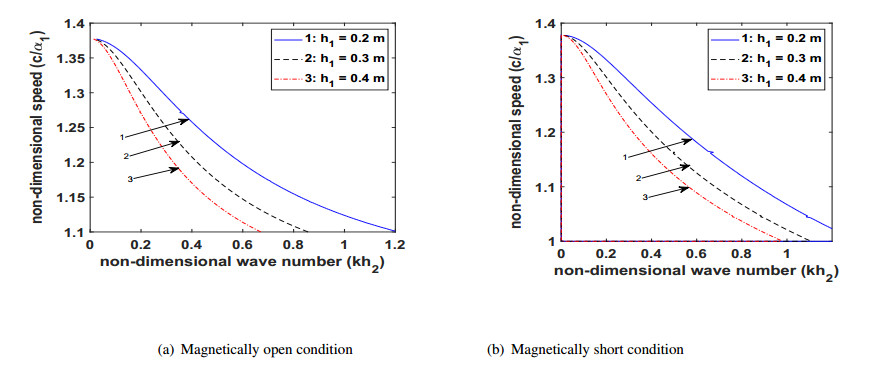
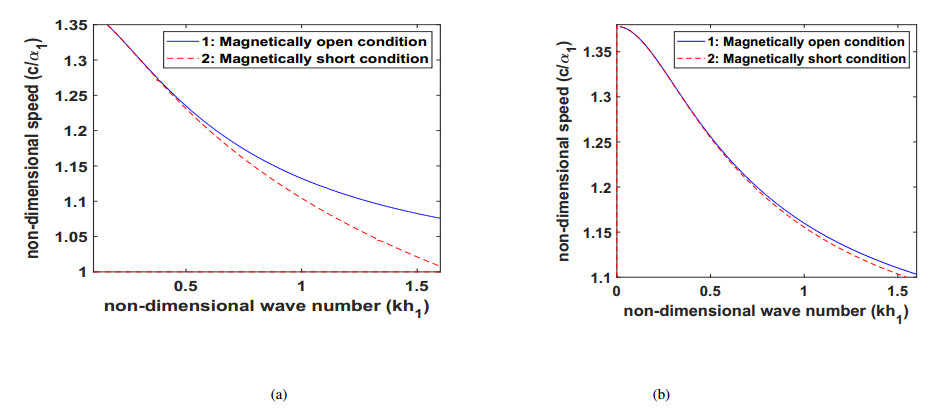
Due to the fluctuations in the environmental conditions such as rising or dropping of the temperature, scrutinizing the effects of the liquid mass density and the coefficient of viscosity on the wave propagation is essential. Figures 8(a) and 8(b) reveals the effect of the liquid mass density and Figures 9(a) and 9(b) reveals the effect of the coefficient of viscosity, on the velocity of the propagating wave in the considered structure for magnetically open and short conditions, respectively. These figures advocate that the liquid mass density has a suppressing effect on the phase velocity of the wave. The increment in the value of the liquid mass density leads to decrease in the phase velocity of the wave while the coefficient of viscosity has a favoring effect on the phase velocity of the wave. With the rising value of the coefficient of viscosity, the phase velocity of the wave increases. For magnetically open and short conditions, Figures 10(a) and 10(b), respectively delineate that an increase in the thickness of VL layer results in the decrease in the phase velocity of the wave. To compare the effect of VL loading on the phase velocity of the wave for magnetically open and short conditions Figure 11(a) is plotted under VL loading and Figure 11(b) is plotted without VL loading. From Figures 11(a) and 11(b), it can be visualized that for a large value of $kh_1$, the phase velocity of the considered wave is always more in case of magnetically open condition as compared to magnetically short condition.

7.   Concluding remarks

In the present work, we have scrutinized the propagation of a Love-type wave in a PM layer overlying a semi-infinite MP elastic substrate, loaded with VL layer. The dispersion equations are obtained in closed form for magnetically open and short cases. The dispersion equations are plotted to apprise the influence of various affecting parameters, viz. the coefficient of viscosity, the liquid mass density, the length scale parameter, the thickness of VL layer, and PM parameters, viz. PM constant, magnetic permeability, elastic constant and the thickness of PM layer on the phase velocity of Love-type waves. Following conclusions can be deduced from the study.

● Phase velocity of the considered wave decreases with the increase in the values of wave number.

● Micropolarity constant has a prominent effect on the phase velocity. As the value of the parameter increases the phase velocity also increases.

● Characteristic length scale parameter has a decaying effect on the phase velocity of the Love-type wave.

● Larger the width of the PM layer, lower is the phase velocity of the Love-type wave in the considered structure.

● As the magnitude of the thickness of the VL layer is increased, the phase velocity of the propagating wave decreases.

● The coefficient of viscosity of the VL layer favors the phase velocity of the wave. As the value of the coefficient of viscosity increases, the phase velocity of the wave also increases.

● With the decrease in values of the liquid mass density, the phase velocity of the considered wave also decreases.

● The phase velocity of the wave increases with an increase in values of magnetic permeability.

● With the increment in the values of elastic constant, the phase velocity of the transferring wave decreases.

● With the increase in the magnitude of PM constant, the phase velocity of the wave decreases.

● Phase velocity curve of Love-type wave in the considered structure for the magnetically open condition is always greater than that obtained for magnetically short condition.

Physical applications

● Love wave biosensors can be used to measure a huge number of biological substances (analytes) with a significant sensitivity and accuracy. These sensors have numerous applications in biology, chemistry, healthcare, defense, environmental monitoring and medicine (clinical practice). These surface waves employing in biosensors have a huge potential.

● The basic principle of Surface Acoustic Wave devices depends on the phase delay. PM materials are able to create an entanglement of the wave, which lowers the phase velocity of the propagating wave and enhances the sensitivity of the Love wave sensors.

● For further optimization high-intensity PM material can be considered. These features aid in the confinement of wave for a longer period which leads to high sensitivity of the device.

● Magnetostrictive vibrators are used as electroacoustic transducers to generate or to receive ultrasonic waves.

● Extremely thin magnetic sensor (called thin films) have numerous applications found in medical devices, weapon detection and data storage.

● The pertinent outcome of the present study depicting the propagation behavior of a Love-type wave in a layered structure comprising of a PM layer followed by a semi-infinite MP elastic substrate, loaded with a VL layer helps in enhancing the efficiency of Love-type wave sensors comprising of PM material working in liquid media.

Acknowledgments

The authors sincerely thank the Council of Scientific and Industrial Research, New Delhi, India for providing financial assistance through CSIR [grant number CSIR/25(0289)/18/EMR-II].

Conflict of interest

All authors declare no conflicts of interest.

Appendix