A general result on the spectral radii of nonnegative k-uniform tensors

1.   Introduction

Let $k, n$ be two positive integers. An order $k$ dimension $n$ tensor $\mathbb{A} = (a_{i_{1}\cdots i_{k}})$ over the real field $\mathbb{R}$, is a multidimensional array with $n^{k}$ entries $a_{i_{1}\cdots i_{k}}\in\mathbb{R}$, where $i_{j}\in [n] = \{1, 2, \ldots, n\}, j\in [k]$. A tensor $\mathbb{A}$ is called nonnegative, denoted by $\mathbb{A}\geq0$, if every entry of tensor $\mathbb{A}$ satisfies $a_{i_{1}\cdots i_{k}}\geq 0$.

Obviously, an $n$ dimensional vector is an order $1$ dimension $n$ tensor and a square matrix is an order $2$ dimension $n$ tensor. A tensor $\mathbb{A} = (a_{i_{1}\cdots i_{k}})$ is called symmetric if $a_{i_{1}\cdots i_{k}} = a_{\sigma (i_{1})\cdots \sigma (i_{k})}$, where $\sigma$ is any permutation on the set $\{i_{1}, \ldots, i_{k}\}$.

Let $\mathbb{A}$ be an order $k$ dimension $n$ tensor. If there is a complex number $\lambda$ and an $n$ dimensional nonzero complex vector $x = (x_{1}, x_{2}, \ldots, x_{n})^{T}$ such that

then $\lambda$ is called an eigenvalue of $\mathbb{A}$ and $x$ an eigenvector of $\mathbb{A}$ corresponding to the eigenvalue $\lambda$ (^[4,16,17,23]). Here $\mathbb{A}x^{k-1}$ and $x^{[k-1]}$ are vectors, whose $i$-th components are

and $(x^{[k-1]})_{i} = x_{i}^{k-1}$, respectively. Moreover, the spectral radius $\rho(\mathbb{A})$ of a tensor $\mathbb{A}$ is defined as $\rho(\mathbb{A}) = \max\{|\lambda|: \lambda \ \mbox{is an eigenvalue of}\ \mathbb{A}\}.$

More properties and applications of the spectral radius of a nonnegative tensor can be found in ^{[4,10,13,15,16,17,20,23,24,29,30,31]}.

A hypergraph is a natural generalization of an ordinary graph ^[2]. A hypergraph $\mathcal{H} = (V(\mathcal{H}), E(\mathcal{H}))$ on $n$ vertices is a set of vertices, say, $V(\mathcal{H}) = [n]$ and a set of edges, say, $E(\mathcal{H}) = \{e_1, e_2, \ldots, e_m\},$ where $e_i = \{i_1, i_2, \ldots, i_l\}, i_j\in [n], j = 1, 2, \ldots, l.$ Let $k\geq 2$, if $\mid e_i\mid = k$ for any $i = 1, 2, \ldots, m$, then $\mathcal{H}$ is called a $k$-uniform hypergraph. When $k = 2$, then $\mathcal{H}$ is an ordinary graph. The degree $d_i$ of vertex $i$ is defined as $d_i = |\{e_j:i\in e_j\in E(\mathcal{H})\}|.$ If $d_i = d$ for any vertex $i$ of a hypergraph $\mathcal{H}$, then $\mathcal{H}$ is called $d$-regular. A walk $W$ of length $\ell$ in $\mathcal{H}$ is a alternate sequence of vertices and edges: $v_0, e_1, v_1, e_2, \ldots, e_\ell, v_\ell,$ where $\{v_i, v_{i+1}\}\subseteq e_{i+1}$ for $i = 0, 1, \ldots, \ell-1$. The hypergraph $\mathcal{H}$ is said to be connected if every two vertices are connected by a walk.

The authors (^[7,17,18]) proposed the study of the spectra of hypergraphs via the spectra of tensors, introduced the adjacency tensor $\mathbb{A}(\mathcal{H})$ of a hypergraph $\mathcal{H}$, and defined the eigenvalues (and spectrum) of a uniform hypergraph as the eigenvalues (and spectrum) of the adjacency tensor.

Definition 1.1. (^[7,17]) Let $\mathcal{H} = (V(\mathcal{H}), E(\mathcal{H}))$ be a $k$-uniform hypergraph on $n$ vertices. The adjacency tensor of $\mathcal{H}$ is defined as the order $k$ dimension $n$ tensor $\mathbb{A}(\mathcal{H})$, whose $(i_1i_2\cdots i_k)$-entry is

Let $\mathbb{D}(\mathcal{H})$ be an order $k$ dimension $n$ diagonal tensor with its diagonal entry $\mathbb{D}_{ii\cdots i}$ being $d_i$, the degree of vertex $i$, for all $i\in V(\mathcal{H}) = [n]$. In 2014, Qi ^[24] defined the signless Laplacian tensor $\mathbb{Q}(\mathcal{H}) = \mathbb{D(\mathcal{H})}+ \mathbb{A(\mathcal{H})}$ of the hypergraph $\mathcal{H}$, and defined the signless Laplacian eigenvalues (and spectrum) of a uniform hypergraph as the eigenvalues (and spectrum) of the signless Laplacian tensor. Clearly, the adjacency tensor $\mathbb{A}(\mathcal{H})$ and the signless Laplacian tensor $\mathbb{Q}(\mathcal{H})$ of a $k$-uniform hypergraph $\mathcal{H}$ are nonnegative and symmetric.

The spectral radii of $\mathbb{A(\mathcal{H})}$ and $\mathbb{Q(\mathcal{H})}$, denoted by $\rho(\mathbb{A(\mathcal{H})})$ and $\rho(\mathbb{Q(\mathcal{H})})$, are called the (adjacency) spectral radius and the signless Laplacian spectral radius of $\mathcal{H}$, respectively.

In general, the zero-nonzero pattern of an order $k$ dimension $n$ tensor $\mathbb{A}$ may not be regarded as the zero-nonzero pattern of the adjacency tensor or the signless Laplacian tensor of some $k$-uniform hypergraph.

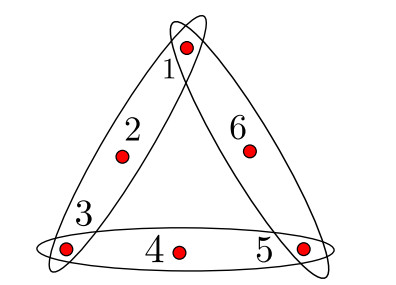
Example 1.2. Let $\mathcal{H}$ be an 3-uniform hypergraph of order 6 as Figure 1, $\mathbb{A}(\mathcal{H})$ and $\mathbb{Q}(\mathcal{H})$ be the adjacency tensor and signless Laplacian tensor of $\mathcal{H}$. Then by Definition 1, for $\mathbb{A}(\mathcal{H})$, we have

and $(\mathbb{A}(\mathcal{H}))_{i_{1}i_{2}i_{3}} = 0$ for the others; for $\mathbb{Q}(\mathcal{H})$, we have

and $(\mathbb{Q}(\mathcal{H}))_{i_{1}i_{2}i_{3}} = (\mathbb{A}(\mathcal{H}))_{i_{1}i_{2}i_{3}}$ for the others.

We can see that $(\mathbb{A}(\mathcal{H}))_{i_1i_2i_3} = 0$ and $(\mathbb{Q}(\mathcal{H}))_{i_1i_2i_3} = 0$ if $i_1 = i_2\not = i_3$, or $i_1 = i_3\not = i_2$, or $i_2 = i_3\not = i_1$.

In order to better study the spectral $k$-uniform hypergraphs theory via the spectra of tensors, we define $k$-uniform tensors, which are more closely related to the $k$-uniform hypergraphs than the general tensors.

Let $S = \{s_1, s_2, \ldots, s_n\}$ be an $n$-element set, noting that $s_i\not = s_j$ if $i\not = j$.

Definition 1.3. Let $n\geq 2, k\geq 2$ and $\mathbb{A} = (a_{i_{1}\cdots i_{k}})$ be an order $k$ dimension $n$ tensor. For any entry $a_{i_{1}i_{2}\cdots i_{k}}\neq0$, if $\{i_1, i_2, \ldots, i_k\}$ is a $k$-element set or $i_{1} = i_{2} = \cdots = i_{k}$, then we call such $\mathbb{A}$ a $k$-uniform tensor.

Obviously, a $2$-uniform tensor is an ordinary matrix. Both the adjacency tensor $\mathbb{A}(\mathcal{H})$ and the signless Laplacian tensor $\mathbb{Q}(\mathcal{H})$ of a $k$-uniform hypergraph $\mathcal{H}$ are nonnegative symmetric $k$-uniform tensors.

What's more, we can see that the zero-nonzero pattern of an order $k$ dimension $n$ symmetric $k$-uniform tensor $\mathbb{A}$ must be regarded as the zero-nonzero pattern of the adjacency tensor or the signless Laplacian tensor of some $k$-uniform hypergraph.

Let $A = (a_{ij})$ be a nonnegative matrix with order $n$. For $1\leq i \leq n$, the $i$-th row sum of $A$ is $r_{i}(A) = \sum\limits_{j = 1}^{n}a_{ij}(\geq 0)$. When $r_{i}(A) > 0$ for $1\leq i \leq n$, we take

and we call $m_{i}(A)$ the $i$-th average $2$-row sum of $A$, and $\omega_{i}(A)$ the $i$-th average of average $2$-row sum (^[1]) of $A$.

Let $\mathbb{A} = (a_{i_{1}\cdots i_{k}})$ be an order $k$ dimension $n$ nonnegative tensor. The $i$-th slice of $\mathbb{A}$, denoted by $\mathbb{A}_{i}$ in ^[26], is the subtensor of $\mathbb{A}$ with order $k-1$ and dimension $n$ such that $(\mathbb{A}_{i})_{i_{2}\cdots i_{k}} = a_{ii_{2}\cdots i_{k}},$ and $r_i(\mathbb{A}) = \sum\limits_{i_{2}, \ldots, i_{k} = 1}^{n}a_{ii_{2}\cdots i_{k}}(\geq 0)$ is called the $i$-th slice sum of the tensor $\mathbb{A}$. Clearly, the $i$-th slice sum of the tensor $\mathbb{A}$ is the generalization of the $i$-th row sum of the matrix $A$.

Similarly, when $r_i(\mathbb{A}) > 0$ for $1\leq i \leq n$, we take

and we call $m_{i}(\mathbb{A})$ the $i$-th average $2$-slice sum of $\mathbb{A}$, and $\omega_{i}(\mathbb{A})$ the $i$-th average of average $2$-slice sum of $\mathbb{A}$.

Duan and Zhou ^[8], Xing and Zhou ^[27], and Adam, Aggeli and Aretaki ^[1] obtained the upper and lower bounds on the spectral radius of a nonnegative matrix by the row sum, the average $2$-row sum, and the average of average $2$-row sum, respectively, and characterized the equality cases if the matrix is irreducible. In ^[20], the paper obtained the upper bound on the spectral radius of a nonnegative $k$-uniform tensor by the slice sum, and characterized the equality cases if the tensor is weakly irreducible.

Motivated by the above results, for $q\geq0, 1\leq i \leq n$, we introduce a new quantity $r^{(q)}_{i}(\mathbb{A})$, called the $i$-th $q$-times-average slice sum:

and when $q\geq 2$, if $r^{(1)}_{i}(\mathbb{A}) > 0$ for any $i\in[n]$, then

We can see that for any $i\in [n]$,

whether $\mathbb{A}$ is a matrix (the case of $k = 2$) or a tensor (the case of $k\geq 3$).

By using the notation $r_{i}^{(q)}(\mathbb{A})$, we will generalize the upper bounds on the spectral radius of nonnegative matrices in ^[1,8,27] and nonnegative $k$-uniform hypergraphs in ^[5] to nonnegative $k$-uniform tensors, and obtain a general result of the upper bound on the spectral radius in Section 3. By applying the general upper bounds, we will obtain some known or new results on the spectral radius and signless Laplacian spectral radius of the $k$-uniform (directed) hypergraphs.

2.   Preliminaries

In 2013, Shao ^[25] defined the general product and similarity of two tensors, which are very useful to study the spectrum of nonnegative tensors.

Definition 2.1. (^[25]) Let $\mathbb{A} = (a_{i_1i_2\cdots i_m})$ and $\mathbb{B} = (b_{i_1i_2\cdots i_k})$ be two tensors with order $m\geq 2$ and $k\geq1$ dimension $n$, respectively. The general product $\mathbb{A}\cdot\mathbb{B}$ (sometimes simplified as $\mathbb{A}\mathbb{B}$) of $\mathbb{A}$ and $\mathbb{B}$ is the following tensor $\mathbb{C}$ with order $(m-1)(k-1)+1$ and dimension $n$:

for $i\in[n], \alpha_{1}, \ldots, \alpha_{m-1}\in[n]^{k-1}.$

The tensor product is a generalization of the usual matrix product, and satisfies a very useful property: The associative law (Theorem 1.1 of ^[25]). In this paper, all the tensor product obey (2.1). According to (2.1), the former $\mathbb{A}x^{k-1}$ can be expressed as the product $\mathbb{A}x$, and

Definition 2.2. (^[25]) Let $\mathbb{A}$ and $\mathbb{B}$ be two order $k$ dimension $n$ tensors. Suppose that there exist two matrices $P$ and $Q$ of order $n$ with $P\mathbb{I}Q = \mathbb{I}$ such that $\mathbb{B} = P\mathbb{A}Q$, then we say that the two tensor $\mathbb{A}$ and $\mathbb{B}$ are similar.

Definition 2.3. (^[25]) Let $\mathbb{A} = (a_{i_{1}i_2\cdots i_{k}})$ and $\mathbb{B} = (b_{i_{1}i_2\cdots i_{k}})$ be two order $k$ dimension $n$ tensors. We say that $\mathbb{A}$ and $\mathbb{B}$ are diagonal similar, if there exists some invertible diagonal matrix $D = (d_{11}, d_{22}, \ldots, d_{nn})$ of order $n$ such that $\mathbb{B} = D^{-(k-1)}\mathbb{A}D$ with entries $b_{i_{1}i_{2}\cdots i_{k}} = d_{i_{1}i_{1}}^{-(k-1)}a_{i_{1}i_{2}\cdots i_{k}}d_{i_{2}i_{2}}\cdots d_{i_{k}i_{k}}.$

Definition 2.4. (^[25]) Let $\mathbb{A} = (a_{i_{1}i_2\cdots i_{k}})$ and $\mathbb{B} = (b_{i_{1}i_2\cdots i_{k}})$ be two order $k$ dimension $n$ tensors. We say that $\mathbb{A}$ and $\mathbb{B}$ are permutational similar, if there exists some permutation matrix $P = P_{\sigma} = (p_{ij})$ such that $\mathbb{B} = P\mathbb{A}P^{T}$ with the entries $b_{i_{1}i_{2}\cdots i_{k}} = a_{\sigma(i_{1})\sigma(i_{2})\cdots \sigma(i_{k})},$ where $p_{ij} = 1\Leftrightarrow j = \sigma(i)$ and $\sigma$ is a permutation on the set $[n]$.

Clearly, both diagonal similar and permutational similar are special kind of similarity of tensors.

Theorem 2.5. (^[25]) Let the two order $k$ dimension $n$ tensors $\mathbb{A}$ and $\mathbb{B}$ be similar. Then they have the same eigenvalues including multiplicity and same spectral radius.

Definition 2.6. (^[10,30]) Let $\mathbb{A}$ be an order $k$ dimensional $n$ tensor. If there exists a nonempty proper subset $I$ of the set $[n]$, such that

then $\mathbb{A}$ is called weakly reducible. If $\mathbb{A}$ is not weakly reducible, then $\mathbb{A}$ is called weakly irreducible.

It is obvious that a weakly irreducible tensor is a generalization of an irreducible matrix.

Lemma 2.7. (Lemma 3.8 of ^[12], Lemma 5.3 of ^[29]) Let $\mathbb{A}$ be a nonnegative tensor of order $k\geq2$ and dimension $n\geq2$, and $x = (x_{1}, x_{2}, \ldots, x_{n})^{T}$ be a positive vector. Then

Moreover, if $\mathbb{A}$ is weakly irreducible, then one of the equalities in (2.2) holds if and only if $\mathbb{A}x = \rho(\mathbb{A})x^{[k-1]}$.

By taking $x = (r_{1}^{(q-1)}(\mathbb{A}), r_{2}^{(q-1)}(\mathbb{A}), \ldots, r_{n}^{(q-1)}(\mathbb{A}))^{T}$ in Lemma 2.7, we can obtain the following Lemma 2.8 immediately.

Lemma 2.8. Let $k\geq2, n\geq2, q\geq1$, $\mathbb{A}$ be a nonnegative tensor with order $k$ dimension $n$, the notation $r_{i}^{(q)}(\mathbb{A})$ for $i\in[n]$ defined as in Section 1, where $r_{i}^{(1)}(\mathbb{A}) > 0$ for $i\in[n]$ when $q\geq 2$. Then for $q\geq 1$, we have

Moreover, if $\mathbb{A}$ is weakly irreducible, then one of the equalities in (2.3) holds if and only if $r_{1}^{(q)}(\mathbb{A}) = r_{2}^{(q)}(\mathbb{A}) = \cdots = r_{n}^{(q)}(\mathbb{A})$.

In fact, we can obtain some known or new results from Lemma 2.8. For example, if $k = 2$, $q = 1, 2$, we can obtain Theorems 1.1 and 1.2 in Chapter 2 of ^[21]; if $k = 2$ and $q = 3$, we can obtain Proposition 3 in ^[1]; if $k\geq 3$ and $q = 1$, we can obtain Lemma 5.2 in ^[29] and Lemma 3.8 in ^[12]; if $k\geq 3$ and $q = 2$, we can obtain Proposition 2.1 in ^[19]; if $k\geq 3$ and $q = 3$, we can obtain the following Corollary 2.4 with the parameter $\omega_{i}(\mathbb{A})$.

Corollary 2.9. Let $\mathbb{A}$ be a nonnegative tensor of order $k\geq2$ and dimension $n$ with all positive slice sums, say, $r_{i}(\mathbb{A}) > 0$ for any $i\in [n]$. Then

Moreover, if $\mathbb{A}$ is weakly irreducible, then one of the equalities in (2.4) holds if and only if $\omega_{1}(\mathbb{A}) = \omega_{2}(\mathbb{A}) = \cdots = \omega_{n}(\mathbb{A})$.

We denote by $\binom{n}{r}$ the number of $r$-combinations of an $n$-element set, and let $\binom{n}{r} = 0$ if $r > n$ or $r < 0$. Clearly, $\binom{n}{r} = \frac{n!}{r!(n-r)!}$ when $0\leq r\leq n$.

Lemma 2.10. (^[3]) Let $n$, $k$ and $m$ be positive integers. Then

$(1)\sum\limits_{r = 0}^{k}\binom{n}{r}\binom{m}{k-r} = \binom{n+m}{k}$, where $n+m\geq k;$

$(2) \binom{n}{k} = \frac{n}{k}\binom{n-1}{k-1}$, where $n\geq k \geq 1.$

Lemma 2.11. Let $n\geq2$, $k\geq2$, $s\geq2$ and $i\in [n]$ be positive integers, $x_{j}\geq1$ for $1\leq j\leq s-1$, and $x_{j} = 1$ for $s\leq j\leq n$. For any $r\in\{0, 1, \ldots, k-1\}$, we take $N_{r}^{s}(i) = \{\{i_{2}, \ldots, i_{k}\}\hskip.15cm |\hskip.15cm i_{2}, \ldots, i_{k}\in \{1, 2, \ldots, n\}\setminus \{i\}$, and there are exactly $r$ elements in $\{i_{2}, \ldots, i_{k}\}$ such that they are not less than $s\}$. Then

Proof. Obviously, the family of all $(k-1)$-element subsets of $\{1, 2, \ldots, n\}\setminus \{i\}$ is just equal to $\bigcup\limits_{r = 0}^{k-1}N_{r}^{s}(i)$.

Case 1: $s\leq i \leq n$, and $s\geq2$.

Clearly, $\{i_{2}, \ldots, i_{k}\}\in N_{r}^{s}(i)$ and $s\leq i \leq n$ imply that we should choose $r$ elements from the set $\{s, \ldots, n\}\setminus \{i\}$ and choose $k-1-r$ elements from the set $\{1, 2, \ldots, s-1\}$, then we have

where we choose $x_{t}$ for $1\leq t\leq s-1$ which implies we should choose $r$ elements from the set $\{s, \ldots, n\}\setminus \{i\}$ and choose $k-2-r$ elements from the set $\{1, 2, \ldots, s-1\}\setminus \{t\}$, and the contribution to the sum is $x_{t}^{k-1}$; similarly, we choose $x_{t}$ for $t\in\{s, \ldots, n\}\setminus \{i\}$ which implies we should choose $r-1$ elements from the set $\{s, \ldots, n\}\setminus \{i, t\}$ and choose $k-1-r$ elements from the set $\{1, 2, \ldots, s-1\}$.

When $r = k-1$, we know $i_2, \ldots, i_k\in \{s, \ldots, n\}$ and $x_{i_{2}}^{k-1}+\cdots +x_{i_{k}}^{k-1}-(k-1) = 0$ by $x_s = \cdots = x_{n} = 1$. Then combining (2.5), (2.6) and Lemma 2.10, we have

Case 2: $1\leq i \leq s-1$, and $s\geq3$.

Clearly, $\{i_{2}, \ldots, i_{k}\}\in N_{r}^{s}(i)$ and $1\leq i \leq s-1$ imply that we should choose $r$ elements from the set $\{s, \ldots, n\}$ and choose $k-1-r$ elements from the set $\{1, 2, \ldots, s-1\}\setminus \{i\}$, then we have

Combining (2.7), (2.8) and Lemma 2.10, we have

The proof is completed.

3.   Main results

In this section, we shall obtain a sharp upper bound on the spectral radius of a nonnegative $k$-uniform tensor by using the notation $r^{(q)}_{i}(\mathbb{A})$ for $q\geq1$, which is the generalization of the main result in ^[1,8,27] for nonnegative matrices and the main result in ^[5] for $k$-uniform hypergraphs. Furthermore, we give two examples to show the upper bounds for different $q$ are not comparable.

Recall the definition of $r^{(q)}_{i}(\mathbb{A})$ in Section 1, we denote $r^{(q)}_{i}(\mathbb{A}) = r^{(q)}_{i}$ for simplify. Especially, $r_{i}(\mathbb{A}) = r_{i}$, $m_{i}(\mathbb{A}) = m_{i}$ and $\omega_{i}(\mathbb{A}) = \omega_{i}$.

Theorem 3.1. Let $n\geq 2, k\geq 2, q\geq1$, $\mathbb{A} = (a_{i_{1}i_{2}\cdots i_{k}})$ be a nonnegative $k$-uniform tensor with order $k$ dimension $n$, the notation $r^{(q)}_{1}\geq r^{(q)}_{2} \geq \cdots \geq r^{(q)}_{n}$, where $r_{i}^{(1)} > 0$ for $i\in[n]$ when $q\geq2$. Let $M$ be the largest diagonal element and $N (>0)$ be the largest non-diagonal element of $\mathbb{A}$, $b = \max\limits_{1\leq i, j\leq n}\frac{r^{(q-1)}_{j}}{r^{(q-1)}_{i}}$, $L = Nb^{k-1}(k-2)!\binom{n-2}{k-2},$ $\psi^{(q)}_1 = r^{(q)}_1$, and for $2\leq s\leq n$,

Then $\rho(\mathbb{A})\leq \min\limits_{1\leq s\leq n}\psi^{(q)}_{s}.$

Moreover, if $\mathbb{A}$ is weakly irreducible, and $\psi^{(q)}_l = \min\limits_{1\leq s\leq n}\psi^{(q)}_{s}$ for some $l\in [n]$, then

$(1)$ when $k = 2$, $\rho(\mathbb{A}) = \psi^{(q)}_{l}$ if and only if $r^{(q)}_{1} = r^{(q)}_{2} = \cdots = r^{(q)}_{n}$ or for some $t\hskip.15cm (2\leq t\leq l)$, $\mathbb{A}$ satisfies the following conditions:

(ⅰ) $a_{ii} = M$ for $1\leq i\leq t-1$;

(ⅱ) $a_{ih} = N$ and $\frac{r^{(q-1)}_{h}}{r^{(q-1)}_{i}} = b$ for $1\leq i\leq n$, $1\leq h\leq t-1$ and $i\neq h$;

(ⅲ) $r^{(q)}_{t} = r^{(q)}_{t+1} = \cdots = r^{(q)}_{n}$.

(2) when $k\geq 3$, $\rho(\mathbb{A}) = \psi^{(q)}_{l}$ if and only if $r^{(q)}_{1} = r^{(q)}_{2} = \cdots = r^{(q)}_{n}$.

Proof. By (1.1) and (1.2), we have $r^{(q)}_{i}\geq a_{ii\cdots i}$ for $1\leq i\leq n$ and $q\geq 1$, then $r^{(q)}_{1}\geq M$.

First, we show $\rho(\mathbb{A})\leq \psi^{(q)}_{s}$ for $1\leq s\leq n$.

If $s = 1$, then we have $\rho(\mathbb{A})\leq\psi^{(q)}_{1}$ by $\psi^{(q)}_{1} = r^{(q)}_{1}$ and Lemma 2.8.

If $2\leq s\leq n$. Let

where $x_{i}^{k-1} = 1+\frac{r^{(q)}_i-r^{(q)}_s}{\psi^{(q)}_s+L-M}$ for $1\leq i\leq s-1$ and $x_s = \cdots = x_n = 1$.

Now we show $x_{i}\geq 1$ for $1\leq i\leq s-1$. By $r^{(q)}_{1}\geq r^{(q)}_{2} \geq \cdots \geq r^{(q)}_{n}$, we only need to show $\psi^{(q)}_s+L-M > 0$.

If $\sum\limits_{t = 1}^{s-1}(r^{(q)}_{t}-r^{(q)}_{s}) > 0$, then by (3.1), we have

and thus $\psi^{(q)}_{s}-M+L > 0$.

If $\sum\limits_{t = 1}^{s-1}(r^{(q)}_{t}-r^{(q)}_{s}) = 0$, then $r^{(q)}_1 = r^{(q)}_2 = \cdots = r^{(q)}_s$. Thus $\psi_{s}-M+L > 0$ by $r^{(q)}_1\geq M$ and $\psi_{s} = r^{(q)}_s$ from (3.1).

Combining the above arguments, we have $x_{i}\geq 1$, and then $U$ is an invertible diagonal matrix. Let $\mathbb{B} = U^{-(k-1)}\mathbb{A}U = (b_{i_{1}\cdots i_{k}}).$ By Theorem 2.5, we have

By (3.1), it is easy to see that

Then by $x_{t}^{k-1} = 1+\frac{r^{(q)}_t-r^{(q)}_s}{\psi^{(q)}_s+L-M}$, we have

Therefore, by $\psi^{(q)}_{s}-M+L > 0$, we have

In the following we will show $r_i(\mathbb{B})\leq \psi^{(q)}_s$ for any $i\in [n]$.

Let $S(i) = \{\{i, i_2, \ldots, i_k\}|a_{ii_2\cdots i_k}\not = 0\}$. Since $M$ be the largest diagonal element and $N > 0$ be the largest non-diagonal element of tensor $\mathbb{A}$, by the definition of $r^{(q)}_i(\mathbb{A})$, Definition 2.3, Theorem 2.5, we have

where $\{i_{2}, \ldots, i_{k}\}\subseteq \{1, 2, \ldots, n\}\setminus \{i\}$ and $N_{r}^{s}(i)$ defined in Lemma 2.6 for $0\leq r\leq k-1$, and then $|S(i)|\leq \sum\limits_{r = 0}^{k-1}|N_r^s(i)|$ for $i\in[n]$.

Furthermore, the equality holds in (3.4) if and only if the following (a), (b), (c) and (d) hold:

(a) $x_{i}^{k-1} = 1$ or $a_{i\cdots i} = M$ for $x_{i} > 1$;

(b) for any $\{i, i_{2}, \ldots, i_{k}\}\in S(i)$, $x_{i_{2}}\cdots x_{i_{k}} = 1$ or $a_{ii_{2}\cdots i_{k}} = N$ and $\frac{r^{(q-1)}_{i_j}}{r^{(q-1)}_{i}} = b$ for any $j\in\{2, \ldots, k\}$ and $x_{i_{2}}\cdots x_{i_{k}} > 1$;

(c) $x_{i_{2}} = \cdots = x_{i_{k}}$ for any $\{i, i_{2}, \ldots, i_{k}\}\in S(i)$;

(d) $\sum\limits_{\{i, i_{2}, \ldots, i_{k}\}\in S(i)}\left(\frac{x_{i_{2}}^{k-1}+\cdots +x_{i_{k}}^{k-1}}{k-1}-1\right) = \sum\limits_{r = 0}^{k-1}\sum\limits_{ \{i_{2}, \ldots, i_{k}\}\in N_{r}^{s}(i)}\left(\frac{x_{i_{2}}^{k-1}+\cdots +x_{i_{k}}^{k-1}}{k-1}-1\right)$.

Case 1: $s\leq i\leq n$.

We note $x_s = \cdots = x_n = 1$ and $r^{(q)}_1\geq \cdots \geq r^{(q)}_s\geq \cdots \geq r^{(q)}_i\geq \cdots \geq r^{(q)}_n$. By (3.3), (3.4) and Lemma 2.11, we have

where the second equality holds if and only if the following condition (e) holds: (e) $r^{(q)}_{i} = r^{(q)}_{s}$.

Case 2: $1\leq i\leq s-1$.

In this case, $x_{i}^{k-1} = 1+\frac{r^{(q)}_i-r^{(q)}_s}{\psi^{(q)}_s+L-M}$ for $1\leq i\leq s-1$.

Subcase 2.1: $s\geq 3$.

By (3.3), (3.4) and Lemma 2.11, we have

Subcase 2.2: $s = 2$.

In this subcase, we have $i = 1$ by $1\leq i\leq s-1$ and we only need to show $r_1(\mathbb{B})\leq \psi^{(q)}_2$.

By the definition of $N_{r}^{2}(1)$, and $x_2 = \cdots = x_n = 1$, we have

On the other hand, by (3.3), we have $x_1^{k-1} = \frac{\psi^{(q)}_2-r^{(q)}_{2}+L}{L}.$ Then by (3.1) and (3.4), we have

Combining Subcases 2.1 and 2.2, we have $r_{i}(\mathbb{B})\leq \psi^{(q)}_s$ for $1\leq i\leq s-1$, and combining Cases 1 and 2, we have $r_{i}(\mathbb{B})\leq \psi^{(q)}_s$ for $1\leq i\leq n$. Then $\rho(\mathbb{A}) = \rho(\mathbb{B})\leq \max\limits_{1\leq i\leq n}r_{i}(\mathbb{B})\leq \psi^{(q)}_s$ for $2\leq s\leq n$ by (3.2) and Lemma 2.8.

Therefore, we know $\rho(\mathbb{A})\leq \psi^{(q)}_s$ for $1\leq s\leq n$ and thus $\rho(\mathbb{A})\leq \min\limits_{1\leq s\leq n}\psi^{(q)}_s$.

Now suppose that $\mathbb{A}$ is weakly irreducible. Then $\mathbb{B}$ is also weakly irreducible by $\mathbb{B} = U^{-(k-1)}\mathbb{A}U$. Let $\psi^{(q)}_l = \min\limits_{1\leq s\leq n}\psi^{(q)}_s$.

Case 1: $l = 1$.

By Lemma 2.8 and the fact $r^{(q)}_1 = \max\limits_{1\leq i\leq n}r^{(q)}_i$, we have $\rho(\mathbb{A}) = \psi^{(q)}_{1}$ if and only if $r^{(q)}_{1} = r^{(q)}_{2} = \cdots = r^{(q)}_{n}$.

Case 2: $2\leq l\leq n$.

Then $\rho(\mathbb{B}) = \max\limits_{1\leq i\leq n}r_i(\mathbb{B})$ and thus $r_1(\mathbb{B}) = r_2(\mathbb{B}) = \cdots = r_n(\mathbb{B}) = \psi^{(q)}_l$ by $\psi^{(q)}_l = \rho(\mathbb{A}) = \rho(\mathbb{B})\leq \max\limits_{1\leq i\leq n}r_i(\mathbb{B})\leq \psi^{(q)}_l$ and Lemma 2.8. Therefore, (a), (b), (c) and (d) hold for $1\leq i\leq n$, (e) holds for $l\leq i\leq n$.

Subcase 2.1: $r^{(q)}_{1} = r^{(q)}_{l}$.

By $r^{(q)}_{1}\geq r^{(q)}_{2} \geq \cdots \geq r^{(q)}_{n}$ and (e) $r^{(q)}_{i} = r^{(q)}_{l}$ for $l\leq i\leq n$, then we have $r^{(q)}_{1} = r^{(q)}_{2} = \cdots = r^{(q)}_{n}$.

Subcase 2.2: $r^{(q)}_{1} > r^{(q)}_{l}$.

Let $t$ be the smallest integer such that $r^{(q)}_{t} = r^{(q)}_{l}$ for $1 < t\leq l$. By $r^{(q)}_{1}\geq r^{(q)}_{2} \geq \cdots \geq r^{(q)}_{n}$ and (e) $r^{(q)}_{i} = r^{(q)}_{l}$ for $l\leq i\leq n$, we have $r^{(q)}_{1}\geq r^{(q)}_{2}\geq \cdots\geq r^{(q)}_{t-1} > r^{(q)}_{t} = r^{(q)}_{t+1} = \cdots = r^{(q)}_{n}$, and $x_{1}\geq x_2\cdots\geq x_{t-1} > x_t = \cdots = x_l\cdots = x_n = 1$.

When $k\geq 3$, (d) implies there exists some $r$ $(1\leq r\leq k-2)$ such that $\{i_2, \ldots, i_k\}\in N_r^l(i)$, $\{i, i_2, \ldots, i_k\}\in S(i)$ and there are $q(\geq r)$ elements in $\{i_2, \ldots, i_k\}$ chosen from $\{t, \ldots, l,$ $\ldots, n\}$, $k-1-q$ elements in $\{i_2, \ldots, i_k\}$ chosen from $\{1, \ldots, t-1\}$, which is a contradiction with (c): $x_{i_2} = \cdots = x_{i_k}$. Thus we only consider the case of $k = 2$.

In the case of $k = 2$, (d) implies

Then (ⅰ)–(ⅲ) follow from (a), (b), (c), (d) for $1\leq i\leq n$, and (e) for $l\leq i\leq n$, and thus (1) and (2) hold.

Conversely, if $r^{(q)}_{1} = r^{(q)}_{2} = \cdots = r^{(q)}_{n}$, then $\psi^{(q)}_{s} = r^{(q)}_{s}$ for $1\leq s\leq n$. By Lemma 2.8, we have $\rho(\mathbb{A}) = \min\limits_{1\leq s\leq n}\psi^{(q)}_{s}$.

Especially, if $k = 2$ and (ⅰ)–(ⅲ) hold, then (a), (b), (c) and (d) hold for $1\leq i\leq n$, (e) holds for $l\leq i\leq n$. Then we have $r_{i}(\mathbb{B}) = \psi^{(q)}_{l}$ for $1\leq i\leq n$. Therefore by Lemma 2.8, we have $\rho(\mathbb{A}) = \rho(\mathbb{B}) = \max\limits_{1\leq i\leq n}r_i(\mathbb{B}) = \psi^{(q)}_{l} = \min\limits_{1\leq s\leq n}\psi^{(q)}_{s}$.

We note that when $k = 2$, a tensor is a matrix, and weak irreducibility for tensors corresponds to irreducibility for matrices. Then we can obtain Theorem 2.1 of ^[8], Theorem 2.1 of ^[27], and Theorem 4 of ^[1] from Theorem 3.1 by taking $q = 1, 2, 3$ immediately.

When $k\geq 2$ and $q = 1$, we can obtain Theorem 2.1 of ^[20] from Theorem 3.1, which is the generalization of Theorems 1 and 2 in ^[5]. Similarly, we can obtain more if we take $q = 2, 3$. Now we list these three results as follows.

Let $\psi^{(1)}_1 = r_1$, $\psi^{(2)}_1 = m_1$, $\psi^{(3)}_1 = \omega_1$, and for $2\leq s\leq n$,

Now we give two examples to show the upper bounds for different $q$ are not comparable.

Example 3.2. Let $\mathbb{A}$ be a nonnegative 3-uniform tensor with order 3 dimension 3, the slices of $\mathbb{A}$ are given as follows:

We can get the following table with the help of MATLAB software.

From the above table, we see that $r_1^{(2)}(\mathbb{A}) > r_2^{(2)}(\mathbb{A}) > r_3^{(2)}(\mathbb{A})$ holds, it implies that when $q = 2$ we can apply Theorem 3.1 to $\mathbb{A}$, and we obtain $\rho(\mathbb{A})\leq \min\limits_{1\leq i\leq 3}\psi^{(2)}_{i} = \psi^{(2)}_{2} = 38.5154.$

In order to apply Theorem 3.1 when $q = 1, 3$, we let $P$ be a permutation matrix of order 3 as follows, then $\mathbb{A}$ is permutation similar to $\mathbb{A}^{\prime} = P\mathbb{A}P^{T}$ by definition 2.4 and $\rho(\mathbb{A}) = \rho(\mathbb{A}^{\prime})$ by Theorem 2.5. We also write the slices of $\mathbb{A}^{\prime}$, and get the following table of tensor $\mathbb{A^{\prime}}$ as follows, where $\chi^{(q)}_{i}$ be the $\psi^{(q)}_{i}$ of $\mathbb{A}^{\prime}$ for $q\in [3]$ and $i\in [3]$.

From the above table, we see that $r_1^{(1)}(\mathbb{A}^{\prime}) > r_2^{(1)}(\mathbb{A}^{\prime}) > r_3^{(1)}(\mathbb{A}^{\prime})$ and $r_1^{(3)}(\mathbb{A}^{\prime}) > r_2^{(3)}(\mathbb{A}^{\prime}) > r_3^{(3)}(\mathbb{A}^{\prime})$ hold, it implies that when $q = 1, 3$ we can apply Theorem 3.1 to $\mathbb{A}^{\prime}$, and we obtain $\rho(\mathbb{A}) = \rho(\mathbb{A}^{\prime})\leq \min\limits_{1\leq i\leq 3}\chi^{(1)}_{i} = \chi^{(1)}_{3} = 21.9444$ when $q = 1$, and $\rho(\mathbb{A}) = \rho(\mathbb{A}^{\prime})\leq \min\limits_{1\leq i\leq 3}\chi^{(3)}_{i} = \chi^{(3)}_{2} = 75.3899$ when $q = 3$.

From the above arguments, we can see that the upper bound of $q = 1$ is better than the upper bound of $q = 2$ or $q = 3$.

Example 3.3. Let $\mathbb{B}$ be a nonnegative 3-uniform tensor with order 3 dimension 3, the slices of $\mathbb{B}$ are given as follows, and we get the following table with the help of MATLAB software.

Similar to the arguments of Example 3.2, we can apply Theorem 3.1 to $\mathbb{B}$, and we obtain $\rho(\mathbb{B})\leq \min\limits_{1\leq i\leq 3}\psi^{(1)}_{i} = \psi^{(1)}_{2} = 1.1292$ when $q = 1$, and $\rho(\mathbb{B})\leq \min\limits_{1\leq i\leq 3}\psi^{(2)}_{i} = \psi^{(2)}_{2} = 1.0754$ when $q = 2$.

In order to apply Theorem 3.1 when $q = 3$, we let $P$ be a permutation matrix of order 3 as follows, then $\mathbb{B}$ is permutation similar to $\mathbb{B}^{\prime} = P\mathbb{B}P^{T}$ by Theorem 2.4 and $\rho(\mathbb{B}) = \rho(\mathbb{B}^{\prime})$ by Theorem 2.5. We also write the slices of $\mathbb{B}^{\prime}$, and get the following table of tensor $\mathbb{B^{\prime}}$ as follows, where $\chi^{(q)}_{i}$ be the $\psi^{(q)}_{i}$ of $\mathbb{B}^{\prime}$ for $q\in [3]$ and $i\in [3]$.

Clearly, we can apply Theorem 3.1 when $q = 3$, and we have $\rho(\mathbb{B}) = \rho(\mathbb{B^{\prime}})\leq \min\limits_{1\leq i\leq 3}\chi^{(3)}_{i} = \chi^{(3)}_{2} = 1.1130$ when $q = 3$.

From the above arguments, we can see that the upper bound of $q = 2$ is better than the upper bounds of $q = 1$ and $q = 3$.

Combining the above two examples, we know the upper bounds for different $q$ are not comparable.

4.   Applications to hypergraphs

Let $\mathcal{H}$ be a $k$-uniform hypergraph on $n$ vertices, $\mathbb{A}(\mathcal{H})$ and $\mathbb{Q}(\mathcal{H})$ are the adjacency tensor and the signless Laplacian tensor of $\mathcal{H}$, respectively. It was proved in ^[10,22] that a $k$-uniform hypergraph $\mathcal{H}$ is connected if and only if its adjacency tensor $\mathbb{A}(\mathcal{H})$ (and thus the signless Laplacian tensor $\mathbb{Q}(\mathcal{H})$) is weakly irreducible.

Recently, several papers studied the spectral radii of $\mathbb{A}(\mathcal{H})$ and $\mathbb{Q}(\mathcal{H})$ of a $k$-uniform hypergraph $\mathcal{H}$ (see ^{[5,7,17,19,31,32]} and so on).

In this section, we will apply Theorem 3.1 to the adjacency tensor $\mathbb{A}(\mathcal{H})$ and the signless Laplacian tensor $\mathbb{Q}(\mathcal{H})$ of a $k$-uniform hypergraph $\mathcal{H}$.

Theorem 4.1. Let $k\geq 2, q\geq1, n\geq2$, $\mathcal{H}$ be an $n$ vertices $k$-uniform hypergraph, the notation $r_i^{(q)} = r_i^{(q)}(\mathbb{A}(\mathcal{H}))$ for all $i\in [n]$ with $r^{(q)}_{1}\geq \cdots \geq r^{(q)}_{n}$, where $r_{i}^{(1)} > 0$ for $i\in[n]$ when $q\geq2$. Let $b = \max\limits_{1\leq i, j\leq n}\frac{r^{(q-1)}_{j}}{r^{(q-1)}_{i}}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$, $\psi^{(q)}_1 = r^{(q)}_1$, and for $2\leq s\leq n$,

Then

Moreover, if $k\geq 3$ and $\mathcal{H}$ is connected, then the equality in (4.1) holds if and only if $r^{(q)}_{1} = \cdots = r^{(q)}_{n}$.

Proof. Let $\mathbb{A} = \mathbb{A}(\mathcal{H})$, $M = 0, N = \frac{1}{(k-1)!}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$. The proof is completed from Theorem 3.1 immediately.

In fact, if we take $\mathcal{H}$ to be a $k$-uniform hypergraph or a graph, $\mathbb{A} = \mathbb{A}(\mathcal{H})$, $r_i^{(q)} = r_i^{(q)}(\mathbb{A}(\mathcal{H}))$ in Theorem 4.1, then we have the following table.

Theorem 4.2. Let $k\geq2, q\geq1, n\geq2$, $\mathcal{H}$ be an $n$ vertices $k$-uniform hypergraph, the notation $r_i^{(q)} = r_i^{(q)}(\mathbb{Q}(\mathcal{H}))$ for all $i\in [n]$ with $r^{(q)}_{1} \geq r^{(q)}_{2}\geq \cdots \geq r^{(q)}_{n}$, where $r_{i}^{(1)} > 0$ for $i\in[n]$ when $q\geq2$. Let $\Delta$ be the maximal degree of $\mathcal{H}$, $b = \max\limits_{1\leq i, j\leq n}\frac{r^{(q-1)}_{j}}{r^{(q-1)}_{i}}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$, $\psi^{(q)}_1 = r^{(q)}_1$, and for $2\leq s\leq n$,

Then

Moreover, if $k\geq 3$ and $\mathcal{H}$ is connected, then the equality in (4.2) holds if and only if $r^{(q)}_{1} = \cdots = r^{(q)}_{n}$.

Proof. Let $\mathbb{A} = \mathbb{Q}(\mathcal{H})$, $M = \Delta, N = \frac{1}{(k-1)!}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$. The proof is completed from Theorem 3.1 immediately.

Similarly, if we take $\mathcal{H}$ to be a $k$-uniform hypergraph or a graph, $\mathbb{A} = \mathbb{Q}(\mathcal{H})$, $r_i^{(q)} = r_i^{(q)}(\mathbb{Q}(\mathcal{H}))$ in Theorem 4.2, then we have the following table.

5.   Applications to directed hypergraphs

Directed hypergraphs have found applications in imaging processing ^[9], optical network communications ^[14], computer science and combinatorial optimization ^[11]. However, unlike spectral theory of undirected hypergraphs, there are very few results in spectral theory of directed hypergraphs.

A directed hypergraphs $\overrightarrow{\mathcal{H}}$ is a pair $(V(\overrightarrow{\mathcal{H}}), E(\overrightarrow{\mathcal{H}}))$, where $V(\overrightarrow{\mathcal{H}}) = [n]$ is the set of vertices and $E(\overrightarrow{\mathcal{H}}) = \{e_{1}, e_{2}, \ldots, e_{m}\}$ is the set of arcs. An arc $e\in E(\overrightarrow{\mathcal{H}})$ is a pair $e = (j_{1}, e(j_{1}))$, where $e(j_{1}) = \{j_{2}, \ldots, j_{t}\}$, $j_{l}\in V(\overrightarrow{\mathcal{H}})$ and $j_{l}\neq j_{h}$ if $l\neq h$, for $l, h\in[t]$ and $t\in[n]$. The vertex $j_{1}$ is called the tail (or out-vertex) and each other vertex $j_{2}, \ldots, j_{t}$ is called a head (or in-vertex) of the arc $e$. The out-degree of a vertex $j\in V(\overrightarrow{\mathcal{H}})$ is defined as $d_{j}^{+} = |E_{j}^{+}|$, where $E_{j}^{+} = \{e\in E(\overrightarrow{\mathcal{H}}): j \ \mbox{is the tail of} \ e\}$.

Two distinct vertices $i$ and $j$ are strong-connected, denoted by $i\rightarrow j$, if there is a sequence of arcs $(e_{1}, \ldots, e_{t})$ such that $i$ is the tail of $e_{1}$, $j$ is a head of $e_{t}$, and a head of $e_{r}$ is the tail of $e_{r+1}$ for all $r\in[t-1]$. A directed hypergraph is called strongly connected, if every pair of different vertices $i$ and $j$ of $\overrightarrow{\mathcal{H}}$ satisfying $i\rightarrow j$ and $j\rightarrow i$.

Similar to the definition of a $k$-uniform hypergraph, we define a $k$-uniform directed hypergraph as follows: A directed hypergraph $\overrightarrow{\mathcal{H}} = (V(\overrightarrow{\mathcal{H}}), E(\overrightarrow{\mathcal{H}}))$ is called a $k$-uniform directed hypergraph if $|e| = k$ for any arc $e\in E(\overrightarrow{\mathcal{H}})$. When $k = 2$, then $\overrightarrow{\mathcal{H}}$ is an ordinary digraph.

The following definitions for the adjacency tensor and signless Laplacian tensor of a directed hypergraph was proposed by Chen and Qi in ^[6].

Definition 5.1. (^[6]) Let $\overrightarrow{\mathcal{H}} = (V(\overrightarrow{\mathcal{H}}), E(\overrightarrow{\mathcal{H}}))$ be a $k$-uniform directed hypergraph. The adjacency tensor of the directed hypergraph $\overrightarrow{\mathcal{H}}$ is defined as the order $k$ dimension $n$ tensor $\mathbb{A}(\overrightarrow{\mathcal{H}})$, whose $(i_1i_2\cdots i_k)$-entry is:

Let $\mathbb{D}(\overrightarrow{\mathcal{H}})$ be an order $k$ dimension $n$ diagonal tensor with its diagonal entry $d_{ii\cdots i}$ being $d_i^{+}$, the out-degree of vertex $i$, for all $i\in V(\overrightarrow{\mathcal{H}}) = [n]$. Then $\mathbb{Q}(\overrightarrow{\mathcal{H}}) = \mathbb{D(\overrightarrow{\mathcal{H}})}+ \mathbb{A(\overrightarrow{\mathcal{H}})}$ is the signless Laplacian tensor of the directed hypergraph $\overrightarrow{\mathcal{H}}$.

Xie and Qi ^[28] defined the eigenvalues (signless Laplacian eigenvalues) of a uniform directed hypergraph $\overrightarrow{\mathcal{H}}$ as the eigenvalues of the adjacency (signless Laplacian) tensor $\mathbb{A(\overrightarrow{\mathcal{H}})}$ ($\mathbb{Q(\overrightarrow{\mathcal{H}})}$) of $\overrightarrow{\mathcal{H}}$. The spectral radii of $\mathbb{A(\mathcal{\overrightarrow{\mathcal{H}}})}$ and $\mathbb{Q(\mathcal{\overrightarrow{\mathcal{H}}})}$, denoted by $\rho(\mathbb{A(\mathcal{\overrightarrow{\mathcal{H}}})})$ and $\rho(\mathbb{Q(\mathcal{\overrightarrow{\mathcal{H}}})})$, are called the (adjacency) spectral radius and the signless Laplacian spectral radius of $\mathcal{\overrightarrow{\mathcal{H}}}$, respectively.

Clearly, the adjacency tensor and the signless Laplacian tensor of a $k$-uniform directed hypergraph $\overrightarrow{\mathcal{H}}$ are nonnegative $k$-uniform tensors, but not symmetric in general. It was proved in ^[20] that a $k$-uniform directed hypergraph $\mathcal{\overrightarrow{H}}$ is strongly connected if and only if its adjacency tensor $\mathbb{A}(\mathcal{\overrightarrow{H}})$ (and thus the signless Laplacian tensor $\mathbb{Q}(\mathcal{\overrightarrow{H}})$) is weakly irreducible.

Recently, several papers studied the spectral radii of the adjacency tensor $\mathbb{A}(\overrightarrow{\mathcal{H}})$ and the signless Laplacian tensor $\mathbb{Q}(\overrightarrow{\mathcal{H}})$ of a $k$-uniform directed hypergraph $\overrightarrow{\mathcal{H}}$ (see ^[6,20,28,31] and so on).

In this section, we apply Theorem 3.1 to the adjacency tensor $\mathbb{A}(\overrightarrow{\mathcal{H}})$ and the signless Laplacian tensor $\mathbb{Q}(\overrightarrow{\mathcal{H}})$ of a (strongly connected) $k$-uniform directed hypergraph $\overrightarrow{\mathcal{H}}$, and obtain some new results about $\rho(\mathbb{A}(\overrightarrow{\mathcal{H}}))$ and $\rho(\mathbb{Q}(\overrightarrow{\mathcal{H}}))$.

Theorem 5.2. Let $k\geq2, q\geq1, n\geq2$, $\overrightarrow{\mathcal{H}}$ be a $k$-uniform directed hypergraph with $n$ vertices, the notation $r^{(q)}_{i} = r^{(q)}_{i}(\mathbb{A}(\overrightarrow{\mathcal{H}}))$ for all $i\in [n]$ and $q\geq 1$ with $r^{(q)}_{1}\geq \cdots \geq r^{(q)}_{n}$, where $r_{i}^{(1)} > 0$ for $i\in[n]$ when $q\geq2$. Let $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$, $b = \max\limits_{1\leq i, j\leq n}\frac{r^{(q-1)}_{j}}{r^{(q-1)}_{i}}$, $\psi^{(q)}_1 = r^{(q)}_1$, and

for $2\leq s\leq n$. Then

Moreover, if $k\geq 3$ and $\overrightarrow{\mathcal{H}}$ is strongly connected, then the equality in (5.1) holds if and only if $r^{(q)}_{1} = \cdots = r^{(q)}_{n}$.

Proof. Let $\mathbb{A} = \mathbb{A}(\overrightarrow{\mathcal{H}})$, $M = 0,$ $N = \frac{1}{(k-1)!}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$. Then the result holds by Theorem 3.1.

Theorem 5.3. Let $k\geq2, q\geq1, n\geq2$, $\overrightarrow{\mathcal{H}}$ be a $k$-uniform directed hypergraph with $n$ vertices, the notation $r^{(q)}_{i} = r^{(q)}_{i}(\mathbb{Q}(\overrightarrow{\mathcal{H}}))$ for all $i\in [n]$ and $q\geq 1$ with $r^{(q)}_{1}\geq r^{(q)}_{2} \geq \cdots \geq r^{(q)}_{n}$, where $r_{i}^{(1)} > 0$ for $i\in[n]$ when $q\geq2$. Let $\Delta^{+}$ be the maximal out-degree of $\overrightarrow{\mathcal{H}}$, $b = \max\limits_{1\leq i, j\leq n}\frac{r^{(q-1)}_{j}}{r^{(q-1)}_{i}}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$, $\psi^{(q)}_1 = r^{(q)}_1$, and

for $2\leq s\leq n$. Then

Moreover, if $k\geq 3$ and $\overrightarrow{\mathcal{H}}$ is strongly connected, then the equality in (5.2) holds if and only if $r^{(q)}_{1} = \cdots = r^{(q)}_{n}$.

Proof. Let $\mathbb{A} = \mathbb{Q}(\overrightarrow{\mathcal{H}})$, $M = \Delta^{+},$ $N = \frac{1}{(k-1)!}$, $L = \frac{b^{k-1}}{k-1}\binom{n-2}{k-2}$. Then the result holds by Theorem 3.1.

In fact, we can obtain some known or new upper bounds for digraphs by taking $k = 2$, $q = 1, 2, 3, \; ...$ in Theorems 5.1 and 5.2, and we can also obtain some known (for example, Theorems 4.4 and 4.5 in ^[20]) or new upper bounds for uniform directed hypergraphs by taking $k\geq3$, $q = 1, 2, 3, \; ...$ in Theorems 5.1 and 5.2, and we omit them here.

Acknowledgments

The authors would like to thank the referees for their valuable comments, corrections, and suggestions, which lead to an improvement of the original manuscript.

The research is supported by the National Natural Science Foundation of China (Grant Nos. 11971180, 11571123, 11501139), the Guangdong Provincial Natural Science Foundation (Grant No. 2019A1515012052), the Key Project at School Level of Guangzhou Civil Aviation College (Grant No. 18X0429)

Conflict of interest

The authors declare that they have no competing interests.