Response mechanism of heat-sensitive neurons under combined noise stimulation

1.   Introduction

The human brain is the most advanced and complex organ known in the world. Highly advanced and organized, the human brain is undoubtedly an excellent computer and signal processor composed of neurons with different functions. Different regions correspond to different specific functions, and neurons primarily contribute to these functions ^[1,2,3,4]. For example, auditory neurons are responsible for transmitting sound signals to the brain for processing and interpretation, and the auditory nerve is very sensitive to the frequency, intensity, and direction of sound, allowing us to perceive the source and distance of sound ^[5,6,7]. Olfactory neurons are responsible for transmitting odor information and can distinguish different odors by comparing and analyzing different olfactory signals ^[8,9,10]. Visual neurons can distinguish different shapes and sizes of objects under certain circumstances ^[11,12,13]. Skin and temperature-sensitive neurons can effectively sense changes in temperature ^[14,15,16]. These functional neurons not only operate independently but also interact with one another to form complex neural networks. This interconnectedness allows for enhanced processing capabilities and the emergence of intricate behaviors, which are essential for understanding the dynamics of neural circuits. The study of neural networks, constructed from these functional neurons, reveals how individual neuron properties contribute to the overall dynamics of the system. Understanding the interactions among these neurons is critical for elucidating the mechanisms underlying their collective behavior. Yamakou et al. ^[17] designed scale-free FHN neural networks through mixed coupled slow recovery variables and studied the stochastic resonance phenomenon of the networks. Murza et al. ^[18] analyzed the dynamic oscillator of an electrically coupled modified FHN network. Yu et al. ^[19] analyzed the effects of bounded noise and delay on subthreshold signal transmission in FHN neural networks. Jiang et al. ^[20] reported the chimera state of non-local attractively repulsive coupling in FHN neural networks. In bipartite neural networks of the FHN model, in which nodes interact with one another only when they are in separate layers, Wu et al. ^[21] examined chimera states. The bipartite networks discovered rich chimera behaviors and multistability. In the study by Yang et al. ^[22], the basic FHN neural circuit was enhanced by simultaneously integrating a thermistor and a phototube into distinct branches of the circuit. This modification renders the neuron sensitive to both light and temperature. The references mentioned above can provide some direction for this study of the FHN neuron model. In order to understand in detail the propagation and interaction of electrical signals within and between neurons, it is necessary to simplify the model setup of individual neurons.

In this paper, a highly simplified dynamic model with appropriate parameters can be used to describe the main characteristics of neural firing behavior by applying appropriate external stimuli and adding a Gaussian white noise. To simulate the FHN neuron model, we have taken into account a basic circuit that is powered by an external voltage source or a photocell that has been activated. For a biological neuron, its internal field energy is represented by changes in action potential and membrane potential. The main biophysical properties of biological neurons can be reproduced by functional biophysical neural circuits, and their internal energy can be described by equivalent Hamilton energy function ^[23,24,25]. The Hamilton energy balance based on Helmholtz's theorem by Leutcho in ^[26] explains the dependence of the initial conditions on the macrostability mechanism and shows how the isosurface with constant Hamilton energy is strongly dependent on the state variable. In the presence of noise interference ^[27,28], most neurons can be tamed in the form of external periodic currents to form regular discharge patterns and high neural activity regularity ^[29]. In the absence of periodic stimulation, a certain intensity of noise can also effectively induce nonlinear resonance ^[30,31,32]. In addition, similar coherent resonances and regular spatial patterns can be formed when noise is applied to a network of neurons ^[33,34]. However, little research has been designed to investigate the effect of AWGN white Gaussian noise added to the original stimuli on different firing patterns of heat-sensitive neurons. A neural circuit using a thermistor and phototube adjusts neuron excitability in response to temperature and light, effectively simulating various firing patterns. Through bifurcation analysis, this model offers insights into neuron dynamics and potential sensor applications ^[35,36].

When a single stimulus from a single channel acts on a neuron, most neurons can be activated, showing different firing patterns. When neurons are stimulated by multiple channels at the same time, their mode selection becomes complex and variable. For example, when two different external stimuli are applied to an isolated neuron, which external stimulus will predominantly determine the firing pattern? The isolated neuron will respond preferentially to which external stimulus? Discovering and studying this mechanism is interesting. Taking it a step further, it is even more meaningful to discover the underlying biophysical mechanisms of information encoding and processing in these biophysical neurons. For example, by studying the response kinetics and excitability of Moris-Lecar neurons to two kinds of temperature-sensitive ion channels, calcium ion channel and leakage current, the co-dimensional bifurcation and frequency response curves under different temperatures show that the excitability of neurons varies from grade Ⅱ to grade Ⅰ with the increase of temperature under temperature-sensitive conditions ^[37].

The first motivation for this research was to build a heat-sensitive neuron model based on the simple FHN neural circuit. Our model is designed to simulate the behavior of heat-sensitive neurons by incorporating both chaotic stimuli and noise, allowing for the analysis of adaptive neuronal responses. The advantage of this model lies in its ability to reproduce complex firing behaviors in response to multiple stimuli, particularly the ability to switch between different firing patterns based on external inputs. The self-adaptive property is reflected in the neuron's ability to filter and select specific stimuli frequencies, a process akin to synaptic plasticity and wave filtering. We will elaborate further on this mechanism, supported by recent studies such as Ma et al. and Xu et al., which discuss that any activation of biophysical function and self-adaption of biological neurons may be dependent on energy flow, and synapse connection is controlled to reach energy balance between neurons ^[38,39]. The second motivation for this research was to investigate the effect of AWGN white Gaussian noise added to the original stimuli on different firing patterns of heat-sensitive neurons. Gammaitoni et al. supported this claim by explaining that it manifests in nonlinear systems, where generally weak input signals can be amplified and optimized with the assistance of noise ^[40]. In this paper, we attempted to explore the potential response mechanism of heat-sensitive neurons when two different external stimuli, both supplemented with Gaussian white noise, stimulate the FHN neural circuit. From a physical perspective, any type of external stimulus to a nonlinear circuit is simply the injection of a certain amount of energy, some of which is absorbed and propagated to more electronic components. The interference of multi-channel synchronous input will cause some conflicts in the nonlinear response, and the nonlinear system will show different emission modes under the guidance of energy flow. By calculating the field energy in the neural circuit and equivalent Hamilton energy in functional neurons ^[41], it is confirmed that neurons tend to respond to any external stimulus only when stimulated, showing higher Hamilton energy and certain regularity. That is to say, neurons are more responsive to external stimuli with higher energy, and neural activity can be regularly induced by particular stimuli, so as to effectively capture the energy injected by the outside world. However, neurons and neural circuits must meet particular energy absorption standards, which can greatly enhance nonlinear resonance, and obtain higher Hamilton energy through appropriate discharge modes; also, they must remain silent to some external stimuli of lower energy and maintain robustness to some incentives that destroy regularity. In order to clearly explain the principle of this phenomenon, we employed two distinct external stimulus types, which added Gaussian white noise to identify the priority of pattern selection in neural activity, and calculated the Hamilton energy under different discharge modes.

The key contributions of this research are two-fold: first, the final emission mode is mainly controlled by a stimulus that activates a higher Hamilton energy within the neuron. Second, the addition of periodic excitation modes helps to excite nonlinear resonances, and new periodic excitation modes can be generated even at lower Hamilton energies. The structure of this article is as follows: a detailed description of the model and stimulus is given in Section 2, the process of numerical simulation is introduced in Section 3, and conclusions are drawn in Section 4.

2.   Description of model and method

2.1.   Description of improved FHN neural circuit

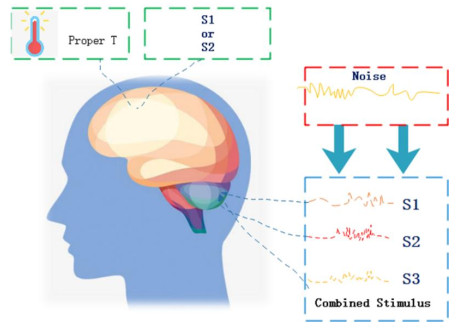
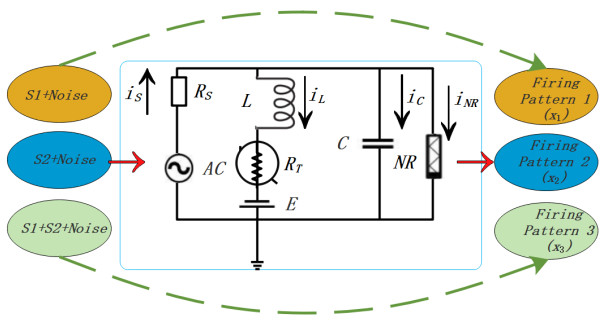
By adding thermistors to different branches of a simple FHN neural circuit, a temperature-thermistor neural circuit is constructed, with its schematic diagram shown in Figure 1. The modified neural circuit consists of a nonlinear resistor NR, an induction coil L, a thermistor R_T, an external constant voltage source E, a capacitor C, a photocell, and a linear resistor R_S. When signal S1 (W1) and white Gaussian noise stimulate neurons, firing mode 1 (x₁) is triggered; firing mode 2 (x₂) is triggered when the neurons are stimulated with signal S2 (W2) and white Gaussian noise; and firing mode 3 (x₃) is generated by stimulating the piezoelectric neurons with signal S1 and signal S2 (W1 + W2) and Gaussian white noise.

Figure 1.  Schematic diagram for neural circuit. The thermistor, C, L, R_T, E, NR, and AC represent the capacitor, induction coil, thermistor, constant voltage source, nonlinear resistance, and AC current, respectively.

DownLoad: Full-Size Img PowerPoint

2.2.   Description of the neural principle

Figure 2.  Schematic diagram of the response mechanism of heat-sensitive neurons under combined noise stimulation. The neural principle depicted here involves the neuron's ability to process and respond to external stimuli (S1 or S2) and noise inputs, resulting in distinct firing patterns. The combination of temperature control (Proper T), stimuli, and noise leads to specific neural responses, illustrating how heat-sensitive neurons integrate multiple signals to generate coordinated activity.

DownLoad: Full-Size Img PowerPoint

2.3.   Derivation of related formulas

In accordance with Kirchhoff's current law and Kirchhoff's voltage law, the circuit equation of the neural circuit drawn in Figure 1 is composed of

where V represents the voltage of the capacitor C and is the current through the inductor L. The current through the nonlinear resistance i_NR can be estimated as

when the linear resistor R_S in series with the photocell is selected with high resistance, the phototube behaves as a voltage source, and its current can be estimated by

where V_p represents the output voltages of the photocell; the resistance of a negative temperature coefficient thermistor can be determined by

In the above equation, q is the activation energy, T is the temperature, K is the Boltzmann constant, and R_∞ is the maximum resistance at T→∞. The physical parameters and variables are updated to the following dimensionless form

The dynamics of thermal neurons powered by photocurrent are calculated by changing the circuit equation to an analogous form

where the variables x and y represent the film potential and recovery variables, respectively, at slow currents. The firing pattern of biophysical neurons can be altered by parameters a, b($T'$), c, ξ and external physical stimuli that we select in the form of cycles

In the above formula, B and w represent amplitude and angular frequency, respectively. The dimensionless Hamilton energy HZ can take the place of the field energy present in an electrical component

As shown in (8), this neuron's Hamilton energy is determined by the intrinsic parameter c and two variables (x, y). Therefore, any change in the firing patterns and parameters of neurons can have a noticeable effect on the Hamilton energy of isolated neurons. In this paper, we will discuss switching external stimuli to detect mode shifts in electrical activity and the dependence of different modes on Hamilton energy.

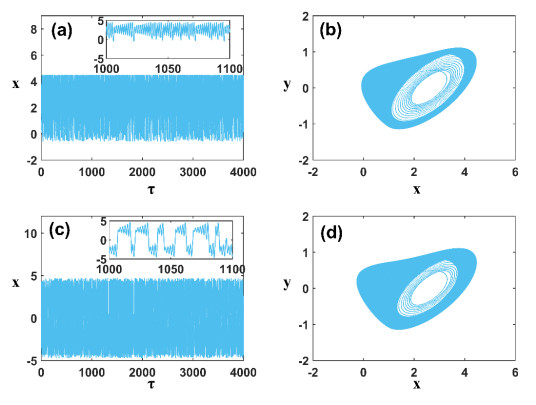
Additionally, the chaotic sequence of Chua's circuit (Figure 3) is used as a chaotic sound wave, and the dynamics of Chua's system can be represented by (9), with x', y', and z' standing for the variables representing the voltage of the two capacitors and the induced current on the induction coil. α, β, γ are normalized parameters that describe the capacitance, inductance, and resistance in a circuit.

Figure 3.  Chaotic sequence and attractor of Chua's circuit. (a) β = 19.5; (b) β = 19.9; (c) β = 14; (d) β = 19.7. Parameters are fixed to α = 8, γ = 0, m0 = -1.664, m1 = -0.598, initial value for (x', y', z') = (0.1, 0.1, 1).

DownLoad: Full-Size Img PowerPoint

Where m₀ and m₁ are normalized parameters for the conductance in the curve i-v for Chua's diode. The nonlinear function f (x') describes the dimensionless current across the nonlinear resistor (diode) of Chua's circuit. By setting appropriate parameters, Chua's system can present chaotic state and periodic state, and then the first variable x' will be used as a realistic signal source for checking the sensitivity of the neural circuit.

Additional Gaussian white noise is described by formula (11):

The AWGN white Gaussian noise is added to the vector signal x. The scalar SNR specifies the ratio of signal to noise in dB at each sampling point. If x is complex, AWGN will add complex noise. This syntax assumes that the energy of x is 0 dBW. The initial value of signal power is fixed at 10 dBW and the SNR is 20 dBW ^[42].

A statistical correlation function, where the symbol < * > denotes the average calculation of the variable over time over a specific transient duration, is constructed in order to identify the influence of various external stimuli on neural mode selection and firing mode. Additionally, the correlation function in (11) is normalized to calculate the pattern selection's dependence on external stimuli ^[43].

When r₁(x₁, x₃) is greater than r₂(x₂, x₃), it shows that the firing mode will be more similar to the r₁ sampling time series, and the firing mode is mainly determined by the external stimulus W1 and noise. Otherwise, when the two external stimuli (W1+W2) and noise are applied simultaneously, the external W2 will completely control the firing mode and the firing mode r_2.

3.   Numerical simulation and discussion

3.1.   Same amplitude and different frequency

Calculations are made in the MATLAB environment in our simulation. The classical fourth-order Runge–Kutta method is used to solve, and the integration step is chosen to be 1 ms, the initial values for the two variables are (0.2, 0.1), and the transient period for the calculation is around 4000 time units. The excitability can be managed by external forcing current and, thereby, the firing mode in membrane potential is regulated fully. A discrete mode transition from a quiescent state, simple oscillation, peaking, r-clonic, to a chaotic state can be induced by carefully controlling the amplitude and frequency of the external stimuli. Furthermore, it is possible to choose the right parameters to activate the chaotic attractor in Chua's circuit; the outcomes are displayed in Figure 3 ^[44,45].

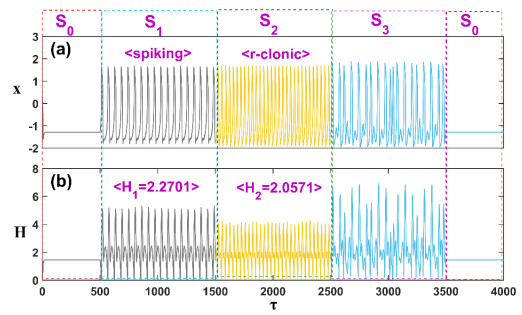
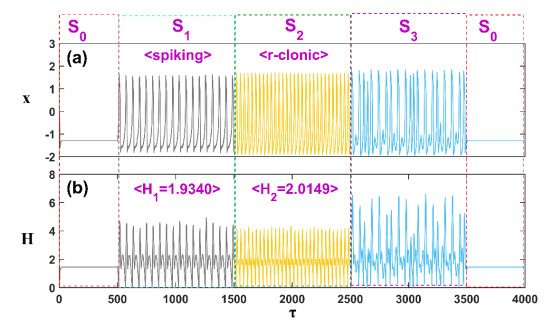
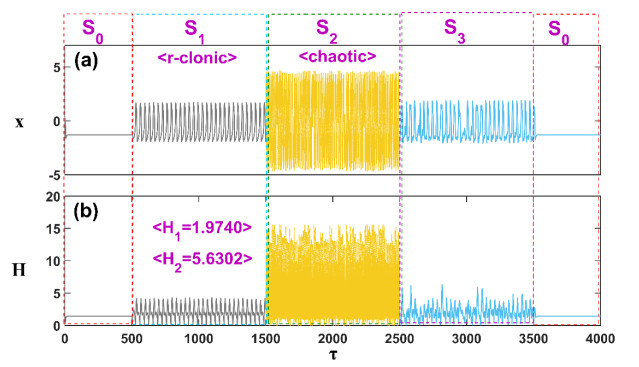
First, with the same amplitude (B1 = B2 = 0.48), we assigned two external stimuli while applying Gaussian white noise of the same intensity. In the S₀ stage, the neuronal membrane potential reached a static state within 0–500 time units without external stimulation. In stage S₁, the spiking discharge state was triggered by W1 and Gaussian white noise in 500–1500 time units. In THE S₂ stage, the W1 and Gaussian white noise stimuli are removed, and the W2 and Gaussian white noise stimuli are used to generate r-clonic discharge patterns in 1500–2500 time units ^[46]. In stage S₃, W1 and W2 combined with white Gaussian noise stimulus simultaneously trigger a hybrid emission mode close to both in 2500–3500 time units. Then, the W1, W2, and Gaussian white noise are removed, the static state is maintained within 3500 ~ 4000 time units, and the correlation function is computed. Figure 4 plots the emission mode change process and the evolution of Hamilton energy at each stage when the external stimulus switches over time. As depicted in Figure 4, when periodic stimulation of W1 and W2 is combined with Gaussian white noise and applied simultaneously to the neurons, the periodic discharge state is suppressed. The resulting discharge mode tends to be a mixed mode of W1 and W2, with a tendency to align more closely to the peak discharge mode. This periodic behavior can be confirmed through the formation of attractors and analysis of the power spectrum. Periodic firing coexists with spiking, and the Hamilton energy further increases compared with that in the S₁ stage.

Figure 4.  Evolution of the membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In S₀ stage, static state without external stimuli. In S₁ stage, periodic W1 is applied with w₁ = 0.11, and peak mode is triggered. In S₂ stage, periodic W2 is applied with w₂ = 0.19, and r-clonic mode is triggered. In S₃ stage, periodic W1 and W2 are applied with w₁ = 0.11 and w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, B1 = B2 = 0.48, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

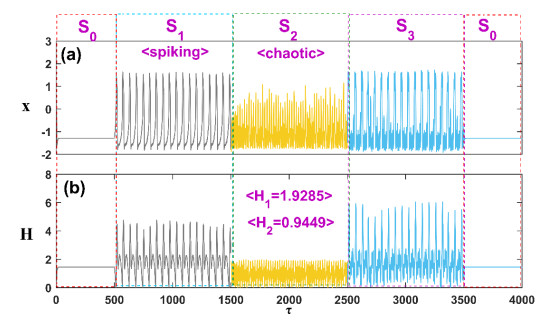
The value of the correlation function r₁(x₁, x₃) is 1.3162, and the value of r₂(x₂, x₃) is –0.3162. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), indicating that external stimulus W1 and white Gaussian noise play a significant part in regulating the discharge pattern, and the excitation from W2 and white Gaussian noise can be suppressed in neurons. Due to this, neurons tend to respond quickly to external stimuli W1 and Gaussian white noise. It is worthwhile to mention the situation in which two external stimuli can induce a chaotic state and a periodic spiking state, whose outcomes are displayed in Figure 5. The Hamilton energy of neurons varies greatly when they change from the spiking state to the chaotic state, with much higher Hamilton energy in the spiking state. When W1, W2, and Gaussian white noise are applied simultaneously, the neurons show a combination of chaotic state and spiking firing mode and a higher Hamilton energy. This is somewhat different from the result in Figure 4, since the final discharge mode is a combination of chaotic state and spiking discharge mode. The occurrence of periodic spiking discharge mode creates a certain periodic oscillation profile in the final discharge mode; the correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), and the outcomes show that the peak discharge mode has a significant impact on the chaotic mode with low Hamilton energy, which leads to the sensitivity of neurons to both kinds of external stimuli. A large number of studies have demonstrated that periodic attractors with multiple orbits are formed under two different types of external stimuli. When the final state of electrical activity is not represented by a different discharge, the electrical response of the neuron is sensitive to both kinds of external stimulus; otherwise, the neuron tends to respond to the external stimulus only when it is effectively stimulated to take on a higher Hamilton energy.

Figure 5.  Evolution of membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with w₁ = 0.11 and peak mode is triggered. In S₂ stage, chaotic W2 is applied with w₂ = 0.65 and chaotic mode is triggered. In S₃ stage, periodic W1 and chaotic W2 are applied with w₁ = 0.11 and w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, B1 = B2 = 0.48, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

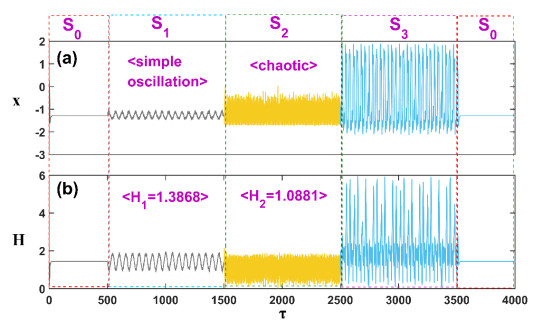
As shown in Figure 6, the simple oscillation pattern of neuronal activity shows a higher Hamilton energy than the chaotic state of neurons driven by a single cycle of stimulation. When the two external stimuli and Gaussian white noise activate neurons at the same time, the final firing mode shows an oscillation state close to the blasting mode, and the Hamilton energy increases greatly. In fact, the introduction of simple oscillatory discharge will enhance the nonlinear oscillation of the pulse train and then make the chaotic mode close to the blasting mode. The value of the correlation function r₁(x₁, x₃) is -0.2291 and the value of r₂(x₂, x₃) is 1.2291. The correlation function r₁(x₁, x₃) is less than r₂(x₂, x₃), indicating that the chaotic state has a great influence on the simple oscillatory discharge mode, resulting in neurons being sensitive to both kinds of external stimuli. It is worth noting that the intensity of the Gaussian white noise remains constant regardless of the difference in the amplitude and frequency of the two external stimuli, which means that the average Hamilton of the various periods and transient periods may differ depending on the two inputs ^[47].

Figure 6.  Evolution of membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with w₁ = 0.19 and simple oscillation mode is triggered. In the S₂ stage, chaotic W2 is applied with w₂ = 0.65 and chaotic mode is triggered. In the S₃ stage, periodic W1 and chaotic W2 are applied with w₁ = 0.19 and w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, B1 = B2 = 0.48, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

3.2.   Different amplitudes and different frequencies

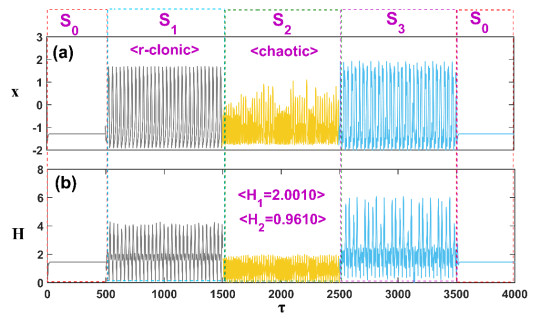
As depicted in Figure 7, we considered two distinct external stimuli, one that effectively triggers the spike discharge pattern and the other that effectively induces the r-clonic pattern. By altering the external stimulus, the neural activity changed from the spiking mode to the r-clonic mode, and the Hamilton energy increased. The value of the correlation function r₁(x₁, x₃) is 1.3793, and the value of r₂(x₂, x₃) is -0.3793. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), indicating that neurons are perceptive of external stimuli and can induce the spiking mode rather than the r-clonic mode. Thus, when two periodic stimuli fire neurons by absorbing more energy, the r-clonic mode can be suppressed by the r-clonic mode. Therefore, the peak discharge mode is more effective in controlling the emission mode. This process can be compared with Figure 4. With the change of amplitude, the level of Hamilton energy of the two shows opposite results, indicating that the change of amplitude can affect the level of Hamilton energy to a certain extent and neurons are more inclined to respond to external stimuli with higher amplitude and present higher Hamilton energy when other conditions remain unchanged.

Figure 7.  Evolution of membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with B1 = 0.41, w₁ = 0.19, and peak mode is triggered. In the S₂ stage, periodic W2 is applied with B2 = 0.48, w₂ = 0.65, and r-clonic mode is triggered. In the S₃ stage, periodic W1 and W2 are applied with B1 = 0.41, w₁ = 0.19, and B2 = 0.48, w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

As shown in Figure 8, under the two kinds of periodic stimuli, the S₁ stage presents the spiking discharge stage, and the S₂ stage presents the blasting mode. Moreover, under the strong amplitude (B2 > B1), the burst sequence can be suppressed by the spiking discharge mode to a certain extent. Because W2 has a higher amplitude and more energy injected into neurons than W1, the Hamilton energy corresponding to W2 is lower than that corresponding to W1. Therefore, the periodic spiking discharge state is accompanied by a higher Hamilton energy. Moreover, the value of the correlation function r₁(x₁, x₃) is 1.5891, and the value of r₂(x₂, x₃) is -0.5891. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), confirming that neurons are more sensitive to W1.

Figure 8.  Evolution of membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with B1 = 0.41, w₁ = 0.11, and peak mode is triggered. In the S₂ stage, chaotic W2 is applied with B2 = 0.55, w₂ = 0.65, and chaotic mode is triggered. In the S₃ stage, periodic W1 and chaotic W2 are applied with B1 = 0.41, w₁ = 0.11, and B2 = 0.55, w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

In a similar way, competition between the r-clonic mode and the chaotic state is considered in the presence of external stimuli and Gaussian white noise, and the outcomes are shown in Figure 9. In the event that both external stimuli are activated, the neurons exhibit r-clonic mode in the S1 stage of electrical activity, which is effectively modulated due to the higher amplitude (B2 > B1) of neurons with chaotic firing mode. The r-clonic pattern of neurons shows a higher Hamilton energy than the chaotic state. The balance between two separate discharge patterns brought on by two different stimuli determines the final discharge pattern. The value of the correlation function r₁(x₁, x₃) is 0.8130, and the value of r₂(x₂, x₃) is 0.1870. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), which indicates that in the final developed mode, the r-clonic discharge mode contributes more than the chaotic discharge mode due to the higher Hamilton energy provided by the r-clonic mode, and the neurons tend to respond preferentially to the r-clonic mode. The results of Figure 9 and Figure 10 show that neurons are more inclined to respond to stimuli that exhibit continuous regularity rather than chaotic or explosive states, and exhibit higher Hamilton energies, thus forming different periodic firing patterns.

Figure 9.  Evolution of membrane potential firing patterns (a) neuron membrane potential and (b) Hamilton energy of isolated neuron. In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with B1 = 0.48, w₁ = 0.19, and r-clonic mode is triggered. In the S₂ stage, chaotic W2 is applied with B2 = 0.55, w₂ = 0.65, and chaotic mode is triggered. In the S₃ stage, periodic W1 and chaotic W2 are applied with B1 = 0.48, w₁ = 0.19, and B2 = 0.55, w₂ = 0.65. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, $T'$ = 2.1, SNR = 20, and the initial value is (0.2, 0.1).

DownLoad: Full-Size Img PowerPoint

3.3.   Chua's circuit stimulus

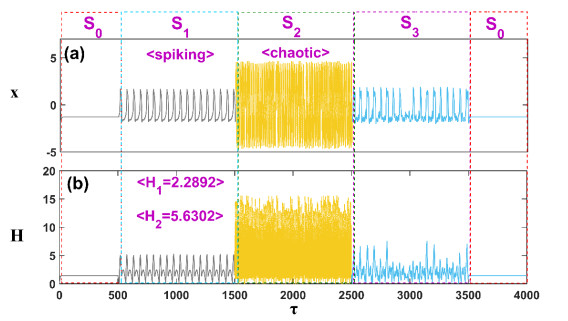
As shown in Figure 10, the study of mode selection is also interesting when external stimuli trigger chaotic and periodic spike discharge patterns. When the external stimulus is forced to change from periodic spiking mode to chaotic mode, the Hamilton energy increases greatly. In addition, when spiking and chaotic stimuli are applied at the same time, the final firing pattern of neurons begins to oscillate irregularly and is accompanied by chaotic patterns. The value of the correlation function r₁(x₁, x₃) is 0.9312, and the value of r₂(x₂, x₃) is 0.0688. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), indicating that neurons are more inclined to react to the burst mode induced by the spiking discharge mode stimulus than the chaotic discharge mode induced by the chaotic stimulus. A large number of numerical findings confirm the emergence and growth of chaotic attractors. The combination of chaotic activity and peak discharge activity causes Hamilton energy to fall dramatically, as can also be seen from the S₃ stage. The Hamilton energy of the S₂ stage is much larger than that of the S₁ stage, indicating that the energy change caused by Chua's circuit stimulation is larger.

Figure 10.  Evolution of membrane potential firing patterns (a) and Hamilton firing patterns in isolated neuron (b). In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with B = 0.48, w = 0.11, and peak mode is triggered. In the S₂ stage, chaotic W2 is applied by setting β = 17 in Chua's circuit and chaotic patterns occur. In the S₃ stage, periodic W1 and chaotic W2 are applied with B = 0.48, w = 0.11, and β = 17. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, $T'$ = 2.1, SNR = 20, α = 8, γ = 0, m₀ = ‒1.664, m₁ = ‒0.598, and the initial values are (0.2, 0.1) in Eq (12) and (0.01, 0.1, 1.0) in Eq (9).

DownLoad: Full-Size Img PowerPoint

As shown in Figure 11, when periodic and chaotic stimuli are used to trigger both the r-clonic pattern and chaotic neural activity, the resulting discharge pattern is dominated by an oscillatory state accompanying the chaotic pattern. The value of the correlation function r₁(x₁, x₃) is 1.2850, and the value of r₂(x₂, x₃) is -0.2850. The correlation function r₁(x₁, x₃) is greater than r₂(x₂, x₃), indicating that r-clonic mode mostly regulated mode choice, so neurons are more sensitive to periodic stimulation than chaotic stimulation. Numerous numerical studies have also confirmed the emergence of dense orbital chaotic attractors in the S₃ stage. The attractors of the S₃ stage of development show chaotic and dense orbits.

Figure 11.  Evolution of membrane potential firing patterns (a) and Hamilton firing patterns in isolated neuron (b). In the S₀ stage, static state without external stimuli. In the S₁ stage, periodic W1 is applied with B = 0.48, w = 0.19, and r-clonic mode is triggered. In the S₂ stage, chaotic W2 is applied by setting β = 17 in Chua's circuit and chaotic patterns occur. In the S₃ stage, periodic W1 and chaotic W2 are applied with B = 0.48, w = 0.19, and β = 17. The parameters are fixed as a = 0.7, b = 0.8, c = 0.1, ξ = 0.175, $T'$ = 2.1, SNR = 20, α = 8, γ = 0, m₀ = ‒1.664, m₁ = ‒0.598, and the initial values are (0.2, 0.1) in Eq (12) and (0.01, 0.1, 1.0) in Eq (9).

DownLoad: Full-Size Img PowerPoint

In conclusion, an external drive can regulate the firing pattern of a single heat-sensitive neuron. A proper firing pattern can be created for any generic and functional neuron because its excitability and intrinsic energy pumping are also regulated. In other words, a neuron can only fire in a single pattern in response to a single channel of input, and when two distinct external stimuli are supplied at the same time, the final firing pattern becomes competitive. In the case of multi-channel stimulation, the competition between the two isolated discharge states as well as the injection and absorption of energy all affect the final discharge pattern of electrical activity. While inducing lower Hamilton energies, the periodic stimuli can significantly increase the occurrence of nonlinear resonance. When the periodic discharge mode of peak discharge and r-clonic discharge is induced, the participation of the periodic discharge mode helps to increase the sensitivity to the external signal. The chaotic excitation is increased, and the chaotic attractor's contour is altered when the chaotic discharge mode is activated. When the spiking emission mode interacts with the chaotic mode, the final discharge mode is more inclined to oscillate irregularly and is accompanied by the chaotic mode, because the spiking mode releases higher Hamilton energy than the chaotic mode, and the developed attractors tend to exhibit periodic orbits. In summary, neurons are more likely to react to stimuli that have higher amplitudes and energies, as well as those that cause more resonance and regularity in neuronal activity.

4.   Conclusions

The main goal of the present study was to discuss which external stimulus can be rapidly received in neurons driven by two separate stimuli and white Gaussian noise, and then to analyze the potential response mechanism of the electrical activity of heat-sensitive neurons. Three main contributions can be drawn from the research:

(1) When neurons are excited, the firing pattern is related to the level of Hamilton energy. For example, the Hamilton energy of the peak mode is higher than that of the r-clonic mode and the chaotic mode. Physically speaking, any external stimulus has the ability to inject energy, some of which is absorbed by neurons. We have defined a correlation function to estimate the primary effect and contribution of each external stimulus and its corresponding pattern. Appropriate excitation in the peak mode can suppress r-clonic as well as chaotic mode, the final emission mode usually remains close to the mixed emission mode profile, and periodic attractors can be developed.

(2) The participation of periodic emission modes tends to cause significant emission mode changes and certain regularity, while other emission modes are suppressed due to possible nonlinear resonances. This means that external stimuli that produce periodic discharge patterns are more easily sensed and responded to.

(3) The main excited states and attractors show periodic and chaotic characteristics when peak mode interacts with r-clonic and chaotic modes. When a chaotic stimulus is applied, the chaotic discharge patterns remain active, and the profile of attractors can be changed due to the interaction with pulses, spike patterns, or even periodic discharge states that can provide a certain amount of energy to the neuron. However, variations in the chaotic attractor profile mean that interactions between chaotic modes, spikes, r-clonic, and periodic states can be efficiently detected, as chaotic states typically exhibit lower Hamilton energies than other emission modes. However, the Hamilton energy of Chua's circuit is often higher than that of the peak mode and r-clonic mode. These findings imply that energy flow controls competition between various discharge patterns, which ultimately results in regularity of neuronal activity, and that energy input from external stimuli is essential. This implies that controlling energy input may be another effective method for regulating neural activity.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12172210 and 11502139). The authors would like to thank the anonymous referees for their efforts and valuable comments.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.