Bifurcation analysis on the reduced dopamine neuronal model

1.   Introduction

Tiny living things called microorganisms cause infectious diseases. Although some of these creatures are normally found in certain organs within the body, they can cause disease when they move to different organs and tissues. Some microorganisms cause disease when found in soil or other sources and are transmitted to humans.

Infectious diseases have many methods of transmission. Some infectious diseases are passed from person to person. Some diseases are transmitted by insects or other animals. Additionally, spoiled food or contaminated water sources can also cause infectious diseases. Infectious diseases can be caused by different microorganisms such as bacteria, viruses, fungi and parasites. Infectious diseases can be transmitted through either direct or indirect contact, or through insect bites or food that carry viruses or bacteria.

Most infectious diseases have only minor complications, and each has its own unique symptoms. Fever, diarrhea, fatigue, muscle aches, and a cough are among the general signs and symptoms of infectious diseases. However, some infections, such as pneumonia, acquired immunodeficiency syndrome (AIDS), and meningitis, can be life-threatening. Research has shown that several types of infections are associated with an increased long-term risk of cancer. Human papillomavirus has been linked to cervical cancer, Helicobacter pylori, stomach cancer, and peptic ulcers; additionally, Hepatitis B and C have been linked to liver cancer. Either laboratory work or an imaging scan is ordered to diagnose infectious diseases. Antibiotics, antivirals, antifungals, and anti-parasitics are used in the treatment of infectious diseases [1].

Hepatitis occurs due to the inflammation of cells in the liver. This is a disorder that occurs when inflammation occurs without microbes. An example of this is the contact of drugs with the liver. There are no microbes within the liver. However, drugs can disrupt the structure of the liver. In other words, drugs can cause inflammation [2]. The Hepatitis B virus (HBV) is a DNA virus from the hepadnavirus family, and is widely known around the world. It is estimated that approximately 400 million people are chronically infected with HBV, and 300,000 new cases are identified in the USA every year. Several new cases are identified in children every year [3].

Chronic HBV carriage begins in early childhood, especially before the age of 2, and is caused by infection [4]. In addition to reducing the rate of carriers and the prevalence of HBV infections in the current younger generation, the universal vaccination program has also resulted in a reduced rate of childhood hepatocellular carcinoma (the most common liver cancer) [5]. The path followed for HBV treatment in childhood is that the disease is mild at first, but there is a risk of progression of the disease in later ages. The decision should be made by considering the direct and side effects of these treatments. For this reason, children who carry the HBV virus should be monitored at certain periods, and the treatment process should be shaped according to the results of each monitored stage [6].

Mathematical modeling of infectious diseases provides information about the course of the disease in the subsequent years. Many models have been created to examine the impact of infectious diseases on different populations. These models have been adapted to a variety of infectious diseases [7]. Mathematical models provide information about whether a disease will become an epidemic or not and what can be done to control diseases [8]. In a study conducted in 1927, Kermack and Mckendrick [9] revealed the course of the disease by modeling an epidemic disease with the SIR model, which uses Susceptible (S), Infected (I), and Recovered (R) populations. After this study, mathematical modeling became a method to examine the transmission of diseases. Various studies have begun to model infectious diseases using similar parameters.

Models are devised using differential operators. Fractional differential operators are operators that allow the integral or derivative of the function to be taken in non-integer degrees (fractional). It helps in modeling anomalous dynamics and complex systems. Fractional differential operators have a memory effect, which ensures that the system depends on past states as well as its current state. Preferring to use fractional derivatives in the epidemiological modeling of infectious diseases such as to HBV helps model the impact of the past experiences of diseases on their future dynamics. Thus, it plays an important role in the development of measures to be taken for infectious diseases over time.

In order to understand them well, some important definitions (such as Gamma function, Beta function, Mittag-Leffler capacity, and Laplace capacity) must first be well-nourished and known. Similar to classical calculus, there is no single derivative definition in the content of fractional calculus. The existence of more than one derivative definition in fractional calculus allows for the type of problem to be sectioned appropriately and thus the best solution of the problem can be obtained. The fact that there are numerous and different definitions for fractional calculus existing simultaneously that are used in the operating processes has caused many difficulties. However, the types of problems that arise have been better classified, and it has become clear which type of definition can be more useful in different problems. Fractional calculus can be applied when known analytical methods are applied and the systems cannot be fully explained.

The fractional operator differs from classical integer variants in modeling disease transmission. For example, infectious diseases may follow an abnormal journey. Therefore, when modeling infectious diseases, instead of using classical integer derivatives, fractional derivatives that are suitable for the abnormal course are preferred. While classical integer derivatives only consider the current state of a function without taking past information into account, fractional derivatives create a memory effect by taking into account the past state of the system. While classical integer derivatives provide limited flexibility because they can take integer degrees, fractional derivatives allow for a more flexible model because they can take non-integer degrees. This allows the system to model more complex and non-linear behaviors. While classical integer derivatives require additional terms in modeling the delay processes, delayed responses can be modeled with fractional derivatives. In this way, the model reaches a structure that is more flexible, realistic, and covers complex dynamics.

In mathematical modeling, transitions between populations are calculated according to the time period defined on the established model for the course of the disease. The contagiousness of the disease is represented with the help of various parameters such as the infection rate. In this study, a new mathematical model is created for the course of HBV. There are studies in the literature that model HBV infectious disease, some of which are provided below.

Kamyad et. al. [10] examined the dynamics of HBV, which can be controlled by vaccinations and treatments. They created a model with five compartments. Normally, models that address horizontal and vertical transmissions consist of different populations such as exposed and carrier. They made calculations such as the basic reproduction number of the model and provided a numerical simulation. Ciupe and Hews [11] created a model that investigated the Hepatitis B e-antigen during HBV infection. They concluded that the models they created could trigger immune activation by either seroconversion or mutations. Guedj et. al. [12] mathematically modeled the surface antigen kinetics of the Hepatitis D and Hepatitis B viruses. They created a model with five compartments, and modeled the HDV RNA and HBsAg kinetics together. Wodajo and Mekonnen [13] created a non-linear HBV model. In their six-compartment model, they took the contact rate of the susceptible population and the transmission rate of the disease into account. They used compartments such as chronically infected, acutely infected, and treated. As a result, they showed that vaccination and treatments could stop the progression of the disease.

Goyal et. al. [14] created a model that addressed the clearance of acute infections in humans. They investigated which mechanisms played a role in clearing the infection by creating a three-compartment model. As a result, they concluded that the clearance of HBV was associated with the proliferation of one infected cell and the production of two healthy cells. Carracedo et. al. [15] created a mathematical model that enabled them to understand the complex dynamics of HBV in drug treatments. They used three compartments in their model and utilized infected and uninfected hepatocytes. Ciupe [16], who was interested in HBV infection, which is one of the causes of cirrhosis and liver cancer, researched studies on mathematical modeling of HBV. The study examined models that addressed effects such as virus-host interactions and the effectiveness of drug therapies. Dahari et. al. [17] modeled the complex degradation profiles of the HBV virus during antiviral treatments. In the model, they showed uninfected hepatocytes(i.e., target cells), infected cells, and infected hepatocytes. They reached various conclusions regarding the importance of the drug in the treatment of HBV patients. Goyal and Murray [18] modeled the cell-to-cell transmission of HBV. They developed an agent-based model and used seven compartments in the model. The study results revealed that factors such as cell-to-cell transmission strength and cytokine production may determine the fate of HBV.

Colombatto et. al. [19] designed a multi-stage bio-mathematical model. In their studies, their models of HBV dynamics revealed that peg-IFN-α2a and 3TC have inhibitory activities on HBV replication. Chronic HBV has affected hundreds of millions of people. Therefore, Cangelosi et. al. [20] conducted a study that modeled the representation of HBV in the liver. The study results revealed that the spatial properties of HBV in the liver could be exploited. Khan et. al. [21] created a model that addressed the impact of HBV on immigrants. In a model that consisted of six compartments, they defined the migration effect with the migration class. Since similar studies in the literature did not explain the numerical results, they produced a study in which the parameters obtained from the numerical simulation and their numerical results were interpreted.

Din and Abidin [22] wrote a fractional order model of vaccinated HBV patients and analyzed it with Mittag-Leffler kernels. Their models consisted of five compartments. Additionally, the entity-unity state and stability of the model for disease-free balance points were examined. As a result, it was that the epidemic caused by the HBV infectious disease can be prevented using the appropriate parameter and the optimal control strategy to minimize the infected class. Yavuz et. al. [23] modeled HBV using real data and a fractional order. They carried out a stability analysis by finding balance points in the model. Moreover, they performed numerical simulations with the help of the Adams-Bashforth numerical scheme. Mustapha et. al. [24] created an age-structured model of HBV. They estimated model parameters using real data from South Africa and performed numerical simulations. As a result, they revealed that in order to eliminate HBV in South Africa, it is very important to treat children with chronic HBV and to reduce its transmission to adults. Wodajo et. al. [25] developed a nonlinear mathematical model for the transmission dynamics of HBV. They created the mathematical model by taking the effects of vaccination, treatment, migration, and the screening parameters into account.

In their study, Xu et. al. [26] built a dynamic model that included a compartment for potentially infectious HBV infections, based on data from the National Bureau of Statistics of China from 2003 to 2021. Khatun et. al. [27] obtained the production number R₀ in all models, which can be exploited for the stability of the equilibrium state. By analyzing the model, they showed that the virus-free equilibrium is asymptotically stable if the basic reproductive number of the viruses is less than one, and that the endemic equilibrium is locally asymptotically stable if the basic reproduction rate is greater than one. Aniji et. al. [28] modeled the relationship between the hepatitis B virus and liver cells using Liao's homotopy analysis method (LHAM). Endashaw and Mekonnen [29] proposed a deterministic mathematical model to investigate the impact of vaccines for the hepatitis B virus and treatments for other viruses on the transmission of HBV-HIV/AIDS viruses in a population (i.e., A mathematical model of hepatitis B virus transmission and its application for vaccination strategy in China).

Khan et. al. [30] built a model that suggested acute and chronic stages of infection using the Caputo-Fabrizio (CF) operator. Using the stochastic Lyapunov function theory, Khan et. al. [31] built a model for the transmission of the hepatitis B virus under the influence of a fluctuating environment. Since 1976, large-scale studies of HBV infections have been conducted, and a wealth of data has been collected. In Zhao et. al. [32], they described a mathematical model developed to predict the HBV transmission dynamics and evaluate the long-term effectiveness of the vaccination program.

Danane et. al. [33] presented and investigated a fractional differential mathematical model that described the dynamics of a hepatitis B viral infection with DNA-containing viruses, liver principal cells, and the humoral immune response. Goldstein et. al. [34] developed a model to calculate the age-specific risk of contracting an HBV infection, acute hepatitis B, and a chronic HBV infection. Liang et. al. [35] revealed that the dynamic model of HBV transmission only simulates the spread of HBV in the population from a macroscopic point of view, and highlighted some major shortcomings in the model structure and parameter estimation. Li and Zu [36] reviewed the viral dynamics in HBV infections; this will help us better understand the dynamic mechanism of HBV infections and the effectiveness of antiviral therapy. Min et. al. [37] formulated a standard event-based model that replaced the basic virus infection model (BVIM) and corrected the model artifact caused by this mass action. Goyal et. al. [38] provided information about HBV infections in humans and provided a brief overview of the development of mathematical models of HBV infection. Zhang and Zhou [39] formulated a mathematical model to explain the spread of an hepatitis B. In this study, the stability of the balance and the persistence of the disease were analyzed.

In addition, many studies have been conducted on mathematical modeling for other infectious diseases such as Hepatitis C (HCV) [40], Cholera [41], [42], [43], tuberculosis (TB) [44], influenza A [45], Mumps [46], cancer [47], [48], the plastic waste model [49], compound biochemical calcium oscillations [50], atmospheric dynamics [51], fish farming [52], brucellosis transmission [53], and predator-prey [54], [55].

Zika virus, which is an infectious diseases, was first discovered in 1947. Complementary teratogenic effects with microcephaly in newborns are the greatest threats to public health. Extended models by Wiratsudakul et. al. [56] were included to describe the relevant distribution dynamics. Möhler et. al. [57] presented a mathematical model that explained the replication of the influenza a virus in animal cells in large-scale microcarrier culture.

The fractional order determines the dynamics of the infection spread and the process of the disease spread. Changes in the fractional order can affect the rate of the disease spread and the long-term dynamics. The fractional order allows for a more realistic modeling of the spread of the disease. This can help to analyze the epidemiological data more accurately and to develop more effective public health policies. Certain values of the fractional order may cause the infection to persist in the community for longer or to spread more rapidly. This may have a direct impact on the timing and intensity of the interventions. The model may either lead to continuous fluctuations or to periodic epidemics under certain conditions. Periodic epidemics indicate that the community may experience periodic outbreaks of disease. This may be related to waning immunities, inadequate vaccinations, or environmental factors. Continuous fluctuations represent a situation where the disease is uncontrollable in the community and may wax and wane over time. This requires a continuous public health response.

In this study, mathematical modeling is studied to examine the effect of vertical transmission and the migration parameters of HBV on the course of the HBV infectious disease. In the mathematical model, consisting of 5 compartments, the susceptible population, latent population, acute population, carrier population, and protected infected (in the sense of recovered) are considered. The rest of the study is organized as follows: In Section 2, we provide several definitions that will be used throughout the study; in Section 3, the derivation of the mathematical model for HBV infection is explained; in Section 4, the mathematical analysis such as positivity, boundedness, and finding equilibria of the model is given; in Section 5, the calibration of the model parameters is set; the numerical results and discussion are presented in Section 6; and the conclusion is explained in Section 7.

2.   Preliminaries

This section provides several definitions to be used in the next stages of the paper.

Definition 2.1. [58] The Caputo fractional derivative of order λ of Ω(t), t > 0 is defined as follows:

where Γ(·) is the Gamma function, λ∈(n−1,n), $n \in \mathbb{Z}^{+}$.

Definition 2.2. [58] The fractional integral operator of Riemann-Liouville type for a function $\xi:(0,\infty )\to \mathcal{R}$ of order λ > 0 is denoted as either

or

Definition 2.3. [58] The fractional derivative of Riemann-Liouville type for a function $\xi:(0,\infty )\to \mathcal{R}$ of order λ > 0 is denoted as follows:

3.   Derivation of the mathematical model for HBV infection

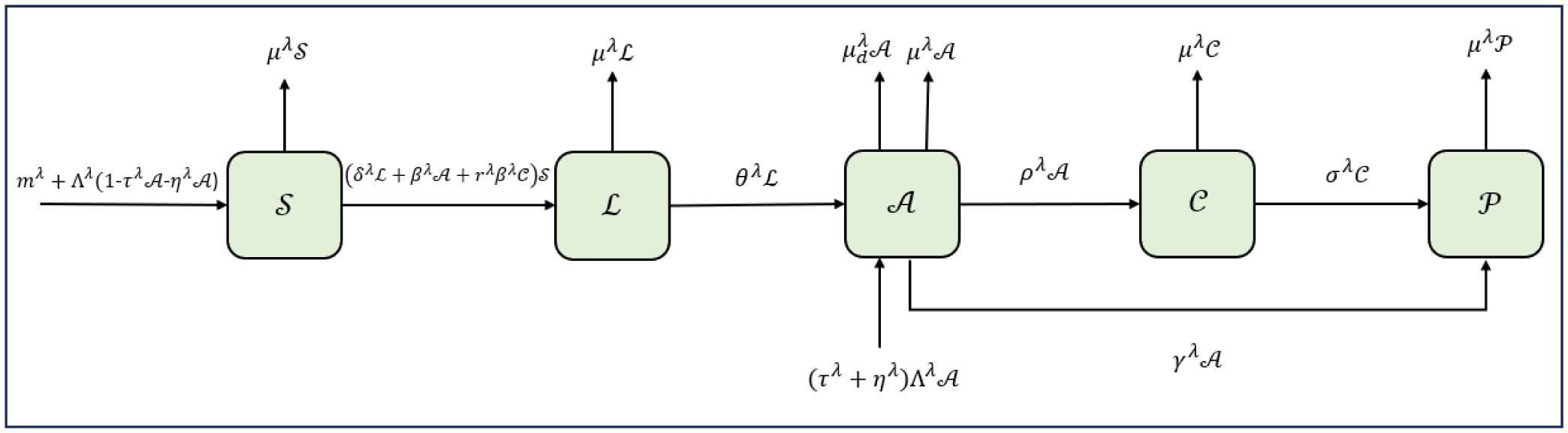
In this section, with the help of real data, the basic $\mathcal SLACP$ mathematical model for the impact of HBV on the vertical transmission and migration factor is proposed and analyzed. The total population, susceptible population $\mathcal S(t)$, latent population $\mathcal L(t)$, acute population $\mathcal A(t)$, carrier population $\mathcal C(t)$, and protective rescued ?? are divided into five mutually exclusive parts. The provided parameters form elements of a mathematical model that describe the transmission dynamics and migration effect of HBV. Λ indicates the rate at which individuals join the susceptible population. µ stands for the natural mortality rate, and β signifies the transmission rate. r indicates a reduced transmission compared to an acute infection. τ signifies the proportion of infected mothers that transmit HBV to their offspring. γ is the recovery rate from an acute infection, and σ is the recovery rate of the carriers. ρ is the transition rate from the acute to the carrier status, and µ_d is the HBV-related death rate. m represents the rate of new individuals that join the community through migration. η denotes the transition rate from susceptible to a latent infection, and θ is the transition rate from a latent to an acute infection. These parameters collectively depict the interaction of various processes in the HBV transmission dynamics, thus providing information about the course of the disease by understanding its spread and control measures. Moreover, it helps predict various parameters of the disease. A model that explains these situations is depicted with a schematic diagram and is stated in Figure 1.

Additionally, the following basic assumptions were taken into account when creating the new HBV model:

The study is important because of the following four items:

A significant contribution to the literature was provided by using real data in the model alongside fractional modeling of the vertical migration and migration effects.

The equation system of the given schematic diagram is given in Eq (3.1).

Figure 1.  Schematic diagram of the SLACP model.

DownLoad: Full-Size Img PowerPoint

Hence, by considering this assumption, the rate of change of susceptible, latent, acute, carrier, and protected infected (protective rescued) are described in the following nonlinear system of differential equations:

with initial conditions $\mathcal S(0) = {\mathcal S_0} \ge 0,{\rm{ }}\mathcal L(0) = {\mathcal L_0} \ge 0,{\rm{ }}\mathcal A(0) = {\mathcal A_0} \ge 0,{\rm{ }}\mathcal C(0) = {\mathcal C_0} \ge 0, {\rm{ }}\mathcal P(0) = {\mathcal P_0} \ge 0 {\rm{ }} .$ The used model parameters and their biological descriptions are listed in Table 1.

4.   Mathematical analysis of the model

4.1.   Positivity and boundedness

Since each class in system (3.1) denotes the human population, we should show that all classes $\mathcal S(t),\ \mathcal L(t), \ \mathcal A(t),\ \mathcal C(t),\ \text{and} \ \mathcal P(t)$ are positive for time t ≥ 0. We provide this fact in the form of the following theorem. Prior to proving the main theorem on the non-negativity of the resulting solutions, we must first establish the following Lemma [59], [60]:

Lemma 1. Take the function $\zeta(t)\in C[f,g]$ and Caputo fractional derivative ${{}^C_0\omega}^{\lambda}_t\zeta (t)\in C(f,g]$ for 0 < λ ≤ 1; then, we have the following:

with $0\leq \psi\leq t, \forall t\in (f,g].$

Remark 1. Take the function $\zeta(t)\in C[0,g]$ and Caputo fractional derivative $\zeta(t)\in C[0,g]$ for 0 < λ ≤ 1. It is clear from Lemma 1 that if ${{}^C_0\omega}^{\lambda}_t\zeta (t)\geq0, \forall t\in (0,g]$, then the function ζ(t) is non-decreasing; moreover, if ${{}^C_0\omega}^{\lambda}_t\zeta (t)\leq0, \forall t\in (0,g]$, then the function ζ(t) is non-increasing $\forall t\in (0,g]$.

Theorem 1. All the solutions of model (3.1) with nonnegative initial conditions remain positive for all t ≥ 0.

Proof. To prove the non-negativity of each component in system (3.1), we use the assumption of the contradiction process, that is, let's suppose that there exists a first time t₀, such that

Here, $\mathcal X(t)=\mathcal{S}(t),\ \mathcal{L}(t), \ \mathcal{A}(t), \ \mathcal{C}(t), and \ \mathcal{P}(t)$ separately. According to our assumption, we first let,

This gives $\mathcal{S}(t_0)=0 \ \mathrm{and}\ \mathcal{S}(t)>0 \ \ \mathrm{for \ all} \ \ t\in[0,t_0).$ However, from the first equation of system (3.1), we obtain the following:

from which we have the following:

which contradicts our assumption $\mathcal{S}(t_0)=0.$ Hence, $\mathcal{S}(t)>0 \ \mathrm{for \ all} \ \ t\geq0.$ In a similar way, we can prove that all solution components are nonnegative in all other cases for all t ≥ 0. Therefore, according to Lin [59] and benefiting from Lemma 1 and Remark 1, we obtain the proof of Theorem 1.

Theorem 2. The closed region

is a biologically feasible region, which means it is a positively invariant set for model (3.1) that attracts all positive solutions, where $\phi(t)$ is the total population.

Proof. To prove the theorem, we have from the total population $\phi(t)$ for model (3.1) after taking its derivation as follows:

Therefore, it follows that

More precisely, $0<\phi(t) \leq \frac{\Lambda^\lambda+m^\lambda}{\mu^\lambda}; \ \mathrm{if} \ \phi(0)\leq \frac{\Lambda^\lambda+m^\lambda}{\mu^\lambda},$ then it means that $\phi(t)$ is bounded and all solutions beginning in $\mathcal{D}$ approach, enter, and remain in $\mathcal{D}$. Therefore, according to Lemma 1, on each hyperplane bounding the non-negative orthant, the vector field points into ${\mathcal{R}}^5_+$. As a result, the model represented by (3.1) can be regarded as a positively invariant set being well-posed. This proves Theorem 2.

4.2.   Equilibria of the model

In this section, we evaluate the disease-free equilibrium (DFE), which has a significant role in determining the basic reproduction number, and its stability to study the steady-state behavior of the model constructed for the HBV disease model. In order to achieve this, we reconsider the following system of Eqs:

By solving the system of equations, we obtain the following DFE point:

where $\mathcal S_0=\dfrac{\Lambda^\lambda+m^\lambda}{\mu^\lambda}$, and the provided endemic equilibrium (EE) is given by the following:

where

$\mathcal{C}^* =\dfrac{\rho^\lambda}{\sigma^\lambda +\mu^\lambda}\mathcal{A}^*,$

$\mathcal{P}^* =\Big(\gamma^\lambda+\dfrac{\sigma^\lambda \rho^\lambda}{\sigma^\lambda+\mu^\lambda}\Big)\mathcal{A}^*,$

$\mathcal{L}^*=\dfrac{\mu^\lambda+\mu_d^\lambda+\rho^\lambda+\gamma^\lambda-\Lambda^\lambda \eta^\lambda-\Lambda^\lambda \tau^\lambda}{\theta^\lambda}\mathcal{A}^*,$

$\mathcal{S}^*=\dfrac{\mu^\lambda+\theta^\lambda}{\beta^\lambda \mathcal{A}^*+r^\lambda \beta^\lambda \mathcal{C}^*+ \delta^\lambda \mathcal{L}^*}\mathcal{L}^*,$

and where $\mu^\lambda+\mu_d^\lambda+\rho^\lambda+\gamma^\lambda>\Lambda^\lambda \eta^\lambda+\Lambda^\lambda \tau^\lambda$.

4.3.   Reproduction number for the suggested disease

For the calculation of the reproduction number $\mathcal R_0$, we compute two matrices, namely the transmission matrix $\mathcal F$, which denotes the transmission part that gives new infections in the dynamic process, and the transition matrix $\mathcal V$, which expresses the state change during the epidemics by employing the next-generation matrix method [61]. Therefore, we have

and

where $z_1=\mathcal{S}(t), z_2=\mathcal{L}(t), z_3=\mathcal{A}(t), z_4=\mathcal{C}(t)$, and $z_5=\mathcal{P}(t)$.

Therefore, $\mathcal R_0$ is calculated as the spectral radius of the next generation matrix $\mathcal{H}=\mathcal{GK}^{-1}$, where,

Hence, the expression we have for $\mathcal R_0$ from $\mathcal{H}=\mathcal{GK}^{-1}$ is given by the following:

where $\mathcal R_0$ represents the average number of new infections caused by a single infectious person in the latent class $\mathcal{L}(t)$, the acute class $\mathcal{A}(t)$, and the carrier class $\mathcal{C}(t)$.

4.4.   Stability conditions of the disease-free equilibrium

In this section, we provide the stability conditions of the DFE, which gives important information about the future course of the disease. Then, we have the following theorem:

Theorem 3. The HBV-free equilibrium point is locally asymptotically stable as long as $\mathcal R_0<1$, otherwise it is unstable.

Proof. To study the stability criterion of disease-free equilibrium Ψ⁰, the general Jacobian matrix of system (3.1) is calculated as follows:

Therefore, at Ψ⁰, the Jacobian matrix takes the following form:

Furthermore, it can be rearranged as follows:

where $\varpi_1 =-\delta^\lambda \frac{\Lambda^\lambda+m^\lambda}{\mu^\lambda}$, $\varpi_2 =-\beta^\lambda \frac{\Lambda^\lambda+m^\lambda}{\mu^\lambda}$, $\varpi_3 =-\Lambda^\lambda (\tau^\lambda+\eta^\lambda)$, $\varpi_4 =-(\mu^\lambda+\mu_d^\lambda+\rho^\lambda+\gamma^\lambda)$, $\varpi_5 =-(\sigma^\lambda+\mu^\lambda)$, and $\varpi_6 =-(\theta^\lambda+\mu^\lambda)$. Thus, the disease-free equilibrium Ψ⁰ is locally asymptotically stable if all the eigenvalues ${\xi}_i,\ i=\mathrm{1,2},\dots ,5$ of the matrix $\mathbb{J}(\Psi^0)$ satisfy the following condition [62]:

We can examine the mentioned eigenvalues by solving the following characteristic equation:

where Î is an identity matrix and ξ represents the eigenvalues. Therefore, we obtain an equation of the following form:

where the coefficients $\vartheta_1$, $\vartheta_2$, $\vartheta_3$, $\vartheta_4$ are given as follows:

Therefore, the eigenvalues of Eq.(4.6) are given by $\xi_1=-\mu^\lambda,$ and $\xi_2, \xi_3, \xi_4, \xi_5$, where $\xi_2, \xi_3, \xi_4, \xi_5$ are the roots of the following equation:

As long as $\mathcal{R}_0>1$, we have the following:

Clearly, when $\mu^\lambda+\mu_d^\lambda+\rho^\lambda+\gamma^\lambda>\Lambda^\lambda \eta^\lambda$, it can be seen that if $\mathcal{R}_0<1$, then $\vartheta_4>0$ of Eq (4.7) are positive since all the model parameters are positive. Therefore, by remembering that all $\varpi$ values are negative, it follows from the Routh-Hurwitz criteria [63], [64], [65], [66] and from condition (5) of Lemma 2 [62] that the condition (4.4) becomes satisfied, which means that all roots of Eq(4.6) have negative real parts, which further imply that the disease-free equilibrium (DFE) Ψ⁰ is locally asymptotically stable (LAS). On the other hand, if $\mathcal{R}_0>1$, then at least one root $\xi_2, \xi_3, \xi_4, \xi_5$ of Eq (4.7) has a positive real part, since $\vartheta_4<0$ indicates that the DFE Ψ⁰ is unstable.

5.   Calibration of the model parameters

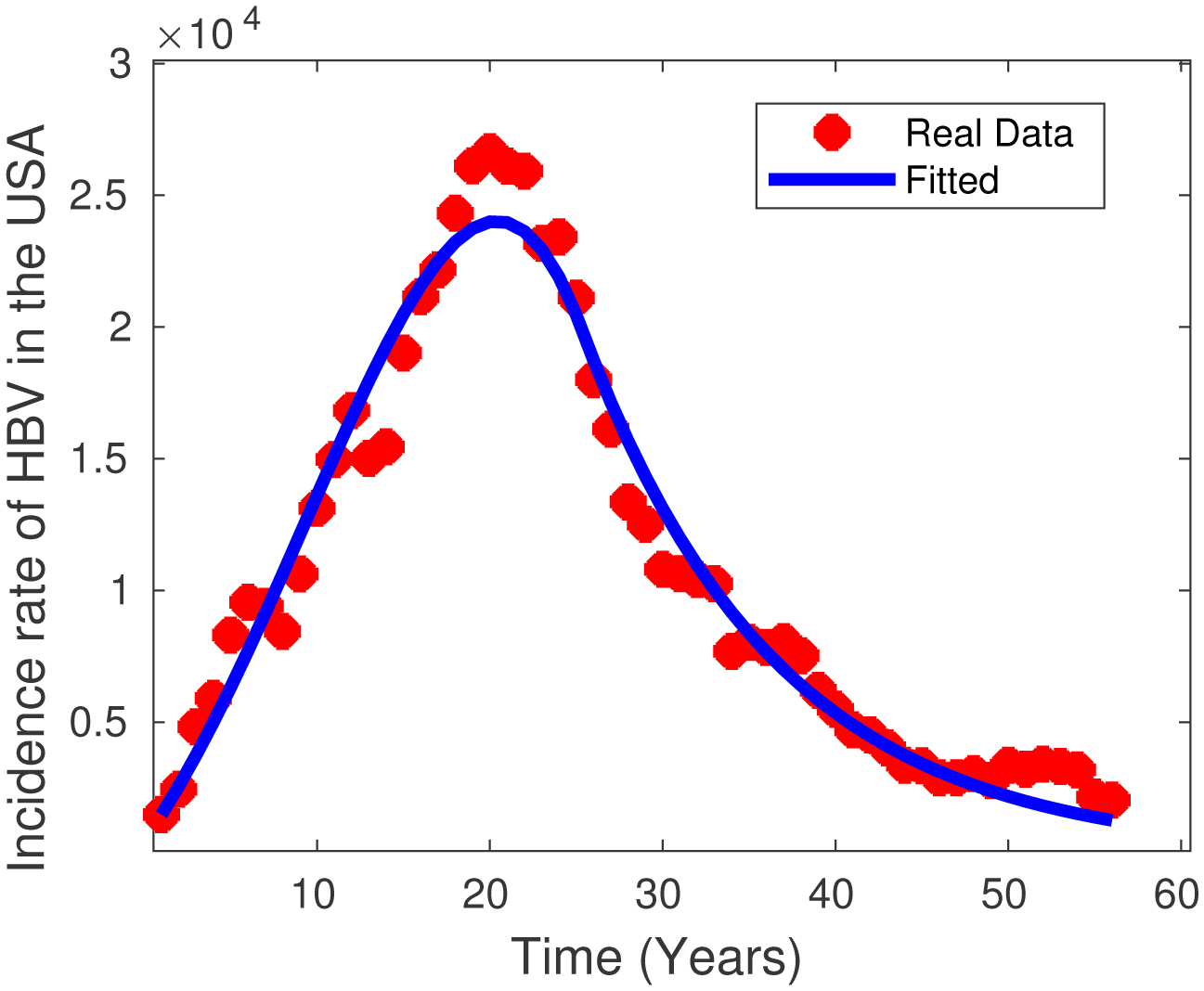
When conducting an epidemic investigation, the most important factor for the validation of the model is the most accurate determination of the parameters. These determined values contribute to the accuracy of the model to better visualize the course of the epidemic. Therefore, in this part of our research, we aim to determine and explain the parameters using the least squares curve fitting technique. We chose exactly 13 different parameters in the model we proposed for the hepatitis-B infectious disease. Among the parameters we chose, we took the parameter µ=3.4857e-05 from the literature [67] and took performed the numerical simulation by estimating the other parameters. We set the initial conditions as follows: $\mathcal S(0)=7000, \mathcal L(0)=400, \mathcal A(0)=1497, \mathcal C(0)=90, \text{and} \,\ \mathcal P(0)=250.$ Figure 2 displays the result of the 12 biological parameters we obtained from the literature and fit with the help of the least squares curve fitting method. The produced Hepatitis-B model expresses the real cases of this epidemic in a very transparent way. The most accurate solution of this model for the Hepatitis-B cases and the epidemic category was to reach the ideal values of the relevant parameters in order to keep the average absolute relative error between the actual data and the prediction to a minimum. Real Hepatitis-B cases are shown with red stars, while the best-fit prediction curve for our model is shown with a blue line. The chosen parameters for our model are shown in Table 1, along with the best estimates that can be made using the least squares method.

Figure 2.  Time series of annual hepatitis-B cases for the USA from 1966 to 2021 and best-fitted curve associated with the proposed model.

DownLoad: Full-Size Img PowerPoint

6.   Numerical result and discussion

In this study, we want to examine the effect of HBV on the course of the disease by establishing a new model that measures the effect of vertical transmission and takes the migration effect parameters into account. For this, we built a mathematical model with 5 compartments: susceptible population $\mathcal S(t)$, latent population $\mathcal L(t)$, and acute population $\mathcal A(t)$, carrier population $\mathcal C(t)$, protected infected (protective rescued) $\mathcal P(t)$. We used the fractional version of the 4th order Runge-Kutta method to obtain numerical solutions of the model within these compartments [68], [69]. In general, the m-order Runge-Kutta method has the following advantages:

The model is built using fractional differential operators. The memory effect captured by fractional differential operators improves the accuracy of our model. First, fractional models are more effective in modeling anomalous behavior. Such dynamics may not be captured with classical models. Infectious diseases such as HBV have contributed to increasing the model accuracy because they show abnormal dynamics, which helps obtain more accurate results by creating a more realistic propagation scenario. Thanks to the memory effect, fractional models are more accurate in long-term forecasts than ordinary models. The accuracy of our model has been increased thanks to the memory-effective fractional order model instead of the ordinary order model [58], [71].

We obtained some results after obtaining the numerical solutions of the SLACP model. We utilized the literature [67], [72] for some of our parameters in the model and estimated other parameters. Our resulting parameter estimates are shown in Table 1:

Table 1.  Parameters used for the HBV model.

Par.	Biological description	Value	Sources
Λ	Recruitment rate	0.22996	fitted
µ	Natural mortality rate	3.4857e-05	[67]
β	Transmission rate	0.001	fitted
r	Reduced transmission rate relative to acute	0.24	fitted
τ	Infected rate of mothers with HBV acute virus	0.029	fitted
γ	Recovery rate of individuals with acute infection	0.2	fitted
σ	Recovery rate of individuals in the carrier class	0.183	fitted
ρ	Transition rate from Acute to Carrier	0.212	fitted
µd	Death rate from HBV disease	0.1	fitted
m	Rate of community coming from outside	0.54	fitted
δ	Transition rate from susceptible to latent	0.02	fitted
θ	Transition rate from latent to acute	0.251	fitted
η	Rate of babies born infected	0.3	fitted
$\mathcal S(0)$	Initial Susceptible Population	7000	fitted
$\mathcal L(0)$	Initial Latent Population	400	fitted
$\mathcal A(0)$	Initial Acute Population	1497	[72]
$\mathcal C(0)$	Initial Carrier Population	90	fitted
$\mathcal P(0)$	Initial Protected Infected Population	250	fitted

---

 | Show Table

DownLoad: CSV

In addition, we examine the transition rate on these populations from acute to carrier in Figure 3, the recovery rate of individuals in the carrier class in Figure 4, and the infected rate of mothers with an acute HBV virus in Figure 5.

Figure 3.  Acute population dynamics for various variables of the transition rate.

DownLoad: Full-Size Img PowerPoint

Figure 3, which contains the graph of the rate of transition from the acute state to the carrier state, graphically shows the acute population and the rate of transition from the acute state to the carrier state. It helps in to examine the spread of HBV at different stages over the years, and shows the change in the acutely infected population over time.

Figure 4.  Recovery rate of individuals in the carrier class.

DownLoad: Full-Size Img PowerPoint

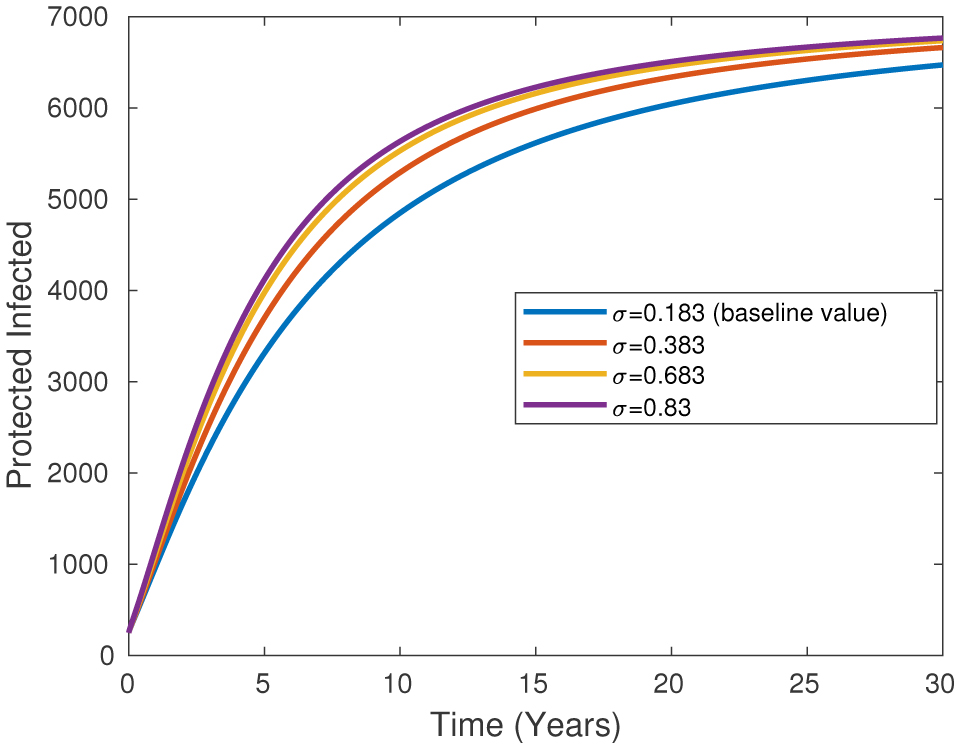
Individuals in the Protected Class are individuals who have recovered from the disease and become immune. Over time, infected individuals recover and move into the protected class. This transition is modeled in Figure 4, in which the rate of recovery results in a decrease in the number of infected individuals and an increase in the number of protected individuals over a given period of time.

Figure 5.  Infected rate of mothers with HBV acute virus.

DownLoad: Full-Size Img PowerPoint

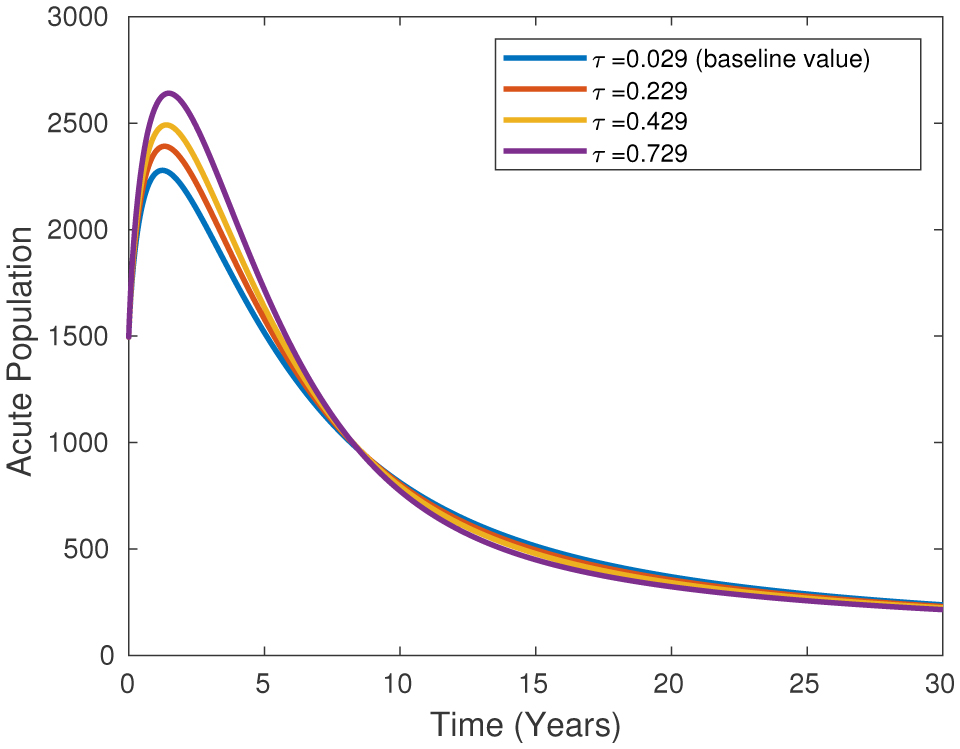
It is important to examine the infection rate of mothers with an HBV infection and the risk of transmitting this infection to babies during or after birth. Vertical transmission refers to transmission from mother to baby during or shortly after birth. Due to the high risk of transmission in mothers with an acute infection, it is of great importance to reduce this risk with measures such as prenatal and postnatal screenings and vaccinations. Figure 5 shows the change in the rate of mothers infected with an acute HBV virus over the years. In Figure 2, the data we have collected shows that there has been a noticeable increase in the number of people infected with this virus in the first 20 years since 1966. In the following years, we see that these numbers gradually decrease due to vaccinations and necessary precautions; even today (in a 50-year period), they have reached the same level as the numbers we achieved in 1966.

Figure 6.  Population densities of the HBV model for the estimated values.

DownLoad: Full-Size Img PowerPoint

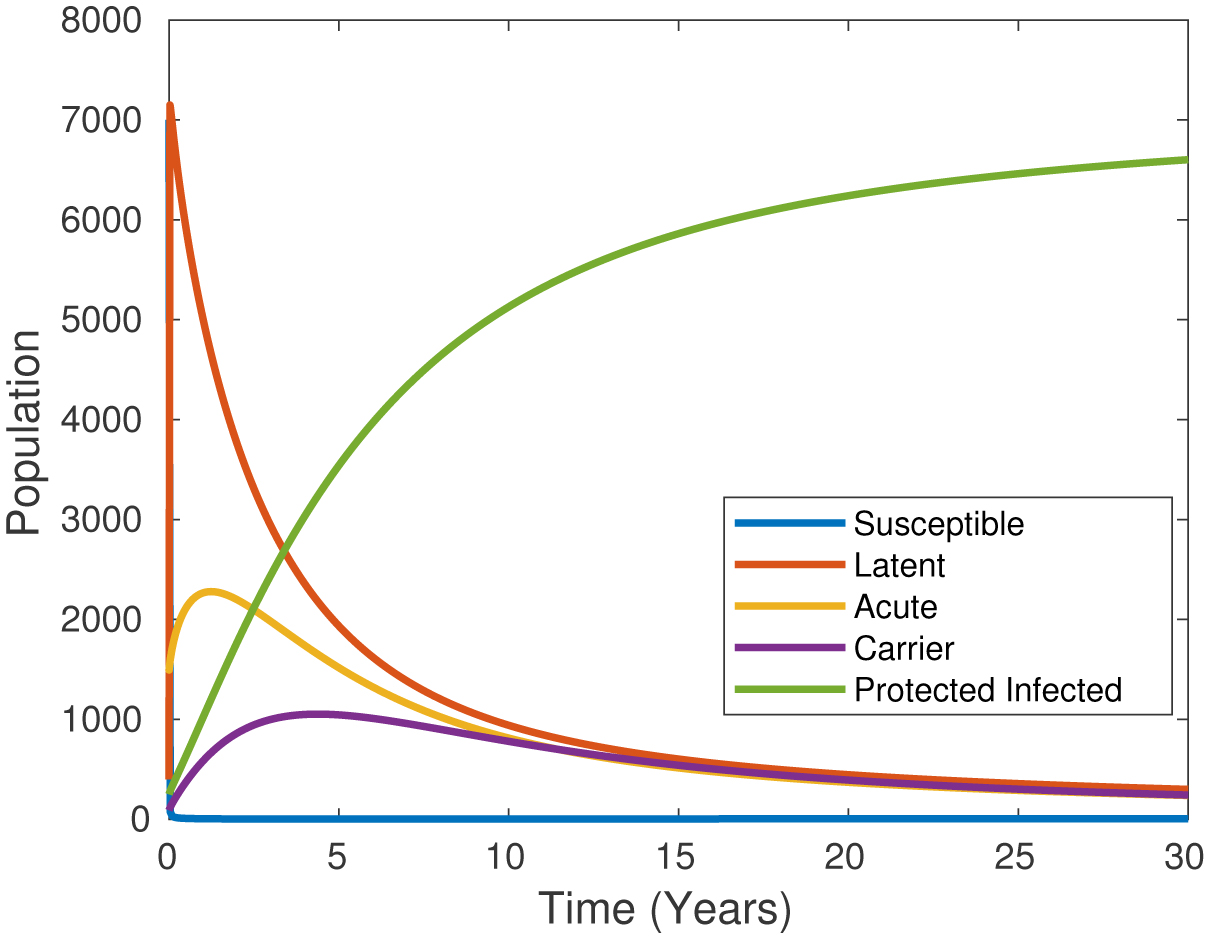
Additionally, we examined the development and change of some populations in our model over time. In Figure 6, we examine the change and development of susceptible, latent, acute, carrier, and protected infected individuals, that is, all the populations in the model, over time. Figure 6 represents the all population densities of the HBV model for the estimated values. According to the model and the real data, the protected infected population (i.e., recovered from infectiousness) gradually increases as time passes.

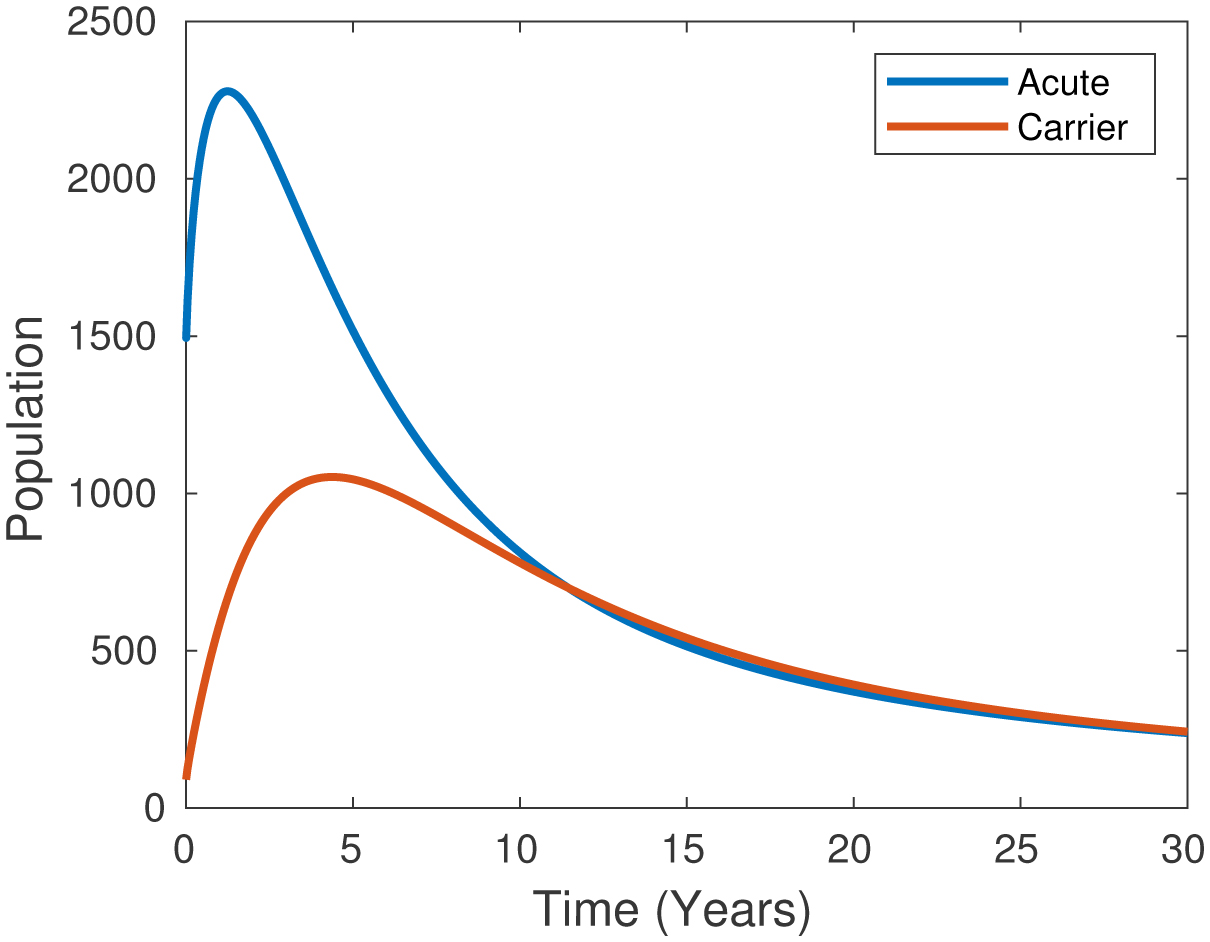
In Figure 7, we examine the relative status of the acute and carrier populations over time. According to Figure 7, up until the 10th year, the acutely infected population was always higher than the carrier population. Additionally, the figure points out the relationship between the acutely infected and the carrier classes was during the simulation process. The numbers used in the graphs were obtained by careful, repeated attempts to construct the most accurate and closest graph to the model. Since our model was created from scratch, we do not have any literature to reference; however, the first feature that distinguishes it from other models is that it was created using real data.

Figure 7.  Status of acute and carrier populations relative to each other.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Effect of different fractional orders on the recovery rate of carrier class in the acute population.

DownLoad: Full-Size Img PowerPoint

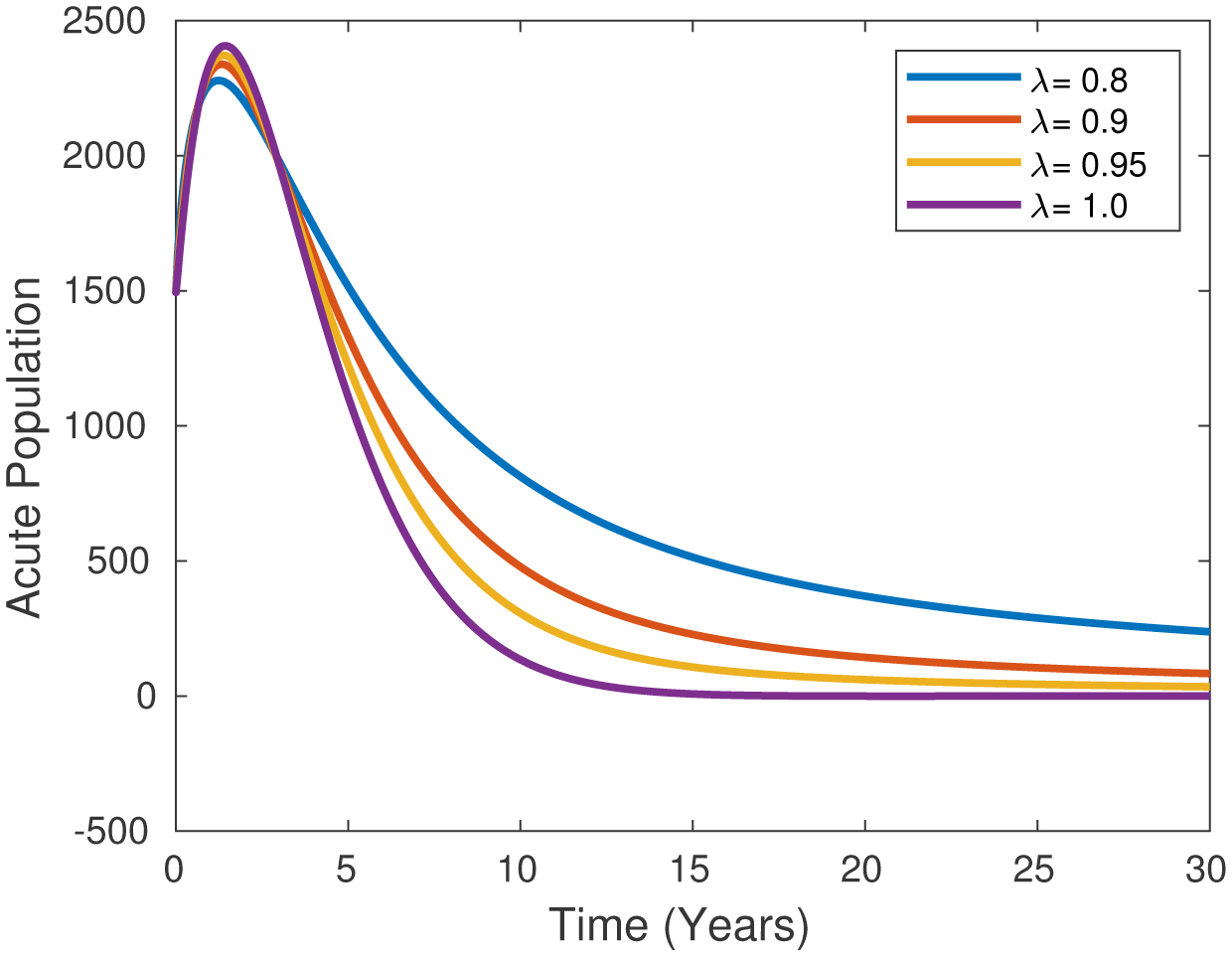
Figure 8 shows the recovery rate of individuals within the carrier class, known as σ in the acute population, for different fractional λ levels of 0.8, 0.9, 0.95, and 1.0. It is seen that as the fractional order value increases, the number of individuals with acute illnesses decreases over the years. The chart is based on σ = 0.183.

Figure 9.  Transition rate from acute to carrier class in carrier population of different fractional orders.

DownLoad: Full-Size Img PowerPoint

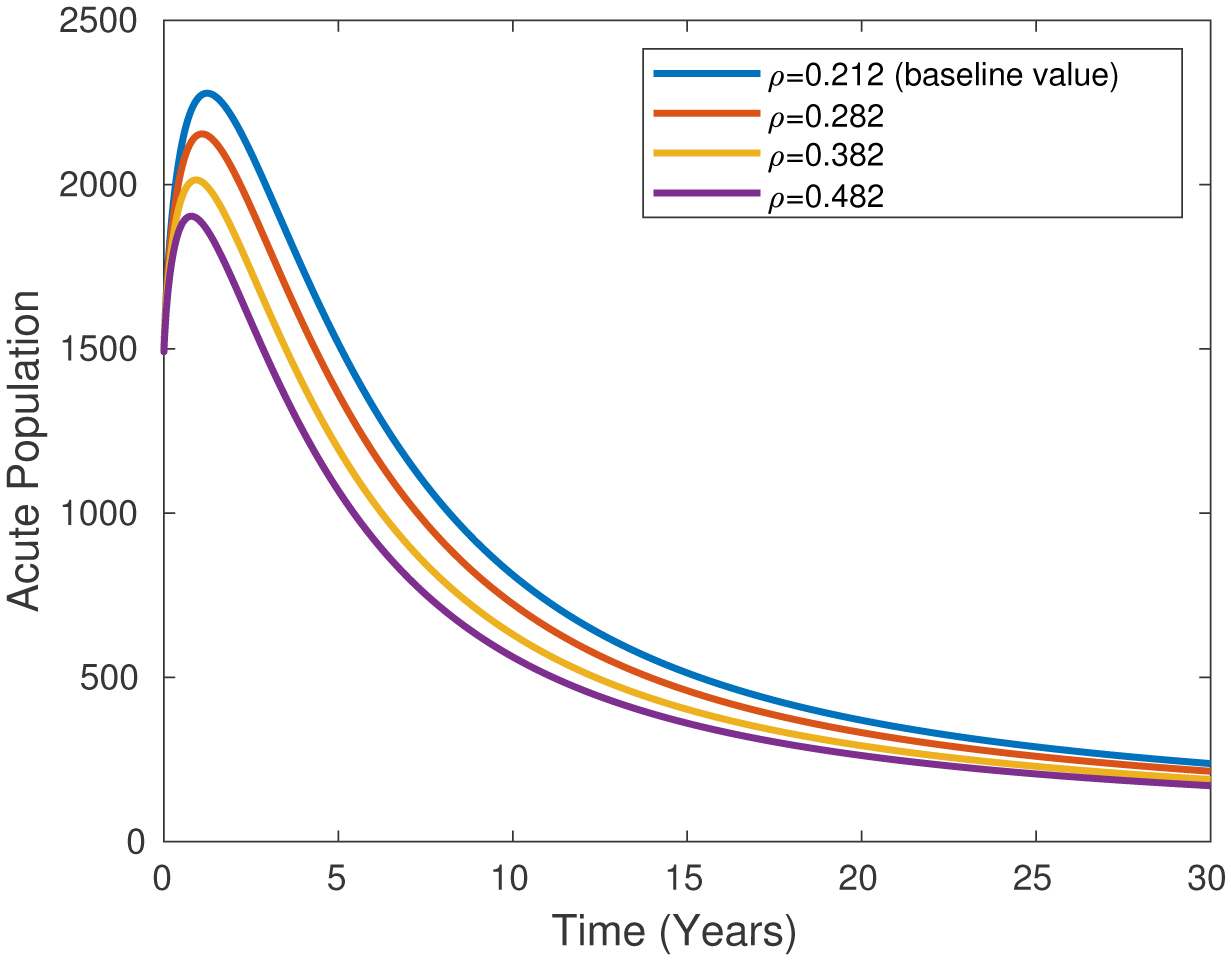
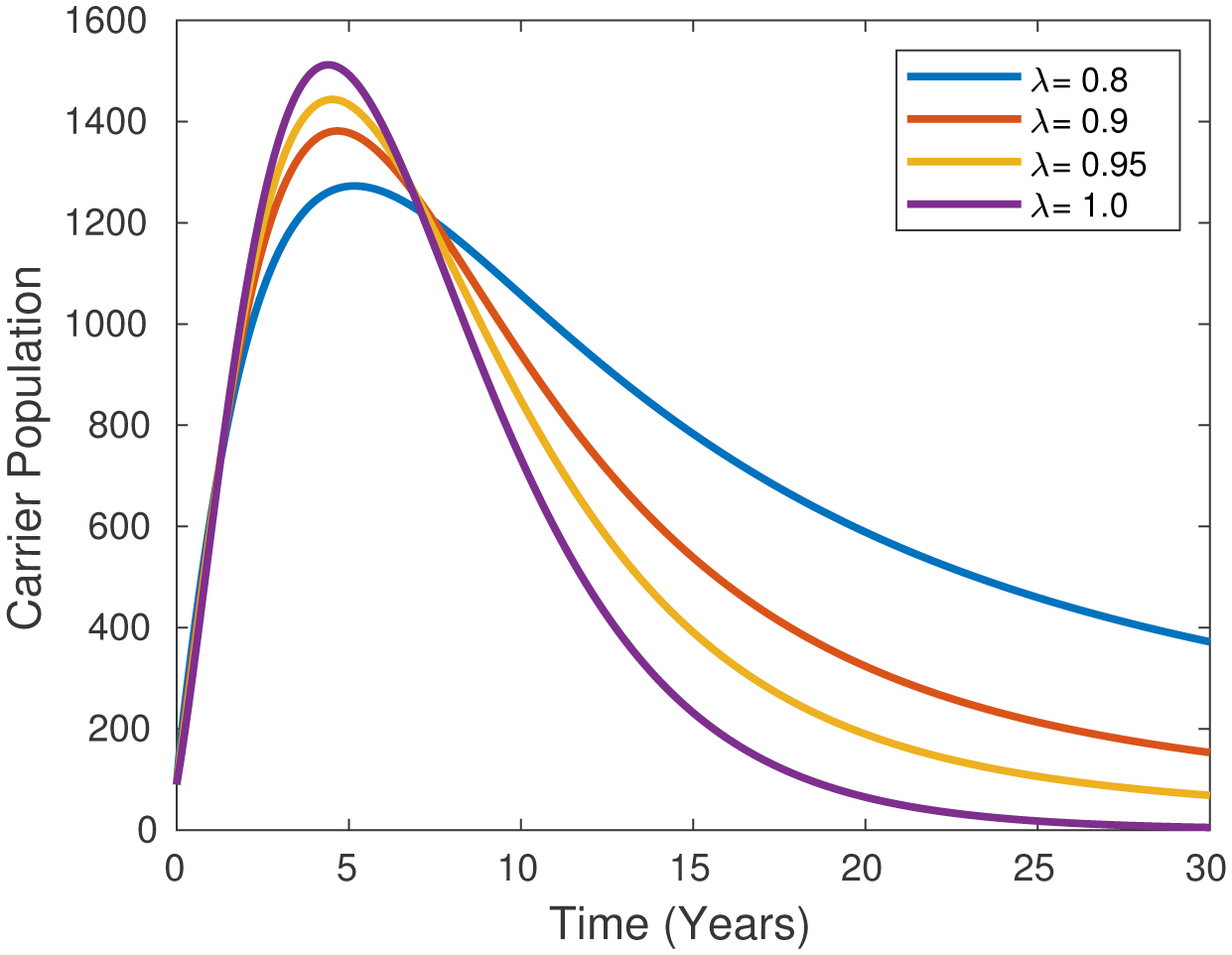
Figure 9 shows the transition rate from acute to carrier in the carrier class, known as ρ in the carrier population, for different fractional λ levels as 0.8, 0.9, 0.95, and 1.0. As the fractional order value increases, the rate of transition from acute to carrier increases in the carrier class in the period between 0 and 10 years, while a reverse decrease is observed in the following years. The chart is based on ρ = 0.212.

7.   Conclusion

In this paper, we developed a new Hepatitis-B mathematical model that contained a vertical transmission from mothers to newborn babies. Additionally, we evaluated the disease-free equilibrium point and its stability analysis. Thus, the conditions under which the disease-free equilibrium points of the system are stable were determined. In order to investigate the virus transmission dynamics of the Hepatitis-B virus, we listed the estimated parameter values for the system of Eq (3.1) with our new clustered model for the Hepatitis-B virus. This section of the article presents the results obtained throughout our study process, the effectiveness of this model, and its performance by developing a new expanding structure that models Hepatitis-B by selecting the appropriate effect for the model. The model we developed provides a protective dose to people with susceptible $\mathcal S(t)$, latent $\mathcal L(t)$, acute $\mathcal A(t)$, and carrier $\mathcal C(t)$, which are considered the basic components of Hepatitis-B diseases. It was partitioned by adding rescued $\mathcal P(t)$ individuals. Our results determined that the course of Hepatitis-B disease is modeled by predictions, of which the predictions about its process were obtained. Non-negative solutions were obtained to ensure the biological augmentation of our system of equations of the model. The replica of our Hepatitis-B model was estimated using the ‘least squares curve fitting’ method. Numerical simulations of data from the USA were performed based on these predicted values. In this model, digital simulations were used to predict how the Hepatitis-B disease would progress to determine how the country would progress. The model we considered in our study included a fractional order differential operator. Thus, the memory effect was considered in the model. Various fractional orders have been tried in our simulations. Thus, various scenarios have been created and supported with graphics and comments. This model considered the effect of vertical transmission and migration on the spread of the disease. For vertical transmissions, it can provide methods to prevent or minimize the spread of the virus before and during birth; for migration, it can make it easier to observe how the virus affects the body under the conditions in the places where the immigrant population lives. Moreover, it plays a role in understanding the relationship between the acute and carrier populations and determining the transmission rate and transmission routes of the virus. This allows us to evaluate the development of the virus. Our model can also provide information to observe the impact of protective rescued populations on future epidemic risks. In short, this model can be preferred when trying to develop important strategies to control the virusby providing a more comprehensive perspective in examining the dynamics of the virus; this may help to develop more effective and targeted health interventions in future research.) For the future directions of the paper, an age-structured model can be developed to investigate the disease process according to the population's age. Additionally, different types of fractional operators may be taken into account to point out the differences and similarities of the mentioned fractional operators.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.