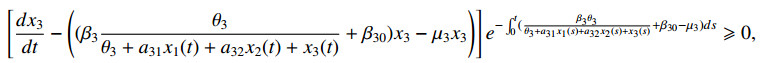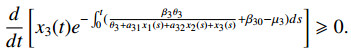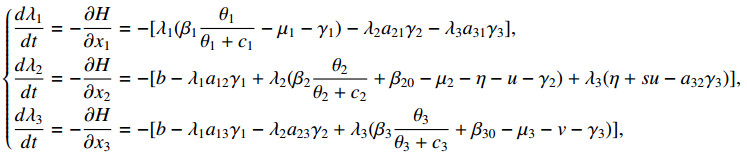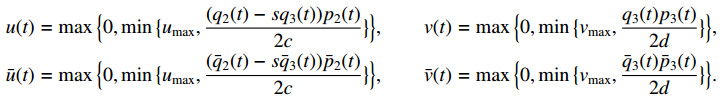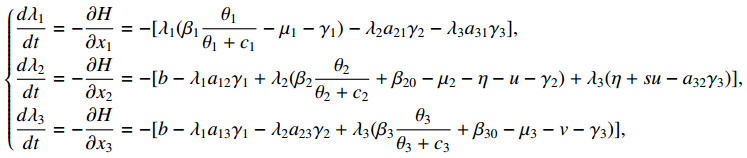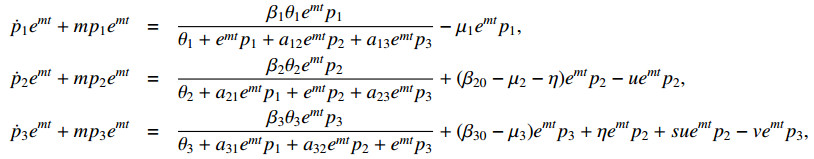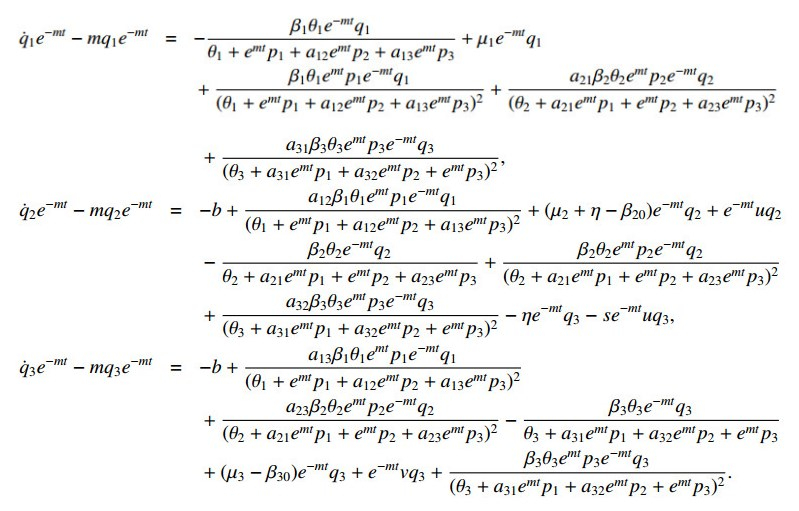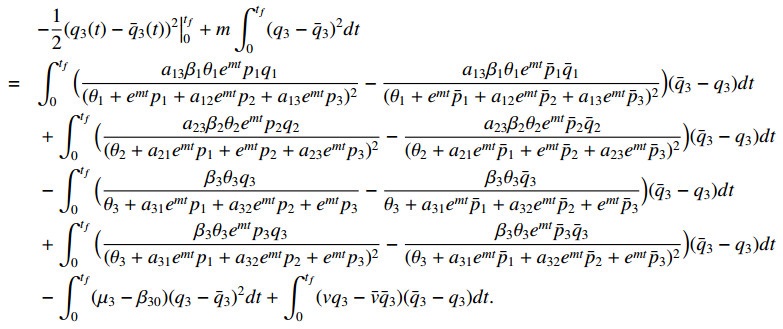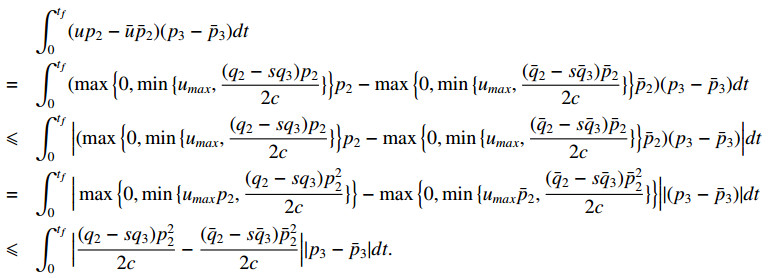1.
Introduction
Intratumor heterogeneity contributes to the emergence of therapy resistance, which plays a vital role in cancer relapse. Biologically, heterogeneity may originate from cellular genetic and epigenetic modifications as well as the environmental changes [1,2]. Clinically, adaptive responses to targeted therapies can facilitate both the expansion of pre-existing drug-resistant subpopulations and the acquisition of new mutations, which yields heterogeneity [2,3,4]. However, the dynamics of how intratumor heterogeneity may affect tumor evolution is not well understood, and is important for us to understand the mechanisms of drug resistance in cancer therapy.
There are mounting evidences that mutation can create favorable conditions for heterogeneity and result in cancer therapy resistance. A critical question arises that whether mutation is prior to or after the onset of therapy. Experiments have showed that mutations in KRAS, TP53, ABL or MET can pre-exist before the initiation of therapy, and contribute to the development of drug resistance [5,6,7,8,9,10]. In addition, it is shown that mutations can also emerge in response to treatment stress and promote drug resistance [11,12,13,14,15,16]. The two mechanisms may imply different dynamics of cancer relapse, and quantitative studies are necessary to uncover the process of how mutation may affect treatment resistance over time.
Many mathematical models have been developed to study the complex dynamics of cancer resistance/recurrence [17,18,19,20,21,22,23,24]. For example, various ordinary differential equations models were developed to describe how the interaction between drug-sensitive and drug-resistant cancer cells may shape the progression of drug resistance [17,18,19,20]. Moreover, the interaction between cancer cells and stroma [21] or immune cells [22,23,24] are considered in different types of models. In addition to the tumor cells, the competition between normal cells and tumor cells can be important for tumor progression [25,26]. Most existing models consider the tumor progression dynamics with pre-existing resistant cells, which interact with sensitive tumor cells through the competition in resources. Nevertheless, resistance cells can also be induced by the treatment behavior, by which sensitive cells can transit to resistant cells due to treatment stress. The mechanism of cell plasticity induced drug resistance is important clinically, however, to our knowledge, is not well studied quantitatively.
In recent years, the idea of adaptive therapy has attracted the attention of many researchers, and the mathematical tool of optimal control theory was applied to obtain the optimal therapy schemes in adaptive therapy. For example, from the standpoint of optimal control, minimization of the total drug count was analyzed in order to control IgG multiple myeloma [27]. The optimal control method was utilized in treatments of various types of cancers, including metastatic prostate cancer [17], immunotherapeutic treatment [28,29], chemotherapy [30], combination of chemotherapy and stem cell transplants for acute myeloid leukemia [31], combination therapy of chronic myeloid leukemia [32], combination chemotherapy of antiangiogenic treatment [33], and bone metastasis treatment [34]. In these studies, the effects of cell plasticity induced drug resistance and the competition between tumor cells and normal cells are not included. Here, we ask how optimal control theory can help us to determine the optimal therapy strategy when both effects of the cell plasticity and competitions are considered.
In this study, to have a better understanding of tumor progression in the base of competitions between normal cells and various types of cancer cells, we develop a mathematical model that includes normal cells, drug-sensitive tumor cells and drug-resistant tumor cells, and apply the model to study the dynamics of tumor progression and treatment responses. First, mathematically, we consider the nonnegativity and boundedness of the model solutions, and the existence and stability of steady states. Next, applying the Pontryagin's maximum(or minimum) principle (PMP) [35], we derive the optimal treatment schedule that can minimize the tumor burden during the treatment and the total drug dose of combination therapy. Two types of optimal control problems are considered with different designations of cost functionals, including the quadratic and linear drug control, respectively.
2.
Model formulation
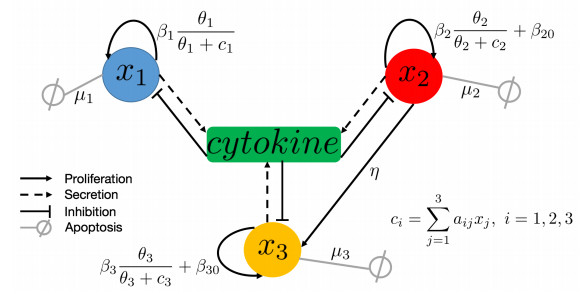
To model the interaction between normal and tumor cells, we consider a mathematical model of tumor progression dynamics that includes normal cells, drug-sensitive and drug-resistant tumor cells (Figure 1). In the model, each type of cells proliferate with different rates that are dependent on the cell numbers and the microenvironmental cytokines regulating the cell proliferation pathway, and are removed due to cell death. All cells can secrete cytokines to regulate the proliferation of all cells, which form the competition between different types of cells. To consider the occurrence of mutation induced by treatment stress, we assume a possible transition from drug-sensitive to drug-resistant cells.
To formulate the model, we consider the numbers of normal, drug-sensitive and drug-resistant cells, which are represented by x1(t), x2(t) and x3(t), respectively. Dynamically, these three types of cells different from each other in their associated proliferation rates and removal rates.
Biologically, the self-renewal ability of a cell is determined by both microenvironmental conditions, e.g., growth factor receptors and cell cycle checkpoints, such as fibroblast growth factors (FGFs) and the transforming growth factor beta (TGF-β) family [36,37,38]. The exact activation pathways that regulate the self-renewal of cells are poorly understood. However, a Hill type proliferation function can be derived based on simple but general assumptions on either positive or negative regulation growth factors [39,40]. Let
represent the overall effects of how cytokines secreted from all types of cells may regulate the self-renewal of type i cells, the competitions from cell type j to cell type i are given by the coefficients aij (i,j=1,2,3). Thus, according to the Hill type function proposed in [39,40], the proliferation rate for normal cells can be formulated as
where β1 represents the maximum proliferation rate of normal cells, and θ1 is the 50% effective coefficient (EC50) that is associated with the effective concentration of cytokines. Here, we take the Hill coefficient to be 1 for simplicity. The proliferation rates of tumor cells are given similarly. However, tumor cells can escape the antigrowth signals due to the capability of self-sufficiency to growth signals and insensitivity to anti-growth signals [41], we thus introduce an additional nonzero constant βi0 (i=2,3) for the effects of self-sustained growth signals of tumor cells. Hence, the proliferation rates of drug-sensitive and drug-resistance cells are formulated as
respectively.
The three types of cells undergo cell death with rates μi, respectively. Moreover, we assume that drug-sensitive cells can transit to drug-resistant cells with a rate η. These arguments give rise to the following model
Biologically, all parameters are non-negative, i.e.
Without loss of generality, we let
In the model (2.2), we apply Hill type functions to describe the proliferation rates of cells, which are derived based on the assumption of cell proliferation regulated by cytokines. Nevertheless, we note that in many studies, logistic growth or Gompertizian growth are often applied to model the dynamics of tumor growth [17,18,19,22,23,24,30]. These growth rate functions are consistent in describing the same property that cell growth rates decrease with the cell number, however are originated from difference biological assumptions. Biologically, Hill type growth rate is more proper to model tumor growth, by which the effects of cytokines are described explicitly.
In the current study, we would be always interested at the situation with positive cell numbers prior treatment. Thus, we have the following assumptions:
(H1) The maximal proliferation rate β1 is greater than the death rate μ1 of normal cells, i.e.,
(H2) The maximal proliferation rate of drug-sensitive cells (β2+β20) is larger than the total removal rate due to either cell death or transition (μ2+η), and the residual proliferation rate β20 should be smaller than the total removal rate to avoid infinity cell numbers (uncontrolled cell growth). These assumptions give
(H3) The maximal proliferation rate of drug-resistance cells (β3+β30) is larger than the cell death rate (μ3), and the residual proliferation rate β30 should be smaller than the death rate to avoid infinity cell numbers (uncontrolled cell growth). These assumptions give
The assumptions (H1)–(H3) give biologically natural restrictions to the proliferation and death rates for the three types of cells.
3.
Results
In this section, we first study the mathematical properties of the model (2.2), next consider the optimal strategy using PMP.
3.1. Invariant set of model solutions
Theorem 1. Assume the conditions (2.3)–(2.6), let
then Ω is an invariant set of the model (2.2), i.e., any solution of (2.2) with initial condition (x10,x20,x30)∈Ω satisfies
Proof. Let (x1(t),x2(t),x3(t)) be the solution of the model (2.2) with initial condition (x10,x20,x30)∈Ω.
Firstly, it is easy to have
and
From the third equation of (2.2), we have
Multiplying both sides of (3.2) by 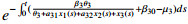 , we have
, we have
which gives
Integrating (3.3) over (0,t) with x3(0)=x30, we have
which gives
Thus, any solution of (2.2) with nonnegative initial condition remains nonnegative over t>0.
Next, we show that any nonnegative solution of (2.2) has finite upper bound. From the initial condition x1(0)=x10⩽ξ1θ1 and
we have x1(t)⩽ξ1θ1,∀t⩾0.
Similar calculations yield x2(t)⩽ξ2θ2 and x3(t)⩽β3θ3+ηξ2θ2μ3−β30,∀t⩾0. This completes the proof.
3.2. Steady state solutions
3.2.1. Existence of steady state solutions
Now, we consider the steady state solutions of the model (2.2). Let (x∗1,x∗2,x∗3) be the nonnegative steady state, we have
where
We are only interested at the steady states that the cell numbers are nonnegative, which can be divided into one of the 8 possible types (+/0,+/0,+/0), here '+' means a positive number, and '0' means zero. It is easy to see that, there always exists a zero steady sate E0=(0,0,0), however this state represents the state of death and is biologically not interested. Since η>0, x∗3=0 always implies x∗2=0, there is no steady state of form (0,+,0) or (+,+,0). Thus, there are 6 possible steady states (here x∗i>0)
The theorem below gives the existence of nonnegative steady states.
Theorem 2. Consider the model (2.2), and assume that all parameters satisfy (2.3).
(1) There always exists the zero steady state E0=(0,0,0).
(2) If (2.4) holds, (2.2) has tumor-free equilibrium E1=(ξ1θ1,0,0).
(3) If (2.6) holds, (2.2) has normal-free equilibrium E3=(0,0,ξ3θ3).
(4) If both (2.4) and (2.6) hold, let
(2.2) has one steady state of form E13=(ξ4s2,0,ξ5s2) only when s2, ξ4 and ξ5 are non-zero and have the same sign.
(5) If both (2.5) and (2.6) hold, then
(i) if a23>ξ2θ2ξ3θ3, let
if
(2.2) has two (or one) steady state of E23-type; otherwise, (2.2) has no steady state of E23-type.
(ii) if a23<ξ2θ2ξ3θ3, (2.2) has one and only one steady state of E23-type.
(6) If (2.4)–(2.6) hold, (2.2) has at most two steady states of form E123=(x∗1,x∗2,x∗3). Moreover, let
where s3=1−a21a12≠0, the E123-type steady states are determined by the solutions x3=x∗3 of the equation
and the solution x∗3 satisfy: if s3>0,
and if s3<0,
In this case, x∗1 and x∗2 are given by
Proof. (1). It is trivial to see that model (2.2) always has the zero steady state E0.
(2). Let x∗2=x∗3=0 and x∗1≠0, from the first equation of (2.2), x∗1 satisfies
which gives
Hence, condition (2.4) implies
(3). Let x∗1=x∗2=0 and x∗3≠0. From the third equation of (3.4), we have
which gives
Thus, condition (2.6) implies
(4) Let x∗2=0, the first and the third equation of (3.4) become
Given x∗1,x∗3≠0, (3.19) can be rewritten as
which yields
From (3.21), we obtain
when s2,ξ4 and ξ5 are given by (3.6). Thus, (2.2) has a steady state of form E13 only when s2,ξ4 and ξ5 are non-zero and have the same sign.
(5). To consider the steady state of form E23, let x∗1=0 in (3.4), we obtain
When x∗2,x∗3≠0, (3.22) can be rewritten as
Thus, we have
Dividing both sides of (3.24) by x∗3, we have
Denote y∗=x∗2x∗3 and z∗=1x∗3, then
and (3.25) becomes
The first equation of (3.26) implies
The second equation of (3.26) implies
Hence, (3.27) and (3.28) together give the equation for y=y∗,
which implies
where p1,q1,r1 are given by (3.7). Thus, to get the positive solution of (3.26), we only need to solve the equation (3.29) for the solution 0<y∗<μ3−β30η.
When (3.29) has a solution y∗∈(0,μ3−β30η), we have z∗>0 from (3.27), and the nonnegative steady state E23=(0,x∗2,x∗3) is given by x∗2=y∗z∗ and x∗3=1z∗. Now, we identify the conditions to have such a solution based on the competition coefficient a23.
(i) If a23>ξ2θ2ξ3θ3, we have p1>0, and
Moreover,
Hence, if
(3.29) has two (or one) positive solutions in the interval (0,μ3−β30η), i.e., (2.2) has two (or one) steady states of E23-type; otherwise, (2.2) has no steady state of E23-type.
(ii) If a23<ξ2θ2ξ3θ3, similar to the above argument of (3.30), we have
Thus, since,
the quadratic function f(y) has one and only one root in (0,μ3−β30η), i.e., (2.2) has one and only one steady state of E23-type.
(6). To consider the positive steady sate of form E123=(x∗1,x∗2,x∗3), we need to find the positive solution of
From the first and the second equations of (3.31), we have
which gives
where s3=1−a21a12≠0.
Substituting (3.33) into the third equation of (3.31), x∗3 satisfies the quadratic equation
where p2, q2 and r2 are given by (3.9). Moreover, from (3.32) and (3.33), if s3>0, x∗3 should satisfy
and if s3<0, x∗3 satisfies
Thus, (2.2) has at most two steady states of form E123, which are determined by the solutions of (3.34) and (3.33) with x∗3 satisfies (3.35) when s3>0, or (3.36) when s3<0.
Theorem 2 establishes the conditions for the existence of nonnegative steady states of different types. Biologically, the conditions (2.4)–(2.6) are satisfied by most tissue cells, and hence the steady states of types E0,E1 and E3 always exist. Moreover, under the extreme condition when the competition coefficients aij=0 for any i≠j, it is easy to have the existence of the steady states of types E13 and E23 from (4) and (5), and from (6),
which yield the existence of a steady state of type E123. Thus, from the continuous dependence, the proposed model (2.2) have steady states of all types in (3.5) when the competition coefficients aij>0 (i≠j) are small enough.
3.2.2. Stability of steady states
Now, we study the stability of the steady state E∗=(x∗1,x∗2,x∗3). Let x=x1−x∗1, y=x2−x∗2 and z=x3−x∗3, and linearize the model (2.2) at E∗, we have the linearization equation
where
The characteristic equation of (3.37) is written as
where
Based on the characteristic Eq (3.39), the condition for asymptotical stability of steady states are given by the Theorem below.
Theorem 3. Consider the model(2.2), and assume that all parameters satisfy (2.3) and the conditions for the existence of steady states listed in Theorem 2, we have the following results.
(1) The zero steady state E0=(0,0,0) is asymptotically stable if and only if none of the conditions (2.4)–(2.6) holds, i.e.,
Furthermore, if
E0 is globally stable for any solutions in Ω.
(2) If (2.4) holds, the steady state E1=(x∗1,0,0) is asymptotically stable if and only if
(3) If (2.6) holds, the steady state E3=(0,0,x∗3) is asymptotically stable if and only if
(4) If (2.4) and (2.6) hold, the steady state E13=(x∗1,0,x∗3) is asymptotically stable if and only if
(5) If (2.5) and (2.6) hold, the steady state E23=(0,x∗2,x∗3) is asymptotically stable if and only if
(6) If (2.4)–(2.6) hold, the steady state E123=(x∗1,x∗2,x∗3) is asymptotically stable if and only if
where a,b,c are defined by (3.39). Particularly, if the following conditions are satisfied
E123 is asymptotically stable.
Proof. (1) For the steady state E0, the coefficient matrix of the linearized Eq (3.37) is
It is straight forward to obtain the corresponding eigenvalues
Thus, E0 is asymptotically stable if and only if λ1,λ2,λ3<0, i.e., none of the conditions (2.4)–(2.6) holds.
Next, to show the global stability of E0, we construct a Lyapunov function V(x1,x2,x3) as
It is easy to see that V(x1,x2,x3) is positive definite, and the derivative of V(x1(t),x2(t),x3(t)) along any solution of (2.2) is given by
From Theorem 1 and the proof therein, any solution of (2.2) with initial condition (x10,x20,x30)∈Ω remains in Ω for all t>0, i.e., x1(t),x2(t),x3(t)⩾0. Hence, when (3.41) is satisfied, the derivative (3.50) along any solution in Ω is negative definite. According to Theorem 1.1 in chapter X.1 of [36], E0 is globally stable for any solutions in Ω.
(2) For the steady state E1=(x∗1,0,0), the coefficient matrix of Eq (3.37) is
It is easy to have the eigenvalues
When (2.4) holds, we have ξ1>0, and λ1<0. Moreover, we have
and
Thus, E1 is asymptotically stable if and only if λ2<0 and λ3<0, i.e., ξ2θ2ξ1θ1<a21 and ξ3θ3ξ1θ1<a31.
(3) For the steady state E3=(0,0,x∗3), the coefficient matrix of (3.37) is given by
This, it is straight forward to have the eigenvalues λ1, λ2, and λ3 as:
From the condition (2.6), we have ξ3>0, and hence λ3<0. Moreover, note x∗3=ξ3θ3, similar to the argument in (2), we have
and
Hence, E3 is asymptotically stable if and only if λ1<0 and λ2<0, i.e., ξ1θ1ξ3θ3<a13 and ξ2θ2ξ3θ3<a23.
(4) For the steady state E13=(x∗1,0,x∗3), the coefficient matrix of (3.37) is given by
where
The eigenvalues λ1, λ2 and λ3 of JE13 satisfy
and
Since α4>0,α5>0, we have λ1<0,λ3<0 if and only if 1−a13a31>0. Moreover, similar to the previous argument,
Thus, E13 is asymptotically stable if and only if (3.44) is satisfied.
(5) For the steady state E23=(0,x∗2,x∗3), the coefficient matrix of (3.37) is given by
where
The eigenvalues λ1, λ2 and λ3 of JE23 satisfy
and
Similar to the previous argument,
Moreover, since α6>0 and α7>0, we have
Thus, E23 is asymptotically stable if and only if (3.45) is satisfied.
(6) For the steady state E123=(x∗1,x∗2,x∗3), the characteristic equation for (3.37) is given by (3.38).
From the Routh-Hurwitz stability criterion, all eigenvalues have negative real parts if and only if a>0, ab−c>0 and c>0. Hence, E123 is asymptotically stable if and only if (3.46) is satisfied.
Let
and applying (3.31), the coefficient matrix of (3.37) at E123 is given by
Since α1,α2,α3,x∗2,x∗3>0, we have
When the conditions in (3.47) are satisfied, we have
and hence
Furthermore, since
we have
Hence, from the Routh-Hurwitz stability criterion, E123 is asymptotically stable.
Theorem 3 gives the conditions for the asymptotical stability of steady states of different types. Specifically, the zero steady state E0 is asymptotically stable if none of the biological restrictions (2.4)–(2.6) holds, i.e., there is no steady state with non-zero cell numbers. When (2.4)–(2.6) are satisfied, and the competition coefficients aij=0 (i≠j), the steady state E123=(x∗1,x∗2,x∗3) exists, and is asymptotically stable, however other nonnegative steady states (E1, E3, E13 and E23) are unstable. The steady state E123 becomes unstable when the competition coefficients increase, and other corresponding nonnegative steady states become stable.
3.3. Therapy strategy
Now, we consider the problem of optimal therapy strategy when both drug-sensitive and drug-resistant tumor cells are co-existence. To this end, we extend the model to include the effect of drug-induced tumor cell death and transition. Here, we consider the possible combination therapy with two drugs, targeted to sensitive cells and resistant cells, respectively. Thus, we introduce the parameters u and v to represent the extra removal rates of drug-sensitive and drug-resistant cells due to treatment stress, respectively. In addition, we assume that the drug targeted to sensitive cells can induce transitions from sensitive cells to resistant cells, the transition rate is represented as su. Thus, the model (2.2) is modified as
Next we discuss the optimal therapy strategies based on (3.56) by designing the objective functionals with quadratic and linear controls, respectively.
3.3.1. Quadratic control
Firstly, we analyze the quadratic control problem, and study the existence and uniqueness of optimal solutions. In cancer therapy, we try to minimize the total quantity of drugs and the tumor burden during treatment, and hence the associated objective functional can be defined as
where tf denotes the duration of treatment, and b>0,c,d are constants, which represent non-negative weights of the three parts. Thus, the optimization problem is formulated as
Now, we prove the existence of the solution for the optimal control of (3.58).
Theorem 4. There exists at least one pair of optimal control (u∗,v∗) such that
Proof. First, we show properties below for the control problem (3.57).
(1). First, similar to the argument in Theorem 1, any solutions of (2.2) with initial condition in Ω1 is bounded with (x1(t),x2(t),x3(t))∈Ω1 for any t>0. From the Carathéodory Theorem (Theorem 5.1 in chapter I.5 of [42]), there exist (x10,x20,x30)∈Ω1 and (u,v)∈A so that the solution of Eq (3.56) with initial condition (x1(0),x2(0),x3(0))=(x10,x20,x30) is well defined in the interval t∈(0,tf).
(2). Since the intervals [0,umax] and [0,vmax] are closed and convex, the admissible control set A is also closed and convex.
(3). The the right hand side of (3.56) is continuous. Moreover, we can write the right hand side as
where
Since (x1,x2,x3)∈Ω1 is bounded, there exists K>0 so that
Thus,
(4). It is easy to verify that L = b (x_2(t) + x_3(t)) + c u(t)^2 + d v(t)^2 is convex with respect to u and v . Moreover, let c_1 = \min \{c, d \} , \beta = 2 , we have
Finally, the existence of the optimal control (u^*, v^*) is followed from the above properties and Corollary 4.1 in [43].
Now, we try to solve the optimal control solution (u^*, v^*) . To this end, applying the Pontryagin's maximum(or minimum) principle (PMP), the associated Hamiltonian H is defined as
Therewith, the associated co-state equations are
here,
and the associated transversality conditions are
On the interior of the control set \mathscr{A}, the optimal controls satisfy the condition
Furthermore, a standard optimality technique implies the optimal controls are given by
and
Now, analogous to the discussions in previous studies [29,30,34], we consider the uniqueness of the optimal control problem. Similar to the argument in Theorem 1, the state variables (x_1, x_2, x_3) of (3.56) are bounded, and there exists an invariant set \Omega_1 for the Eq (3.56) with
where b_1, b_2, b_3 > 0 . Moreover, the solutions of the co-state system (3.60) are bounded with t\in (0, t_f) .
Theorem 5. There exists a sufficiently small final time t_f such that the optimal control solution is unique.
Proof. We assume that there are two different solutions (x_1, x_2, x_3, \lambda_1, \lambda_2, \lambda_3) and (\bar{x}_1, \bar{x}_2, \bar{x}_3, \bar{\lambda}_1, \bar{\lambda}_2, \bar{\lambda}_3) that solve (3.56) and (3.60), and will come out with a contradiction.
For a given positive parameter m > 0 (to be determined latter), set
The optimal control solutions u(t), v(t), \bar{u}(t), \bar{v}(t) are given by p_i(t), q_i(t), \bar{p}_i(t), \bar{q}_i(t) as
Substituting x_i(t) = p_i(t) e^{mt}, \lambda_i(t) = q_i(t) e^{-mt} into Eqs (3.56) and (3.60), after a tedious calculation (see the Appendix), we obtain that there exist L_{1, i} > 0, L_{2, i} > 0 so that
and
Thus, adding up (3.65) and (3.66) for i = 1, 2, 3 , there exists L_3 = \max_{i = 1, 2, 3}\{L_{1, i} + L_{2, i}\} so that
and L_3 only depends on all equation coefficients.
Now, while we choose m = L_3 (1 + 3 e) and t_f < \dfrac{1}{ 3 m} , then m - L(1 + e^{ m t_f} + e^{ 2 m t_f} + e^{ 3 m t_f}) > 0 , which come out with a contradiction with (3.67) if (p_j, q_j) \not = (\bar{p}_j, \bar{q}_j) . Thus, we conclude p_i = \bar{p}_i and q_i = \bar{q}_i , and hence u = \bar{u} and v = \bar{v} from (3.64).
3.3.2. Linear control
Now, we consider the situation of linear control problem, and seek to minimize the pay-off functional J_1 that is defined as
Similar to discussions in Theorem 4, we have the existence of optimal control strategy (u, v) that minimizes J_1(u, v) .
Now, the necessary conditions of the above optimal problem can be given by the PMP [44]. According to PMP, the associated Hamiltonian H is written as
Thus, the associated co-state equations are
where
and the associated transversality conditions are
The optimal control solution (u, v) satisfies
Hence the optimal control solution is given by
and
From (3.72) and (3.73), the optimal controls for the linear problem is a bang-bang control with either zero or maximum dose drugs.
3.3.3. Numerical results
Now, we perform numerical simulations to verify the above analytic discussions. To carry out the numerical simulation, firstly we need to specify parameter values in our model. Since our model is proposed to describe the dynamics of tumor growth with both drug-sensitive and drug-resistant cells, we assume that the proliferation rate of drug-sensitive cancer cells is larger than that of normal cells, and the self-sustained growth rates of cancer cells are nonzero. Moreover, the proliferation rate of drug-resistant cells is larger than that of sensitive cells, but sensitive cells can strongly inhibit the proliferation of drug-resistant cells. Thus, we should have
Different types of cells response differently to the cytokines, and hence we assume that \theta_i can be different for different types of cells. Default parameter values used in numerical simulation are listed in the Table 1. Figure 2(a) shows the cell number dynamics in the case without treatment, in which the system states (x_1, x_2, x_3) approaches the steady state of E_{123} -type. At this state, drug-sensitive cells are dominant in the system, and there are a small fraction of pre-existing drug-resistant cells.
Now, we consider the effect of sequential treatment, with only one drug at one period. To this end, we run the model Eq (3.56) with u = v = 0 to t = 200\ \mathrm{days} so that cancer cells numbers reach a high level near the steady state. Next, we set u = u_{\max} to turn on the drug targeted to sensitive cells ( u -drug for short) for 200 days. Then, we set u = 0 and v = v_{\max} to turn on the drug targeted to resistant cells ( v -drug for short). Figure 2(b) shows the cell number dynamics after sequential treatment. From Figure 2(b), after the administration of u -drug, sensitive cell numbers rapidly decreases to an extreme low level, however resistant cells number increases to a high level and becomes dominant. Next, after the administration of v -drug, resistant cells number decreases, and sensitive cells number increases again, which show the clinical symptom of tumor relapse.
Now, we investigate the dynamics of cell number ratios under different treatment strategies with either u -drug or v -drug alone, or sequential treatment with the two drugs. Here, the drug is applied at t = 200 as in Figure 2 by which sensitive cells are dominant. After the administration of u -drug for 60 days, the ratio of sensitive cells decrease over time, however the ratio of resistant cells increase along with treatment, and the ratio of total cancer cells slowly increases following the decreasing phase in the early stage after treatment (Figure 3(a), (b)). If v -drug is applied alone, there is no obvious decreases in the cancer cells ratio after treatment (Figure 3(c), (d)). The reason is obvious, since the v -drug targeted cells contribute only a small fraction of cancer cells before treatment. Finally, in the case with sequential treatment of two drugs, the total cancer cells ratio shows continuous decrease over time, and reaches a level below 0.2 after 60 days treatment (Figure 3). These results suggest that various treatment strategies can result in different outcomes.
To investigate the effect of optimal control strategy, we numerically solve the optimal control problem with the method of forward-backward sweep method (FBSM) [45]. Figure 4 shows the result corresponding to the quadratic control problem. Here, we take the weight coefficients b = 1 , c = 70 and d = 0.15 (Table 1). The optimal solution in Figure 4 suggests that we should apply the maximum dose drugs simultaneously, and continuously reduce the drug doses at the end point of treatment. In this case, the total cancer cells ratio continuously decreases toward a level ( 2.93 \% ) much lower than those in Figure 3.
In the Eq (3.56), we introduce a parameter s to represent the effect of transition from sensitive cells to resistant cells. Biologically, the transition can be induced by epigenetic, adaptive changes, or gene mutation due to drug stress. To investigate how the transition may affect the optimal control treatment, we vary the relative strength of the transition rate (measured by the ratio s u_{\max} / \eta ), and calculate the total drug doses
and the ratio of cancer cells at t = 60 for each value s u_{\max} . Results show that both total doses and the ratio of cancer cells are insensitive with changes in the relative strength of the transition rate (Figure 5).
Similarly, we solve the optimal control problem with linear control pay-off functional, which yields a bang-bang control. We obtain similar optimal solutions as in the case of quadratic control, in which both drugs are administrated simultaneously with maximum doses, and stop the treatment at later stage (Figure 6). Correspondingly, the final total cancer cells ratio at t = 60 decreases to about 4.54 \% . Moreover, we vary the relative strength of the transition rate s u_{\max} / \eta to examine the dependences of the total drug doses and final cancer ratios on the relative strength of the transition rate s u_{\max} / \eta . Similar to the situation of quadratic control problem, both the total drug doses and final cancer cells ratio are nonsensitive with the transition rate s u_{\max} / \eta (Figure 7).
4.
Conclusions
Intratumor heterogeneity is important to cell competition, and may play important roles in cancer evolution. Here, we study a mathematical model of cancer evolution that includes competition between normal cells and two types of cancer cells, as well as the transition between cancer cells. Moreover, the potential transition from drug-sensitive cancer cells to drug-resistant cancer cells is also involved in the model. Based on the model, the invariant set of the nonnegative solutions, and the existence and the stability of steady sates are discussed. We further discuss the optimal control problem that trying to find the treatment strategy to minimize the optimal functional for both tumor burden and drug doses. We prove the existence and uniqueness of the optimal control strategy for the proposed model. Finally, numerical simulations are performed to verify the optimal control solutions.
In the present study, we study the problem of optimal treatment strategy of cancer through a simple differential equation model. This model considers the competition between different types of cells. In the realistic world, optimal treatment of cancer relies on two techniques: (1) effective method to measure the state of tumor growth; (2) reliable prediction of tumor growth. However, neither of these two techniques are available at present, and there is still a long way toward real world application of the concept of optimal control treatment. This paper is rather a conceptual study that try to explore the possible cell population dynamics when there are competitions between different types of cells, and the possible benefit of optimal treatment in comparing with traditional maximum dose treatment (MDT). The current study is based on a toy model of cell competitions in which different types of cells are assumed to be homogeneous, and the effects of microenvironment are not included in the model, the immune response are not included explicitly. To develop a more realistic and applicable model, these factors are for sure to be included, which is a big ambition in the field of computational cancer biology.
Acknowledgments
This work was funded by National Natural Science Foundation of China (NSFC 11831015).
Conflict of interest
The authors declare there is no conflict of interest.
Appendix
Proof of the inequalities (3.65) and (3.66)
Substituting x_i(t) = p_i(t) e^{mt}, \lambda_i(t) = q_i(t) e^{-mt} into equations (3.56) and (3.60), we have (hereafter, \dot{} means \dfrac{d\ }{d t} )
and
Multiplying both sides of the first three equation by e^{-m t} , and the last three equations by e^{mt} , respectively, we obtain
Similarly, we obtain the same form equations of \bar{p}_i and \bar{\lambda}_i , i = 1, 2, 3 .
Next, subtracting the equations for p_i and \bar{p}_i , and the equations for q_i and \bar{q}_1 , we have
and
Now, we consider the equations for (p_3 - \bar{p}_3) and (-q_3 + \bar{q}_3) , and other equations can be treated similarly. Multiplying the equation for (p_3 - \bar{p}_3) by (p_3 - \bar{p}_3) , and integrating the obtained equation from 0 to t_f , we have
Multiplying the equation for (q_3 - \bar{q}_3) by (- q_3 + \bar{q}_3) , and integrating the obtained equation from 0 to t_f , we have
We note that p_3(0) = \bar{p}_3(0) = x_{30} , equation (4.1) implies
Since the solutions of (3.56) are nonnegative, namely p_i, \bar{p}_i \geqslant 0 , we have
Hence,
Now, we perform estimations to some terms of (4.4), and the other terms can be obtained by similar discussions. Applying the Cauchy inequality, there exists M_1 > 0 such that
Next, since p_i(t) and \bar{p}_i(t) are nonnegative functions for t\in (0, t_f) ,
Moreover, since the function f(p_2, q_2, q_3) = \dfrac{ (q_2 - s q_3) p_2^2 }{2 c} is locally Lipschitz, there exists M_2 > 0 so that
Hence,
Similarly, there exists M_3 > 0 so that
Thus, from (4.4) and (4.5)-(4.7), and note (p_3(t_f) - \bar{p}_3(t_f))^2 \geqslant 0 , there exists L_{1, 3} > 0 so that
which gives an inequality of form (3.65).
Applying the analogous scheme, we obtain for L_{2, 3} > 0 so that
which gives an inequality of form (3.66).









 DownLoad:
DownLoad:
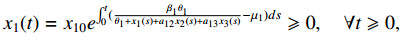
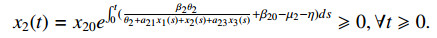
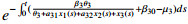 , we have
, we have