Analysis on security-related concerns of unmanned aerial vehicle: attacks, limitations, and recommendations

1.   Introduction

The notion of resolving sets (RSs) in networks has been the subject of a great deal of research over the last few years, mostly because of its practical applications in a variety of domains, including pattern recognition, coding theory, error correction, network design, and distance labelling systems. The RSs are basically subsets of nodes in a network with the capacity to differentiate between each node according to their distances from each other. RSs are often referred to as locating sets and metric bases.

In ^[1], Slater presents the idea of locating sets, or RSs, first, and he also created the phrase location number to indicate the size of the smallest RS. By following the Slater's work, Melter and Harary expanded on the idea of locating sets and introduced the term metric dimension (MD). They further investigated the MD of trees ^[2], providing a comprehensive understanding of this idea. The application of the MD problem has gained significant attention in addressing various real-world issues in recent times. Its utilization spans several domains: establishing reliable sensor networks ^[3], authenticating network intrusions by leveraging the network's metric base, tackling coin weighing challenges ^[4], and connected joins in networks ^[5]. Moreover, MD is applied in different branches of navigation ^[6], and chemistry ^[7].

Murtaza et al. ^[8] estimated the constant MD of cycle-related networks. It was also discovered that finding the MD of a connected network is an NP-hard task ^[9]. Chartrand et al. calculated the MD of both unicyclic and path networks ^[7]. Furthermore, they provided a characterization of all connected networks of order $p$ that possess MD $1$, $p-1$, and $p-2$. For calculating the MD of networks, Murdiansyah and Adiwijaya ^[10] presented the particle swarm optimization technique. Fernau et al. ^[11] introduced an algorithm with linear-time complexity to calculate the MD of chain networks. These networks are bipartite and have vertices that can be arranged based on neighborhood inclusion. In ^[12], Mulyono et al. focused on establishing the MD for three types of networks: the friendship network $\mathbb{F}_n$, the Petersen network $\mathbb{P}(n, m)$, and the lollipop network $\mathbb{L}(m, n)$. Moreover, the MD is thought to be paramount for studying many other structures, such as the RS of silicate stars ^[13], the exact values of MD and domination-related parameters of complete multipartite networks ^[14], and the sharp bounds on the MD of honeycomb networks studied in ^[15].

Determining the fault-tolerant MD of a network poses a complex combinatorial challenge, offering potential implications for sensor networks. In their exploration of the MD and fault-tolerant MD within various interconnection networks ^[16], Hayat et al. discovered that silicate, Benes, and butterfly networks have infinite fault-tolerant resolvability. Saha et al., in their research outlined in ^[17], delved into the $k$-MD of the circulant networks for a range of possible values of $n$ and $k$, representing the required fault-tolerant MD. Investigations conducted by authors in ^[18,19] focused on the fault-tolerant MD within recognized families of convex polytope structures. Additionally, Saha et al. tackled the $2$-MD problem regarding circulant networks specifically, contributing to the field of network resilience, as discussed in ^[20]. Raza et al. ^[21] demonstrate specific lower and upper limits regarding the FTMD for infinite of regular graphs. For more details, see ^[22].

Caceres et al. ^[23] have pioneered the exploration of doubly resolving sets (DRSs) within graph theory, showcasing the strong correlation between the MD of the Cartesian products and these minimal DRSs in network $\mathbb{G}$. DRSs are essential in source localization because they help reduce ambiguity, improve accuracy, enhance robustness, and enable efficient algorithms for determining the locations of multiple sources ^[24,25]. DRSs are a valuable tool in various applications, including radar, sonar, wireless communication, and more, where source localization is a critical task.

In ^[26], Kratica et al. demonstrated that the minimal DRS problem is NP-hard and proposed the utilization of a genetic algorithm to address large-scale instances of the problem. The problem of determining the MDRSs has been investigated for various network families. Notably, prior research has delved into the investigation of minimal DRSs within prisms ^[27], convex polytopes ^[28], and Hamming networks ^[29]. In the work by Chen et al. ^[30], they established the upper and lower bounds for the DRS problem. Additionally, in the study by Ahmad et al. ^[31], it was noted that circulant networks in the same family exhibit identical MD and DRS properties.

Lately, Ahmad et al. have made significant strides in addressing the DRS problem within various network families, as evidenced in their work ^[32,33]. Jannesari ^[34] provided a characterization for networks $\mathbb{G}$ with a double metric dimension (DMD) of $2$, utilizing $2$-connected subnetworks within network $\mathbb{G}$. In another recent research endeavor, Ahmad et al. ^[35] delved into the study of minimal DRSs specifically in the context of chordal ring networks.

There are many different kinds of network metric generators in use right now, and each kind is the subject of theoretical and practical research based on how useful and well-linked it is (for details see: ^[36]). However, while defining networks utilizing these metric generators, there are other viewpoints that have not yet been fully considered. Assume a network where vertices are accurately monitored and uniquely identified by a metric generator. However, if an intruder enters the network through its edges rather than its vertices, it is impossible to pinpoint their location, which makes surveillance impossible.

To address these kinds of issues, Ahmad et al. introduced a novel metric generator called EVDRSs in ^[37]. For the edge form of DRSs, only a few network families have been studied in the literature. The EVDRSs for the sunlet networks and prisms were found in ^[37]. The concept of the minimal EVDRSs has also been examined in ^[38] concerning the family of layer-sun networks. Moreover, the investigation of minimum-ordered EVDRSs in chorded cycles was carried out in ^[39], where the authors established that the least size of the EVDRSs for the chorded cycles is precisely one more than its edge version of MD. Additionally, the EVDRS problem for cocktail networks, jellyfish networks, and necklace networks has been examined in previous works, such as ^[40], and ^[41], respectively. In another study ^[42], Ahmad et al. tackled the problem of identifying the minimum EVDRSs for kayak paddle networks.

In this research article, we focus on EVDRSs in circulant networks $C_n(1, 2)$. A set is considered an EVDRS in a network if it has the ability to uniquely distinguish between any two edges of the network using any pair of edges from a subset of that network. The study of EVDRSs is relatively new and has gained attention as it provides additional information about the structure of a network. The main objective of this research is to investigate the existence, size, and structure of EVDRSs in circulant networks $C_n(1, 2)$. By providing insights into the EVDRSs of circulant networks $C_n(1, 2)$, we contribute to the broader understanding of this intriguing class of networks and expand the knowledge base of RSs. The research findings in this study hold implications for real-life situations in various domains; a few of them are as follows:

Communication Networks: The EVDRSs can help improve error detection and correction mechanisms in communication networks, which will increase the dependability of data transfer.

Distributed Sensor Networks: The design and optimization of distributed sensor networks, where effective data collection and processing are essential, may find applications from the insights gained from this study.

Furthermore, these findings may have an impact on the development of network navigation and localization algorithms. The characterization of EVDRSs in circulant networks $C_{n}(1, 2)$ provides the groundwork for the development of location-aware systems that are more reliable and accurate, influencing domains like tracking, surveillance, and autonomous navigation. To summarize, the study of EVDRSs in circulant networks $C_{n}(1, 2)$ has both theoretical and practical implications for enhancing the performance, efficiency, and reliability of different kinds of communication and sensing systems in real-world applications. The key contribution of the article is explained below:

● The Section $2$ introduces the notation and preliminary definitions required for our study.

● Section $3$ presents our main results on the existence and structure of EVDRSs in $C_n(1, 2)$.

● We discuss the implications and applications of these results in Section $4$.

● Finally, we conclude the article in Section $5$ by summarizing our findings, highlighting their significance and limitations, and suggesting directions for future research.

2.   Preliminaries

We take an undirected, connected, and simple network $\mathbb{G}$ consisting of the set of vertices $V(\mathbb{G})$ and $E(\mathbb{G})$, which is the set of edges. Let $v_1, v_2$ $\in$ $V(\mathbb{G})$, then the distance $d(v_1, v_2)$ is the smallest path between $v_1$ and $v_2$. Let an ordered subset $\mathbb{R} = \{r_i, 1\leq i\leq l \} \subseteq V(\mathbb{G})$, and for any $v$ $\in$ $V(\mathbb{G})$, the representation of $v$ with respect to $\mathbb{R}$ is the $l$-tuple $\big(d(v, r_1), d(v, r_2), \ldots, d(v, r_l)\big)$ and written as $r(v, \mathbb{R})$. The set $\mathbb{R}$ is said to be a RS, when different vertices of $\mathbb{G}$ have different representations with respect to $\mathbb{R}$. The minimum number of vertices in subset $\mathbb{R}$ is called a basis for $\mathbb{G}$, and the cardinality or size of the basis is known as the MD of $\mathbb{G}$, represented by $\dim(\mathbb{G})$. For $\mathbb{R} \subset V(\mathbb{G})$, $r(x, \mathbb{R})$ $=$ $0,$ whenever $x = r_{i},$ the $i^{th}$ component of $\mathbb{R}$. Therefore, to prove that $\mathbb{R}$ is resolvable, we have to demonstrate that $r(x, \mathbb{R}) \neq r(y, \mathbb{R}),$ whenever $x \neq y$ $\in$ $V(\mathbb{G})$ $\backslash$ $\mathbb{R}$. Let $w$ and $x$ be any two vertices of $\mathbb{G}$, where $|\mathbb{V(G)}| \geq 2$. If for the vertices $u, v\in \mathbb{G}$, $d(u, w) - d(u, x) \neq d(v, w) - d(v, x)$, i.e., the difference between their distances to $w$ and $x$ is not equal, then we say that $u$ and $v$ are doubly resolved by $w$ and $x$. A subset $\mathbb{D}$ is said to be DRS, if some of its vertices doubly resolve every pair of the vertices in $\mathbb{G}.$ A DRS with the smallest possible size is said to be a minimal DRS, and its size is called as the double metric dimension (DMD), denoted by the $\psi(\mathbb{G})$.

If $e_1$ and $e_2$ are edges of the network $\mathbb{G}$, with the condition that $|E(\mathbb{G})|\geq 2$ and $d_E(f_{1}, e_1)-d_E(f_{1}, e_2)\neq d_E(f_{2}, e_1)-d_E(f_{2}, e_2)$, then $f_1$ and $f_2$ are said to be doubly resolved by $e_1$ and $e_2$. If an ordered subset $\mathbb{D}_{\mathbb{G}} = \{e_t, 1\leq t \leq k\}$ of edges in $\mathbb{G}$ doubly resolves any pair of edges $f_1$ and $f_2$ in $E(\mathbb{G})$, then such a subset $\mathbb{D}_{\mathbb{G}}$ is called an EVDRS of $\mathbb{G}$. The minimum size of an EVDRS of $\mathbb{G}$ is denoted as $\psi_E(\mathbb{G})$. For more research on these basic concepts, see ^[37].

3.   Edge-version of doubly resolving sets in circulant network $C_n(1, 2)$

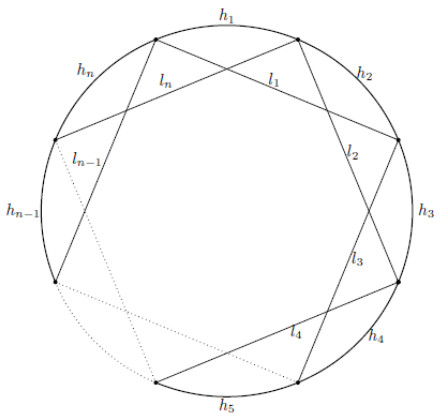
The family of circulant network, denoted by $C_n(1, 2)$ is the family of networks obtained by constructing a cycle of length $n$ and connecting each vertex $v_\lambda$ with $v_\lambda+2$ modulo $n$ with a vertex set $V_{C_n(1, 2)} = \{v_1, v_2, \ldots, v_n\}$ and edge set $E_{C_n(1, 2)} = H\cup L$, as shown in Figure 1, where $H = \{h_1, h_2, \ldots, h_n\}$ and $L = \{l_1, l_2, \ldots, l_n\}.$

Figure 1.  The family of circulant networks $C_n(1, 2)$.

DownLoad: Full-Size Img PowerPoint

The edge version of MD for $C_n(1, 2)$ was studied in ^[43], and the result is given below:

Theorem 3.1. ^[43] Let $C_n(1, 2)$ be the circulant networks, then $\dim_E(C_n(1, 2)) = 4$, $\forall$ $n\geq 6$.

The following proposition will be helpful in calculating the EVDRSs:

Proposition 3.1. ^[26] A subset $\mathbb{D}_{C_n(1, 2)} = \{y_1, y_2, \ldots y_k\}\subseteq E(C_n(1, 2))$ is an EVDRS of $C_n(1, 2)$ if, and only if, for every $v, y \in E(C_n(1, 2))$, there exists $\lambda \in \{2, 3, \ldots, k\}$ such that $d_E(v, y\lambda) - d_E(v, y_1)$ is not equal to $d_E(y, y_\lambda) - d_E(y, y_1)$.

For every edge $e\in E(C_n(1, 2))$, we define $r'_E(e, \mathbb{D}_{C_n(1, 2)}) = (d_E(e, y_2)-d_E(e, y_1), \ldots, d_E(e, y_k)-d_E(e, y_1))$. The above proposition states that $\mathbb{D}_{C_n(1, 2)}$ is a minimal EVDRS if and only if these distance vectors $r'E(e, \mathbb{D}_{C_n(1, 2)})$ are all distinct for every edge $e\in E(C_n(1, 2))$.

The statement of the theorem for EVDRSs in circulant networks is as follows:

Theorem 3.2. Let $C_n(1, 2)$ be the circulant networks, then $\psi_E(C_n(1, 2)) = 4,$ for $n\geq 6.$

Proof. To compute EVDRSs for circulant networks, we will address the following four scenarios:

Case 1. When $n$ $\equiv$ $0(mod$ $4)$ or $n = 4k$, where $k\geq2$.

Consider the set of edges $\mathbb{R}_{C_n(1, 2)} = \{h_1, h_2, h_{\frac{n}{2}-1}, h_{\frac{n}{2}}\},$ then the distance vectors of the edges in relation to $\mathbb{R}_{C_n(1, 2)}$ are shown in Tables 1 and 2 as follows:

Table 1.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, 1, \frac{n}{4}, \frac{n}{4})$	${\ if}\ \lambda=1;$
$(\lambda, \lambda-1, \frac{n}{4}-\lambda+1, \frac{n}{4}-\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(\frac{n}{4}, \frac{n}{4}-1, 0, 1)$	${\ if}\ \lambda=\frac{n}{4};$
$(\lambda, \frac{n}{4}, 2, 1)$	${\ if}\ \lambda=\frac{n}{4}+1;$
$(\frac{n}{2}-\lambda+2, \frac{n}{2}-\lambda+2, \lambda-\frac{n}{4}+1, \lambda-\frac{n}{4})$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}.$
$r'_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(1, \frac{n}{4}, \frac{n}{4})$	${\ if}\ \lambda=1;$
$(-1, \frac{n}{4}-2\lambda+1, \frac{n}{4}-2\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(-1, -\frac{n}{4}, 1-\frac{n}{4})$	${\ if}\ \lambda=\frac{n}{4};$
$(\frac{n}{4}-\lambda, 2-\lambda, 1-\lambda)$	${\ if}\ \lambda=\frac{n}{4}+1;$
$(0, 2\lambda-\frac{3n}{4}-1, 2\lambda-\frac{3n}{4}-2)$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}.$
$r_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(1, 0, \frac{n}{4}-1, \frac{n}{4})$	${\ if}\ \lambda=1;$
$(\lambda, \lambda, \frac{n}{4}-\lambda, \frac{n}{4}-\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(\frac{n}{4}, \frac{n}{4}, 1, 0)$	${\ if}\ \lambda= \frac{n}{4};$
$(\frac{n}{2}-\lambda+1, \frac{n}{2}-\lambda+2, \lambda-\frac{n}{4}+1, \lambda-\frac{n}{4}+1)$	${\ if}\ \frac{n}{4}+1 \leq \lambda \leq \frac{n}{2}.$
$r'_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(-1, \frac{n}{4}-2, \frac{n}{4}-1)$	${\ if}\ \lambda=1;$
$(0, \frac{n}{4}-2\lambda, \frac{n}{4}-2\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(0, 1-\frac{n}{4}, -\frac{n}{4})$	${\ if}\ \lambda= \frac{n}{4};$
$(1, 2\lambda-\frac{3n}{4}, 2\lambda-\frac{3n}{4})$	${\ if}\ \frac{n}{4}+1 \leq \lambda \leq \frac{n}{2}.$

---

 | Show Table

DownLoad: CSV

Table 2.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(1, 1, \frac{n}{4}-1, \frac{n}{4})$	${\ if}\ \lambda= 1;$
$(\lambda, \lambda-1, \frac{n}{4}-\lambda, \frac{n}{4}-\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(\frac{n}{4}, \lambda-\frac{n}{4}+4, \lambda-\frac{n}{4}+1, 1)$	${\ if}\ \frac{n}{4} \leq \lambda \leq \frac{n}{4}+1;$
$(\frac{n}{2}-\lambda+1, \frac{n}{2}-\lambda+2, \lambda-\frac{n}{4}+1, \lambda-\frac{n}{4})$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}-1;$
$(1, 2, \frac{n}{4}, \frac{n}{4})$	${\ if}\ \lambda= \frac{n}{2}.$
$r'_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, \frac{n}{4}-2, \frac{n}{4}-1)$	${\ if}\ \lambda= 1;$
$(-1, \frac{n}{4}-2\lambda, \frac{n}{4}-2\lambda+1)$	${\ if}\ 2 \leq \lambda \leq \frac{n}{4}-1;$
$(\lambda-\frac{n}{2}+4, \lambda-\frac{n}{2}+1, 1-\frac{n}{4})$	${\ if}\ \frac{n}{4} \leq \lambda \leq \frac{n}{4}+1;$
$(1, 2\lambda-\frac{3n}{4}, 2\lambda-\frac{3n}{4}-1)$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}-1;$
$(1, \frac{n}{4}-1, \frac{n}{4}-1)$	${\ if}\ \lambda= \frac{n}{2}.$
$r_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \lambda, \frac{n}{4}-\lambda, \frac{n}{4}-\lambda)$	${\ if}\ 1 \leq \lambda \leq \frac{n}{4}-1;$
$(\frac{n}{4}, \frac{n}{4}, \lambda-\frac{n}{4}+1, \lambda-\frac{n}{4}+1)$	${\ if}\ \frac{n}{4}\leq \lambda \leq \frac{n}{4}+1;$
$(\frac{n}{2}-\lambda+1, \frac{n}{2}-\lambda+1, \lambda-\frac{n}{4}+1, \lambda-\frac{n}{4}+1)$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}-1;$
$(1, 1, \frac{n}{4}, \frac{n}{4})$	${\ if}\ \lambda= \frac{n}{2}.$
$r'_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, \frac{n}{4}-2\lambda, \frac{n}{4}-2\lambda)$	${\ if}\ 1 \leq \lambda \leq \frac{n}{4}-1;$
$(0, \lambda-\frac{n}{2}+1, \lambda-\frac{n}{2}+1)$	${\ if}\ \frac{n}{4}\leq \lambda \leq \frac{n}{4}+1;$
$(0, 2\lambda-\frac{3n}{4}, 2\lambda-\frac{3n}{4})$	${\ if}\ \frac{n}{4}+2 \leq \lambda \leq \frac{n}{2}-1;$
$(0, \frac{n}{4}-1, \frac{n}{4}-1)$	${\ if}\ \lambda= \frac{n}{2}.$

---

 | Show Table

DownLoad: CSV

Case 2. When $n$ $\equiv$ $1(mod$ $4)$ or $n = 4k+1$, where $k\geq 2$.

Consider the set of edges $\mathbb{R}_{C_n(1, 2)} = \{h_1, h_{\lfloor\frac{n}{2}\rfloor}, h_{\lfloor\frac{n}{2}\rfloor+1}, h_{n}\},$ then the distance vectors of the edges in relation to $\mathbb{R}_{C_n(1, 2)}$ are shown in Tables 3 and 4 as follows:

Table 3.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, \frac{n-1}{4}, \frac{n-1}{4}+1, 1)$	${\ if}\ \lambda=1;$
$(\lambda, \frac{n-1}{4}-\lambda+1, \frac{n-1}{4}-\lambda+2, \lambda)$	${\ if}\ 2 \leq \lambda \leq \frac{n-1}{4};$
$(\frac{n-1}{4}+1, 1, 0, \frac{n-1}{4}+1)$	${\ if}\ \lambda=\frac{n-1}{4}+1;$
$(\frac{n-1}{2}-\lambda+2, \lambda-\frac{n-1}{4}, \lambda-\frac{n-1}{4}, \frac{n-1}{2}-\lambda+2)$	${\ if}\ \frac{n-1}{4}+2 \leq \lambda \leq \frac{n-1}{2};$
$(1, \frac{n-1}{4}+1, \frac{n-1}{4}+1, 0)$	${\ if}\ \lambda=\frac{n-1}{2}+1.$
$r'_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-1}{4}, \frac{n-1}{4}+1, 1)$	${\ if}\ \lambda=1;$
$(\frac{n-1}{4}-2\lambda+1, \frac{n-1}{4}-2\lambda+2, 0)$	${\ if}\ 2 \leq \lambda \leq \frac{n-1}{4};$
$(-\frac{n-1}{4}, -\frac{n-1}{4}-1, 0)$	${\ if}\ \lambda=\frac{n-1}{4}+1;$
$(2\lambda-\frac{3n-3}{4}-2, 2\lambda-\frac{3n-3}{4}-2, 0)$	${\ if}\ \frac{n-1}{4}+2 \leq \lambda \leq \frac{n-1}{2};$
$(\frac{n-1}{4}, \frac{n-1}{4}, -1)$	${\ if}\ \lambda=\frac{n-1}{2}+1.$
$r_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-1}{4}-\lambda+1, \frac{n-1}{4}-\lambda+1, \lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4}-1;$
$(\frac{n-1}{4}, 0, 1, \frac{n-1}{4}+1)$	${\ if}\ \lambda = \frac{n-1}{4};$
$(\frac{n-1}{2}-\lambda+2, \lambda-\frac{n-1}{4}+1, \lambda-\frac{n-1}{4}, \frac{n-1}{2}-\lambda+1)$	${\ if}\ \frac{n-1}{4}+1 \leq \lambda \leq \frac{n-1}{2}.$
$r'_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-1}{4}-2\lambda+1, \frac{n-1}{4}-2\lambda+1, 1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4}-1;$
$(-\frac{n-1}{4}, 1-\frac{n-1}{4}, 1)$	${\ if}\ \lambda = \frac{n-1}{4};$
$(2\lambda-\frac{3n-3}{4}-1, 2\lambda-\frac{3n-3}{4}-2, -1)$	${\ if}\ \frac{n-1}{4}+1 \leq \lambda \leq \frac{n-1}{2}.$

---

 | Show Table

DownLoad: CSV

Table 4.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-1}{4}-\lambda+1, \frac{n-1}{4}-\lambda+1, \lambda)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4};$
$(\frac{n-1}{2}-\lambda+2, \lambda-\frac{n-1}{4}, \lambda-\frac{n-1}{4}, \frac{n-1}{2}-\lambda+1)$	${\ if}\ \frac{n-1}{4}+1 \leq \lambda \leq \frac{n-1}{2};$
$(1, \frac{n-1}{4}, \frac{n-1}{4}+1, 1)$	${\ if}\ \lambda=\frac{n-1}{2}+1.$
$r'_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-1}{4}-2\lambda+1, \frac{n-1}{4}-2\lambda+1, 0)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4};$
$(2\lambda-3k-2, 2\lambda-3k-2, -1)$	${\ if}\ k+1 \leq \lambda \leq 2k;$
$(\frac{n-1}{4}-1, \frac{n-1}{4}, 0)$	${\ if}\ \lambda=\frac{n-1}{2}+1.$
$r_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-1}{4}-\lambda, \frac{n-1}{4}-\lambda+1, \lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4}-1;$
$(\frac{n-1}{4}, 1, 1, \frac{n-1}{4}+1)$	${\ if}\ \lambda = \frac{n-1}{4};$
$(\frac{n-1}{2}-\lambda+1, \lambda-\frac{n-1}{4}+1, \lambda-\frac{n-1}{4}, \frac{n-1}{2}-\lambda+1)$	${\ if}\ \frac{n-1}{4}+1 \leq \lambda \leq \frac{n-1}{2}.$
$r'_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-1}{4}-2\lambda, \frac{n-1}{4}-2\lambda+1, 1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-1}{4}-1;$
$(1-\frac{n-1}{4}, 1-\frac{n-1}{4}, 1)$	${\ if}\ \lambda = \frac{n-1}{4};$
$(2\lambda-\frac{3n-3}{4}, 2\lambda-\frac{3n-3}{4}-1, 0)$	${\ if}\ \frac{n-1}{4}+1 \leq \lambda \leq \frac{n-1}{2}.$

---

 | Show Table

DownLoad: CSV

Case 3. When $n$ $\equiv$ $2(mod$ $4)$ or $n = 4k+2$, where $k\geq 1$.

Consider the set of edges $\mathbb{R}_{C_n(1, 2)} = \{h_1, h_{\frac{n}{2}-1}, h_{\frac{n}{2}}, h_{n}\},$ then the distance vectors of the edges in relation to $\mathbb{R}_{C_n(1, 2)}$ are shown in Tables 5 and 6 as follows:

Table 5.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, \frac{n-2}{4}, \frac{n-2}{4}+1, 1)$	${\ if}\ \lambda=1;$
$(\lambda, \frac{n-2}{4}-\lambda+1, \frac{n-2}{4}-\lambda+2, \lambda)$	${\ if}\ 2 \leq \lambda \leq \frac{n-2}{4};$
$(\frac{n-2}{4}+1, 1, 0, \frac{n-2}{4}+1)$	${\ if}\ \lambda=\frac{n-2}{4}+1;$
$(\frac{n-2}{2}-\lambda+3, \lambda-\frac{n-2}{4}, \lambda-\frac{n-2}{4}, \frac{n-2}{2}-\lambda+2)$	${\ if}\ \frac{n-2}{4}+2 \leq \lambda \leq \frac{n-2}{2}+1.$
$r'_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-2}{4}, \frac{n-2}{4}+1, 1)$	${\ if}\ \lambda=1;$
$(\frac{n-2}{4}-2i+1, \frac{n-2}{4}-2\lambda+2, 0)$	${\ if}\ 2 \leq \lambda \leq \frac{n-2}{4};$
$(-\frac{n-2}{4}, -\frac{n-2}{4}-1, 0)$	${\ if}\ \lambda=\frac{n-2}{4}+1;$
$(2\lambda-\frac{3n-6}{4}-3, 2\lambda-\frac{3n-6}{4}-3, -1)$	${\ if}\ \frac{n-2}{4}+2 \leq \lambda \leq \frac{n-2}{2}+1.$
$r_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-2}{4}-\lambda+1, \frac{n-2}{4}-\lambda+1, \lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4}-1;$
$(\frac{n-2}{4}, 0, 1, \frac{n-2}{4}+1)$	${\ if}\ \lambda = \frac{n-2}{4};$
$(\frac{n-2}{2}-\lambda+2, \lambda-\frac{n-2}{4}+1, \lambda-\frac{n-2}{4}, \frac{n-2}{2}-\lambda+2)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2};$
$(1, \frac{n-2}{4}+1, \frac{n-2}{4}+1, 0)$	${\ if}\ \lambda= \frac{n-2}{2}+1.$
$r'_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-2}{4}-2\lambda+1, \frac{n-2}{4}-2\lambda+1, 1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4}-1;$
$(-\frac{n-2}{4}, 1-\frac{n-2}{4}, 1)$	${\ if}\ \lambda = \frac{n-2}{4};$
$(2\lambda-\frac{3n-6}{4}-1, 2\lambda-\frac{3n-6}{4}-2, 0)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2};$
$(\frac{n-2}{4}, \frac{n-2}{4}, -1)$	${\ if}\ \lambda= \frac{n-2}{2}+1.$

---

 | Show Table

DownLoad: CSV

Table 6.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-2}{4}-\lambda+1, \frac{n-2}{4}-\lambda+1, \lambda)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4};$
$(\frac{n-2}{2}-\lambda+2, \lambda-\frac{n-2}{4}, \lambda-\frac{n-2}{4}, \frac{n-2}{2}-\lambda+2)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2}+1.$
$r'_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-2}{4}-2\lambda+1, \frac{n-2}{4}-2\lambda+1, 0)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4};$
$(2\lambda-\frac{3n-6}{4}-2, 2\lambda-\frac{3n-6}{4}-2, 0)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2}+1.$
$r_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \frac{n-2}{4}-\lambda, \frac{n-2}{4}-\lambda+1, \lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4}-1;$
$(\frac{n-2}{4}, 1, 1, \frac{n-2}{4}+1)$	${\ if}\ \lambda = \frac{n-2}{4};$
$(\frac{n-2}{2}-\lambda+2, \lambda-\frac{n-2}{4}+1, -\frac{n-2}{4}, \frac{n-2}{2}-\lambda+1)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2};$
$(1, \frac{n-2}{4}, \frac{n-2}{4}+1, 1)$	${\ if}\ \lambda= \frac{n-2}{2}+1.$
$r'_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\frac{n-2}{4}-2\lambda, \frac{n-2}{4}-2\lambda+1, 1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-2}{4}-1;$
$(1-\frac{n-2}{4}, 1-\frac{n-2}{4}, 1)$	${\ if}\ \lambda = \frac{n-2}{4};$
$(2\lambda-\frac{3n-6}{4}-1, 2\lambda-\frac{3n-6}{4}-2, -1)$	${\ if}\ \frac{n-2}{4}+1 \leq \lambda \leq \frac{n-2}{2};$
$(\frac{n-2}{4}-1, \frac{n-2}{4}, 0)$	${\ if}\ \lambda= \frac{n-2}{2}+1.$

---

 | Show Table

DownLoad: CSV

Case 4. When $n$ $\equiv$ $3(mod$ $4)$ or $n = 4k+3$, where $k\geq 1$.

Consider the set of edges $\mathbb{R}_{C_n(1, 2)} = \{h_1, h_{n-2}, l_{\lfloor\frac{n}{2}\rfloor-1}, l_{\lfloor\frac{n}{2}\rfloor}\},$ then the distance vectors of the edges in relation to $\mathbb{R}_{C_n(1, 2)}$ are shown in Tables 7 and 8 as follows:

Table 7.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(0, 2, \frac{n-3}{4}, \frac{n-3}{4}+1)$	${\ if}\ \lambda=1;$
$(\lambda, \lambda+1, \frac{n-3}{4}-\lambda+1, \frac{n-3}{4}-\lambda+2)$	${\ if}\ 2 \leq \lambda \leq \frac{n-3}{4};$
$(\frac{n-3}{4}+1, \frac{n-3}{4}+1, 1, 1)$	${\ if}\ \lambda=\frac{n-3}{4}+1;$
$(\frac{n-3}{2}-\lambda+3, \frac{n-3}{2}-\lambda+2, \lambda-\frac{n-3}{4}, \frac{n-3}{4}-\lambda-1)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(2, 0, \frac{n-3}{4}+1, \frac{n-3}{4})$	${\ if}\ \lambda=\frac{n-3}{2}+1;$
$(1, 2, \frac{n-3}{4}+1, \frac{n-3}{4}+1)$	${\ if}\ \lambda=\lfloor\frac{n-3}{2}+2\rfloor.$
$r'_E(h_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(2, \frac{n-3}{4}, \frac{n-3}{4}+1)$	${\ if}\ \lambda=1;$
$(1, \frac{n-3}{4}-2\lambda+1, \frac{n-3}{4}-2\lambda+2)$	${\ if}\ 2 \leq \lambda \leq \frac{n-3}{4};$
$(0, -\frac{n-3}{4}, -\frac{n-3}{4})$	${\ if}\ \lambda=\frac{n-3}{4}+1;$
$(-1, 2\lambda-\frac{3n-9}{4}-3, -\frac{n-3}{4}-4)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(-2, \frac{n-3}{4}-1, \frac{n-3}{4}-2)$	${\ if}\ \lambda=\frac{n-3}{2}+1;$
$(1, \frac{n-3}{4}, \frac{n-3}{4})$	${\ if}\ \lambda=\lfloor\frac{n-3}{2}+2\rfloor.$
$r_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \lambda+2, \frac{n-3}{4}-\lambda+1, \frac{n-3}{4}-\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\lambda, \frac{n-3}{2}-\lambda+1, 1, 1)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(\frac{n-3}{2}-\lambda+3, \frac{n-3}{2}-\lambda+1, \lambda-\frac{n-3}{4}, \lambda-\frac{n-3}{4})$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(2, 1, \frac{n-3}{4}+1, \frac{n-3}{4}+1)$	${\ if}\ \lambda= \frac{n-3}{2}+1.$
$r'_E(h_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(2, \frac{n-3}{4}-2\lambda+1, \frac{n-3}{4}-2\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\frac{n-3}{2}-2\lambda+1, 1-\lambda, 1-\lambda)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(-2, 2\lambda-\frac{3n-9}{4}-3, 2\lambda-\frac{3n-9}{4}-3)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(-1, \frac{n-3}{4}+1, \frac{n-3}{4}+1)$	${\ if}\ \lambda= \frac{n-3}{2}+1.$

---

 | Show Table

DownLoad: CSV

Table 8.  Distance vectors $r$ and $r'$ of the edges in $C_n(1, 2)$.

$r_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \lambda+1, \frac{n-3}{4}-\lambda+1, \frac{n-3}{4}-\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\lambda, \frac{n-3}{2}-\lambda+1, 2, \frac{n-3}{4}-\lambda+1)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(\frac{n-3}{2}-\lambda+3, \frac{n-3}{2}-+1, \lambda-\frac{n-3}{4}, \lambda-\frac{n-3}{4}-1)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(-\frac{n-3}{2}+1, \lambda-\frac{n-3}{2}, \frac{3n-9}{4}-\lambda+2, -\frac{n-3}{4}-1)$	${\ if}\ \frac{n-3}{2}+1 \leq \lambda \leq \lfloor\frac{n-3}{4}+2\rfloor.$
$r'_E(l_{2\lambda-1}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(1, \frac{n-3}{4}-2\lambda+1, \frac{n-3}{4}-2\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\frac{n-3}{2}-2\lambda+1, 2-\lambda, \frac{n-3}{4}-2\lambda+1)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(-2, 2\lambda-\frac{3n-9}{4}-3, 2\lambda-\frac{3n-9}{4}-4)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(-1, \frac{5n-15}{4}-2\lambda-1, \frac{n-3}{4}-2)$	${\ if}\ \frac{n-3}{2}+1 \leq \lambda \leq \lfloor\frac{n+1}{2}\rfloor.$
$r_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(\lambda, \lambda+2, \frac{n-3}{4}-\lambda, \frac{n-3}{4}-\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\lambda, \frac{n-3}{2}-\lambda+1, \lambda-\frac{n-3}{4}, 2)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(\frac{n-3}{2}-\lambda+2, \frac{n-3}{2}-\lambda+1, \lambda-\frac{n-3}{4}, \lambda-\frac{n-3}{4})$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(1, 1, \frac{n-3}{4}+1, \frac{n-3}{4}+1)$	${\ if}\ \lambda= \frac{n-3}{2}+1.$
$r'_E(l_{2\lambda}, \mathbb{R}_{C_n(1, 2)})$	$\lambda$
$(2, \frac{n-3}{4}-2\lambda, \frac{n-3}{4}-2\lambda+1)$	${\ if}\ 1 \leq \lambda \leq \frac{n-3}{4}-1;$
$(\frac{n-3}{2}-2\lambda+1, -\frac{n-3}{4}, 2-\lambda)$	${\ if}\ \frac{n-3}{4} \leq \lambda \leq \frac{n-3}{4}+1;$
$(-1, 2\lambda-\frac{3n-9}{4}-2, 2\lambda-\frac{3n-9}{4}-2)$	${\ if}\ \frac{n-3}{4}+2 \leq \lambda \leq \frac{n-3}{2};$
$(0, \frac{n-3}{4}, \frac{n-3}{4})$	${\ if}\ \lambda= \frac{n-3}{2}+1.$

---

 | Show Table

DownLoad: CSV

The distance vectors in the above four cases show that each distance vector $r'_E$ is unique, resulting in $\psi_E(C_{n}(1, 2))$ $=$ $4.$ □

4.   Application

EVDRSs is a mathematical tool within the field of graph theory. They serve as a tool for locating particular edges inside a graph (network) by recognizing a collection of edges that are capable of precisely locating a different edge or set of related edges. In practical scenarios, this variant of graph theory finds numerous applications, including fault detection in various network types such as computer networks and network security systems, as well as tracing the origins of epidemics within social networks and contagious diseases, among other uses (for further information, see ^[44]).

An EVDRS essentially represents a set of measurements or tests that can be helpful in source localization to detect the origin of a viral disease outbreak or a virus source in complex networks. The term "doubly resolving" is used because it possesses the capability to not only identify the existence of contamination but also differentiate between various source categories. Let us explore the following example to better understand how an EVDRS might be used to identify the origins of epidemics during contagious disease outbreaks.

In a viral disease outbreak scenario, where the city is represented as a circulant network $C_8(1, 2)$ with edges $\{h_1, h_2, h_3, h_4, h_5, h_6, h_7, h_8, l_1, l_2, l_3, l_4, l_5, l_6, l_7, l_8\}$ as shown in Figure 2, we can employ the minimal EVDRSs to effectively track and control the spread of the virus.

Figure 2.  Origin of disease outbreak within the city.

DownLoad: Full-Size Img PowerPoint

Let us consider the following situation:

● The edges $h_1, h_2, h_3, h_4, h_5,$ and $h_6$ represent residential areas.

● The edges $l_1, l_2, l_3, l_4, l_5,$ and $l_6$ represent commercial areas.

● The edges $h_7, h_8, l_7,$ and $l_8$ represent medical facilities.

A quick solution can be achieved by carefully placing observers across the city and ensuring exact and well-documented distances between these edges. However, executing this comprehensive procedure would incur substantial expenses and consume a significant amount of time. As a result, the question arises: how many observers must be deployed to trace the origin of infection when the initial time of commencement is unknown and transmission delays across edges vary? This demands a system in which each edge is distinguished by its minimal distance from strategically placed observers.

For this purpose, we need to identify a minimal set of edges (observers) that, when infection spreads, would uniquely determine the source of the infection and help in containing the spread. In the case where a city is represented by the circulant network $C_8(1, 2)$, we can choose the following minimal EVDRS: $\mathbb{R}_{C_8(1, 2)} = \{h_1, h_2 h_3, h_4\}$.

Let us examine how this works:

Residential Areas: If anyone from the residential areas gets infected, then the source of infection would be uniquely identified from these residential areas using the information collected by the placed observers. This information can help in implementing targeted measures like quarantine, testing, and contact tracing within the residential areas.

Commercial Areas: If an infection spreads in any one of these commercial areas, similarly, by employing the collected data by the placed observer, the source of the infection would point to one of these commercial areas. This knowledge can be used to implement measures like temporary closure, sanitation, and testing within commercial areas.

Medical Facilities: If the infection has reached one of the medical facilities, then by finding the unknown starting time and edge-to-edge transmission delays using EVDRSs, the source of infection would be uniquely identified. This information is crucial for implementing measures to protect healthcare workers and patients and prevent further transmission within medical facilities.

By means of the careful monitoring and tracking of infection via these basic EVDRSs, health authorities and decision-makers can efficiently allocate resources, identify interventions, and make informed decisions to control the viral disease outbreak in the city.

There are numerous practical uses for circulant networks, particularly in distributed computing and computer networks. Particularly, circulant networks can be used for task assignments, load balancing, and data spreading in distributed computing systems. Circulant networks are beneficial for efficient routing and resource allocation due to their regular nature. Also, circulant networks offer an effective way to organize the communication architecture in sensor networks, where multiple sensors send data to a central node (or edge) or among one another.

Moreover, these networks can be utilized in wireless mesh networks, which expand network coverage by using wireless communication among nodes, or edges. Because of their regular structure, circulant networks are suitable for distributing computational workloads among multiple nodes (or edges) in an efficient manner. Moreover, they can be applied in social areas, in which coordination and a communication mechanism between distant units are needed. For instance, a social network or Internet of Things system.

5.   Conclusions

The present paper has tackled the notion of EVDRSs in circulant networks $C_n(1, 2)$, EVDRSs being a set of edges in a network that ascertains that each edge has a unique representation in relation to the elements of an EVDRS. The main goals were to characterize the minimal size of EVDRS for circulant networks $C_n(1, 2)$ as well as to understand their structural properties. To sum up, the present study has focused on EVDRSs in circulant networks $C_n(1, 2)$ and has made significant advances in comprehending their structural features, determining their minimal size, and highlighting their independence from the parity of $n$. The results of the above investigations extend the understanding of graph theory and have practical implications in several fields, such as telecommunications and distributed computing, which rely on well-built and efficient networks. Our research findings are important for helping to create more robust and efficient networks, as well as for developing the theory of graph-based communication systems.

Because the obtained results are specific to circulant networks $C_n(1, 2)$, they may not hold true for other network topologies. It could be difficult to convert theoretical results into practical implementations, especially in complex and dynamic networks. Collaborating with specialists in related fields such as network engineering, epidemiology, and computer science may be necessary for fully comprehending the potential impact of the research in several domains. In fact, bridging the gap between theoretical research and practical applications can be greatly aided by disciplinary collaboration. Interdisciplinary collaboration can solve the shortcomings of specific disciplines by combining ideas and techniques from other domains, producing more trustworthy and useful research results. This could then lead to a greater impact from these discoveries in a variety of domains, eventually resulting in useful answers and breakthroughs in various disciplines of research.

Open Problem 5.1. Investigate the EVDRSs for the Chordal Ring network $CR_n(1, 3, 5)$, $\forall$ even integers $n\geq 6$.

Author contributions

Ruby Nasir and Muhammad Ahmad conducted the final review and made sure the results were validated at the problem discussion. Zohaib Zahid was helpful in initiating the problem, obtaining necessary information, and offering continuous supervision. Initiating the study's drafting process and contributing significantly to its analysis and computation was Sanaa A. Bajri. In addition to contributing to the methodology, Hamiden Abd El-Wahed Khalifa actively discussed the issue and carefully proofread the final draft.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

The Research is funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R527), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia

Conflict of interest

The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.