Resolving set and exchange property in nanotube

1.   Introduction

Chemical graph theory allows for the discussion of chemical structures and mathematical molecular representations. The structural characteristics of crystals, processes, clusters, molecules, polymers and other materials are described using chemical graph theory. Recent advances and discoveries of mathematical models of chemical circumstance and the application of mathematical techniques and concepts to chemistry have led to the development of mathematical chemistry with a wide range of perspectives to deal with chemical structures that support existing chemical concepts^[1]. Very large and complex chemical structures in their original form are not easy for understanding, and chemical graph theory is used to make them simple and understandable.

A nanotube derived from an quadrilateral-octagonal grid belongs to essential and extensively studied compounds in materials science ^[2,3,4]. Nanostructures have many applications due to their thickness, such as those used in the medical field and nanotechnology. We resolve these structures and find mixed metric dimensions ^[5]. For further discussion of mathematical chemistry related to graph theory, see ^[7].

Let the distance be denoted by $\xi$ and a vertex $k$ is resolved to a pair of $p, q$ vertices if the distances from $k$ to $p$ and $q$ satisfy $\xi (k, p)\neq \xi (k, q).$ Let $W_{1}$ and $W_{2}$ be two resolving sets and $W_{1}$ $\neq$ $W_{2}$. Then, we can say that the graph $G$ has double resolving set. The resolving or locating set recognizes a unique representation of the chemical structures ^[8]. The smallest cardinality of the resolving set is called the metric dimension ^[9,10,11]. The notion of the locating set of a graph was introduced by ^[12] in $1975.$ The same notion was introduced by ^[13] in $1976,$ which they called the metric dimension of a graph. The concept of the revolving set and the metric dimension Blumenthal had long ago been described in his monograph theory in the general context of metric space and the applications of distance geometry ^[14,15].

When $W_1$ and $W_2$ are any two minimal resolving sets for $G$ and each vertex $u$ $in$ $W_1$ has a vertex $v \in W_2$, then $\backslash$$\{u\})$$\cup$$v$ is also a minimal resolving set. Resolving sets are afterward said to possess the exchange property in the graph (for details see^[16]. In this study, only finite, simple, and linked graphs are taken into consideration. Additionally, every group that is taken into consideration is finite. A graph's exchange property also refers to its set resolution property.

In daily life, metric dimension has many applications that inspire researchers and has been studied widely. Be determining similar patterns of a variety of many medicines, the metric dimension is used ^[17]. Some various other uses of metric dimensions are combinatorial optimization ^[18], robot navigation ^[19], Pharmaceutical chemistry ^[20], computer networks ^[21], canonically labeling graphs ^[22], location problems, sonar and coast guard Loran ^[12], image processing facility, weighing problems^[23], mastermind game's coding and decoding discussed in ^[24]. For further detail of physical and chemical properties of metric dimension see ^{[26,27,28,29,30,31,32,33,34]}.

In chemistry, the double-resolving set has several applications, and the double-resolving set of different chemical structures was studied in various articles. Double resolving set of Jellyfish Graph and Cocktail Party Graph are studied in ^[35], Computing minimal doubly resolving sets of graphs are discussed in ^[36], Minimal doubly resolving sets of prism graphs are studied in ^[37]. The mixed metric dimension and a resolving set of silicate stars discussed in ^[38], metric dimension's upper bonds of cellulose networks determined in ^[39], metric dimension of crystal cubic carbon structure determined in ^[40], discussion about Convex polytopes graph was given in ^[41], edge metric dimension of Cayley graphs barycentric subdivision was done in ^[42], due to its variety, many difficult problems are solved by applying the concept of metric dimension. For resolvability parameters of various chemical structures, we refer to ^[43,44,45].

For more physical and chemical properties of the quadrilateral-octagonal grids, we refer to see ^[46,47,48]. Some basic mathematical definitions of distance, resolving set and metric dimension are given below that are used in this article.

Definition 1.1. Let G be the simple, undirected graph in which set of vertices are represented by V(G) and set of edges denoted by E(G), the distance which is also known as geodesics between $\beta_{1}, \beta_{2}$ $\in V(G)$ two vertices is the length of the smallest path between $\beta_{1}-\beta_{2}$ in G. It is denoted by $\xi$ ($\beta_{1}, \beta_{2}).$

Definition 1.2. Consider $V(G)$ is the order set of vertices labeled as $L = \{{\beta_{1}}, {\beta_{2}}, {\beta_{3}}, \dots, {\beta_{h}}\}$ and $\beta \in V(G).$ The representation $r(\beta \vert L)$of $\beta$-vertex concerning order subset L is the h-tuple distances $(\xi ((\beta, \beta_{1}), (\beta, \beta_{2}), (\beta, \beta_{3}), (\beta, \beta_{4}), \dots, (\beta, \beta_{h})$. If the representation shown by each vertex of G is unique according to L, then L is known as the resolving set of G, the smallest cardinality of $L$ is the metric dimension, and it is denoted by $dim(G)$.

Definition 1.3. Let Let $R_{m} = \{{v}_{1}, {v}_{2}\}$ be a mixed metric resolving set then $r(v\mid R_{m})$ and $r(e\mid R_{m})$ should be unique and it is denoted by $dim_{m}(G)$.

Some basic theorems are used in this article. In ^[49] the author prove that $dim(G) = 1$ if and only if $G = P_{n},$ and in ^[13] it is proved that $dim(C_{n}) = 2$, for $n\geq 3$ where the $C_{n}$ is a cycle graph. The mixed metric dimension one is also for the path graph.

Theorem 1.1. Let $NT_{{h}, {v}}$ be a nanotube with ${h}, {v}\geq 1.$ Then double resolving sets of cardinality $3$ exist.

Proof. To prove this claim we have to show that the nanotube has two resolving sets of cardinality $3$. Let $W_{1}$ and $W_{2}$ be two resolving sets of nanotube such that $R_{1}$ $\ne$ $R_{2}$. □

2.   Construction of nanotube $N T_{{h}, {v}}$ for resolving set $W_{1}$

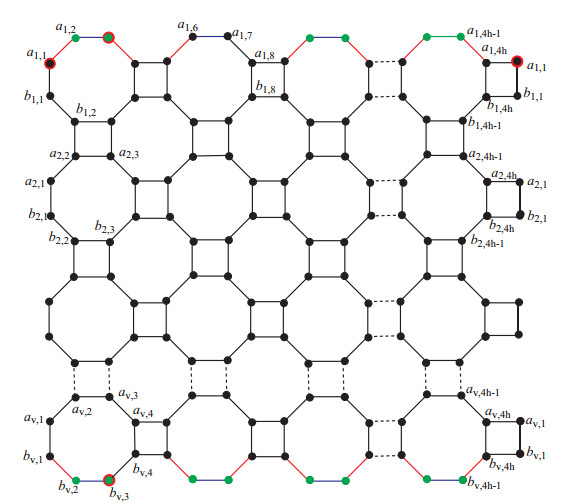
In Figure 1, red is used for those edges that have endpoints of degree $2$ and $3$. The blue color is used for those edges that have endpoints of degree $2$ and the black color is used for all edges that have endpoints of degree $3.$ The green color is used for $2$-degree vertex and the black color vertex has a degree $3.$ The double color is used for that vertex which makes a revolving set. ${a_{1, 1}}$ is black and red due to the degree of $3$ and the point of resolving set. Vertices ${a_{1, 3}}$, ${b_{v, 2}}$ are green and red due to degree $2$ and point of resolving set. Suppose ${h}$ and ${v}$ denote the horizontal and vertical number of $C_{8}.$ The $2$ degree vertices are $2{h},$ and vertices of degree $3$ are $8{h}{v}-2{h}.$ The order of $NT_{{h}, {v}} is \vert O(NT_{{h}, {v}})\vert = 8{h}{v}$ and the size of $NS_{{h}, {v}}$ is $\vert E(NT_{{h}, {v}})\vert = 12{h}{v}+2{v}.$

Two parameters ${h}, \ {v}$ and tow index ${m},$ ${n}$are used in labelling. ${m}$ vary two times with ${v}$ and ${n}$ change $4$ time with ${h}.$ The vertex and edge sets of the nanotube are resp.

Carbon nanotube production exceeded several thousand tons per year, used for applications in automotive parts, molecular electronics, catalyst supports, energy storage, boat hulls, device modeling, biomedical, air and water filtration, sporting goods, thin-film electronics, water filters, actuators, coatings and electromagnetic shields. Over three decades, carbon nanotubes have been used in important applications, such as microelectronic circuitry and microscopy, as well as devices designed to model biological systems and probe quantum mechanics. The two types of carbon nanotubes are single-wall carbon nanotubes and multi-wall carbon nanotubes. Carbon nanotube has multiple properties like strength and elasticity, electrical conductivity, electron emission, aspect ratio, thermal conductivity and expansion. Some researchers find the topological indices of this nanotube and many other people work on nanotubes in fluid flow but in the research area of graph theory. Our aim in this section is to determine the metric dimension of this nanotube. However, first we will construct the nanotube derived from an quadrilateral-octagonal grid and we will denote it by $NT_{{h}, {v}}$.

Theorem 2.1. Let $N T_{{h}, {v}}$ be a nanotube with ${h}, {v}\geq 1.$ Then $W_{1}$ is minimal resolving set of cardinality $3$.

Proof. Let $W_{1} = \{{a}_{1, 1}, {a}_{1, 3}, {b}_{v, 3}\},$ be a subset of the vertices of $N T_{{h}, {v}}$. To prove that $W_{1}$ is a minimal resolving set of cardinality $3$ we follow the definition of resolving set. Given below are the unique representation of all vertices of $NT_{{h}, {v}}$ for ${h}, {v}\geq 1$ (See Figure 2).

The representation of $W_{1} = \{{a}_{1, 1}, {a}_{1, 3}, {b}_{1, 3}\}$ for ${h} = 1 = {v}$ show in Table 1.

This is a unique representation of vertices of nanotube for $h$ = 1 = $v$.

2.1.   Generalized results

The generalized formulas of distances of all vertices of the quadrilateral-octagonal nanosheet show that the minimal resolving set has cardinality $2$ because all distances are different. Let the distance is represented by $\xi.$ Given below are the generalized formulas of distances. Now representation of $W_{1} = \{{a}_{1, 1}, {a}_{1, 3}, {b}_{v, 2}\}.$ for ${h}, {v} > 1.$ Let $\xi (a_{m, n}, a_{1, 1 }) = \alpha_{1},$ $\xi (a_{m, n}, a_{1, 3}) = \alpha_{2},$ $\xi (a_{m, n}, b_{v, 2}) = \alpha_{3}$ and $r({a}_{m, {n}}\mid W_{1}) = (\alpha_{1}, \alpha_{2}, \alpha_{3}).$

where $z_{1} = 2 \left\lfloor\frac{{n}-2}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{{n}-2{h}+2}{4}\right\rfloor, z_{3} = 2\left\lfloor\frac{{n}-2{h}+2}{4}\right\rfloor.$

where $z_{1} = 2\left\lfloor\frac{{n}-6}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{4{h}-{n}-1}{4}\right\rfloor.$

where

Let $\xi (b_{m, n}, a_{1, 1 }) = \alpha^{\prime}_{1},$ $\xi (b_{m, n}, a_{1, 3}) = \alpha^{\prime}_{2},$ $\xi (b_{m, n}, b_{v, 2}) = \alpha^{\prime}_{3}$ and $r({b}_{{m}, {n}}\mid W_{1}^) = (\alpha_{1}^{\prime}, \alpha_{2}^{\prime}, \alpha_{3}^{\prime})$

where $z_{1} = 2\left\lfloor\frac{{n}-4}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{{n}-2{h}+2}{4}\right\rfloor, z_{3} = 2\left\lfloor\frac{{n}-2{h}+2}{4}\right\rfloor.$

where $z_{1} = 2\left\lfloor\frac{{n}-4}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{4{h}-{n}-3}{4}\right\rfloor.$

where

Let $p$ and $q$ be two any arbitrary vertices on nanotube $NT_{{h}, {v}}$. Let $W_{1} = \{a_{1, 1}, a_{1, 3}, b_{v, 3}\}$.

Case Ⅰ: When $p = a_{m, n}$ and $q = a_{m^{'}, n^{'}}$ then further three Subcases arise.

Subcase 1: if $m = m^{'}$, $n \neq n^{'}$ then w. l. o. g. say $n < n^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})+t$ where $t = n^{'}-n$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 2: if $m \neq m^{'}$, $n = n^{'}$ then w. l. o. g. say $m < m^{'}$ this would implies that $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$, because $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})+s$ where $s = 2(m^{'} -m)$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 3: if $m \neq m^{'}$, $n\neq n^{'}$ then w. l. o. g. say $n < n^{'}$, $m < m^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})+(s+t)$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Case Ⅱ: When $p = b_{m, n}$ and $q = b_{m^{'}, n^{'}}$.

Subcase 1: if $m = m^{'}$, $n \neq n^{'}$ then w. l. o. g. say $n < n^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})+t$ where $t = n^{'}-n$ is so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 2: if $m \neq m^{'}$, $n = n^{'}$ then w. l. o. g. say $m < m^{'}$ this would implies that $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$, because $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})+s$ where $s = 2(m^{'} -m)$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 3: if $m \neq m^{'}$, $n\neq n^{'}$ then w. l. o. g. say $n < n^{'}$, $m < m^{'}$ this would implies that $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$, because $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})+(s+t)$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Case Ⅲ: When $p = a_{m, n}$ and $q = b_{m^{'}, n^{'}}$ then further four Subcases arise.

Subcase 1: if $m = m^{'}$, $n = n^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1})$ at least is equal to $\xi (q, a_{1, 1})+1$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 2: if $m = m^{'}$, $n \neq n^{'}$ then w. l. o. g. say $n < n^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1})$ at least is equal to $\xi (q, a_{1, 1})+2$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 3: if $m \neq m^{'}$, $n = n^{'}$ then w. l. o. g. say $m < m^{'}$ this would implies that $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$, because $\xi (p, a_{1, 3})$ at least is equal to $\xi (q, a_{1, 3})+3$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$

Subcase 4: if $m \neq m^{'}$, $n\neq n^{'}$ then w. l. o. g. say $n < n^{'}$, $m < m^{'}$ this would implies that $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, because $\xi (p, a_{1, 1})$ al least is equal to $\xi (q, a_{1, 1})+2$ so $r(p\mid W_{1}) \neq r(q\mid W_{1}).$ When $m \neq m^{'}$, $n\neq n^{'}$ the positions of $p$ and $q$ where $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})$, then $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$ if at these positions $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$ then it is clearly $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$.

We discuss all cases in which $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$ whatever $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})$ if $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})$ then one of these is different $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})$ or $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, a_{1, 1}) \neq \xi (q, a_{1, 1})$, $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})$ or $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})$, $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, a_{1, 1}) = \xi (q, a_{1, 1})$, $\xi (p, a_{1, 3} = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$.

From the above discussion in the form of representation, we note that unique representation is given by all the vertex and satisfies the resolution set condition, which shows that $\vert R\vert = 3.$

Conversely, for $dim(NT_{{h}, {v}})\geq 3 \sim dim(NT_{{h}, {v}}) < 3 \Rightarrow dim(NT_{{h}, {v}}) = 1 \ or \ 2.$ Dimension $1$ is not possible because that is only for the path graph. Now for the dimension is not $2$ we discuss some cases.

Case 1: Suppose $W_{1}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}, 4{n}+1} \vert W_{1}^{\prime}) = r({b}_{{m}, 4{n}}\vert W_{1}^{\prime}).$

Case 2: Suppose $W_{1}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {b}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}+1}\vert W_{1}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert W_{1}^{\prime}).$

Case 3: Suppose $W_{1}^{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}-1}\vert W_{1}^{\prime}) = r({b}_{{m}, 4{n}}\vert W_{1}^{\prime}).$

Case 4: suppose $W_{1}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}+1, {n}}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}-2}\vert W_{1}^{\prime}) = r({b}_{{m}+1, 4{n}-1}\vert W_{1}^{\prime}).$

Case 5: suppose $W_{1}^{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}+1, {n}}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}-2}\vert W_{1}^{\prime}) = r({b}_{{m}+1, 4{n}-1}\vert W_{1}^{\prime}).$

Case 6: suppose $W_{1}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}+1, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}+1}\vert W_{1}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert W_{1}^{\prime}).$

Case 7: suppose $W_{1}^{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}+1, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}+1}\vert W_{1}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert R ^{\prime}).$

Consonantly, there is no possibility of the above collection which are $^\vert {} ^{v}{}^\vert G_2 = \frac{\vert {v} \vert!}{2!(\vert {v} \vert-2)!} = \frac{8({h}{v})!}{2!(8({h}{v})-2)!}$ of vertex set of ${NT_{{h}, {v}}}.$ This shows that locating or resolving a set of 2-cardinality does not have a unique representation, so a minimal resolving set of 2 cardinalities is impossible. Hence the minimal resolving set has cardinality of $3$. □

3.   Construction of nanotube $N T_{{h}, {v}}$ for resolving set $W_{2}$

In Figure 3, red is used for those edges that have endpoints of degree $2$ and $3$. The blue color is used for those edges with endpoints of degree $2$ and the black color is used for all edges that have endpoints of degree $3.$ The green color is used for $2$-degree vertex and the black color vertex has a degree $3.$ The double color is used for those vertexes which make a resolving set. ${b_{1, 1}}$ is black and red color due to the degree $3$ and the point of resolving set. ${a_{1, 3}}$, ${b_{V, 3}}$ are green and red due to degree $2$ and point of resolving set. suppose ${h}$ and ${v}$ denotes the horizontal and vertical number of $C_{8}.$ The $2$ degree vertices are $2{h},$ and the number of vertices of degree $3$ are $8{h}{v}-2{h}.$ The order of $NT_{{h}, {v}} is \ \ \vert O(NT_{{h}, {v}})\vert = 8{h}{v}$ and the size of $NT_{{h}, {v}}$ is $\vert E(NT_{{h}, {v}})\vert = 12{h}{v}+2{h}.$

Two parameters ${h}$, ${v}$ and tow index ${m},$ ${n}$are used in labeling. ${m}$ carry along two time with ${v}$ and ${n}$ change $4$ time with ${h}.$ The vertex and edge sets of the nanotube are

Theorem 3.1. Let $N T_{{h}, {v}}$ be a nanotube with ${h}, {v}\geq 1.$ Then $W_{2}$ is also an other resolving set of cardinality $3.$

Proof. Let $W_{2} = \{{b}_{1, 1}, {a}_{1, 3}, {b}_{v, 3}\},$ be a subset of the vertices of $N T_{{h}, {v}}$. To prove that $W_{2}$ is a minimal resolving set of cardinality $3$ we follow the definition of resolving set. Given below are the unique representation of all vertices of $N T_{{h}, {v}}$ for ${h}, {v}\geq 1$ (See Figure 4).

The representation of $W_{2} = \{{a}_{1, 1}, {a}_{1, 3}, {b}_{1, 3}\}$ for ${h} = 1 = {v}$ show in Table 2.

This is a unique representation of vertices of nanotube for $h$ = 1 = $v$.

3.1.   Generalized results

The generalized formulas of distances of all vertices of the quadrilateral-octagonal nanosheet show that the minimal resolving set has cardinality $2$ because all distances are different. Given below are the generalized formulas of distances. Let $\xi (a_{m, n}, b_{1, 1 }) = \alpha_{1},$ $\xi (a_{m, n}, a_{1, 3}) = \alpha_{2},$ $\xi (a_{m, n}, b_{v, 3}) = \alpha_{3}$ and $r({e}_{m, {n}}\mid {R}) = ({\alpha}_{1}, {{\alpha}}_{2}, {{\alpha}}_{3}).$

where

where $z_{1} = 2\left\lfloor\frac{{n}-6}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{4{h}-{n}-1}{4}\right\rfloor.$

where

Let $\xi (a_{m, n}, b_{1, 1 }) = \alpha^{\prime}_{1},$ $\xi (a_{m, n}, a_{1, 3}) = \alpha^{\prime}_{2},$ $\xi (a_{m, n}, b_{v, 3}) = \alpha^{\prime}_{3}$ and $r(a_{m, {n}}\mid {R}) = ({\alpha}^{\prime}_{1}, {{\alpha}^{\prime}}_{2}, {{\alpha^{\prime}}}_{3}).$

where

where $z_{1} = 2\left\lfloor\frac{{n}-4}{4}\right\rfloor, z_{2} = 2\left\lfloor\frac{4{h}-{n}-3}{4}\right\rfloor.$

where

Let $p$ and $q$ be two any arbitrary vertices on nanotube $NT_{{h}, {v}}$. Let $W_{2} = \{b_{1, 1}, a_{1, 3}, b_{v, 2}\}$.

Case Ⅰ: When $p = b_{m, n}$ and $q = b_{m^{'}, n^{'}}$ then further three Subcases arise.

Subcase 1: if $m = m^{'}$, $n \neq n^{'}$ and without loss of generality we can say that $n < n^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})+t$ where $t = n^{'}-n$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 2: if $m \neq m^{'}$, $n = n^{'}$ and without loss of generality we can say that $m < m^{'}$ then $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$ Because $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})+s$ where $s = 2(m^{'} -m)$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 3: if $m \neq m^{'}$, $n\neq n^{'}$ and without loss of generality we can say that $n < n^{'}$, $m < m^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})+(s+t)$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Case Ⅱ: When $p = a_{m, n}$ and $q = a_{m^{'}, n^{'}}$.

Subcase 1: if $m = m^{'}$, $n \neq n^{'}$ and without loss of generality we can say that $n < n^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})+t$ where $t = n^{'}-n$ is so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 2: if $m \neq m^{'}$, $n = n^{'}$ and without loss of generality we can say that $m < m^{'}$ then $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$ Because $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})+s$ where $s = 2(m^{'} -m)$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 3: if $m \neq m^{'}$, $n\neq n^{'}$ and without loss of generality we can say that $n < n^{'}$, $m < m^{'}$ then $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ Because $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})+(s+t)$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Case Ⅲ: When $p = b_{m, n}$ and $q = b_{m^{'}, n^{'}}$ then further four Subcases arise.

Subcase 1: if $m = m^{'}$, $n = n^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1})$ at least is equal to $\xi (q, b_{1, 1})+1$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 2: if $m = m^{'}$, $n \neq n^{'}$ and without loss of generality we can say that $n < n^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1})$ at least is equal to $\xi (q, a_{b, 1})+2$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 3: if $m \neq m^{'}$, $n = n^{'}$ and without loss of generality we can say that $m < m^{'}$ then $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$ Because $\xi (p, a_{1, 3})$ at least is equal to $\xi (q, a_{1, 3})+3$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

Subcase 4: if $m \neq m^{'}$, $n\neq n^{'}$ and without loss of generality we can say that $n < n^{'}$, $m < m^{'}$ then $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ Because $\xi (p, b_{1, 1})$ al least is equal to $\xi (q, b_{1, 1})+2$ so $r(p\mid W_{2}) \neq r(q\mid W_{2}).$

When $m \neq m^{'}$, $n\neq n^{'}$ the positions of $p$ and $q$ where $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})$ then $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$ if at these positions $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$ then it is clearly $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$.

We discuss all cases in which $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$ whatever $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})$ if $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})$ then one of these is different $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})$ or $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$, $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$, $\xi (p, a_{1, 3}) = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, b_{1, 1}) \neq \xi (q, b_{1, 1})$, $\xi (p, a_{1, 3})\neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) = \xi (q, b_{v, 3})$ or $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})$, $\xi (p, a_{1, 3}) \neq \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ or $\xi (p, b_{1, 1}) = \xi (q, b_{1, 1})$, $\xi (p, a_{1, 3} = \xi (q, a_{1, 3})$, $\xi (p, b_{v, 3}) \neq \xi (q, b_{v, 3})$ No possibility shows two representations are equal. From the above discussion in the form of representation, we note that unique representation is given by all the vertex and satisfies the condition of resolving set which shows that $\vert W_{2}\vert = 3.$

Conversely, for $dim_e(NT_{{h}, {v}})\geq 3 \sim dim_e(NT_{{h}, {v}}) < 3 \Rightarrow dim_e(NT_{{h}, {v}}) = 1 \ or \ 2.$ Dimension $1$ is not possible because that is only for the path graph. Now for the dimension is not $2$ we discuss some cases.

Case 1: Suppose $W_{2}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}, 4{n}+1} \vert W_{2}^{\prime}) = r({b}_{{m}, 4{n}}\vert W_{2}^{\prime}).$

Case 2: Suppose $W_{2}^{\prime}\subseteq\{{{a}_{{m}, {n}}, {b}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}+1}\vert W_{2}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert W_{2}^{\prime}).$

Case 3: Suppose $W{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}-1}\vert W_{2}^{\prime}) = r({b}_{{m}, 4{n}}\vert W_{2}^{\prime}).$

Case 4: suppose $W{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}+1, {n}}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}-2}\vert W_{2}^{\prime}) = r({b}_{{m}+1, 4{n}-1}\vert W_{2}^{\prime}).$

Case 5: suppose $W{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}+1, {n}}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}-2}\vert W_{2}^{\prime}) = r({b}_{{m}+1, 4{n}-1}\vert W_{2}^{\prime}).$

Case 6: suppose $W^{\prime}\subseteq\{{{a}_{{m}, {n}}, {a}_{{m}+1, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+1, 4{n}+1}\vert W_{2}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert W_{2}^{\prime}).$

Case 7: suppose $W^{\prime}\subseteq\{{{b}_{{m}, {n}}, {b}_{{m}+1, {n}+1}}:1\leq{m}\leq{v}, 1\leq{n}\leq 4{h}\}$ having 2-cardinality, then similar representations are given by; $r({a}_{{m}+2, 4{n}+1}\vert W_{2}^{\prime}) = r({b}_{{m}+1, 4{n}}\vert R ^{\prime}).$

Consonantly, there is no possibility of the above collection which are $^\vert {} ^{v}{}^\vert G_2 = \frac{\vert {v} \vert!}{2!(\vert {v} \vert-2)!} = \frac{8({h}{v})!}{2!(8({h}{v})-2)!}$ of vertex set of ${NT_{{h}, {v}}}.$ This shows that locating or resolving a set of 2-cardinality does not have a unique representation, so a minimal resolving set of 2 cardinality is impossible. so the minimal resolving set has cardinality of $3$. Hence prove that $W_{2}$ ia an other resolving set of nanotube has cardinality $3.$ □

4.   Exchange property

In graph theory, a resolving set of a graph is a subset of vertices that uniquely identifies every vertex in the graph. More formally, a resolving set S of a graph G is a subset of vertices such that for every pair of distinct vertices u and v, there exists a vertex w in S such that the distance from u to w is different from the distance from v to w.

The exchange property of a resolving set refers to a property that allows one to exchange vertices between resolving sets in a graph without losing the resolving property. Specifically, if $S$ and $T$ are two resolving sets of a graph G, and there exists a vertex v in $S\setminus T$ (S minus T) such that $(T{v})\cup{u}$ is also a resolving set for every vertex $u$ in $S\setminus T,$ then we say that the resolving sets $S$ and $T$ have the exchange property.

In other words, the exchange property means that if there is a vertex in one resolving set that is not in the other resolving set, but by removing it from the first and adding a vertex from the second, we still obtain a resolving set. This property allows us to manipulate and transform resolving sets while maintaining their essential property of uniquely identifying every vertex in the graph.

The exchange property is useful in various applications of resolving sets, such as graph reconstruction, fault diagnosis and network localization. It allows for the efficient construction and modification of resolving sets, enabling better analysis and understanding of graph structures.

Note that not all resolving sets have the exchange property. The exchange property is a desirable characteristic but is not a necessary condition for a set to be a resolving set. There may be resolving sets that do not satisfy the exchange property.

The components of a vector space's basis determine each vector in a finite-dimensional space in a unique way (expressed as a linear combination). The exchange property applies to a vector space's basis. The vertices of a minimal resolving set can also be used to uniquely identify each vertex of a finite graph. As a result, resolving sets of a finite graph behave like bases in a vector space with finite dimensions. The exchange property is not always present in the minimal resolving sets, unlike a linear basis of a vector space. The literature contains findings regarding the exchange property for various graphs. For instance, the exchange property is true for resolving sets in trees, but it is false for $n$ $\geq$8 in wheels graph $W_{n}$.

Theorem 4.1. Let $N T_{{h}, {v}}$ be an quadrilateral-octagonal Nanotube with ${h}, {v}\geq 1$ then exchange property hold for this structure.

Now to prove this claim we follow the definition of the exchange property. Let $u = a_{1, 1}$ and $u$$\in$ $W_{1}$, $v = b_{1, 1}$ and $v$ $\in$ $W_{2}$ then $(W_{1}$$\backslash$$\{u\})$$\cup$$v$ is also a minimal resolving set. Suppose $(W_{1}$$\backslash$$\{u\})$$\cup$$v = K$ Now we have to prove that $K$ is also a minimal resolving set for $N T_{{h}, {v}}$. We know that $W_{1} = \{a_{1, 1}, a_{1, 3}, b_{v, 3}\}$ and $W_{2} = \{b_{1, 1}, a_{1, 3}, b_{v, 3}\}$ so $(W_{1}$$\backslash$$\{u\})$$= \{a_{1, 3}, b_{v, 3}\}$$\cup$$v = \{b_{1, 1}, a_{1, 3}, b_{v, 3}\} = W_{2}$ and in theorem $4.1$ we prove that $W_{2}$ is a minimal resolving set of cardinality $3$. Hence prove that the exchange property hold in $N T_{{h}, {v}}$. $a_{1, 3} and b_{v, 3}$ are common point in $W_{1}$ and $W_{2}$. So $W_{1}$, $W_{2}$ exchange $u$ and $v$ point with each other.

5.   Conclusions

This article discusses two structures of nanotubes derived from the quadrilateral-octagonal grid. We have found the resolving sets of the nanotubes based on the distance of the graph. The Resolving sets of nanotubes are cardinality $3$. Moreover, we found that when a nanosheet folds and makes a nanotube, the 2D structure converts into 3D. Due to this phenomenon, the cardinality of resolving sets increases one. We ensure that the exchange property is also held for this structure.

5.1.   Implications, limitations

The metric dimension in graph theory refers to the minimum number of vertices required to uniquely identify every vertex in a graph. While it is a well-studied concept with various applications, there are certain limitations and potential future directions to consider.

Computational Complexity: Computing the exact metric dimension of a graph is known to be NP-hard, which means that there is no known efficient algorithm to solve it in general. The problem becomes even more challenging for larger graphs, limiting its applicability in practical scenarios. Thus, developing approximation algorithms or finding efficient algorithms for special graph classes are areas of interest.

Lack of Structural Understanding: The metric dimension does not always provide insight into the structural properties of a graph. Even graphs with the same metric dimension can exhibit different structural characteristics. Understanding the relationship between the metric dimension and other graph parameters, such as connectivity, diameter or degree distribution, is an avenue for further research.

Dynamic Graphs: Most studies on metric dimension assume static graphs, where the underlying structure does not change. However, in real-world scenarios, graphs often evolve dynamically. Exploring the metric dimension in dynamic graphs, where edges and vertices are added or removed over time, is an important direction for future research.

Robustness and Fault-Tolerance: Analyzing the resilience of metric dimension under vertex or edge failures is another interesting aspect. Investigating how the metric dimension changes in the presence of faults or attacks can provide insights into the fault-tolerance and robustness of networks.

Application-Specific Metrics: Different applications may require tailored metrics for vertex identification. Developing and studying alternative measures that capture specific characteristics of graphs in different contexts can be valuable. For instance, considering weighted or probabilistic graphs, where vertices have different importance or uncertainties, can lead to novel perspectives on metric dimension.

Beyond Traditional Graphs: Exploring the metric dimension in non-traditional graph structures, such as hypergraphs, temporal networks, or spatial networks, can provide new insights and challenges. These extended graph models require rethinking the notion of distance and vertex identification, pushing the boundaries of metric dimension research.

Overall, the limitations in the metric dimension topic present opportunities for further investigation and the development of new methodologies, algorithms and applications. By addressing these limitations, we can deepen our understanding of graph structures and expand the utility of metric dimension in diverse fields. For more work on the metric dimension, we refer to see ^[50,51,52].

5.2.   Future study

In this draft, we did the computation of only resolving set and its exchange property. One can also consider to discuss the other variants of resolving set, like fault-tolerant resolving set ^[53,54,55], partition resolvability of these chemical compounds ^[56,57] and other similar theoretical parameters as well.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflicts of interest

The authors declare that they have no conflicts of interest to report regarding the present study.