A fractional mathematical model for assessing cancer risk due to smoking habits

1.   Introduction

The smoking disease, also known as chronic obstructive pulmonary disease (COPD), is a group of progressive lung diseases that cause breathing difficulties ^[1]. It is primarily caused by long-term exposure to cigarette smoke, although exposure to second-hand smoke, air pollution, and certain occupational fumes can also contribute to its development. Common symptoms of COPD include chest tightness, wheezing, shortness of breath, and persistent cough. Over time, the disease progressively worsens, resulting in a reduced ability to carry out physical activities and everyday tasks. Individuals with COPD may also experience frequent respiratory infections, fatigue, unintended weight loss, and swelling in the ankles, feet, or legs ^[2].

This smoking-related disease mainly affects the lungs' alveoli, or air sacs, and airways. The toxic compounds in tobacco smoke affect the respiratory system and cause damage to the airways, leading to a narrowing of the air passages and mucus production ^[3]. As a result, the lungs become less efficient at transferring oxygen into the bloodstream, making breathing more difficult. In advanced stages, COPD can also affect the heart, leading to complications such as heart failure ^[4]. While there is currently no cure for COPD, there are treatments that can help to control the symptoms and delay the illness's progression. In order to effectively manage COPD, changes in lifestyle like giving up smoking, avoiding triggers in the environment, and engaging in regular exercise are essential. Medications like bronchodilators, inhaled corticosteroids, and oxygen therapy are commonly prescribed to improve breathing and reduce inflammation ^[5].

Smoking is a major cause of various types of cancer, including lung, oral, throat, bladder, kidney, pancreas, and stomach cancer, among others ^[6]. It is estimated that smoking is responsible for nearly one-third of all cancer deaths in the United States. When tobacco is smoked, thousands of harmful chemicals are released into the body. These chemicals can cause damage to the DNA in cells, leading to the formation of cancerous cells. Smoking also weakens the immune system, making it harder for the body to fight off cancer cells ^[7].

Lung cancer is the most common and deadliest form of cancer associated with smoking. The risk of developing lung cancer is directly related to the duration and intensity of smoking. The longer a person smokes and the more cigarettes they consume, the higher their risk of developing lung cancer. Oral and throat cancers are also strongly linked to smoking ^[8]. The toxic chemicals from tobacco can cause mutations in the cells of the mouth and throat, leading to the formation of cancerous growths. Smokers are also at a higher risk of developing bladder, kidney, pancreas, and stomach cancer, as these organs come into contact with the harmful chemicals through the bloodstream or urine ^[9].

Quitting smoking significantly decreases the risk of developing cancer. Although it can be challenging, quitting smoking at any age can provide immediate and long-term health benefits. Additionally, early detection through cancer screening programs and regular medical check-ups is crucial for detecting and treating cancer at an early stage, improving the chances of successful treatment and survival ^[10,11].

Mathematical modeling is highly significant in various fields and has numerous practical applications. Mathematical models provide a means to simulate and analyze real-world phenomena, allowing scientists to conduct virtual experiments and test hypotheses. This enables researchers to explore complex systems and generate insights that may be difficult or impossible through direct experimentation ^[12,13]. Therefore, mathematical modeling is a great tool as it provides a framework for understanding complex systems, predicting future outcomes, solving problems, making informed decisions, optimizing designs, evaluating policies, conducting scientific research, and fostering education ^[14,15].

Mathematical models can be used to determine the probability of developing different types of cancer due to smoking. Researchers can incorporate various factors such as smoking duration, intensity, and exposure to second-hand smoke to estimate individual and population-level cancer risks. We can simulate the natural history and progression of smoking-related cancers with the help of modeling ^[16,17]. Researchers can create models that simulate the effects of implementing intervention strategies like tobacco taxes, smoking cessation programs, or smoke-free regulations, allowing policy-makers to make evidence-based decisions ^[18].

Models can assist in optimizing treatment strategies for smoking-related cancers. By simulating treatment outcomes and comparing different treatment approaches, researchers can identify the most effective combinations of surgery, chemotherapy, radiation therapy and targeted therapies ^[19]. This can improve patient outcomes and resource allocation. Mathematical modeling can also be used to evaluate the economic implications of different smoking-related cancer interventions. By considering factors such as healthcare costs, productivity losses, and quality-adjusted life years gained, policymakers can assess the value of various interventions and allocate resources accordingly (see ^[20]).

Fractional differential equations (FDEs) are a type of differential equation that involve fractional order derivatives. They provide a more flexible and accurate mathematical tool for modeling complex physical phenomena with memory effects, such as viscoelastic materials, anomalous diffusion, and biological systems ^[21]. To implement FDEs in modeling, one can use semi-analytical or numerical methods that approximate the fractional-order derivatives, as exact closed-form solutions are often unavailable. Several popular numerical methods for FDEs include the Riemann-Liouville, Caputo, Atangana-Baleanu fractional derivative in Caputo sense (ABC), or any other fractional-order operator. Once the system of FDEs is solved, we can analyze and interpret the obtained solution in the context of the physical problem being modeled ^[22,23]. This may involve calculating key quantities of interest or comparing the results with experimental data.

In the last few decades, many studies have been noted as significant in fractional-order modeling, which include optimal systems, series solutions and conservation laws for a time fractional cancer tumor model ^[24,25], the Mittag-Leffler kernel approach for time-fractional advection-reaction-diffusion equations ^[26,27], codimension two Lie invariant solutions of the modified Khokhlov-Zabolotskaya-Kuznetsov equation ^[28,29], mathematical studies of the solution of Burgers' equations ^[30,31], numerical studies of the neural network-based fractional mathematical model of immunotherapy and chemotherapy for breast cancer ^[32], mathematical modeling of integer and fractional order and its simulations for Q-fever ^[33], an examination of the glucose-insulin alliance scheme in the fractional-order diabetes model ^[34,35], evaluation of a fractional vector-host disease system mathematically using the Caputo-Fabrizio operator ^[36], the Atangana-Baleanu-Caputo derivative-based numerical and geometric interpretation of a fractional-order model of the cancer-immune mode ^[37], the solution of fractional sawada-kotera-ito equation employing the derivatives of Caputo and Atangana-Baleanu ^[38], and the new semi-analytical approach to solve the fractional-order Sharma-Tasso-Olver equation with the derivatives of Caputo and Atangana-Baleanu ^[39]. In addition, we have Hopf bifurcation control of a fractional-order delayed turbidostat model, delayed chemostat model, and three-triangle multi-delayed neural networks ^[40,41,42], the COVID-19 stochastic model, the plankton–oxygen dynamical model owning delay, and a control technique in a predator-prey system ^[43,44,45], hybrid controller design of a 2D Lotka-Volterra commensal symbiosis system, fractional order uncertain BAM neural networks, and as well as a Hopf bifurcation of a type of BAM neural network model concerning three nonidentical delays ^[46,47,48].

The present work is organized as follows: Section 2 includes the fractional smoking-related cancer model, its diagram, and detailing of the parameters. Section 3 covers the well-defined definitions and theorems which we have used in this work. Qualitative and stability analysis are discussed in Sections 4 and 5, respectively. Numerical computation and its behavior in the form of figures are displayed in Section 6. Valedictory results and graphical interpretation are discussed in Section 7.

2.   Model formation

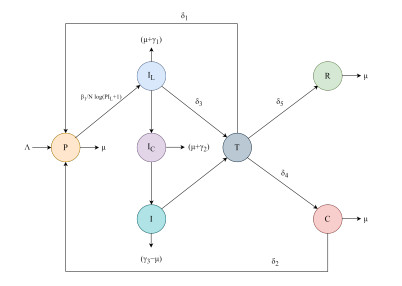
The present mathematical model of smoking-related cancer is classified into seven specific compartments: smoking individuals as the susceptible class $P(t)$, lately infected individuals as $I_L(t)$, chronically infected individuals without treatment as $I_C(t)$, infected individuals with and without treatment as $T(t)$ and $I(t)$, smoking-related cancer individuals as $C(t)$, and recovered individuals as $R(t)$. We contemplated some parameters in the formation of the model. The disease transmission coefficient from the susceptible $P(t)$ to the lately infected class $I_L(t)$ is $\beta_1$, and from the lately infected $I_L(t)$ to the chronically infected class $I_C(t)$ is $\beta_2$. The total population size is denoted as $\Delta$. The infected individuals without treatment $I(t)$ to with treatment $T(t)$ transmission rate is defined as $\delta_1$, and smoker individuals $P(t)$ to cancer patient $C(t)$ transmit rate is $\delta_2$. For TB-infected patients that transmit from the lately infected $I_L(t)$ to infected with treatment class $T(t)$ is defined as $\delta_3$, those infected with treatment $T(t)$ that transmit to the smoking-related cancer class $C(t)$ as $\delta_4$, and those that transmit from the infected with treatment $T(t)$ to recovered class $R(t)$ as $\delta_5$. The death rate due to smoking is marked as $\mu$. Notations $\alpha_1, \alpha_2$, and $\alpha_3$ are assigned for infection growth from $I_L(t)$ to $I_C(t)$ class, from $I_C(t)$ to $I(t)$ class, and from $I(t)$ to $T(t)$ class, respectively. The disease death rate in the $I_L(t), I_C(t)$, and $I(t)$ compartments are $\gamma_1, \gamma_2$, and $\gamma_3$, respectively.

By linking the above-mentioned parameters, the mathematical model as a system of differential equations is represented as:

with the initial conditions

Here, the total population by adding all of the compartments is defined as

The proposed smoking-related cancer model, by implementing the ABC fractional derivative ^[49], is as follows:

3.   Preliminaries

Definition 3.1. ^[49] Let $G \in \mathbb{H}^{1}(a, b), a > b$, then the ABC fractional derivative is given as:

where $E_\alpha (\cdot)$ is the Mittag-Leffler function of order one and can be expressed as

Definition 3.2. ^[49] The ABC fractional integral of order $\alpha$ is defined as:

where $\Gamma (\cdot)$ denotes the Gamma function and it can be defined as

Lemma 3.1. ^[50] The solution of any fractional differential equation

with $\psi(0) = {\psi_0},$ is given by

4.   Existence and uniqueness

The existence and uniqueness of the considered model (2.2) will be covered in this section. The considered model (2.2) can be rewritten as follows:

where

For the purpose of simplicity, we refer to the suggested model (4.1) as follows:

where,

Applying fractional ABC integral (3.2) on (4.3), we get:

Utilizing $\chi = [0, T]$ as

under the norm specified as follows, let us define the Banach space as:

Assume that the function $\Delta \left(t, \mathbb{G}(t)\right)$ satisfies the following two conditions for each $\mathbb{G}\in \Omega$ and $t \in [0, T]$.

● $\exists$ constants $\mu_\Delta$ and $\nu_\Delta$ such that:

● $\exists$ constant $\lambda_\Delta > 0$ such that:

Now we define the operators $\Lambda_1$ and $\Lambda_2$ such that:

where

Theorem 4.1. Suppose that the above-mentioned Lipschitz and growth conditions hold. If the following are true, then there is at least one solution for (4.4):

(I) $\frac{(1-\alpha)}{\mathbb{N}(\alpha)} \lambda_\Delta < 1$.

(II) $\Psi_1 = \left[\frac{(1-\alpha)}{\mathbb{N}(\alpha)} + \frac{T^ {\alpha}}{\mathbb{N}(\alpha)\Gamma(\alpha)} \right] \nu_\Delta < 1.$

(III) $\Psi_2 = \left[\frac{(1-\alpha)}{\mathbb{N}(\alpha)} + \frac{T^ {\alpha}}{\mathbb{N}(\alpha)\Gamma(\alpha)} \right] \mu_\Delta < 1.$

Proof. Assume a closed convex set

In order to establish that $\Lambda_1 \mathbb{G}_1 + \Lambda_2 \mathbb{G}_2 \in B_\tau$ for any $\mathbb{G}_1$, $\mathbb{G}_2$ $\in B_\tau$. Using the growth condition, we get:

This shows that

Next, we will show that $\Lambda_1$ is a contraction. For any $\mathbb{G}_1$, $\mathbb{G}_2$ $\in B_\tau$, and using the Lipschitz condition, we get

where

Thus, $\Lambda_1$ is a contraction.

Let us now demonstrate the relative compactness of $\Lambda_2$. Considering $\mathbb{G} \in B_\tau$ for this

Therefore, on $B_\tau$, $\Lambda_2$ is uniformly bounded. Lastly, we demonstrate the equicontinuous nature of $\Lambda_2$. Let $t_1$, $t_2$ $\in [0, T]$ such that $t_1 < t_2$. Let $\mathbb{G} \in B_\tau$. Following that:

Thus, $\left\|\Lambda_2 \mathbb{G}(t_1) - \Lambda_2 \mathbb{G}(t_2) \right\| \rightarrow 0$ as $t_2 \rightarrow t_1$. The operator $\Lambda_2$ is equicontinuous because it is relatively compact, according to the Arzela-Ascoli theorem. Hence, there is at least one solution for Eq (4.4). The considered model has at least one solution since the proposed model is equivalent to Eq (4.4). □

Theorem 4.2. Assuming that the Lipschitz condition is satisfied, then the unique solution of Eq (4.4) can be found if

Proof. Considering $t \in [0, T]$ and for any $\mathbb{G}$, $\mathbb{G^*}$ $\in \Omega$, we have

The operator $\Lambda$ is a contraction as per the hypothesis

The solution to Eq (4.4) is unique according to the Banach contraction theorem. As a result, the solution for the suggested model (2.2) is unique. □

5.   Stability analysis

5.1.   Local stability

We discuss the equilibrium points of presented model (2.1). Here, we consider the two stage of the population.

(1) Disease-free equilibrium point $E^0$

At this stage, there is no contamination due to the smoking habit in the class. Hence, we set every infection class to zero. Therefore, the disease-free equilibrium point $E^0$ can be defined as:

(2) Endemic equilibrium point $E^{end}$

To obtain the value of endemic stage $E^{end},$ we will equate the system of Eq (2.1) with zero. By solving the system of linear equations, we achieve the endemic equilibrium point $E^{end}$ as:

where

5.1.1.   Reproduction number $R_0$

To calculate $R_0,$ we employ the next generation matrix method. Let us consider the following sub-system by involving the infective compartments as below:

Now we find the eigenvalues for the matrix $FV^{-1}$ to evaluate $R_0,$ where matrix $F$ and $V$ for the system (5.1) can be defined as:

and

Next, we find the inverse of matrix $V^{-1}$ and with simple matrix multiplication, we get

Further, the dominant eigenvalues can be found by

The basic reproduction number $R_0$ can be defined as

where

and

Theorem 5.1. The disease-free stage of smoking-related cancer model (2.1) is locally asymptotically stable if the basic reproduction number $R_0 < 0.$

Proof. Available in ^[51]. □

Theorem 5.2. The endemic stage of smoking-rated cancer model (2.1) is locally asymptotically stable if the endemic Lyaponove function $L < 0$ and the basic reproduction number $R_0 > 0.$

Proof. Available in ^[51]. □

5.2.   Global stability

Using the concept of nonlinear functional analysis, we address the Ulam-Hyres (UH) stability of the suggested fractional model (2.2) in this section.

Definition 5.1. If the following property holds true and $\exists$ ${\omega} > 0$, then the proposed system (2.2) is UH stable. For any $\overline {\mathbb{G}} \in \Omega$ and $\epsilon > 0$, If

then $\exists\ \mathbb{G} \in \Omega$ satisfies the system (2.2) with the initial condition

such that

Where

Remark 5.1. Consider a small perturbation $\rho \in \mathsf{C}[0, \mathsf{T}]$ such that $\rho(0) = 0$ along with the following property:

for $t \in [0, \mathsf{T}]$ and $\overline{\epsilon} > 0$.

Lemma 5.3. The solution $\overline{\mathbb{G}}_\rho(t)$ of the perturbed system

satisfies the relation

where

Proof. Applying fractional integral (3.2) on (5.5), we get

and also,

Using Remark 5.1,

This completes the proof. □

Theorem 5.4. The proposed fractional system (2.2) is UM stable if

Proof. Since $\mathbb{G}$ is a unique solution of the system (5.5) and $\overline{\mathbb{G}}$ is the solution of (5.4), then

which implies that

where

and

For

then

Hence, the considered fractional system (2.2) is UM stable. □

6.   Numerical results and discussion

In this work, we obtain the solution of the fractional-order smoking-related cancer model (2.2) using the Adams-Bashforth-Moulton method ^[52]. We take some specific values of the necessary parameters

with the initial values

Figures 1–7 represent the behavior of each compartment when we utilized the ABC with some fractional orders between 0.9 and 1. We plot the 3D behavior of the transmission rate from the $I_{L}(t)$ class to the $I_{C}(t)$ class when $\beta_2$ and $\alpha_1$ are between 0 and 0.004 in Figures 8 and 9, respectively. When infective parameter $\delta_4$ is between 0.0001 and 0.0004, the rate of transmission from the $I(t)$ and $C(t)$ class is demonstrated as Figure 10. When another infective parameter $\delta_5$ is between 0 and 0.0004, the rate of transmission from $I(t)$ to $R(t)$ class is obtained as in Figure 11. Figure 12 is the plot of the transmission rate from infected to recovered individuals when infective parameter $\delta_5$ change.

7.   Conclusions

We demonstrated a fractional-order smoking-related cancer mathematical model with seven compartments under the duration of 60 days. We utilized the ABC fractional operator as it has non-local and non-singular properties. Further, we acquired a well-known Adams-Bashforth-Moulton method which provided a fast convergence to the solution. The existence and uniqueness of the system was proved with the help of Banach's fix point theorem. By calculating the equilibrium points and basic reproduction number, we validated the local stability and, with the use of Ulam-Hyres stability, we admitted the global stability of the suggested model. From Figures 1–8, we see that the behavior of the solution of each class having a stable region. Figures 9 and 10 show that when transmission coefficients $\beta_2$ and $\alpha_1$ change, the lately infected individuals transmit to chronically infected individuals. Figure 11 displays the transmission rate from infected individuals to cancer due to smoking individuals when infective parameter $\delta_4$ differs. By incorporating data on smoking-related cancer and its treatment effectiveness, researchers can gain insights into how different factors affect the cancer progression and design strategies for prevention, diagnosis, and treatment. It can help to evaluate the impact of different tobacco control policies on cancer incidence and mortality.

The use of the smoking-related cancer model in research can support the UN's sustainable development goals in several ways. Researchers can contribute valuable insights into the causes and mechanisms of cancer development, which can ultimately lead to improved prevention, early detection, and treatment strategies. This can have a significant impact on good health and well-being, by reducing the burden of cancer worldwide and improving overall public health. Additionally, research on the smoking-related cancer model can also contribute to quality education, by providing valuable training and educational opportunities for researchers and healthcare professionals. By sharing knowledge and expertise gained from studying the smoking cancer model, researchers can help build capacity in cancer research and care, ultimately improving the quality of education and healthcare delivery in this field.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors have no conflicts of interest to declare.