On the criteria for diagnosing depression in bereaved individuals: a self-organizing map approach

1.   Introduction

With the emergence of large scientific devices in various scientific fields around the world, scientific discovery has entered the era of big data. Scientific discovery cannot completely rely on expert experience to find rare scientific events from massive data, and a large amount of historical data cannot be used effectively. At the same time, it is becoming more and more prominent in real-time and high precision. The mode of scientific events is rare, and the general algorithm is not suitable for the field of science. Therefore, the problem of intelligent discovery of scientific data came into being. Scientific data intelligent discovery aims to accelerate the discovery of scientific events by using data intelligent method. However, intelligent discovery of scientific data lacks the overall framework design, which is embodied in the lack of comprehensive analysis system of scientific data and efficient knowledge fusion mechanism of heterogeneous scientific data. From the perspective of data management, the long-term storage and mining of massive historical data is inefficient. This paper puts forward the framework and related challenges of scientific data intelligent discovery and management, in order to promote the progress of scientific discovery.

Another description form of neural network model is based on memristor. In 2008, the Hewlett-Packard(HP) laboratory research group in the United States first confirmed the existence of memristor in nanometre electronic components, and also described it in detail with mathematical and physical models ^[1]. As a new type of nanometre circuit element, the memristor has many good characteristics, such as low energy dissipation and powerful memory function. Memristor has attracted the attention of scientific research institutions in different fields all over the world. Its strong learning ability can consent memristor to replace the existing transistors in the future. If the resistance is used to replace the self-feedback connection weight, the Hopfield neural network system will have a simple memory storage function ^[2,3]. Similarly, further, if the memristor is used to replace the traditional resistor, a simple memristor model can be established. It also proves that memristor plays an important role in circuit theory, especially in the field of modeling and non-traditional signal processing. The connection weight is completely determined by the memristor in the artificial neural network. The memristor model based on neural networks can be established by simulating the structure of human brain which is very similar to the structure of neural networks (the structure diagram of four circuit elements of memristor). At the same time, due to the extremely rich dynamic behavior in the neural network system (especially the memristor system), the storage, reading and writing abilities of n-node neural network system with memristor are dozens of times that of the neural network system without memristor ^[4]. Compared with the traditional model, this kind of model has stronger computing power and information storage capacity. Another neural network model, recurrent neural network, has also received a lot of attention and has a wide range of applications, such as the four-tank benchmark problem, the nonlinear constrained optimization problem, the statistical model, the phase structure and the pattern recognition ^[5,6,7]. Therefore, combined with memristor and recurrent neural network model, considering its rich theoretical significance and practical achievements, many scholars are committed to the synchronization of recurrent neural network model with memristor. From the perspective of mathematical theory, this kind of new neural network model is a switched dynamic system model that depends on the initial state. In essence, it can be described by the discontinuous functional differential equation. Through the methods of set-valued analysis theory and functional differential equation, the mathematical theory and neural network engineering model are effectively combined. As a powerful analysis tool and an effective technical means, this paper makes a comprehensive discussion and dynamic analysis on the time-delay recurrent neural network model based on memristor, which not only improves the system of discontinuous functional differential equations at the right end of mathematics at the theoretical level, but also provides a more practical idea for the neural network model in engineering at the application level.

In order to better obtain the stability results on the neural network model, the way to realize stabilization is also divided into different categories. Among them, the popular stabilization methods include exponential stabilization ^[8], asymptotic stabilization ^[9], exponential adaptive stabilization ^[10], anti-stabilization ^[11], robust stabilization ^[12], finite-time stabilization and fixed-time synchronization. However, the previous results about asymptotic stabilization and exponential stabilization can be guaranteed only when the time is close to infinity. Since the service life of organisms and equipment is limited, the criteria of asymptotic stability and exponential stability are not applicable in practice. In order to improve convergence and efficiency, another finite-time stabilization has been widely studied in recent years ^{[13,14,15,16,17,18,19,20]}. Finite-time stabilization means that stabilization can reach the so-called stable time within the specified time. When the initial values are known, some effective controllers with adjustable parameters can be designed, in which the parameters considered can be stabilized before a given fixed time. Obviously, the efficiency of engineering such as image processing and secure communication will be greatly improved based on finite-time technology. Finite-time stabilization has better robustness and anti-interference ability than asymptotic stabilization. On the other hand, the stable time of finite-time stabilization depends on the selection of initial values. The stabilization stable settling time is not fixed for different initial values. In addition, considering the environmental constraints in practice and other factors, not all initial values are applicable in the system, so finite-time stabilization also has some limitations. Therefore, in recent years, a more suitable stabilization method for realizing finite-time stability, called fixed-time stabilization(FTS), was proposed by A. Polyakov et al. in ^[21,22]. Its advantage over finite-time stabilization method is that its stability time does not depend on the selection of the initial value. Under the framework of fixed-time technology, many scholars also made outstanding contributions to the finite-time stabilization problem. A unified control strategy is designed and it is revealed that a parameter value in the controller completely decides the memristors-based neural networks are stabilized whether in finite time or in fixed time, which is described in ^{[23,24,25,26,27,28]}. Meanwhile, the author designed a class of memristive neural networks with time-varying delays and general activation functions. They investigate the exponential stabilization problem of such systems in ^[29]. And Wen studied a new convolution algorithm: convolution kernel first operated (CKFO), which can solve the problem that the actual calculation is not reduced after pruning the weight of the convolution neural network ^[30].

However, in the intricate relationship within neurons, we must first consider the coupling network and understand the interaction between different neurons. In ^[31,32], the authors introduced an ordinary differential equation model with neuron nodes with mutual coupling relationship, and the following interesting dynamic behaviors will occur in the model: self-organization phenomenon, synchronization behavior, traveling wave solution, spatiotemporal chaos and defect propagation. In ^[33], a dynamic element was introduced as a neuron node. Considering the interaction and influence between neurons, the existing neural network models are considered from the static and dynamic levels respectively. At the same time, in practice, one can not control every neuron, so the introduction of a new containment control theory is very necessary. For the problem of non-strongly connected networks or undirected spanning trees, a lot of references have studied the stable traction control theory of complex networks ^{[34,35,36,37,38,39]}. The theory can be used for network topological features, such as strongly connected networks, undirected networks, scale-free networks and random networks, to realize global traction stable control under the stability framework. In addition, this brief considers a single system. If two drive response systems are considered, the finite-time stabilization problem can also be transformed into a variety of synchronization problems. Synchronization means that the state variables of these two systems are often consistent under control input. There have been many excellent works before, such as quasi-uniform synchronization ^[40,41], global synchronization for BAM delayed reaction-diffusion neural networks^[42].

Based on the above statements, this brief presents a pinning control scheme for FTS of delayed CMNNs with nonlinear coupling. The main contributions of this paper are summarized as follows:

1) This paper comprehensively considers a class of complex systems with time-delayed and nonlinear coupling. Considering the interaction of internal neurons, the coupling function of neuron nodes is found through topological graph theory.

2) The Lyapunov method of the indefinite derivative is used in this paper. We consider the non-autonomous system with variable coefficients which is state-dependent, the stability of the system is better discussed according to the real-time state of neurons.

3) By designing a suitable pinning controller and considering the FTS problem of CMNNs. Compared with the previous research results, this paper can ensure the stability faster and the settling time shorter by controlling only a small number of neurons.

This brief mainly studies the fixed-time stabilization problem of CMNNs system based on the idea of the indefinite derivative, through the design of an appropriate pinning controller to make the system achieve finite-time stabilization as soon as possible. In the next section, we give the model description and some preliminaries. In Section 3, it is our main part. The main challenge of this section is to use the finite-time stability theory different from the traditional theory to stabilize the system as soon as possible. In the last section, two numerical simulation examples are given.

2.   Model description and preliminaries

This part gives some basic definitions, lemmas and assumptions, which can be obtained from some basic references ^{[43,44,45,46,47,48,49]}.

This section we introduce a mathematical model of MNNs as follows:

another expression of the above system (2.1) is:

where $z(t) = (z_{1}(t), z_{2}(t), \ldots, z_{n}(t))^{T}$ denotes the potential of capacitor $c_{i}$, $d_{i} > 0$ expresses the self-inhibition of the $i$th neuron; $f(z(t))$ expresses the activation function with $f_{i}(0) = 0$ for every $i\in {\mathbb N}$; $a_{ij}(\cdot)$ and $b_{ij}(\cdot)$ are two measurable functions representing the weight of memristor, which can be shown as:

where ${\bf W}^{f}_{ij}$ indicate the memductances of memristors. ${\bf M}^{f}_{ij}$ stands for the memristors between the activation function $f_{i}(z_{i}(t))$ and $z_{i}(t)$, and ${\bf C}_{i}$ is the invariant capacitor when the memductances of memristors ${\bf W}^{f}_{ij}$ and ${\bf M}^{f}_{ij}$ respond to change in pinched hysteresis loops. Moreover,

According to the characteristics of memristor and the discussion in previous literature, we give the mathematical expression of the connection functions of memristor as follows:

where $h_{i}: {\mathbb R}\rightarrow {\mathbb R}$ are threshold level functions, $r_{i}\in {\mathbb R}$ are threshold level, and $\check{a}_{ij}$, $\check{b}_{ij}$, $\hat{a}_{ij}$, $\hat{b}_{ij}$ are constant numbers.

Through the idea of differential inclusion and Filippove theory, because $a_{ij}$ and $b_{ij}$ have discontinuous characteristics, we can get that $\frac{\mathrm{d}z_{i}(t)}{\mathrm{d}t}\in-d_{i}z_{i}(t)+\sum\limits^{n}_{j = 1}\overline{co} [a_{ij}(z_{j}(t))]f_{j}(z_{j}(t))+\sum\limits^{n}_{j = 1}\overline{co} [b_{ij}(z_{j}(t))]f_{j}(z_{j}(t-\tau))$, where

with $\underline{a}_{ij} = \min\{\check{a}_{ij}, \hat{a}_{ij}\}$, $\overline{a}_{ij} = \max\{\check{a}_{ij}, \hat{a}_{ij}\}$ and $\underline{b}_{ij} = \min\{\check{b}_{ij}, \hat{b}_{ij}\}$, $\overline{b}_{ij} = \max\{\check{b}_{ij}, \hat{b}_{ij}\}$.

Then for a.e. $t\geq0$ and $i = 1, 2, \ldots, n$, there exist $\widetilde{a}_{ij}(t)\in\overline{co}[a_{ij}(z_{i})]$ and $\widetilde{b}_{ij}(t)\in\overline{co}[b_{ij}(z_{i})]$ such that

and the initial value of the system is definition as $\psi(s) = (\psi_{1}(s), \psi_{2}(s), \ldots, \psi_{n}(s))^{T}\in C[(-\tau, 0), {\mathbb R}^{n}]$.

Our goal is to gain the FTS issue of the above system. Before that, we need to make the basic assumption of the activation function as follow:

(Hypothesis 1). For every $j\in {\mathbb N}$, the neuron activation $f_{j}$ are bounded and satisfy that

where $x\neq y$ and $h_{j}^{-}, h_{j}^{+}$ are constants.

Definition 2.1 (see ^[8]). The solution of system (2.1) is said to gain stabilized in a finite time, if there exists a settling time $T^{*}(z_{0}, t_{0})$ such that

Moreover, if the settling time $T^{*}(z_{0}, t_{0})$ is not depend on the initial values, the solution of system (2.1) is said to be fixed-time stabilized.

Definition 2.2 (see ^[8]). For the function $\psi: {\mathbb R}_{+}\rightarrow {\mathbb R}_{+}$, if it is continuous and strictly increasing with $\psi(0) = 0$, $\psi$ is called a $\mathcal{K}$-function and it can be expressed as $\psi\in\mathcal{K}$. Moreover, if $\lim_{s\rightarrow +\infty}\psi(s) = +\infty$ holds, the function $\psi$ is called a $\mathcal{K}_{\infty}$-function with $\psi\in\mathcal{K}_{\infty}$.

Lemma 2.3 (C-Regular see ^[48]). The function $V: {\mathbb R}^{n}\rightarrow {\mathbb R}^{n}$ is C-Regular if and only if $V(z)$ satisfies:

1) regularity in ${\mathbb R}^{n}$;

2) $V(z) > 0$ for $z\neq0$ and $V(0) = 0$;

3) $V(z)\rightarrow +\infty$ as $\|z\|\rightarrow +\infty$.

Lemma 2.4 (Chain Rule see ^[48]). $V(z)$ is C-regular and for $z(t)$ denotes absolute continuity function in $[t_{0}, +\infty)\rightarrow {\mathbb R}^{n}$, then $V(z(t))$ is differentiable for a.e. $t\geq t_{0}$, and $\frac{\mathrm{d}V(z(t))}{\mathrm{d}t} = \langle\mathcal{L}(t), \frac{\mathrm{d}z(t)}{\mathrm{d}t}\rangle$, where $\mathcal{L}(t)\in\partial V(z(t))$.

Lemma 2.5 (See ^[24]). For an undirected graph $\mathcal{G}(\mathcal{A})$, and the corresponding adjacency matrix and Laplace matrix are $C = [c_{ij}]$ and $L$ respectively, the following formula holds for arbitrary $z = (z_{1}, z_{2}, \ldots, z_{n})\in {\mathbb R}^{n}$:

Moreover, if there exists an undirected and connected nonnegative column vector ${\bf w}$, $L(\mathcal{A})+\mathrm{diag}({\bf w})$ is positive definite.

Lemma 2.6 (Jesen inequality ^[49]). If $a_{1}, a_{2}, \ldots, a_{n}$ are positive numbers and $0 < r < p$, then

and

3.   Main results

This section we introduce the FTS for $N$ identical discontinuous MNNs (2.1), when consider the internal relationship of neurons and adding the nonlinear coupling relationship to the system, one can rewrite the system (2.3) as

where $i = 1, 2, \cdots, N$, and $x_{i}(t) = (x_{i1}(t), x_{i2}(t), \cdots, x_{in}(t))^{T}\in {\mathbb R}^{n}$ is the state vector representing the state variables of node $i$ at time $t$. $f = f(x_{i}(t)): {\mathbb R}^{n}\rightarrow {\mathbb R}^{n}$ is a vector-value function standing for the activity of an individual subsystem. $\widetilde{A}$ and $\widetilde{B}$ express $[\widetilde{a}_{ij}]$ and $[\widetilde{b}_{ij}]$, respectively. $\phi$ is the nonlinear coupling function and $\phi_{s+1}(z) = |z|^{s}\mathrm{sign}(z)$. $0 < \alpha < 1$ and $\beta > 1$. Matrix $C = [c_{ij}]$ denotes the adjacency matrix of subsystems, which corresponding Laplacian matrix is represented as $L$, and all of them are applicable to undirected weighted networks. $u_{i}(t)$ is the controller.

In order to achieve the FTS and the convenience of engineering practice, it is generally impossible to control every neuron. Then we introduce the method of pinning control. In this paper, a random number $\delta(\frac{1}{N} < \delta < 1)$ is selected, and let $l = [\delta N]$, that is, the control is applied to these $l$ neurons. Without losing generality, we can select the first $l$ neurons (which are also regarded as a random choice) as the control objects. Then the controller $u_{i}(t)$ can be given as

where $Q(t)$ is a $K_{\infty}$-function $p$, $q$ are nonnegative coefficients.

For the sake of convenience, we denote $d^{\min} = \min\{d_{i}\}$ and $h^{\max} = \max\{h_{j}^{-}, h_{j}^{+}\}$ for every $i, j\in {\mathbb N}$. Then the main results in this paper are given by the following theorems.

Theorem 3.1. If the activation function $f$ of the system is assumed as the above Hypothesis. The coupled system (3.1) with novel controller (3.2) can be fixed-time stabilized if the following equal holds for every $i\in {\mathbb N}$ and $k, l = 1, 2, \ldots, n$:

(A) $d^{\min} > h^{\max}\cdot\max\limits_{k, l\in {\mathbb N}}\{\sup\limits_{t\in[t_{0}, +\infty)}|\widetilde{a}_{kl}(t)|\}+nh^{\max}\cdot\max\limits_{k, l\in {\mathbb N}}\{\sup\limits_{t\in[t_{0}, +\infty)}|\widetilde{b}_{kl}(t)|\}$.

Proof. Define the Lyapunov function $V(t, x)$ as follows:

Differentiating the derivative of $V(t, x)$ along the trajectories of (3.1)

From the above discussion of measurable functions $\widetilde{a}_{ij}(t)$, $\widetilde{b}_{ij}(t)$ and the Hypothesis 1, one can obtain that

According to the hypothesis (A) of this theorem and two inequalities (Eqs 3.4 and 3.5), we can reduce the Eq (3.3) to

According the first Jesen inequality of Lemma 2.6, let $p_{i} = p$ when $i = 1, \ldots, l$ and $p_{i} = 0$ when $i = l+1, \ldots, N$ and $q_{i} = q$ when $i = 1, \ldots, l$ and $q_{i} = 0$ when $i = l+1, \ldots, N$, one can reduce

and by the second Jesen inequality of Lemma 2.6, similarly one can have

Given two new matrices as $C_{1} = (c^{\frac{2}{1+\alpha}}_{ij})$ and $C_{2} = (c^{\frac{2}{1+\beta}}_{ij})$. $L_{C_{1}}$ and $L_{C_{2}}$ denote the Laplacian matrices of the Graph $\mathcal{G}(C_{1})$ and $\mathcal{G}(C_{2})$, respectively. Let $D_{p} = \mathrm{diag}\big(\underbrace{(2p)^{\frac{2}{1+\alpha}}, \ldots, (2p)^{\frac{2}{1+\alpha}}}_{l}, \underbrace{0, \ldots, 0}_{N-l}\big)$ and $D_{q} = \mathrm{diag}\big(\underbrace{(2q)^{\frac{2}{1+\alpha}}, \ldots, (2q)^{\frac{2}{1+\beta}}}_{l}, \underbrace{0, \ldots, 0}_{N-l}\big)$. Recalling the Lemma 2.5, (3.7) and (3.8), the Eq (3.6) can be rewritten as

where $\lambda_{1} = \lambda_{\min}(2L_{C_{1}}+D_{p})$ and $\lambda_{2} = \lambda_{\min}(2L_{C_{2}}+D_{q})$.

Let $\breve{p} = 2^{\frac{\alpha-1}{2}}\lambda^{\frac{1+\alpha}{2}}_{1}$ and $\breve{q} = 2^{\frac{\beta-1}{2}}N^{\frac{1-\beta}{2}}\lambda_{2}^{\frac{1+\beta}{2}}$, because $0 < \frac{1+\alpha}{2} < 1$ and $\frac{1+\beta}{2} > 1$, multiplying both sides of (3.9) by $V^{-\frac{1+\alpha}{2}}(t, x)$, one can have

let $W(t, x) = V^{\frac{1-\alpha}{2}}(t, x)$, then we can expand the inequality (Eq 3.10) as

multiplying both sides of (3.11) by $e^{-\int^{t}_{t^{*}}Q(\varsigma)\mathrm{d}\varsigma}$, for a.e. $t\geq t^{*}$ we get

Integrate both sides of (3.14) from $t^{*}$ to $t$ and according to the definition of $K_{\infty}$-function, which implies $\int^{t}_{t_{0}}Q(s)\mathrm{d}s\leq -\lambda(t-t_{0})+M$, then one can get

which implies

Moreover, from (3.9) it's easily to see that $\frac{\mathrm{d}V(t, x)}{\mathrm{d}t}\leq Q(t)V(t, x)$, which yields for $t^{*} > t_{0}$

Combined with (3.14) and (3.15), it is easy to see $V(t, x(t))\equiv0$ if the following inequality holds:

which yield

where $t^{*}$ is a priori condition to make inequality (Eq 3.15) true, it is not difficult to find that when $t_{0}$ and $x_{0}$ are determined, one can find the corresponding $t^{*}$, then according to (3.14)–(3.17) and the fact $e^{\int^{t}_{t^{*}}Q(\varsigma)\mathrm{d}\varsigma} > 0$, when $t\geq T^{*}(t_{0}, x_{0}) = t^{*}+\frac{1}{\lambda}\ln\Big(1+\frac{2\lambda e^{M}\Upsilon}{(1-\alpha)\breve{p}}\Big)$, one can obtain $V(t, x(t))\equiv0$. Then the FTS can be finally realized and the settling time can be estimated by $T^{*}(t_{0}, x_{0})$.

Remark 3.2. Many previous literatures ^{[21,22,23,24]} have used Polyakov's classical finite/fixed-time theorem. In this paper, a term $Q(t)$ is added to the controller $u_{i}$, and the method of indefinite $V$-function derivative is used to further popularize Polyakov's finite/fixed-time theorem. We can see that fewer conditions are required in our model and the stable settling time is faster. Our results generalize the previous conclusion.

The corresponding adaptive controller of (3.2)can be designed as

where $\Delta_{i} = \mathrm{diag}(\zeta_{i1}, \zeta_{i2}, \ldots, \zeta_{in})$, $\Pi_{i} = \mathrm{diag}(\pi_{i1}, \pi_{i2}, \ldots, \pi_{in})$, and for $k = 1, 2, \ldots, n$ the controller rules of $\zeta_{ik}$, $\pi_{ik}$ satisfy:

where $p_{ik}$, $q_{ik}$ are adaptive coefficients need to be determined.

Theorem 3.3. If the condition (A) of Theorem 3.1 holds and the activation function $f$ of the system is assumed as the above Hypothesis. The coupled system (3.1) can be fixed-time stabilized by adding the adaptive controller (3.18) and choosing the suitable adaptive coefficients.

Proof. We construct the following Lyapunov function:

Taking the derivative of $V(t, x)$ along the trajectories of (3.2)

Through the hypothesis (A) of Theorem 3.1 and recalling the previous discussion (3.4) and (3.5), one can have

Then we return to the evolution in Eq (3.6) in Theorem 3.1, and we can see that the FTS of the coupled system can be achieved by adding the pinning adaptive controller. Moreover, the settling time $T(x_{0}, t_{0})$ can be estimated by (3.17), the corresponding parameters of (3.17) in this theorem can be adjusted adaptively with the coefficients of the controller (3.18).

Remark 3.4. In fact, in this paper, it is a classical fixed stability problem when $Q(t)$ is equal to 0. This paper breaks the conventional restrictions and uses inequality skill to deduce derivative term of indefinite function. Compared with the previous articles^[26,27], the FTS problem is obtained from the two aspects of pinning state controller and pinning adaptive controller. In particular, the coefficient of adaptive adjustment is added to make the parameters more flexible to adapt to the system.

Remark 3.5. In this paper, a novel coupling parameter is introduced to study the fixed time problem, which combines the parameters $\alpha$, $\beta$ in the controller. Based on Lemma 2.5, the FTS problem can be simplified by converting fewer conditional requirements. In addition, if $\breve{q} = 0$ in (3.9), we can find that it is the global asymptotic stability or finite-time criteria problem of complex network systems in ^{[9,10,18,19,20]}. This method of the indefinite derivative is also applicable. This means that our results can generalize the previous conclusion.

Remark 3.6. In this brief, the finite-time stabilization of the CDMMs is studied mainly by choosing the suitable pinning controller. Compared with other methods, this brief has a wider scope of application and more advantages: 1) The controller only randomly controls a part of nodes. 2) In the proof, the derivative of $V$ function is not necessarily strictly negative. It has an indefinite term, and the calculation is more complex. Meanwhile, this article also has some shortcomings. If we want to achieve finite/fixed-time stabilization, although the convergence speed is faster, it will consume more components, that is, the cost will be higher. Moreover, compared with the traditional Polyakov finite-time theorem ^[21] used by the $V$ function, when the derivative of the $V$ function has an indefinite term, the calculation is more complex, and it is more difficult to achieve a fixed-time stabilization.

4.   Examples and simulation experiment

In this section, we introduce two examples and simulations to prove our results' effectiveness. The dimension of the system (3.1) in the example is three-dimensional, and its model and parameters are defined as follows:

where $d_{1} = d_{2} = d_{3} = 9$; $f(\cdot) = \begin{pmatrix} \tanh(\cdot) \\ \tanh(\cdot) \\ \tanh(\cdot) \end{pmatrix}$. Moreover, $A$ and $B$ are expressed as follows:

$A = \begin{pmatrix} a_{11} & 0.3 & 0.5 \\ 0.2 & a_{22} & 0.3 \\ 0.1 & 0.5 & a_{33} \end{pmatrix}$; $B = \begin{pmatrix} b_{11} & 0.1 & 0.8 \\ -0.1 & b_{22} & 0.8 \\ 0.2 & 1 & b_{33} \end{pmatrix}$;

where

Example 4.1. Consider the model (4.1) i.e., it is easy to check that the neuron function satisfies the Hypothesis 1 with $h^{\max} = 1$. Moreover, let $N = 6$, we randomly select a relationship between different neurons of coupling network, and its topology rule and the corresponding adjacency matrix $C$ can be shown as follows:

and the corresponding Laplace is $L$, one can see that $\lambda_{\min}(L) = 0$. Then we choose the control rule by $u_{i}(t) = Q(t)\mathrm{SIGN}(x_{i}(t))|x_{i}(t)|-p_{i}\mathrm{SIGN}(x_{i}(t))|x_{i}(t)|^{\alpha}-q_{i}\mathrm{SIGN}(x_{i}(t))|x_{i}(t)|^{\beta}$ with $Q(t) = \frac{1}{1+t^{2}}$, $p_{i} = q_{i} = 1$ for $i = 1, 2$, and $\alpha = 0.5$, $\beta = 2$, one can check that:

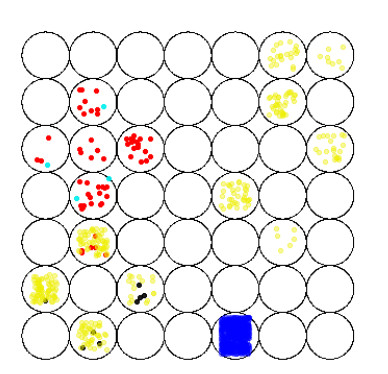
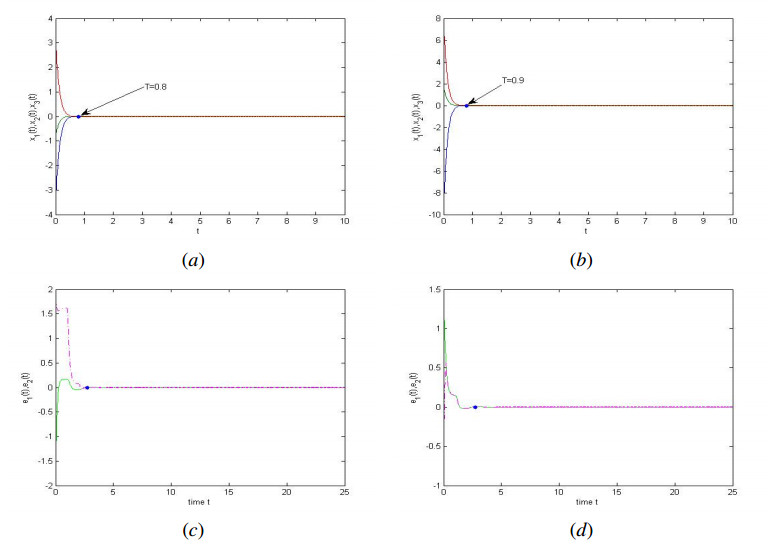
then Hypothesis (A) holds. By using Theorem 3.1, the coupled system (4.1) can be fixed-time stabilized by randomly choosing 3 groups of initial values 2.5, -0.5 and -3. The simulation results are described by Figure 1(a). Moreover, the settling time can be estimated as $T^{*}(t_{0}, x^{0}) = 0.8$.

Example 4.2. Recalling (4.1) again, let $N = 4$, and the topological connection of the coupling neurons network and the corresponding configuration matrix are illustrated by the following structure:

which easily have $\lambda_{\min}(L) = 0$.

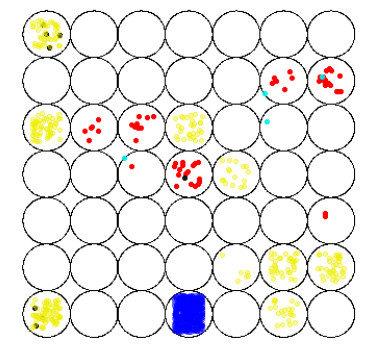
Then we choose the control rule $u_{i}(t)$ in (3.18) and only control the first three nodes. The same as Example 4.1, we can see that the Hypothesis $({\bf A})$ is true. By using Theorem 3.3, the coupled system (4.1) can be fixed-time stabilized by randomly choosing 3 groups of initial values 0.8, 6.2 and -8. The simulation results are described by Figure 1(b), the settling time can be estimated as $T^{*}(t_{0}, x^{0}) = 0.9$.

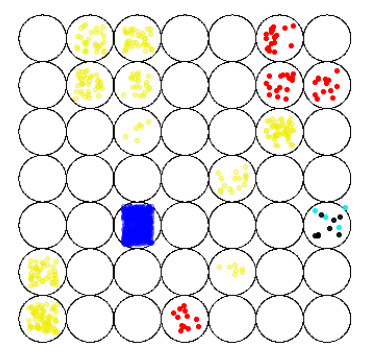
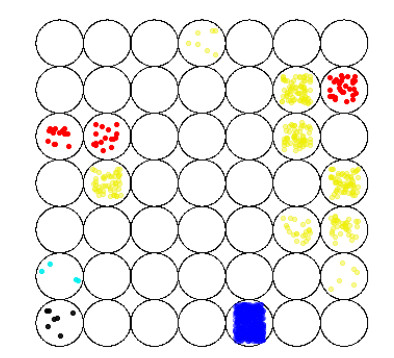
Remark 4.3. Through the above two examples, we can find that the number of control nodes in the example is randomly selected, and the initial value is also arbitrary. According to the simulation image, it can be seen that the stability of the system can be achieved quickly, and the stability of the system has nothing to do with the selection of the initial value and the number of nodes. This fully demonstrates the advanced nature and effectiveness of our results. We can see from Figure 1(c) and Figure 1(d) that when the controller is cancelled, the system settling time $T_{0}$ is obviously longer than that with the controller.

5.   Conclusions

This paper introduces the FTS problem of CMNNs system. The main method is to establish a novel state-dependent pinning controller and the corresponding adaptive pinning controller in the form of vector based on Lyapunov functional and undirected topological graph theory. In addition, we use the method of the indefinite derivative to solve the FTS issue of CMNNs with nonlinear coupling, which is independent of the initial value. The limit that the conventional $V$-function must be negative definite is broken. Finally, through experimental analysis and numerical simulation, it is verified that the experimental and theoretical methods in this brief are effective. Moreover, the control method and the calculation technology of the indefinite derivative established in this brief are relatively novel and can be extended to many fields, such as recurrent neural networks ^[4,5], statistical language modeling ^[6], stochastic memristive chaotic systems ^{[10,35,36,37]}, muti-agent systems ^[14], fuzzy neural networks ^[38], chaotic systems ^[39] and so on.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (11801042, 12171056 and 11671011), Training Program for Excellent Young Innovators of Changsha (kq20106072) and Scientific Research Foundation of Hunan Provincial Education Department (21B0771).

Conflict of interest

The authors declare there is no conflicts of interest.

Data availability statements

Data sharing allows researchers to verify the results of the article, replicate the analysis, and conduct secondary analyses. The data used to support the findings of this study are available from the corresponding author upon request.