Mean square synchronization for stochastic delayed neural networks via pinning impulsive control

1.   Introduction

During the last several decades, neural networks have attracted much attention from mathematics, medicine, biology, computer science, and many others. It is all about the broad applications in various fields, including pattern recognition, signal processing, industrial automation and classification, combinatorial optimization ^[1,2,3,4,5]. Synchronization of neural networks is a typical and significant collective behavior, which has been exploited widely in real-world applications, such as secure communications ^[6,7,8]; UAV formation control ^[9,10]; image encryption and protection ^[11,12]. To be specific, synchronization in the brain means a group of neurons reach the same state through interaction. Nevertheless, the neural network can not synchronize with some desired trajectory, relying only on self-coupling. For achieving the coordination of neurons, the control strategy plays a vital role.

As an innovation of the integrating single control method, PIC was primitively raised in ^[13]. Before that, pinning state-feedback control strategy and impulsive control strategy are used in the synchronization problem of networks respectively ^[14,15,16]. Moreover, Lu et al. ^[13] also put forward a criterion for determining which fraction of nodes in the whole network should be controlled. As we can see, this criterion has been extensively utilized in many articles (see ^[17,18,19] for references), including this paper. Owing to its efficiency and convenience, PIC has drawn many scholars' attention. Initially, the authors applied PIC to solve stabilization problem of nonlinear dynamical networks ^[13]. More recently, PIC was also applied effectively to the synchronization problem of discrete-time dynamical networks in ^[20]. Afterwards, researchers found that PIC can be used to synchronize the networks mentioned above, and has the same effect on the neural networks. In ^[21], an impulsive pinning controller has been developed to realize the synchronization of reaction-diffusion neural networks. In terms of control strategy, nowadays there exist many different ways, such as adaptive feedback control, distributed control, sliding mode control, and so on. However, to the best of our knowledge, PIC characterize by inheriting the merits of pinning control and impulsive control. Compared to adaptive feedback control, PIC is a discontinuous control strategy, which means there is no need to control the system constantly. We just need to exert influence at some instants, so, by comparison, PIC is more economic. For distributed control, it can be challenging to apply it for impulsive system. So compared with distributed control, we apply PIC as our control strategy which has the superiority of reducing the adverse effects of impulse. Although sliding mode control has the advantages like ignoring external disturbances, but it'll inevitably bring tremor behavior and how to reduce this behavior can be challenging. Compared to sliding mode control, PIC is more suitable for synchronous analysis of systems with stochastic disturbance, because we can select impulse instants artificially when using PIC. Through the analysis above, PIC is undoubtedly a powerful technique for synchronizing the networks.

It is noteworthy that in a real-life scenario, the transmission of control tasks is not always timely and the controller cannot be updated in time. As a result, this leads to so-called delayed impulses, the interval between sending and execution of the control task. Delayed impulses are sometimes regarded as a preferable way to describe numerous practical problems. For instance, due to the limited speed of signal sampling in impulsive transients in communication systems based on impulsive synchronization, a delay called sampling delay that depends on the previous states at the sample locations will occur in impulsive transients ^[22]. Regrettably, some existing results did not take delayed impulses into account in using PIC^[13,20,21]. Nowadays, the finite speeds of transmission and traffic congestion have become an indisputable fact. Thus, more and more researchers are devoted to studying delayed impulses. In ^[23], a constant delay $h$ $(h > 0)$ is utilized to describe time delays in impulse terms which mean delayed impulses are assumed to be fixed. In addition, $\tau_{ij}(k)$ is used to describe time-varying communication delay at time $t_{k}$, where the delayed impulses are assumed with a strict upper bound ^[24]. In fact, the assumptions mentioned above about delayed impulses may result in conservativeness of corresponding results. Therefore, from a more holistic perspective, a better mechanism for describing delayed impulses is required in this paper.

From the perspective of the system under consideration, the chaotic neural network and the corresponding response system realize synchronization via impulsive control in ^[25]. Unfortunately, we can observe that the neural network model in ^[25] did not contain internal delay and stochastic disturbance on the network structure. With the unremitting efforts of researchers, the research on neural networks has developed to concerning the synchronization issues of fractional-order neural networks ^[40,41]. However, because of the interference of the external environment, it is challenging to maintain a fixed state. On the one hand, the time delays in impulses mentioned above, and internal delay occurring inside the dynamical nodes ubiquitously exist in neural networks ^[26]. The internal time delay is usually described by a continuous function $\tau(t)$ (see ^[17,21,27] for references), and it usually is assumed to be bounded. On the other hand, more than internal time delay, the signal transmission is unavoidably influenced by noises owing to random fluctuations from subtle changes of surrounding environment that lead to stochastic disturbance. This indicated that take noises into account is necessary and meaningful. Many solutions to the synchronization and stability challenges for neural networks with stochastic disturbances have been found so far. For example, Lu et al. ^[28] examined the synchronization of stochastic dynamical networks with noises using pinning impulsive strategy. Since the perturbations induced by stochastic processes are all one-dimensional, the same noise effects the signal broadcast by nodes ^[30].

Inspired by the preceding considerations, the purpose of this paper is to handle the issue of mean square synchronization for a class of general stochastic neural networks with both internal and impulsive delay by utilizing a pinning impulsive control strategy. The main novelties of the study are as follows:

$1)$ Considering the influence of time-varying delay and external interference on the neural network, we take a type of stochastic delayed neural networks. Compared to the neural networks proposed in ^[25], the stochastic delayed neural network model considered here is more practical. At the same time, the difficulties and challenges of the theoretical analysis are also added, so it can meet a broader range of applications and a topic worth investigating.

$2)$ The PIC strategy utilized here, in fact, is the combination of pinning feedback control and impulsive control, which is different from the majority of literature that used PIC. In other words, the controller is excited at the impulsive instants and executed between any two consecutive impulse moments, which means that the convergence rate of the system is accelerated under the proposed controller. Compared with the control method in ^[4] and ^[33], the design of this controller inherits the merits of the two control mechanisms.

$3)$ AID is introduced to design the controller as a novel concept to deal with delayed impulses. Compared with ^[23] and ^[24], we relax the upper constraint on impulsive control input delays. Equally, certain adjustable synchronization requirements for stochastic delayed neural networks are derived. By means of the Lyapunov stability theory, several sufficient criteria are given to guarantee the mean square synchronization of the stochastic delayed neural networks.

This paper is organized as follows. Section 2 presents the stochastic delayed neural networks. Moreover, some lemmas and definitions are presented. Section 3 compares the impulsive synchronization criteria between two conditions (with and without impulsive delay). Two numerical examples are given in Section 4. And finally, in Section 5, we restate the paper's context and draw the conclusions.

Notations: $\mathbb{R}$ represents the set of real numbers. Let $||\cdot||$ denotes the Euclidean norm. $A^{s} = (A+A^{T})/2$ represents the symmetric part of matrix $A$. $\otimes$ indicates Kronecker product in the usual sense. For a symmetric matrix $P$, $P > 0$ $(P < 0)$ means that the matrix $P$ is positive definite (negative definite).

The notations $P^{T}$ and $P^{-1}$ represent for the transpose and the inverse of $P$, respectively. $\# \mathcal{O}$ denotes the number of members in a finite set $\mathcal{O}$. The Dini derivative of $\phi(t)$ is defined as $D^{+}\phi(t) = \limsup_{s\rightarrow 0^{+}}\frac{\phi(t+s)-\phi(t)}{s}$. $(\Omega, \mathcal{F}, P)$ is the standard probability space. $\mathbb{E}(\cdot)$ denotes the expectation operator with respect to some probability measure $P$.

2.   Preliminaries

2.1.   Modle description

Consider the following stochastic delayed neural network:

where $x_{i}(t) = (x_{i1}(t), x_{i2}(t), \dots, x_{in}(t))^{T} \in \mathbb{R}^{n}$ denotes the state of the $i$-th neural network; $C = diag\lbrace c_{1}, c_{2}, \dots, c_{n}\rbrace > 0$ denotes the rate with which the $i$-th cell resets its potential to the resting state when being isolated from other cells and inputs; $f : \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is an activation function; $A = (a_{i j})_{n \times n},$ $B = (b_{i j})_{n \times n} \in \mathbb{R}^{n \times n}$ are the connection weight matrices. $L = (l_{ij})_{N \times N}$ is the Laplacian coupling matrix representing the coupling topology of the dynamic network. The elements $l_{ij}$ of the matrix $L$ are defined as follows : if there is a connection between nodes $i$ and $j\ (i\neq j)$, $l_{ij} = l_{ji} > 0$; otherwise $l_{ij} = l_{ji} = 0\ (i\neq j)$, and the diffusivity coupling condition $l_{ii} = - \sum_{j = 1, j\neq i}^{N}l_{ij}$ is satisfied for the diagonal elements $l_{ii} (i = 1, 2, \dots, N)$. $\tau(t)$ is transmittal time-varying delay satisfying $0 < \tau(t) < \tau$ and $0 < \dot{\tau}(t) \le \bar{\tau} < 1$ with positive constants $\tau$ and $\bar{\tau}$; $u_{i}(t)$ represents the control input. $g(t, x(t), x(t-\tau(t))) = g(t, x_{1}(t), \dots, x_{n}(t), x_{1}(t-\tau(t)), \dots, x_{n}(t-\tau(t)))\in \mathbb{R}^{n\times n}$ is the noise intensity matrix in signal transmission and learning process; $\omega(t) = (\omega_{1}(t), \omega_{2}(t), \dots, \omega_{n}(t))^{T} \in \mathbb{R}^{n}$ is a $n$-dimensional Brownian motion on complete probability space $(\Omega, \mathcal{F}, P)$, satisfying

The initial values of the system (2.1) are given by $x_{i}(s) = \phi_{i}(s) \in \mathcal{C}(\lbrack-\tau, 0 \rbrack, \mathbb{R}^{n}), i = 1, 2, \dots, N$, where $\mathcal{C}(\lbrack-\tau, 0 \rbrack, \mathbb{R}^{n})$ denotes the set of all $n-$dimensional continuous functions defined on the interval $\lbrack-\tau, 0\rbrack$.

Let $s(t)$ be a desired leader of network (2.1) satisfying

The initial condition is $s(t) = \phi(t)$ where $\phi(t)\in \mathcal{C}(\lbrack-\tau, 0 \rbrack, \mathbb{R}^{n})$.

Remark 1. The neural network considered in this paper including time-varying delay and external stochastic disturbance, so compared to the neural networks proposed in ^[25], the model considered here is more practical. Jiang et al.^[25] investigate the chaos synchronization problem of chaotic neural network via impulsive control. Although the neural network we study are different, we all use impulsive control because it only needs discrete control input so can achieve the reduction of communication pressure and control cost.

Define $e_{i}(t) = x_{i}(t) - s(t)$ be the error signal of node $i$ between the current state $x_{i}(t)$ and the reference state $s(t)$. The impulsive controller can be constructed as follows by applying impulsive effects on a subset of systems nodes (2.1):

where $| d_{k} | < 1$ are constants which means impulsive effects, $\rho > 0$ represents control strength and denote $\Pi = diag\lbrace\rho, \dots, \rho, 0, \dots, 0\rbrace\in \mathbb{R}^{n\times n}$. The impulse instants $\lbrace t_{1}, t_{2}, t_{3}, \dots \rbrace$ satisfy $\lim_{k \rightarrow +\infty} t_{k} = +\infty$. The index set of $l$ nodes belongs to $\mathcal{O}(t)$ which should be impulsively controlled is determined as follows: At time $t$, the expectation of $||e_{1}\left(t\right)||, ||e_{2}\left(t\right)||, \dots, ||e_{N}\left(t\right)||$ can reorder such that

Then, the index set of $l$ controlled nodes $\mathcal{O}(t)$ is defined as $\mathcal{O}(t) = \lbrace j_{1}, j_{2}, \dotsc, j_{l} \rbrace$.

Remark 2. As for the criterion on determining which fraction of nodes in the whole network should be controlled, subtle distinctions can be drawn between the criterion in ^[13] and this article. In practice, this is because the neural network studied in this paper considers external interference so we need to select the nodes with larger expectation rather than norm, while the network in ^[13] doesn't. In ^[34], the authors also utilize the criterion with expectation to arrange the node errors, which explains that as the complexity of the system under consideration increases, the research methods need to be improved accordingly.

Under the impulsive controller (2.3), the error system can be described by

where $\rho (i) = \Big \lbrace\begin{array}{l} \rho, i \in \mathcal{O}(t_{k}) \\ 0, i \notin \mathcal{O}(t_{k}) \end{array}$ and $\tilde{f}(e_{i}(t))$ = $f(x_{i}(t)) - f(s(t))$, $\tilde{g}(t, e(t), e(t-\tau(t)))$ = $g(t, x(t), x(t-\tau(t)))- g(t, s(t), s(t-\tau(t)))$, $e_{i}(t_{k}^{+})$ = $\lim\limits_{h \rightarrow 0^{+}} e_{i}(t_{k}+h)$.

In the next section, we will propose the conditions for realizing the mean square synchronization of the network (2.1) and (2.2).

2.2.   Definitions and assumptions

In this part, some useful definitions and lemmas are presented as a preparation for later theoretical analysis.

Definition 1. (^[35]) The stochastic delayed neural networks (2.1) and (2.2) are said to reach mean square synchronization if the following equations holds:

Definition 2. (Average Impulsive Interval ^[13]) The Average Impulsive Interval $T_{a}$ of the impulsive sequence $\{ t_{k} \}_{k\in \mathbb{N}^{\ast}}$ is defined as follows:

where $N\left(t, t_{0}\right)$ stands for the number of impulse times of $\lbrace t_{k} \rbrace_{k\in \mathbb{N}^{\ast} }$ on the interval $[t_{0}, t)$.

Definition 3. (Average Impulsive Delay ^[25]) The Average Impulsive Delay (AID) of impulsive delay sequence $\lbrace \tau_{k} \rbrace_{k\in \mathbb{N}^{\ast}}$ is defined as follows:

where $N\left(t, t_{0}\right)$ has the same meaning as Definition 2 and we suppose that $\tau_{k} < t_{k} - t_{k-1}, \forall k\in \mathbb{N}^{\ast}$.

Lemma 1. For all $x, y \in \mathbb{R}^{n}$ and scalar $\epsilon > 0$, we have

Lemma 2. (Fubini's Theorem ^[38]) Let $\mu$ be a probability measure on $A$, and $\nu$ be a probability measure on $B$, and let $\mu \times \nu$ be product measure on $A \times B$. If $f: A \times B \rightarrow R$ is measurable with respect to $\mu \times \nu$, then

The following assumptions also be used throughout this paper in constructing synchronization conditions.

Assumption 1. (^[39]) For $\tilde{g}(t, e(t), e(t-\tau(t)))$ $\triangleq$ $g(t, x(t), x(t-\tau(t)))- g(t, s(t), s(t-\tau(t)))\in \mathbb{R}^{n\times n}$, there exist appropriate dimensional positive definite constant matrices $\Lambda_{1}, \Lambda_{2}$ such that

Assumption 2. Let $f(\cdot): \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ be a continuous vector-valued function and satisfy the following condition for all $x, y \in \mathbb{R}^{n}$

where $\kappa > 0$ is a constant also called Lipschitz constant.

3.   Main results

In order to make the mechanism of impulsive delay clear, the following theorems are discussed for two cases, respectively. (ⅰ) The case that doesn't take impulsive delay into account. (ⅱ) The case that take impulsive delay into account. It can be seen in the following proof that impulsive delay sometimes effectively effects for the synchronization of the system. Then, sufficient criteria are established to guarantee the mean square synchronization of the stochastic delayed neural networks.

3.1.   The case of mean square synchronization without impulsive delay

Theorem 1. Assume that Assumptions 1 and 2 hold, if there exist a positive definite matrix $P$, and constants $\delta_{1}$, $\delta_{2} > 0$, $\epsilon_{1}, \epsilon_{2} > 0$ such that the following conditions hold:

(i)

(ii)

then the stochastic delayed neural networks (2.1) and (2.2) can reach mean square synchronization, where $\gamma > 0$ is the smallest root of the equation

Proof: Construct a Lyapunov function as shown below

For $t \in (t_{k}, t_{k+1} \rbrack, k\in \mathbb{N}$ according to Lemma 2, we have

Based on Lemma 1 and Assumption 2

and

From Assumption 1, we can obtain

Substituting (3.3)–(3.5) into (3.2) we have

where $E(t) = \left(e_{1}^{T}(t), e_{2}^{T}(t), \cdots, e_{N}^{T}(t)\right)^{T}$.

Let

where $\gamma$ is the smallest root of Eq (3.1). For convenience, we denote $\widetilde{V}(t)$ = $\mathbb{E}V(t)$. Then by inequality (Eq 3.6), one gets

The generalized It$\hat{o}$'s formula gives

for any $t \in (t_{k}, t_{k+1}]$. Hence we have

By changing variables $s - \tau(s) = u$, we can deduce that

Substituting Eq (3.8) into Eq (3.7), we obtain

Then using Gronwall inequality, we get

where $\delta = \gamma -\delta_{1} +\frac{\delta_{2}e^{\gamma \tau}}{1-\bar{\tau}}$. On the other hand, when $t = t_{k}$, one can conclude

According to the rule of nodes belongs to $\mathcal{O}(t_{k})$, we have

then it yields that

Furthermore, the mathematical induction is utilized to prove the following inequality holds for all $t \in (t_{m-1}, t_{m}]$ and all $m \in \mathbb{N}^{\ast}$.

where $\widetilde{V}_{0} = \widetilde{V}\left(e\left(t_{0}\right)\right)$. For convenience, we define $\tau_{0} \triangleq 0$. Then according to (3.9) we infer :

in which $\bar{d}_{0} \triangleq 1$. Thus, (3.10) holds for $m = 1$. Now, we'll assume that (3.10) also applies to $m = l$ ($l \ge$ 1).

To be precise

We shall demonstrate that (3.10) holds for $m = l+1$. When $t \in\left(t_{l}, t_{l+1}\right]$, we have

i.e., (3.10) holds for $m = l + 1$. Till now, we conclude that (3.10) holds for all $m \in \mathbb{N}^{\ast}$. Then we infer that

for all $t \ge t_{0}$. By using condition (ⅱ) and the definition of $T_{a}$ one can obtain that

Therefore, $\mathbb{E}\left[\sum_{i = 1}^{N}\left\|e_{i}(t)\right\|^{2}\right] \rightarrow 0$ as $t \rightarrow \infty$.

Remark 3. It can be seen from the proof process of Theorem 1 that PIC is an effective method to make stochastic delayed neural network to achieve synchronization. Compared to ^[29], although the system we considered is similar, but Wong et al. ^[29] adopted the average impulsive interval approach and the comparison principle to make the system realize synchronization. So in comparison, PIC makes the control more convenient to implement since only a small fraction of nodes is directly controlled at each impulsive instant.

3.2.   The case of mean square synchronization with impulsive delay

The investigation of impulse time delays begins with the premise that it is a constant or has a rigid upper constraint. (see ^{[19,20,23,24]}). However, it should be mentioned that in some practical systems, the delays may be variable. As a result, we take impulsive delay into account in this section to make out how it works to synchronization. First of all, the controller with impulsive delay is designed as :

Remark 4. As shown in (2.3) and (3.15), the controller in (2.3) only use the information of the node belongs to $\mathcal{O}(t_{k})$ at $t_{k}$, meanwhile (3.15) uses the information at $t_{k}-\tau_{k}$. The different effect of the two controllers will be compared in numerical simulations.

Remark 5. According to the screening property of Dirac function $\delta(\cdot)$, we notice that $e_{i}(t)$ in controller (2.3) and $e_{i}[(t-\tau_{k})^{-}]$ in controller (3.15) should be modified to $e_{i}(t_{k})$ and $e_{i}[(t_{k}-\tau_{k})^{-}]$, separately. Due to $g(x(t))$ is discontinuous at $t_{k}$, so according to the screening property of Dirac function $\delta(\cdot)$, $\int_{t_{k}-\varepsilon}^{t_k+\varepsilon} g(x(t)) \delta(t-t_{k}) dt = g\left(x\left(t_{k}\right)\right)$ doesn't hold. We need to replace $g(x(t))$ to $g(x(t_{k}))$ to make Dirac function's property correctly. That is, $\int_{t_{k}-\varepsilon}^{t_{k}+\varepsilon} g\left(x\left(t_{k}\right)\right) \delta\left(t-t_{k}\right) d t = g\left(x\left(t_{k}\right)\right)$.

Under controller (3.15), the error system is described by

then we obtain the theorem below.

Theorem 2. Assume that Assumptions 1 and 2 hold, if there exist a positive definite matrix $P$, and constants $\delta_{1}$, $\delta_{2} > 0$, $\epsilon_{1}, \epsilon_{2} > 0$ such that the following conditions hold:

(i)

(ii)

where $\hat d_{t} = \max \limits_{0 \le k \le N(t, t_{0})} \lbrace \hat{d_{k}} \rbrace$ and the other parameters are the same as the ones in Theorem 1. Then the mean square synchronization can be achieved with controller (3.15).

Proof: Construct a Lyapunov function as it's in Theorem 3.1. Then we will find that the estimation of $\mathcal{L} \widetilde{V}(t)$ is same to Theorem 1, so just focus on $\widetilde{V}\left(t_{k}^{+}\right)$ is enough. When $t = t_{k}$, we reach the conclusion that

where $\varphi(t_{k}) = \min \{\mathbb{E}||e_{i}(t_{k})||: i \in \mathcal{O}(t_{k})\}$ and $\psi\left(t_{k}\right) = \max \left\{\mathbb{E}\left\|e_{i}\left(t_{k}\right)\right\|: i \notin \mathcal{O}\left(t_{k}\right)\right\}.$ The next discussions will be derived from (3.17).

Furthermore, the mathematical induction is also utilized to prove the following inequality holds for all $t \in (t_{m-1}, t_{m}]$ and all $m \in \mathbb{N}^{\ast}$.

where $\widetilde{V}_{0} = \widetilde{V}\left(e\left(t_{0}\right)\right)$. Also define $\tau_{0} \triangleq 0$, it follows from (3.17) that

Thus, we infer that (3.18) holds for $m = 1$. Now, we'll assume that (3.18) also applies to $m = l$ ($l \ge$ 1).

To be precise,

We shall demonstrate that (3.18) holds for $m = l+1$.

Based on the assumptions that $\tau_{k} < t_{k} - t_{k-1}$ for all $k\in \mathbb{N^{\ast}}$, which infers that $t_{l} - \tau_{l} \in (t_{l-1}, t_{l}]$, then we get

According to $\widetilde{V}(t) \leq \widetilde{V}\left(t_{l}^{+}\right) e^{\delta\left(t-t_{l}+\tau+\gamma(t_{l}-t)\right)}$, then for all $t \in\left(t_{l}, t_{l+1}\right]$ we have

i.e., (3.18) holds for $m = l + 1$. As a result, by mathematical induction, it is possible to verify that (3.18) holds for each $m \in \mathbb{N}^{\ast}$. We can then conclude that

for all $t \ge t_{0}$. By using condition (ⅱ) and the definitions of $T_{a}$ and $\tau^{\ast}$ it's possible to obtain that

Therefore, $\mathbb{E}\left[\sum_{i = 1}^{N}\left\|e_{i}(t)\right\|^{2}\right] \rightarrow 0$ as $t \rightarrow 0$.

Remark 6. Controller (3.15) is the result that take impulsive control input delays into account. Yi et al. investigated hybrid time-varying delays including transmittal delay, discrete delay, distributed delay in ^[16], but hardly concerned about impulsive control input delays. Compared to ^[16], the situation considered here is more realistic. Due to the introduction of impulsive control input delays, we complete the proof of three criteria with the help of AID method.

Notice that condition (ⅰ) in Theorem 2 means that $|d_{k}| < \sqrt{\frac{1}{1+\frac{N-l}{l}\frac{\lambda_\ {\max}\ \ (P)}{\lambda_\ {\min}\ \ (P)}}}\ \ \ $. In fact, if there satisfied special conditions for certain $k, k\in { 1, 2, \dots, N }$ at $t_{k}-\tau_{k}$, then the restrictions on $d_{k}$ can be further relaxed to $|d_{k}| < \sqrt{\frac{1}{1+\frac{N-l}{l}(\frac{\lambda_\ {\max}\ \ (P)}{\lambda_\ {\min}\ \ (P)}\ \ -\frac{\lambda_\ {\min}\ \ (P)}{\lambda_\ {\max}\ \ (P)}\ \ \ \ )}}$. The following theorem can be obtained by further estimating $\widetilde{V}(t_{k}^{+})$.

Theorem 3. Assume that Assumptions 1 and 2 hold, if there exist a positive definite matrix $P$, and constants $\delta_{1}$, $\delta_{2} > 0$, $\epsilon_{1}, \epsilon_{2} > 0$ such that the following conditions hold:

(i)

(ii)

where $\hat{\varphi}(t_{k}) = \max \{\mathbb{E}||e_{i}(t_{k})||: i \in \mathcal{O}(t_{k})\}$, $\hat{\psi}(t_{k}) = \min \{\mathbb{E}||e_{i}(t_{k})||: i \notin \mathcal{O}(t_{k})\}$, $\hat d_{t} = \max \limits_{0 \le k \le N(t, t_{0})} \lbrace \hat{d_{k}} \rbrace$ and the other parameters are the same as the ones in Theorem 1. Then the mean square synchronization can be achieves with controller (3.15).

Proof: We can deduce from Theorem 2. that

Focus on the second term, when $\hat{\varphi}\left(t_{k}-\tau_{k}\right) \le \hat{\psi}\left(t_{k}-\tau_{k}\right)$

The following proof is the same as Theorem 2.

Remark 7. Theorem 3 indicates that when $\hat{\psi} (t_{k}-\tau_{k}) < \hat{\varphi}(t_{k}-\tau_{k})$, the range of values for $d_{k}$ is larger than it in Theorem 2. Obviously, there exist $\hat{\psi}(t_{k}) < \psi(t_{k}) < \varphi(t_{k}) < \hat{\varphi}(t_{k})$ when $t = t_{k}$. Nevertheless, $\hat{\psi}(t_{k}-\tau_{k}) < \psi({t_{k}-\tau_{k}}) < \varphi(t_{k}-\tau_{k}) < \hat{\varphi}(t_{k}-\tau_{k})$ doesn't always stand up when $t = t_{k}-\tau_{k}$. For instance, we suppose that $\mathcal{O}(t_{k}) = \lbrace 1, 2, \dots, l\rbrace$ and $\left\|e_{1}\left(t\right)\right\| \geq \left\|e_{2}\left(t\right)\right\| \geq \cdots \geq \left\|e_{l}\left(t\right)\right\| \geq ||e_{l+1}(t)||\geq \cdots \geq ||e_{N}(t)||$, then we can get $\varphi(t_{k}) = \min \{||e_{i}(t_{k})||: i \in \mathcal{O}(t_{k})\} = ||e_{l}(t_{k})|| \ge \psi(t_{k}) = \max \{||e_{i}(t_{k})||: i \notin \mathcal{O}(t_{k})\} = ||e_{l+1}(t_{k})||.$ But when $\tau_{k} \neq 0$, $||e_{l}(t_{k}-\tau_{k})|| \ge ||e_{l+1}(t_{k}-\tau_{k})||$ may not be true. Furthermore, the situations $\hat{\psi}(t_{k}-\tau_{k}) < \psi(t_{k}-\tau_{k})$ and $\hat{\varphi}(t_{k}-\tau_{k}) < \varphi(t_{k}-\tau_{k})$ may also not be true. In other words, although the nodes are divided into two groups when $t = t_{k}$ (the nodes belong to $\mathcal{O}$ become a group while the others become another group), the relationship of their norm is only true at $t_{k}$, not necessarily at other times.

4.   Numerical simulations

Two numerical simulations are presented to demonstrate the applicability of the theoretic analysis presented in this paper.

Example 1: Consider the stochastic cellar neural network (2.1) composed of 10 units with 2-D and associated leader (2.2), whose parameters are selected as follows: $f(x_{i}(t))$ = (tanh$x_{i1}(t)$, tanh$x_{i2}(t))^{\mathrm{T}}$, $\tau(t) = 0.1 \frac{e^{t}}{1+e^{t}}$,

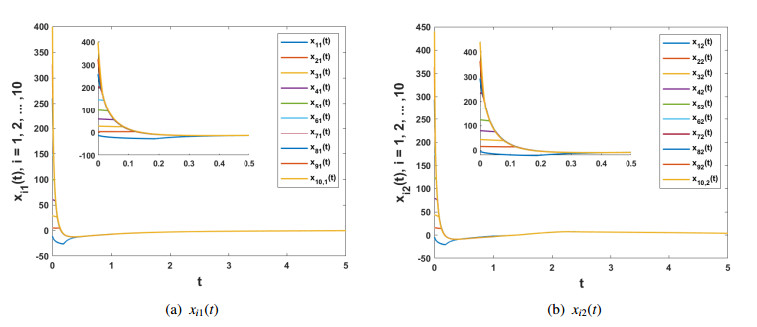
Figure 1 describes $x_{i}, i = 1, 2, \dots, 10$ under 3 pinned nodes, from which one can see that the stochastic cellar neural network approach associated target as time goes.

In addition to depict the change trend of $x_{i}(t), i = 1, 2, \dots, 10$, the state curve of error system can also be observed.

The norm of error system $E(t)$ is displayed in Figure 2. It can be seen that the norm of $E(t)$ has exceeded 1000 at the beginning, while converge to $0$ in about 0.42s, which indicates that effectiveness of PIC on synchronizing stochastic delayed neural networks (2.1) and (2.2).

Example 2: When the impulsive delay is considered, we build an impulsive delay sequence in which $\tau_{k} = ((-1)^{k}/200)$ + 0.005$|$sin$(k^{2})|$, it suggests that $\tau^{*} = 0.0064$. In order to find out the influence of impulsive control input delays, the parameters are assumed to be the same as those given in Example 1.

Focused on Figure 3, one can observe that under controller (3.15) which contains impulsive control input delay $\tau_{k}$, stochastic delayed neural networks (2.1) and (2.2) can also realize synchronization. With the data given before, the norm of synchronization error $E(t)$ is plotted in Figure 4.

Comparing the results of Examples 1 and 2, especially $||E(t)||$ in Figures 2 and 4, we could observe that although the instant of realizing synchronization are different, however, the effect of the synchronization almost the same. Therefore, in view of after the impulsive signal is sent, the control task is often not been executed immediately, so it's more realistic and widely applicable to take impulsive delay into account.

5.   Conclusions

The mean square synchronization of stochastic delayed neural networks was investigated in this research using mixed PIC. We solve the problem with an impulsive control strategy. Considering the time delay in impulsive signal transmission, we design two kinds of pinning impulsive controllers to compare the convergence speed of the system with and without impulsive delay. The controller we designed is effective because the nodes which belong to the controlled node set at some impulsive instant are those with the larger norm, and the size of the controlled node set is determined. To ensure the neural network's mean square synchronization, some sufficient conditions are derived. Eventually, two simulations are performed to verify the authenticity of our findings.

Acknowledgments

The authors would like to thank the associate editor and the anonymous reviewers for their insightful suggestions. This work was supported in part by the National Natural Science Foundation of China under Grant 61873171 and 61872429, in part by the National Key Research and Development Program under Grant 2020YFB1806405.

Conflict of interest

All authors declare no conflicts of interest in this paper.