An improved finite-time stabilization of discontinuous non-autonomous IT2 T-S fuzzy interconnected complex-valued systems: A fuzzy switching state-feedback control method

1.   Introduction

It is well known that a lot of information in communications, fluid mechanics, signal processing and related fields is described by complex numbers ^[1,2,3]. Since a complex-valued neural network was first proposed by Hirose ^[4], it has become a hot issue for its excellent computing power and high capabilities ^[5,6,7]. Compared with real-valued neural networks, complex-valued neural networks have more complicated dynamic characteristics and can solve some problems that real-valued neural networks did not handle, such as XOR problems and detection of symmetry ^[8,9]. Recently, some dynamics, including stability and synchronization, of discontinuous complex-valued neural networks have been extensively studied ^[10,11,12]. However, how to describe the instantaneous changes of the signal transmission between neurons is not considered in the existing articles. As pointed out in ^[13], the information interactions between biological neurons are changing all the time. When it comes to the mathematical model, the change of signal transmission between different neurons is expressed by the elements of the connection matrix. Thus, it is more reasonable to integrate the time-varying parameters into network models. So, proposing a new discontinuous interconnected dynamical system (IDS) with complex-valued state variables and time-varying systematic parameters is the first motivation.

Interconnected dynamical systems, modeled by interconnection of several lower-dimensional systems, are widely used in many fields, such as electric power systems, social networks and cyber physical systems ^[14,15]. The dynamics of IDS, such as stability and control scheme, have become the main subjects of intense investigation over the past few decades, as witnessed by many publications in various fields ^{[16,17,18,19]}. Most of the previous results were obtained under a strict assumption, which was the Lipschitz continuity of the interconnection function. However, as pointed out in ^[20], the transmission of signals between lower dimensional systems shows characteristics of the high-slope hypothesis. As we know, the interconnection function with a high-gain hypothesis in classical neural networks would approximate a discontinuous function ^[21]. In addition, the lower-dimensional systems exchange information through physical connections or communication networks. Due to the fact that physical connections are vulnerable to the external environment, the parameters of IDS should relay on time variables. Generally speaking, we model this kind of IDS by a discontinuous differential equation with time-varying parameters, which is more accurate than the continuous one. Recently, a few research results on the FTS problem of IDS possessing discontinuous interconnection functions ^[22,23,24] were presented under the framework of the Filippov solution. However, as far as we know, there is almost no work on the dynamics of discontinuous interconnected complex-valued systems. Thus, the discontinuous interconnected complex-valued dynamical system (ICVDS) should be further studied. So, how to use complex-valued differential inclusion theory to handle the difficulties caused by the discontinuous interconnection function is the second motivation.

Fuzzy logic systems and their control have become a hot research topic ^[25,26] since Takagi-Sugeno first proposed the T-S fuzzy model ^[27]. Because the upper membership functions, the lower membership functions and weighting coefficients depend on system states, the type-2 fuzzy control method has better performance in dealing with system uncertainties than the type-1 fuzzy control method ^[28]. Recently, many excellent results concerning IT2 T-S fuzzy control systems have been presented ^{[29,30,31,32]}. For example, an event-triggered adaptive fuzzy control was developed to stabilize active vehicle suspension systems in ^[31]. In ^[32], the stability analysis and control synthesis of IT2 Polynomial-Fuzzy-Model-Based networked control systems are investigated under the event-triggered control framework. Recently, fuzzy logic and fuzzy complex-valued neural networks have become hot topics^[33,34]. However, these works are focused on small-scaled networks with continuous activation functions and constant parameters. Thus, it is worth further studying the dynamical behavior of a discontinuous IT2 T-S fuzzy ICVDS with time-varying coefficients. So, how to use indefinite-derivative LF method to deal with the difficulties caused by the time-varying parameters is the third motivation.

Inspired by the above discussion, the discontinuous non-autonomous interconnected complex-valued systems is modeled as follows. The $k$th subsystem of ICVDS is described by

where $k, l = 1, 2, \cdots, s$ and $s$ means the subsystems' number; $z_{k}(t) = [z_{k1}(t), z_{k2}(t), \cdots, z_{kn_{k}}(t)]^{T}\in\mathbb{C}^{n_{k}}$ denotes the complex-valued state of the subsystem ${{W}_{k}}$; $h_{k}(\cdot)$ represents a set of nonlinear functions; $f_{kl}(\cdot) = [f_{kln_{1}}(\cdot), f_{kln_{2}}(\cdot), \cdots, f_{kln_{k}}(\cdot)]^{T}$ represents the discontinuous complex-valued interconnection function between the subsystems $W_{k}$ and $W_{l}$ when $k\ne l$.

Assumption 1 The complex-valued activation function $f_{kl}:\mathbb{R}\times \mathbb{C}^{n_{l}}\rightarrow \mathbb{C}^{n_{k}}$ is piecewise-continuous on $\mathbb{C}$. For $r = 1, 2, \cdots, m$, $(m > 1)$, $f_{kl}(z_{l})$ is continuous in finitely many open domains $G^{kl}_{r}$ and discontinuous on $\partial G^{kl}_{r}$, which is composed of finitely many smooth curves. Moreover, $G^{kl}_{r}$, $(r = 1, 2, \cdots, m)$ satisfies $\bigcup\limits_{r = 1}^{m}(G^{kl}_{r}\bigcup\partial G^{kl}_{k}) = \mathbb{C}$ and $G^{kl}_{p}\bigcap G^{kl}_{q} = \emptyset$ for $1\leqslant q\neq p\leqslant m$. For every $r$, the limitation $f_{kl}(z_{0}) = \lim\limits_{z\rightarrow z_{0}, z\in G^{kl}_{r}}f_{kl}(z)$ exists, where $z_{0}\in\partial G^{kl}_{r}$.

Remark 1.1 As we all know, the main difference between an interconnected system and others is the composition of interacting subsystems. In general, taking the properties of the interconnection function as an example, there are two types, continuous ones ^[16,17] and discontinuous ones ^[22,23]. Compared with the existing articles, there are two main differences. The first one is that both the nonlinear function and interconnection function in (1.1) are described by complex-valued functions. Second, the interconnection function depends on time variables to reflect the impact of the external environment on the system model.

Finite-time stabilization (FTS) means that the system's states can achieve a desired position in finite time under a suitable designed controller. Due to its good character of faster convergence rate, FTS has been extensively studied since it was first proposed by Bhat in 2000^[35]. Later, the FTS problem of discontinuous differential equations was investigated under the framework of differential inclusion ^[36]. Recently, the finite-time stabilization control of IT2 T-S fuzzy IDS with discontinuous interconnection functions was studied^[22,23]. However, the system parameters in articles ^[22,23] are assumed to be unchangeable, and the system state is expressed by a real value. Moreover, though the stabilization was studied by the Lyapunov function (LF) method under the framework of differential inclusion, the derivative of the constructed LF is required to be negative. Recently, an improved LF method with indefinite-derivative, which is effective to handle time-varying coefficients of differential systems, has been widely used to study the stability or the FTS of different kinds of models, such as a discontinuous system^[24] and impulsive systems ^[37,38]. However, there is no related result on FTS of IT2 T-S fuzzy discontinuous ICVDS. Thus, it is meaningful to investigate the FTS problem of T-S fuzzy discontinuous ICVDS. Based on the complex-valued differential inclusion theory and indefinite-derivative LF method, to design a novel control protocol to achieve FTS of T-S fuzzy discontinuous ICVDS is the fourth motivation.

In this article, complex-valued differential inclusion is used to deal with the discontinuity of the interconnection function, and the indefinite-derivative Lyapunov function method is used to deal with the time-varying parameters. Moreover, an IT2 T-S Fuzzy control protocol is used to realize FTS of discontinuous ICVDS. The main contributions are summarized in four aspects. (1) Compared with the studied models in ^{[16,17,22,23,24,33,34]}, the considered ICVDS is more general, since the system state is expressed by a complex-valued vector, the systematic parameters are time-varying, and the interconnection function is discontinuous. (2) Complex-valued differential inclusion theory is used to handle the difficulty caused by the discontinuity of the interconnection function. (3) Different from the traditional LF method, an improved indefinite-derivative LF method is used to establish the sufficient FTS criteria for discontinuous ICVDS. (4) A novel fuzzy switching state feedback controller is designed to achieve the FTS of discontinuous ICVDS, and the estimated settling time is more flexible.

Notations : $\mathbb{R}$ and $\mathbb{C}$ denote real and complex domains, respectively. ${{\mathbb{R}}^{n}}$ and ${{\mathbb{C}}^{n}}$ denote the $n$-dimensional Euclidean space and the $n$-dimensional Unitary space, respectively. ${{\mathbb{R}}^{n\times n}}$ and ${{\mathbb{C}}^{n\times n}}$ are the set of $n\times n$ real matrices and the set of $n\times n$ complex matrices, respectively. $||\cdot||$ denotes the Euclidean vector norm. For any column vector $v = {{({{v}_{1}}, {{v}_{2}}, \cdots, {{v}_{n}})}^{T}}\in {{\mathbb{R}}^{n}}$, define $||v|| = \sqrt{{{v}^{T}}v}$. $\varphi\in K_{\infty }$ if and only if $\varphi$ is strictly increasing and continuous with $\varphi (0) = 0$ and $\mathop {\lim }\limits_{s \to + \infty } {\mkern 1mu} \varphi (s) = + \infty$.

2.   Model description and some preliminaries

2.1.   Model description

In ^[22,23], the FTS of IDS is achieved by designing a suitable IT2 T-S fuzzy control protocol. Based on this control protocol, the discontinuous ICVDS (1.1) is given as follows:

Fuzzy Rule $i$: IF $\alpha_{k1}(z_{k}(t))$ is $\beth_{k1}^{i}$ and $\cdots$ and ${{\alpha }_{kb}}(z_{k}(t))$ is $\beth_{kb}^{i}$

THEN

where $i = 1, 2, \cdots, {{m}_{k}}$, and ${{m}_{k}}$ is the fuzzy rules' number in $k$th subsystem $W_{k}$; $B_{k}^{i}(t)$ represents a known complex-valued matrix; $f_{kl}(\cdot) = {{[{{f}_{kl{{n}_{1}}}}(\cdot), {{f}_{kl{{n}_{2}}}}(\cdot), \cdots, {{f}_{kl{{n_{k}}}}}(\cdot)]}^{T}}$ represents the discontinuous complex-valued interconnection function between the subsystem $W_{k}$ and $W_{l}$ when $k\ne l$; ${{\alpha }_{ka}}({{z}_{k}}(t)) (a = 1, 2, \cdots, b)$ are measurable premise variables; and $\beth_{ka}^{i}(a = 1, 2, \cdots, b)$ denote the linguistic fuzzy sets.

On the basis of the method proposed in ^[22,23], using a weighted average fuzzifier and singleton fuzzifier product inference, the expression of discontinuous ICVDS (2.1) is derived as follows:

where

where $\hat{\mu}_{k}^{i}(\cdot)\geq 0$ ($\breve{\mu}_{k}^{i}(\cdot)\geq 0$) denotes the upper (lower) membership function, and $0\leq\bar{\mu}_{k}^{i}(\cdot)\leq1$ ($0\leq\underline{\mu}_{k}^{i}(\cdot)\leq1$) means the weighting coefficient function to describe the change of uncertain parameters, respectively. For convenience, $\mu_{k}^{i}(z_{k}(t))$ is denoted as $\mu_{k}^{i}$.

For further investigating FTS of discontinuous IT2 T-S fuzzy ICVDS (2.2), a novel fuzzy switching state feedback controller is designed as follows:

Fuzzy Rule $j$: IF ${{\beta}_{k1}}(z_{k}(t))$ is $\daleth_{k1}^{j}$ and $\cdots$ and ${{\beta}_{kd}}(z_{k}(t))$ is $\daleth_{kd}^{j}$

THEN

Here, ${\rm sign}(z_{k}(t)) = {{[{\rm sign}({{z}_{k1}}(t)), {\rm sign}({{z}_{k2}}(t)), \cdots, {\rm sign}({{z}_{k{{n}_{k}}}}(t))]}^{T}}$, in which ${\rm sign}(z_{kq}(t)) = {\rm sign}(x_{kq}(t))+{\textbf{i}} {\rm sign}(y_{kq}(t))$; $c_{k}^{j}(t)$ and $m_{k}^{j}(t)$ denote the time-varying gain coefficients; $\beta_{kc}(z_{k}(t))(c = 1, 2, \cdots, d)$ represent the measurable premise variable; and $\daleth_{kc}^{j}(c = 1, 2, \cdots, d)$ denote the linguistic fuzzy sets. Thus, the designed controller is described as follows:

with

where ${{\varphi}_{k}}$ denotes the number of fuzzy rules in the $n$-th controller, $\hat{\nu}_{k}^{j}(\cdot)\geq 0$ ($\breve{\nu}_{k}^{j}(\cdot)\geq 0$) denotes the upper (lower) membership function, and $0\leq\bar{\nu}_{k}^{j}(\cdot)\leq1$ ($0\leq\underline{\nu}_{k}^{j}(\cdot)\leq1$) shows the weighting factor function for uncertain parameter changes. For convenience, $\nu_{k}^{j}(z_{k}(t))$ is denoted as $\nu_{k}^{j}$.

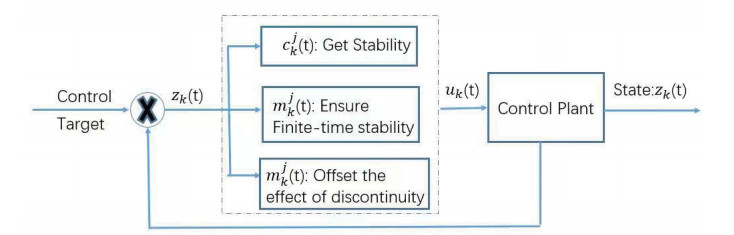
The fuzzy control scheme is shown in Figure 1, where $c_{k}^{j}(t)$ and $m_{k}^{j}(t)$ denote the designed control gain coefficients under the control fuzzy rules. There are two parts of the designed controller. The first part $c_{k}^{j}(t)z_{k}(t)$ ensures the stability of the plant. The second part $m_{k}^{j}(t){\rm sign}(z_{k}(t))$ offsets the effect of the discontinuous interconnection function and guarantees the finite-time stability.

Remark 2.1 There is a special term ${\rm sign}(z_{k}(t))$ in the designed control protocol (2.3), which is used to deal with the discontinuities caused by the discontinuous interconnection function effectively. From the definition of ${\rm sign}(z)$, it is easy to see that the designed control protocol is switching corresponding to the state $z_{k}(t)$. So, the designed controller (2.3) is a fuzzy switching state-feedback controller. As shown in Figure 1, there are two effects of the switching term ${\rm sign}(z_{k}(t))$. The first one is to offset the effect caused by the discontinuous interconnection function. The second is that it plays an important role in realizing finite-time stabilization.

Remark 2.2 Obviously, the precondition membership function and fuzzy rules' number of the designed controller are different from those described in the plant model (2.1). Therefore, the designed controller is more flexible. Moreover, since the upper and lower membership functions of the designed controller (2.3) can well express the uncertainty characteristics, the designed controller has much better performance.

2.2.   Some preliminaries

In this part, some basic knowledge of complex-valued differential inclusion and non-smooth theories are introduced. More details can be found in ^[10,39].

Definition 1 For a discontinuous function $g(t, z)$, the complex-valued differential inclusion is defined to be a multi-valued map $\mathbb{G}:\mathbb{R}\times\mathbb{C}^{n}\rightarrow 2^{\mathbb{C}^{n}}$, where

where $\mu(\gimel)$ is the Lebesgue measure of $\gimel$ and $B(z, \xi) = \{u|\|u-z\|\leq\xi\}$.

Definition 2 A complex-valued function $z(t):I \mapsto \mathbb{C}^{n}$ is a solution of the complex-valued differential equation $\dot{z}(t) = g(t, z(t))$ in sense of Filippov, if it is absolutely continuous on any interval $[t_{1}, t_{2}]\subseteq I$ and satisfies

for almost all $t\in I$.

Following the above discussion, if $z(t)$ is the Filippov solution of (2.2), then

for a.e. $t\in [t_{0}, +\infty)$. According to the measurable selection theorem ^[39], there exists a set of measurable functions $\digamma_{kl}(t, z_{k}(t))\in \overline{\rm co}f_{kl}[(t, z_{l}(t))]$ satisfying

for a.e. $t\in [t_{0}, +\infty)$.

Assumption 2 There exist $\mathcal{P}_{kl}(t)$ and $\mathcal{Q}_{kl}(t)$ such that

holds for all $\digamma_{kl}(t, z_{l}(t))\in \overline{\rm co}f_{kl}[(t, z_{l}(t))]$ and $\bar{\digamma}_{kl}(t, \bar{z}_{l}(t))\in \overline{\rm co}f_{kl}[(t, \bar{z}_{l}(t))]$. Moreover, for all $k, l$ and $t\geq t_{0}$, $0\in \overline{\rm co}f_{kl}[(t, 0)]$.

Definition 3 The zero solution $z = 0$ of (2.6) is said to be FTS, if it is Lyapunov stable and finite-time attractive, i.e., there exists $\mathcal{T}(t_{0}, z_{0})$ such that $\lim\limits_{t\rightarrow \mathcal{T}(t_{0}, z_{0})}\|z(t)\| = 0$ and ${z}(t) = 0$ for $t > \mathcal{T}(t_{0}, z_{0})$, in which $\mathcal{T}(t_{0}, z_{0})$ is called the settling-time.

Definition 4 We say that $(\mu(t), \rho(t))\in\mathcal {F}\mathcal {P}$ if and only if $\mu(t)$ is integrable, $\rho(t)$ is semi-negative definite and integrable, and there are $L, M\ge 0, \lambda > 0$ and $0 < \alpha < 1$ satisfying

Lemma 1 ^[40] Assume $(\mu(t), \rho(t))\in\mathcal {F}\mathcal {P}$ and ${{\kappa }_{1}}, {{\kappa }_{2}}\in {{K}_{\infty }}$. If there exists a $C-$regular function $V:{{\mathbb{R}}_{+}}\times {{\mathbb{R}}^{n}}\to {{\mathbb{R}}_{+}}$ with $V(t, 0) = 0$, for almost every $t\in[{{t}_{0}}, +\infty)$ satisfying

1) ${{\kappa }_{1}}(||x||)\le V(t, x(t))\le {{\kappa }_{2}}(||x||)$, $\forall (t, x)\in {{\mathbb{R}}_{+}}\times {{\mathbb{R}}^{n}}$,

2) $\dot{V}(t, x(t))\le \mu (t)V(t, x(t))+\rho (t){{V}^{\alpha }}(t, x(t))$,

then the system is able to realize FTS. In addition, the settling time is estimated as

Under the designed novel fuzzy switching state feedback controller (2.3), the discontinuous IT2 T-S fuzzy ICVDS (2.2) is described as follows:

Remark 2.3 In ^[16,17], the interconnection function of IDS is assumed to be continuous. In ^[22,23,24], the state of the studied model is described by a real-valued vector. In ^[33,34], the systematic parameters of the studied model are required to be autonomous, and the activation function is required to satisfy the Lipschitz condition. Since complex values, a discontinuous interconnection function, time-varying coefficients and Takagi-Sugeno fuzzy logic are incorporated in this model, the considered discontinuous IT2 T-S fuzzy ICVDS is more general than those models considered in previous articles ^{[16,17,22,23,24,33,34]}.

For further investigating the FTS, we adapt the real-image separation method here. Let $z_{k}(t) = x_{k}(t)+{\textbf{i}}y_{k}(t)$, $B_{k}^{i}(t) = (B_{k}^{i})^{\rm R}(t)+{\textbf{i}}(B_{k}^{i})^{\rm I}(t)$ and $\digamma_{kl}(t, z_{k}(t)) = \digamma_{kl}^{\rm R}(t)+{\textbf{i}}\digamma_{kl}^{\rm I}(t)$, and then the system (2.11) is transformed into

Next, we give an important Lemma and some notations.

Lemma 2 ^[41] For some positive constants $m_{1}, m_{2}, \cdots, m_{k}$ and $0 < p < q$, one has

For a set of given real-valued matrices

where $k = 1, 2, \ldots, s$, we define $\pi_{k}^{\max} = \max\limits_{1\leq u, v\leq n_{k}}\{|\pi_{kuv}|\}$,

$\bar{b}^{\rm R \max}_{k}(t) = \max\limits_{1\leq i\leq s}\{\max\limits_{1\leq u, v\leq n_{k}}\{|\bar{b}^{i\rm R}_{kuv}(t)|\}\}$ and $\bar{b}^{\rm I \max}_{k}(t) = \max\limits_{1\leq i\leq s}\{\max\limits_{1\leq u, v\leq n_{k}}\{|\bar{b}^{i\rm I}_{kuv}(t)|\}\}$. Moreover, it is easy to get the following inequalities from Assumption 2:

and

3.   Finite-time stabilization analysis

Theorem 1 If both Assumption 1 and Assumption 2 are satisfied,

Assumption H₁: there exists a set of positive-definite matrices $\Pi_{k} = (\pi_{kuv})_{n_{k}\times n_{k}}$, $k = 1, 2, \ldots, s$, such that

and

hold, and $(\mu(t), \rho(t))\in\mathcal {F}\mathcal {P}$, then the zero solution of discontinuous ICVDS (2.2) is FTS under the fuzzy switching state feedback controller (2.3).

Proof: Consider a $C-$regular Lyapunov function:

Calculating the derivative of $V(t, x)$ along the solution of system (2.12), for a. e. $t\geq t_{0}$, one obtains

By computation, this yields

Based on $\sum\limits_{i = 1}^{m_{k}}\mu_{k}^{i} = 1$ and $\sum\limits_{j = 1}^{\varphi_{k}}\nu_{k}^{j} = 1$, one has

and

By using the Cauchy-Schwarz inequality and Assumption 2, this implies

Moreover, it is obvious that

According to Lemma 2 and the fact $m_{k}^{j}(t) > 0$ for all $k, j$, it is deduced that

With a similar analysis as that used in (3.4)–(3.8), one gets

According to Assumption ${\bf{H}}_{{\bf{1}}}$, combined with formula (3.4)–(3.9), it follows that

where $\bar{\rho}(t) = 2\max\limits_{1\leq k\leq s}\{\pi_{k}^{\max}\}\cdot\max\limits_{1\leq k\leq s}\{\sum\limits_{l = 1}^{s}\mathcal{Q}_{kl}(t)\}-2\min\limits_{1\leq k\leq s}\{\min\limits_{1\leq j\leq \varphi_{k}}\{m_{k}^{j}(t)\}\lambda_{\min}(\Pi_{k})\}$.

From Lemma 2, it follows that

Based on the above discussion, this yields

where $\mu (t)$ and $\rho (t)$ have been given in Theorem 1. By Lemma 1, the zero solution of discontinuous ICVDS (2.2) achieves FTS under the fuzzy switching state feedback controller (2.3). Moreover, the settling time is estimated by $\mathcal{T}({{t}_{0}}, {{x}_{0}}) = {{t}_{0}}+\frac{{{V}^{1-\alpha }}({{t}_{0}}, {{x}_{0}}){{e}^{(1-\alpha)L}}+(1-\alpha)M}{(1-\alpha)\lambda}$.

Remark 3.1 In ^[32], the stability condition of an event-triggered IT2 PFMB control system is given in the form of a linear matrix inequality (LMI). In ^[42], the asymptotical stability of a large-scale fuzzy system under a distributed event-triggering piecewise controller is studied by using the LMI technique and free-weighting matrix method. Compared with the LMI technique used in ^[32,42], the inequalities (3.3)–(3.11) here indeed induce much conservatism. However, the proposed conditions in this paper are simple and easily verified. In addition, how to reduce the conservatism caused by inequalities is one topic of our future work.

Remark 3.2 In most of the existing results on FTS in ^[22,23,33], the constructed Lyapunov functions are required to possess semi-negative/negative definite derivative with respect to the time variable. In this theorem, the constructed function may not have semi-negative/negative definite derivative since the estimation of the Lyapunov function's derivative contains an indefinite function $\mu(t)$.

Remark 3.3 In ^[22,23], the control gain coefficients are preassigned to be constants. The designed control gain coefficients in this paper are time-varying functions, which means the design control protocol is novel. Moreover, the estimation of settling time for FTS depends on the designed time-varying control gain coefficients. Thus, the estimated settling time is more flexible than in ^[22,23].

As a special case, $\Pi_{k}$ is taken to be a positive-definite diagonal matrix for every $k = 1, 2, \ldots, s$, i.e. $\Pi_{k} = {\rm diag}\{\pi_{k1}, \pi_{k2}, \ldots, \pi_{kn_{k}}\}$ and $\pi_{ku} > 0$ for $u = 1, 2, \ldots, n_{k}$. Define $\hat{\pi}_{k}^{\max} = \max\limits_{1\leq u\leq n_{k}}\{\pi_{ku}\}$ and $\hat{\pi}_{k}^{\min} = \min\limits_{1\leq u\leq n_{k}}\{\pi_{ku}\}$, and then $\lambda_{\min}(\Pi_{k}) = \hat{\pi}_{k}^{\min}$ and $\lambda_{\max}(\Pi_{k}) = \hat{\pi}_{k}^{\max}$. Then, we can get the following corollary.

Corollary 1 If Assumption 1 and Assumption 2 are satisfied,

Assumption H₂: there exist positive-definite diagonal matrices $\Pi_{k} = {\rm diag}\{\pi_{k1}, \pi_{k2}, \ldots, \pi_{kn_{k}}\}$, $k = 1, 2, \ldots, s$, such that

and

hold, and $(\mu_{1}(t), \rho_{1}(t))\in\mathcal {F}\mathcal {P}$, then the zero solution of discontinuous ICVDS (2.2) is FTS under the fuzzy switching state feedback controller (2.3).

In corollary 1, if $\Pi_{k} = I_{n_{k}\times n_{k}}$, then $\hat{\pi}_{k}^{\max} = \hat{\pi}_{k}^{\min} = 1$, and the corresponding corollary can be obtained.

Corollary 2 If Assumption 1 and Assumption 2 are satisfied, and $(\mu_{2}(t), \rho_{2}(t))\in\mathcal {F}\mathcal {P}$, where

and

then the zero solution of discontinuous ICVDS (2.2) is FTS under the fuzzy switching state feedback controller (2.3).

Remark 3.4 Compared with the FTS results on the IT-2 T-S fuzzy IDS proposed in ^[22,23,24], the system states are complex valued. Compared with the stabilization results on T-S fuzzy complex-valued neural networks in ^[33,34], the interconnection function is discontinuous. Moreover, the systematic parameters are time-varying in this article. In order to handle the time-varying parameters, we use a different version of the indefinite-derivative Lyapunov function method to investigate FTS of the discontinuous fuzzy ICVDS.

4.   Numerical simulation

In this part, two practical applications are provided to illustrate the validity of the obtained results.

Example 1. As a special type of interconnected dynamics, a large-scale IT2 fuzzy neural network model is given to show the effectiveness of the proposed theoretical results. As we know, neural networks have wide applications in many fields, such as pattern recognition, intelligent robots, predictive estimates and image processing. Here, we consider the IT2 T-S fuzzy complex-valued neural networks with two neurons. Each neuron state is expressed by a two-dimensional differential equation. For every subsystem $W_{k}$ $(k = 1, 2)$, the fuzzy rule number $m_{k} = 3$, and $\varphi_{k} = 2$.

The system parameters are chosen as

The discontinuous complex-valued interconnection functions are selected as $f_{kl}(t, z_{l}) = (f_{kl1}(t, z_{l1}), f_{kl2}(t, z_{l2}))^{\rm T}$, where $f_{klm}(t, s) = [(0.8-0.3\sin t)(s^{\rm R}-0.5){\rm{sgn}}(s^{\rm R})+(0.8-0.3\sin t){\rm tanh}(s^{\rm I})]+{\textbf{i}}$$[(0.8-0.3\sin t)(s^{\rm I}-0.5){\rm{sgn}}(s^{\rm I})+(0.8-0.3\sin t){\rm tanh}(s^{\rm R})]$ for $s = s_{lm}\in \mathbb{C}$ and $k, l, m = 1, 2$. Obviously, the interconnection function $f_{klm}(t, s)$ is discontinuous on variable $s$ and it satisfies $\|f_{klm}(t, s)\|\leq (0.8-0.3\sin t)\|s\|+(0.4-0.15\sin t)$. Thus, Assumption 1 and Assumption 2 are satisfied with $\mathcal{P}_{kl}(t) = 0.8-0.3\sin t$ and $\mathcal{Q}_{kl}(t) = 0.4-0.15\sin t$.

The upper and lower membership functions of the plant and the controller are shown in Table 1. The corresponding curves of the plant's upper and lower membership functions are depicted in Figures 2 and 3, and the weighting coefficient functions of the plant are shown in Figure 4. In addition, the corresponding curves of the controller's upper and lower membership functions are depicted in Figures 5 and 6, and the weighting coefficient functions of the controller are shown in Figure 7. Through simple computation, it is easy to get that $\mu_{1}^{i}(z_{1}) = \mu_{2}^{i}(z_{2})$ and $\nu_{1}^{j}(z_{1}) = \nu_{2}^{j}(z_{2})$ with $i = 1, 2, 3$ and $j = 1, 2$. Obviously, $z = (0, 0, 0, 0)^{\rm T}$ is an equilibrium point of the ICVDS. If the initial values are selected as $z_{1}(0) = (1-0.5{\textbf{i}}, -1+0.5{\textbf{i}})^{\rm T}$ and $z_{2}(0) = (-0.5+{\textbf{i}}, 0.5-{\textbf{i}})^{\rm T}$, the dynamic behaviors of the real part and imaginary part of the ICVDS without any controller are shown in Figures 8 and 9, which show that $z = (0, 0, 0, 0)^{\rm T}$ is not a stable equilibrium point.

Design a novel fuzzy switching state-feedback controller with $k = 1, 2$ and $j = 1, 2$. Taking the time-varying control gains $c_{k}^{j}(t) = (\frac{1}{1+t^{2}}+2.4\sin t)-16.2$ and $m_{k}^{j}(t) = 1-0.5\sin t$ in (2.3), one has $\mu_{2}(t) = \frac{2}{1+t^{2}}$, $\rho_{2}(t) = -0.4+0.4\sin t$ in Corollary 2. It is obvious that $(\mu_{2}(t), \rho_{2}(t))\in\mathcal {F}\mathcal {P}$ since $\int_{0}^{+\infty }{|\mu_{2} (s)|ds < \pi}$, and $\int_{{{t}_{0}}}^{t}{\rho_{2}(s)ds < -0.4(t-{{t}_{0}})+0.8}$. Thus, all conditions in Corollary 2 are satisfied, and this yields that the zero solution of the ICVDS is FTS under the designed novel fuzzy switching state-feedback controller (2.3). Under the designed controllers, the real parts and the imaginary parts of the ICVDS are shown in Figures 10 and 11. As shown in Figures 10 and 11, the zero solution $z = (0, 0, 0, 0)^{\rm T}$ is FTS, and the ICVDS achieves stabilization in 0.32 (sec).

Remark 4.1 As shown in Figures 10 and 11, as the time $t$ tends to infinity, the real part and three imaginary parts of state trajectories converge to zero in finite time under the designed controller. In ^[33,34], the stabilization and synchronization of complex-valued neural networks were investigated. However, the convergence rate of the state (error) trajectories is asymptotic or exponential. This means that our convergence rate is faster than the convergence rate in ^[33,34].

In the following, we focus on the dynamics of complex-valued neural networks under the type-1 fuzzy approach. We replace the type-2 membership functions by type-1 ones, that is, $\mu_{k}^{1}(z_{k}) = 1-\sin(\|z_{k}\|-2), \mu_{k}^{2}(z_{k}) = \cos(\|z_{k}\|-2), \mu_{k}^{3}(z_{k}) = 1-\mu_{k}^{1}(z_{k})-\mu_{k}^{2}(z_{k}),$ $\nu_{k}^{1}(z_{k}) = \frac{1}{1+e^{0.5+\|z_{k}\|}}, \nu_{k}^{}(z_{k}) = 1-\nu_{k}^{1}(z_{k})$, and set the other related parameters unchanged. Figures 12 and 13 show the state responses of subsystem $W_{1}$ and $W_{2}$ under the type-1 fuzzy approach. Obviously, the type-2 fuzzy approach has better performance than the type-1 fuzzy approach.

Example 2. It is well known that complex-valued chaotic systems arise in various important fields, such as fluids, superconductors, plasma physics and electromagnetic fields, secure communications. The complex-valued Lorenz system ^[43] is described by

where the Rayleigh number $r$ and parameters $a, c$ are complex numbers, and $b$ is a real and positive number. In model (4.1), the complex variables $z_{1}, z_{2}$ and real variable $z_{3}$ have relations with the electric field, the atomic polarization amplitudes and the population inversion in a ring laser system of two-level atoms, respectively.

Here, we consider the FTS of the ICVDS composed by two 3-dimensional complex-valued Lorenz systems interconnected by discontinuous functions. With a similar fuzzy method as used in ^[44], we choose the fuzzy rule number $m_{k} = 2$ and $\varphi_{k} = 2$ for every subsystem $W_{k}$ $(k = 1, 2)$. The complex-valued Lorenz system parameters are chosen as

The discontinuous complex-valued interconnection functions are selected as $f_{kl}(t, z_{l}) = (0, -z_{l1}z_{l3}+0.5(sign(z^{R}_{l1})+{\textbf{i}}sign(z^{I}_{l1})), 0.5(\bar{z}_{l1}z_{l2}+z_{l1}\bar{z}_{l2}))^{\rm T}$ for $k, l = 1, 2$. Obviously, the interconnection function $f_{kl}(t, z_{l})$ is discontinuous, and it satisfies Assumption 1 and Assumption 2.

The upper and lower membership functions of the plant and the controller are shown in Table 2. Through simple computation, it is easy to get that $\mu_{1}^{i}(z_{1}) = \mu_{2}^{i}(z_{2})$ and $\nu_{1}^{j}(z_{1}) = \nu_{2}^{j}(z_{2})$ with $i = 1, 2$ and $j = 1, 2$. Obviously, $z = (0, 0, 0, 0, 0, 0)^{\rm T}$ is an equilibrium point of the ICVDS. If the initial values are selected as $z_{1}(0) = (1-0.5{\textbf{i}}, -1+0.5{\textbf{i}}, 0.5)^{\rm T}$ and $z_{2}(0) = (-0.5+{\textbf{i}}, 0.5-{\textbf{i}}, 1.5)^{\rm T}$, the dynamic behavior of the real part and imaginary part of the ICVDS without any controller are shown in Figures 14–17, which show that $z = (0, 0, 0, 0, 0, 0)^{\rm T}$ is not a stable equilibrium point.

Design a novel fuzzy switching state-feedback controller with $k = 1, 2$ and $j = 1, 2$. Take the time-varying control gains $c_{k}^{j}(t) = \frac{2}{1+t}-t|\cos t|-7.2$ and $m_{k}^{j}(t) = 12.4-0.3\sin t$ in (2.3). Under the designed novel fuzzy switching state-feedback controller, the zero solution of the ICVDS is FTS. The trajectories of the ICVDS are shown in Figures 18 and 19, which show that the zero solution $z = (0, 0, 0, 0, 0, 0)^{\rm T}$ is FTS.

5.   Conclusions

In this paper, a complex-valued IDS with discontinuous interconnection function and time-varying coefficients is formulated by the IT-2 T-S fuzzy method. Under the differential inclusion framework and using an improved Lyapunov function with indefinite derivative, we established some sufficient criteria to achieve FTS via designing a novel fuzzy switching state-feedback controller. In the future, it will be interesting to investigate the FTS of IT-2 T-S fuzzy complex-valued neural networks.

Acknowledgments

This work was supported by National Natural Science Foundation of China (No. 12171056), National Natural Science Foundation of Hunan Province (No. 2020JJ4012), and China Postdoctoral Science Foundation (No. 2018M632207).

Conflict of interest

The authors declare there is no conflicts of interest.