Stability analysis of discrete-time switched systems with bipartite PDT switching

1.   Introduction

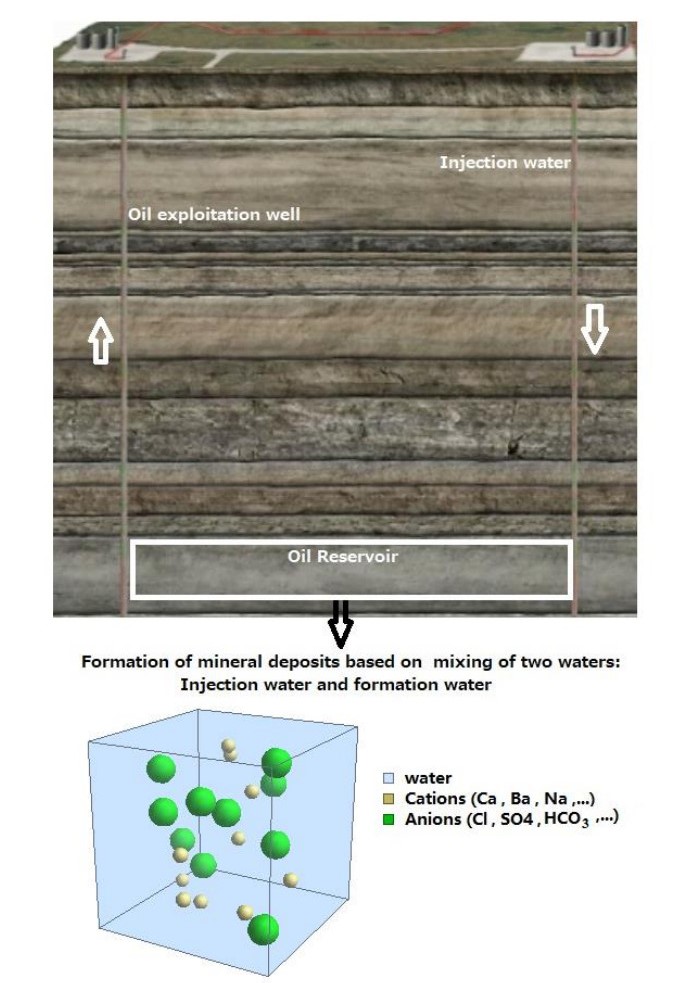
Water is recognized as an important fluid in the oil fields, being in direct contact with the reservoir materials. Therefore, by careful analysis, important geological and geochemical information can be obtained. All the waters of the reservoir formation contain dissolved minerals, including cations such as sodium, calcium, barium, strontium, potassium, and iron, as well as common anions such as chloride, sulfate, sulfide, and carbonate ions ^[1,2,3]. According to available reports, the concentration of dissolved minerals in the formation waters in oil fields is frequently higher (up to 300,000 ppm) than in seawater (around 35,000 ppm) ^[3]. One of the reasons for this abundance is the effect of ion exchange from formation rocks to water. The concentration of mineral ions in the formation water is affected by factors such as dilution with groundwater, the presence of anaerobic bacteria and petroleum components, ion exchange of cations with clay, dissolution of mineral solutes (due to the movement of formation waters), exchange of magnesium and calcium during dolomite formation, and the passage of mineral solutes through the cracks ^[3,4]. In the process of oil recovery operations (especially when seawater is used for injection operations), mineral precipitates may be formed in surface and subsurface equipment ^[3,5,6,7,8]. In other words, with the mixing of the injection water and the formation water, the concentration of mineral ions in the solution increases, and changes in the solubility of minerals may occur, which is also dependent on temperature and pressure. These changes may lead to the formation of mineral precipitates in the reservoir and oil wells, thus reducing production efficiency (Figure 1).

Figure 1.  Schematic of mineral sediment formation during oil well operation.

DownLoad: Full-Size Img PowerPoint

Considering the various challenges of mineral deposits in the oil industry, many studies have been conducted by researchers in this field in the last few decades. Jonnes (1964) ^[9] showed that the adsorption properties of clays with calcium and magnesium mineral ions are higher than that of sodium minerals, leading to a blockage of the oilfield subsurface reservoir. Mongan (1965) ^[10] examined the effect of pH and ion concentration on the blockage of the pores with mineral particles and the reduction of permeability. Oddo et al. (1991) ^[11] pointed to the increase in temperature and pressure drop as the main factors for calcium carbonate and calcium sulfate mineral deposits in floating pumps in offshore wells. Chong and Sheikholeslami (2001) ^[12] investigated the effect of accumulation and deposition of calcium sulfate and calcium carbonate sediments in a mineral solution under different temperatures. Bagci et al. (2001) ^[13] investigated the effect of alkaline fluids and injection rates on permeability in monolithic and non-monolithic calcareous cores, showing the influence of salt concentration for permeability. Voloshin et al. (2003) ^[14] showed that the mineral composition of injection water is an effective factor in the process of mineral deposition in the reservoir and wells during oil recovery operations. Abu Khamsin and Ahmad (2005) ^[15] investigated the process of calcium sulfate deposition in the presence of sandstone using a mixture of calcium-containing saline water with sulfate-rich impure water, showing that the rate of accumulation and sedimentation of inorganic calcium sulfate is markedly increased despite the high injection rate and high temperature. Hashemi et al. (2019) ^[16] studied the accumulation of barium and strontium sulfates in Siri and Nosrat oilfields, including a thermodynamic model (with different temperatures and pressures) for the conditions and composition of both formation water and injection water operations. Hashemi and Hashemi (2020) ^[17] studied the prediction of carbonate and sulfate mineral deposits in the Nosrat Oil field under different operating conditions. According to the results of their study, the formation of mineral deposits of calcium carbonate, magnesium carbonate, and barium sulfate could cause serious problems during operations.

Based on the results obtained by previous researchers (especially the ones mentioned above), the formation of mineral deposits in the subsurface reservoir and the surface facilities in the oil industry can be expected, and due to the increasing use of water injection operations, investigation of the formation of mineral deposits is important. For this reason, in this study, the mineral deposition of calcium carbonate, magnesium carbonate, calcium sulfate, and gypsum in operating conditions in Rag-e Sefid Oil and Gas Field have been evaluated. Therefore, formation waters of 5 wells have been analyzed with the StimCade2 software (Schlumberger).

The thermodynamic properties of aqueous electrolyte systems, such as the activity coefficient and osmotic coefficients of mineral ions ^[18,19,20] and interfacial tension of water/oil system with the presence surfactants and salt ^[2], are of interest to investigate the behavior of cations and anions in solution. Saturation index is another thermodynamic property of electrolyte systems, which is required in this study to investigate the formation of sulfate and carbonate mineral deposits based on ion concentration and operating conditions (temperature and pressure). In other words, the saturation index of mineral deposits in the oil industry is calculated based on thermodynamic equations, which is based on the percentage of saturation in the StimCade2 software.

2.   The geological area of investigation

Rag-e Sefid oil field is one of the southwestern Iranian oil fields, located on the border between Khuzestan and Kohgiluyeh and Boyer-Ahmad provinces (Figure 2). Oil production in the Rag-e Sefid oil and gas field is carried out in the hydrocarbon layer of the Asmari and Bangistan reservoirs. The Asmari reservoir of the Rag-e Sefid oil field was discovered by surface geological operations in the year 1951, and finally, the existence of oil and gas reserves in the Rag-e Sefid oil field was proven by drilling a well in the year 1964. This oil field is geologically located at the bottom of the Zagros Sedimentary Zone. The Rag-e Sefid oil field in the southeast is associated with the Bibi Hikmieh oil field, in the northeast with Poznan, in the northwest with Ramshir, and in the southwest with Zagheh, Hindijan-Behrganasar, and Tango ^[21]. The Rag-e Sefid field is located in Khuzestan province, southwest Iran and is more than 6 km away from the Persian Gulf. This field has an arcuate asymmetrical anticline structure. This structure is 45 km long and 5–9 km wide. This structure has three horizon reservoirs, which in ascending stratigraphical order are the Khami Group (gas bearing), Bangestan Group, and Asmari Formation (oil/gas bearing).

Figure 2.  Location map of Rag-e Sefid field ^[25].

DownLoad: Full-Size Img PowerPoint

The first exploration well in the Rag-e Sefid structures was drilled in 1963 and reached the Asmari Formation. This was followed with drilling programs for evaluation of the Bangestan and Khami groups in 1964. The estimated hydrocarbon of this reservoir is 2.4 billion barrels of oil and 20 trillion cubic feet of gas ^[22]. The Asmari oil reservoir is characterized by 30° API and low sulfur, whereas the Bangestan Oil reservoir is marked by 25° API and 3.5% sulfur. Based on data from oil production, it has been indicated that the amount of sulfur in the crude oil of the Asmari Formation increases during production. This phenomenon suggests that the oil of Asmari and Bangestan Reservoirs is connected by fractures and faults. It should be mentioned that more than 118 wells have been drilled in this structure up until now. 95 out of 118 wells have been drilled in the Asmari reservoir, 11 in the Bangestan reservoir, and the remaining 12 in the Khami reservoir ^[21]. The Asmari Formation is of Oligocene-Miocene age, which is the most important reservoir rock in the oil fields of southwestern Iran, including the Reg-e Sefid oil field ^[23]. Also, a Meistrichtian age has been determined for the Gurpi Formation in the Sefid Vein field. The thickness of the Gorpi Formation in Rag-e Sefid field has decreased from the north towards the central areas ^[24].

3.   Materials and methods

In this study, 5 water samples of Asmari formation from Reg-e Sefid oil field have been considered (depth of about 8000 ft).

In this study, measurement methods for bicarbonate based on Betz Handbook (1962) ^[26], calcium and magnesium ions based on the ASTM-D511 standard, chloride ions based on ASTM-D512, iron ions based on HACH 8008, sodium ions using flame photometer and sulfate ions based on HACH 8051 were used. Also, the ASTM D-4007 standard was used to determine the percentage of sediment in the formation water.

The StimCad 2 software was used for the prediction of sulfate and carbonate mineral deposition. This software is intended to simulate the acidification of wells and to predict mineral deposition in oilfields. The StimCad 2 software has a temperature range of −50 to 600 degrees Fahrenheit and a compression range of 15.99 to 24999.988 psia. The software reports saturation percentage, sedimentation rate, and pH. This application software is shown in Figure 3. 5 samples from rock reservoirs in the studied field were analyzed with XRF using a PW1410 Philips instrument for comparison with water analysis.

Figure 3.  Stimcade2 Software.

DownLoad: Full-Size Img PowerPoint

In this study, based on Stimcade2 software, the concentration of mineral ions analyzed according to the 5 studied well samples is entered into the software as input information, and then the target temperature and pressure are applied. Therefore, based on the input data to the program, the percentage of saturation is calculated to predict the formation of sulfate and carbonate mineral deposits, and if there is a possibility of scale formation, its amount is estimated.

4.   Results and discussion

4.1.   Geochemistry

Table 1 presents the analysis of inorganic ions in 5 samples of Rag-e Sefid oil and gas field wells. Based on the results in Table 1, calcium, magnesium and sodium cations, as well as sulfate, chloride and bicarbonate anions are significant in the oil field water. The pH levels in the 5 samples studied are between 5.98 and 6.42.

Table 1.  Formation water analysis for 5 samples of Rag-e Sefid oil and gas field.

Components (mg/lit)	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5
Na+	80224	59087	77458	66409	58056
Ca2+	8000	7600	8000	7600	7200
Mg2+	2187	972	1701	1458	1701
Cl-	142000	106500	136675	118925	106500
SO42-	2400	1200	2100	1600	925
HCO3-	1098	244	854	244	293
Total Dissolved Solid	235909	175603	226788	196236	174675
Ph	5.98	6.42	6.05	6.42	6.38

---

 | Show Table

DownLoad: CSV

Based on the analysis, iron ions in the 5 samples studied are non-detectable. Sulfate ions (SO₄^2-) are more concentrated than bicarbonate, possibly due to the intense dissolution of gypsum. Cl^- ions are significantly present in the Rag-e Sefid Formation.

Based on the results of Table 1, the solubility of the aqueous solution mineral water changes as a result of the change in the concentration of sodium, calcium, magnesium, chloride, sulfate, and bicarbonate ions. In other words, the electrolyte solutions due to the electrostatic forces between the ions and the short-range forces between the ions and the water can form a saturated solution in the formation water. By changing the solubility of the mineral ions, in the case of appropriate temperature and pressure conditions of the reservoir, it is possible to form mineral deposits.

In carbonate gas reservoirs, several chemical reactions occur during geological periods ^[27]. High concentrations of Ca²⁺ in the water of the Rag-e Sefied Formation can indicate a carbonate sedimentary environment. The concentration of Mg²⁺ also indicates a strong reaction between the reservoir rock of Rag-e Sefid oil and gas field and the formation water, associated with the precipitation of dolomite and dissolution of anhydrite ^[28,29,30].

The high concentration of chloride ions in the formation water, when compared to sulfate and bicarbonate mineral ions, can be related to the concentration of sodium chloride in ancient seawater and the low solubility of CaSO₄ and CaCO₃ ^[28,31].

Table 2 presents the analysis of the percentage of water-soluble materials in the Rag-e Sefid oil field. According to the results of Table 2, the volume percentage of sediments (organic and inorganic) in the water of the Rag-e Sefid formation for samples 1 to 5 were 90%, 46%, 95%, 24%, and 95% respectively. Such high ionic concentrations can cause problems in the operating system.

Table 2.  Volume percentage of water-soluble sediments in formation water of Rag-e Sefid oil and gas field.

Formation Water	volume percentage of sediments (organic and inorganic)
Sample 1	90%
Sample 2	46%
Sample 3	95%
Sample 4	24%
Sample 5	95%

---

 | Show Table

DownLoad: CSV

Table 3 presents the prediction of mineral deposition of calcium carbonate, magnesium carbonate, calcium sulfate, and gypsum for 5 wells in the Rag-e Sefid oil and gas field. Calcium carbonate sediment formation is significant for samples 1 to 5, and calcium sulfate mineral precipitates for samples 1, 2, 3, and 4 are significant. However, it is not possible to form gypsum and magnesium carbonate mineral deposits based on the concentration of water-soluble ions and the temperature and pressure conditions of the well. According to the results of Table 3, with increasing temperature and pressure, the saturation rate of gypsum and magnesium carbonate mineral deposits decreases and increases, respectively. This can be related to the solubility of magnesium carbonate and gypsum as well as the activity coefficient of calcium, magnesium, bicarbonate, and sulfate ions.

Table 3.  Prediction of sulfate and carbonate mineral scale formation index at different pressures and temperatures.

Well	Deposition (% Saturation*)	Survey Data
		3093 psia & 177.96 °F	3156 psia & 181.6 °F	3220 psia & 184.79 °F	3358 psia & 186.63 °F
Sample 1	CaSO4	100	100	100	100
	CaSO4·2H2O	23.38	21.88	20.81	20.13
	CaCO3	100	100	100	100
	MgCO3	17.93	19.38	20.53	21.33
Sample 2	CaSO4	100	100	100	100
	CaSO4·2H2O	25.16	23.55	22.4	21.33
	CaCO3	100	100	100	100
	MgCO3	7.5	8.11	8.59	8.92
Sample 3	CaSO4	100	100	100	100
	CaSO4·2H2O	23.64	22.12	21.04	20.35
	CaCO3	100	100	100	100
	MgCO3	13.56	14.66	15.53	16.13
Sample 4	CaSO4	100	100	100	100
	CaSO4·2H2O	24.56	22.99	21.86	21.14
	CaCO3	100	100	100	100
	MgCO3	11.57	12.5	13.24	13.76
Sample 5	CaSO4	91.4	94.81	97.43	99.2
	CaSO4·2H2O	23.05	22.37	21.86	21.53
	CaCO3	100	100	100	100
	MgCO3	13.72	14.8	15.65	16.24
Note: * % Saturation (% SR) = 100: Scale Formation. Saturation ratio is usually expressed as the ratio obtained by multiplying the activity of the ions by the chemical equilibrium constant.

---

 | Show Table

DownLoad: CSV

Mineral ions such as calcium, sodium, magnesium, iron, sulfate, chloride, and bicarbonate affect each other's behavior in the solid-liquid equilibrium system due to their electrical charges. This effect can cause supersaturation conditions in the formation water and in sediments, both in surface and subsurface facilities of oil and gas fields. Also, the presence of intermolecular forces of mineral anions and cations in water and the formation of ion pairs can be other factors affecting the behavior of mineral ions forming mineral precipitates in oil and gas field facilities.

In this study, in order to predict the formation of mineral deposits, different temperatures and pressures including 3093 psia/177.96 °F, 3156 psia/181.6 °F, 3220 psia/184.79 °F and 3358 psia/186.63 °F were considered. In the water analysis, SO₄^2- and Cl^- are major components (Figures 4 and 5). Based on geochemical analysis, Ca²⁺ and Mg²⁺ ions are major components in the reservoir rock samples. (Figure 6). Therefore, this comparison shows that the source of ions (except for calcium and magnesium ions) in the reservoir water is not the rock but waters of marine origin.

Figure 4.  Stiff diagram for water ion distribution in the water reservoir of the studied fieldF.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Piper diagram for distribution of ion in reservoir water in the 5 samples.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Distribution of elements in the rock reservoir in the studied field. LOI (Loss on ignition) is formed by components in the sample that evaporate due to heat and leave the system to reduce the total percentage of samples to less than 100. These include components such as water and carbon dioxide.

DownLoad: Full-Size Img PowerPoint

Table 4 shows the amount of mineral sediment in 5 samples collected at the Rag-e Sefid oil and gas field, according to StimCad 2 software based on the percentage of saturation index.

Table 4.  The amount of mineral precipitates in Rag-e Sefid oil field according to StimCad 2 software based on the percentage of saturation index.

Well	Deposition (mg/lit)	Survey Data
		3093 psia/178 °F	3156 psia/182 °F	3220 psia/185 °F	3358 psia/187 °F
Sample 1	CaSO4	1772.138	1822.854	1868.5	1894.7
	CaCO3	715.4	719.43	723.11	725.25
Sample 2	CaSO4	326.57	373.64	407.67	429.75
	CaCO3	129.51	131.01	132.12	132.85
Sample 3	CaSO4	1396.87	1451.48	1490.99	1516.66
	CaCO3	544.73	548.44	551.17	552.97
Sample 4	CaSO4	788.78	839.61	876.37	900.24
	CaCO3	127.42	128.95	130.1	130.85
Sample 5	CaCO3	160.52	162.314	163.63	164.5

---

 | Show Table

DownLoad: CSV

According to the results of Table 4, the formation of calcium sulfate and calcium carbonate deposits in the Rag-e Sefid Oil and Gas field is significant, with a higher rate for calcium sulfate. The amount of mineral precipitation in sample 1 was the highest, and sample 5 was the lowest. According to the results of Table 4, CaSO₄·2H₂O and magnesium carbonate mineral deposits cannot be formed due to the concentration of ions in the formation water. For sample 1, at a pressure of 3093 psia and a temperature of 178 °F, the amount of mineral sediment formation for calcium sulfate and calcium carbonate is 1772.138 and 715.4 mg/lit, respectively. However, based on the concentration of mineral ions in the formation water (Sample 1), at a pressure of 3358 psia and a temperature of 187 °F, the amount of mineral precipitates for calcium sulfate and calcium carbonate is 1894.7 and 725.25 mg/lit, respectively.

In this study, based on StimCad software, calcium carbonate deposit is the most important deposit that can be formed in the Rag-e Sefid oil and gas field, which is confirmed by the field results of Bijani and Khamechi's research. In the research of Bijani and Khamechi (2019) ^[32] the formation of mineral deposits in the desalination unit and the core pipes of the disposal well of the oil field and Reg-e Sefid gas has been investigated. The results of their work emphasize the formation of calcium carbonate deposits.

4.2.   Hydrocarbon preservation

Table 5 presents the hydrochemical properties of the mineral ions in the water of the Rag-e Sefid oil field. Based on the analysis of the concentration of mineral ions in the formation water of this field, a relation between these and hydrocarbon preservation can be obtained (Table 5), which can be expressed as follows:

Table 5.  Ion ratio for estimation of preservation of hydrocarbons in the studied field.

Formation water	Na+/Cl- (mg/l)	Cl--Na+/Mg2+ (mg/l)	HCO3-/Cl- (mg/l)	HCO-/Ca2+ (mg/l)	Mg2+/Ca2+ (mg/l)
Sample 1	0.565	28.24	0.0077	0.137	0.273
Sample 2	0.555	48.77	0.00229	0.032	0.127
Sample 3	0.567	34.81	0.00624	0.106	0.213
Sample 4	0.558	36.02	0.00205	0.032	0.192
Sample 5	0.545	28.48	0.00275	0.041	0.236

---

 | Show Table

DownLoad: CSV

Na⁺/Cl^- ratio. According to the table, the ratio of sodium to chloride in the water samples is in the range of 0.565 to 0.567. The numerical ratio of sodium to chlorine in the 5 samples studied (because it is less than one) can emphasize that the water in the Rag-e Sefid oil and gas field formation is ancient residual seawater that is sealed in the reservoir (without being associated with shallow water or active aquifers). Based on the ionic ratio obtained from sodium and chloride concentration, this formation is useful for storing hydrocarbons ^[33,34,35].

(Cl^--Na⁺)/Mg²⁺ ratio. This ratio is named as "metamorphic coefficient" and considered to evaluate the degree of water-rock interaction and ion replacement ^[36,37]. The ratio (Cl^--Na⁺)/Mg²⁺ in 5 water samples of the formation in the Rag-e Sefid oil and gas field ranges from 28.24 to 48.77. This high metamorphic coefficient, in the studied samples, indicates strong interactions between water and rock ^[38], so Na⁺ and Mg²⁺ are mainly displaced by Ca²⁺ and therefore have high metamorphic coefficients.

Mg²⁺/Ca²⁺ ratio. The ratio of magnesium to calcium in the water of the study formation is less than one. Dolomite formation leads to a high concentration of Ca²⁺ versus a low concentration of Mg²⁺ in the formation water. Therefore, dolomitization has an essential role in controlling Ca²⁺ and Mg²⁺ concentrations. Dolomite formation occurs in sealed reservoirs ^[39], so Mg²⁺/Ca²⁺ ratios have low ratios and can indicate sealing conditions ^{[27,33,40,41,42,43,44]}. Higher magnesium to calcium ratios can reduce hydrocarbon storage ^[38].

(HCO₃^--CO₃^2-)/Ca²⁺ ratio. This ratio is considered to test the decarbonization property ^[45]. The ratios of (HCO₃^--CO₃^2-)/Ca²⁺ in the formation water are mostly less than 0.5. Bicarbonate is the product of the dissolution of carbonate by oxygenated water. Previous studies have shown that low ratios of (HCO₃-CO₃^2-)/Ca²⁺ are typically associated with a high acid content, which is closely related to petroleum water organic matter ^[46,47,48]. It is therefore suitable for storing hydrocarbons ^[49,50,51].

(HCO₃^-)/Cl ratio. In the studied samples, this ratio is in the range of 0.00205 to 0.0077. Considering the ratio of 0.006 ≥ (HCO₃-)/Cl^- and also the ratio of (Cl^--Na⁺)/Mg²⁺ > 17.855 ^[38], the formation of the Rag-e Sefid oil and gas field has suitable conditions for gas production.

5.   Conclusions

The analysis of mineral ions in aqueous solutions is of great interest due to the saturation of mineral ions and the formation of mineral deposits in chemical systems such as oil fields. Lack of adequate analysis and sampling can lead to many technical problems. One of the most important problems is the presence of ions in the oil fields and the formation of mineral deposits in surface installations as well as reservoirs and wells. For this reason, in this study, for 5 wells of the Rag-e Sefid oil and gas field, mineral ions in formation water were studied. The main conclusions of the study of the 5 samples of formation water of the Rag-e Sefid oil and gas field are as follows:

ⅰ) the total amount of minerals dissolved in the formation water ranges from 174675 to 235909 mg/l; (ⅱ) the concentration of inorganic ions such as calcium, sodium, magnesium, sulfate, chloride, and bicarbonate in the formation water can affect the conditions of oil exploration processes; (ⅲ) the formation of calcium carbonate and calcium sulfate deposits, modeled for the the Rag-e Sefid oil and gas field, is significant and can affect operations; (ⅳ) the geochemical properties of formation water point to suitable conditions for gas production; (ⅴ) based on a comparison of formation waters and formation rocks, the source of ions (except for calcium and magnesium ions) in the water is mostly related to original marine water (and not to the sedimentary rocks); (ⅵ) the relation between geochemical properties and water distribution of the Rag-e Sefid Formation, points to favorable conditions for hydrocarbon production.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We are extremely grateful for the cooperation of Mr. Seyed Abdulrasoul Hashemi and managers of different departments of Gachsaran Oil and Gas Exploitation Company, as well as the constructive comments of both reviewers.

Conflict of interest

The authors declare no conflict of interest.