Conditional Ulam stability and its application to von Bertalanffy growth model

1.   Introduction

Fractional differential equations constitute an interesting area of research in view of their extensive applications in a variety of fields such as economics, financial issues, disease models, physical and chemical processes, etc. For theoretical and applications details of the subject, see the monographs ^{[6,12,16,19,23,24,26]} and the papers ^{[1,4,7,13,25,29,30]}. An important factor accounting for the popularity of the topic is the nonlocal nature of fractional order differential and integral operators, which provides insight into the past history of the phenomena. On the other hand, this aspect was missing in the models based on the tools of classical (integer order) calculus.

The Langevin equation (proposed by Langevin in 1908) is an important equation of mathematical physics, which can describe the evolution of physical phenomena in fluctuating environments ^[9]. For some new developments on the fractional Langevin equation, see, for example, ^[3,22,28] and references cited therein.

In the literature there are many papers dealing with boundary value problems for fractional Langevin equation of the form:

equipped with different kinds of boundary conditions, such as Dirichlet boundary conditions ^[2], nonlocal conditions ^[27], etc. Moreover, the fractional derivatives involved in Langevin equation are both Caputo type or Riemann-Liouville type or Hadamard type.

In the present paper we introduce a new nonlocal-terminal value problem for Langevin equation containing both Riemann-Liouville and Caputo type fractional derivatives and variable coefficient, supplemented with nonlocal-terminal fractional integro-differential conditions. In precise terms, we consider the following problem:

where ${}^{RL}D^q$ denotes the Riemann-Liouville fractional derivative of order $q \in (0, 1),$ ${}^{C}D^r,$ ${}^{C}D^{\nu}$ denote the Caputo fractional derivatives of orders $r$ and $\nu$ respectively, $0 < r < 1, 0 < \nu < r,$ $I^{p}$ is the Riemann-Liouville fractional integral of order $p > 0$, $\lambda\in C({\mathbb R}^+, {\mathbb R}),$ $f: [0, T]\times {\mathbb R}$ $\to {\mathbb R}$ and $\alpha, \beta\in {\mathbb R}.$

Concerning the motivation for the equation considered in (1.1), we refer the reader to the applications of such equations in physical phenomena exhibiting anomalous diffusion ^[15] and the height loss over time of the granular material contained in a silo ^[21]. The nonlocal conditions involved in the problem (1.1) are flux-integral type boundary conditions, which appear in several applications of diffusion processes and computational fluid dynamics (CFD) studies of blood flow problems, for instance, see ^[5].

The existence and uniqueness results for the problem (1.1), based on modern methods of functional analysis (fixed point theorems due to Banach, Krasnoselskii and nonlinear alternative of Leray-Schauder type), are obtained in Section 3. In Section 4 we extend our study to the multivalued analogue of the problem (1.1), that is, we investigate the following multivalued problem:

where $F: [0, T] \times {\mathbb{R}}\rightarrow {\mathcal P}({\mathbb{R}})$ is a multi-valued map, (${\mathcal P}({\mathbb{R}})$ is the family of all nonempty subsets of ${\mathbb R}$) and all other constants are as in problem (1.1).

We derive the existence results for the problem (1.2) with the aid of standard fixed point theorems for multivalued maps. In case of convex valued right-hand side of the inclusion, we use Leray-Schauder nonlinear alternative for multi-valued maps. In case of non-convex valued right hand side of the inclusion, we apply a fixed point theorem for multivalued contractions due to Covitz and Nadler. Examples illustrating the obtained results are presented in Section 5. Some basic concepts of fractional calculus, multivalued analysis and fixed point theory are outlined in Section 2. We also prove a basic result associated with the linear variant of the problem (1.1) in this section. Section 6 contains some interesting observations and a short discussion for the case when Caputo and Riemann-Liouville fractional derivatives are interchanged in the fractional Langevin equation in (1.1).

2.   Preliminaries

Let us recall some basic concepts of fractional calculus, multivalued analysis and state fixed point results related to our work.

2.1.   Fractional Calculus

In this subsection, we recall some basic concepts of fractional calculus ^[16,24] and present known results needed in our forthcoming analysis.

Definition 2.1. The Riemann-Liouville fractional derivative of order $q$ for a function $f: (0, \infty)\rightarrow{\mathbb R}$ is defined by

where $[q]$ denotes the integer part of the real number $q$, provided the right-hand side is pointwise defined on $(0, \infty)$.

Definition 2.2. The Riemann-Liouville fractional integral of order $q$ for a function $f: (0, \infty)\rightarrow{\mathbb R}$ is defined by

provided the right-hand side is pointwise defined on $(0, \infty)$.

Definition 2.3. The Caputo derivative of fractional order $q$ for a $n$-times derivative function $f: (0, \infty)\rightarrow{\mathbb R}$ is defined as

Lemma 2.1. If $\alpha+\beta > 1,$ then the equation $(I^{\alpha}I^{\beta}u)(t) = (I^{\alpha+\beta}u)(t), t\in [a, b]$ is satisfied for $u\in L^1([a, b], {\mathbb R}), 0 \le a < b < \infty.$

Lemma 2.2. Let $\beta > \alpha.$ Then the equation $(D^{\alpha}I^{\beta}u)(t) = (I^{\beta-\alpha}u)(t), t\in [a, b]$ is satisfied for $u\in C([a, b], {\mathbb R}).$

Lemma 2.3. Let $n = [\alpha]+1]$ if $\alpha\not\in {\mathbb N}$ and $n = \alpha$ if $\alpha\in {\mathbb N}.$ Then the following relations hold:

(i) for $k\in \{0, 1, 2, \ldots, n-1\}, \; D^{\alpha}t^k = 0;$

(ii) if $\beta > n$ then $D^{\alpha}t^{\beta-1} = \frac{\Gamma(\beta)}{\Gamma(\beta-\alpha)}t^{\beta-\alpha-1};$

(iii) $I^{\alpha}t^{\beta-1} = \frac{\Gamma(\beta)}{\Gamma(\beta+\alpha)}t^{\beta+\alpha-1}.$

Lemma 2.4. (see [16]) Let $q > 0$. Then for $y\in C(0, T)\cap L(0, T)$ holds

where $c_i\in \mathbb{R}$, $i = 1, 2, \ldots, n$ and $n-1 < q < n$.

Lemma 2.5. (see [16]) Let $q > 0$. Then for $y\in C(0, T)\cap L(0, T)$ holds

where $c_i\in \mathbb{R}$, $i = 0, 1, 2, \ldots, n-1$ and $n = [q]+1$.

Lemma 2.6. Let $\Lambda: = A\Gamma-B\ne0$ and $y\in C([0, T], {\mathbb R}).$ Then the linear problem

is equivalent to the integral equation

where

Proof. Firstly, we apply the Riemann-Liouville fractional integral of order $q$ to both sides of equation in (2.1), and then use Lemma 2.5 to obtain

where $c_1\in {\mathbb R}.$ Applying Riemann-Liouville fractional integral of order $r$ to both sides of (2.3), we get

where $c_2\in \mathbb{R}$.

From (2.4), we have

Using the above expressions in the fractional nonlocal-terminal conditions of the problem (2.1), we find that

Substituting the values of $c_1$ and $c_2$ into equation (2.4) we have

which yields the required solution. By direct computation we can prove the converse. This ends the proof.

Remark 2.1. In Lemma 2.6, note that the conditions $\Lambda\ne0$ corresponds to non-resonance case.

Corollary 2.1. (Special case: $\lambda(t) = \lambda$ = constant) Let $\Lambda\ne 0$ and $y\in C([0, T], {\mathbb R})$. Then the unique solution of the linear problem

is given by

3.   Existence results for the problem (1.1)

In order to transform the problem (1.1) into a fixed point problem, we introduce an operator $\mathcal{A}:\mathcal{C}\rightarrow\mathcal{C}$ by Lemma 2.6 as follows:

where $\mathcal{C}$ is the Banach space of continuous functions from $[0, T]$ to $\mathbb{R}$ equipped with the norm $\|x\| = \sup_{t\in[0, T]}|x(t)|.$ Evidently the existence of solutions for the problem (1.1) is related to the existence of fixed points for the operator $\mathcal{A}$.

For computational convenience, we use the notations:

where

Remark 3.1. In the special case of constant function $\lambda(t) = \lambda,$ $\Phi_{\lambda}$ becomes

We are now in a position to give our first existence and uniqueness result, which relies on the contraction mapping principle due to Banach.

Theorem 3.1. Let $f: [0, T]\times {\mathbb R}\to {\mathbb R}$ be a continuous function. Assume that:

$(H_1)$ there exists a positive constant $L$ such that

If

where $\Phi$ and $\Phi_{\lambda}$ are respectively given by (3.2) and (3.3), then the nonlocal-terminal value problem (1.1) has a unique solution on $[0, T].$

Proof. The hypothesis of contraction mapping principle will be verified in two steps. In the first step, we show that $\mathcal{A} B_r \subset B_r,$ where $\mathcal{A}$ is the operator defined by (3.1), $B_r = \{x \in \mathcal{C}: \|x\|\le r \},$ $r \ge M \Phi (1-L\Phi-\Phi_{\lambda})^{-1},$ $\sup_{t \in [0, T]}|f(t, 0)| = M < \infty.$ For any $x \in B_r,$ and taking into account assumption $(H_1)$, we obtain

which implies that $\mathcal{A}B_r\subset B_r$. In the next step, it will be shown that the operator $\mathcal{A}$ given by (3.1) is a contraction. For $t\in [0, T]$ and for $x, y\in \mathcal{C},$ we have

which leads to $\|\mathcal{A}x-\mathcal{A}y\|\le (L\Phi+\Phi_{\lambda}) \|x-y\|$. As $L\Phi+\Phi_{\lambda} < 1$, therefore $\mathcal{A}$ is a contraction. Since the hypothesis of Banach contraction mapping principle is satisfied, therefore we deduce by its conclusion that the operator $\mathcal{A}$ has a unique fixed point, which corresponds to a unique solution of the problem (1.1). The proof is completed.

Next, we prove an existence result for the problem (1.1) by using Krasnoselskii fixed point theorem ^[18].

Theorem 3.2. Assume that $f: [0, T]\times {\mathbb R}\to {\mathbb R}$ is a continuous function satisfying the assumptions:

$(H_2)$ $|f(t, x)|\leq \delta(t)$, $\forall (t, x)\in [0, T]\times \mathbb{R},$ $\delta \in C([0, T], \mathbb{R}^+)$ with $\|\delta\| = \sup_{t\in [0, T]}|\delta(t)|.$

$(\overline{H}_2)$ $\Phi_{\lambda} < 1,$ where $\Phi_{\lambda}$ is given by (3.4).

Then the nonlocal-terminal value problem (1.1) has at least one solution on $[0, T]$.

Proof. Let us select a positive number $\overline{r}$ such that $\overline{r}\geq \|\delta\|\Phi(1-\Phi_{\lambda})^{-1}$ and define operators $\mathcal{A}_1$ and $\mathcal{A}_2$ on $B_{\overline{r}} = \{x\in \mathcal{C}:\|x\|\leq \overline{r}\}$ as

Observe that $\mathcal{A}x = \mathcal{A}_1x+\mathcal{A}_2x$. For $x, y \in B_{\overline{r}}$, we have

This shows that $\mathcal{A}_1 x+ \mathcal{A}_2 y\in B_{\overline{r}}$. With the aid of the assumption $(\overline{H}_2)$, it is easy to show that $\mathcal{A}_2$ is a contraction. Further the operator $\mathcal{A}_1$ is continuous in view of continuity of $f$. Further $\mathcal{A}_1$ is uniformly bounded on $B_{\overline{r}}$ as

Next, we prove the compactness of the operator $\mathcal{A}_1$. Let us set $\sup_{(t, x)\in [0, T]\times B_{\overline{r}}}|f(t, x)| = \overline{f} < \infty$ and take $t_1, t_2\in [0, T]$ with $t_1 < t_2.$ Then we have

which tends to zero as $t_2\rightarrow t_1$ independent of $x$. Thus, $\mathcal{A}_1$ is equicontinuous. So $\mathcal{A}_1$ is relatively compact on $B_{\overline{r}}$. Hence, by the Arzelá-Ascoli theorem, $\mathcal{A}_1$ is compact on $B_{\overline{r}}$. Thus the operators $\mathcal{A}_1$ and $\mathcal{A}_2$ satisfy the hypothesis of Krasnoselskii fixed point theorem ^[18]. Hence it follows by the conclusion of Krasnoselskii fixed point theorem ^[18] that the operator $\mathcal{A} ( = \mathcal{A}_1+\mathcal{A}_2)$ has a fixed point, which corresponds to a solution of the problem (1.1) on $[0, T]$. The proof is completed.

In the following result, we prove the existence of solutions for the problem (1.1) by means of Leray-Schauder nonlinear alternative ^[14].

Theorem 3.3. Let $f: [0, T]\times {\mathbb R}\to {\mathbb R}$ be a continuous function satisfying the conditions:

$(H_3)$ there exist a continuous nondecreasing functions $\psi:[0, \infty)\rightarrow(0, \infty)$ and a function $\phi \in C([0, T], \mathbb{R}^+)$ such that $|f(t, x)|\leq \phi(t)\psi(|x|)$ for each $(t, x)\in [0, T]\times \mathbb{R}$;

$(H_4)$ there exists a constant $N > 0$ such that

where $\Phi$ and $\Phi_{\lambda}$ are respectively given by (3.2) and (3.3).

Then there exists at least one solution for the nonlocal-terminal value problem (1.1) on $[0, T].$

Proof. We verify the hypothesis of Leray-Schauder nonlinear alternative ^[14] in several steps. Let us first show that the operator $\mathcal{A},$ defined by $(3.1),$ maps bounded sets (balls) into bounded sets in $\mathcal{C}$. For a positive number $R$, let $B_{R} = \{x\in \mathcal{C}:\|x\|\leq R\}$ be a bounded ball in $\mathcal{C}$. Then, for $t\in [0, T]$, we have

In view of (3.2) and (3.3), the above inequality takes the form:

Secondly, we show that $\mathcal{A}$ maps bounded sets into equicontinuous sets of $\mathcal{C}$. Let $\nu_1, \nu_2\in [0, T]$ with $\nu_1 < \nu_2$ and $x\in B_{R}$. Then we have

Obviously the right hand side of the above inequality tends to zero independently of $x\in B_{R}$ as $\nu_2\rightarrow \nu_1$. Therefore it follows by the Arzelá-Ascoli theorem that $\mathcal{F}:\mathcal{C}\rightarrow \mathcal{C}$ is completely continuous.

In order to complete the hypothesis of the Leray-Schauder nonlinear alternative ^[14], it will be shown that the set of all solutions to the equation $x = \theta {\mathcal A}x$ is bounded for $\theta \in [ 0, 1].$ For that, let $x$ be a solution of $x = \theta {\mathcal A}x$ for $\theta \in [ 0, 1]$. Then, for $t\in [0, T],$ we apply the strategy used in the first step to obtain

where $\Phi$ and $\Phi_{\lambda}$ are respectively given by (3.3) and (3.4). Consequently, we have

By the condition $(H_4)$, we can find a positive number $N$ such that $\|x\|\neq N$. Introduce a set

and observe that the operator $\mathcal{A}:\overline{U}\rightarrow \mathcal{C}$ is continuous and completely continuous. With this choice of $U$, we cannot find $x\in \partial U$ satisfying the relation $x = \theta \mathcal{A}x$ for some $\theta\in(0, 1)$. Therefore, it follows by nonlinear alternative of Leray-Schauder type ^[14] that the operator ${\mathcal A}$ has a fixed point in $\overline{U}.$ Thus there exists a solution of the problem (1.1) on $[0, T]$. The proof is complete.

4.   Multi-valued case

We begin this section with the definition of a solution for the multi-valued problem (1.2).

Definition 4.1. A function $x\in C([0, T], {\mathbb R})$ is said to be a solution of the problem (1.2) if there exists a function $v\in L^1([0, T], \mathbb{R})$ with $v(t)\in F(t, x)$ a.e. on $[0, T]$ such that $x(\xi) = \lambda ^CD^{\nu}x(\eta), \; x(T) = \mu I^p x(\zeta)$ and

4.1.   The upper semicontinuous case

Our first result, dealing with the convex-valued $F$, is based on Leray-Schauder nonlinear alternative for multi-valued maps.

Definition 4.2. A multivalued map $F : [0, T] \times \mathbb{R} \to {\mathcal{P}}(\mathbb{R})$ is said to be Carathéodory if (i) $t \longmapsto F(t, x)$ is measurable for each $x \in \mathbb{R}$ and (ii) $x \longmapsto F(t, x)$ is upper semicontinuous for almost all $t\in [0, T].$ Further a Carathéodory function $F$ is called $L^1-$Carathéodory if (iii) for each $\rho > 0$, there exists $\varphi_{\rho} \in L^1([0, T], \mathbb{R}^+)$ such that $\|F (t, x)\| = \sup \{|v| : v \in F (t, x)\} \le \varphi_{\rho} (t)$ for all $x\in {\mathbb R}$ with $\|x\| \le \rho$ and for a.e. $t \in [0, T].$

Theorem 4.1. Assume that:

$(A_1)$ $F : {[0, T]} \times \mathbb{R} \to {\mathcal{P}_{cp, c}}(\mathbb{R})$ is $L^1$-Carathéodory, where ${\mathcal P}_{cp, c}(\mathbb{R}) = \{Y \in {\mathcal{P}}(\mathbb{R}) :$ Yiscompactandconvex};

$(A_2)$ there exist a continuous nondecreasing function $Q: [0, \infty) \to (0, \infty)$ and a function $P \in C([0, T], \mathbb{R}^+)$ such that $\|F(t, x)\|_\mathcal{P}: = \sup\{|y|: y \in F(t, x)\}\le P(t)Q(|x|) \; \; \mathit{\mbox{for each}}\; \; (t, x)$ $\in [0, T] \times \mathbb{R};$

$(A_3)$ there exists a constant $M > 0$ such that

where $\Phi$ and $\Phi_{\lambda}$ are respectively given by (3.3) and (3.4).

Then the nonlocal-terminal value problem (1.2) has at least one solution on $[0, T]$.

Proof. Firstly, we transform the problem (1.2) into a fixed point problem by defining a multi-valued map: $N:C([0, T], {\mathbb R})\rightarrow {\mathcal P}(C([0, T], {\mathbb R}))$ as

for $v \in S_{F, x}.$

It is clear that fixed points of $N$ are solutions of problem (1.2). So we need to verify that the operator $N$ satisfies all the conditions of Leray-Schauder nonlinear alternative ^[14]. This will be done in several steps.

Step 1. $N(x)$ is convex for each $x \in C([0, T], \mathbb{R}).$

Indeed, if $h_1, h_2$ belongs to $N(x)$, then there exist $v_1, v_2\in S_{F, x}$ such that, for each $t\in [0, T]$, we have

$i = 1, 2.$ Let $0\leq \theta\leq 1$. Then, for each $t\in [0, T]$, we have

Since $F$ has convex values ($S_{F, x}$ is convex), therefore, $\theta h_1+(1-\theta)h_2\in N(x).$

Step 2. $N(x)$ maps bounded sets (balls) into bounded sets in $C([0, T], \mathbb{R}).$

For a positive number $r$, let $B_r = \{x \in C([0, T], \mathbb{R}): \|x\| \le r \}$ be a bounded ball in $C([0, T], \mathbb{R})$. Then, for each $h\in N(x), x\in B_r,$ there exists $v\in S_{F, x}$ such that

In view of $(H_2),$ for each $t\in {[0, T]},$ we have

which yields

Step 3. $N(x)$ maps bounded sets into equicontinuous sets of $C({[0, T]}, \mathbb{R}).$

Let $x$ be any element in $B_r$ and $h\in N(x)$. Then there exists a function $v\in S_{F, x}$ such that, for each $t\in {[0, T]}$ we have

Let $\tau_1, \ \tau_2\in {[0, T]}, \ \tau_1 < \tau_2$. Then

The right hand of the above inequality tends to zero independently of $x\in B_r$ as $\nu_1\rightarrow \nu_2$.

Combining the outcome of Steps 1–3 with Arzelá-Ascoli theorem, we deduce that $N: C({[0, T]}, \mathbb{R}) \to {\mathcal{P}}(C({[0, T]}, \mathbb{R}))$ is completely continuous.

In order to prove that the operator $N$ is u.s.c., it is enough to establish that it has a closed graph by Proposition 1.2 in ^[11], as it is already shown to be completely continuous. This is done in the next step.

Step 4. $N$ has a closed graph.

Let $x_n\rightarrow x_*$, $h_n\in N(x_n)$ and $h_n\rightarrow h_*$. We need to show that $h_*\in N(x_*)$. Now $h_n\in N(x_n)$ implies that there exists $v_n\in S_{F, x_n}$ such that, for each $t\in {[0, T]}$,

Therefore, we must show that there exists $v_*\in S_{F, x_*}$ such that, for each $t\in {[0, T]}$,

Consider the continuous linear operator $\Theta:L^1({[0, T]}, {\mathbb{R}})\rightarrow C({[0, T]}, {\mathbb R})$ given by

Observe that $\|h_n(t)-h_*(t)\|\to 0$ as $n\to \infty.$ So it follows from by a closed graph result obtained in ^[20] that $\Theta\circ S_{F, x}$ is a closed graph operator. Moreover, we have $h_n\in\Theta(S_{F, x_n}).$ Since $x_n\rightarrow x_*$, therefore we have

for some $v_*\in S_{F, x_*}$

Step 5. We show there exists an open set ${\mathcal V} \subseteq C({[0, T]}, {\mathbb R})$ with $x\notin \theta N (x)$ for any $\theta\in (0, 1)$ and all $x\in \partial {\mathcal V}.$

Let $\theta\in (0, 1)$ and $x\in \theta N (x).$ Then there exists $v \in L^1({[0, T]}, \mathbb{R})$ with $v \in S_{F, x}$ such that, for $t \in {[0, T]}$, we have

Using the computations done in Step 2, for each $t\in {[0, T]},$ we get

which can alternatively be written as

In view of $(A_{3})$, there exists $M$ such that $\|x\| \ne M$. Let us define a set

The operator $N :\overline{{\mathcal V}} \to \mathcal{P}(C({[0, T]},$ $\mathbb{R}))$ is a compact multi-valued map, u.s.c. with convex closed values. With the given choice of ${\mathcal V}$, it is not possible to find $x \in \partial {\mathcal V}$ satisfying $x \in \theta N (x)$ for some $\theta \in (0, 1)$. In consequence, we deduce by the nonlinear alternative of Leray-Schauder type ^[14] that the operator $N$ has a fixed point $x \in \overline{{\mathcal V}},$ which corresponds to a solution of the problem (1.2). This completes the proof.

4.2.   The Lipschitz case

Let $({\mathcal X}, d)$ be a metric space induced from the normed space $({\mathcal X}; \|\cdot\|)$. Consider $H_d : {\mathcal{P}}({\mathcal X}) \times {\mathcal{P}}({\mathcal X}) \to \mathbb{R} \cup \{\infty\}$ defined by $H_d(A, B) = \max\{ \sup _{a \in A}d(a, B), \sup _{b \in B}d(A, b)\},$ where $d(A, b) = \inf_{a\in A}d(a; b)$ and $d(a, B) = \inf_{b\in B}d(a; b)$. Then $({\mathcal P}_{b, cl}({\mathcal X}),$ $H_d)$ is a metric space (see ^[17]), where ${\mathcal P}_{b, cl}({\mathcal X}) = \{{\mathcal Y} \in {\mathcal{P}}({\mathcal X}) : {\mathcal Y} \mbox{ is bounded and closed}\},$

Now we present our existence result for the problem (1.2) with a non-convex valued right hand side by applying a fixed point theorem for multivalued maps due to Covitz and Nadler ^[10]: ``If $N : {\mathcal X} \to {\mathcal P}_{cl}({\mathcal X})$ is a contraction, then $Fix N \ne \emptyset$, where ${\mathcal P}_{cl}({\mathcal X}) = \{{\mathcal Y} \in {\mathcal{P}}({\mathcal X}) : {\mathcal Y} \mbox{ is closed}\}".$

Theorem 4.2. Assume that the following conditions hold:

$(A_4)$ $F : {[0, T]} \times \mathbb{R} \to {\mathcal P}_{cp}(\mathbb{R})$ is such that $F(\cdot, x) : {[0, T]} \to {\mathcal P}_{cp}(\mathbb{R})$ is measurable for each $x \in \mathbb{R},$ where ${\mathcal P}_{cp}(\mathbb{R}) = \{{\mathcal Y} \in {\mathcal{P}}(\mathbb{R}) : {\mathcal Y} \mathit{\mbox{is compact}}\}$;

$(A_5)$ $H_d(F(t, x), F(t, \bar{x}))\le \varrho(t)|x-\bar{x}|$ for almost all $t \in {[0, T]}$ and $x, \bar{x} \in \mathbb{R}$ with $\varrho \in C({[0, T]}, \mathbb{R}^+)$ and $d(0, F(t, 0))\le \varrho(t)$ for almost all $t \in {[0, T]}$.

Then the nonlocal-terminal value problem (1.2) has at least one solution on ${[0, T]}$ if

where $\Phi$ and $\Phi_{\lambda}$ are respectively given by (3.3) and (3.4).

Proof. Once it is shown that the operator $N: C({[0, T]}, \mathbb{R})\to {\mathcal P}(C({[0, T]}, \mathbb{R})),$ defined in the beginning of the proof of Theorem 4.1, satisfies the assumptions of Covitz and Nadler fixed point theorem ^[10], we are done. We establish in two steps.

Step Ⅰ. $N(x)$ is nonempty and closed for every $v\in S_{F, x}.$

Observe that the set-valued map $F(\cdot, x(\cdot))$ admits a measurable selection $v: {[0, T]} \to \mathbb{R}$ as it is measurable by the measurable selection theorem (e.g., [8, Theorem Ⅲ.6]). Moreover, by the assumption $(A_5),$ we have

that is, $v \in L^1({[0, T]}, \mathbb{R})$ and hence $F$ is integrably bounded. Therefore, $S_{F, x} \ne \emptyset$.

Next we show that $N(x)$ is closed for each $x \in C({[0, T]}, \mathbb{R}).$ Let $\{u_n\}_{n \ge 0} \in N(x)$ be such that $u_n \to u$ as $n \to \infty$ in $C({[0, T]}, \mathbb{R}).$ Then $u \in C({[0, T]}, \mathbb{R})$ and there exists $v_n \in S_{F, x_n}$ such that, for each $t \in {[0, T]}$,

As $F$ has compact values, we pass onto a subsequence (if necessary) to obtain that $v_n$ converges to $v$ in $L^1 ({[0, T]}, \mathbb{R}).$ Thus $v \in S_{F, x}$ and for each $t \in {[0, T]}$, we have

Hence $u \in N(x).$

Step Ⅱ. We show that there exists $0 < \hat \theta < 1$ ($\hat\theta = \Phi \|\varrho\|+\Phi_{\lambda}$) such that

Let $x, \bar{x} \in C({[0, T]}, \mathbb{R})$ and $h_1 \in N(x)$. Then there exists $v_1(t) \in F(t, x(t))$ such that, for each $t \in {[0, T]}$,

By $(A_5)$, we have

So, there exists $w(t) \in F(t, \bar{x}(t))$ such that

Define ${\mathcal U} : {[0, T]} \to \mathcal{P}(\mathbb{R})$ by

As the multivalued operator ${\mathcal U}(t)\cap F(t, \bar{x}(t))$ is measurable (see Proposition Ⅲ.4 [8]), there exists a function $v_2(t)$ which is a measurable selection for ${\mathcal U}$. So $v_2(t) \in F(t, \bar{x}(t))$ and for each $t \in {[0, T]}$, we have $|v_1(t)-v_2(t)|\le \varrho(t)|x(t)-\bar{x}(t)|$.

For each $t \in {[0, T]}$, let us define

In consequence, we get

Hence

Analogously, interchanging the roles of $x$ and $\overline{x}$, we obtain

Therefore, $N$ is a contraction in view of the given condition($(\Phi\|\varrho\|+\Phi_{\lambda}) < 1$). Hence it follows by the conclusion of Covitz and Nadler fixed point theorem ^[10] that $N$ has a fixed point $x$, which corresponds to a solution of (1.2). The proof is complete.

5.   Examples

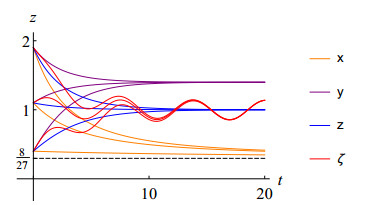
Consider the following nonlocal-terminal value problem

Here $q = 2/3, r = 3/4, \xi = 2/3, \eta = 1/3, \nu = 1/2, \alpha = 5, \beta = 4, \zeta = 4/5, p = 1, T = 1.$ Using the given data in (2.2), we find that $A\approx -5.739178, B \approx -1.616533, \Gamma \approx -1.915888,$ and $\Lambda \approx 12.612155.$ From (3.5), we have $\bar\lambda_1 \approx 0.360215$ and $\bar\lambda_2 \approx 0.576166.$ Inserting the given values in (3.3) and (3.4), we obtain $\Phi \approx 2.538503$ and $\Phi_\lambda \approx 0.502890.$

In order to illustrate Theorem 3.1, we take

in (5.1), where $L$ is to be fixed later. Obviously $|f(t, x)-f(t, y)|\leq L |x-y|, \, t\in [0, 1], \, x, y \in {\mathbb R}$ and $L\Phi+\Phi_{\lambda} < 1$ is satisfied for $L < 0.195828.$ Thus all the assumptions of Theorem 3.1 are satisfied. Hence, by the conclusion of Theorem 3.1, the problem (5.1) with $f(t, x)$ given by (5.2) has a unique solution on $[0, 1]$.

Also the conclusion of Theorem 3.2 applies to the problem (5.1) with $f(t, x)$ given by (5.2) as $|f(t, x)|\le [\pi+2 +\sqrt{t^4+3}] = \delta(t),$ where $L = 4.$

For the illustration of Theorem 3.3, let us take

and note that $|f(t, x)| \le \phi(t) \psi(|x|),$ where $\phi(t) = e^{-t^2}/\sqrt{t^4+100},$ and $\psi(|x|) = (|x|+1/10).$ So the assumption $(H_3)$ holds. Moreover, there exists $N > 0.1043536$ satisfying $(H_4)$. Thus all the conditions of Theorem 3.3 are satisfied and consequently the problem (5.1) with $f(t, x)$ given by (5.3) has at least one solution on $[0, 1].$

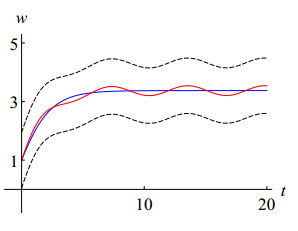
Now we illustrate Theorem 4.2 by considering the following multivalued problem:

where

Clearly $H_d(F(t, x), F(t, \bar{x}))\leq \varrho(t)|x-\bar{x}|,$ where $\varrho(t) = \frac{2}{(t+4)^2}.$ Also $d(0, F(t, 0))\le \varrho(t)$ for almost all $t \in [0, 1]$ and $\Phi \|\varrho\|+\Phi_{\lambda} \approx 0.820203 < 1.$ As the hypothesis of Theorem 4.2 is satisfied, therefore we conclude that the multivalued problem (5.4) has at least one solution on $[0, 1].$

6.   Conclusions

We have studied a new nonlocal-terminal value problem consisting of Langevin equation with variable coefficient involving both Riemann-Liouville and Caputo fractional derivatives, and equipped with nonlocal-terminal fractional integro-differential conditions. The results presented in this paper are new and enrich the existing literature on boundary value problems of Langevin equation.

As an analogue of the problem (1.1), we interchange the role of Riemann-Liouville and Caputo fractional derivatives in the Langevin equation given by (1.1) and consider the following nonlocal boundary value problem:

As argued in the proof of Lemma 2.6, the solution of the Langevin equation in (6.1) can be written as

Using the condition $x(0) = 0$ in (6.2) implies that $c_2 = 0$. Inserting the value of $c_2$ in (6.2) and then using the resulting expression for $x(t)$ in the condition $x(T) = \beta\; I^px(\zeta)$, we find that

where

Thus the solution of the problem (6.1) is

One can notice that the solution (6.2) becomes unbounded at $t = 0$ in view of the values of $q \in (0, 1)$, in contrast to the problem (1.1). So we impose the condition $x(0) = 0$ to ensure the boundedness of the solution of the Langevin equation in (6.1). It is equivalent to saying that the problem (1.1) is now well-posed one. The existence results for the problem (6.1), analogue to the ones for (1.1), can be obtained in a similar manner.

Special cases. We can obtain several new results as special cases of the work presented in this paper by fixing the values of parameters involved in the problem at hand, which are listed below.

● By taking $\alpha = 0,$ our results correspond to the ones for nonlocal-terminal fractional integral conditions: $x(\xi) = 0, x(T) = \beta\; I^px(\zeta), \xi, \zeta\in (0, T)$.

● The results of this paper reduce to the ones with boundary conditions of the form: $x(\xi) = \alpha\; ^C D^{\nu}x(\eta), \; x(T) = 0, \; \xi, \eta \in (0, T)$ by fixing $\beta = 0.$

● Letting $\alpha = 0, \beta = 0$ in the results of this paper, we obtain the ones associated with the nonlocal-terminal conditions: $x(\xi) = 0, x(T) = 0$.

Acknowledgment

The authors thank the reviewers for their useful remarks on our paper.

Conflict of interest

All authors declare no conflicts of interest in this paper.