Figure 1.
The 2D cross section along the transverse plane of the 3D finite element model of cervical spinal cord.
Citation: Rui Zhu, Yuhang Chen, Qianqian Yu, Siqing Liu, Jianjie Wang, Zhili Zeng, Liming Cheng. Effects of contusion load on cervical spinal cord: A finite element study[J]. Mathematical Biosciences and Engineering, 2020, 17(3): 2272-2283. doi: 10.3934/mbe.2020120
| [1] | Won Man Park, Young Joon Kim, Shaobai Wang, Yoon Hyuk Kim, Guoan Li . Investigation of lumbar spine biomechanics using global convergence optimization and constant loading path methods. Mathematical Biosciences and Engineering, 2020, 17(4): 2970-2983. doi: 10.3934/mbe.2020168 |
| [2] | Xiaoyu Du, Yijun Zhou, Lingzhen Li, Cecilia Persson, Stephen J. Ferguson . The porous cantilever beam as a model for spinal implants: Experimental, analytical and finite element analysis of dynamic properties. Mathematical Biosciences and Engineering, 2023, 20(4): 6273-6293. doi: 10.3934/mbe.2023270 |
| [3] | Shanzheng Wang, Xinhui Xie, Chao Li, Jun Jia, Changhong Chen . Integrative network analysis of N6 methylation-related genes reveal potential therapeutic targets for spinal cord injury. Mathematical Biosciences and Engineering, 2021, 18(6): 8174-8187. doi: 10.3934/mbe.2021405 |
| [4] | Han Zhou, Yikun Li, Ying Gu, Zetian Shen, Xixu Zhu, Yun Ge . A deep learning based automatic segmentation approach for anatomical structures in intensity modulation radiotherapy. Mathematical Biosciences and Engineering, 2021, 18(6): 7506-7524. doi: 10.3934/mbe.2021371 |
| [5] | Huihao Wang, Kuan Wang, Zhen Deng, Xiaofei Li, Yi-Xian Qin, Hongsheng Zhan, Wenxin Niu . Effects of facet joint degeneration on stress alterations in cervical spine C5–C6: A finite element analysis. Mathematical Biosciences and Engineering, 2019, 16(6): 7447-7457. doi: 10.3934/mbe.2019373 |
| [6] | Jana Zatloukalova, Kay Raum . High frequency ultrasound assesses transient changes in cartilage under osmotic loading. Mathematical Biosciences and Engineering, 2020, 17(5): 5190-5211. doi: 10.3934/mbe.2020281 |
| [7] | Fang Wang, Jiaming Wang, Mingxin Li, Jun Hu, Kehua Song, Jianguo Zhang, Yubo Fan . Biomechanical study of the effect of traction on elbow joint capsule contracture. Mathematical Biosciences and Engineering, 2023, 20(12): 21451-21466. doi: 10.3934/mbe.2023949 |
| [8] | Christian Engwer, Markus Knappitsch, Christina Surulescu . A multiscale model for glioma spread including cell-tissue interactions and proliferation. Mathematical Biosciences and Engineering, 2016, 13(2): 443-460. doi: 10.3934/mbe.2015011 |
| [9] | Lin Chen, Mingjun Wang, Zhanyu Wu, Jinbo Sun, Jianglong Li, Chun Chen, Chuan Ye . Advancements in health informatics: finite element insights into medial open-wedge high tibial osteotomy and lateral meniscal tears. Mathematical Biosciences and Engineering, 2024, 21(4): 5394-5410. doi: 10.3934/mbe.2024237 |
| [10] | Yan Yan, Yong Qian, Hongzhong Ma, Changwu Hu . Research on imbalanced data fault diagnosis of on-load tap changers based on IGWO-WELM. Mathematical Biosciences and Engineering, 2023, 20(3): 4877-4895. doi: 10.3934/mbe.2023226 |
Injury of cervical spine, a common injury of locomotor system usually accompanied by spinal cord injury, could bring heavy burden to patients [1]. The clinical features include incomplete injury of the spinal cord, which could lead to such clinical syndromes as central cord syndrome, anterior/posterior cord syndrome or Brown-Sequard syndrome. Currently the causes of such clinical symptoms and injury mechanisms are still unclear, therefore it is of clinical interest to understand the damage mechanism and its interplay with the pathophysiological changes.
Clinical data such as those obtained from medical imaging can provide useful information for the mechanism analysis, diagnosis and treatment of the cervical spinal cord injury. Quencer et al. [2] studied MRI images from 11 patients with central cord syndrome. The lesions were found mainly in the axons of the lateral funiculus of white matter, while the central area of gray matter showed no signs of bleeding. Curt et al. [3] reported that, in central cord syndrome, axons that control hand movement are more susceptible than those for lower limb movement, suggesting that axon characteristics could have greater influences in neurological dysfunction of the upper limb than the lower limbs. Despite of these findings, few biomechanical studies have been reported, possibly due to the fact that it is not trivial to design in vivo experiments therefore some parameters cannot be measured directly in patients. Same can be said to in vitro studies, as it is difficult in specimen preparation, preservation and control of loading conditions.
Finite Element (FE) has been widely used as a complementary tool to experimental biomechanical study and is a candidate to address this issue, particularly in characterising the stress and strain distributions. However, it has certain challenges, such as the modelling of soft tissue and muscle tension [4,5]. Scifert et al. [6] developed a three-dimensional (3D) FE model to quantify the physiological strains and stresses in the cervical spinal cord in C5-C6 motion segment. Li et al. [7] conducted an FE analysis of C5-C6 spinal cord and analyze the features of stress distributions in the cervical spinal cord under different injury conditions. They concluded that hyperpathia may be resulted from injuries at the posterior horn, the anterior funiculus or the fasciculus cuneatus. Moreover, Khuyagbaatar et al. [8] studied the von-Mises stress and maximum principal strain in the spinal cord as well as its cross-sectional area of cord for three mechanisms of spinal cord injury. Afterwards, biomechanical effects on cervical spinal cord and nerve root following laminoplasty were compared between open-door and double-door laminoplasty using a similar spinal cord FE model [9]. Zareen et al. [10] used a FE model of motor cortex and spinal cord to direct trans-spinal direct current stimulation in order to investigate the recovery of corticospinal tract axonal outgrowth and motor after cervical contusion spinal cord injury. Although the aforementioned studies provided useful data for the investigation of injury mechanisms of spinal cord, anatomical components such as pia mater, which may have significant roles in the deformation mechanisms of the spinal cord [11,12,13], were not included. In addition, the variation in loading direction applied and the injury process with different extents of spinal cord compression were not taken into account.
This study aims to establish and validate a 3D FE biomechanical model of cervical spinal cord and, more importantly, to investigate its injury mechanism associated with the contusion load, with different extents of spinal cord compression.
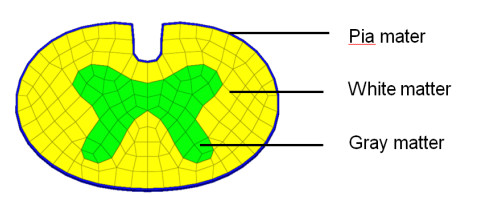
A 3D FE biomechanical model of three segments of the human cervical spinal cord, namely the gray matter, white matter and pia mater which were assumed symmetrical with respect to the mid-sagittal plane, was proposed here and illustrated in Figure 1. The geometries of the gray matter and white matter were recontructed from MR images of a 25 years old male who has no diagnosed spine disease. A segment, 60 mm long, of the spinal cord was modeled to represent three vertebrae [14] and meshed using 6-node wedge and 8-node hexahedral FE elements. The pia mater, not visible in the MR images [15], was modeled as a shell surrounding the white matter, with a thickness of 0.1 mm [16]. The curvature of the spine, not illustrated here, was obtained from the MR images of the volunteer showing lordosis.
The mechanical properties for all three modeled materials are summarised here in Table 1. The nonlinear, hyperelastic Ogden model was employed to model the white and gray matter [8,17]. The pia mater was considered to be elastic and its material properties were adopted from previous studies [18,19]. The mesh convergence test, where the mesh density of the entire model was doubled or halved until convergence, was carried out.
| Material Properties | References | |
| Gray matter | Hyperelastic (Ogden): Μ = 0.0041 MPa, α = 14.7 |
[8,17] |
| White matter | Hyperelastic (Ogden): Μ = 0.004 MPa, α = 12.5 |
[8,17] |
| Pia matter | Elastic: E = 2.3 MPa, υ = 0.3 | [13,18,19] |
DownLoad:
CSV
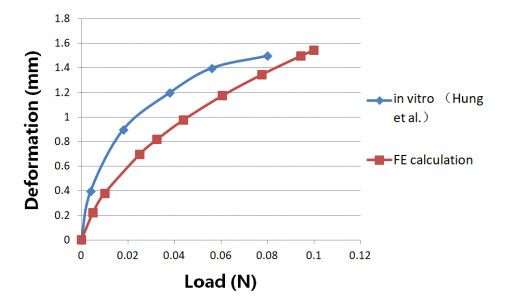
For the validation purpose, compressive forces of 0–0.1 N, in the saggital plane and acting perpendicular to the axial direction of the spinal cord, was applied at the middle section of the spinal cord. This was considered to match the experimental conditions from the previous study [20], in which the force and deformation of the spinal cord of animal subject to force perpendicular to the long axis of the spinal cord were studied. The relationship between the calculated displacement and the compressive force was then compared to data extracted from this experimental study [20].
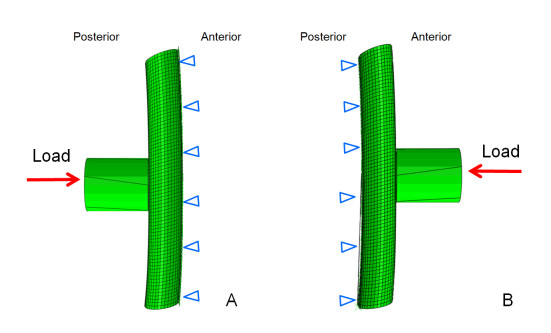
In this study, the contusion load was applied from back to front of the spinal cord to represent the scenario of compression of the fracture fragment, while the load along the reversed direction, i.e. from front to back, was applied to represent that of disc herniation or ligament ossification. The load is applied by a rigid cylinder with cross-sectional diameter of 13 mm (scaled to be equivalent to the diameter of the lateral cord), as illustrated in Figure 2. The direction of the cylinder is along the loading direction, perpendicular to the cervical spinal cord. A set of displacements, equivalent to 10% (0.84 mm), 20% (1.68 mm), 30% (2.52 mm) and 40% (3.36 mm) of the sagittal diameter of the spinal cord representing different extents of contusion, was applied to the rigid cylinder to the spinal cord, as shown. Although different from the way how the load was applied for the purpose of validation as aforementioned, applying a displacement enabled the data comparison between two different loading conditions (i.e. front-to-back and back-to-front) and made it possible to have progressive stages of contusion that can be linked to its severity with reference to the relative position among all parts of the spine involved. The FE analysis was carried out in ABAQUS (Valley Street, Providence, RI, USA).
The mesh convergence test was carried out on the proposed spinal cord model using different mesh densities, until the maximum deformation and von Mises stress only change by less than 5% between two consecutive simulations. As aforementioned, compressive forces of 0–0.1 N in the saggital plane and acting perpendicular to the axial direction of the spinal cord, were applied at the center section of the spinal cord for validation purpose. The derived displacement is ploted against the applied force, in comparison with the data extracted from a previous experimental study [20], as shown in Figure 3. The results from the FE model showed a similar trend to the data measured from the in vitro experiment.
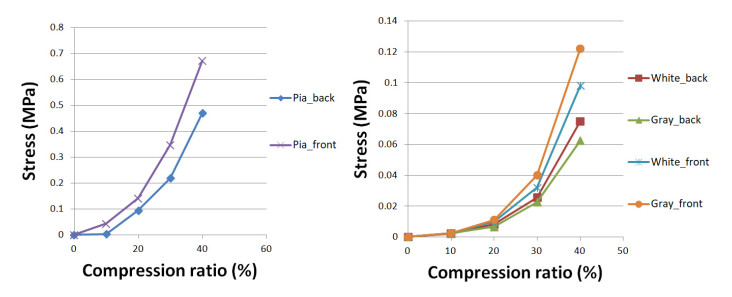
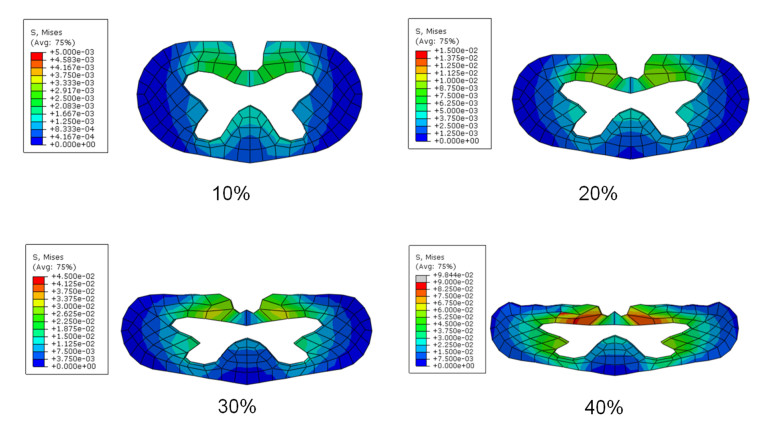
The maximum von Mises stress across the middle transverse section is shown in Figure 4. The stress in the pia mater is significantly higher than that in the gray and white matter and, in general, the stress is higher in the scenario of front-to-back load than the back-to-front load case. Interestingly, under the same loading condition, areas of gray and white matter are in similar stress level, and the maximum stress is in gray matter in the case of front-to-back load.
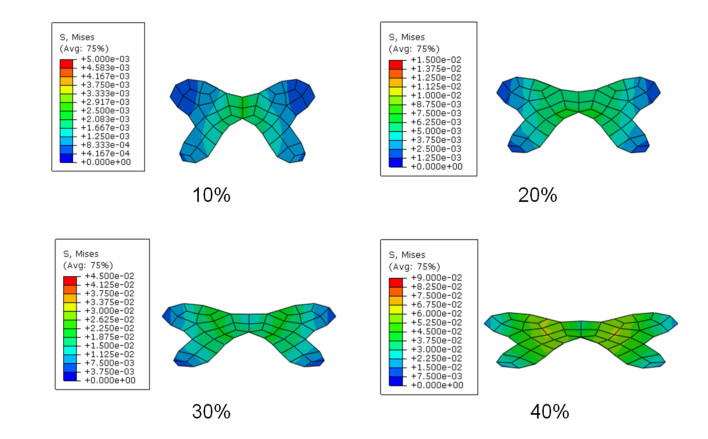
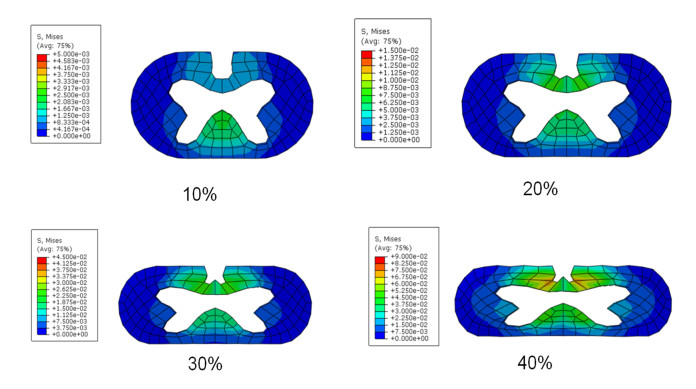
The von-Mises stress distributions in the transverse cross sections of gray matter with back-to-front load were presented in Figure 5. The high level of von Mises stress was mainly located at the central canal area of the gray matter under the compression of 10% and 20%. When the compression further increases, the distribution of von Mises stress displayed a different pattern and the highest stress area extended to both left and right sides near the central canal. The unified scale bar was used for each compression ratio for clear comparison, while cases under different compression ratio had different scale bars.
For the white matter with back-to-front load, as shown in Figure 6, the highest von Mises stress was located in the central canal area under 10% compression. When the compression ratio increased, the pattern of stress distribution changed and the location of maximum stress switched to the area closed to anterior median fissure.
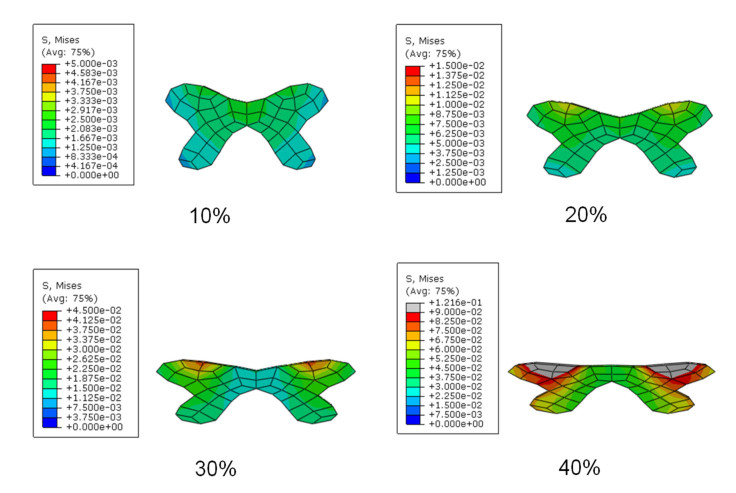
The von-Mises stress distributions in the transverse cross sections of gray matter subjected to the front-to-back load were presented in Figure 7. The highest von Mises stress was seen at the central canal area when subject to 10% compression, whilst it appeared at the anterior horn of the spinal cord when the compression increased.
For the white matter in the scenario of front-to-back load, the highest von Mises stress appeared in the area of the anterior funiculus close to anterior median fissure. Such an area was close to the location of the highest stress in the gray matter in Figure 7. Unlike the gray matter, the location of maximum stress in the white matter remained unchanged when the compression increased.
In back-to-front loading scenario, the posterior funiculus and posterior median sulcus had the largest displacement in posterior-anterior direction. The gray matter was affected less in this direction but mainly shifts left and right. In front-to-back loading scenario, the anterior funiculus had the largest displacement and the anterior horn was also affected to some extent in anterior-posterior direction.
A finite element model of cervical spinal cord was established and two scenarios of contusion injury loading conditions, i.e. back-to-front and front-to-back load, were applied. In addition, four different compression displacements were applied to the middle section of the cervical spinal cord. The maximum of von Mises stress, stress distribution and displacement in middle transverse cross section were obtained from the FE analysis and explored for understanding the mechanism of spinal cord injury. Through injury biomechanics studies, data may be used to develop appropriate injury classification criteria [21], or design more realistic braces and protective gear [22].
Stress distribution could provide key information to exploring the damage mechanism of spinal cord and has been extensively studied. Since biological tissues in general have nonlinear stress–strain responses [23], the hyperelastic material model was utilized for the white and gray matters. Little mechanical measurement data was available for human pia matter therefore elastic properties were adopted from previous studies [18,19], despite the fact that such data was acquired from animal tissue.
In order to validate the proposed FE model, data from a previous experimental study [20] was used. Despite of a similar trend in the load-displacement curves between the experimental and FE data, a certain extent of discrepancy can be observed. This can be resulted, particularly, from the fact that the experimental study was conducted on small animals, as well as from the possible difference in load contact area which was not reported in the literature.
The maximum von Mises stress in the middle transverse cross section was obtained from the FE model. Kato et al. [24] showed the maximum stress in gray and white matter was 0.06 MPa in a case of 40% compression by ossification of the posterior longitudinal ligament, while Khuyagbaata et al. [25] showed 0.08 MPa. Therefore, the feasibility of this study is evident from results showing that maximum stresses in gray and white matter were from 0.06 MPa to 0.12 MPa in different areas under 40% compression. Relative injury possibilities were explored to provide some data for discussion about clinical symptoms and injury mechanisms. The stress was significantly greater, by an order of magnitude, in the pia matter than the gray and white matters, as shown in Fig. 4. The pia matter can avoid direct injury to gray matter and white matter and have significant effect on spinal cord deformation which is consistent with previous literatures [11,12]. Thus, modelling of pia matter is important to the stress analysis of spinal cord using FE approach. Even in the electrically related study of the effect of intradural spinal cord stimulation, pia matter was constructed to calculate electrochemical stress and showed important feature [26] as well.
One mechanism of cervical spine injury is high energy injury in the cases of young patients [27], however it is unclear how the injury relates to the stress distribution in the spinal cord subject to a specific type of loading condition. Firstly, for the gray matter when subjected to the back-to-front load, in the cases of 10% and 20% compression, stress was largely concentrated in the region near the central canal, which may lead to central cord syndrome. As the compression ratio increases, the high stress region propagated to both sides and the stress-induced damage may occur around the central canal. This progressive formation and propagation of stress could be key to explaining the significant damage to the area at and near the central canal under the high displacement load [28]. On the other hand, for the white matter subject to back-to-front load, the highest von Mises stress also located in the central canal area in the case of 10% compression. When the compression increased, the maximum stress location switched to the area near the anterior median fissure, which was also observed in literature [7]. This may be due to the internal geometry of anterior median fissure. In the internal, white matter has a similar level of stress compared to that of gray matter which is mainly composed of neuronal cell bodies and dendrite. White matter, however, is mainly composed of longitudinally fiber bundle and the tissue is relatively tough, therefore is less vulnerable to damage. When the spinal cord is under contusion load, the gray matter closer to the central canal is more vulnerable to damage, which is in line with what has been reported in literature [29]. The compression firstly appeared at the central hematoma of the gray matter [30], gradually propagating to the white matter near the anterior funiculus, causing potential damage and further clinical symptoms.
The front-to-back load can be given arise by several degenerative factors, such as disc herniation, ligament ossification and osteophyma [31]. The stress is higher than that in the back-to-front load, in all three tissue components. Under 10% compression, the highest stress was located in the region around central canal, similar to that in the back-to-front load. As a result, regions around the central canal may be damaged first and lead to central cord syndrome. Under the increasing compression, the anterior horn of the spinal cord became most affected and symptoms of anterior cord syndrome may become more predominant. Meanwhile, multiple areas presented high levels of stress concentrations subject to a high displacement load, which could account for the appearance of complicated and diverse clinical symptoms.
This study, as it currently stands, has certain limitations. Firstly, as mentioned above, the material property of the pia matter was adopted from an animal study and only elastic properties were used. The tendency inferred from the comparison affectd a little as all loading conditions used same parameters. Secondly, the contusion load was modeled using the displacement from a rigid cylinder. To better reflect both the front-to-back and back-to-front loading conditions given rise by compression of adjacent anatomical structures, more complicated geometries of the load sources need to be considered. Thirdly, the model has certain simplifications and the dura matter, cerebrospinal fluid and nerve roots were not modeled. When the fracture frame hits the spinal cord, the cerebrospinal fluid can provide certain buffering effect, which would depend on the strain rate of the applied load. Thus the influence of the cerebrospinal fluid to this study maybe small under non-impact load. Future developments of the proposed FE model will include more anatomical structures to improve its effectiveness in simulating the stress field in cervical spinal cord under complex loading conditions. Better experimental data and refinement validation process could confirm the estimated results and should be maped out in further investigations.
The model was firstly compared to the experimental measurements carried out in literature and a similar trend was found in the force-deformation data. For the back-to-front loading scenario, the stress concentration was found in the area at and near the central canal and the damage may lead to the central canal syndrome from biomechanical point of view. As the displacement further increased, high levels of von Mises stress were also observed in the area of the anterior median fissure of the white matter, and the damage may result in further complications. With the front-to-back load, the maximum von Mises stress located in central canal area of gray matter when subject to 10% compression, whilst it appeared at the anterior horn when the compression increased. For the white matter, the maximum von Mises stress appeared in the area of the anterior funiculus. This leads to complicated symptoms given rise by damage to multiple locations in the cervial spinal cord. The illustrative results demonstrated the need of considering different loading scenarios in understanding the damage mechanisms of the cervial spinal cord, particularly when the loading conditions were given rise by different patho-physiological causes.
This work was supported by the National Natural Science Foundation of China (No. 81772337), Shanghai Health and Family Planning System Excellent Young Medical Talents Training Program (No. 2018YQ32), National Key R & D Program of China (No. 2018YFB1105600) and British Council Newton Fund (UK-China Joint Research and Innovation Partnership Fund–440004097).
The authors declare that there is no conflict of interest regarding the publication of this paper.
| [1] | A. E. Nkusi, S. Muneza, D. Hakizimana, S. Nshuti, P. Munyemana, Missed or delayed cervical spine or spinal cord injuries treated at a tertiary referral hospital in rwanda, World Neurosurg., 87 (2016), 269-276. |
| [2] | R. M. Quencer, R. P. Bunge, M. Egnor, B. A. Green, W. Puckett, T. P. Naidich, et al., Acute traumatic central cord syndrome: MRI-pathological correlations, Neuroradiology, 34 (1992), 85-94. |
| [3] | A. Curt, P. H. Ellaway, Clinical neurophysiology in the prognosis and monitoring of traumatic spinal cord injury, in Handbook of clinical neurology, Elsevier, 109 (2012), 63-75. |
| [4] | R. Zhu, T. Zander, M. Dreischarf, G. N. Duda, A. Rohlmann, H. Schmidt, Considerations when loading spinal finite element model with predicted muscle forces from inverse static analyses, J. Biomech., 46 (2013), 1376-1378. |
| [5] | R. Zhu, A. Rohlmann, Discrepancies in anthropometric parameters between different models affect intervertebral rotations when loading finite element models with muscle forces from inverse static analyses, Biomed. Eng./Biomed. Tech., 59 (2014), 197-202. |
| [6] | J. Scifert, K. Totoribe, V. Goel, J. Huntzinger, Spinal cord mechanics during flexion and extension of the cervical spine: a finite element study, Pain Physician, 5 (2002), 394-400. |
| [7] | X. F. Li, L. Y. Dai, Acute central cord syndrome: injury mechanisms and stress features, Spine, 35 (2010), 955-964. |
| [8] | B. Khuyagbaatar, K. Kim, W. Man Park, et al., Biomechanical behaviors in three types of spinal cord injury mechanisms, J. Biomech. Eng., 138 (2016). |
| [9] | B. Khuyagbaatar, K. Kim, T. Purevsuren, S. H. Lee, Y. H. Kim, Biomechanical effects on cervical spinal cord and nerve root following laminoplasty for ossification of the posterior longitudinal ligament in the cervical spine: A comparison between open-door and double-door laminoplasty using finite element analysis, J. Biomech. Eng., 140 (2018), 071006. |
| [10] | N. Zareen, M. Shinozaki, D. Ryan, H. Alexander, A. Amer, D. Q. Truong, et al., Motor cortex and spinal cord neuromodulation promote corticospinal tract axonal outgrowth and motor recovery after cervical contusion spinal cord injury, Exp. Neurol., 297 (2017), 179-189. |
| [11] | C. Persson, J. Summers, R. M. Hall, The importance of fluid-structure interaction in spinal trauma models, J. Neurotrauma., 28 (2011), 113-125. |
| [12] | N. Nishida, Y. Kato, Y. Imajo, S. Kawano, T. Taguchi, Biomechanical study of the spinal cord in thoracic ossification of the posterior longitudinal ligament, J. Spinal Cord Med., 34 (2011), 518-522. |
| [13] | K. Polak-Krasna, S. Robak-Nawrocka, S. Szotek, M. Czyż, D. Gheek, C. Pezowicz, The denticulate ligament-tensile characterisation and finite element micro-scale model of the structure stabilising spinal cord, J. Mech. Behav. Biomed. Mater., 91 (2019), 10-17. |
| [14] | C. Y. Greaves, M. S. Gadala, T. R. Oxland, A three-dimensional finite element model of the cervical spine with spinal cord: an investigation of three injury mechanisms, Ann. Biomed. Eng., 36 (2008), 396-405. |
| [15] | K. H. Stoverud, M. Alnaes, H. P. Langtangen, V. Haughton, K. A. Mardal, Poro-elastic modeling of Syringomyelia - a systematic study of the effects of pia mater, central canal, median fissure, white and gray matter on pressure wave propagation and fluid movement within the cervical spinal cord, Comput. Methods Biomech. Biomed. Engin., 19 (2016), 686-698. |
| [16] | Y. B. Yan, W. Qi, Z. X. Wu, T. X. Qiu, E. C. Teo, W. Lei, Finite element study of the mechanical response in spinal cord during the thoracolumbar burst fracture, PLoS One, 7 (2012), e41397. |
| [17] | R. W. Ogden, Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids, Proc. R. Soc. London, Ser. A, 326 (1972), 565-584. |
| [18] | H. Ozawa, T. Matsumoto, T. Ohashi, M. Sato, S. Kokubun, Mechanical properties and function of the spinal pia mater, J. Neurosurg. Spine, 1 (2004), 122-127. |
| [19] | M. Czyz, K. Scigala, W. Jarmundowicz, R. Bedzinski, The biomechanical analysis of the traumatic cervical spinal cord injury using finite element approach, Acta Bioeng. Biomech., 10 (2008), 43-54. |
| [20] | T. K. Hung, H. S. Lin, L. Bunegin, M. S. Albin, Mechanical and neurological response of cat spinal cord under static loading, Surg. Neurol., 17 (1982), 213-217. |
| [21] | Z. Cai, Z. Li, L. Wang, H. Y. Hsu, Z. Xiao, C. J. Xian, A three-dimensional finite element modelling of human chest injury following front or side impact loading, J. Vibroeng., 18 (2016), 539-550. |
| [22] | Z. Cai, Z. Li, J. Dong, Z. Mao, L. Wang, C. J. Xian, A study on protective performance of bullet-proof helmet under impact loading, J. Vibroeng., 18 (2016), 2027-2079. |
| [23] | L. E. Bilston. L. E. Thibault, The mechanical properties of the human cervical spinal cord in vitro, Ann. Biomed. Eng., 24 (1996), 67-74. |
| [24] | Y. Kato, T. Kanchiku, Y. Imajo, K. Kimura, K. Ichihara, S. Kawano, et al., Biomechanical study of the effect of degree of static compression of the spinal cord in ossification of the posterior longitudinal ligament, J. Neurosurg. Spine, 12 (2010), 301-305. |
| [25] | B. Khuyagbaatar, K. Kim, W. M. Park, Y. H. Kim, Effect of posterior decompression extent on biomechanical parameters of the spinal cord in cervical ossification of the posterior longitudinal ligament, Proc. Inst. Mech. Eng. H, 230 (2016), 545-552. |
| [26] | D. J. Anderson, D. R. Kipke, S. J. Nagel, S. Lempka, A. G. Machado, M. T. Holland, et al., Intradural spinal cord stimulation: Performance modeling of a new modality, Front. Neurosci., 13 (2019), 253. |
| [27] | N. B. Ramirez, R. E. Arias-Berrios, C. Lopez-Acevedo, E. Ramos, Traumatic central cord syndrome after blunt cervical trauma: a pediatric case report, Spinal Cord Ser. Cases, 2 (2016), 16014. |
| [28] | R. C. Schneider, G. Cherry, H. Pantek, The syndrome of acute central cervical spinal cord injury; with special reference to the mechanisms involved in hyperextension injuries of cervical spine, J. Neurosurg., 11 (1954), 546-577. |
| [29] | B. Aarabi, M. N. Hadley, S. S. Dhall, D. E. Gelb, R. J. Hurlbert, C. J. Rozzelle, Management of acute traumatic central cord syndrome (ATCCS), Neurosurgery, 72 (2013), 195-204. |
| [30] | S. Z. Hashmi, A. Marra, L. G. Jenis, A. A. Patel, Current concepts: Central cord syndrome, Clin. Spine Surg., 31 (2018), 407-412. |
| [31] | C. Xiaofei, N. Bin, L. Qi, J. Chen, H. Guan, Q. Guo, Clinical and radiological outcomes of spinal cord injury without radiologic evidence of trauma with cervical disc herniation, Arch. Orthop. Trauma Surg., 133 (2013), 193-198. |
| 1. | Salim Meddahi, Ricardo Ruiz-Baier, A Mixed Discontinuous Galerkin Method for a Linear Viscoelasticity Problem With Strongly Imposed Symmetry, 2023, 45, 1064-8275, B27, 10.1137/22M1482081 | |
| 2. | Alba Díaz-Baamonde, Roberto Peláez-Cruz, Maria J. Téllez, Junping Chen, Jacques Lara-Reyna, Sedat Ulkatan, Quadriplegia, an Unusual Outcome After Anterior Cervical Discectomy and Fusion, 2021, 11, 2160-3251, 10.2106/JBJS.CC.20.00487 | |
| 3. | Fan Xue, Hao Deng, Zujiang Chen, Han Yang, Yikai Li, Shiguo Yuan, Nansheng Zheng, Meixiong Chen, Effects of cervical rotatory manipulation on the cervical spinal cord complex with ossification of the posterior longitudinal ligament in the vertebral canal: A finite element study, 2023, 11, 2296-4185, 10.3389/fbioe.2023.1095587 | |
| 4. | Meng-lei Xu, Hui-zi Zeng, Liang-dong Zheng, Chen Jin, Shi-jie Zhu, Yi-ting Yang, Yu-ting Cao, Rui Zhu, Li-ming Cheng, Effect of degenerative factors on cervical spinal cord during flexion and extension: a dynamic finite element analysis, 2022, 21, 1617-7959, 1743, 10.1007/s10237-022-01617-x | |
| 5. | Symeon Naoum, Angelo V. Vasiliadis, Christos Koutserimpas, Nikolaos Mylonakis, Michail Kotsapas, Konstantinos Katakalos, Finite Element Method for the Evaluation of the Human Spine: A Literature Overview, 2021, 12, 2079-4983, 43, 10.3390/jfb12030043 | |
| 6. | Ishan Singhal, Balaji Harinathan, Ali Warraich, Yuvaraj Purushothaman, Matthew D. Budde, Narayan Yoganandan, Aditya Vedantam, Finite element modeling of the human cervical spinal cord and its applications: A systematic review, 2023, 15, 26665484, 100246, 10.1016/j.xnsj.2023.100246 | |
| 7. | Benjamin Davies, Samuel Schaefer, Amir Rafati Fard, Virginia Newcombe, Michael Sutcliffe, Finite Element Analysis for Degenerative Cervical Myelopathy: Scoping Review of the Current Findings and Design Approaches, Including Recommendations on the Choice of Material Properties, 2024, 9, 2561-3278, e48146, 10.2196/48146 |
Rui Zhu, Yuhang Chen, Qianqian Yu, Siqing Liu, Jianjie Wang, Zhili Zeng, Liming Cheng. Effects of contusion load on cervical spinal cord: A finite element study[J]. Mathematical Biosciences and Engineering, 2020, 17(3): 2272-2283. doi: 10.3934/mbe.2020120
| Material Properties | References | |
| Gray matter | Hyperelastic (Ogden): Μ = 0.0041 MPa, α = 14.7 |
[8,17] |
| White matter | Hyperelastic (Ogden): Μ = 0.004 MPa, α = 12.5 |
[8,17] |
| Pia matter | Elastic: E = 2.3 MPa, υ = 0.3 | [13,18,19] |
DownLoad:
CSV
