Innovation of prescribe conditions for radiative Casson micropolar hybrid nanofluid flow with inclined MHD over a stretching sheet/cylinder

1.   Introduction

Hybrid nanofluids are an advanced type of fluid generated by combining two or more different categories of nanoparticles with a base fluid. This combination enhances the thermal and mechanical characteristics of the base fluid, surpassing traditional single-component nanofluids. The thermal conductivity, viscosity, and heat transfer capabilities can be improved by including nanoparticles such as metals, oxides, carbides, or carbon-based materials such as graphene. The study of hybrid nanofluid flow has gained noteworthy consideration due to its potential uses in various engineering and industrial processes, including cooling systems, microelectronics, biomedical devices, and energy systems. Analyzing the flow of hybrid nanofluids is a challenging but crucial area of research due to the complex interactions between these factors. Suresh et al. ^[1] presented the experimental model of hybrid nanofluids. Moin ^[2] considered the mixed conviction for hybrid nanofluids and performed experimental results using the laminar flow. Madhesh and Kalaiselvam ^[3] performed the experimental results for cooling using hybrid nanofluids, and explored the force convection and thermal features. Xian et al. ^[4] reported the impact of hybrid nanofluids and prepared techniques introduced for engineering applications. Shoaib et al. ^[5] reported a comprehensive analysis of hybrid nanofluids using the radiation impact of a stretchable sheet. They considered the rotating flow having magnetohydrodynamic (MHD) impacts for the phase flow model. Yashkun et al. ^[6] considered the permeable surface for both stretching and shrinking to analyze the impression of hybrid nanofluids. They applied MHD on the flow to more convenient results for hybrid nanofluids under radiation. Akbar et al. ^[7] discussed the hybrid nanofluid flow under the with an open-cell metallic foam. Ramesh et al. ^[8] debated the influence of hybrid nanofluids, while Madhukesh et al. ^[9] inspected the impression of hybrid nanofluids. Waqas et al. ^[10] provided comparative results of hybrid nanofluids at a stretchable sheet. Nadeem et al. ^[11] highlighted the features of the phase flow model using two nanoparticles and a base fluid. They considered the Brinkman phase flow model and produced analytical results. Few authors have developed the feature of their analysis using the phase flow model for different flow assumptions; see Refs. ^[12,13].

In the study of heat transfer, particularly in boundary layer problems involving fluid flow over the surface, two essential boundary conditions are commonly used: the prescribed surface temperature and the prescribed heat flux. These conditions are crucial for accurately modeling the thermal behavior and solving practical engineering problems. The prescribed surface temperature specifies that the temperature of the surface remains constant regardless of the heat flux or other thermal conditions of the fluid. This condition is often used when the surface is maintained at a uniform temperature due to external heating or cooling sources. The prescribed heat flux conditions dictate that the rate of heat transfer per unit area across the surface is kept constant. Bataller ^[14] discussed the impact of the prescribed thermal effects at the stretchable surface. Aman and Ishak ^[15] debated on the numerically prescribed conditions on the vertical stretching sheet. Qasim et al. ^[16] deliberated the slip phenomena using the prescribed thermal conditions. They applied the ferrofluid model under the MHD impression to numerically deliberate the consequences. Nabwey et al. ^[17] highlighted the impression of the prescribed surface temperature on the nanofluid. Ramesh et al. ^[18] reported the work for the prescribed surface temperature on the nanofluid flow. Reddy et al. ^[19] explained the features of activation energy for nanofluids. Waini et al. ^[20] worked on the stability for a shrinking cylinder using the prescribed thermal conditions. Nabwey et al. ^[21] discussed the impact of nanofluids within a rotating desk. Abdal et al. ^[22] reported the impact of the prescribed thermal conditions for the Maxwell fluid model. The bioconvection and heat transfer phenomena were comprehensively discussed. Sadighi et al. ^[23] debated the analysis of the nanofluid model with MHD having prescribed thermal conditions. Recently, authors have studied the prescribed thermal conditions for different fluid models; see Refs. ^[24,25].

The Casson fluid theory explains the behavior of non-Newtonian fluids with yield stress. Below this stress, they act like a solid; above it, they flow like a fluid. The model is used for fluids with microstructural compositions such as blood, chocolate, certain slurries, and cosmetic products. It captures the nonlinear flow characteristics of these fluids, which is important to understand their behavior under different flow conditions. The study of Casson fluid flow over a stretchable surface is significant in industrial and biomedical applications because the yield stress of Casson fluid means that the flow behavior is strongly affected by the applied shear stress, which changes across the stretching surface. Batra and Das ^[26] considered the rotating cylinder to analyze the Casson fluid. In their analysis, the inner cylinder was fixed and outer cylinder was rotating. Vajravelu et al. ^[27] emphasized the impression of a mixed convection for the Casson fluid at a stretchable vertical sheet. The variable thermal properties have been highlighted analytically. Mustafa et al. ^[28] considered the stagnation region for the Casson fluid flow at a stretchable sheet. Mukhopadhyay et al. ^[29] studied the impact of The Casson fluid flow having temperature dependent characteristics over a stretchable sheet. Khan et al. ^[30] discussed the impact of the Casson fluid and developed the results for closed solutions. The linear stretchable sheet was taken into account. Nawaz et al. ^[31] numerically implemented the technique of Predictor–corrector on the Casson fluid model. Authors have debated the impact of the Casson fluid model for different assumptions; see refs. ^[32,33].

The theory of micropolar fluids extends classical fluid dynamics in view of the fluid particles, microstructure, and local angular momentum. The micropolar fluid theory is particularly useful for studying fluids with internal microstructures, such as liquid crystals, polymeric suspensions, colloidal fluids, and biological fluids. Micropolar fluids contain microelements that can rotate and exhibit micro-inertia effects, offering a more comprehensive description of the fluid behavior, especially when these microstructural effects are significant. One important area of study is the flow of micropolar fluids over a stretchable surface, which is of interest in both theoretical research and practical applications. Often modeled as a linearly or exponentially stretching sheet, a stretchable surface creates complex flow fields that significantly differ from flow over a non-stretchable surface. Such stretching sheets are commonly encountered in industrial processes such as the extrusion of polymer sheets, the cooling of metallic plates in a stretching motion, and manufacturing processes that involve fluids with microstructural components interacting with moving boundaries. Takhar et al. ^[34] initiated the work on the micropolar fluid with convection effects at a stretching sheet. The numerical scheme was used to develop the theoretical results. Abo-Eldahab and Ghonaim ^[35] considered the micropolar fluid with electrically conducting with heat convection impression at a stretchable sheet. Mahmoud ^[36] initiated the work on the micropolar fluid with thermal impacts over a stretching sheet. They considered the variable features of the fluid to analyze the effect of MHD and thermal radiation. Hayat et al. ^[37] considered the nonlinear stretching sheet to develop the results for the micropolar fluid. The stagnation region with electrically conducting fluid impression has been studied. Ahmad et al. ^[38] worked on the time dependent flow of micropolar fluids due to a stretchable sheet. The implicit finite difference scheme has been implemented on the fluid model. Hayat et al. ^[39] considered the chemical reaction with a micropolar fluid by taking the curved sheet into account. Bilal et al. ^[40] considered the porous surface to analyze the micropolar fluid features. Thermal radiation was studied in their analysis. Sharma et al. ^[41] initiated the results of micropolar MHD with slip phenomena over a stretching sheet. Authors have studied micropolar fluids with different flow assumptions; see Refs. ^[42,43].

Viewing the above literature, we considered the hybrid Casson micropolar nanofluid flow over a permeable stretching cylinder/sheet. The prescribed thermal conditions were implemented, and the flow features were studied. The inclined magnetic field was studied under viscous dissipation and thermal radiation, and the variable temperature features were discussed. The nanoparticles of Ag and CuO with an Ethylene Glycol (EG) base fluid EG were discussed. Additionally, the study explored the impact of an inclined magnetic field on the flow behavior. The governing partial differential equations described the conservation of mass, momentum, and energy, which were transformed into a nonlinear ordinary differential equation using appropriate similarity transformations. Then, these equations were numerically cracked using a reliable computational technique, and the results were presented in detail. The current study addresses the following scientific questions:

● How do various Casson fluids, micropolar, temperature properties, radiation, porosity, heat generation, suction, magnetic, and nanoparticle concentration factors impact the fluid temperature (PST and PHF) for both cases under flow conditions over a stretching cylinder/sheet?

● How does the rate of heat transfer and skin friction in a Casson micropolar hybrid nanofluid under the flow assumptions differ for both cases of the prescribed conditions (PST and PHF) over a stretching cylinder/sheet?

● The numerical outcomes compare the coefficient of Skin friction and the Nusselt number tabulated graphically.

2.   Mathematical formulation

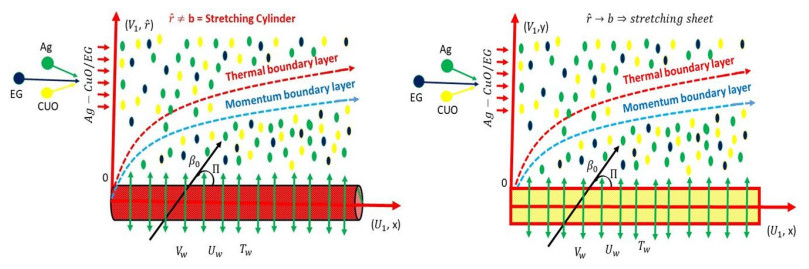
The steady incompressible flow of a hybrid micropolar Casson nanofluid flow over a permeable stretching cylinder/sheet is deliberated, which is seen in Figure 1. The thermal radiation and temperature dependent properties were considered in the present analysis. The accurate angle of inclined magnetic field $\mathrm{\Pi }$ was applied in the y-direction. As $\varPi = \frac{\pi }{2}$, the magnetic field behaves as a transverse magnetic field. ${U}_{1}$ and ${V}_{1}$ are the velocity mechanisms along the axial and radial directions, respectively, in the case of a stretching cylinder (in case of stretching sheet in $x-$, $y-$ directions). The flow is expected to be in the axial ($x$) direction, with the radial direction being perpendicular to $x$. The entire analysis is conducted under the assumptions of the boundary layer theory. The expression is presented as follows (see Refs. ^{[7,8,12,18,38]}):

with the following suitable boundary conditions:

where ${\gamma }_{1} = {\mu }_{B}\frac{\sqrt{{2\pi }_{c}}}{{P}_{\widehat{r}}}$ is the Casson fluid parameter. The thermal expansion coefficient is ${\beta }_{0}$. ${\mathrm{\gamma }}_{hNF} = {\mu }_{hNF}\left(T\right)+\frac{{k}^{*}}{2}$ is the viscosity of the spin radiation of the hybrid nanofluid. ${\mu }_{hNF}$ is the viscosity of the hybrid nanofluid. The special transformation is introduced as follows:

The non-dimensional equations become the following:

with the following boundary condition:

2.1.   Heat transfer phenomena

The equation of the temperature with boundary layer approximations can be expressed as follows (see Refs. ^[7,8,25]):

${K}_{HNF}\left(T\right) = {k}_{hNF}\left(1+E\mathrm{\Theta }\left(\zeta \right)\right)$ is the variable thermal conductivity of the hybrid nanofluid. ${\sigma }_{hNF}$ is the electric conductivity of hybrid nanofluid. The thermal expansion coefficient is ${\beta }_{0}$. ${q}_{\widehat{r}}$ is the radiative heat flux. The Reynold approximation of the radiative heat flux is presented as ${q}_{\widehat{r}} = -\frac{4{\sigma }^{*}}{3{k}_{1}}\frac{\partial {T}^{4}}{\partial \widehat{r}}$. The constant Steffen Boltzmann is ${\sigma }^{*}$. ${k}_{1}$ is the absorption coefficient. The differences of temperature within the flow are considered to be sufficiently small, so ${T}^{4}$ presented as a temperature linear function. ${T}^{4}$ expands using the Taylor series about ${T}_{\mathrm{\infty }}$ and diminishes the higher order terms, which is considered as ${T}^{4}\cong 4{{T}_{\mathrm{\infty }}}^{3}T-3{{T}_{\mathrm{\infty }}}^{4}$.

2.1.1.   Case-I (Prescribed surface temperature)

The special transformation is introduced as follows (see Ref. ^[7,25]):

The relevant boundary conditions are as follows:

The dimensionless system becomes the followings:

with the following boundary condition:

2.1.2.   Case-ii (Prescribed heat flux)

The special transformation is introduced as follows:

The relevant boundary conditions are as follows:

The dimensionless system becomes the following:

with the following boundary condition:

The thermodynamic characteristics are defined in Table 1. The expressions for the thermodynamic properties of the base fluid and nanoparticles are as follows:

Nomenclature

Skin friction and the Nusselt number are physical quantities, which are presented as follows:

The Eq 18 becomes non dimensional and is defined as follows:

The Reynold number is $Re$.

3.   Numerical procedure

The bvp4c numerical technique is used to elucidate non-linear higher order differential equations that have specific boundary conditions. The Bvp4c method involves breaking down the intricate higher-order differential system into a system of first order differential equations, which can then be numerically elucidated. The model convergence is performed by reducing the residual error and achieving the tolerance threshold. The steps involved in this numerical technique include the following:

The boundary condition at the surface is as follows:

4.   Results and discussions

A system of differential equations were developed under the flow assumptions and boundary layer approximations. The mathematical model was cracked through a numerical scheme and involved physical factor impact phenomena offered in the form of graphs and in tabular form. Figures 2–9 report the physical features of external forces on the temperature (PST and PHF). The difference of joule heating and the prescribed condition for temperature are presented in Figures 2 and 3. The thickness of the thermal layer was enriched due to an increment in the joule heating for both cases of the stretching cylinder and the sheet. As more thermal energy is created within the fluid, the temperature naturally rises because temperature measures the average kinetic energy of the fluid molecules. As more heat is generated, the molecules move more energetically, thus leading to a rise in temperature. Figures 4 and 5 report the difference of variable thermal conductivity and the prescribed condition on temperature. For the case of the prescribed surface temperature (PST) and the variable thermal conductivity, there was a direct relation, which is reported in Figure 4. The prescribed surface temperature (PST) increased as the thermal conductivity parameter values increased, as a higher thermal conductivity improves the heat conduction within the fluid and raises its temperature. Alternatively, the opposite relation found in the case of the prescribed temperature (PHF) and the variable thermal conductivity, which is reported in Figure 5. The prescribed heat flux (PHF) declined due to the increased variable thermal conductivity parameter values. As the thermal conductivity increases, heat spreads more effectively within the fluid, thus reducing the temperature gradient near the surface. Since heat flux is proportional to the temperature gradient, a lower gradient leads to a decrease in the PHF. The difference between the solid nanoconcentration and the prescribed conditions (PHF and PST) for temperature is reported in Figures 6 and 7. The thickness of the thermal layer is boosted up due to an increment in the nanoconcentration factor for both cases for the prescribed conditions (PHF and PST). Due to the physical properties, the thermal conductivity of the fluid gradually enlarg4es due to an enrichment in the nanoconcentration factor. Therefore, the fluid temperature is boosted up. The difference between the solid radiation and the prescribed conditions (PHF and PST) for temperature is reported in Figures 8-9. The thermal thickness of the prescribed conditions (PHF and PST) for temperature is enhanced due to an increment in the factor of radiation. As more radiative heat is absorbed, the fluid internal energy increases, thus leading to a rise in temperature because the absorbed radiation boosts the kinetic energy of the fluid molecules, thereby increasing the fluid temperature.

Table 2 displays the physical features of the external forces on the Nusselt number for both cases of temperature (PST and PHF). Moreover, the differences between the variable thermal conductivity and the Nusselt number (PST and PHF) are presented in Table 2. The heat transfer becomes low due to an enrichment in the variable thermal conductivity in both cases of the stretching cylinder and the sheet. As the Nusselt number reflects the efficiency of convection, a decrease in the temperature gradient results in a lower Nusselt number, which indicates a reduced convective heat transfer compared to a conductive heat transfer. Table 2 compares the micropolar factor and Nusselt number (PST and PHF). The higher the micropolar factor, the richer the heat transfer fluid. The enhanced Nusselt number signifies the efficiency, thereby showing that the hybrid nanofluid with more pronounced micropolar characteristics excels in heat transfer through convection compared to one with weaker micropolar effects. The variation of the porosity factor and the Nusselt number is reported in Table 2. The Nusselt number found declines in its behavior by enlarging the values of the porosity factor. The decline in the Nusselt number with an increasing porosity factor indicates that the porous medium structure allows the hybrid nanofluid to flow with less resistance, thus reducing the effectiveness of a convective heat transfer. The nanoconcentration of the particles affects the Nusselt number, which is revealed in Table 2. The temperature gradient shows a decline due to higher values of the solid nanoconcentration. The Nusselt number decreased as the concentration of the solid nanoparticles increased because the hybrid nanofluid improves the internal heat conduction, though it decreases its ability to transfer heat through convection. The Nusselt number becomes enriched due to an increment in the section factor. The Nusselt number increased as the section parameter values rose, thus enhancing the heat transfer efficiency. As the section parameter and the thermal boundary layer increased, the convective heat transport away from the surface improved. The Nusselt number reduced due to an increment in the Casson fluid factor A reduced fluid flow decreased the heat transfer by convection due to a thicker boundary layer, lower shear rates, and the temperature gradient, leading to a decrease in the Nusselt number. The temperature gradient deteriorated due to an addition in the thermal radiation. Increased thermal radiation results in a thicker thermal boundary layer, thereby extending the region where temperature changes occur and reducing the temperature gradient near the surface. The temperature gradient deteriorated due to an addition in the joule heating and the magnetic field. The rate of convective heat transfer decreased as the fluid velocity decreased. Convection depends on the fluid movement to transfer heat from the surface to the bulk of the fluid. Table 3 displays the physical features of external forces on Skin friction for both cases of temperature (PST and PHF). The variation in skin friction remains constant due to different thermal conductivity values. The variation of skin friction diminishes while improving the values of the micropolar polar fluid factor. The rotation dominated the fluid velocity, thus improving the velocity and reducing the friction between the surface and the fluid. The skin friction enriches due to improving the values of the porosity and suction factors. Increasing the porosity improved the fluid permeability at the surface, thus enabling more fluid to flow through. This change disrupted the velocity gradient and increased the resistance to fluid motion. As a result, the shear stress at the wall intensified, thus leading to a higher skin friction. The variation of skin friction is enriched while improving the values of the nanoconcentration. A higher concentration led to an increased effective viscosity, thus enhancing the flow resistance near the surface and raising the skin friction. The variation of skin friction is enriched while improving the values of the Casson factor. A higher yield stress resulted in a greater velocity gradient near the surface, which increased the skin friction. The variation in skin friction remains constant due to different radiation values and joule heating values. The variation of skin friction is enriched while improving the values of the magnetic field. By increasing the values of the magnetic field, the rate of fluid near the surface declined, as well as the friction between the fluid and the surface. Table 4 reports the comparison of present analysis with decay results from Hayat et al. ^[44] and Fang et al. ^[45] for different values of $\mathrm{\Omega }$, while the other values are as follos: $E\to 0, {K}_{1}\to 0.0, \chi \to 0.0, {\varphi }_{2}\to 0.0, {\varphi }_{1}\to 0.0, Q\to 0.0, R\to \infty, Rd\to 0.0, S\to 0.0, \mathrm{\Pi }\to 90°.$ It is noted that our results have been found to be in a good agreement with the decay results.

5.   Final remarks

We conducted an analysis of the flow and heat transfer characteristics of a Casson micropolar hybrid nanofluid over a stretching sheet or cylinder. Our study includes factors such as Joule heating, thermal radiation, and variable thermal conductivity. We assessed the prescribed thermal conditions in detail. The governing equations were developed and solved using numerical methods with the Maple software. Below, we highlight the main key findings from our analysis:

● The thickness of the thermal layer is enriched due to an increment in the joule heating for both cases of a stretching cylinder and a sheet. As more heat is generated, the molecules move more energetically, thus leading to an increase in temperature.

● The thickness of the thermal layer is boosted up due to an increment in the nanoconcentration factor for both cases of the prescribed condition (PHF and PST) for temperature. Due to the physical characteristics, the thermal conductivity of fluid gradually enlarged due to an enrichment in the nanoconcentration factor. As a results, the fluid temperature boosted up.

● The enhanced Nusselt number signifies efficiency, showing that the hybrid nanofluid with more pronounced micropolar characteristics excels in heat transfer through convection compared to one with weaker micropolar effects.

● The Nusselt number was reduced due to an increment in the Casson fluid factor. A reduced fluid flow decreases the heat transfer by convection due to a thicker boundary layer, lower shear rates, and temperature gradient, leading to a decrease in the Nusselt number.

● The PST achieved more heat transfer and friction factor compared to the PHF. The stretching sheet achieved more temperature as compared to the stretching cylinder.

6.   Limitations of present work

The limitations associated with the current computational model are as follows:

● Models often assume that the nanoparticle dispersion is uniform, overlooking the effects of agglomeration or clustering, which can significantly alter the thermal conductivity and viscosity in real-world applications.

● Models may not adequately consider complex heat transfer mechanisms, including particle-particle thermal interactions, thermal resistance, and nanolayer effects.

● Computational results are often insufficiently validated against experimental data, which leads to uncertainties regarding the accuracy and reliability of the models.

In the future, this study can be expanded through various approaches to enhance the understanding and appreciation of the topic. This can be achieved by incorporating diverse geometries with a non-Newtonian fluid model and considering physical impacts that could alter the model performance, such as non-Fourier thermal flux, activation energy, and the Hall and current effects. Additionally, exploring a more complex combination of nanoparticles within the hybrid nanofluid could further extend the scope of this research.

Author contributions

Nadeem Abbas: Writing–review & editing, Writing–original draft, Investigation, Formal analysis, Conceptualization; Wasfi Shatanawi: Writing–review & editing, Writing–original draft, Data curation, Validation, Supervision, Formal analysis; Taqi A.M. Shatnawi: Writing–original draft, Validation, Software, Project administration, Methodology, Visualization, Software, Resources, Investigation, Conceptualization. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare(s) they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The authors extend their appreciation to the TAS Lab at Prince Sultan University for funding this work through SEED Project under grant number SEED-CHS-2024-163.

Conflict of interest

The authors declare no competing interests.