An efficient eigenvector-based crossover for differential evolution: Simplifying with rank-one updates

1.   Introduction

Rumors are pieces of information that are not verified and often spread quickly through word of mouth, social media, or other means of communication. They can have serious consequences, causing panic, fear, and even violence. Therefore, understanding how rumors start and spread is crucial to prevent their negative impacts.

In order to better predict and control rumors, the commonly used method is to utilize mathematics to study the mathematical rumor model, analyze its nature, and apply it to real life to reduce the adverse effects of rumors. For example, in ^[1], the authors studied the local stability and optimal control of the rumor propagation model in online social networks as the number of total users changes. Because the transmission mechanism of rumors is very similar to that of infectious diseases, the research method of infectious diseases can be used to study the model of rumor transmission. Besides, many scholars have studied the rumor propagation model of ordinary differential equations, and a large number of brilliant results have appeared. In 1965, Daley and Kendall ^[2] proposed a mathematical model of rumor propagation, namely the DK model, and the model divided the population into three categories, namely, ignorant people, disseminators, and rational people. In 1973, Maki and Thomson ^[3] developed the DK model on the basis of mathematical theoretical analysis, introducting an immune population, and established the MT rumor model. Afterwards, subsequent studies based on the MT rumor model have been expanded and promoted, and most of the research literature assumes that rumor spreading can ignore the skeptical population, that is, upon hearing the rumor, every ignorant person will immediately spread it, become a spreader, and then wake up and acquire permanent or temporary immunity. For such models, we call them SIR models or SIRS models based on the infectious disease model. For example, in ^[4], Wang et al. introduced the trust mechanism into the SIR model to obtain a new model of removal of susceptible persons, which reduced the size of the final rumor and the speed of rumor propagation, and delayed the end time of the rumor.

When rumors spread more and more widely, and even emergency situations such as subway congestion or car accidents occur, it is crucial to improve the ability to deal with such emergencies. In this regard, the authors in ^[5] established an improved SIRS model of the spread of passenger panic in subway emergencies, which provides certain reference significance for the construction and implementation of rail transit emergency treatment modes. Then, in ^[6], Zhang et al. took into account a forgetting mechanism and a memory mechanism, and analyzed the final scale of rumor propagation.

Moreover, many rumors are not propagated immediately by the disseminators after hearing the rumors, and some people are skeptical and do not spread rumors during the wait-and-see period. For such populations, skeptics are introduced into the model, and the resulting models are called SEIR models or SEIRS models, respectively, depending on whether the sober person is permanently awake. For example, in research ^[7], Liu et al. proposed a novel SEIR heterogeneous network model for rumor propagation and analyzed the global dynamic behavior of the rumor-free equilibrium point. In the research ^[8], Chen et al. considered a new model, it was known as the susceptibility-exposure-infection-recovery-susceptibility (SEIRS-V) model. However, the above studies do not consider the effects of time delay.

It is worth noting that time delay is a real and common phenomenon in social networks. Considering this factor, many scholars have established a rumor propagation model with delay. In ^[9], the authors proposed a delayed rumor propagation model in social networks and analyzed and discussed the Hopf bifurcation between time delay and rumor propagation rate.

It is well known that optimal control by media intervention refers to the use of media channels and strategies to influence or manipulate public opinion, shape narratives, and control information flow for a specific agenda or outcome. While media intervention can be used for various purposes, such as promoting positive social change or raising awareness about important issues, it can also be utilized for more manipulative purposes. For example, in ^[10], Misra et al. proposed a nonlinear susceptible-infected-susceptible (SIS) infectious disease model that incorporated media-induced behavioral responses and integrated media publicity activities into the modeling process to encourage individuals to adopt protective measures. This approach resulted in a decline in the transmission rate, which in turn altered the contact rate and effectively controlled the spread of infectious diseases. This study illustrates the significant impact of implementing media control strategies on the future course of an epidemic. Chen ^[11] has extended the traditional rumor theory to incorporate crisis management by establishing an ignorants-latents-spreaders-cooled-removed (ILSCR) rumor propagation model, and explored the media's control of rumors in emergencies, taking into account factors such as the cooling-off period, which is more reflective of real-world situations, and the mobility of personnel in specific regions. The numerical results of the study demonstrate that enhancing the credibility of mainstream media could potentially serve as an effective measure for controlling rumors. Meanwhile, optimal control has also been discussed to reduce the frequency of rumor propagation ^[12,13,14]. For example, Zhu and Wang ^[12] proposed a rumor propagation model with the function of forced silence in online social networks to further strengthen the supervision of network information security. Their research also analyzed the Hopf bifurcation phenomenon caused by time delay during rumor propagation. Because of the negative impact of rumors on society, researchers have focused on the optimal control of rumors after studying the mechanism of rumor propagation. In ^[14], the authors introduced a new classification for the pages that propagate rumors within the network, and proposed a cholera-based model to depict the dynamic process of rumor dissemination via social media. This study also implemented an optimal control strategy to counter the spread of rumors on social media. The effectiveness of this strategy was validated through final numerical results. In addition, in ^[15] the author studied a constant rumor propagation model with an age-dependent propagation coefficient among people with age structure; in ^[16,17,18], the authors considered random factors and studied stochastic rumor propagation models. In ^[19], Zhang and Teng improved the SEIRS disease transmission model with exponential population structure in ^[20], in which they not only analyzed the stability of disease-free balance and the existence, uniqueness and stability of endemic balance, but they also proved the uniform persistence of the disease.

However, in previous studies, most scholars did not consider the logistic growth of the spread population. This logistic growth phenomenon means that rumors spread quickly at the beginning, but after a period of time, the increase rate of the number of sober people will gradually slow down the increase rate of the spreading population. As time goes by, people lose interest in rumors, and rumors gradually stop spreading. Therefore, this kind of growth phenomenon is more realistic in the process of rumor propagation, and it is necessary to consider the logistic growth of the spreading population in the rumor propagation model. Although some previous studies have discussed the optimal control strategy for controlling rumors, it is a very new perspective to control rumors in unexpected situations through media publicity activities. It is the most direct and easiest way for media to refute rumors through social software. Therefore, analyzing media control is a necessary way to curb rumors. In this paper, we consider the effects of two time delays. When a controversial topic appears, people will be confused, they will hesitate, wait and see, and then analyze and demonstrate, where the time spent in the middle is the time lag. The two time delays reflect real-life more effectively, and most previous studies have been based on a single time delay. In addition, differing from the linear propagation rate and the standard propagation rate, we choose the saturated propagation rate because of the large target population base. The main purpose of this paper is to study the spreading mechanism and influencing factors of a rumor model using an epidemic-like model.

The content of this paper is organized as follows: Section 2 presents the considered model and some preliminaries. Section 3 studies the boundedness of the system and analyzes the conditions for the existence of a positive equilibrium point. Section 4 gives the conditions for the stability of the rumor-free equilibrium point. Section 5 discusses the permanence of the rumor. In Section 6, sufficient conditions for the global stability (including local stability) of the local equilibrium point of system (3) are given. In Section 7, the optimal control by media for the system is given. Section 8 gives three examples with numerical simulations to illustrate the main results of this paper. Finally, Section 9 gives the conclusions of this paper.

2.   The model and preliminaries

Based on the above works and the model discussed in ^[20], the components $X$, $D$, $Y$, and $Z$ stand, respectively, for the ignorant, the doubters (doubting but not spreading rumors), the communicators, and the sober, and thus we can obtain the rumor propagation model with exponential population structure

The spread rate of rumors, like the incidence rate in epidemiological models, plays a very important role in the rumor spreading model. We can refer to the definition of incidence rate to write a general expression of transmission rate: $\beta C(N)\frac{XY}{N}$ where $N(t)$ represents the total population at time $t$. In most models of rumor spreading, the linear incidence rate $\beta XY$ and standard incidence rate $\frac{\beta XY}{N}$ are frequently used. Linear incidence is more suitable for propagation in a chain of relationships than in a network. For standard incidence rates, a large target base of the rumor and higher actual exposure per person than assumed by the theory provides a good approximation. However, when the target base is low, the authors ^[19] combined the two previous approaches by assuming that the number of actual per capita partners $C(N)$ is proportional to $N$, whereas, if the number of available partners is large, there is a saturation effect which makes the number of actual partners constant. Specifically, it has the form (Michaelis-Menten contact rate):

Clearly, the transmission rate of the above form indicates that the number of new communicators per unit time is saturated with the total population. If the propagation rate of the ignorant or the spreader is saturated, two forms of propagation are used in the rumor propagation dynamics model: $\frac{\beta XY}{1+\alpha X}$, $\frac{\beta XY}{1+\alpha Y}$.

The parameter $b$ is the rate that an event will cause a rumor in the crowd, $d$ is related to a specific event, about which the group is no longer active, $b$ represents the probability that the rumor generated is equal to the probability that the rumor is no longer interesting. $\beta$ is the average number of adequate contacts of an infectious individuals per unit time, $\eta$ is the rate that the spreader will become awake after contact with an awake person, the delay $\omega$ is the time it takes for an ignorant person to think about its authenticity before spreading it, the delay $\tau$ is the time required for the communicator to undergo continuous analysis and demonstration in the process of becoming conscious, and $\epsilon$ is the rate that a sober person becomes suspicious after hearing too many rumors ($\varepsilon > 0$, the sober becomes the ignorant; $\varepsilon = 0$, always awake).

However, based on the dynamics of rumor propagation, we need to consider more realistic factors. In the beginning, the rumor spreads quickly, but after a while, almost everyone has heard the rumor, and it is difficult to find an ignorant person who has not heard the rumor; at this time, the spread rate will slow down to zero. Therefore, it is very important to consider the logical growth of the disseminator group in the rumor propagation model. We calculated the threshold of a rumor's influence, that is, the situation in which a rumor prevails until it finally disappears.

Additionally, the total population has a boundary, the rate of increase in the number of sober people reduces the rate of increase in the number of communicators, and with the passage of time, people lose interest in rumors. So, after a while, the rumor stops spreading and incrementally increases to a constant $K$. Therefore, for model (1) we consider the logical growth $Y(1-\frac{Y}{K})$ and obtain

Because the variable $D$ does not appear in the first, third, and fourth equations of system (2), so we consider the subsystem of system (2)

Let $\iota = \max \{\tau, \omega\}$ and $M$ be the Banach space of continuous functions $\psi$: $[-\iota, 0] \rightarrow R^{3}$ with norm

where $\psi = (\psi _{1}, \psi _{2}, \psi _{3})$. Further, let

The initial conditions for system (6) are given by

where $\psi = (\psi _{1}, \psi _{2}, \psi _{3}) \in M_{+}$.

Now, we present a useful definition and a useful lemma.

Definition 2.1. The rumor in system (3) is said to be permanent if there exist constants $l > 0$ and $L > 0$ such that the any solution $(X(t), Y(t), Z(t))$ of system (3) with initial conditions satisfies

Lemma 2.1. The solutions of system (3) with initial conditions are positive for all $t \geqslant 0$.

3.   Boundedness and existence of positive equilibrium points

In this section, we will obtain the boundedness and positive equilibrium point of system (3).

From

we can see that

is positively invariant with respect to system (3).

Theorem 3.1. The positive solutions of system (3) with initial conditions are ultimately bounded.

Proof. Let $(X(t), Y(t), Z(t))$ be any positive solution of system (3), then from system (3) we can obtain

where

One can derive that the function $\rho(Y)$ reaches its maximum value $\frac{K}{4}$ when $Y$ is equal to $\frac{K}{2}$. Then, from above equation, we have

which yields

It follows from the above inequality when $t\to\infty$,

Hence, there exists a constant $T > 0$ such that

for $t > T.$

Therefore, we obtain

for $t > T.$ □

One can see that there are two equilibria points of system (3):

(1) Rumor-free equilibrium point $E_{0} = (\bar{x}, 0, 0)$ where $\bar{x} = 1$. This means that the rumors will eventually disappear.

(2) Rumor prevailing equilibrium point or rumor existing equilibrium point $E_{+} = (\hat{X}, \hat{Y}, \hat{Z})$ with $\hat{Y} \neq0$. This means that the rumors will continue to spread.

Next, by the interior equilibrium point and system (3), we obtain

Then, solving the first and third equations of system (4), we have

From the values of $\hat{X}$ and $\hat{Z}$ and the second equation of system (5), one has the following cubic equation of $Y^{*}$

where

It is clear that this fixed point exists only if Eq (6) has a positive root. Thus, $L_{1}$ and $L_{2}$ are positive. Now we can suppose that $L_{4} < 0$ or $R_{0} > 1$. If this condition is true, then there are two cases:

(ⅰ) $L_{3} < 0$, meaning that Eq (6) has only one positive root.

(ⅱ) $L_{3} > 0$, meaning Eq (6) has three roots or exactly one positive root.

If the condition is not true, then there are two possibilities:

(ⅰ') $L_{3} < 0$, meaning Eq (6) has two positive real roots or no real roots (according to Descartes' rule of sign).

(ⅱ') $L_{3} > 0$, meaning Eq (6) has two positive real roots or no real roots (according to Descartes' rule of sign).

In order to find the one positive real root of Eq (6), first we need to find the value of $\hat{Y}$, and then we can find the values of $\hat{X}$ and $\hat{Z}$. Thus, we want to get a positive real root of Eq (6).

From the above discussion, one can see that system (3) has at least one positive rumor local equilibrium point.

Now, by the next generation matrix method ^[21], we can obtain the basic regeneration number (which is analogous to the basic reproduction number in a disease transmission model)

and then one can easily get that, when $R_{0} \le 1$, system (3) only has $E_{0}$, and, when $R_{0} > 1$, system (3) has $E_{+}$ except for $E_{0}$ and $E_{+}$ is unique.

4.   Stability of rumor-free equilibrium point $E_{0}$

On the stability of the rumor-free equilibrium point $E_{0}$ of system (3), we have the following result:

Theorem 4.1. In $\Gamma$, the equilibrium point $E_{0}$ of system (3) is globally stable if $R_{0} \le 1$, and the equilibrium point $E_{0}$ of system (3) is unstable if $R_{0} > 1$.

Proof. Denote

where

is any positive solution of system (3) with initial function $(\psi _ {1}, \psi_ {2}, \psi_ {3})$.

Construct a Lyapunov functional as follows:

Then by calculation we obtain

Let

and take the largest set $\Psi\in G$ which is invariant with respect to system (3). Obviously, $\Psi$ is not empty, because $(1, 0, 0) \in \Psi$. If $R_{0} < 1$, from $X(t)\le 1$ we get

Hence,

It follows from system (3) that

If $R_{0} = 1$, we have

Hence,

By

and when $X(t) = 1$, one can get

By means of the Lyapunov-LaSalle invariance principle, we have that, when $R_{0} \le1$, the equilibrium point $E_{0}$ is globally stable in $\Gamma$. Next, when $R_ {0} > 1$, we let

and then we have the following linearization equations of system (3) at $E_ {0}$

Further, we have the characteristic equation of system (7)

Consequently,

Set

Obviously,

and, by $R_{0} > 1$, when $\lambda\to+\infty$ we have $f(\lambda)\to+\infty$. In this case, there must be a $\lambda_{0} > 0$ such that $f(\lambda_{0}) = 0$. Therefore, there exists at least one root of (8) with positive real part. Thus, $E_{0}$ is unstable. □

5.   Permanence of rumor

On the permanence of the rumor of system (3), we have the following result.

Theorem 5.1. In system (3), if $R_{0} > 1$, then the rumor is permanent.

Proof. From

there are small enough $\alpha_{0} > 0$ and large enough $T_{0} > 0$ such that

Consider the derivative of the function

where

Now, we claim that for all $t\ge t_{0}\ge T_{0}$, $Y(t)\le \alpha_{0}$ is impossible. Suppose the contrary is true. Then for $t\ge t_{1}$, we have

Therefore, when $t\ge t_{1}+T_{0}$,

where

Let $t_{1} = T_{0}$, and then from the above inequality, for $t\ge 2T_{0}$, we get

Take

Now, we prove that $Y(t) \ge\underline{y}$ for all $t\ge 2T_{0}$. If the condition is not true, then there is a $T\ge 0$ satisfies $T\ge 0$, $Y(t) \ge \underline{y}$ for all

and

In addition, from the second equation of system (3), we get

This is a contradiction. Therefore, $Y(t) \ge \underline{y}$ for all $t\ge 2T_{0}$. Consequently, for all $t\ge 2T_{0}$, we obtain

This means that $V(t)\to+\infty$ as $t\to+\infty$ contradicts the boundedness of $V(t)$. Thus, the claim is valid. Then, we will discuss the following two possibilities for all large $t$:

(ⅰ) $Y(t)\geqslant \alpha_{0}$;

(ⅱ) $Y(t)$ oscillates about $\alpha_{0}$.

At last, for a sufficiently large $t$, we will get the result

Therefore, we only need to consider case (ⅱ).

Set $t_{1}$ and $t_{2}$ large enough satisfying

and $Y(t) < \alpha_{0}$ for all $t \in(t_{1}, t_{2})$.

If

since

we get

for all $t \in[t_{1}, t_{2}]$. If $t_{2}-t_{1} > T_{0}+\omega,$ then, it is easy to see that

for all $t \in[t_{1}, t_{1}+T_{0}+\omega]$. Therefore, based on the analysis and proof of the above claims, we observe that

on $[t_{1}+T_{0}+\omega, t_{2}]$. If it does not hold, then there exists a $\tilde{T} \geqslant0$ such that

for all $t \in[t_{1}, t_{1}+T_{0}+\omega+\tilde{T}]$, and

and

Next, from (10) and by the second equation of system (3), we get for

which is a contradiction. Thus,

holds for any $t\in[t_{1}, t_{2}]$. Therefore, we obtain

□

Remark 5.1. From Theorems 4.1 and 5.1, one can see that the condition $R_{0} > 1$ is a sufficient and necessary condition for the permanence of the rumor in system (3). Moreover, the condition $R_{0} \leqslant1$ is a sufficient and necessary condition for global stability of the rumor-free equilibrium point of system (3).

6.   Stability of the rumor prevailing equilibrium point $E_{+}$

In this part, we will derive some conditions on the locally asymptotic stability and global stability of the rumor prevailing equilibrium point of system (3). First, let

Then, system (3) takes the form

The linear part of system (11) is

where

It is clear that in order to prove the locally uniform asymptotic stability of the rumor prevailing equilibrium point $E_{+}$ of system (3), we only need to prove the locally uniform asymptotic stability of the zero solution of system (12).

Theorem 6.1. If $R_{0} > 1$ holds and conditions $G_{i}$ $(i = 1, 2, 3)$ hold, then the equilibrium point $E_{+}$ of system (3) is locally uniformly asymptotically stable, where

($G_{1}$) $2k_{11}+k_{12}-k_{13}-k_{21}\left(1+k_{23} \omega\right) > 0$;

($G_{2}$) $-k_{31}\left(1+k_{33}\tau\right)+(k_{24}-3k_{23}-2k_{21}-k_{22})+k_{12} > 0$;

($G_{3}$) $2k_{32}+k_{33}-k_{31}-k_{33}\tau(k_{31}+2k_{32}+2k_{33}) > 0$.

Proof. First, we define

Then, by $a^{2}+b^{2}\geqslant 2|ab|$ and system (12), we get

Let

Then, from the derivatives of $F_{11}(t)$ and $F_{12}(t)$, we have

where

Rewriting the second equation of (12), we get

Define

and from system (12), we get

Using the inequality $a^{2}+b^{2}\geqslant2|ab|$, we further get

Define

Then, from the derivatives of $F_{21}(t)$ and $F_{22}(t)$, we have

Next, let

where

Then, we have

Similarly, rewriting the third equation of (12) we get

Let

Then, using the inequality $a^{2}+b^{2}\geqslant 2|ab|$, we further derive

Define $F_{32}(t)$ as

Then, from the derivatives of $F_{31}(t)$ and $F_{32}(t)$, we have

Define

where

Then, we get

Finally, let

Then, we get

where

Obviously, from the assumptions of Theorem 6.1, we can see that

and then $\frac{\mathrm{d}F}{\mathrm{d}t}$ is negative definite in $\Gamma$. □

Now, we will consider the global stability of the rumor prevailing equilibrium point $E_{+}$. We need the positive invariant set of system (11)

and the following lemma:

Lemma 6.1. Suppose that (X(t), Y(t), Z(t)) is any positive solution of system (3). Then,

Proof. For any positive constant $\theta$, there exists a sufficiently large $t_{1} > 0$, such that $Y(t)\leqslant1+\theta$ as $t\geqslant t_{1}$. Then, from system (3), we get

for $t\geqslant t_{1}$. Since $\theta$ is arbitrary and it follows from the above inequality when $t\to\infty$,

Hence, there exists a constant $T_0 > 0$ such that

for $t > T_0$.

Based on the above lemma, we can assume

First, define functions $J_{i}(i = 1, 2, 3)$ as follows:

Next, by calculation of the derivatives of $J_{i}$ $(i = 1, 2, 3)$ along system (11), we get

and

Finally, we construct the Lyapunov functional

where

Then, calculating the derivative of $J(t)$, we get

where

□

Based on the above analysis and discussion on the globally asymptotic stability of rumor prevailing equilibrium point $E_{+}$ of system (3), we have the following result:

Theorem 6.2. If $R_{0} > 1$ and $e_{i} > 0$ $(i = 1, 2, 3)$ hold, then the rumor prevailing equilibrium point of system (3) is globally asymptotically stable in $\Gamma$.

7.   Optimal control by media intervention

If there is an emergency or a situation becomes very urgent, in order to curb the spread of rumors, the government will usually control or intervene in the trend of rumors through the media ^[22,23,24]. This paper uses the most common media interventions to study the role of control mechanisms in the system. For a clearer understanding, a period of time can be selected as the effective time, during which the control is added, and the control is removed when the number of spreaders is reduced enough to restore the stability of the system. At this time, both the ignorant and the conscious are actively or passively taking control. Therefore, when the system performs media intervention controls, we calculate the cost per user. Now, assume that $u$ is the media control variable, then we have the following assumptions:

(1) Let $u^{2}(t)(X(t)+Y(t)+Z(t))$ be the cost function of the control, where the media control are effective for all users. Although our goal is to minimize the spread of false information, the spread of false information through the media cannot be applied to any specific group, but to all groups.

(2) The ignorant population directly enters the aware class with the rate $\zeta _{1}$, whereas the spreader population transfers to the aware class with the rate $\zeta _{2}$. It is evident that $\zeta _{1}$ is greater than $\zeta _{2}$.

with the initial condition $X(0)\ge 0,$ $Y(0)\ge 0,$ $Z(0)\ge 0$. Here our objective is to minimize the total number of spreaders and the corresponding cost. So,

where

By ^[25], to find the optimal solution, we find the Hamiltonian of our optimal control problem (13) as given by

where the $f_{i}$ $(i = 1, 2, 3)$ are adjoint variables.

7.1.   Existence of optimal control

Theorem 7.1. For system (13) and objective function (14), there exists an optimal control $u^{\ast } \in \hat{\Theta }$ for which

Proof. As all the state variables and co-state variables are non-negative, so too is the control variable $u$. The control space $\hat{\Theta }$ is convex and closed. According to Theorems 3.1 and 5.1 and their proofs in ^[26], one can see that there is a minimum value, so the control coefficient $u$ has a minimum value, and thus there is an optimal control, and the proof is complete. □

7.2.   Analysis of the control

Here we find the set of necessary conditions for our optimal control problem with the help of Pontryagin's maximum principle.

Theorem 7.2. If $u^{\ast }$ is the optimal control variable which optimizes (14) for system (13), with optimal state variables $X^{\ast }, Y^{\ast },$ and $Z^{\ast}$, and optimal co-state variable $f_{i}\; (i = 1, 2, 3)$ where $f_{i}$ satisfies the system

with transversality condition

then we obtain

Proof. Using Pontryagin's maximum principle on the Hamiltonian (15), we obtain the mathematical expression of the adjoint system (16), which is

From the optimality condition

we obtain

By definition, the highest and the lowest value of control are 1 and 0, respectively. That is, if $u^{*} \le 0$ then $u^{*} = 0$, and if $u^{*} \ge 1$, then $u^{*} = 1$. So, for $u^{\ast }$ we get the optimum value of $W(X, Y, Z)$ for system (16). □

8.   Numerical simulations

In this section, three examples are given to illustrate the effectiveness of our results obtained in this paper.

Example 8.1. First, we take a set of parameters and consider the following system

Directly from calculation, we get $R_{0} = 0.7996 < 1$. On the basis of Theorem 3.1, we have that the rumor-free equilibrium point $E_{0} = (1, 0, 0)$ is globally stable, which means the rumor disappears. The corresponding simulations are shown in Figure 1.

Next, we take another set of parameters and consider the following system

Directly from calculation, we get $R_{0} = 0.6696 < 1$. From Theorem 3.1, we also have that the rumor-free equilibrium point $E_{0} = (1, 0, 0)$ is globally stable, which means the rumor disappears. The corresponding simulations are shown in Figure 2.

Example 8.2. Next, we consider the system

Directly from calculation, we get $R_{0} = 4.0651 > 1.$

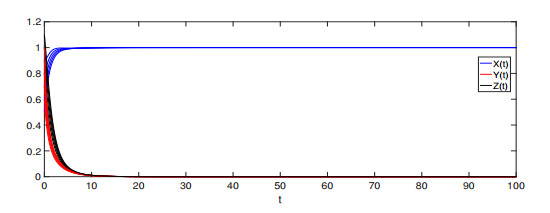
From Theorem 5.1, we have that the rumor is permanent, which means the rumor exists for a long time. The corresponding simulations are shown in Figure 3.

Example 8.3. Finally, we consider the system

where $\tau = 0.38, \ \omega = 0.07$. Directly from calculation, we get

and

The corresponding simulations are shown in Figure 4 ($a_1, b_1, c_1, d_1, e_1, f_1, g_1$).

In system (23), if we take

then, we have

The corresponding simulations are shown in Figure 5 ($a_2, b_2, c_2, d_2, e_2, f_2, g_2$).

In system (23), if we take

then we have

and

The corresponding simulations are shown in Figure 6 ($a_3, b_3, c_3, d_3, e_3, f_3, g_3$).

In system (23), if we take

then we have

and

The corresponding simulations are shown in Figure 7 ($a_4, b_4, c_4, d_4, e_4, f_4, g_4$).

Remark 8.1. From the above numerical simulation figures in Example 8.3 and the values of the time delays $\tau$, $\omega$, we can see that if $\tau = 0.38, \ \omega = 0.07$, then the rumor prevailing equilibrium point $E_{+}$ of system (23) is globally asymptotically stable; if $\tau = 0.38$, $\omega = 0.24$, then the rumor prevailing equilibrium point $E_{+}$ of system (23) is unstable; if $\tau = 0.38$, $\omega = 0.72$, then the rumor prevailing equilibrium point $E_{+}$ of system (22) is globally asymptotically stable; if $\tau = 1.48$, $\omega = 0.72$, then the rumor prevailing equilibrium point $E_{+}$ of system (22) is globally asymptotically stable. From the above analysis, we can conclude that the time delay $\omega$ has an effect on the global asymptotic stability of the rumor prevailing equilibrium point $E_{+}$.

9.   Conclusions

Social networks have become an important medium for rumor propagation, and it may cause some serious negative effects on our society. Hence, studying the ways in which rumors spread and controlling them is of great significance. This paper considers the delayed $XDYZ$ rumor propagation model based on social networks with logistic growth and saturation incidence, and the dynamical behavior of the model is studied by using of the next generation matrix method, some inequality techniques, the Lyapunov-LaSalle invariance principle, and the Lyapunov functional. First, the positiveness and boundedness of the system are obtained. Second, the rumor-free equilibrium point, the rumor prevailing equilibrium point, and the basic regeneration number $R_{0}$ of the model are obtained. Meanwhile, the global stability of the rumor-free equilibrium point $E_{0}$, the permanence of the rumor, and the global asymptotic stability of the rumor prevailing equilibrium point $E_{+}$ are obtained. Then, the minimum cost of controlling rumors is given. Finally, the validity of the theoretical results and the influence of different parameters and time delays on the model are shown by numerical simulations. Additionally, we can see from the results and numerical simulation examples that the time delay $\omega$ has an effect on the aforementioned dynamic behaviors of the considered system. Because of this, system (2) can be seen as a general model compared to the models in ^{[1,2,3,4,5,6,7,8,9,10,11,13,14,15,16,17,18]}, and the theoretical results obtained in this article and model (2) can be seen as extensions of and supplements to the previously known theoretical results and models.

From the dynamic analysis of the rumor propagation model, one can find that rumor propagation is a very complicated process. Mathematical analysis can provide a theoretical basis for reducing and controlling the harmful effects of rumor propagation and to reduce the disturbance or panic caused by widely circulated rumors (viral scenes) in society. In conclusion, studying the ways in which rumors spread and controlling them is essential to preventing their negative impacts. By using social network analysis, debunking false claims, and addressing the underlying emotions that drive rumor-mongering, governments and organizations can effectively manage rumors and protect their communities. This model can also use different time delays required by users of different age structures or take into account the role of a trust mechanism to study a more realistic rumor propagation model.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported by the Open Project of Key Laboratory of Applied Mathematics of Xinjiang Uygur Autonomous Region (grant No. 2023D04045) and the National Natural Science Foundation of Xinjiang (grant No. 2021D01C067).

Conflict of interest

The authors declare that they have no competing interests.