Dynamic analysis and optimum control of a rumor spreading model with multivariate gatekeepers

1.   Introduction

Rumor spreading, a ubiquitous phenomenon, is typically defined as the spreading of unverified messages on social platforms, easily attracting public attention and causing social panic ^[1]. With recent advancements of mobile internet technologies, social platforms not only provide a convenient way for netizens to access and exchange information but also facilitate rumor spreading ^[2]. The internet mediums have more remarkable characteristics than traditional oral communication, such as faster speed, broader scope, and more substantial harm. Rumors significantly affect human affairs and social order by failing to be reasonably controlled in an emergency. Practical experience shows that scientific defense and intervention of rumor spreading can be effectively carried out with an in-depth understanding of the scientific laws of rumor spreading ^[3], thereby undoubtedly stimulating the current intensive study of the rumor-spreading model on social networks.

Recently, rumor spreading has drawn considerable attention due to the universality and harmfulness of rumors, which involve many disciplines, such as psychology ^[2], mathematics ^[4], physics ^[5], and so on. Early on, epidemic models were used to study the spreading of smallpox ^[6,7,8], which marked the advent of the epidemic model era. Due to the obvious similarity of the law between rumor spreading and disease spreading ^[9,10,11,12], researchers proposed some classical models based on epidemic models to investigate the dynamics laws of rumor spreading, such as susceptible-infected (SI) ^[13], susceptible-infected-susceptible (SIS) ^[14], and susceptible-infected-recovered (SIR) ^[15]. Daley et al. first put forward the classic Daley-Kendall (DK) model in 1964 ^[16]. Consequently, Mak et al. further presented the improved Maki-Thompson (MT) model^[17]. Sudbury et al. explored the dynamics of rumor spreading with the SIR model in 1985 ^[18]. Building upon this, researchers continually advance various variant models, which are used to explore the impact of different mechanisms on rumor spreading. The isolation mechanism can effectively avoid contact between users, thereby reducing information flow and controlling the scope of rumor spreading. Zhu et al. investigated the compulsory silence functionality ^[1]. Jiang et al. found that the isolation mechanism was the most effective strategy to restrain rumor propagation with a two-stage rumor-spreading model ^[4]. Subsequently, Liu et al. ^[19] also adopted the isolation transformation strategies as external and soft control strategies. Meanwhile, there are physiological characteristics that strikingly impact rumor spreading ^[20,21,22], such as the forgetting mechanisms. Ding et al. found that the forgetting mechanism greatly alleviates the harmfulness of rumor spreading. Ding et al.^[20] and Ferraz et al.^[21] explored the effect of the forgetting mechanism on rumor spreading and observed that the forgetting mechanism was closely related to the lifespan of rumors. What is more, the information disclosure mechanism can enable netizens to timely access real information and eliminate misunderstandings caused by rumors. To capture the dynamic interaction law between rumors and anti-rumors, Ghosh et al.^[22] and Yin et al.^[23] investigated the counteractive role.

Although the existing efforts have verified that disclosure, enforced silence, and forgetting mechanisms can largely affect rumor spreading, they fail to simultaneously combine them. In fact, rumor spreading is a complex and dynamic process affected by various factors in real scenarios. Meanwhile, curbing rumor spreading is consistently an enduring topic^[24] due to the serious harmfulness for the nation and society. Our goal is to essentially eliminate rumor spreading on social networks as much as possible at the minimum cost within the expected time. Thereby rumor control mechanisms are necessary to mitigate the harm done, such as deleting posts^[25], education mechanism^[26,27], and releasing anti-rumor information^[28,29]. However, the existing works primarily focus on no more than two control strategies and ignore the role of multivariate factors, thereby failing to be suitable in complex real-world scenarios. Therefore, it has profound practical significance and application value to explore the dynamic behaviors of rumor spreading considering joint disclosure, forgetting, enforced silence, and control mechanisms. Undoubtedly, this also increases the complexity of rumor spreading models.

In response to the above challenges, in this paper, we propose an innovative ISEHR rumor-spreading model with a multivariate gatekeeper mechanism. Specifically, we first calculate the threshold of our model by using the next-generation matrix. Further, based on the Routh-Hurwitz judgment, Lyapunov theory, and LaSalle's invariance principle, we analyze the existence and stability of the rumor-free/rumor equilibrium points. In addition, the optimized control is investigated to optimize the multivariate gatekeeper mechanism. Finally, extensive numerical simulations are conducted to validate the correctness of the theoretical analysis. In a nutshell, the main contributions of this paper are described as follows:

1) Under appropriate assumptions, considering the disclosure, forgetting, and enforced silence mechanisms, we establish an innovative ISEHR model with a multivariate gatekeeper mechanism, which is beneficial for understanding the laws of rumor spreading.

2) We introduce the concept of multivariate gatekeepers from the communication discipline. We present an optimized control model with the multivariate gatekeeper strategies, such as the nation, social platforms, and administrators.

3) Extensive numerical simulations validate the correctness of the theoretical analysis with sensitivity analysis under different initialization values. Our findings indicate that the proposed mechanisms and strategies seriously affect rumor spreading, and complex interactions exist among different factors. These findings provide an effective and scientific basis of decisions for society and national governance.

The structure the rest of this paper is as follows: The establishment process of our model is first introduced, and the meaning of each variable is clarified, in Section 2. In Section 3, the existence and distribution of the equilibrium point are discussed. In Section 4, the optimal control problem is studied. Numerical simulations of the theorems mentioned are given in Section 5. The last section includes the summary of this paper, followed by the display of references.

2.   Model formulation with basic properties

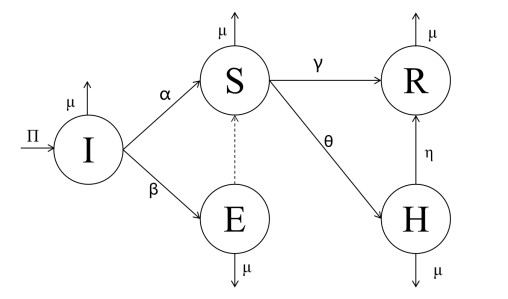
In this paper, we propose a novel ISEHR model with a multivariate gatekeeper mechanism, which considers disclosure, forgetting, and enforced silence mechanisms and introduce the expositor and hibernator roles. The total population of the system is dynamically changed over time, hence ushering an entering and leaving mechanism for the dynamic system. Meanwhile, we divide them into five categories, specifically Ignorant, Expositor, Spreader, Hibernator, and Remover, where I (Ignorant) represents the Ignorant have not been exposed to rumors and are easily influenced; the E (Expositor) group who know and spread the truth; the S (Spreader) group who believe and spread rumors; the H (Hibernator) describes the Hibernator who cannot spread rumors temporarily but can spread them in the future; and the R (Remover) group who used to be rumor-believers, but have been made conscious that rumors are incorrect and will no longer spread them. The densities of Ignorant, Spreader, Expositor, Hibernator, and Remover are denoted by I(t), S(t), E(t), H(t), and R(t) at time t, respectively. Additionally, our model only considers the disclosure, forgetting, and enforced silence mechanisms and ignores other factors, such as time delay^[30] and topology structure^[31], which will be considered in our future work. Our model is schematically shown in Figure 1.

According to the facts about rumor spreading, the parameters of the system (2.1) are non-negative constants, which are outlined in Table 1, such as $\Pi$, $\alpha$, $\mu$, $\beta$, $\gamma$, $\theta$, and $\eta$, and the range is between zero and one. The assumptions of our model are as follows:

1) When an Ignorant comes into contact with a rumor posted by the Spreaders on social networks, they may become a Spreader with the probability $\alpha$. Meanwhile, due to differences in the Ignorants' abilities to identify rumors, part of the Ignorant group may become Expositors with the probability $\beta$, avoiding rumor spreading to a certain extent.

2) After a Spreader exposes the truths published by the Expositors, the Spreader realizes that the information encountered is incorrect, hence the Spreader will actively become a Removal with the probability $\gamma$. Meanwhile, considering the phenomenon of hardcore fans among Spreaders on social networks, they firmly believe that the rumor released is correct. Social platforms alleviate rumor spreading with the enforced silence mechanism, such as blocking the account. The Spreader will passively become a Hibernator with the probability $\theta$ and will no longer spread rumors.

3) Due to the inherent property of forgetting information for the population, a Hibernator become a Removal with the probability $\theta$.

4) The density of the individuals entering the dynamic system is $\Pi$, the density of the Ignorant, Expositor, Spreader, Hibernator, and Remover leaving the system is $\mu$.

According to the above propagation criteria, our model can be expressed as shown in the following nonlinear differential equations (2.1).

The initial conditions of the dynamic system (2.1) satisfies the following Eq (2.2).

The total population of the system (2.1) is $N(t)$, as shown in Eq (2.3).

Taking the derivative on both sides of Eq (2.3), and then substituting Eq (2.1), we can obtain Eq (2.4).

We achieve the following results by using the variation constants method.

If $t \to + \infty$, the total population of the system (2.1) is $N(t) = \frac{\Pi }{\mu }$.

In conclusion, the total population of the system (2.1) at any moment is non-negative. Therefore, the positive invariant set of the system (2.1) is presented as shown in Eq (2.6).

We can clearly observe that the $R$ state does not affect the stability of the system from Eq (2.1). For simplicity, we simplify the system (2.1) as shown in the following Eq (2.7).

3.   Stability analysis

In the following, we mainly focus on the stability analysis of our model. Specifically, we utilize the next-generation matrix method to solve the basic reproduction number and apply in the Lyapunov theory to analyze the stability of the rumor-free/rumor equilibrium point in the dynamic system (2.7).

Let $\phi \left(t \right) = {\left({I(t), S(t), E(t), H(t)} \right)^T}$, and the dynamic system (2.7) is simplified as shown in the following Eq (3.1).

Deriving for $\phi (t)$, the Eq (3.1) is written as shown in the following Eq (3.2).

where $F\left(\phi \right) = \left({\begin{array}{*{20}{c}} 0\\ {\alpha I(t)S(t)}\\ {\beta I(t)S(t)}\\ {\theta S(t)E(t)} \end{array}} \right)$, and $V\left(\phi \right) = \left({\begin{array}{*{20}{c}} {\alpha I(t)S(t) + \beta I(t)S(t) + \mu I(t) - \Pi }\\ {\gamma S(t)E(t) + \theta S(t)E(t) + \mu S(t)}\\ {\mu E(t)}\\ {\eta H(t) + \mu H(t)} \end{array}} \right)$.

The Jacobian matrices of $F(\phi)$ and $V(\phi)$ are described as shown in the following Eqs (3.3) and (3.4), respectively.

For simplicity, the rumor-free equilibrium point is substituted into Eqs (3.3) and (3.4), obtaining Eqs (3.5)–(3.7).

The basic reproduction number ${\Re _0}$ of the dynamic system (2.1) is the spectral radius of the matrix $F{V^{ - 1}}$, as shown in Eq (3.8).

Solving for the eigenvalues of Eq (3.8), we obtain Eq (3.9).

The basic reproduction number ${\Re _0}$ of the dynamic system (2.1) is shown in Eq (3.10).

3.1.   The stability analysis of rumor-free equilibrium

3.1.1.   The local stability analysis of rumor-free equilibrium

Theorem 1. For the dynamic system (2.7), if ${\Re_0} < 1$, the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$ is locally asymptotically stable; if ${\Re_0} > 1$, then the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$ is unstable.

Proof: The Jacobian matrix of the dynamic system (2.7) at the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$ is described as shown in Eq (3.11).

The eigenvalues of Eq (3.11) are

Furthermore, we can obtain

The eigenvalues of Eq (3.13) are given by

According to Eq (3.14), if ${\lambda _4} < 0$, then the following Eq (3.15) needs to be satisfied.

If ${\Re _0} < 1$, then ${\lambda _1} < 0$, ${\lambda _2} < 0$, ${\lambda _3} < 0$, and ${\lambda _4} < 0$ hold, and all eigenvalues of the Eq (3.13) are all negative. Therefore, the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$ is locally asymptotically stable. Furthermore, if ${\Re _0} > 1$, and then the eigenvalue ${\lambda _4}$ is positive, then the dynamic system (2.7) is unstable at the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$.

3.1.2.   The global stability analysis of rumor-free equilibrium

Theorem 2. For the dynamic system (2.7), if ${\Re _0} < 1$, the rumor-free equilibrium ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$ is globally asymptotically stable.

Proof: We define the Lyapunov function of the dynamic system (2.7) as shown in Eq (3.16).

Deriving both sides of Eq (3.16) and substituting Eq (2.1) into Eq (3.16), we can obtain

If the Eq (3.17) holds, we can obtain

Combining Eqs (3.17) and (3.18), we obviously find that if ${\Re _0} < 1$, then $\frac{{dV(t)}}{{dt}} < 0$. Then $\frac{{dV(t)}}{{dt}} = 0$, if and only if ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$.

According to the Lyapunov theory, it can be inferred that if ${\Re _0} < 1$, the dynamic system (2.7) is globally asymptotically stable at ${E_0} = \left({\frac{\Pi }{d}, 0, 0, 0} \right)$.

3.2.   The stability analysis of rumor equilibrium

In this section, we primarily discuss the properties of rumor equilibrium. We first assume that there exists the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$. The dynamic system (2.7) satisfies the following Eq (3.19).

We can obtain Eqs (3.20)–(3.23) from Eq (3.19).

Combining Eqs (3.19)–(3.23), we can obtain the expression ${R^*}$ with ${S^*}$. Therefore, the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$ exists.

3.2.1.   The local stability analysis of rumor equilibrium

Theorem 3. If $H({S^*}) > 0$, $G({S^*}) > 0$, $K({S^*}) > 0$, and $H({S^*})G({S^*}) > K({S^*})$, the dynamic system (2.7) is locally asymptotically stable at the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$.

Proof: The Jacobian matrix of the dynamic system (2.7) at the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$ is as shown in Eq (3.24).

The characteristic equation is written as shown in Eq (3.25).

For brevity, let $a = \alpha {S^*} + \beta {S^*} + \mu$, $b = \frac{{\beta \Pi \left({\gamma + \theta } \right){S^*}}}{{\mu \left[{\left({\alpha + \beta } \right){S^*} + \mu } \right]}} - \frac{{\alpha \Pi }}{{\left({\alpha + \beta } \right){S^*} + \mu }} + \mu$, $c = \frac{{ - \beta \Pi \left({\alpha + \beta } \right)\left({\gamma + \theta } \right){S^{*2}}}}{{\left({\alpha + \beta } \right){S^*} + \mu }}$, $d = \frac{{\alpha \Pi \left({\alpha + \beta } \right){S^*}}}{{\left({\alpha + \beta } \right){S^*} + \mu }}$, and $e = \frac{{\beta \Pi \left({\gamma + \theta } \right){S^*}}}{{\left({\alpha + \beta } \right){S^*} + \mu }}$.

Further, we can obtain

Combining Eqs (3.26)–(3.28), the simplified form of Eq (3.25) is obtained.

Remarkably, we observe the following from Eq (3.29).

According to the Routh-Hurwitz criterion and Eq (3.31), if $H({S^*}) > 0$, $G({S^*}) > 0$, $K({S^*}) > 0$, and $H({S^*})G({S^*}) > K({S^*})$, then ${\lambda _2}$, ${\lambda _3}$, and ${\lambda _4}$ have negative real parts. Therefore, the dynamic system (2.7) is locally asymptotically stable at the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$.

3.2.2.   The global stability analysis of rumor equilibrium

Theorem 4. For the dynamic system (2.7), the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$ is globally asymptotically stable if ${\Re _0} > 1$.

Proof: Let $g(a) = a - 1 - \ln a$, where $a > 0$ and $g(a) \ge 0$. We construct the Lyapunov function, as shown in Eq (3.32).

Assuming $x = \frac{{I(t)}}{{{I^*}}}$, $y = \frac{{S(t)}}{{{S^*}}}$, and $z = \frac{{E(t)}}{{{E^*}}}$, where $A$, $B$, and $C$ are all positive constants, then Eq (3.32) is derived, obtaining Eq (3.33).

According to Eqs (2.7) and (3.19), we obtain the following Eq (3.34).

Eq (3.35) is given from Eqs (3.33) and (3.34).

We can find the suitable constants A, B, and C to ensure that the following Eqs (3.36)–(3.40) hold.

We can find that $\frac{{dV(t)}}{{dt}} \le 0$ holds. If and only if $I(t) = {I^*}$, $S(t) = {S^*}$, and $E(t) = {E^*}$, then $\frac{{dV(t)}}{{dt}} = 0$. Therefore, the dynamic system (2.7) is globally asymptotically stable at the rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}} \right)$.

4.   The optimal control

In this section, we introduce a real-time optimization control strategy. Our goal is to contain rumor spreading in the expected time with minimal cost. Due to the severe harmfulness of rumors for the nation and society, all level subjects must take effective measures to curb rumor spreading. The nation improves the ability of the Ignorant to identify rumors with educational technology and rumor-disclosure mechanisms, the platform organizer adopts the control technology to filter and block rumors, and the administrators continuously communicate with the Hibernator, gradually alleviating rumor spreading. The above strategies constitute a multivariate gatekeeper mechanism to govern rumor spreading. After adding optimized control, Eq (4.1) is given as shown in the following:

where ${\psi _1}$, ${\psi _2}$, and ${\psi _3}$ represent the control intensity of the nation, the social platforms, and the administrators, respectively. To calculate the control cost, ${\Omega _i}$ and ${\varphi _i}$ $(i = 1, 2, 3)$ represent the average cost of controlling the Ignorant, Spreader, and Hibernator at the nation, social platform, and administrator level, respectively, and the control cycle time is $\left[{0, T} \right]$. The constructed optimal control objective function is shown as the following Eq (4.2).

where the feasible regions of ${\psi _1}(t)$, ${\psi _2}(t)$, and ${\psi _3}(t)$ are shown in Eq (4.3).

where ${\psi _1}^{\max } \le 1$, ${\psi _2}^{\max } \le 1$, and ${\psi _3}^{\max } \le 1$ are the upper bound of ${\psi _1}(t)$, ${\psi _2}(t)$, and ${\psi _3}(t)$, respectively. The optimal control ${\psi _1}^*$, ${\psi _2}^*$, and ${\psi _3}^*$ satisfy $J\left({{\psi _1}^*, {\psi _2}^*, {\psi _3}^*} \right) = \min \left\{ {J\left({{\psi _1}\left(t \right), {\psi _2}\left(t \right), {\psi _3}\left(t \right)} \right) \in \Delta } \right\}$.

We construct the following Lagrange function to obtain the optimal control, as shown in Eq (4.4).

We define the Hamiltonian function for the optimized dynamic control system, as shown in Eq (4.5).

where $i = 1, 2, 3, 4, 5$. We apply the Pontryagin maximum principle to obtain the following Lemma 1:

Lemma 1. Let ${I^*}$, ${S^*}$, ${E^*}$, ${H^*}$, and ${R^*}$ are the optimal solutions corresponding to the optimal control $\left({{\psi _1}^*, {\psi _2}^*, {\psi _3}^*} \right)$. The existing variables ${\lambda _i}(t), i = 1, 2, 3, 4, 5$, satisfy Eq (4.6).

According to the boundary conditions of ${\lambda _i}(t), i = 1, 2, 3, 4, 5$, the optimal control $\left({{\psi _1}^*, {\psi _2}^*, {\psi _3}^*} \right)$ can be described as the following Eqs (4.7)–(4.9) from Eq (4.6).

Proof: Let $I(t) = {I^*}$, $S(t) = {S^*}$, $E(t) = {E^*}$, $H(t) = {H^*}$, and $R(t) = {R^*}$, and then, we can obtain the following equation by using Pontryagin's Maximum Principle.

Combining the optimization conditions, Eq (4.5) is derived for ${\psi _1}(t)$, ${\psi _2}(t)$, and ${\psi _3}(t)$. We obtain the following Eqs (4.11)–(4.13).

By solving the above Eqs (4.11)–(4.13), we have the optimized control values (4.14)–(4.16).

According to the property of the boundary $\Delta$, the intervals of values ${\psi_1}^*$, ${\psi_2}^*$, and ${\psi_3}^*$ can be obviously obtained, as shown in Eqs (4.17)–(4.19), respectively.

5.   Numerical simulations

In this section, extensive numerical simulations are conducted to verify the effectiveness of our model and the proposed optimal control under different parameter values.

5.1.   The stability analysis of rumor-free equilibrium

In dynamic system (2.1), we choose $\Pi = 0.001$, $\alpha = 0.09$, $\beta = 0.04$, $\gamma = 0.025$, $\theta = 0.05$, $\eta = 0.02$, and $\mu = 0.01$, where $\Pi$ is the density of an individual entering the dynamic system with 0.001, $\alpha$ corresponds to the probability of an Ignorant becoming a Spreader with 0.09, $\beta$ signifies the probability of an Ignorant becoming an Expositor with 0.04, $\gamma$ presents the probability of a Spreader becoming a Removal with 0.025, $\theta$ is the probability of a Spreader becoming a Hibernator with 0.05, $\eta$ symbolizes the probability of the Hibernator becoming the Removal with 0.02, and $\mu$ refers to the density of each state leaving the dynamic system with 0.01. The basic reproduction number ${\Re _0} = 0.9 < 1$ is calculated. The results are shown in Figure 2.

Under ${\Re _0} = 0.9 < 1$, Figure 2(a) shows the changes in the density for five groups over time. The density of the Ignorant group shows a decreasing trend, but the densities present first increasing and then decreasing for the Expositor, Spreader, Hibernator, and Removal groups over time, and they finally reach 0. This indicates that there are no more Spreaders in the system (2.1) after reaching the rumor-free equilibrium. Figures 2(b)–(c) show the trend of the density change for the Ignorant, Hibernator, Removal, Spreader, and Expositor groups over time under different initial values until they converge to the equilibrium points ${E_0}$. Meanwhile, under different initial conditions for the Ignorant group, Figures 2(d)–(e) show the trajectory of the density change for the Ignorant, Spreader, and Expositor group in the solution space of the dynamic system (2.1), respectively. We observe that Expositors and Spreaders first increase to a maximum and then decrease as Ignorant decreases. Figure 2(f) shows the trajectory of the density change for the Ignorant, Spreader, and Expositor groups. We observe that from different initial states, they all converge to the same equilibrium point ${E_0}$. In conclusion, the dynamic system (2.1) has a unique rumor-free equilibrium ${E_0}$ from Theorem 1, which is locally asymptotic stable, as shown in Figure 2(a). Meanwhile, the unique rumor-free equilibrium ${E_0}$ is also globally asymptotically stable from Theorem 2. We provide numerical simulations to verify the global asymptotic stability of the dynamic system (2.1), as shown in Figures 2(b)–(f). We observe that $\left(I\left(t \right), S\left(t \right), E\left(t \right), H\left(t \right), R\left(t \right)\right)$ converges to $E_0$, which means that ${E_0}$ is globally asymptotically stable.

5.2.   The stability analysis of rumor equilibrium

Considering the dynamic system (2.1) under initialization parameters $\Pi = 0.01$, $\; \alpha = 0.06$, $\; \beta = 0.01$, $\; \gamma = 0.06$, $\; \theta = 0.04$, $\; \eta = 0.01$, and $\; \mu = 0.008$, where $\Pi$ denotes the density of an individual entering the dynamic system with 0.01, $\alpha$ corresponds to the probability of an Ignorant becoming a Spreader with 0.06, $\beta$ signifies the probability of an Ignorant becoming an Expositor with 0.01, $\gamma$ presents the probability of a Spreader becoming a Removal with 0.06, $\theta$ symbolizes the probability of a Spreader becoming a Hibernator with 0.04, $\eta$ refers to the probability of a Hibernator becoming a Removal with 0.01, and $\mu$ is the density of each state leaving the dynamic system with 0.008. We can obtain ${\Re _0} = 9.375 > 1$ by calculation. The dynamic system (2.1) has a rumor equilibrium ${E_1}^* = \left({{I^*}, {S^*}, {E^*}, {H^*}, {R^*}} \right)$. According to Theorems 3 and 4, the rumor equilibrium ${E_1}^*$ is locally and globally asymptotically stable. We provide simulation experiments to verify the correctness of Theorems 3 and 4, and the results are shown in Figure 3.

Under ${\Re _0} = 9.375 > 1$, Figure 3(a) shows the density changes for five groups over time. We observe that the density of the Ignorant group first decreases and then increases. The density first increases and then decreases for the Spreaders. At the same time, for the Expositor, Hibernator, and Removal individuals, we observe that their density shows an upward trend over time. Finally, the density of all states converge to the equilibrium point ${E_1}^*$, which is non-zero. Figure 3(b) shows that under different initial values for Spreaders, the density of the Spreader and Expositor groups respectively show a trend of first increasing, then decreasing and increasing, converging to the equilibrium point ${E_1}^*$. Meanwhile, Figures 3(c)–(f) show that the density of the Ignorant, Hibernator, Spreader, and Removal groups change over time until they approach the equilibrium point ${E_1}^*$. Among them, the Ignorant group generally indicates a downward trend, while Hibernator and Removal show an upward trend. In conclusion, the dynamic system (2.1) has a unique rumor equilibrium ${E_1}^*$ from Theorem 3, which is locally asymptotic stable, as shown in Figure 3(a). Meanwhile, the unique rumor equilibrium ${E_1}^*$ is also globally asymptotic stable from Theorem 4. We provide numerical simulations to verify the global asymptotic stability of the dynamic system (2.1), as shown in Figures 3(b)–(f). We observe that $\left(I\left(t \right), S\left(t \right), E\left(t \right), H\left(t \right), R\left(t \right)\right)$ converges to ${E_1}^*$, which means that ${E_1}^*$ is globally asymptotic stable.

5.3.   The feasibility and effectiveness of optimal control

To verify the impact of the multivariate gatekeeper strategy from different levels on rumor spreading, we construct the optimal control system, as shown in Eq (4.1). Based on the parameters in Section 5.2, we add the optimal control parameters and provide some numerical simulations. The results are shown in Figure 4.

Under ${\Re _0} = 9.375 > 1$, Figure 4(a) shows the trends of the change for the Ignorant, Spreader, and Hibernator groups with or without optimal conditions, respectively. Meanwhile, Figures 4(b)–(f) show the trends of the change for the Expositor, Removal, Ignorant, Spreader, and Hibernator, respectively, under their respective control strength changes over time. We observe that the greater the strength of control, the smaller the scale of rumor spreading. At the same time, it can weaken the possibility of rumors erupting again. In conclusion, as the control conditions increase, the density for the Removal group increases. This means that compared to a single control factor, the multivariate gatekeeper strategy introduced can better increase the number of removals, thereby faster controlling the rumor diffusion. The above analysis is in line with practical application scenarios. Therefore, the multivariate gatekeeper strategy proposed in this paper can effectively curb rumor diffusion.

5.4.   Model comparison

In this subsection, we compare our model with the classical SIRE model ^[32], where the parameters of the SIRE are described that $b = 0.7$, $\beta = 0.7$, $\mu = 0.1$, $\gamma = 0.15$, $\Upsilon = 0.05$, $< k > = 1.9231$, and $\alpha = 0.9$. The comparison of our model and the SIRE model is as shown in Figure 5.

From Figure 5, we can observe that the peak density of the Spreader group in our model is smaller than that in the SIRE model, meaning that the disclosure, forgetting, and enforced silence mechanisms can better suppress rumor spreading. Thereby, the proposed mechanisms are effective and reasonable in our model.

6.   Conclusions

In this paper, considering the disclosure, forgetting, and enforced silence mechanisms, we propose an innovative ISEHR rumor-spreading model with the multivariate gatekeeper strategy. The threshold behavior and dynamics are carried out by analyzing the dynamic system. We obtain some meaningful theoretical results ensuring local/global asymptotic stable rumor/rumor-free equilibrium points. We further introduce the optimal control to efficiently curb the rumor spreading at the minimum cost within the expected time. Some numerical simulations are conducted to verify the correctness of the theoretical analysis. Our findings can essentially help us understand rumor spreading on social networks, effectively alleviating the harm to human affairs and social order. In the future works, we will consider dual-layer rumor spreading models with time delay on social networks and explore more complex control strategies, such as the pulse control strategy.

Author contributions

Yanchao Liu: conceptualization, methodology, data curation, writing–original draft; Pengzhou Zhang: funding acquisition, resources; Deyu Li: formal analysis; Junpeng Gong: supervision, writing–review & editing.

All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by the National Key Research and Development Program of China (No. 2022YFC3302101).

Conflict of interest

All authors declare no conflicts of interest in this paper.