On the list injective coloring of planar graphs without a ${4^ - }$-cycle intersecting with a ${5^ - }$-cycle

1.   Introduction

Let $G$ be a finite, simple, and planar graphs throughout this paper. A 2-$distance$ $k$-$coloring$ of $G$ is a mapping $c:V(G) \to \{ 1, 2, \cdots, k\}$ such that the vertices whose distance is at most two receive distinct colors. The 2-$distance$ $chromatic$ $number$ is the least integer $k$ such that $G$ has a 2-distance $k$-coloring, denoted by ${\chi _2}(G)$. In $1977$, Wegner ^[15] first defined the 2-distance coloring and proposed the following conjecture:

Conjecture 1.1. Let $G$ be a planar graph with maximum degree $\Delta$. Then

Recently, Kim and Lian ^[10] showed that each subcubic planar graph $G$ has $\chi _2(G) \le 7$ if $g(G) \ge 6$. Then Yu et al. ^[16] proved that every planar graph $G$ has $\chi _2(G) \le 18$ if $\Delta \le 5$, and $\chi _2(G) \le 4\Delta -3$ if $\Delta \ge 6$.

An $injective$ $k$-$coloring$ of $G$ is a mapping $c:V(G) \to \{ 1, 2, \cdots, k\}$ such that $c(u) \ne c(v)$ if there is a path of length two between $u$ and $v$. The $injective$ $chromatic$ $number$ of $G$ is the smallest positive integer $k$ such that $G$ is injectively $k$-colorable, denoted by ${\chi _i}(G)$. So it is clear that ${\chi _i}(G) \le {\chi _2}(G)$. Give a list assignment, $L = \{ L(v):v \in V(G)\}$. A list injective coloring of $G$ is an injective coloring of $G$ such that $c(v)\in L(v)$ for each vertex $v\in G$. An injective $L$-$coloring$ is an injective coloring such that $c(v) \in L(v)$ for any vertex $v$ of $G$. Moreover, $G$ is $injectively$ $k$-$choosable$ if $G$ has an injective $L$-coloring for any $L$ with $\left| {L(v)} \right| \ge k$. The $injective$ $choosability$ $number$ of $G$ is the smallest positive integer $k$ such that $G$ is injectively $k$-choosable, denoted by $\chi _i^l(G)$.

In $2002$, Hahn et al. ^[9] first defined the concept of injective coloring, and they applied it to the theory of error-correcting codes. If the injective chromatic number of the hypercube $Q_n$ had been shown to be exponential in $n$, then there would have been consequences for some complexity concerns on random access machines. They gave a slightly smaller upper bound: ${\chi _i}(G) \le { \Delta ^2} - \Delta + 1$. The upper bound is strengthened to ${\chi _i}(G) \le {\Delta ^2} - \Delta$ if $\Delta \ge 3$ by Chen et al. ^[7]. In 2010, Lužar ^[12] gave the following conjecture by studying Conjecture 1.1:

Conjecture 1.2. Let $G$ be a planar graph with maximum degree $\Delta$.

Many researchers have done many studies on this conjecture. For every ${K_4}$-minor-free graph $G$, Chen et al. ^[7] showed ${\chi _i}(G) \le \left\lceil {\frac{3}{2}\Delta } \right\rceil$. They conjectured ${\chi _i}(G) \le \left\lceil {\frac{3}{2}\Delta } \right\rceil$ for every planar graph $G$, but Lužar and Škrekovski ^[13] proved it was wrong.

Also, there are many results about planar graph $G$ with girth restrictions.

Theorem 1.3. (Lužar et al. ^[14]) Let $G$ be a planar graph and $\Delta \le 3$.

$(1)$ If $g(G)\ge 19$, then ${\chi _i}(G) \le 3;$

$(2)$ If $g(G)\ge 10$, then ${\chi _i}(G) \le 4;$

$(3)$ If $g(G)\ge 7$, then ${\chi _i}(G) \le 5$.

Theorem 1.4. Suppose that planar graph $G$ has $g(G)\ge 6.$

$(1)$ ^[6] ${\chi _i^l}(G) \le \Delta + 3;$

$(2)$ ^[3] If $\Delta \ge 8$, then ${\chi _i^l}(G) \le \Delta + 2;$

$(3)$ ^[1] If $\Delta \ge 24$, then ${\chi _i^l}(G) \le \Delta + 1.$

Theorem 1.5. Suppose that planar graph $G$ has $g(G)\ge 5$.

$(1)\;$ ^[5] ${\chi _i^l}(G) \le \Delta + 6;$

$(2)\;$ ^[2] If $\Delta \ge 11$, then ${\chi _i^l}(G) \le \Delta + 4;$

$(3)\;$ ^[8] If $\Delta \ge 2339$, then ${\chi _i}(G) \le \Delta + 1.$

More recently, Li et al. ^[11] proved that if $G$ is a planar graph with $\Delta \ge 22$ that has no intersecting 4-cycles or triangles, then $\chi _i^l(G) \le \Delta + 4$. Cai et al. ^[4] showed that $\chi _i^l(G) \le \Delta + 4$ if $G$ is a planar graph with $\Delta \ge 12$ that has disjoint ${5^ - }$-cycles. We strengthen the result of Cai et al. ^[4] and allow that $G$ has 5-cycles intersecting 5-cycles by proving Theorem 1.6.

Theorem 1.6. If $G$ is a planar graph with $\Delta \ge 12$ that has no ${4^ - }$-cycles intersecting with ${5^ - }$-cycles, then $\chi _i^l(G) \le \Delta + 4$.

We define $N(v) = \{ {v_1}, {v_2}, \cdots, {v_k}\}$ and $D(v) = \sum\nolimits_{1 \le i \le k} {d({v_i})}$ for a $k$-vertex $v$. The number of $k$-neighbors of $v$ is denoted by ${n_k}(v)$. For a ${2^ + }$-vetex $v$, if $D(v) \ge \Delta + 4 + d(v)$, then $v$ is called a $heavy$ vertex; otherwise, $v$ is called a $light$ vertex. A $k(l)$-vertex is a $k$-vertex that has $l$ 2-neighbors. For a path $xwy$, if $d(w) = 2$, then we say $x$ and $y$ are $fake$-$adjacent$. The number of $k$-faces that are incident with $v$, denoted $m_k(v)$. We say that 2-vertex $v$ is of $Class\; one$($resp$., $Class\; two$, $Class\; three$, $Class\; four$, $Class\; five$) if ${m_3}(v) = 1$($resp$., ${m_4}(v) = 1$, ${m_5}(v) = 2$, ${m_5}(v) = {m_{6^+}}(v) = 1$, ${m_{6^+}}(v) = 2$). If a 3(1)-vertex $w$ has a Class one 2-neighbor, then $w$ is called a $strong$ 3(1)-vertex; otherwise, $w$ is called a $weak$ 3(1)-vertex. The number of strong 3(1)-neighbors of $w$ is denoted by ${n_{st}}(w)$. For $k$-vertex $v$, we define ${f_1}, {f_2}, \cdots, {f_k}$ as being incident with $v$. If two cycles have a common vertex, then we say they are intersecting with each other.

Observation. If $v$ is a Class one 2-vertex, then ${m_{7^+}}(v) = 1$; if $v$ is a Class two 2-vertex, then ${m_{6^+}}(v) = 1$.

2.   Structural properties of critical graphs

With the intention of proving Theorem 1.6, we suppose instead that $G$ is a counterexample with the fewest edges, which indicates that $\chi _i^l(G) > \Delta + 4$ and $\chi _i^l(H) \le \Delta + 4$ for any $H \subset G$. For a partial vertex coloring $c$ of $G$ and each vertex $v$, the forbidden color set is denoted by $F(v)$, and $L$ denotes an arbitrary list assignment with $\left| {L(v)} \right| \ge \Delta + 4$.

Lemma 2.1. There are no adjacent light vertices.

Proof. Suppose that $u$ and $v$ are distinct light vertices and $uv \in E(G)$. By $G$ having the fewest edges, $G - uv$ is injective $L$-choosable. Decolor $u$ and $v$. Clearly, $\left| {F(v)} \right| \le D(u) - d(u) \le \Delta + 3$ and $\left| {F(u)} \right| \le D(u) - d(u) \le \Delta + 3$. So recolor $u$ and $v$ by $c(u) \in L(u) - F(u)$ and $c(v) \in L(v) - F(v)$. Then $G$ has an injective $L$-coloring, a contradiction. □

It is easy to know the following corollaries from Lemma 2.1.

Corollary 2.2. There are no adjacent $2$-vertices, and $\delta (G) \ge 2$.

Corollary 2.3. Suppose $3 \le d(v) \le 5$. If ${n_2}(v) \ge 1$, then $v$ is a heavy vertex and $n_2(v) \le d(v) - 2$.

Lemma 2.4. Let $v$ be a 3(1)-vertex and $u$ be a 5-vertex. If ${n_2}(u) \ge 1$, then $uv \notin E(G)$.

Proof. Assume the assertion of the lemma is false that $u$ is adjacent to $v$. Suppose that ${v_1}$ is the 2-neighbor of $v$ and ${u_1}$ is the 2-neighbor of $u$. By the choice of $G$, $G - v{v_1}$ is injective $L$-choosable. Remove the colors of $v$, ${u_1}$, and ${v_1}$. Clearly, $\left| {F(v)} \right| \le \Delta + 3$. Note that ${v_1}$ and ${u_1}$ are light vertices, which indicates that $\left| {F({v_1})} \right| \le D({v_1}) - d({v_1}) \le \Delta + 3$ and $\left| {F({u_1})} \right| \le D({u_1}) - d({u_1}) \le \Delta + 3$. Thereby, we recolor $v$, ${u_1}$, and ${v_1}$ in sequence, a contradiction. □

Lemma 2.5. Suppose that $d(v) = 6$ and ${v_1}$ is a 2-neighbor of $v$. If ${m_4}({v_1}) = 1$, then $v$ is a heavy vertex.

Proof. Assume to the contrary that $v$ is a light vertex. By $G$ having the fewest edges, $G-v{v_1}$ has an injective $L$-coloring. Decolor $v$ and ${v_1}$. Clearly, $\left| {F({v_1})} \right| \le 5 + \Delta -2 = \Delta +3$. Since $v$ is a light vertex, we have $\left| {F(v)} \right| \le D(v) - d(v) \le \Delta + 3$. So we can recolor ${v_1}$ and $v$ in sequence, a contradiction. □

Lemma 2.6. Let $f = [ {v'_1}{v_1}v{v_2}{v'_2}]$ be a 5-face with $d(v) = 6$, $d({v_1}) = d({v'_2}) = 2$, and $d({v_2}) = 3$. Then $v$ is a heavy vertex.

Proof. Assume to the contrary that $v$ is a light vertex. Clearly, $G-v{v_1}$ has an injective $L$-coloring. Decolor $v$, ${v_1}$, and ${v'_2}$. Clearly, $\left| {F({v_1})} \right| \le d(v) -1 + \Delta -2 = \Delta +3$. It follows from $v$ and ${v'_2}$ being light vertices that we can recolor ${v_1}$, $v$, and ${v'_2}$ in sequence, a contradiction. □

Lemma 2.7. Let $v$ be a 3(1)-vertex. If ${v_1}$ is a Class one 2-neighbor, then $D(v) \ge \Delta + 8$.

Proof. Suppose to the contrary that $D(v) \le \Delta + 7$. By Corollary 2.3, we need to consider that $D(v) = \Delta + 7$. It follows from $G$ having the fewest edges that $G - v{v_1}$ has an injective $L$-coloring. Decolor $v$ and ${v_1}$. Obviously, $\left| {F(v)} \right| \le D(v) - d(v) -1 \le \Delta + 3$. Notice that ${v_1}$ is a light vertex. So, we recolor $v$ and ${v_1}$ in sequence, a contradiction. □

3.   Proof of Theorem 1.6

Note that $G$ has no ${4^ - }$-cycles intersect with ${5^ - }$-cycles. According to Euler's formula $|V(G)|+|F(G)|-|E(G)| = 2$, and $\sum\limits_{v \in V(G)} {d(v)} = \sum\limits_{f \in F(G)} {d(f)} = 2\left| E(G) \right|$, we derive the following equation:

Then we construct the weight function $\omega (v) = d(v) - 6$ for each $v\in V(G)$ and $\omega (f) = 2d(f) - 6$ for each $f\in F(G)$, which means that $\sum\nolimits_{x \in V(G)\bigcup F (G)} {\omega (x) = - 12}$. In this section, we get a new weight function ${\omega'}(x)$ by assigning the weight. Thereby, we have the following contradiction:

It shows that $G$ does not exist, so Theorem 1.6 is proved. Then $\tau(u\rightarrow v)$ shows the weight that $u$ transfers to $v$, and $\tau (u \to f \to v)$ denotes the weight that $u$ transfers to $v$ by $f$, where $u, v\in V(G)$ and $f\in F(G)$. Next, we introduce two face types of $configuration\; A$ and $configuration\; B$. We define the number of configuration A-face($resp$., B-face) contain $v$ as ${m_A}(v)$($resp$., ${m_B}(v)$).

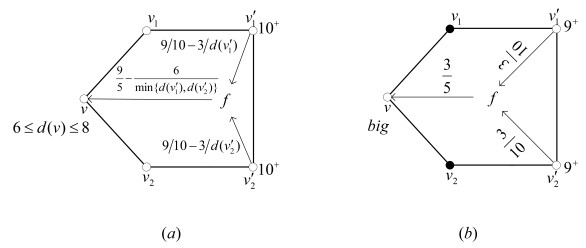
$configuration\; A$-face: Suppose $f = [{v'_1}{v_1}v{v_2}{v'_2}]$ with $6 \le d(v) \le 8$, $2 \le d({v_i})\le 3$, and $d({v'_i})\ge 10$($i = 1, 2$) (See Figure 1(a)). $configuration\; B$-face: Suppose $f = [{v'_1}{v_1}v{v_2}{v'_2}]$ with $d(v) = 9$, $d({v_i}) = 2$ and $d({v'_i})\ge 9$($i = 1, 2$) (See Figure 1(b)).

The discharging rules

R1 Let $f$ be a ${4^ + }$-face. Then $\tau(f \to incident\; vertices) = 2 - \frac{6}{{d(f)}}$.

R2 Let $uv \in E(G)$ and $d(u)\ge 3$. If $v$ is a Class one($resp$., Class two, Class three, Class four, Class five) 2-vertex, then $\tau(u\rightarrow v) = \frac{10}{7}(resp., \frac{5}{4}, \frac{6}{5}, \frac{11}{10}, 1)$.

R3 Let $d(v) = 3$ and $uv \in E(G)$.

R3.1 Suppose that $v$ is a light 3(0)-vertex and $u$ is a heavy vertex with $3 \le d(u) \le 7$. Then $\tau(u\rightarrow v) = \frac{1}{3}$.

R3.2 Suppose that $v$ is a heavy 3(0)-vertex. If $d(u) = 4$($resp$., $5 \le d(u) \le 7$), then $\tau(u\rightarrow v) = \frac{1}{30}$($resp$., $\frac{1}{3}$).

R3.3 Suppose that $v$ is a weak 3(1)-vertex. Assume ${m_3}(v) = 1$, if $d(u) = 5$($resp.$, 6, 7, 8, 9), then $\tau(u\rightarrow v) = \frac{7}{10}(resp., \frac{3}{4}, \frac{4}{5}, \frac{9}{10}, \frac{11}{10})$. Assume ${m_{4^+}}(v) = 3$, if $d(u) = 5$($resp.$, 6, 7, 8, 9), then $\tau(u\rightarrow v) = \frac{1}{2}(resp., \frac{11}{20}, \frac{3}{5}, \frac{9}{10}, 1)$.

R3.4 Suppose that $v$ is a strong 3(1)-vertex. If $d(u) = 6(resp., 7, 8, 9)$, then $\tau(u\rightarrow v) = \frac{7}{8}(resp., \frac{12}{13}, 1, \frac{8}{7})$. If $d(u) \ge 10$, then $\tau(u\rightarrow v) = 2-\frac{7}{d(u)}$.

R4 Let $d(v) = 4$ and $uv \in E(G)$. If $d(u) = 5$($resp$., $6 \le d(u) \le 7$), then $\tau(u\rightarrow v) = \frac{1}{30}$($resp$., $\frac{2}{7}$).

R5 Suppose $8 \le d(u) \le 9$ such that $uv \in E(G)$.

R5.1 If $d(v) = 3, 4$ except for 3(1)-vertex, then $\tau(u \to v) = \frac{9}{10}$ when $d(u) = 8$ and $\tau(u \to v) = 1$ when $d(u) = 9$.

R5.2 If $d(v) = 5$, then $\tau(u \to v) = \frac{3}{5}$.

R5.3 If $d(v) = 6$, then $\tau(u \to v) = \frac{3}{5}$ when $d(u) = 9$.

R6 Suppose $3 \le d(v) \le 8$ except for strong 3(1)-vertex. If $d(u) \ge 10$ such that $uv \in E(G)$, then $\tau(u\rightarrow v) = \frac{9}{5}-\frac{6}{d(u)} \ge \frac{6}{5}$.

R7 Let $d(u) \ge 10$ and $6 \le d(v) \le 8$. If $u$ is fake-adjacent to $v$ by a Class five 2-vertex, then $\tau(u\rightarrow v) = \frac{4}{5}-\frac{6}{d(u)}$.

R8 Suppose $f = [{v'_1}{v_1}v{v_2}{v'_2}]$. After R1$\sim$R6, the 9-vertex $v$ is called $big$ 9-vertex if $\omega '(v) < 0$.

R8.1 If $f$ is a configuration A-face, then $\tau ({v'_i} \to f) = \frac{9}{{10}} - \frac{3}{{d({v'_i})}}(i = 1, 2)$ through ${v'_1}{v'_2}$ and $\tau(f \to v) \ge \frac{9}{5} - \frac{6}{{\min \{ d({v'_1}), d({v'_2})\} }}$ (See Figure 1(a)).

R8.2 If $v$ is a big vertex and $f$ is a configuration B-face, then $\tau ({v'_i} \to f) = \frac{3}{{10}}$ through ${v'_1}{v'_2}$ and $f$ transfers $\frac{3}{5}$ to each big 9-vertex equally (See Figure 1(b)).

Firstly, we check $\omega '(v)$ for each $v \in V(G)$.

Case 1. $d(v) = 2$ and then $\omega(v) = -4$.

If $v$ is a Class one 2-vertex, then ${m_3}(v) = {m_{7^+}}(v) = 1$, which means that $\sum\limits_{i = 1}^2 {\tau ({f_i} \to v) \ge \frac{8}{7}}$ by R1. Hence, $\omega '(v) \ge - 4 + \frac{8}{7} + \frac{{10}}{7} \times 2 = 0$ by R2. If $v$ is a Class two 2-vertex, then ${m_4}(v) = {m_{6^+}}(v) = 1$, which indicates that $\sum\limits_{i = 1}^2 {\tau ({f_i} \to v)} \ge \frac{1}{2} + 1 = \frac{3}{2}$ by R1. So $\omega '(v) \ge - 4 + \frac{3}{2} + \frac{{5}}{4} \times 2 = 0$ by R2. Next, consider that $v$ is a Class three, Class four, or Class five 2-vertex. It resembles the above arguments that can be obtained that $\omega '(v) \ge - 4 + \min \{ \frac{6}{5} \times 2 + \frac{4}{5}\times 2, \frac{{11}}{{10}} \times 2 + \frac{4}{5}+1, 2 + 2\} = 0$ by R1, R2.

Case 2. $d(v) = 3$ and then $\omega (v) = - 3$. Let $N(v) = \{ {v_1}, {v_2}, {v_3}\}$ with $d({v_1}) \le d({v_2})\le d({v_3})$.

Subcase 2.1. Suppose ${n_2}(v) = 0$. If ${m_{4^-}}(v) = 1$, then ${m_{6^+}}(v) = 2$; otherwise, ${m_{5^+}}(v) = 3$. Then $\sum\limits_{i = 1}^3 {\tau ({f_i} \to v)} \ge \min \{ 2, \frac{4}{5} \times 3\} = 2$ by R1. Consider that $v$ is a light vertex, which means that ${v_i}(i = 1, 2, 3)$ are heavy vertices by Lemma 2.1. According to R3.1, R5.1, R6, $\sum\limits_{i = 1}^3 {\tau ({v_i} \to v)} \ge \frac{1}{3} \times 3 = 1$. Then $\omega '(v) \ge - 3 + 2 + 1 = 0$. Otherwise, consider that $v$ is a heavy vertex. Suppose ${n_3}(v) = 0$. If ${n_4}(v) = 0$, then ${n_{5^+}}(v) = 3$; if ${n_4}(v) \ge 1$, then either ${n_{9^+}}(v) \ge 1$ or ${n_7}(v) = {n_8}(v) = 1$, which means that $\sum\limits_{i = 1}^3 {\tau ({v_i} \to v)} \ge \min \{ \frac{1}{3} \times 3, \frac{1}{{30}} + 1, \frac{1}{{30}} + \frac{1}{3} + \frac{9}{{10}}\} = 1$ by R3.2, R5.1, R6. Hence, $\omega '(v) \ge - 3 + 2 + 1 = 0$. Suppose $d({v_1}) = 3$, which indicates that $\tau(v \to {v_1}) \le \frac{1}{3}$ by R3.1. If $d({v_2}) = 4$, then $d({v_3}) \ge 12$; if $5\le d({v_2}) \le 7$, then $d({v_3}) \ge 9$; otherwise, $d({v_2}), d({v_3}) \ge 8$. So $\sum\limits_{i = 2}^3 {\tau ({v_i} \to v)} \ge \min \{ \frac{1}{{30}} + (\frac{9}{5} - \frac{6}{{12}}), \frac{1}{3} + 1, \frac{9}{{10}} \times 2\} = \frac{4}{3}$ by R3.2, R5.1, R6. Furthermore, $\omega '(v) \ge - 3 + 2 - \frac{1}{3} + \frac{4}{3} = 0$.

Subcase 2.2. Suppose $d({v_1}) = 2$. By Corollary 2.3, $d({v_2})+d({v_3}) \ge \Delta + 5$. Consider that $v$ is a weak 3(1)-vertex. Suppose ${m_3}(v) = 1$. If $d({v_2}) = 5$, then $d({v_3}) \ge 12$; if $d({v_2}) = 6$, then $d({v_3}) \ge 11$; if $d({v_2}) = 7$, then $d({v_3}) \ge 10$; otherwise, $d({v_2}) \ge 8$ and $d({v_3}) \ge 9$. Therefore, $\sum\limits_{i = 2}^3 {\tau ({v_i} \to v)} \ge \min \{ \frac{7}{{10}} + (\frac{9}{5} - \frac{6}{{12}}), \frac{3}{4} + (\frac{9}{5} - \frac{6}{{11}}), \frac{4}{5} + (\frac{9}{5} - \frac{6}{{10}}), \frac{9}{{10}} + \frac{{11}}{{10}}\} = 2$ by R3.3, R5, R6. Thereby, $\omega '(v) \ge - 3 + 2 - 1 + 2 = 0$ by R1, R2. If ${m_{4^+}}(v) = 3$, then $- \tau (v \to {v_1}) + \sum\limits_{i = 1}^3 {\tau ({f_i} \to v)} \ge \min \{ - \frac{5}{4} + \frac{1}{2} + 2, - \frac{6}{5} + \frac{4}{5} \times 3\} = \frac{6}{5}$ by R1, R2. So $\omega '(v) \ge - 3 + \frac{6}{5} + \min \{ \frac{1}{2} + (\frac{9}{5} - \frac{6}{{12}}), \frac{{11}}{{20}} + (\frac{9}{5} - \frac{6}{{11}}), \frac{3}{5} + (\frac{9}{5} - \frac{6}{{10}}), \frac{9}{{10}} + 1\} = 0$ by R3.3, R6. Next, consider that $v$ is a strong 3(1)-vertex. By Lemma 2.7, $d({v_2})+d({v_3}) \ge \Delta + 6$. Moreover, $- \tau(v \to {v_1}) + \sum\limits_{i = 1}^3 {\tau ({f_i} \to v)} \ge - \frac{10}{7} + \frac{8}{7} + 1 = \frac{5}{7}$ by R1, R2. Thus, $\omega '(v) \ge - 3 + \frac{5}{7} + \min \{ \frac{7}{8} + (2 - \frac{7}{{12}}), \frac{{12}}{{13}} + (2 - \frac{7}{{11}}), 1 + (2 - \frac{7}{{10}}), \frac{8}{7} + \frac{8}{7}\} = 0$ by R3.4.

Case 3. $d(v) = 4$ and then $\omega (v) = -2$. Let $N(v) = \{ {v_1}, {v_2}, {v_3}, {v_4}\}$ with $d({v_1}) \le d({v_2})\le d({v_3})\le d({v_4})$.

Subcase 3.1. Suppose ${n_2}(v) = 0$. If ${m_{4^-}}(v) = 1$, then ${m_{6^+}}(v) = 3$; otherwise, ${m_{5^+}}(v) = 4$. So $\sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge \min \{ 3, \frac{4}{5} \times 4\} = 3$ by R1. If $v$ is a heavy vertex, then ${n_3}(v) \le 3$. Note that ${n_{11^+}}(v) \ge 1$ if ${n_3}(v) = 3$. Therefore, $-\tau(v \to 3$-$neighbors)+\tau({11^+}$-$neighbor \to v) \ge \min \{ - \frac{1}{3} \times 3 + (\frac{9}{5} - \frac{6}{{11}}), - \frac{1}{3} \times 2\} = -\frac{2}{3}$ by R3.1, R6. Hence, $\omega '(v) \ge - 2 + 3 - \frac{2}{3} = \frac{1}{3}$. Otherwise, suppose that $v$ is a light vertex, which implies that ${v_i}(1\le i \le 4)$ are not light 3-vertices by Lemma 2.1. Clearly, $\omega '(v) \ge - 2 + 3 - \frac{1}{{30}} \times 4 = \frac{{13}}{{15}}$ by R3.2.

Subcase 3.2. Suppose $d({v_1}) = 2$. By Corollary 2.3, $d({v_2})+d({v_3})+d({v_4}) \ge \Delta +6$. According to R1, R2, if ${v_1}$ is a Class one 2-vertex, then $-\tau(v \to {v_1})+ \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge - \frac{{10}}{7} + \frac{8}{7} + 2 = \frac{12}{7}$; if ${v_1}$ is a Class two 2-vertex, then $-\tau(v \to {v_1})+ \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge - \frac{5}{4} + \frac{1}{2} + 3 = \frac{9}{4}$; if ${m_{5^+}}(v) = 4$, then $-\tau(v \to {v_1})+ \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge - \frac{6}{5} + \frac{4}{5} \times 4 = 2$; otherwise ${m_{6^+}}({v_1}) = 2$ and ${m_{4^-}}(v) = 1$, then $-\tau(v \to {v_1})+ \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge -1 + 3 = 2$. Therefore, $-\tau(v \to {v_1})+ \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge \min \{ \frac{{12}}{7}, \frac{9}{4}, 2, 2\} = \frac{{12}}{7}$. If ${n_3}(v) = 0$, then ${n_{6^+}}(v) \ge 1$; if ${n_3}(v) = 1$, then ${n_{8^+}}(v) \ge 1$; if ${n_3}(v) = 2$, then ${n_{12^+}}(v) = 1$. This implies that $-\tau(v \to 3$-$neighbors)+\tau({6^+}$-$neighbors \to v) \ge \min \{ \frac{2}{7}, - \frac{1}{3} + \frac{9}{{10}}, - \frac{1}{3} \times 2 + (\frac{9}{5} - \frac{6}{{12}})\} = \frac{2}{7}$ by R3.1, R4, R5.1, R6. Moreover, $\omega '(v) \ge - 2 + \frac{12}{7} + \frac{2}{7} = 0$.

Subcase 3.3. Suppose $d({v_1}) = d({v_2}) = 2$, which means that $d({v_3})+d({v_4}) \ge \Delta +4$ by Corollary 2.3. According to R1, R2, $-\tau(v \to {v_1}) -\tau(v \to {v_2}) + \sum\limits_{i = 1}^4 {\tau ({f_i} \to v)} \ge\min \{ - \frac{{10}}{7} - 1 + \frac{8}{7} + 2, - \frac{5}{4} \times 2 + \frac{1}{2} + 3, - \frac{6}{5} \times 2 + \frac{4}{5} \times 4, - 2 + 3\} = \frac{5}{7}$. If $d({v_3}) = 4$, then $d({v_4})\ge 12$; if $d({v_3}) = 5$, then $d({v_4})\ge 11$; if $6 \le d({v_3}) \le 7$, then $d({v_4})\ge 9$; otherwise, $d({v_3}), d({v_4}) \ge 8$. This indicates that $\sum\limits_{i = 3}^4 {\tau ({v_i} \to v)} \ge \min \{ \frac{9}{5} - \frac{6}{{12}}, \frac{1}{{30}} + (\frac{9}{5} - \frac{6}{{11}}), \frac{2}{7} + 1, \frac{9}{{10}} \times 2\} = \frac{9}{7}$ by R4, R5.1, R6. So $\omega '(v) \ge - 2 + \frac{5}{7} + \frac{9}{7} = 0$.

Claim 3.1. Let $5 \le d(v) \le 7$. Note that $v$ is adjacent to at most one weak 3(1)-vertex that is incident with a 3-face.

Case 4. $d(v) = 5$ and then $\omega (v) = -1$.

Subcase 4.1. Suppose ${n_2}(v) = 0$. According to R1, $\sum\limits_{i = 1}^5 {\tau ({f_i} \to v)} \ge \min \{ 4, 4 + \frac{1}{2}, \frac{4}{5} \times 5\} = 4$. Therefore, $\omega '(v) \ge - 1 + 4 - \frac{7}{{10}} - \frac{1}{2} \times 4 = \frac{3}{{10}}$ by R3.3 and Claim 3.1. Suppose ${n_2}(v) = 1$, which implies that $v$ is a heavy vertex by Corollary 2.3 and ${n_{3(1)}}(v) = 0$ by Lemma 2.4. Then ${n_3}(v)+{n_4}(v) \le 3$. According to R1, R2, $-\tau(v \to 2$-$neighbor)+ \sum\limits_{i = 1}^5 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{10}}{7} + \frac{8}{7} + 3, - \frac{5}{4} + \frac{1}{2} + 4, - \frac{6}{5} + \frac{4}{5} \times 5, - 1 + 4\} = \frac{{19}}{7}$. Note that ${n_{10^+}}(v) = 1$ if ${n_3}(v) = 3$. Therefore, $-\tau(v \to 3$-$neighbors) -\tau(v \to 4$-$neighbors) +\tau({10^+}$-$neighbors \to v) \ge \min \{ - \frac{1}{3} \times 3 + (\frac{9}{5} - \frac{6}{10}), - \frac{1}{3} \times 2 - \frac{1}{{30}} \times 2\} = -\frac{11}{15}$ by R3.1, R3.2, R4, R6. Hence, $\omega '(v) \ge - 1 + \frac{{19}}{7} -\frac{11}{15} = \frac{{103}}{{105}}$.

Subcase 4.2. Suppose ${n_2}(v) = 2$. This implies that $v$ is a heavy vertex by Corollary 2.3, and ${n_{3(1)}}(v) = 0$ by Lemma 2.4. Then ${n_3}(v)+{n_4}(v) \le 2$. According to R1, R2, $-\tau(v \to 2$-$neighbors)+ \sum\limits_{i = 1}^5 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{10}}{7}- 1 + \frac{8}{7} + 3, - \frac{5}{4} \times 2 + \frac{1}{2} + 4, - \frac{6}{5} \times 2 + \frac{4}{5} \times 5, - 2 + 4\} = \frac{8}{5}$. Note that ${n_{11^+}}(v) = 1$ if ${n_3}(v) = 2$. Moreover, $-\tau(v \to 3$-$neighbors)-\tau(v \to 4$-$neighbors)+\tau({11^+}$-$neighbor \to v) \ge \min \{ - \frac{1}{3} \times 2 + (\frac{9}{5} - \frac{6}{{11}}), - \frac{1}{3} - \frac{1}{{30}} \times 2 \} = - \frac{2}{5}$ by R3.1, R4, R6. Thus, $\omega '(v) \ge - 1 + \frac{8}{5} - \frac{2}{5} = \frac{1}{{5}}$. Suppose ${n_2}(v) = 3$, which means that $v$ is a heavy vertex by Corollary 2.3, and ${n_{3(1)}}(v) = 0$ by Lemma 2.4. Then ${n_3}(v)+{n_4}(v) \le 1$. Clearly, $-\tau(v \to 2$-$neighbors)+ \sum\limits_{i = 1}^5 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{10}}{7}- 2 + \frac{8}{7} + 3, - \frac{5}{4} \times 2 - 1+ \frac{1}{2} + 4, - \frac{6}{5} \times 3 + \frac{4}{5} \times 5, - 3 + 4\} = \frac{2}{5}$ by R1, R2. If ${n_3}(v) = {n_4}(v) = 0$, then ${n_{8^+}}(v) \ge 1$; if ${n_3}(v) = 1$, then ${n_{12^+}}(v) = 1$; if ${n_4}(v) = 1$, then ${n_{11^+}}(v) = 1$. Moreover, $\omega '(v) \ge - 1 + \frac{2}{5} + \min \{ \frac{3}{5}, - \frac{1}{3} + (\frac{9}{5} - \frac{6}{{12}}), - \frac{1}{{30}} + (\frac{9}{5} - \frac{6}{{11}})\} = 0$ by R3.1, R4, R5.2, R6.

Claim 3.2. Suppose $d(v) \ge 6$, ${m_{5^+}}(v) = d(v)$, and ${n_{st}}(v) = t$. If $1 \le t \le d(v)-1$, then ${m_{6^+}}(v) \ge t+1$, w.l.o.g., ${m_{6^+}}(v) \ge t$ for $t \ge 0$.

Case 5. $d(v) = 6$ and then $\omega (v) = 0$.

Claim 3.3. Consider that $v$ is a light vertex. Suppose that $w$ is a 2-neighbor of $v$ and $u$ is a 3(1)-neighbor of $v$. Then ${m_{4^-}}(w) = 0$ and $uv$ is not incident with 3-face. If $v$ is incident with a configuration A-face $f$ contains 2-neighbors and 3(1)-neighbor of $v$, then $\tau(f \to v) \ge \frac{69}{55}$.

Proof. By Lemma 2.5, ${m_4}(w) = 0$. If ${m_3}(w) = 1$, then there is a $\Delta$-vertex in $N(v)$ by Lemma 2.1, which means $v$ is a heavy vertex, a contradiction. Suppose that $uv$ is incident with 3-face. Then there is a $(\Delta-1)^+$-vertex in $N(v)$, which implies that $v$ is a heavy vertex, a contradiction. Next, consider that $v$ is incident with the configuration A-face $f$ and $f$ is incident with a 2-neighbor and a 3(1)-neighbor of $v$. By R8.1, it is easy to know that $\tau(f \to v) \ge \frac{9}{5} - \frac{6}{{11}} = \frac{69}{55}$. □

Subcase 5.1. Suppose ${n_2}(v) = 0$. If $v$ is a heavy vertex, then ${n_3}(v) \le 5$. According to R1, $\sum\limits_{i = 1}^6 {\tau ({f_i} \to v)} \ge \min \{ \frac{4}{5} \times 6, 5\} = \frac{24}{5}$. Therefore, $\omega '(v) \ge \frac{24}{5} - 5 \times \frac{7}{8}- \frac{2}{7} = \frac{{39}}{{280}}$ by R3.4, R4. Otherwise, consider that $v$ is a light vertex. If ${m_{4^-}}(v) = 1$, then ${n_{st}}(v) \le 4$ by Claim 3.2. Then $\omega '(v) \ge 5 - 4 \times \frac{7}{8} - \frac{3}{4} - \frac{{11}}{{20}} = \frac{1}{5}$ by R1, R3.3, R3.4 and Claim 3.1. Consider that ${m_{5^+}}(v) = 6$. If ${n_{st}}(v) \le 4$, then $\omega '(v) \ge \frac{{4}}{5}\times 6 - 4 \times \frac{7}{8} - \frac{{11}}{{20}} \times 2 = \frac{1}{5}$ by R1, R3.3, R3.4. If ${n_{st}}(v) \ge 5$, then ${m_{6^+}}(v) = 6$ by Claim 3.2. It follows that $\omega '(v) \ge 6 - 6 \times \frac{7}{8} = \frac{3}{4}$ by R1, R3.4.

Subcase 5.2. Suppose ${n_2}(v) = 1$. If $v$ is a heavy vertex, then either ${n_3}(v)+{n_4}(v) \le 4$ or ${n_4}(v) = 5$, which derives that $\tau(v \to 3$-$neighbors)+\tau(v \to 4$-$neighbors) \le \max \{ \frac{7}{8} \times 4, \frac{2}{7} \times 5\} = \frac{7}{2}$ by R3.4, R4. According to R1, R2, $-\tau(v \to 2$-$neighbor)+ \sum\limits_{i = 1}^6 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{10}}{7} + \frac{8}{7} + 4, - \frac{5}{4} + \frac{1}{2} + 5, - \frac{6}{5} + \frac{4}{5} \times 6, - 1 + 5\} = \frac{{18}}{5}$. Therefore, $\omega '(v) \ge \frac{18}{5} - \frac{7}{2} = \frac{1}{{10}}$. Consider that $v$ is a light vertex. If ${m_{4^-}}(v) = 1$, then ${n_{st}}(v) \le 3$ by Claim 3.2 and Claim 3.3, and $\tau(v \to 2$-$neighbor) = 1$ by R2 and Claim 3.3. So $\omega '(v) \ge - 1 + 5 - \frac{7}{8} \times 3 - \frac{3}{4} - \frac{{11}}{{20}} = \frac{3}{{40}}$ by R1, R3.3, R3.4, and Claim 3.1. Consider that ${m_{5^+}}(v) = 6$. Suppose ${n_{st}}(v) = t \le 5$. Then $-\tau(v \to 2$-$neighbor)+ \sum\limits_{i = 1}^6 {\tau ({f_i} \to v)} \ge - \frac{6}{5} + t + \frac{4}{5}(6 - t) = \frac{1}{5}t + \frac{18}{5}$ by R1, R2 and Claim 3.2. Thereby, $\omega '(v) \ge \frac{1}{5}t + \frac{18}{5}- \frac{7}{8}t - \frac{{11}}{{20}}(5 - t) = - \frac{1}{8}t + \frac{{17}}{{20}} \ge \frac{9}{{40}}$ by R3.3, R3.4.

Subcase 5.3. Suppose ${n_2}(v) = 2$. If $v$ is a heavy vertex, then ${n_3}(v) +{n_4}(v)\le 3$. According to R1, R2, $-\tau(v \to 2$-$neighbors)+ \sum\limits_{i = 1}^6 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{10}}{7} - 1 + \frac{8}{7} + 4, - \frac{5}{4} \times 2 + \frac{1}{2} + 5, - \frac{6}{5} \times 2 + \frac{4}{5} \times 6, - 2 + 5\} = \frac{{12}}{5}$. Note that ${n_{9^+}}(v) = 1$ if ${n_3}(v) = 3$. Clearly, $\omega '(v) \ge \frac{12}{5}+ \min \{ - \frac{7}{8} \times 3 + \frac{3}{5}, - \frac{7}{8} \times 2 - \frac{2}{7}\} = \frac{51}{140}$ by R3.4, R4, R5.3. Otherwise, consider that $v$ is a light vertex. By Claim 3.3 and R2, $\tau(v \to 2$-$neighbors) = 2$. If ${m_3}(v) = 1$, then ${n_{3(1)}}(v) \le 2$ by Claim 3.3. Then $\omega '(v) \ge 5 - 2 - \frac{7}{8} \times 2 - \frac{{1}}{{3}} \times 2 = \frac{7}{{12}}$ by R1, R2, R3.2, R3.4. If ${m_4}(v) = 1$, then ${n_{st}}(v) \le 2$ by Claim 3.2 and Claim 3.3. Obviously, $\omega '(v) \ge - 2+ 5 + \frac{1}{2} - \frac{7}{8} \times 2 - \frac{{11}}{{20}} \times 2 = \frac{{13}}{{20}}$ by R1, R2, R3.3, R3.4, and Claim 3.1. Finally, consider that ${m_{5^+}}(v) = 6$. Suppose ${n_{st}}(v) = t \le 4$. If $t = 0$, then $\omega '(v) \ge - \frac{6}{5} \times 2 + \frac{{4}}{5}\times 6 - \frac{{11}}{{20}} \times 4 = \frac{1}{5}$ by R1, R2, R3.3; if $1 \le t \le 3$, then $\omega '(v) \ge - \frac{6}{5} \times 2 + t +1 +\frac{4}{5}(5-t)- \frac{7}{8}t - \frac{{11}}{{20}}(4 - t) = - \frac{1}{8}t + \frac{2}{5} \ge \frac{1}{{40}}$ by R1, R2, R3.3, R3.4 and Claim 3.2; if $t = 4$, then ${m_{6^+}}(v) \ge 5$ and $v$ has two 2-neighbors of Class four or Class five. Moreover, $\omega '(v) \ge \min \{ - \frac{{11}}{{10}}, -1 \} \times 2 + 5 + \frac{4}{5} - \frac{7}{8} \times 4 = \frac{1}{{10}}$ by R1, R2, R3.4.

Subcase 5.4. Suppose ${n_2}(v) = 3$. If $v$ is a heavy vertex, then ${n_3}(v) + {n_4}(v)\le 2$. Clearly, ${n_{10^+}}(v) = 1$ if ${n_3}(v) = 2$. Hence, $\omega '(v) \ge - \frac{6}{5} \times 3 + \frac{{4}}{5}\times 6 + \min \{ - \frac{7}{8} \times 2 + (\frac{9}{5}-\frac{6}{10}), - \frac{7}{8} - \frac{2}{7}\} = \frac{{11}}{{280}}$ by R1, R2, R3.4, R4, R6. Otherwise, consider that $v$ is a light vertex. If ${m_3}(v) = 1$, then ${n_{3(1)}}(v) \le 1$ by Claim 3.3. Then $\omega '(v) \ge 5 - 3 - \frac{7}{8} - 2 \times \frac{{1}}{{3}} = \frac{11}{{24}}$ by R1, R2, R3.2, R3.4 and Claim 3.3. If ${m_4}(v) = 1$, then ${n_{st}}(v) \le 1$ by Claim 3.2 and Claim 3.3. So $\omega '(v) \ge 5 + \frac{1}{2} - 3 - \frac{7}{8} - \frac{{11}}{{20}} \times 2 = \frac{{21}}{{40}}$ by R1, R2, R3.3, R3.4, and Claim 3.3. Consider that ${m_{5^+}}(v) = 6$. Suppose ${n_{st}}(v) = t \le 3$. If ${m_A}(v) \ge 1$, then $\omega '(v) \ge - \frac{6}{5} \times 3 + t +\frac{4}{5}(6 - t) + \frac{69}{55} - \frac{7}{8}t - \frac{{11}}{{20}}(3 - t) = - \frac{1}{8}t + \frac{{177}}{{220}} \ge \frac{{189}}{{440}}$ by R1, R2, R3.3, R3.4, Claim 3.2 and Claim 3.3. Consider that ${m_A}(v) = 0$. Suppose ${n_{st}}(v) = 0$. If ${n_{3(1)}}(v) = 0$, then $\omega '(v) \ge - \frac{6}{5} \times 3 + \frac{4}{5} \times 6 - \frac{1}{3} \times 3 = \frac{1}{5}$ by R1, R2, R3.2. If ${n_{3(1)}}(v) \ge 1$, then ${m_{6^+}}(v) \ge 2$ and $v$ has at least two 2-neighbors of Class four or Class five by Lemma 2.6. Hence, $\omega '(v) \ge - \frac{6}{5} - \frac{{11}}{{10}} \times 2 + 2 + \frac{4}{5} \times 4 - \frac{{11}}{{20}} \times 3 = \frac{3}{{20}}$ by R1, R2, R3.3. Consider that ${n_{st}}(v) = 1$. Then ${m_{6^+}}(v) \ge 2$ by Claim 3.2. Note that ${m_{6^+}}(v) \ge 4$ if ${n_{3(1)}}(v) = 2$; ${m_{6^+}}(v) \ge 5$ if ${n_{3(1)}}(v) = 3$ by Lemma 2.6. Therefore, $-\tau(v \to 3$-$neighbors)+ \sum\limits_{i = 1}^6 {\tau ({f_i} \to v)} \ge - \frac{7}{8} + \min \{ - \frac{{11}}{{20}} - \frac{1}{3}+4 + \frac{4}{5} \times 2, - \frac{{11}}{{20}} \times 2 + 5 + \frac{4}{5}, - \frac{1}{3} \times 2 +2 + \frac{4}{5} \times 4 \} = \frac{439}{120}$ by R1, R3.2, R3.3. Hence, $\omega '(v) \ge - \frac{6}{5} \times 3 + \frac{439}{120} = \frac{7}{{120}}$ by R1, R3.4. If ${n_{st}}(v) \ge 2$, then ${m_{6^+}}(v) \ge 4$ and $v$ has one Class five 2-neighbor and two 2-neighbors of Class four or Class five. Note that $v$ is fake-adjacent a $\Delta$-vertex by Class five 2-vertex, which indicates that $v$ receives at least $\frac{4}{5} - \frac{6}{{12}} = \frac{3}{10}$ by R7. Moreover, $\omega '(v) \ge -1 + \min \{ - \frac{{11}}{{10}}, -1\} \times 2 + 4 + \frac{4}{5} \times 2 - \frac{7}{8} \times 3 + \frac{3}{10} = \frac{3}{{40}}$ by R1, R2, R3.4.

Subcase 5.5. Suppose ${n_2}(v) = 4$. If $v$ is a heavy vertex, then ${n_3}(v) + {n_4}(v) \le 1$. Note that ${n_{11^+}}(v) = 1$ if ${n_3}(v) = 1$; ${n_{10^+}}(v) = 1$ if ${n_4}(v) = 1$. So $\omega '(v) \ge - \frac{6}{5} \times 4 + \frac{{4}}{5}\times 6 + \min \{ - \frac{7}{8} + (\frac{9}{5} - \frac{6}{{11}}), - \frac{2}{7} + (\frac{9}{5} - \frac{6}{{10}}), 0\} = 0$ by R1, R2, R3.4, R4, R6. Consider that $v$ is a light vertex. If ${m_3}(v) = 1$, then ${n_{3(1)}}(v) = 0$ by Claim 3.3. So $\omega '(v) \ge 5 - 4 - \frac{{1}}{{3}} \times 2 = \frac{1}{{3}}$ by R1, R2, R3.2. If ${m_4}(v) = 1$, then ${n_{st}}(v) = 0$ by Claim 3.2 and Claim 3.3. Then $\omega '(v) \ge 5 + \frac{1}{2} - 4 - \frac{{11}}{{20}} \times 2 = \frac{{2}}{{5}}$ by R1, R2, R3.3. Next, consider that ${m_{5^+}}(v) = 6$. If ${m_A}(v) \ge 2$, then $\omega '(v) \ge - \frac{6}{5} \times 4 + \frac{{4}}{5}\times 6 + \frac{69}{55} \times 2 - \frac{7}{8} \times 2 = \frac{{167}}{{220}}$ by R1, R2, R3.4, and Claim 3.3. Consider that ${m_A}(v) = 1$. Note that ${m_{6^+}}(v) \ge 3$ if ${n_{st}}(v) \ge 1$. Thus, $\omega '(v) \ge - \frac{6}{5} \times 4 + \frac{69}{55} + \min \{ \frac{4}{5} \times 3 + 3 - \frac{7}{8} \times 2, \frac{4}{5} \times 6 - \frac{{11}}{{20}} \times 2\} = \frac{{23}}{{220}}$ by R1, R2, R3.3, R3.4, and Claim 3.3. Finally, suppose ${m_A}(v) = 0$. If ${n_{3(1)}}(v) = 0$, then ${m_{6^+}}(v) \ge 2$ and $v$ has either at least one Class five 2-neighbor or four Class four 2-neighbors. Hence, $\omega '(v) \ge \min \{ - \frac{6}{5} \times 3 - 1 + 2 + \frac{4}{5} \times 4 - \frac{1}{3} \times 2 + (\frac{4}{5} - \frac{6}{{12}}), - \frac{{11}}{{10}} \times 4 + 2 + \frac{4}{5} \times 4 - \frac{1}{3} \times 2\} = \frac{2}{15}$ by R1, R2, R3.2, R7. If ${n_{3(1)}}(v) = 1$, then ${m_{6^+}}(v) \ge 4$ and $v$ has at least two Class five 2-neighbors by Lemma 2.6. Thus, $\omega '(v) \ge - \frac{6}{5} \times 2 - 2 + 4 + \frac{4}{5} \times 2 - \frac{7}{8} + (\frac{4}{5} - \frac{6}{{12}}) \times 2 - \frac{1}{3} = \frac{71}{120}$ by R1, R2, R3.2, R3.4, R7. If ${n_{3(1)}}(v) = 2$, then ${m_{6^+}}(v) \ge 5$ and $v$ has four Class five 2-neighbors by Lemma 2.6. So $\omega '(v) \ge - 4 + 5 + \frac{4}{5} - \frac{7}{8} \times 2 + (\frac{4}{5} - \frac{6}{{12}}) \times 4 = \frac{5}{{4}}$ by R1, R2, R3.4, R7.

Subcase 5.6. Suppose ${n_2}(v) = 5$. If $v$ is a heavy vertex, then ${n_{12^+}}(v) = 1$. This shows that $\omega '(v) \ge - \frac{6}{5} \times 5 + \frac{{4}}{5}\times 6 + (\frac{9}{5} - \frac{6}{{12}}) = \frac{1}{{10}}$ by R1, R2, R6. Consider that $v$ is a light vertex, which implies that ${m_{5^+}}(v) = 6$ by Claim 3.3. If ${m_A}(v) \ge 2$, then $\omega '(v) \ge - \frac{6}{5} \times 5 + \frac{{4}}{5}\times 6 + \frac{69}{55} \times 2 - \frac{7}{8} = \frac{{191}}{{440}}$ by R1, R2, R3.4, and Claim 3.3. Consider that ${m_A}(v) = 1$. This implies that ${m_{6^+}}(v) \ge 3$ and $v$ has at least one Class five 2-neighbor. It follows from R1, R2, R3.4, R7, and Claim 3.3 that $\omega '(v) \ge - 1 - 4 \times \frac{6}{5} + 3 + 3 \times \frac{4}{5} - \frac{7}{8} + (\frac{4}{5} - \frac{6}{{12}}) + \frac{69}{55} = \frac{{123}}{{440}}$. Finally, suppose ${m_A}(v) = 0$, which means that ${m_{6^+}}(v) \ge 4$ and $v$ has at least three Class five 2-neighbors. So $\omega '(v) \ge - 3 - \frac{6}{5} \times 2 + 4 + \frac{4}{5} \times 2 - \frac{7}{8} + (\frac{4}{5} - \frac{6}{{12}}) \times 3 = \frac{9}{{40}}$ by R1, R2, R3.4, R7.

Subcase 5.7. Suppose ${n_2}(v) = 6$. Obviously, $v$ is a light vertex. Then ${m_{5^+}}(v) = 6$ by Claim 3.3. If ${m_A}(v) \ge 2$, then $\omega '(v) \ge - \frac{6}{5}\times 6 + \frac{4}{5}\times 6 + \frac{69}{55} \times 2 = \frac{6}{{55}}$ by R1, R2 and Claim 3.3. If ${m_A}(v) \le 1$, then ${m_{6^+}}(v) \ge 5$ and $v$ has at least four Class five 2-neighbors. Hence, $\omega '(v) \ge - 4 - \frac{{6}}{5}\times 2 + 5 + \frac{4}{5} + (\frac{4}{5} - \frac{6}{{12}}) \times 4 = \frac{3}{5}$ by R1, R2, R7.

Case 6. $d(v) = 7$ and then $\omega (v) = 1$.

Claim 3.4. If light $v$ is incident with a configuration A-face $f$ and $f$ is incident with 2-neighbors and 3(1)-neighbors of $v$, then $\tau(f \to v) \ge \frac{9}{5} - \frac{6}{{10}} = \frac{6}{5}$.

Subcase 6.1. Suppose ${n_2}(v) = 0$. Clearly, $\omega '(v) \ge 1 + \min \{ 6, \frac{{4}}{5}\times 7\} - \frac{{12}}{{13}} \times 7 = \frac{9}{{65}}$ by R1, R3.4. Suppose ${n_2}(v) = k \ge 1$. If $v$ is a heavy vertex, then ${n_2}(v)+{n_3}(v) \le 6$. If $1 \le k \le 2$, then $\omega '(v) \ge 1 + \min \{ - \frac{{10}}{7}- (k - 1) + \frac{8}{7} + 5, -\frac{5}{4}k+\frac{1}{2}+6, - \frac{6}{5}k + \frac{{4}}{5}\times 7, - k + 6\} - \frac{{12}}{{13}}(6 - k) - \frac{2}{7} = - \frac{{18}}{{65}}k + \frac{{353}}{{455}} \ge \frac{{101}}{{455}}$ by R1, R2, R3.4, R4. Consider that $3 \le k \le 6$. If ${m_{4^-}}(v) = 1$, then $\omega '(v) \ge 1 + \min \{ - \frac{{10}}{7} - (k - 1)+ \frac{8}{7} + 5, -\frac{5}{4}\times 2-(k-2)+ \frac{1}{2} + 6, - k + 6\} - \frac{{12}}{{13}}(6 - k) - \frac{2}{7} = - \frac{1}{{13}}k + \frac{{81}}{{91}} \ge \frac{3}{7}$ by R1, R2, R3.4, R4. Next, suppose ${m_{5^+}}(v) = 7$. If $3 \le k \le 4$, then $\omega '(v) \ge 1 - \frac{6}{5}k + (6 - k) + \frac{4}{5}(k + 1) - \frac{{12}}{{13}}(6 - k) - \frac{2}{7} = - \frac{{31}}{{65}}k + \frac{{899}}{{455}} \ge \frac{{31}}{{455}}$ by R1, R2, R3.4, R4, and Claim 3.2. Assume that $k = 5$, we have ${n_{10^+}}(v) = 1$ if ${n_3}(v) = 1$. Then $\omega '(v) \ge 1 - \frac{6}{5} \times 5 + \frac{4}{5} \times 7 + \min \{ - \frac{{12}}{{13}} + (\frac{9}{5}-\frac{6}{10}), - \frac{2}{7}\} = \frac{11}{35}$ by R1, R2, R3.4, R4, R6. If $k = 6$, then ${n_{11^+}}(v) = 1$. So $\omega '(v) \ge 1 - \frac{6}{5}\times 6 + \frac{4}{5}\times 7 + (\frac{9}{5} - \frac{6}{{11}}) = \frac{{36}}{{55}}$ by R1, R2, R3.4, R6.

Subcase 6.2. Consider that $v$ is a light vertex. If ${m_3}(v) = 1$, then ${n_{3(1)}}(v) \le 6-k$. Then $\omega '(v) \ge 1 + \min \{ - \frac{{10}}{7}- (k - 1) + \frac{8}{7} + 5, - k + 6\} - \frac{{12}}{{13}}(6 - k) - \frac{1}{3} = - \frac{1}{{13}}k + \frac{{230}}{{273}} \ge \frac{{83}}{{273}}$ by R1, R2, R3.2, R3.4. If ${m_4}(v) = 1$, then $\omega '(v) \ge 1 + \min \{ - \frac{5}{4} - (k - 1) + \frac{1}{2} + 6, - \frac{5}{4} \times 2 - (k - 2)+ \frac{1}{2} + 6, - k+ 6\} - \frac{{12}}{{13}}(7 - k) = - \frac{1}{{13}}k + \frac{7}{{13}} \ge 0$ by R1, R2, R3.4. Consider that ${m_{5^+}}(v) = 7$. If $1 \le k \le 3$, then $\omega '(v) \ge 1 - \frac{6}{5}k + \min \{ \frac{4}{5} \times 7 - \frac{3}{5}(7 - k), (7 - k) + \frac{4}{5}k - \frac{{12}}{{13}}(7 - k)\} = - \frac{{31}}{{65}}k + \frac{{20}}{{13}} \ge \frac{7}{{65}}$ by R1, R2, R3.4 and Claim 3.2. Suppose $4 \le k \le 5$. If ${m_A}(v) \ge 1$, then $\omega '(v) \ge - \frac{{31}}{{65}}k + \frac{{20}}{{13}} + \frac{6}{5} \ge \frac{{23}}{{65}}$ by Claim 3.4. Suppose ${m_A}(v) = 0$. Consider that $k = 4$. Note that ${m_{6^+}}(v) \ge 2$ if ${n_{st}}(v) = 1$; ${m_{6^+}}(v) \ge 5$ if ${n_{st}}(v) \ge 2$. Therefore, $-\tau(v \to 3$-$neighbors)+ \sum\limits_{i = 1}^7 {\tau ({f_i} \to v)} \ge \min \{ - \frac{{12}}{{13}} - \frac{3}{5} \times 2 + 2 + \frac{{4}}{5}\times 5, - \frac{{12}}{{13}} \times 3 + 5 + \frac{4}{5}\times 2, - \frac{3}{5} \times 3 + \frac{{4}}{5}\times 7 \} = \frac{19}{5}$ by R1, R3.3, R3.4. So $\omega '(v) \ge 1 - \frac{6}{5} \times 4 + \frac{19}{5} = 0$ by R2. If $k = 5$, then ${m_{6^+}}(v) \ge 3$ and $v$ has either at least two Class five 2-neighbors or one Class five 2-neighbor and four Class four 2-neighbors. Therefore, $\omega '(v) \ge 1 + 3 + \frac{{4}}{5} \times 4 - \frac{{12}}{{13}} \times 2 + \min \{ - \frac{6}{5} \times 3 - 2 + (\frac{4}{5} - \frac{6}{{11}}) \times 2, - \frac{{11}}{{10}} \times 4 - 1 + (\frac{4}{5} - \frac{6}{{11}})\} = \frac{{149}}{{715}}$ by R1, R2, R3.4, R7. Finally, suppose $6 \le k \le 7$. If ${m_A}(v) \ge 2$, then $\omega '(v) \ge - \frac{{31}}{{65}}k + \frac{{20}}{{13}} + \frac{{6}}{5} \times 2 \ge \frac{3}{5}$ by Claim 3.4. Next, consider that ${m_A}(v) = 1$. If $k = 6$, then ${m_{6^+}}(v) \ge 4$ and $v$ has at least two Class five 2-neighbors. Clearly, $\omega '(v) \ge 1 - 2 - \frac{6}{5} \times 4 + 4 + \frac{{4}}{5}\times 3 - \frac{{12}}{{13}}+ (\frac{4}{5} - \frac{6}{{11}}) \times 2 + \frac{6}{5} = \frac{{991}}{{715}}$ by R1, R2, R3, R7, and Claim 3.4. If $k = 7$, then ${m_{6^+}}(v) \ge 6$ and $v$ has at least five Class five 2-neighbors. Obviously, $\omega '(v) \ge 1 -5- \frac{6}{5} \times 2 +6+ \frac{{4}}{5} + (\frac{4}{5} - \frac{6}{{11}}) \times 5 + \frac{6}{5} = \frac{{158}}{{55}}$ by R1, R2, R3.4, R7, and Claim 3.4. Finally, consider that ${m_A}(v) = 0$. If $k = 6$, then ${m_{6^+}}(v) \ge 5$ and $v$ has at least four Class five 2-neighbors. Hence, $\omega '(v) \ge 1 - 4- \frac{6}{5} \times 2 + \frac{{4}}{5}\times 2+5 - \frac{{12}}{{13}} + (\frac{4}{5} - \frac{6}{{11}}) \times 4 = \frac{{926}}{{715}}$ by R1, R2, R3.4, R7. If $k = 7$, then ${m_{6^+}}(v) = 7$. Then $\omega '(v) \ge 1 - 7 +7 = 1$ by R1, R2.

Case 7. $d(v) = 8$ and then $\omega (v) = 2$.

Claim 3.5. If light $v$ is incident with a configuration A-face $f$ and $f$ is incident with 2-neighbors of $v$, then $\tau(f \to v) \ge \frac{9}{5} - \frac{6}{{10}} = \frac{6}{5}$.

If ${m_{4^-}}(v) = 1$, then $\omega '(v) \ge 2 + \min \{ - \frac{{10}}{7} - 7 + \frac{8}{7} + 6, - \frac{5}{4} \times 2 - 6 + \frac{1}{2} + 7, - 8 + 7 \} = \frac{5}{7}$ by R1, R2. Consider that ${m_{5^+}}(v) = 8$. Suppose ${n_2}(v) = k \le 8$. If $k \le 4$, then $\omega '(v) \ge 2 - \frac{6}{5}k + \min \{ \frac{4}{5} \times 8 - \frac{9}{{10}}(8 - k), (8 - k) + \frac{4}{5}k - (8 - k)\} = - \frac{3}{{10}}k + \frac{6}{5} \ge 0$ by R1, R2, R3.4, R5.1. Next, consider that $k \ge 5$.

Consider that $v$ is a heavy vertex. If $k = 5$, then either ${n_3}(v)+{n_4}(v) + {n_5}(v) \le 2$ or ${n_4}(v) \le 1$ and ${n_4}(v) + {n_5}(v) = 3$. Moreover, $\omega '(v) \ge 2 - \frac{6}{5} \times 5 + \frac{4}{5} \times 8 + \min \{ - 1 \times 2, - \frac{9}{{10}} - \frac{3}{5} \times 2\} = \frac{3}{{10}}$ by R1, R2, R3.4, R5.1. If $k = 6$, then ${n_3}(v)+{n_4}(v)+{n_5}(v) \le 1$. So $\omega '(v) \ge 2 - \frac{6}{5} \times 6 + \frac{4}{5} \times 8 + \min \{ - 1, - \frac{9}{{10}}\} = \frac{1}{5}$ by R1, R2, R3.4, R5.1. If $k = 7$, then ${n_{10^+}}(v) = 1$. Thus, $\omega '(v) \ge 2 - \frac{6}{5} \times 7 + \frac{{4}}{5} \times 8 + (\frac{9}{{5}} - \frac{6}{10}) = \frac{6}{{5}}$ by R1, R2, R6. Consider that $v$ is a light vertex. If ${m_A}(v) \ge 1$, then $\omega '(v) \ge 2 + \frac{4}{5} \times 8 - \frac{6}{5} \times 8 + \frac{6}{5} = 0$ by R1, R2 and Claim 3.5. Next, consider that ${m_A}(v) = 0$. If $k = 5$, then ${m_{6^+}}(v) \ge 2$ and $v$ has either at least one Class five 2-vertex or four Class four 2-vertex. It follows from R1, R2, R3.4 that $\omega '(v) \ge 2 + \min \{ - \frac{6}{5} \times 4 - 1, - \frac{6}{5} - \frac{{11}}{{10}} \times 4\} + 2 + \frac{4}{5} \times 6 - 1 \times 3 = 0$. If $k \ge 6$, then ${m_{6^+}}(v) \ge 4$ and $v$ has at least two Class five 2-neighbors. So $\omega '(v) \ge 2 - \frac{6}{5} \times 6 - 2 + \frac{4}{5} \times 4 + 4 + (\frac{4}{5} - \frac{6}{{10}}) \times 2 = \frac{2}{5}$ by R1, R2, R7.

Case 8. $d(v) = 9$ and then $\omega (v) = 3$.

If ${m_{4^-}}(v) = 1$, then $\omega '(v) \ge 3 + \min \{ - \frac{{10}}{7} + \frac{8}{7} + 7 - \frac{8}{7} \times 8, - \frac{5}{4} \times 2 + \frac{1}{2} + 8 - \frac{8}{7} \times 7, - \frac{8}{7} \times 9 + 8\} = \frac{4}{7}$ by R1, R2, R3.4. Consider that ${m_{5^+}}(v) = 9$. Suppose ${n_2}(v) = k \le 8$. If $k \le 6$, then $\omega '(v) \ge 3 - \frac{6}{5}k + \min \left\{ {\frac{{4}}{5}\times 9 - (9 - k), (9 - k) + \frac{4}{5}k - \frac{8}{7}(9 - k)} \right\} = - \frac{1}{5}k + \frac{6}{5} \ge 0$ by R1, R2, R3.4, R5.1, and Claim 3.2. Next, consider $7 \le k \le 9$.

Suppose that $v$ is a heavy vertex. If $k = 7$, then either ${n_3}(v)+{n_4}(v) + {n_5}(v)+{n_6}(v)\le 1$ or ${n_5}(v)+{n_6}(v) = 2$. Clearly, $\omega '(v) \ge 3 - \frac{6}{5} \times 7 + \frac{{4}}{5} \times 9 + \min \left\{ { - \frac{8}{7}, - \frac{3}{5} \times 2} \right\} = \frac{3}{5}$ by R1, R2, R3.4, R5.2. If $k = 8$, then ${n_{9^+}}(v) = 1$. Thereby, $\omega '(v) \ge 3 - \frac{6}{5} \times 8 + \frac{{4}}{5}\times 9 = \frac{3}{5}$ by R1, R2. Consider that $v$ is a light vertex. If $v$ is not a big vertex, then $\omega '(v) \ge 0$. Next, suppose that $v$ is a big vertex. For configuration B-face (See Figure 1(b)), $\omega '({v'_i}) \ge 3 - \frac{6}{5} \times 8 + \frac{4}{5} \times 9 = \frac{3}{5}(i = 1, 2)$ by R1$\sim$R7. So configuration B-face has just one big vertex. If ${m_B}(v) \ge 1$, then $\omega '(v) \ge 3 + \frac{4}{5} \times 9 - \frac{6}{5} \times 9 + \frac{3}{5} = 0$ by R1, R2, R8.2. Suppose ${m_B}(v) = 0$. If $k = 7$, then ${m_{6^+}}(v) \ge 5$. Obviously, $\omega '(v) \ge 3 + \frac{4}{5} \times 4 + 5 - \frac{6}{5} \times 7 - \frac{8}{7} \times 2 = \frac{18}{{35}}$ by R1, R2, R3.4. If $k = 8$, then ${m_{6^+}}(v) \ge 7$. So $\omega '(v) \ge 3 + \frac{4}{5}\times 2 +7 - \frac{6}{5} \times 8 - \frac{8}{7} = \frac{6}{{7}}$. If $k = 9$, then ${m_{6^+}}(v) = 9$, which indicates that $\omega '(v) \ge 3 + 9 - 9 = 3$.

Case 9. $d(v) = k\ge 10$ and then $\omega (v) = k-6$. Note that $2 - \frac{7}{k} > \frac{9}{5} - \frac{6}{k} \ge \frac{6}{5}$.

If ${m_{4^-}}(v) = 1$, then $\omega '(v) \ge k - 6 + \min \{ - \frac{{10}}{7} + k -2 + \frac{8}{7} - (2 - \frac{7}{k})(k - 1), - \frac{5}{4} + k -1 + \frac{1}{2} - (2 - \frac{7}{k})(k - 1), k - 1 - (2 - \frac{7}{k})k\} = 0$ by R1, R2, R3.4. Next, consider that ${m_{5^+}}(v) = k$. Suppose ${n_{st}}(v) = t\ge 0$. Moreover, $\omega '(v) \ge k - 6 + \frac{4}{5}(k-t) + t - (2 - \frac{7}{k})t - (\frac{9}{5} - \frac{6}{k})(k - t) = \frac{1}{k}t \ge 0$ by R1, R3.4, R6, and Claim 3.2. From the above argument, it is clear that $\omega '({v'_i}) \ge \frac{9}{5}-\frac{6}{d({v'_i})}(i = 1, 2)$ for configuration A-face (See Figure 1(a)) by R1$\sim$R7.

Next, it follows from the above argument that $\omega '(f)\ge 0$ if $f$ is a configuration A-face or configuration B-face, which derives that $\omega '(f)\ge 0$ for each $f \in F(G)$.

Therefore, Theorem 1.6 is proved.

4.   Conclusions

It is difficult to consider ${\chi _i}(G)$ and ${\chi _i^l}(G)$ for planar graph $G$ that has $g(G)\ge 4$. So we consider the case of $G$ where it does not have a ${4^ - }$-cycle intersecting with a ${5^ - }$-cycle. In addition, we will try to explore whether there exists a constant $C$ such that ${\chi _i^l}(G)\le \Delta + C$ for $G$ has disjoint ${4^-}$-cycles.

Author contributions

Yuehua Bu: Conceptualization; Hongrui Zheng: Writing-original & draft; Hongrui Zheng and Hongguo Zhu: Writing-review & editing. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (12031018, 12201569).

Conflicts of interest

The authors declare that they have no conflicts of interest.