A smaller upper bound for the list injective chromatic number of planar graphs

1.   Introduction

In the context of this article, all discussed graphs are assumed to be finite, simple, and undirected. In this regard, we use the notations: $V(G)$ for the vertex set, $E(G)$ for the edge set, $F(G)$ for the face set, $\Delta(G)$ (or simply $\Delta$ if no confusion occurs) for the maximum degree, $\delta(G)$ for the minimum degree, and $g(G)$ for the girth of a graph $G$. For a vertex $x$, $N_{G}(x)$ represents the set of vertices adjacent to $x$ in $G$, and $d(x)$ denotes the degree of vertex $x$, i.e., the number of vertices adjacent to $x$.

An injective $k$-coloring of a graph $G$ refers to a mapping $c$ that assigns a color from the set $\{1, 2, \ldots, k\}$ to each vertex in $V(G)$, this coloring satisfies the condition such that for any two vertices $u_{1}$ and $u_{2}$ in $V(G)$, $c(u_{1})\neq c(u_{2})$ if $N(u_{1})\cap N(u_{2})\neq\emptyset$. The injective chromatic number $\chi_{i}(G)$ of $G$ is defined as the smallest integer $k$ for which $G$ has an injective $k$-coloring.

A list assignment of a graph $G$ is a mapping $L$ that assigns a color list $L(x)$ to each vertex $x\in V(G)$. For a list assignment $L$ of $G$, if there is an injective coloring $\varphi$ of $G$ such that $\varphi(x)\in L(x)$ for each $x\in V(G)$, then $\varphi$ is called an injective $L$-coloring. If a graph $G$ can be injectively $L$-colored for any list assignment $L$ with $|L(x)|\geq k$ for each $x\in V(G)$, then $G$ is said to be injectively $k$-choosable. The injective choosability number $\chi_{i}^{l}(G)$ of a graph $G$ is defined as the minimum positive integer $k$ for which the graph $G$ is injectively $k$-choosable. It is important to note that $\chi_{i}(G)\leq\chi_{i}^{l}(G)$ holds for any graph $G$. For planar graphs, Borodin et al. ^[1] demonstrated that $\chi_{i}^{l}(G)$ and $\chi_{i}(G)$ are equivalent to $\Delta$ under certain conditions. These conditions are as follows: (1) $\Delta\geq16$ and $g = 7$; (2) $\Delta\geq10$ and $8\leq g\leq9$; (3) $\Delta\geq6$ and $10\leq g\leq11$; (4) $\Delta = 5$ and $g\geq12$.

The concept of injective coloring was introduced by Hahn et al. ^[11] in 2002. They showed the injective chromatic number of some special graphs such as paths, cycles, complete graphs, and stars. They also proved that for a connected graph $G$ that is not $K_{2}$, it holds that $\chi(G)\leq\chi_{i}(G)\leq\Delta(\Delta-1)+1$.

In 2010, Lu$\check{z}$ar proposed a conjecture for planar graphs in ^[13].

Conjecture A. Suppose $G$ is a planar graph with maximum degree $\Delta$.

(ⅰ) If $\Delta = 3$, then $\chi_{i}(G)\leq5$;

(ⅱ) If $4\leq\Delta\leq7$, then $\chi_{i}(G)\leq\Delta+5$;

(ⅲ) If $\Delta\geq8$, then $\chi_{i}(G)\leq\lfloor\frac{3\Delta}{2}\rfloor+1$.

Lu$\check{z}$ar et al. ^[14] proved that if this conjecture is true, the upper bounds mentioned above are tight.

Several studies have focused on investigating the injective chromatic number of graphs considering the constraints of maximum degree $\Delta$ and girth $g$ in ^{[1,2,3,4,5,6,7,8,9,10,12]}, which can be described as follows:

Theorem 1. Let $G$ be a planar graph with girth $g\geq g'$ and maximum degree $\Delta\geq \Delta'$.

$(1)$ If $(g', \Delta')\in \{(6, 17), (7, 7), (9, 4) \}$, $\chi_{i}(G)\leq\Delta+1$.

$(2)$ If $(g', \Delta')\in \{(6, 9)\}$, $\chi_{i}(G)\leq\Delta+2$.

$(3)$ If $(g', \Delta')\in \{(5, 20)\}$, $\chi_{i}(G)\leq\Delta+3$.

$(4)$ For any $\Delta$, if $g' = 6$, $\chi_{i}(G)\leq\Delta+3$; if $g' = 5$, $\chi_{i}(G)\leq\Delta+6$.

$(5)$ If $(g', \Delta')\in \{(6, 24), (8, 5)\}$, $\chi_{i}^{l}(G)\leq\Delta+1$.

$(6)$ If $(g', \Delta') = \{(6, 8)\}$, $\chi_{i}^{l}(G)\leq\Delta+2$.

$(7)$ If $(g', \Delta') = \{(5, 8)\}$, $\chi_{i}^{l}(G)\leq\Delta+6$; If $(g', \Delta') = \{(5, 10)\}$, $\chi_{i}^{l}(G)\leq\Delta+5$; If $(g', \Delta') = \{(5, 11)\}$, $\chi_{i}^{l}(G)\leq\Delta+4$.

$(8)$ For any $\Delta$, if $g' = 6$, $\chi_{i}^{l}(G)\leq\Delta+3$; if $g' = 5$, $\chi_{i}^{l}(G)\leq\Delta+5$.

For planar graphs $G$ with girth $g\geq5$, Bu et al. ^[7] proved that if the maximum degree $\Delta\geq20$, the inequality $\chi_{i}(G)\leq\Delta+3$ holds. Additionally, if the maximum degree $\Delta\geq10$, they established that $\chi_{i}^{l}(G)\leq\Delta+5$ in ^[5], and if the maximum degree $\Delta\geq11$, they showed that $\chi_{i}^{l}(G)\leq\Delta+4$ ^[2]. However, the best-known result for planar graphs $G$ with girth $g\geq5$ and any maximum degree $\Delta$ is $\chi_{i}^{l}(G)\leq\Delta+5$, as shown in ^[12]. In this paper, for any maximum degree $\Delta$, we present a proof that the list injective chromatic number of planar graphs without 3- and 4-cycles, as well as without intersecting 5-cycles, is at most $\Delta+4$.

Theorem 2. If $G$ is a planar graph with girth $g\geq5$ and without intersecting $5$-cycles, then $\chi_{i}^{l}(G)\leq\Delta+4$.

2.   Properties related to the structure of critical graphs

In this section, we explore various structural properties of $k$-$critical$ graphs, which are graphs that do not admit any injective $L$-coloring with $|L(x)|\geq k$ for every vertex $x\in V(G)$, while every proper subgraph of $G$ does allow such a coloring.

Let us introduce some notations. A vertex $x$ in a graph $G$ is defined to be $k$-vertex, $k^{+}$-vertex, or $k^{-}$-vertex if its degree is equal to $k$, at least $k$, or at most $k$, respectively. Similarly, a $k$-face, $k^{+}$-face, or $k^{-}$-face can be defined. A vertex adjacent to vertex $x$ in a graph $G$ is referred to as a $k$-neighbor, $k^{+}$-neighbor, or $k^{-}$-neighbor of $x$ if it is a $k$-vertex, $k^{+}$-vertex, or $k^{-}$-vertex, respectively. Let $N_{k}(x)$ denote the set of $k$-neighbors of vertex $x$, and let $n_ {k}(x)$ and $n_{k^{+}}(x)$ represent the counts of $k$-neighbors and $k^{+}$-neighbors of $x$, respectively. We can define $S_{G}(x)$ as $\sum_{y\in N(x)}(d(y)-1) = \sum_{y\in N(x)}d(y)-d(x)$. It is evident that the number of vertices in graph $G$ that share a common neighbor with vertex $x$ is at most $S_{G}(x)$. Therefore, if the remaining vertices are injectively colored, vertex $x$ has at most $S_{G}(x)$ forbidden colors. Consider a graph $G$ that is $(\Delta+4)$-critical. If a 3-vertex $x$ of $G$ has a 2-neighbor, we call $x$ a $bad$ vertex. Otherwise, if $x$ does not have a 2-neighbor, we call it a $good$ vertex. A vertex is referred to as a $k(s)$-vertex if it is a $k$-vertex and has exactly $s$ 2-neighbors.

We can represent the adjacent vertices of a vertex $v$ in graph $G$ as $v_{1}, v_{2}, \ldots, v_{d(v)}$ where $d(v_{1})\leq d(v_{2})\leq\ldots\leq d(v_{d(v)})$ in ascending order of their degrees. Then, we call $v$ a $(d(v_{1}), d(v_{2}), \ldots, d(v_{d(v)}))$-vertex. Additionally, if $d(v_{i}) = 2$, we denote the other neighbor of $v_{i}$ as $v_{i}'$.

We present the following properties of $(\Delta+4)$-critical graphs. Their proofs can be found in Reference ^[4].

Lemma 3. $\delta(G)\geq2$.

Lemma 4. For any edge $uv\in E(G)$, $\max\{S_{G}(u), S_{G}(v)\}\geq\Delta+4$.

Lemma 5. $G$ has no adjacent $2$-vertices.

Lemma 6. For a vertex $v$ with $3\leq d(v)\leq5$, if $v_{1}$ is a $2$-neighbor of $v$, $l = n_{3^{+}}(v)$, $u_{i} (i = 1, \ldots, l)$ is the $3^{+}$-neighbor of $v$, then

$(1)$ $l\geq2$,

$(2)$ $\sum_{i = 1}^{l}d(u_{i})\geq\Delta+4+2l-d(v)$.

3.   Proof of Theorem 2

In this part, we will prove Theorem 2 by contradiction, and the graphs discussed below are planar graphs. Suppose that Theorem 2 is not true. Let $G$ be a ($\Delta+4$)-critical graph and $L$ be the corresponding list assignment of $G$ with $|L(x)|\geq\Delta+4$ for each $x\in V(G)$. It is, $G$ does not admit any injective $L$-coloring, while every proper subgraph of $G$ does allow such a coloring. Then $G$ is connected and $\delta(G)\geq2$.

First, we assign an initial charge $\omega(v)$ to each vertex $v$ such that $\omega(v) = \frac{3}{2}d(v)-5$ and a charge $\omega(f) = d(f)-5$ to each face $f$. By Euler's formula, $|V(G)|-|E(G)|+|F(G)| = 2$, we have

$\sum_{v\in V(G)}(\frac{3}{2}d(v)-5)+\sum_{f\in F(G)}(d(f)-5) = -10$.

We then proceed by transferring charges from one element to another, resulting in a new charge $\omega'(t)$ for each $t\in V(G)\cup F(G)$ such that $\sum_{t\in V(G)\cup F(G)}\omega'(t) = -10$ still holds. Our goal is to show that if all transfers result in $\omega'(t)\geq0$ for each $t\in V(G)\cup F(G)$, then we will reach a contradiction:

$0\leq\sum_{t\in V(G)\cup F(G)}\omega'(t) = \sum_{t\in V(G)\cup F(G)}\omega(t) = -10 < 0$.

Hence, the theorem is proved.

Now, we prove the following lemma.

Lemma 7. $\Delta\geq4$.

Proof. According to Lemma 3 and Lemma 5, we have $\Delta\geq3$. If $\Delta = 3$, let $d(v) = 3$, then $S_{G}(v) = d(v_{1})+d(v_{2})+d(v_{3})-3 < \Delta+4$. However, we can observe that $S_{G}(v_{1})\leq\Delta+\Delta+3-3 = 2\Delta < \Delta+4$, which contradicts Lemma 4. Therefore, $\Delta\geq4$.

We will then prove the theorem by distinguishing several cases based on the maximum degree $\Delta$. In the rest, we always give a proper subgraph of $G$, denoted by $G'$. Since $G$ is critical, $G'$ has an injective $L$-coloring $c$. After deleting the colors of some vertices, let $L_{c}'(x)$ denote the set of available colors of $x$.

3.1.   $\Delta=4$

Claim 8. A $4(2)$-vertex is not adjacent to a $4$-vertex with at least one $2$-neighbor.

Proof. Let us consider a 4(2)-vertex denoted as $u$, with its neighbors $u_{1}$ and $u_{2}$ having degrees of 2, and another neighbor $u_{3}$ as a 4-vertex. Let $v$ be the adjacent 2-vertex of $u_{3}$. For convenience, assume that $d(u_{4}) = \Delta$. Let $G' = G-uu_{1}$. Now we delete the colors on $u, u_{1}$ and $v$. Obviously, $|L_{c}'(u)|\geq\Delta+4-(2\times2+4+\Delta-d(u)-1)\geq1$, $|L_{c}'(u_{1})|\geq\Delta+4-(\Delta+4-d(u_{1}))\geq2$, $|L_{c}'(v)|\geq\Delta+4-(\Delta+4-d(v)-1)\geq3$. So we can recolor $u, u_{1}, v$, in turn and an injective $L$-coloring of $G$ is obtained, a contradiction.

We use the following discharging rules.

R1-1. Each 2-vertex receives 1 from each adjacent $3^{+}$-vertex.

R1-2. A 4-vertex sends $\frac{1}{4}$ to each adjacent 3-vertex.

R1-3. A $(3, 4, 4)$-vertex sends $\frac{1}{18}$ to each adjacent $(3, 3, 3)$-vertex.

R1-4. Each $6^{+}$-face equally distributes its positive charge to each incident $3^{+}$-vertex.

R1-5. A $4(0)$-vertex sends $\frac{1}{4}$ to each of its $4(2)$-neighbors.

First, we check $\omega'(v)\geq0$ for each vertex $v\in V(G)$.

Case 1. If $d(v) = 2$, then $\omega(v) = \frac{3}{2}\times2-5 = -2$. By R1-1, $\omega'(v) = -2+1\times2 = 0$.

Case 2. If $d(v) = 3$, then $\omega(v) = \frac{3}{2}\times3-5 = -\frac{1}{2}$. According to Lemma 4, $n_{2}(v) = 0$. If $n_{3}(v)\leq1$, then $\omega'(v)\geq-\frac{1}{2}-\frac{1}{18}+2\times\frac{1}{4}+2\times\frac{1}{6} = \frac{5}{18}$ by R1-2, R1-3, and R1-4. If $n_{3}(v) = 2$, then $\omega'(v)\geq-\frac{1}{2}+\frac{1}{4}+2\times\frac{1}{6} = \frac{1}{12}$ by R1-2 and R1-4. If $n_{3}(v) = 3$, then according to Lemma 4, each 3-neighbor of $v$ must be $(3, 4, 4)$-vertex. Therefore, using R1-3 and R1-4, we have $\omega'(v)\geq-\frac{1}{2}+3\times\frac{1}{18}+2\times\frac{1}{6} = 0$.

Case 3. If $d(v) = 4$, then $\omega(v) = \frac{3}{2}\times4-5 = 1$. According to Lemma 4, $n_{2}(v)\leq2$. If $n_{2}(v) = 0$, then $\omega'(v)\geq1-4\times\frac{1}{4}+3\times\frac{1}{6} = \frac{1}{2}$ by R1-2, R1-4, and R1-5. If $n_{2}(v) = 1$, then according to Lemma 4, $n_{3}(v)\leq2$. So $\omega'(v)\geq1-1-2\times\frac{1}{4}+3\times\frac{1}{6} = 0$ by R1-1, R1-2, and R1-4. If $n_{2}(v) = 2$, then $n_{4}(v) = 2$ by Lemma 4, and each 4-neighbor of $v$ must be a $4(0)$-vertex by Claim 8. It follows that $\omega'(v)\geq1-2+2\times\frac{1}{4}+3\times\frac{1}{6} = 0$ by R1-1, R1-5, and R1-4.

We now check $\omega'(f)\geq0$ for each $f\in F(G)$.

If $f$ is a 5-face, then $\omega'(f) = d(f)-5 = 0$ since no charge is discharged to or from $f$. If $f$ is a $6^{+}$-face, according to R1-4, $f$ gives away its positive charge, so $\omega'(f) = 0$.

We have checked $\omega'(x)\geq0$ for all $x\in V(G)\cup F(G)$. Therefore, the proof is completed when $\Delta = 4$.

3.2.   $\Delta=5$

Claim 9. The following configurations are forbidden.

$(1)$ A $(2, 2, 5, 5)$-vertex adjacent to a $5$-vertex with at least two $2$-neighbors.

$(2)$ A $(2, 2, 4, 5)$-vertex adjacent to a $5$-vertex with at least one $2$-neighbor.

$(3)$ A $(2, 3, 3, 3, 3)$-vertex adjacent to a bad $3$-vertex.

$(4)$ A $5(3)$-vertex adjacent to a bad $3$-vertex.

Proof. (1) Let $v$ be a (2, 2, 5, 5)-vertex with $d(v_{1}) = d(v_{2}) = 2$ and $d(v_{3}) = d(v_{4}) = 5$. Suppose $v_{4}$ is adjacent to at least two 2-vertices $u$ and $w$. Let $G' = G-vv_{1}$. Now we delete the colors on $v, v_{1}, u$, and $w$. It is clear that $|L_{c}'(v)|\geq\Delta+4-(2\times2+5\times2-d(v)-2)\geq1$. If $v_{1}$ and $u$ (or $w$) have no common neighbor, then we have $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+4-d(v_{1}))\geq2$, $|L_{c}'(u)|\geq\Delta+4-(\Delta+5-d(u)-2)\geq3$, and $|L_{c}'(w)|\geq\Delta+4-(\Delta+5-d(w)-2)\geq3$. Thus, we can recolor $v, u, w$, and $v_{1}$ in turn to obtain an injective $L$-coloring of $G$. If $v_{1}$ and $u$ have a common neighbor, then we have $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+4-d(v_{1})-1)\geq3$, $|L_{c}'(u)|\geq\Delta+4-(\Delta+5-d(u)-3)\geq4$, and $|L_{c}'(w)|\geq\Delta+4-(\Delta+5-d(w)-2)\geq3$. Thus, we can recolor $v, v_{1}, w$, and $u$ in turn to obtain an injective $L$-coloring of $G$.

(2) Let $v$ be a (2, 2, 4, 5)-vertex with $d(v_{1}) = d(v_{2}) = 2$, $d(v_{3}) = 4$, $d(v_{4}) = 5$, and $u$ be a 2-neighbor of $v_{4}$. Let $G' = G-vv_{1}$. Now we delete the colors on $v, v_{1}$, and $u$. It is clear that $|L_{c}'(v)|\geq\Delta+4-(2\times2+4+5-d(v)-1)\geq1$. If $N(v_{1})\cap N(u) = \emptyset$, then we have $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+4-d(v_{1}))\geq2$ and $|L_{c}'(u)|\geq\Delta+4-(\Delta+5-d(u)-1)\geq2$. Thus, we can recolor $v, u$, and $v_{1}$ in turn to obtain an injective $L$-coloring of $G$. If $N(v_{1})\cap N(u)\neq\emptyset$, then we have $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+4-d(v_{1})-1)\geq3$ and $|L_{c}'(u)|\geq\Delta+4-(\Delta+5-d(u)-2)\geq3$. Thus, we can recolor $v, v_{1}$, and $u$ in turn to obtain an injective $L$-coloring of $G$.

(3) Let $v$ be a (2, 3, 3, 3, 3)-vertex with $d(v_{1}) = 2$, $d(v_{2}) = d(v_{3}) = d(v_{4}) = d(v_{5}) = 3$, and $u$ be a 2-neighbor of $v_{2}$. Let $G' = G-vv_{1}$. Now we delete the colors on $v, v_{1}$, and $u$. It is clear that $|L_{c}'(v)|\geq\Delta+4-(2+3\times4-d(v)-1)\geq1$, $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+5-d(v_{1}))\geq1$, and $|L_{c}'(u)|\geq\Delta+4-(\Delta+3-d(u)-1)\geq4$. So we can recolor $v, v_{1}$, and $u$ in turn, and an injective $L$-coloring of $G$ is obtained.

(4) Let $v$ be a 5(3)-vertex with $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$, $d(v_{4}) = 3$, and $u$ be a 2-neighbor of $v_{4}$. For convenience, assume $d(v_{5}) = \Delta$. Let $G' = G-vv_{1}$. Now we delete the colors on $v, v_{1}$, and $u$. It is clear that $|L_{c}'(v)|\geq\Delta+4-(2\times3+3+\Delta-d(v)-1)\geq1$, $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+5-d(v_{1}))\geq1$, and $|L_{c}'(u)|\geq\Delta+4-(\Delta+3-d(u)-1)\geq4$. So we can recolor $v, v_{1}$, and $u$ in turn, and an injective $L$-coloring of $G$ is obtained.

We use the following discharging rules.

R2-1. Each 2-vertex receives 1 from each adjacent $3^{+}$-vertex.

R2-2. A 4-vertex sends $\frac{1}{18}$ to each adjacent 3-vertex.

R2-3. A 5-vertex sends $\frac{1}{4}$ to each adjacent $(2, 2, 5, 5)$-vertex, $\frac{1}{2}$ to each adjacent $(2, 2, 4, 5)$-vertex.

R2-4. A 5-vertex sends $\frac{7}{12}$ to each adjacent bad 3-vertex, $\frac{1}{6}$ to each adjacent good 3-vertex.

R2-5. A $(3, 4^{+}, 5)$-vertex sends $\frac{1}{18}$ to each adjacent $(3, 3, 3^{+})$-vertex or adjacent $(3, 4, 4)$-vertex.

R2-6. Each $6^{+}$-face equally distributes its positive charge to each incident $3^{+}$-vertex.

First, we check $\omega'(v)\geq0$ for each vertex $v\in V(G)$.

Case 1. $d(v) = 2$, $\omega(v) = \frac{3}{2}\times2-5 = -2$. By R2-1, $\omega'(v) = -2+1\times2 = 0$.

Case 2. $d(v) = 3$, $\omega(v) = \frac{3}{2}\times3-5 = -\frac{1}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}\}$. By Lemma 6(1), $n_{2}(v)\leq1$.

If $n_{2}(v) = 1$, then according to Lemma 6(2), $n_{5}(v) = 2$. By R2-1, R2-4, and R2-6, $\omega'(v)\geq-\frac{1}{2}-1+2\times\frac{7}{12}+2\times\frac{1}{6} = 0$.

If $n_{2}(v) = 0$ and $n_{3}(v)\geq2$, let $d(v_{1}) = d(v_{2}) = 3$; then $v_{1}$ and $v_{2}$ are both $(3, 4^{+}, 5)$-vertices by Lemma 4. So $\omega'(v)\geq-\frac{1}{2}+2\times\frac{1}{18}+2\times\frac{1}{6}+\min\{\frac{1}{18}, \frac{1}{18}, \frac{1}{6}\} = 0$.

If $n_{2}(v) = 0$ and $n_{3}(v) = 1$, then $v$ must be either a $(3, 4, 4)$-vertex or a $(3, 4^{+}, 5)$-vertex. When $v$ is a $(3, 4, 4)$-vertex, the 3-vertex adjacent to $v$ must be $(3, 4^{+}, 5)$-vertex by Lemma 4, so $\omega'(v)\geq-\frac{1}{2}+\frac{1}{18}+2\times\frac{1}{18}+2\times\frac{1}{6} = 0$; When $v$ is a $(3, 4^{+}, 5)$-vertex, $\omega'(v)\geq-\frac{1}{2}-\frac{1}{18}+\frac{1}{18}+\frac{1}{6}+2\times\frac{1}{6} = 0$.

If $n_{2}(v) = 0$ and $n_{3}(v) = 0$, then $\omega'(v)\geq-\frac{1}{2}+3\times\frac{1}{18}+2\times\frac{1}{6} = 0$.

Case 3. $d(v) = 4$, $\omega(v) = \frac{3}{2}\times4-5 = 1$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}\}$. By Lemma 6(1), $n_{2}(v)\leq2$.

If $n_{2}(v) = 2$, let $d(v_{1}) = d(v_{2}) = 2$, then by Lemma 6(2), $d(v_{3})+d(v_{4})\geq\Delta+4$. So $v$ must be a $(2, 2, 4^{+}, 5)$-vertex. Hence, $\omega'(v)\geq1-2\times1+\min\{\frac{1}{2}, 2\times\frac{1}{4}\}+3\times\frac{1}{6} = 0$ by R2-1, R2-3, and R2-6.

If $n_{2}(v)\leq1$, then $\omega'(v)\geq1-1-3\times\frac{1}{18}+3\times\frac{1}{6} = \frac{1}{3}$ by R2-1, R2-2, and R2-6.

Case 4. $d(v) = 5$, $\omega(v) = \frac{3}{2}\times5-5 = \frac{5}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}\}$. By Lemma 6, $n_{2}(v)\leq3$.

If $n_{2}(v) = 3$, then $n_{3}(v)\leq1$ by Lemma 4. When $n_{2}(v) = 3$ and $n_{3}(v) = 1$, then $v$ is a $(2, 2, 2, 3, 5)$-vertex. By Claim 9(4), $v$ is not adjacent to a bad 3-vertex. Therefore, by R2-1, R2-4 and R2-6, we have $\omega'(v)\geq\frac{5}{2}-3\times1-\frac{1}{6}+4\times\frac{1}{6} = 0$. When $n_{2}(v) = 3$ and $n_{3}(v) = 0$, by Claim 9(1)(2), $v$ is not adjacent to a $(2, 2, 4, 5)$-vertex or a $(2, 2, 5, 5)$-vertex. Thus, $\omega'(v)\geq\frac{5}{2}-3\times1+4\times\frac{1}{6} = \frac{1}{6}$.

If $n_{2}(v) = 2$, then $n_{3}(v)\leq2$ by Lemma 4. By Claim 9(1)(2), $v$ is not adjacent to a $(2, 2, 4, 5)$-vertex or a $(2, 2, 5, 5)$-vertex. Therefore, $\omega'(v)\geq\frac{5}{2}-2\times1-2\times\frac{7}{12}+4\times\frac{1}{6} = 0$.

If $n_{2}(v) = 1$ and $n_{3}(v) = 4$, then by Claim 9(3), $v$ is not adjacent to bad 3-vertices. Thus, $\omega'(v)\geq\frac{5}{2}-1-4\times\frac{1}{6}+4\times\frac{1}{6} = \frac{3}{2}$.

If $n_{2}(v) = 1$ and $n_{3}(v)\leq3$, then by Claim 9(2), $v$ is not adjacent to a $(2, 2, 4, 5)$-vertex. Therefore, $\omega'(v)\geq\frac{5}{2}-1-3\times\frac{7}{12}-\frac{1}{4}+4\times\frac{1}{6} = \frac{1}{6}$.

If $n_{2}(v) = 0$, then $\omega'(v)\geq\frac{5}{2}-5\times\frac{7}{12}+4\times\frac{1}{6} = \frac{1}{4}$ by R2-3, R2-4, and R2-6.

We now check $\omega'(f)\geq0$ for each $f\in F(G)$.

If $f$ is a 5-face, then $\omega'(f) = d(f)-5 = 0$ since no charge is discharged to or from $f$. If $f$ is a $6^{+}$-face, according to R2-6, $f$ gives away its positive charge, so $\omega'(f) = 0$.

We have verified that $\omega'(x)\geq0$ for all $x\in V(G)\cup F(G)$. This completes the proof when $\Delta = 5$.

3.3.   $\Delta=6$

Claim 10. The following configurations are forbidden.

$(1)$ A $5(3)$-vertex adjacent to a $4(2)$-vertex.

$(2)$ A $5(3)$-vertex adjacent to a bad $3$-vertex.

Proof. (1) Let $v$ be a 5(3)-vertex with $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$, $d(v_{4}) = 4$, and $x, y$ as 2-neighbors of $v_{4}$. For convenience, assume $d(v_{5}) = \Delta$. Let $G' = G-vv_{1}$. Now we delete the colors on $v, v_{1}, x$, and $y$. Obviously, $|L_{c}'(v)|\geq\Delta+4-(2\times3+4+\Delta-d(v)-2)\geq1$, $|L_{c}'(v_{1})|\geq\Delta+4-(\Delta+5-d(v_{1}))\geq1$, $|L_{c}'(x)|\geq\Delta+4-(\Delta+4-d(x)-2)\geq4$, and $|L_{c}'(y)|\geq\Delta+4-(\Delta+4-d(y)-2)\geq4$. So we can recolor $v, v_{1}, x$, and $y$ in turn, and an injective $L$-coloring of $G$ is obtained.

(2) The proof can be seen from Claim 9(4).

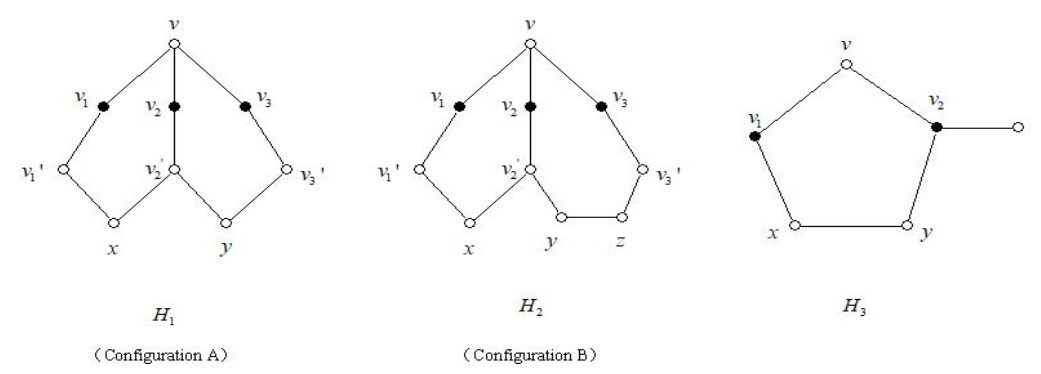
Claim 11. Let $f_{1} = v_{1}'v_{1}vv_{2}v_{2}'x$, $f_{2} = v_{3}'v_{3}vv_{2}v_{2}'y$ be two $6$-faces. Suppose $d(v) = 6$ and $S_{G}(v) < \Delta+4$. If $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$, then $d(x)\geq3$ and $d(y)\geq3$. Additionally, if $d(x) = 3$ and $d(y) = 3$, then at most one of $x$ or $y$ is a bad $3$-vertex. (The configuration composed of $f_{1}$ and $f_{2}$ is called Configuration $A$ of $v$. See $H_{1}$ in Figure 1)

Proof. By Lemma 4, we conclude that $d(v_{1}') = d(v_{2}') = d(v_{3}') = \Delta$. The subsequent steps of the proof follow a similar approach as presented in Claim 3 of the reference paper ^[8] by Chen et al.

Claim 12. Let $f_{1} = v_{1}'v_{1}vv_{2}v_{2}'x$ be a $6$-face, $f_{2} = v_{3}'v_{3}vv_{2}v_{2}'yz$ be a $7$-face. Suppose $d(v) = 6$ and $S_{G}(v) < \Delta+4$. If $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$ and $d(z)\leq5$, then $\min\{d(x), d(y)\}\geq3$. (The configuration composed of $f_{1}$ and $f_{2}$ is called Configuration $B$ of $v$. See $H_{2}$ in Figure 1)

Proof. To prove this claim, we will use a proof by contradiction. Let $G' = G-vv_{1}$. According to Lemma 4, we can deduce that $d(v_{1}') = d(v_{2}') = d(v_{3}') = \Delta$. We will now consider three cases.

Case A. $d(x) = 2$ and $d(y) = 2$. In this case, erase the colors on vertices $v, v_{1}, v_{2}, v_{3}, x$, and $y$. Now, we have $|L_{c}'(v)|\geq(\Delta+4)-S_{G}(v)\geq1$, $|L_{c}'(v_{1})|\geq(\Delta+4)-(\Delta+6-2-3) = 3$, $|L_{c}'(v_{2})|\geq(\Delta+4)-(\Delta+6-2-4) = 4$, $|L_{c}'(v_{3})|\geq(\Delta+4)-(\Delta+6-2-2) = 2$, $|L_{c}'(x)|\geq(\Delta+4)-(\Delta+\Delta-2-3) = 9-\Delta = 3$, and $|L_{c}'(y)|\geq(\Delta+4)-(\Delta+5-2-2) = 3$. Therefore, we can recolor vertices $v, v_{3}, v_{1}, v_{2}, x$, and $y$ sequentially, obtaining an injective $L$-coloring of $G$, which leads to a contradiction.

Case B. $d(x) = 2$ and $d(y)\geq3$. In this case, erase the colors on $v, v_{1}, v_{2}, v_{3}$, and $x$. We have $|L_{c}'(v)|\geq(\Delta+4)-S_{G}(v)\geq1$, $|L_{c}'(v_{1})|\geq(\Delta+4)-(\Delta+6-2-3) = 3$, $|L_{c}'(v_{2})|\geq(\Delta+4)-(\Delta+6-2-3) = 3$, $|L_{c}'(v_{3})|\geq(\Delta+4)-(\Delta+6-2-2) = 2$, and $|L_{c}'(x)|\geq(\Delta+4)-(\Delta+\Delta-2-2) = 8-\Delta = 2$. If $L_{c}'(x)\cap L_{c}'(v_{3})\neq\emptyset$, let $\alpha\in L_{c}'(x)\cap L_{c}'(v_{3})$, then recolor $x$ and $v_{3}$ with $\alpha$, and recolor vertices $v, v_{1}$, and $v_{2}$ sequentially. Suppose $L_{c}'(x)\cap L_{c}'(v_{3}) = \emptyset$. If $L_{c}'(x)\cap L_{c}'(v_{1}) = \emptyset$, we can simply recolor vertices $v, v_{3}, v_{1}, v_{2}$, and $x$ sequentially. If $L_{c}'(x)\cap L_{c}'(v_{1})\neq\emptyset$, let $\beta\in L_{c}'(x)\cap L_{c}'(v_{1})$. Note that $\beta\not\in L_{c}'(v_{3})$. We can recolor vertex $v_{1}$ with color $\beta$, and then recolor vertices $v, x$, and $v_{2}$ sequentially. Since $|L_{c}'(v_{3})|\geq2$ and $\beta\not\in L_{c}'(v_{3})$, there exists at least one color $\gamma\in L_{c}'(v_{3})$ that is different from the color of $v_{2}$ and $\gamma\neq\beta$. Therefore, we can recolor vertex $v_{3}$ with color $\gamma$.

Case C. $d(y) = 2$ and $d(x)\geq3$. In this case, erase the colors on $v, v_{1}, v_{2}, v_{3}$, and $y$. We have$|L_{c}'(v)|\geq(\Delta+4)-S_{G}(v)\geq1$, $|L_{c}'(v_{1})|\geq(\Delta+4)-(\Delta+6-2-2) = 2$, $|L_{c}'(v_{2})|\geq(\Delta+4)-(\Delta+6-2-3) = 3$, $|L_{c}'(v_{3})|\geq(\Delta+4)-(\Delta+6-2-2) = 2$, and $|L_{c}'(y)|\geq(\Delta+4)-(\Delta+5-2-1) = 2$. Therefore, we can recolor vertices $v, v_{1}, v_{3}, v_{2}$, and $y$ sequentially.

In all three cases, we obtain an injective $L$-coloring of $G$, which leads to a contradiction. Therefore, the claim is proved.

Claim 13. Let $f_{1} = xv_{1}vv_{2}y$ be a 5-face. Suppose $d(v) = 6$ and $S_{G}(v) < \Delta+4$. If $d(v_{1}) = 2$ and $d(v_{2}) = 3$, then $d(y)\geq3$. (See $H_{3}$ in Figure 1)

Proof. The proof is carried out by contradiction. Let $G' = G-vv_{1}$. Suppose $d(y) = 2$. Erase the colors on vertices $v, v_{1}$, and $y$. Then we have $|L_{c}'(v)|\geq(\Delta+4)-S_{G}(v)\geq1$, $|L_{c}'(v_{1})|\geq(\Delta+4)-(\Delta+6-2-1) = 1$, and $|L_{c}'(y)|\geq(\Delta+4)-(\Delta+3-2-2) = 5$. We can then recolor $v, v_{1}$, and $y$ in turn.

We use the following discharging rules.

R3-1. Each 2-vertex receives 1 from each adjacent $3^{+}$-vertex.

R3-2. A bad 3-vertex receives $\frac{1}{2}$ from each adjacent 5-vertex, $\frac{19}{30}$ from each adjacent 6-vertex.

R3-3. A good 3-vertex receives $\frac{1}{6}$ from each adjacent 5-vertex, $\frac{1}{3}$ from each adjacent 6-vertex.

R3-4. Suppose $d(v) = 3$. If $S_{_{G}}(v) < \Delta+4$, then $v$ receives $\frac{1}{18}$ from each adjacent 3-vertex or 4-vertex.

R3-5. A 4(2)-vertex receives $\frac{13}{60}$ from each adjacent $5$-vertex, $\frac{13}{30}$ from each adjacent 6-vertex.

R3-6. Each $6^{+}$-face equally distributes its positive charge to each incident $3^{+}$-vertex.

R3-7. In Configuration $A$ or $B$, $v$ receives $\frac{1}{12}$ along edge $v_{2}'x$ from $v_{2}'$, and $\frac{1}{12}$ along edge $v_{2}'y$ from $v_{2}'$, for a total of $\frac{1}{6}$ received from $v_{2}'$. (See Fig. 2)

R3-8. For a 5-face $f = vv_{1}xyv_{2}$, if $d(v) = 6$, $d(v_{1}) = d(v_{2}) = 2$, $d(x) = d(y) = \Delta$, we call it Configuration $C_{1}$ of $v$. In Configuration $C_{1}$, $v$ receives $\frac{1}{6}$ along edge $xv_{1}$ from $x$, and $\frac{1}{6}$ along edge $yv_{2}$ from $y$, for a total of $\frac{1}{3}$ from $x$ and $y$. On the other hand, if $d(v) = 6$, $d(v_{1}) = 2$, $d(v_{2}) = 3$, $d(x) = \Delta$, and $d(y)\geq5$, we call it Configuration $C_{2}$ of $v$. In Configuration $C_{2}$, $v$ receives $\frac{1}{6}$ along edge $xv_{1}$ from $x$.(See Figure 2)

R3-9. For a 7-face $f = yv_{2}'v_{2}vv_{3}v_{3}'z$, if $d(v) = 6$, $d(v_{2}) = d(v_{3}) = 2$ and $d(v_{2}') = d(v_{3}') = d(z) = \Delta$, we call it Configuration $D$ of $v$. In Configuration $D$, $v$ receives $\frac{1}{12}$ along edge $zy$ from $z$, and $\frac{1}{12}$ along edge $v_{3}'v_{3}$ from $v_{3}'$, for a total of $\frac{1}{6}$ from $z$ and $v_{3}'$. (See Figure 2)

Remark 1. Let $d(v) = 6$. In Configuration A, $v$ receives $\frac{1}{6}$ from $v_{2}'$, and receives $\frac{1}{4}+\frac{1}{4}$ from $f_{1}$ and $f_{2}$, so $v$ receives $\frac{2}{3}$ in total; in Configuration B, $v$ receives $\frac{1}{6}$ from $v_{2}'$, receives $\frac{1}{4}$ from $f_{1}$ and receives $\frac{2}{5}$ from $f_{2}$, so $v$ receives $\frac{49}{60}$ in total; in Configuration D, $v$ receives $\frac{1}{6}$ from $v_{3}'$ and $z$, receives $\frac{2}{5}$ from $f$, so $v$ receives $\frac{17}{30}$ in total.

First, we check $\omega'(v)\geq0$ for each vertex $v\in V(G)$.

Case 1. $d(v) = 2$. We have $\omega(v) = \frac{3}{2}\times2-5 = -2$. By applying R3-1, we obtain $\omega'(v) = -2+1\times2 = 0$.

Case 2. $d(v) = 3$. We have $\omega(v) = \frac{3}{2}\times3-5 = -\frac{1}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}\}$. By Lemma 6(1), $n_{2}(v)\leq1$.

If $n_{2}(v) = 1$, let $d(v_{1}) = 2$, then $d(v_{2})+d(v_{3})\geq\Delta+5$ by Lemma 6(2). Using R3-1, R3-2, and R3-6, we have $\omega'(v)\geq-\frac{1}{2}-1+\min\{\frac{1}{2}+\frac{19}{30}, 2\times\frac{19}{30}\}+\frac{1}{6}+\frac{1}{5} = 0$.

If $n_{2}(v) = 0$ and $n_{3}(v)\geq2$, then $S_{G}(v) < \Delta+4$. By applying R3-3, R3-4, and R3-6, we have $\omega'(v)\geq-\frac{1}{2}+\min\{3\times\frac{1}{18}, 2\times\frac{1}{18}+\frac{1}{6}, 2\times\frac{1}{18}+\frac{1}{3}\}+2\times\frac{1}{6} = 0$.

Suppose $n_{2}(v) = 0$ and $n_{3}(v) = 1$; let $d(v_{1}) = 3$. If $S_{G}(v) < \Delta+4$, then $d(v_{2})+d(v_{3}) < \Delta+4 = 10$. By applying R3-4, R3-3 and R3-6, we have $\omega'(v)\geq-\frac{1}{2}+\min\{3\times\frac{1}{18}, 2\times\frac{1}{18}+\frac{1}{6}\}+2\times\frac{1}{6} = 0$. If $S_{G}(v)\geq\Delta+4$, then $d(v_{2})+d(v_{3})\geq\Delta+4 = 10$. By applying R3-4, R3-3, and R3-6, we have $\omega'(v)\geq-\frac{1}{2}-\frac{1}{18}+\min\{\frac{1}{3}, 2\times\frac{1}{6}\}+2\times\frac{1}{6} = \frac{1}{9}$.

Suppose $n_{2}(v) = 0$ and $n_{3}(v) = 0$. If $S_{G}(v) < \Delta+4$, then $d(v_{1}) = d(v_{2}) = d(v_{3}) = 4$. By applying R3-4 and R3-6, we have $\omega'(v)\geq-\frac{1}{2}+3\times\frac{1}{18}+2\times\frac{1}{6} = 0$. If $S_{G}(v)\geq\Delta+4$, $v$ is adjacent to at least one $5^{+}$-vertex. By applying R3-3 and R3-6, we have $\omega'(v)\geq-\frac{1}{2}+\frac{1}{6}+2\times\frac{1}{6} = 0$.

Case 3. $d(v) = 4$. We have $\omega(v) = \frac{3}{2}\times4-5 = 1$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}\}$. By Lemma 6(1), $n_{2}(v)\leq2$.

If $n_{2}(v) = 2$, let $d(v_{1}) = d(v_{2}) = 2$, then $d(v_{3})+d(v_{4})\geq\Delta+4$ by Lemma 6(2). Using R3-1, R3-5, and R3-6, we have $\omega'(v)\geq1-2+\min\{\frac{13}{30}, 2\times\frac{13}{60}\}+\frac{1}{6}+2\times\frac{1}{5} = 0$.

If $n_{2}(v)\leq1$, then $\omega'(v)\geq1-1-3\times\frac{1}{18}+3\times\frac{1}{6} = \frac{1}{3}$ by R3-1, R3-4, and R3-6.

Case 4. $d(v) = 5$. We have $\omega(v) = \frac{3}{2}\times5-5 = \frac{5}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}\}$. By Lemma 6(1), we have $n_{2}(v)\leq3$.

If $n_{2}(v) = 3$, let $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$. Then, using Claim 10 and Lemma 6(2), we see that $v$ is not adjacent to a bad 3-vertex or a 4(2)-vertex, and $d(v_{4})+d(v_{5})\geq\Delta+3$. This means that $v$ is adjacent to at most one good 3-vertex. Using R3-1, R3-3, and R3-6, we have $\omega'(v)\geq\frac{5}{2}-3\times1-\frac{1}{6}+4\times\frac{1}{6} = 0$.

If $n_{2}(v) = 2$, by Lemma 4, we have $n_{3}(v)\leq2$.

Suppose $n_{2}(v) = 2$ and $n_{3}(v) = 2$. Then, another neighbor of $v$ must be $5^{+}$-vertex. Using R3-1, R3-2, and R3-6, we have $\omega'(v)\geq\frac{5}{2}-2\times1-2\times\frac{1}{2}+4\times\frac{1}{6} = \frac{1}{6}$.

If $n_{2}(v) = 2$ and $n_{3}(v)\leq1$, using R3-1, R3-2, R3-5, and R3-6, we have $\omega'(v)\geq\frac{5}{2}-2\times1-\frac{1}{2}-2\times\frac{13}{60}+4\times\frac{1}{6} = \frac{7}{30}$.

If $n_{2}(v)\leq1$, using R3-1, R3-2 and R3-6, we have $\omega'(v)\geq\frac{5}{2}-1-4\times\frac{1}{2}+4\times\frac{1}{6} = \frac{1}{6}$.

Case 5. $d(v) = 6$. We have $\omega(v) = \frac{3}{2}\times6-5 = 4$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}\}$.

Case 5.1. $n_{2}(v) = 0$. If $v$ is incident with a Configuration $D$, $v$ receives at least $-\frac{1}{12}+\frac{2}{5} = \frac{19}{60}$ from the configuration. However, if $v$ is incident with a 6-face $f$, $v$ receives at least $\frac{1}{6}$ from $f$. Therefore, in the worst case scenario, we assume that $v$ is not incident with any Configurations $D$. Using R3-2 and R3-6, we have $\omega'(v)\geq4-6\times\frac{19}{30}+5\times\frac{1}{6} = \frac{31}{30}$.

Case 5.2. $n_{2}(v) = 1$. Similarly to Case 5.1, we assume that $v$ is not incident with any Configurations $D$. Then there exists at most one Configuration $C_{1}$, or one Configuration $C_{2}$, or one Configuration $A$, or one Configuration $B$. Using R3-1, R3-2, R3-3, R3-4, R3-7, R3-8, and R3-6, we have $\omega'(v)\geq4-1-5\times\frac{19}{30}-\max\{\frac{1}{6}, 2\times\frac{1}{12}\}+5\times\frac{1}{6} = \frac{1}{2}$.

Case 5.3. $n_{2}(v) = 2$. Similarly to Case 5.1, we assume that $v$ is not incident with any Configurations $D$. Then there exists at most one Configuration $C_{1}$, or one Configuration $C_{2}$, or two Configurations $A$, or two Configurations $B$. Using R3-1, R3-2, R3-3, R3-4, R3-7, R3-8, and R3-6, we have $\omega'(v)\geq4-2-4\times\frac{19}{30}-\max\{\frac{1}{6}, \frac{1}{6}+2\times\frac{1}{12}, 4\times\frac{1}{12}\}+3\times\frac{1}{6}+2\times\frac{1}{5} = \frac{1}{30}$.

Case 5.4. $n_{2}(v) = 3$. Similarly to Case 5.1, we assume that $v$ is not incident with any Configurations $D$. If $v$ is incident with at most one bad 3-vertex, then there exist at most one Configuration $C_{1}$ (or Configuration $C_{2}$) and two Configurations $A$ (or Configurations $B$), or at most three Configurations $A$ (or Configurations $B$). When $v$ is incident with a Configuration $C_{1}$ (or Configuration $C_{2}$) that requires charges to be sent to it, $v$ must be adjacent to at least one $5^{+}$-vertex. Therefore, in the worst-case scenario, $v$ is incident with three Configurations $A$, $\omega'(v)\geq4-3\times1-\frac{19}{30}-2\times\frac{13}{30}-3\times\frac{1}{6}+6\times\frac{1}{5} = \frac{1}{5}$.

If $v$ is incident with two bad 3-vertices, there exist at most two Configurations $A$ incident with $v$ by Claim 11. So $\omega'(v)\geq4-3\times1-2\times\frac{19}{30}-\frac{13}{30}-2\times\frac{1}{6}+4\times\frac{1}{4}+\min\{-\frac{1}{6}+\frac{1}{4}+\frac{2}{5}, \frac{1}{5}\} = \frac{1}{6}$.

If $v$ is incident with three bad 3-vertices, there exist at most three Configurations $B$ incident with $v$ by Claim 11 and Claim 12. So $\omega'(v)\geq4-3\times1-3\times\frac{19}{30}+\min\{-3\times\frac{1}{6}+3\times\frac{1}{4}+3\times\frac{2}{5}$, $-2\times\frac{1}{6}+2\times\frac{1}{4}+2\times\frac{2}{5}+\frac{1}{5}, -1\times\frac{1}{6}+\frac{1}{4}+\frac{2}{5}+2\times\frac{1}{5}+\frac{1}{6}, 4\times\frac{1}{5}+\frac{1}{6}$, $\frac{1}{4}+2\times\frac{1}{5}+2\times\frac{1}{6}, 5\times\frac{1}{5}\} = \frac{1}{15}$.

Case 5.5. $n_{2}(v) = 4$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 4$. We consider three subcases.

Subcase 5.5.1. $v$ is adjacent to two bad 3-vertices. Let $d(v_{5}) = d(v_{6}) = 3$. Note that $S_{G}(v) = 2\times4+3\times2-6 = 8 < \Delta+4$. By Lemma 4, we have $d(v_{i}') = \Delta$ for $i = 1, \ldots, 4$ and another neighbor of $v_{j}$ must be a $5^{+}$-vertex for $j = 5, 6$.

If $v$ is incident with one Configuration $C_{1}$, say $f_{1}$, there are three cases shown in Figure 3(1)–(3). In (1) and (2), we have $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+2\times\frac{1}{6}+\min\{2\times\frac{1}{4}+2\times\frac{1}{5}+\frac{1}{6}, \frac{1}{4}+4\times\frac{1}{5}\} = \frac{7}{60}$. In (3), there is at most one Configuration B. So $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+2\times\frac{1}{6}+\min\{-2\times\frac{1}{12}+2\times\frac{1}{4}+\frac{2}{5}+2\times\frac{1}{5}, 3\times\frac{1}{4}+2\times\frac{1}{5}\} = \frac{1}{5}$.

If $v$ is incident with one Configuration $C_{2}$, say $f_{6}$, there are three cases shown in Figure 3(4)–(6). We have $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+\frac{1}{6}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{10}$.

If $v$ is incident with a 5-face, but not Configuration $C_{1}$ or Configuration $C_{2}$, there is only one case where $d(f_{5}) = 5$ according to Claim 13 (see Figure 3(7)). If $v$ is incident with at least one Configuration $A$ or $B$, then $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+2\times\frac{1}{12}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{10}$. If $v$ is not incident with any Configurations $A$ or $B$, then $\max\{d(f_{1}), d(f_{2})\}\geq7$ and $\max\{d(f_{2}), d(f_{3})\}\geq7$. Therefore, either $d(f_{2})\geq7$ or $\min\{d(f_{1}), d(f_{3})\}\geq7$. Suppose $d(f_{2}) = 7$ and $\min\{d(f_{1}), d(f_{3})\} = 6$. Since $v$ is not incident with any Configuration $B$, $f_{2}$ must be Configuration $D$. Thus, $v$ receives ($2\times\frac{1}{12}+\frac{2}{5}$) from $f_{2}$, and $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+(2\times\frac{1}{12}+\frac{2}{5})+3\times\frac{1}{4}+\frac{1}{5} = \frac{1}{4}$. If $d(f_{2}) = 7$ and $\min\{d(f_{1}), d(f_{3})\}\geq7$, we have $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+3\times\frac{2}{5}+\frac{1}{4}+\frac{1}{5} = \frac{23}{60}$. If $d(f_{2})\geq8$, then $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+\frac{3}{6}+3\times\frac{1}{4}+\frac{1}{5} = \frac{11}{60}$. Now suppose $\min\{d(f_{1}), d(f_{3})\}\geq7$. In this case, $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+2\times\frac{2}{5}+2\times\frac{1}{4}+\frac{1}{5} = \frac{7}{30}$.

If $v$ is not incident with any 5-faces, then $v$ is incident with at most one Configuration B to which $v$ needs to send charges. So $\omega'(v)\geq4-4\times1-2\times\frac{19}{30}+\min\{-2\times\frac{1}{12}+\frac{2}{5}+5\times\frac{1}{4}, 2\times\frac{1}{4}+4\times\frac{1}{5}\} = \frac{1}{30}$.

Subcase 5.5.2. $v$ is adjacent to one bad 3-vertex. Let $v_{5}$ be a bad 3-vertex. If $d(v_{6})\geq5$, then $v$ is incident with at most one Configuration $C_{1}$ (or $C_{2}$), or at most one Configuration A (or B) that requires charges to be sent to it. Therefore, $\omega'(v)\geq4-4\times1-\frac{19}{30}-\frac{1}{6}+2\times\frac{1}{4}+3\times\frac{1}{5} = \frac{11}{30}$. If $d(v_{6})\leq4$, then according to Lemma 4, $d(v_{i}') = \Delta$, $i = 1, \ldots, 4$. We consider three cases (see Figure 4(1)–(3)). In (1) and (2), we only need to consider the worst case where $v_{6}$ is a 4(2)-vertex and $v$ is incident with a 5-face but not Configuration $C_{1}$ or $C_{2}$. In this case, $\omega'(v)\geq4-4\times1-\frac{19}{30}-\frac{13}{30}+\min\{3\times\frac{1}{4}+\frac{1}{5}+\frac{1}{6}, 2\times\frac{1}{4}+3\times\frac{1}{5}\} = \frac{1}{30}$. In (3), $f_{4}$ and $f_{5}$ may form a Configuration $A$ or $B$. We consider the worst case where $v_{6}$ is a 4(2)-vertex and $v$ is incident with a 5-face but not Configuration $C_{1}$ or $C_{2}$. If $f_{1}$ and $f_{2}$ cannot form configuration $A$, then $\max\{d(f_{1}), d(f_{2})\}\geq7$. In this case, $\omega'(v)\geq4-4\times1-\frac{19}{30}-\frac{13}{30}-2\times\frac{1}{12}+\frac{1}{4}+\frac{2}{5}+3\times\frac{1}{5} = \frac{1}{60}$. If $f_{1}$ and $f_{2}$ form configuration $A$, then $\omega'(v)\geq4-4\times1-\frac{19}{30}-\frac{13}{30}-2\times\frac{1}{12}+2\times\frac{1}{12}+2\times\frac{1}{4}+3\times\frac{1}{5} = \frac{1}{30}$.

Subcase 5.5.3. $v$ is not adjacent to any bad 3-vertices. Let us consider the worst case where $v$ is adjacent to two 4(2)-vertices and is incident with a 5-face, but not Configuration $C_{1}$ or $C_{2}$. In this case, $\omega'(v)\geq4-4\times1-2\times\frac{13}{30}+\min\{3\times\frac{1}{4}+\frac{1}{5}+\frac{1}{6}, 2\times\frac{1}{4}+3\times\frac{1}{5}, -2\times\frac{1}{12}+4\times\frac{1}{4}+\frac{1}{5}\} = \frac{1}{6}$.

Case 5.6. $n_{2}(v) = 5$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 5$. We consider four subcases.

Subcase 5.6.1. $v_{6}$ is a bad 3-vertex. Let $N(v_{6}) = \{v, x, y\}$ and $d(x) = 2$. According to Lemma 4, we have $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$, and $d(x)+d(y)\geq\Delta+1 = 7$. Thus, $d(y)\geq5$. By Claim 13, $v$ is not incident with a 5-face that is not $C_{1}$ or $C_{2}$.

Suppose $v$ is incident with a Configuration $C_{1}$. If $v$ is incident with at least one $7^{+}$-face, then $\omega'(v)\geq4-5\times1-\frac{19}{30}+2\times\frac{1}{6}+4\times\frac{1}{4}+\frac{2}{6} = \frac{1}{30}$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least one Configuration $A$. So $\omega'(v)\geq4-5\times1-\frac{19}{30}+2\times\frac{1}{6}+2\times\frac{1}{12}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{15}$.

Suppose $v$ is incident with a Configuration $C_{2}$. In this case, $C_{2}$ must be $f_{5}$ (see Fig. 5(1)). If $v$ is incident with at least two $7^{+}$-faces, then $\omega'(v)\geq4-5\times1-\frac{19}{30}+\frac{1}{6}+3\times\frac{1}{4}+2\times\frac{2}{5} = \frac{1}{12}$. If $v$ is incident with one $7^{+}$-face, then $v$ is incident with at least one Configuration $A$. So $\omega'(v)\geq4-5\times1-\frac{19}{30}+\frac{1}{6}+2\times\frac{1}{12}+4\times\frac{1}{4}+\frac{2}{5} = \frac{1}{10}$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least three Configurations $A$. So $\omega'(v)\geq4-5\times1-\frac{19}{30}+\frac{1}{6}+5\times\frac{1}{4}+3\times\frac{1}{6} = \frac{17}{60}$.

Suppose $v$ is not incident with any 5-faces. If $v$ is incident with at least two $7^{+}$-faces, then $\omega'(v)\geq4-5\times1-\frac{19}{30}+\min\{2\times\frac{2}{5}+3\times\frac{1}{4}+\frac{1}{5}, \frac{2}{6}+\frac{2}{5}+4\times\frac{1}{4}\} = \frac{1}{10}$. If $v$ is incident with one $7^{+}$-face, then $v$ is incident with at least one Configuration $A$. So $\omega'(v)\geq4-5\times1-\frac{19}{30}+\frac{2}{5}+4\times\frac{1}{4}+\frac{1}{5}+2\times\frac{1}{12} = \frac{2}{15}$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least three Configurations $A$. So $\omega'(v)\geq4-5\times1-\frac{19}{30}+\frac{1}{5}+5\times\frac{1}{4}+3\times\frac{1}{6} = \frac{19}{60}$.

Subcase 5.6.2. $v_{6}$ is a good 3-vertex. Let $N(v_{6}) = \{v, x, y\}$. According to Lemma 4, we have $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$, and $d(x)+d(y)\geq\Delta+1 = 7$.

If $v$ is not incident with a 5-face, then $\omega'(v)\geq4-5\times1-\frac{1}{3}+4\times\frac{1}{4}+2\times\frac{1}{5} = \frac{1}{15}$.

If $v$ is incident with a Configuration $C_{1}$ or $C_{2}$, then $\omega'(v)\geq4-5\times1-\frac{1}{3}+\min\{2\times\frac{1}{5}+3\times\frac{1}{4}+2\times\frac{1}{6}, \frac{1}{5}+4\times\frac{1}{4}+\frac{1}{6}\} = \frac{1}{30}$.

If $v$ is incident with a 5-face but not Configuration $C_{1}$ or $C_{2}$, then the 5-face must be $f_{5}$ or $f_{6}$ (see Figure 5(2)). If $v$ is incident with at least one $7^{+}$-face, then $\omega'(v)\geq4-5\times1-\frac{1}{3}+\min\{\frac{1}{5}+3\times\frac{1}{4}+\frac{2}{5}, 4\times\frac{1}{4}+\frac{2}{6}\} = 0$. If $v$ is not incident with $7^{+}$-faces, then $f_{1}$ and $f_{2}$, $f_{2}$ and $f_{3}$, and $f_{3}$ and $f_{4}$ form three Configurations $A$. Therefore, $\omega'(v)\geq4-5\times1-\frac{1}{3}+4\times\frac{1}{4}+\frac{1}{5}+3\times\frac{1}{6} = \frac{11}{30}$.

Subcase 5.6.3. $v_{6}$ is a 4(2)-vertex. Let $N(v_{6}) = \{v, x, y, z\}$ and $d(x) = d(y) = 2$. According to Lemma 4, we know that $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$, and $d(z)\geq4$. It is clear that $v$ is not incident with a Configuration $C_{2}$.

If $v$ is not incident with a 5-face, then $\omega'(v)\geq4-5\times1-\frac{13}{30}+5\times\frac{1}{4}+\frac{1}{5} = \frac{1}{60}$.

If $v$ is incident with a Configuration $C_{1}$, then $\omega'(v)\geq4-5\times1-\frac{13}{30}+4\times\frac{1}{4}+\frac{1}{5}+2\times\frac{1}{6} = \frac{1}{10}$.

Suppose $v$ is incident with a 5-face but not Configuration $C_{1}$. Then the 5-face must be $f_{5}$ or $f_{6}$ (see Figure 5(3)). If $v$ is incident with at least two $7^{+}$-faces, $\omega'(v)\geq4-5\times1-\frac{13}{30}+\min\{2\times\frac{1}{4}+\frac{1}{5}+2\times\frac{2}{5}, 3\times\frac{1}{4}+\frac{2}{5}+\frac{2}{6}\} = \frac{1}{20}$. If $v$ is incident with one $7^{+}$-face, then $v$ is incident with at least one Configuration $A$. So $\omega'(v)\geq4-5\times1-\frac{13}{30}+\min\{4\times\frac{1}{4}+\frac{2}{6}+2\times\frac{1}{12}, 3\times\frac{1}{4}+\frac{1}{5}+\frac{2}{5}+2\times\frac{1}{12}\} = \frac{1}{15}$. If $v$ is not incident with $7^{+}$-faces, then $f_{1}$ and $f_{2}$, $f_{2}$ and $f_{3}$, and $f_{3}$ and $f_{4}$ form three Configurations $A$. So $\omega'(v)\geq4-5\times1-\frac{13}{30}+4\times\frac{1}{4}+\frac{1}{5}+3\times\frac{1}{6} = \frac{4}{15}$.

Subcase 5.6.4. $v_{6}$ is not a 3-vertex or a 4(2)-vertex. If $v$ is incident with a Configuration $D$, $v$ receives at least $-\frac{1}{12}+\frac{2}{5} = \frac{19}{60}$ from the configuration. However, if $v$ is incident with a 6-face $f$, $v$ receives at least $\frac{1}{6}$ from $f$. Therefore, in the worst-case scenario, we assume that $v$ is not incident with any Configurations $D$. If $v$ is incident with a Configuration $C_{1}$ or $C_{2}$, then $\omega'(v)\geq4-5\times1-\frac{1}{6}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{30}$. If $v$ is not incident with a Configuration $C_{1}$ or $C_{2}$, then $\omega'(v)\geq4-5\times1+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{5}$.

Case 5.7. $n_{2}(v) = 6$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 6$. By Lemma 4, we have $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 6$.

If $v$ is incident with at least four $7^{+}$-faces, then $\omega'(v)\geq4-6\times1+\min\{4\times\frac{2}{5}+2\times\frac{1}{4}, 4\times\frac{2}{5}+\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{10}$ by R3-1, R3-6, and R3-8.

Suppose $v$ is incident with three $7^{+}$-faces. If at least one of the $7^{+}$-faces is an $8^{+}$-face, then $\omega'(v)\geq4-6\times1+\min\{\frac{3}{6}+2\times\frac{2}{5}+3\times\frac{1}{4}, \frac{3}{6}+2\times\frac{2}{5}+2\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{20}$. Now, let us consider the case where $v$ is exactly incident with three 7-faces. If at least one of the three 7-faces is Configuration $D$, then $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+2\times\frac{1}{12}+\min\{3\times\frac{1}{4}, 2\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{7}{60}$. Assume that none of the three 7-faces is Configuration $D$. If $v$ is incident with a 5-face, then the 5-face must be Configuration $C_{1}$. Hence, $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+2\times\frac{1}{6}+2\times\frac{1}{4} = \frac{1}{30}$. If $v$ is not incident with a 5-face, then $v$ is incident with either six Configurations $B$, or one Configuration $A$ and four Configurations $B$, or two Configurations $A$ and two Configurations $B$. In this case, $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+3\times\frac{1}{4}+4\times\frac{1}{6} = \frac{37}{60}$.

Suppose $v$ is incident with two $7^{+}$-faces. If both of the two $7^{+}$-faces are $8^{+}$-faces, then $\omega'(v)\geq4-6\times1+\min\{2\times\frac{3}{6}+4\times\frac{1}{4}, 2\times\frac{3}{6}+3\times\frac{1}{4}+2\times\frac{1}{6}\} = 0$. If one of the two $7^{+}$-faces is an $8^{+}$-face and the other is Configuration $D$, then $\omega'(v)\geq4-6\times1+\frac{3}{6}+(\frac{2}{5}+2\times\frac{1}{12})+\min\{4\times\frac{1}{4}, 3\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{15}$. If one of the two $7^{+}$-faces is an $8^{+}$-face and the other is not Configuration $D$, then the sum of Configurations $A$ and Configurations $B$ incident with $v$ is at least two. So $\omega'(v)\geq4-6\times1+\frac{3}{6}+\min\{4\times\frac{1}{4}+\frac{2}{5}+2\times\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{6}+\frac{2}{5}+2\times\frac{1}{6}\} = \frac{7}{30}$. If the two $7^{+}$-faces are exactly two 7-faces and at least one of them is Configuration $D$, then $v$ is incident with one Configuration $C_{1}$ or at least two Configurations $A$. So $\omega'(v)\geq4-6\times1+2\times\frac{2}{5}+2\times\frac{1}{12}+\min\{3\times\frac{1}{4}+2\times\frac{1}{6}, 4\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{20}$. If both of the two $7^{+}$-faces are exactly two 7-faces and neither of them is Configuration $D$, then the sum of Configurations $A$ and Configurations $B$ incident with $v$ is at least two. So $\omega'(v)\geq4-6\times1+2\times\frac{2}{5}+\min\{4\times\frac{1}{4}+2\times\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{6}+2\times\frac{1}{6}\} = \frac{2}{15}$.

Suppose $v$ is incident with one $7^{+}$-face. Then $v$ is incident with one Configuration $C_{1}$ and at least two Configurations $A$, or at least four Configurations $A$. So $\omega'(v)\geq4-6\times1+\frac{2}{5}+\min\{4\times\frac{1}{4}+2\times\frac{1}{6}+2\times\frac{1}{6}, 5\times\frac{1}{4}+4\times\frac{1}{6}\} = \frac{1}{15}$.

Suppose $v$ is not incident with $7^{+}$-faces. Then $v$ is incident with one Configuration $C_{1}$ and at least four Configurations $A$, or at least six Configurations $A$. So $\omega'(v)\geq4-6\times1+\min\{5\times\frac{1}{4}+2\times\frac{1}{6}+4\times\frac{1}{6}, 6\times\frac{1}{4}+6\times\frac{1}{6}\} = \frac{1}{4}$.

We now check $\omega'(f)\geq0$ for each $f\in F(G)$.

If $f$ is a 5-face, then $\omega'(f) = d(f)-5 = 0$ since no charge is discharged to or from $f$. If $f$ is a $6^{+}$-face, according to R3-6, $f$ gives away its positive charge, so $\omega'(f) = 0$.

We have verified that $\omega'(x)\geq0$ for all $x\in V(G)\cup F(G)$. This completes the proof when $\Delta = 6$.

3.4.   $\Delta=7$

Claim 14. Let $f_{1} = v_{1}'v_{1}vv_{2}v_{2}'x$, $f_{2} = v_{3}'v_{3}vv_{2}v_{2}'y$ be two $6$-faces. Suppose $d(v) = 6$ and $S_{G}(v) < \Delta+4$. If $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$, then $\max\{d(x), d(y)\}\geq3$ (The configuration composed of $f_{1}$ and $f_{2}$ is called Configuration $E$ of $v$. See $H_{4}$ in Figure 6.)

Proof. By Lemma 4, we conclude that $d(v_{1}') = d(v_{2}') = d(v_{3}') = \Delta$. The subsequent steps of the proof follow a similar approach as presented in Claim 4 of the reference paper ^[8] by Chen et al.

Claim 15. Let $f_{1} = v_{1}'v_{1}vv_{2}v_{2}'x$ be a $6$-face, $f_{2} = v_{3}'v_{3}vv_{2}v_{2}'yz$ be a $7$-face. Suppose $d(v) = 6$ and $S_{G}(v) < \Delta+4$. If $d(v_{1}) = d(v_{2}) = d(v_{3}) = 2$ and $d(z)\leq5$, then $\max\{d(x), d(y)\}\geq3$. (The configuration composed of $f_{1}$ and $f_{2}$ is called Configuration $F$ of $v$. See $H_{5}$ in Figure 6.)

Proof. The proof proceeds by contradiction. Let $G' = G-vv_{1}$. According to Lemma 4, we can deduce that $d(v_{1}') = d(v_{2}') = d(v_{3}') = \Delta$.

Suppose $d(x) = 2$ and $d(y) = 2$. Erase the colors on $v, v_{1}, v_{2}, v_{3}, x, y$. Then we have $|L_{c}'(v)|\geq(\Delta+4)-S_{G}(v)\geq1$, $|L_{c}'(v_{1})|\geq(\Delta+4)-(\Delta+6-2-3) = 3$, $|L_{c}'(v_{2})|\geq(\Delta+4)-(\Delta+6-2-4) = 4$, $|L_{c}'(v_{3})|\geq(\Delta+4)-(\Delta+6-2-2) = 2$, $|L_{c}'(x)|\geq(\Delta+4)-(\Delta+\Delta-2-3) = 9-\Delta = 2$, $|L_{c}'(y)|\geq(\Delta+4)-(\Delta+5-2-2) = 3$. Thus, we can sequentially recolor $v, x, v_{3}, v_{1}, v_{2}, y$ and obtain an injective $L$-coloring of $G$, which leads to a contradiction.

Claim 10 and Claim 13 remain valid in this portion.

We use the following discharging rules.

R4-1. Each 2-vertex receives 1 from each adjacent $3^{+}$-vertex.

R4-2. A bad 3-vertex receives $\frac{2}{3}$ from each adjacent 7-vertex, $\frac{17}{30}$ from each adjacent 6-vertex, $\frac{7}{15}$ from each adjacent 5-vertex.

R4-3. A good 3-vertex receives $\frac{1}{3}$ from each adjacent 7-vertex, $\frac{1}{6}$ from each adjacent 5-, 6-vertex.

R4-4. Suppose $d(v) = 3$. If $S_{G}(v) < \Delta+4$, then $v$ receives $\frac{1}{18}$ from each adjacent 3-, 4-vertex.

R4-5. A 4(2)-vertex receives $\frac{13}{30}$ from each adjacent 7-vertex, $\frac{13}{60}$ from each adjacent 5-, 6-vertex.

R4-6. Each $6^{+}$-face equally distributes its positive charge to each incident $3^{+}$-vertex.

R4-7. In configuration $E$ or $F$, $v$ receives $\frac{1}{12}$ along edge $v_{2}'x$ from $v_{2}'$, and $\frac{1}{12}$ along edge $v_{2}'y$ from $v_{2}'$, for a total of $\frac{1}{6}$ received from $v_{2}'$. (See Figure 7)

R4-8. For a 5-face $f = vv_{1}xyv_{2}$, if $d(v) = 6$, $d(v_{1}) = d(v_{2}) = 2$, $d(x)\geq\Delta-1$ and $d(y)\geq\Delta-1$, we call it configuration $G$ of $v$. In configuration $G$, $v$ receives $\frac{1}{6}$ along edge $xv_{1}$ from $x$, and $\frac{1}{6}$ along edge $yv_{2}$ from $y$, for a total of $\frac{1}{3}$ from $x$ and $y$. (See Figure 7)

R4-9. For a 7-face $f = yv_{2}'v_{2}vv_{3}v_{3}'z$, if $d(v) = 6$, $d(v_{2}) = d(v_{3}) = 2$, $d(v_{2}') = d(v_{3}') = \Delta$ and $d(z)\geq6$, we call it Configuration $H$ of $v$. In Configuration $H$, $v$ receives $\frac{1}{12}$ along edge $zy$ from $z$, and $\frac{1}{12}$ along edge $v_{3}'v_{3}$ from $v_{3}'$, for a total of $\frac{1}{6}$ from $z$ and $v_{3}'$. (See Figure 7)

First, we check $\omega'(v)\geq0$ for each vertex $v\in V(G)$.

Case 1. $d(v) = 2$. We have $\omega(v) = \frac{3}{2}\times2-5 = -2$. By R4-1, $\omega'(v) = -2+1\times2 = 0$.

Case 2. $d(v) = 3$. We have $\omega(v) = \frac{3}{2}\times3-5 = -\frac{1}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}\}$. By Lemma 6(1), $n_{2}(v)\leq1$. If $n_{2}(v) = 1$, let $d(v_{1}) = 2$, then by Lemma 6(2), we have $d(v_{2})+d(v_{3})\geq\Delta+5$. So $\omega'(v)\geq-\frac{1}{2}-1+\min\{\frac{7}{15}+\frac{2}{3}, 2\times\frac{17}{30}\}+\frac{1}{6}+\frac{1}{5} = 0$ by R4-1, R4-2, and R4-6. If $n_{2}(v) = 0$ and $n_{5^{+}}(v) = 0$, then $S_{G}(v) < \Delta+4$. By R4-4 and R4-6, $\omega'(v)\geq-\frac{1}{2}+3\times\frac{1}{18}+2\times\frac{1}{6} = 0$. Suppose $n_{2}(v) = 0$ and $n_{5^{+}}(v)\geq1$. If $v$ is not adjacent to a 3-vertex $u$ with $S_{G}(u) < \Delta+4$, then $\omega'(v)\geq-\frac{1}{2}+\frac{1}{6}+2\times\frac{1}{6} = 0$. If $v$ is adjacent to a 3-vertex $u$ with $S_{G}(u) < \Delta+4$, then by Lemma 4, the sum of degrees of the other two neighbors of $v$ is at least $\Delta+4$. So $\omega'(v)\geq-\frac{1}{2}-\frac{1}{18}+\min\{\frac{1}{3}, 2\times\frac{1}{6}\}+2\times\frac{1}{6} = \frac{1}{9}$.

Case 3. $d(v) = 4$. We have $\omega(v) = \frac{3}{2}\times4-5 = 1$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}\}$. By Lemma 6(1), $n_{2}(v)\leq2$. If $n_{2}(v) = 2$, let $d(v_{1}) = d(v_{2}) = 2$, then by Lemma 6(2), we have $d(v_{3})+d(v_{4})\geq\Delta+4$. So $\omega'(v)\geq1-2\times1+\min\{\frac{13}{30}, 2\times\frac{13}{60}\}+\frac{1}{6}+2\times\frac{1}{5} = 0$ by R4-1, R4-5, and R4-6. If $n_{2}(v)\leq1$, then $\omega'(v)\geq1-1-3\times\frac{1}{18}+3\times\frac{1}{6} = \frac{1}{3}$.

Case 4. $d(v) = 5$. We have $\omega(v) = \frac{3}{2}\times5-5 = \frac{5}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}\}$. By Lemma 6, $n_{2}(v)\leq3$. If $n_{2}(v) = 3$, then by Claim 10, $v$ is not adjacent to a bad 3-vertex or a 4(2)-vertex. Additionally, by Lemma 4, $v$ is adjacent to at most one 3-vertex. Thus, $\omega'(v)\geq\frac{5}{2}-3\times1-\frac{1}{6}+4\times\frac{1}{6} = 0$. If $n_{2}(v) = 2$, then by Lemma 4, we know that $n_{3}(v)\leq2$. Therefore, $\omega'(v)\geq\frac{5}{2}-2\times1-2\times\frac{7}{15}-\frac{13}{60}+4\times\frac{1}{6} = \frac{1}{60}$ by our rules. If $n_{2}(v)\leq1$, then $\omega'(v)\geq\frac{5}{2}-1-4\times\frac{7}{15}+4\times\frac{1}{6} = \frac{3}{10}$.

Case 5. $d(v) = 6$. We have $\omega(v) = \frac{3}{2}\times6-5 = 4$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}\}$. We consider four cases.

Case 5.1. $n_{2}(v)\leq3$. In this case, $\omega'(v)\geq4-3\times1-3\times\frac{17}{30}+5\times\frac{1}{6} = \frac{2}{15}$.

Case 5.2. $n_{2}(v) = 4$. Let $d(v_{1}) = d(v_{2}) = d(v_{3}) = d(v_{4}) = 2$.

If at most one of $v_{5}$ and $v_{6}$ is a bad 3-vertex, then $\omega'(v)\geq4-4\times1-\frac{17}{30}-\frac{13}{60}+5\times\frac{1}{6} = \frac{1}{20}$.

Suppose both $v_{5}$ and $v_{6}$ are bad 3-vertices. By Lemma 4, we know that $d(v_{i}') = \Delta$ for $i = 1, \ldots, 4$. If $v$ is not incident with a 5-face, then $\omega'(v)\geq4-4\times1-2\times\frac{17}{30}+\min\{5\times\frac{1}{4}+\frac{1}{6}, 4\times\frac{1}{4}+2\times\frac{1}{5}\} = \frac{4}{15}$. If $v$ is incident with a Configuration $G$, then $\omega'(v)\geq4-4\times1-2\times\frac{17}{30}+2\times\frac{1}{6}+\min\{4\times\frac{1}{4}+\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{5}\} = \frac{23}{60}$. If $v$ is incident with a 5-face but not Configuration $G$, then $\omega'(v)\geq4-4\times1-2\times\frac{17}{30}+\min\{5\times\frac{1}{4}, 4\times\frac{1}{4}+\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{5}, 4\times\frac{1}{4}+\frac{1}{5}\} = \frac{1}{60}$.

Case 5.3. $n_{2}(v) = 5$, let $d(v_{1}) = d(v_{2}) = d(v_{3}) = d(v_{4}) = d(v_{5}) = 2$.

Subcase 5.3.1. $v_{6}$ is not a 3-vertex or a 4(2)-vertex. Then $v$ may incident with a Configuration $G$ that requires charges from $v$. In this case, we have $\omega'(v)\geq4-5\times1-\frac{1}{6}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{30}$.

Subcase 5.3.2. $v_{6}$ is a bad 3-vertex. Let $N(v_{6}) = \{v, x, y\}$ and $d(x) = 2$. By Lemma 4, we have $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$, and $d(x)+d(y)\geq\Delta+1 = 8$, so $d(y)\geq6$.

Suppose $v$ is incident with a Configuration $G$. If $v$ is incident with at least one $7^{+}$-face, then $\omega'(v)\geq4-5\times1-\frac{17}{30}+2\times\frac{1}{6}+\min\{4\times\frac{1}{4}+\frac{2}{6}, 3\times\frac{1}{4}+\frac{1}{5}+\frac{2}{5}\} = \frac{1}{10}$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least one Configuration $E$. So $\omega'(v)\geq4-5\times1-\frac{17}{30}+2\times\frac{1}{6}+2\times\frac{1}{12}+4\times\frac{1}{4}+\frac{1}{5} = \frac{2}{15}$.

Suppose $v$ is incident with a 5-face but not Configuration $G$. Then the 5-face must be $f_{5}$ by Claim 13 (see Figure 8). If $v$ is incident with at least two $7^{+}$-face and at least one of them is an $8^{+}$-face, then $\omega'(v)\geq4-5\times1-\frac{17}{30}+3\times\frac{1}{4}+\frac{2}{5}+\frac{3}{6} = \frac{1}{12}$. So, assume $v$ is incident with at least two $7$-faces. If at least one of them is Configuration $H$, then $\omega'(v)\geq4-5\times1-\frac{17}{30}+3\times\frac{1}{4}+2\times\frac{2}{5}+2\times\frac{1}{12} = \frac{3}{20}$. If neither of the two $7$-faces is Configuration $H$, then $v$ is incident with at least two Configurations $E$ or $F$. So $\omega'(v)\geq4-5\times1-\frac{17}{30}+3\times\frac{1}{4}+2\times\frac{2}{5}+2\times\frac{1}{6} = \frac{19}{60}$. If $v$ is incident with one $7^{+}$-face, then $v$ is incident with at least one Configuration $E$. So $\omega'(v)\geq4-5\times1-\frac{17}{30}+4\times\frac{1}{4}+\frac{2}{5}+2\times\frac{1}{12} = 0$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least three Configurations $E$. So $\omega'(v)\geq4-5\times1-\frac{17}{30}+5\times\frac{1}{4}+3\times\frac{1}{6} = \frac{11}{60}$.

Suppose $v$ is not incident with any 5-faces. If $v$ is incident with at least one $7^{+}$-face, then $\omega'(v)\geq4-5\times1-\frac{17}{30}+\min\{\frac{2}{6}+5\times\frac{1}{4}, \frac{2}{5}+4\times\frac{1}{4}+\frac{1}{5}\} = \frac{1}{60}$. If $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least three Configurations $E$. So $\omega'(v)\geq4-5\times1-\frac{17}{30}+5\times\frac{1}{4}+\frac{1}{5}+3\times\frac{1}{6} = \frac{23}{60}$.

Subcase 5.3.3. $v_{6}$ is a good 3-vertex. By Lemma 4, $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$.

If $v$ is not incident with a 5-face, then $\omega'(v)\geq4-5\times1-\frac{1}{6}+4\times\frac{1}{4}+2\times\frac{1}{5} = \frac{7}{30}$.

If $v$ is incident with a Configuration $G$, then $\omega'(v)\geq4-5\times1-\frac{1}{6}+2\times\frac{1}{5}+3\times\frac{1}{4}+2\times\frac{1}{6} = \frac{19}{60}$.

If $v$ is incident with a 5-face but not Configuration $G$, then $\omega'(v)\geq4-5\times1-\frac{1}{6}+4\times\frac{1}{4}+\frac{1}{5} = \frac{1}{30}$.

Subcase 5.3.4. $v_{6}$ is a 4(2)-vertex. Let $N(v_{6}) = \{v, x, y, z\}$ and $d(x) = d(y) = 2$. By Lemma 4, $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 5$, and $d(z)\geq5$.

If $v$ is not incident with a 5-face, then $\omega'(v)\geq4-5\times1-\frac{13}{60}+5\times\frac{1}{4}+\frac{1}{5} = \frac{7}{30}$.

If $v$ is incident with a Configuration $G$, then $\omega'(v)\geq4-5\times1-\frac{13}{60}+4\times\frac{1}{4}+\frac{1}{5}+2\times\frac{1}{6} = \frac{19}{60}$.

If $v$ is incident with a 5-face but not Configuration $G$, then if $v$ is incident with at least one $7^{+}$-face, $\omega'(v)\geq4-5\times1-\frac{13}{60}+\min\{3\times\frac{1}{4}+\frac{1}{5}+\frac{2}{5}, 4\times\frac{1}{4}+\frac{2}{6}, 4\times\frac{1}{4}+\frac{2}{5}\} = \frac{7}{60}$; if $v$ is not incident with any $7^{+}$-faces, then $v$ is incident with at least three Configurations $E$. So $\omega'(v)\geq4-5\times1-\frac{13}{60}+4\times\frac{1}{4}+\frac{1}{5}+3\times\frac{1}{6} = \frac{29}{60}$.

Case 5.4. $n_{2}(v) = 6$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 6$. According to Lemma 4, we have $d(v_{_{i}}') = \Delta$ for $i = 1, \ldots, 6$. Therefore, if $v$ is incident with a 5-face, it must be Configuration $G$.

If $v$ is incident with at least four $7^{+}$-faces, then $\omega'(v)\geq4-6\times1+\min\{4\times\frac{2}{5}+2\times\frac{1}{4}, 4\times\frac{2}{5}+\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{10}$.

Suppose $v$ is incident with three $7^{+}$-faces. If at least one of the $7^{+}$-faces is an $8^{+}$-face, then $\omega'(v)\geq4-6\times1+\min\{\frac{3}{6}+2\times\frac{2}{5}+3\times\frac{1}{4}, \frac{3}{6}+2\times\frac{2}{5}+2\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{20}$. So we consider the case where $v$ is exactly incident with three 7-faces. If at least one of the three 7-faces is Configuration $H$, then $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+2\times\frac{1}{12}+\min\{3\times\frac{1}{4}, 2\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{7}{60}$. Now let us assume that none of the three 7-faces is Configuration $H$. If $v$ is incident with a 5-face, then $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+2\times\frac{1}{6}+2\times\frac{1}{4} = \frac{1}{30}$. If $v$ is not incident with a 5-face, then $v$ is incident with either six Configurations $F$, or one Configuration $E$ and four Configurations $F$, or two Configurations $E$ and two Configurations $F$. So $\omega'(v)\geq4-6\times1+3\times\frac{2}{5}+3\times\frac{1}{4}+4\times\frac{1}{6} = \frac{37}{60}$.

Suppose $v$ is incident with two $7^{+}$-faces. If both of the two $7^{+}$-faces are $8^{+}$-faces, then $\omega'(v)\geq4-6\times1+\min\{2\times\frac{3}{6}+4\times\frac{1}{4}, 2\times\frac{3}{6}+3\times\frac{1}{4}+2\times\frac{1}{6}\} = 0$. If one of the two $7^{+}$-faces is an $8^{+}$-face, and the other is Configuration $H$, then $\omega'(v)\geq4-6\times1+\frac{3}{6}+(\frac{2}{5}+2\times\frac{1}{12})+\min\{4\times\frac{1}{4}, 3\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{15}$. If one of the two $7^{+}$-faces is an $8^{+}$-face, and the other is not Configuration $H$, then $v$ is incident with at least two Configurations $F$, or one Configuration $F$ and one Configuration $E$, or two Configurations $E$. Therefore, $\omega'(v)\geq4-6\times1+\frac{3}{6}+\min\{4\times\frac{1}{4}+\frac{2}{5}+2\times\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{6}+\frac{2}{5}+2\times\frac{1}{6}\} = \frac{7}{30}$. If the two $7^{+}$-faces are both 7-faces and at least one of them is Configuration $H$, then $v$ must be incident with one Configuration $G$ or at least two Configurations $E$. Thus, $\omega'(v)\geq4-6\times1+2\times\frac{2}{5}+2\times\frac{1}{12}+\min\{3\times\frac{1}{4}+2\times\frac{1}{6}, 4\times\frac{1}{4}+2\times\frac{1}{6}\} = \frac{1}{20}$. If the two $7^{+}$-faces are both 7-faces and neither of them is Configuration $H$, then $v$ must be incident with at least two Configurations $E$ or two Configurations $F$. Hence, $\omega'(v)\geq4-6\times1+2\times\frac{2}{5}+\min\{4\times\frac{1}{4}+2\times\frac{1}{6}, 3\times\frac{1}{4}+2\times\frac{1}{6}+2\times\frac{1}{6}\} = \frac{2}{15}$.

Suppose $v$ is incident with one $7^{+}$-face. Then $v$ is incident with one Configuration $G$ and at least two Configurations $E$, or at least four Configurations $E$. Hence, $\omega'(v)\geq4-6\times1+\frac{2}{5}+\min\{4\times\frac{1}{4}+2\times\frac{1}{6}+2\times\frac{1}{6}, 5\times\frac{1}{4}+4\times\frac{1}{6}\} = \frac{1}{15}$.

Suppose $v$ is not incident with any $7^{+}$-faces. Then $v$ is incident with one Configuration $G$ and at least four Configurations $E$, or at least six Configurations $E$. Therefore, $\omega'(v)\geq4-6\times1+\min\{5\times\frac{1}{4}+2\times\frac{1}{6}+4\times\frac{1}{6}, 6\times\frac{1}{4}+6\times\frac{1}{6}\} = \frac{1}{4}$.

Case 6. $d(v) = 7$. We have $\omega(v) = \frac{3}{2}\times7-5 = \frac{11}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}\}$.

Case 6.1. $n_{2}(v)\leq3$. There are at most $n_{2}(v)$ Configurations $E$ or $F$ that require charges from $v$. Therefore, we have $\omega'(v)\geq\frac{11}{2}-n_{2}(v)\times1-(d(v)-n_{2}(v))\times\frac{2}{3}-n_{2}(v)\times\frac{1}{6}+6\times\frac{1}{6}\geq\frac{1}{3}$.

Case 6.2. $n_{2}(v) = 4$. There are at most four Configurations $E$ or $F$ that require charges from $v$. Therefore, we have $\omega'(v)\geq\frac{11}{2}-4\times1-3\times\frac{2}{3}-4\times\frac{1}{6}+\min\{2\times\frac{1}{5}+2\times\frac{1}{4}+2\times\frac{1}{6}, 6\times\frac{1}{5}, 4\times\frac{1}{5}+\frac{1}{4}+\frac{1}{6}\} = \frac{1}{30}$.

Case 6.3. $n_{2}(v) = 5$. Let $d(v_{i}) = 2$ for $i = 1, \ldots, 5$. We consider three subcases.

Subcase 6.3.1. Both $v_{6}$ and $v_{7}$ are bad 3-vertices. Let $N(v_{6}) = \{v, x_{1}, y_{1}\}$ and $N(v_{7}) = \{v, x_{2}, y_{2}\}$ where $d(x_{1}) = d(x_{2}) = 2$. By Lemma 4, we have $d(v_{i}')\geq\Delta-1$ for $i = 1, \ldots, 5$, and $d(y_{1})\geq5$, $d(y_{2})\geq5$.

If $v$ is incident with a Configuration $G$, without loss of generality, let us say it is $f_{2}$. Then $v$ is incident with at most three Configurations $E$ (or $F$) to which $v$ needs to send charges (see Figure 9. In (1), $f_{7}$ and $f_{1}$, $f_{4}$ and $f_{5}$ may form two Configurations $E$ or $F$; In (2), $f_{7}$ and $f_{1}$, $f_{3}$ and $f_{4}$, and $f_{5}$ and $f_{6}$ may form three Configurations $E$ or $F$; In (3), $f_{7}$ and $f_{1}$, $f_{4}$ and $f_{5}$, and $f_{5}$ and $f_{6}$ may form three Configurations $E$ or $F$). So we have $\omega'(v)\geq\frac{11}{2}-5\times1-2\times\frac{2}{3}-3\times\frac{1}{6}+2\times\frac{1}{6}+6\times\frac{1}{6} = 0$.

If $v$ is incident with a 5-face, but not Configuration $G$, without loss of generality, let us say it is $f_{6}$. Then $v$ is incident with at most three Configurations $E$ (or $F$) to which $v$ needs to send charges (see Figure 9. In (1), $f_{7}$ and $f_{1}$, $f_{4}$ and $f_{5}$ may form two Configurations $E$ or $F$; in (2), $f_{7}$ and $f_{1}$, $f_{3}$ and $f_{4}$ may form two Configurations $E$ or $F$; in (3), $f_{7}$ and $f_{1}$, $f_{2}$ and $f_{3}$, $f_{4}$ and $f_{5}$ may form three Configurations $E$ or $F$). So, we have $\omega'(v)\geq\frac{11}{2}-5\times1-2\times\frac{2}{3}-3\times\frac{1}{6}+\min\{4\times\frac{1}{4}+2\times\frac{1}{5}, 3\times\frac{1}{4}+3\times\frac{1}{5}\} = \frac{1}{60}$.

If $v$ is not incident with any 5-faces, then $v$ is incident with at most four Configurations $E$ (or $F$) to which $v$ needs to send charges (see Figure 9. In (1), $f_{7}$ and $f_{1}$, $f_{4}$ and $f_{5}$ may form two Configurations $E$ or $F$; in (2), $f_{7}$ and $f_{1}$, $f_{3}$ and $f_{4}$, $f_{5}$ and $f_{6}$ may form three Configurations $E$ or $F$; in (3), $f_{7}$ and $f_{1}$, $f_{2}$ and $f_{3}$, $f_{4}$ and $f_{5}$, $f_{5}$ and $f_{6}$ may form four Configurations $E$ or $F$). So, we have $\omega'(v)\geq\frac{11}{2}-5\times1-2\times\frac{2}{3}-4\times\frac{1}{6}+4\times\frac{1}{4}+3\times\frac{1}{6} = \frac{1}{10}$.

Subcase 6.3.2. One of $v_{6}$ and $v_{7}$ is a bad 3-vertex. If $v$ is incident with a 5-face, as discussed in Subcase 6.3.1, $v$ is incident with at most three Configurations $E$ (or $F$) that require charges from $v$ (see Figure 9). Therefore, $\omega'(v)\geq\frac{11}{2}-5\times1-\frac{2}{3}-\max\{\frac{13}{30}, \frac{1}{3}\}-3\times\frac{1}{6}+\min\{4\times\frac{1}{4}+2\times\frac{1}{5}, 3\times\frac{1}{4}+3\times\frac{1}{5}\} = \frac{1}{4}$. If $v$ is not incident with any 5-faces, as discussed in Subcase 6.3.1, $v$ is incident with at most four Configurations $E$ (or $F$) that require charges from $v$ (see Figure 9). Hence, $\omega'(v)\geq\frac{11}{2}-5\times1-\frac{2}{3}-\max\{\frac{13}{30}, \frac{1}{3}\}-4\times\frac{1}{6}+\min\{4\times\frac{1}{4}+2\times\frac{1}{5}+\frac{1}{6}, 3\times\frac{1}{4}+4\times\frac{1}{5}\} = \frac{17}{60}$.

Subcase 6.3.3. Neither $v_{6}$ nor $v_{7}$ is a bad 3-vertex. If $v$ is incident with a 5-face, then $v$ is incident with at most three Configurations $E$ (or $F$) that require charges from $v$ (see Figure 9). So $\omega'(v)\geq\frac{11}{2}-5\times1-\max\{2\times\frac{13}{30}, \frac{13}{30}+\frac{1}{3}, 2\times\frac{1}{3}\}-3\times\frac{1}{6}+6\times\frac{1}{6} = \frac{2}{15}$. If $v$ is not incident with any 5-faces, then $v$ is incident with at most four Configurations $E$ (or $F$) that require charges from $v$ (see Figure 9). So $\omega'(v)\geq\frac{11}{2}-5\times1-\max\{2\times\frac{13}{30}, \frac{13}{30}+\frac{1}{3}, 2\times\frac{1}{3}\}-4\times\frac{1}{6}+3\times\frac{1}{4}+4\times\frac{1}{6} = \frac{23}{60}$.

Case 6.4. $n_{2}(v) = 6$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 6$.

If $d(v_{7})\geq5$ and $v$ is incident with a Configuration $G$ that requires charges from $v$, then $v$ is incident with at most one Configuration $H$, or one Configuration $E$ (or $F$) that requires charges from $v$. Therefore, $\omega'(v)\geq\frac{11}{2}-6\times1-\frac{1}{6}-\max\{\frac{1}{12}, 2\times\frac{1}{12}\}+5\times\frac{1}{4}+\frac{1}{5} = \frac{37}{60}$.

If $d(v_{7})\geq5$ and $v$ is not incident with a Configuration $G$, then $v$ is incident with at most two Configurations $H$, or two Configurations $E$ (or $F$) that require charges from $v$. Therefore, $\omega'(v)\geq\frac{11}{2}-6\times1-\max\{2\times\frac{1}{12}, 2\times\frac{1}{6}\}+5\times\frac{1}{4}+\frac{1}{5} = \frac{49}{60}$.

Suppose $v_{7}$ is a bad 3-vertex or a 4(2)-vertex. If $v$ is incident with a 5-face but not Configuration $G$, then $v$ is incident with at most one Configuration $E$ (or $F$) that requires charges from $v$. Therefore, we have $\omega'(v)\geq\frac{11}{2}-6\times1-\max\{\frac{2}{3}, \frac{13}{30}\}-\frac{1}{6}+5\times\frac{1}{4}+\frac{1}{5} = \frac{7}{60}$. If $v$ is not incident with a 5-face, then $v$ is incident with at most two Configurations $E$ (or $F$) that require charges from $v$. Therefore, we have $\omega'(v)\geq\frac{11}{2}-6\times1-\max\{\frac{2}{3}, \frac{13}{30}\}-2\times\frac{1}{6}+5\times\frac{1}{4}+2\times\frac{1}{5} = \frac{3}{20}$.

Suppose $v_{7}$ is a good 3-vertex or a 4-vertex (not a 4(2)-vertex). Then $v$ is incident with at most two Configurations $E$ (or $F$) that require charges from $v$. Therefore, we have $\omega'(v)\geq\frac{11}{2}-6\times1-\frac{1}{3}-2\times\frac{1}{6}+4\times\frac{1}{4}+2\times\frac{1}{5} = \frac{7}{30}$.

Case 6.5. $n_{2}(v) = 7$. Then $\omega'(v)\geq\frac{11}{2}-7\times1+6\times\frac{1}{4} = 0$.

We now check $\omega'(f)\geq0$ for each $f\in F(G)$.

If $f$ is a 5-face, then $\omega'(f) = d(f)-5 = 0$ since no charge is discharged to or from $f$. If $f$ is a $6^{+}$-face, according to R4-6, $f$ gives away its positive charge, so $\omega'(f) = 0$.

We have verified that $\omega'(x)\geq0$ for all $x\in V(G)\cup F(G)$. This completes the proof when $\Delta = 7$.

3.5.   $\Delta\geq8$

If $p = uwv$ is a path in $G$ and $d(w) = 2$, we say that $u$ is pseudo-adjacent to $v$ if $uv\not\in E(G)$.

We use the following discharging rules.

R5-1. Each 2-vertex receives 1 from each adjacent $3^{+}$-vertex.

R5-2. Let $v$ be a bad 3-vertex, $uv\in E(G)$. If $d(u)\geq8$, $v$ receives 1 from $u$; if $d(u) = 7$, $v$ receives $\frac{2}{3}$ from $u$; if $d(u) = 6$, $v$ receives $\frac{7}{15}$ from $u$; if $d(u) = 5$, $v$ receives $\frac{2}{15}$ from $u$.

R5-3. Let $v$ be a good 3-vertex, $uv\in E(G)$. If $d(u) = \Delta$, $v$ receives $\frac{2}{9}$ from $u$; if $5\leq d(u)\leq\Delta-1$, $v$ receives $\frac{1}{6}$ from $u$.

R5-4. Let $d(v) = 3$, $uv\in E(G)$. If $S_{G}(v) < \Delta+4$ and $3\leq d(u)\leq4$, then $v$ receives $\frac{1}{18}$ from $u$.

R5-5. Let $v$ be a 4(2)-vertex, $uv\in E(G)$. If $d(u)\geq7$, $v$ receives $\frac{13}{30}$ from $u$; if $d(u) = 6$, $v$ receives $\frac{13}{60}$ from $u$.

R5-6. Each $6^{+}$-face equally distributes its positive charge to each of its incident $3^{+}$-vertices.

R5-7. Each 6-vertex receives $\frac{1}{12}$ from each of its pseudo-adjacent $\Delta$-vertices.

R5-8. Let $f = vv_{1}xyv_{2}$ be a 5-face. If $d(v) = 6$, $d(v_{1}) = d(v_{2}) = 2$, $d(x) = d(y) = \Delta$, $f$ is called configuration $I$ of $v$. In configuration $I$, $v$ receives $\frac{1}{8}$ along edge $xv_{1}$ from $x$, and $\frac{1}{8}$ along edge $yv_{2}$ from $y$, for a total of $\frac{1}{4}$ from $x$ and $y$.

First, we check $\omega'(v)\geq0$ for each vertex $v\in V(G)$.

Case 1. $d(v) = 2$, $\omega(v) = \frac{3}{2}\times2-5 = -2$. By R5-1, $\omega'(v) = -2+1\times2 = 0$.

Case 2. $d(v) = 3$, $\omega(v) = \frac{3}{2}\times3-5 = -\frac{1}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}\}$. By Lemma 6(1), we know that $n_{2}(v)\leq1$. If $n_{2}(v) = 1$, let $d(v_{1}) = 2$. Then, by Lemma 6(2), we have $d(v_{2})+d(v_{3})\geq\Delta+5$. Therefore, $\omega'(v)\geq-\frac{1}{2}-1+\min\{1+\frac{2}{15}, \frac{2}{3}+\frac{7}{15}\}+\frac{1}{6}+\frac{1}{5} = 0$ by R5-1, R5-2, and R5-6. If $n_{2}(v) = 0$ and $n_{5^{+}}(v) = 0$, then $S_{G}(v) < \Delta+4$. By applying R5-4 and R5-6, we can conclude that $\omega'(v)\geq-\frac{1}{2}+3\times\frac{1}{18}+2\times\frac{1}{6} = 0$. Suppose $n_{2}(v) = 0$ and $n_{5^{+}}(v)\geq1$. If $v$ is not incident with a 3-vertex $u$ with $S_{G}(u) < \Delta+4$, then we have $\omega'(v)\geq-\frac{1}{2}+\frac{1}{6}+2\times\frac{1}{6} = 0$. If $v$ is incident with a 3-vertex $u$ with $S_{G}(u) < \Delta+4$, then by Lemma 4, the sum of the degrees of the other two neighbors of $v$ is at least $\Delta+4$. Therefore, $\omega'(v)\geq-\frac{1}{2}-\frac{1}{18}+\min\{\frac{2}{9}, 2\times\frac{1}{6}\}+2\times\frac{1}{6} = 0$.

Case 3. $d(v) = 4$, $\omega(v) = \frac{3}{2}\times4-5 = 1$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}\}$. By Lemma 6(1), we know that $n_{2}(v)\leq2$. If $n_{2}(v) = 2$, let $d(v_{1}) = d(v_{2}) = 2$. Then, by Lemma 6(2), we have $d(v_{3})+d(v_{4})\geq\Delta+4$. Therefore, by using R5-1, R5-5, and R5-6, we can conclude that $\omega'(v)\geq1-2\times1+\min\{\frac{13}{30}, 2\times\frac{13}{60}\}+\frac{1}{6}+2\times\frac{1}{5} = 0$. If $n_{2}(v)\leq1$, then $\omega'(v)\geq1-1-3\times\frac{1}{18}+3\times\frac{1}{6} = \frac{1}{3}$.

Case 4. $d(v) = 5$, $\omega(v) = \frac{3}{2}\times5-5 = \frac{5}{2}$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}\}$. According to Lemma 6, we know that $n_{2}(v)\leq3$. If $n_{2}(v) = 3$, using Lemma 4, it follows that $v$ is adjacent to at most one 3-vertex. Therefore, $\omega'(v)\geq\frac{5}{2}-3\times1-\max\{\frac{2}{15}, \frac{1}{6}\}+4\times\frac{1}{6} = 0$. If $n_{2}(v) = 2$, then by Lemma 4, we have $n_{3}(v)\leq2$. So $\omega'(v)\geq\frac{5}{2}-2\times1-\max\{2\times\frac{1}{6}, 2\times\frac{2}{15}, \frac{1}{6}+\frac{2}{15}\}+4\times\frac{1}{6} = \frac{5}{6}$. If $n_{2}(v)\leq1$, then $\omega'(v)\geq\frac{5}{2}-1-4\times\frac{1}{6}+4\times\frac{1}{6} = \frac{3}{2}$.

Case 5. $d(v) = 6$, $\omega(v) = \frac{3}{2}\times6-5 = 4$. Let $N(v) = \{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}\}$. We consider four cases.

Case 5.1. $n_{2}(v)\leq3$. In this case, $\omega'(v)\geq4-3\times1-3\times\frac{7}{15}+5\times\frac{1}{6} = \frac{13}{30}$.

Case 5.2. $n_{2}(v) = 4$. We then have $\omega'(v)\geq4-4\times1-2\times\frac{7}{15}+\min\{\frac{1}{4}+4\times\frac{1}{5}, 2\times\frac{1}{4}+2\times\frac{1}{5}+\frac{1}{6}\} = \frac{7}{60}$.

Case 5.3. $n_{2}(v) = 5$. Let $d(v_{1}) = d(v_{2}) = d(v_{3}) = d(v_{4}) = d(v_{5}) = 2$. If $d(v_{6})\geq5$, then $\omega'(v)\geq4-5\times1+3\times\frac{1}{4}+2\times\frac{1}{5} = \frac{3}{20}$. If $d(v_{6})\leq4$, then by Lemma 4, we have $d(v_{i}') = \Delta$, $i = 1, \ldots, 5$. Therefore, $\omega'(v)\geq4-5\times1-\frac{7}{15}+3\times\frac{1}{4}+2\times\frac{1}{5}+5\times\frac{1}{12} = \frac{1}{10}$ by R5-1, R5-2, R5-3, R5-5, R5-6, and R5-7.

Case 5.4. $n_{2}(v) = 6$. Let $d(v_{i}) = 2$, $i = 1, \ldots, 6$. By Lemma 4, we have $d(v_{i}') = \Delta$, $i = 1, \ldots, 6$. If $v$ is incident with a 5-face, it must be Configuration $I$. Therefore, $\omega'(v)\geq4-6\times1+5\times\frac{1}{4}+\frac{1}{4}+6\times\frac{1}{12} = 0$ by R5-1, R5-6, R5-7 and R5-8.

Case 6. $d(v) = 7$, $\omega(v) = \frac{3}{2}\times7-5 = \frac{11}{2}$.

If $n_{2}(v)\leq5$, then $\omega'(v)\geq\frac{11}{2}-5\times1-2\times\frac{2}{3}+6\times\frac{1}{6} = \frac{1}{6}$.

If $n_{2}(v) = 6$, then $\omega'(v)\geq\frac{11}{2}-6\times1-\frac{2}{3}+4\times\frac{1}{4}+2\times\frac{1}{5} = \frac{7}{30}$.

If $n_{2}(v) = 7$, then $\omega'(v)\geq\frac{11}{2}-7\times1+6\times\frac{1}{4} = 0$.

Case 7. $d(v) = 8$, $\omega(v) = \frac{3}{2}\times8-5 = 7$.

Note that the worst case is that $v$ is adjacent to $t$ 2-vertices and $(8-t)$ bad 3-vertices.

If $t = 8$, then $\omega'(v)\geq7-8\times1-8\times\frac{1}{12}+7\times\frac{1}{4} = \frac{1}{12}$ by R5-1, R5-6 and R5-7.

If $t = 7$, then $\omega'(v)\geq7-8\times1-7\times\frac{1}{12}+5\times\frac{1}{4}+2\times\frac{1}{5} = \frac{1}{15}$ by R5-1, R5-2, R5-3, R5-5, R5-6, and R5-7.

If $t = 6$, then $\omega'(v)\geq7-8\times1-6\times\frac{1}{12}+\min\{4\times\frac{1}{4}+2\times\frac{1}{5}+\frac{1}{6}, 3\times\frac{1}{4}+4\times\frac{1}{5}\} = \frac{1}{15}$.

If $t = 5$, then $\omega'(v)\geq7-8\times1-5\times\frac{1}{12}+\min\{3\times\frac{1}{4}+2\times\frac{1}{5}+2\times\frac{1}{6}, 2\times\frac{1}{4}+4\times\frac{1}{5}+\frac{1}{6}, \frac{1}{4}+6\times\frac{1}{5}\} = \frac{1}{30}$.

If $t = 4$, then $\omega'(v)\geq7-8\times1-4\times\frac{1}{12}+\min\{7\times\frac{1}{5}, 2\times\frac{1}{4}+2\times\frac{1}{5}+3\times\frac{1}{6}, \frac{1}{4}+4\times\frac{1}{5}+2\times\frac{1}{6}, \frac{1}{6}+6\times\frac{1}{5}\} = \frac{7}{10}$.

If $t = 3$, then $\omega'(v)\geq7-8\times1-3\times\frac{1}{12}+\min\{\frac{1}{4}+2\times\frac{1}{5}+4\times\frac{1}{6}, 4\times\frac{1}{5}+3\times\frac{1}{6}, 2\times\frac{1}{6}+5\times\frac{1}{5}\} = \frac{1}{20}$.

If $t\leq2$, then $\omega'(v)\geq7-8\times1-2\times\frac{1}{12}+7\times\frac{1}{6} = 0$.

Case 8. $d(v)\geq9$.

If $n_{2}(v) = d(v)$, then $\omega'(v)\geq\frac{3}{2}d(v)-5-d(v)\times1-\frac{1}{12}n_{2}(v)+\frac{1}{4}(d(v)-1) = \frac{2}{3}d(v)-\frac{21}{4} > 0$.

If $n_{2}(v) = d(v)-1$, then $\omega'(v)\geq\frac{3}{2}d(v)-5-d(v)\times1-\frac{1}{12}n_{2}(v)+\frac{1}{4}(d(v)-3)+2\times\frac{1}{5} = \frac{2}{3}d(v)-\frac{79}{15} > 0$.

If $n_{2}(v) = d(v)-2$, then $\omega'(v)\geq\frac{3}{2}d(v)-5-d(v)\times1-\frac{1}{12}n_{2}(v)+\min\{\frac{1}{4}(d(v)-4)+2\times\frac{1}{5}+\frac{1}{6}, \frac{1}{4}(d(v)-5)+4\times\frac{1}{5}\} = \frac{2}{3}d(v)-\frac{79}{15} > 0$.

If $n_{2}(v)\leq d(v)-3$, then $\omega'(v)\geq\frac{3}{2}d(v)-5-d(v)\times1-\frac{1}{12}n_{2}(v)+\frac{1}{6}(d(v)-1) = \frac{7}{12}d(v)-\frac{59}{12} > 0$.

We now check $\omega'(f)\geq0$ for each $f\in F(G)$.

If $f$ is a 5-face, then $\omega'(f) = d(f)-5 = 0$ since no charge is discharged to or from $f$. If $f$ is a $6^{+}$-face, according to R5-6, $f$ gives away its positive charge, so $\omega'(f) = 0$.

We have checked $\omega'(x)\geq0$ for all $x\in V(G)\cup F(G)$. This completes the proof when $\Delta\geq8$, and hence the proof of the whole Theorem 2.

4.   Conclusions

In this paper, we consider the list injective chromatic index of planar graphs without intersecting 5-cycles and proved that such graphs have $\chi_{i}^{l}(G)\leq\Delta+4$ if $g(G)\geq5$. Based on the result of Theorem 2, the following question is meaningful, namely: for a planar graph $G$ with $g(G)\geq5$, explore the upper bound of $\chi_{i}^{l}(G)$ when $G$ has no adjacent 5-cycles.

Use of Generative-AI tools declaration

The authors declare that no Artificial Intelligence was used.

Author contributions

Hongyu Chen devised the project, the main ideas, proof outline, and wrote the manuscript. Li Zhang verified the results and polished the paper.

Acknowledgments

This work was supported by National Natural Science Foundations of China (Grant No.11401386)

Conflict of interest

The authors declare no conflicts of interest.