Acyclic edge coloring of planar graphs

1.   Introduction

All graphs considered in this paper are finite simple graphs. For a graph $G$, we use $V(G)$, $E(G)$, $F(G)$, $\Delta(G)$ ($\Delta$ for short and reserved), and $g(G)$ to denote the vertex set, edge set, face set, maximum degree and girth, respectively. A graph $G$ is $2$-connected if there are two paths between any two distinct vertices.

Let $G$ be a planar graph. The acyclic edge $k$-coloring of graph $G$ is a mapping $c:E(G)\rightarrow \{1, 2, \ldots, k\}$ such that any two adjacent edges receive different colors, and there are no bichromatic cycles in $G$. The acyclic chromatic index of $G$, denoted by $\chi^{'}_{a}(G)$, is the smallest integer $k$ such that $G$ is acyclically edge $k$-colorable.

Fiam$\check{c}$ik posed a famous conjecture for acyclic edge coloring of any graphs.

Conjecture 1.1. ^[3] For any graph $G$, $\chi^{'}_{a}(G)\leq\Delta(G)+2$.

The conjecture is still open.

For any graph $G$, Alon, McDiarmid and Reed ^[1] proved that $\chi^{'}_{a}(G)\leq64\Delta$. Molloy and Reed ^[8] improved this bound to $16\Delta$. Later, Fialho et al. ^[4] showed that $\chi^{'}_{a}(G)\leq3.569(\Delta-1)$, and most recently to $2\Delta-1$ by Kirousis and Livieratos ^[7].

There have been numerous investigations about acyclic edge coloring of planar graphs.

For any planar graph $G$, Basavaraju et al. ^[2] proved that $\chi^{'}_{a}(G)\leq\Delta+12$, Wang et al. ^[9] proved that $\chi^{'}_{a}(G)\leq\Delta+7$, Wang and Zhang ^[10] proved that $\chi^{'}_{a}(G)\leq\Delta+6$.

Let $G$ be a planar graph with small grith. Shu, Wang and Wang ^[11] proved that $\chi^{'}_{a}(G)\leq\Delta(G)+2$ if $g(G)\geq4$. For planar graph $G$ with $g(G)\geq5$, Hou et al.^[6] proved that $\chi^{'}_{a}(G)\leq\Delta(G)+1$; they also proved that such graph has $\chi^{'}_{a}(G) = \Delta(G)$ if $\Delta(G)\geq9$. For planar graph $G$ without $4$-cycles, Wang and Sheng ^[13] proved that $\chi^{'}_{a}(G)\leq\Delta(G)+3$. Then Wang, Shu and Wang ^[14] improved this bound to $\Delta(G)+2$ when $\Delta(G)\geq5$. In 2012, Fiedorowicz ^[5] proved that the planar graph $G$ without an $i$-cycle intersect to a $j$-cycle has $\chi^{'}_{a}(G)\leq\Delta(G)+2$ for $i, j\in\{3, 4\}$. Most recently, Shu et al. ^[12] proved that the planar graph $G$ without intersecting triangles has $\chi^{'}_{a}(G)\leq\Delta(G)+2$.

In this paper, we consider the planar graph without 3-cycles and intersecting 4-cycles, and prove the following theorem:

Theorem 1.1. Let $G$ be a planar graph without 3-cycles and intersecting 4-cycles. If $\Delta(G)\geq8$, then $\chi^{'}_{a}(G)\leq\Delta(G)+1$.

2.   Notation

Let $G$ be a simple planar graph. For a vertex $v\in V(G)$, $N(v)$ denotes the set of vertices adjacent to $v$, and $d(v) = |N(v)|$ denotes the degree of $v$. For $f\in F(G)$, we use $b(f)$ to denote the boundary walk of $f$ and write $f = [u_{1}u_{2} \ldots u_{n}]$ if $u_{1}, u_{2}, \ldots, u_{n}$ are the vertices on $b(f)$ enumerated in the clockwise direction. For $f = [u_{1}u_{2} \ldots u_{n}]$, let $\delta(f)$ denote the minimum degree of any vertex on $b(f)$. That is, $\delta(f) = \min\{d(u_{i}), i = 1, \ldots, n\}$. The degree of a face $f$, denoted by $d(f)$, is the number of edges in its boundary walk.

For $f\in F(G)$, $f$ is called a $k$-(or $k^{+}$-, or $k^{-}$-) face if $d(f) = k$ (or $d(f)\geq k$, or $d(f)\leq k$). For $v\in V(G)$, $v$ is called a $k$-(or $k^+$-, or $k^-$-) vertex if $d(v) = k$ (or $d(v)\geq k$, or $d(v)\leq k$). If $u\in N(v)$ and $d(u) = k$, then $u$ is called $k$-neighbor of $v$. Let $N_{k}(v) = \{x\in N(v)|d(x) = k\}$, and $n_{k}(v) = |N_{k}(v)|$.

Let $c$ be an edge coloring of $G$ and $v$ be a vertex of $G$. Then, $C(v) = \{c(uv):u\in N(v)\}$, $F_{v}^{c}(uv) = C(v)\setminus\{c(uv)\}$. Let $\alpha, \beta$ be two colors. An $(\alpha, \beta)$-bichromatic path with respect to $c$ is a path consisting of edges that are colored with $\alpha$ and $\beta$ alternately. An $(\alpha, \beta)$-bichromatic path which starts at the vertex $u$ via an edge colored $\alpha$ and ends at $v$ via an edge colored $\alpha$ is an $(\alpha, \beta)_{(u, v)}$-bichromatic path. We use "w.l.o.g." as a shorthand for "without loss of generality".

3.   Proof of Theorem 1.1

We apply a discharging procedure to prove Theorem 1.1. Discharging is a tool in a two-pronged approach to inductive proofs. It can be viewed as an amortized counting argument used to prove that a global hypothesis guarantees the existence of some desirable local configurations. In an application of the resulting structure theorem, one shows that each such local configuration cannot occur in a minimal counterexample to the desired conclusion. Such local configurations are called reducible configurations. In this section, we give some reducible configurations.

Let $G$ be a counterexample with minimum $|V(G)|+|E(G)|$ of Theorem 1.1. In other words, $G$ is a connected simple planar graph without $3$-cycles and intersecting $4$-cycles, $\Delta = \Delta(G)\geq8$, but $\chi^{'}_{a}(G)\geq\Delta+2$. Let $C$ be a color set of $G$, $C = \{1, 2, \ldots, \Delta+1\}$. Now, we discuss the structures of $G$.

3.1.   The properties of minimal counterexample

Lemma 3.1. The graph $G$ is $2$-connected.

Proof. By contradiction, suppose that $v$ is a cut vertex of $G$. Let $C_{1}, C_{2}, \ldots, C_{t}(t\geq2)$ be the connected components of $G\setminus v$. For each $1 \leq i\leq t$, there is an acyclic $(\Delta+1)$-edge coloring $c_{i}$ of $G_{i} = C_{i}\cup\{v\}$. We can adjust the colors in each $c_{i}$ such that the colors appearing on the edges incident with $v$ are all distinct. Now the union of these colorings is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Lemma 3.2. The graph $G$ does not contain a $2$-vertex adjacent to a $3^{-}$-vertex.

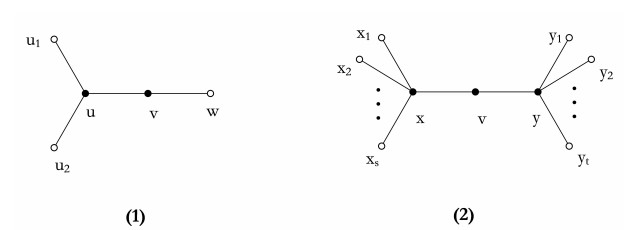
Proof. By contradiction, let $d(v) = 2, \; N(v) = \{u, w\}$, $d(u)\leq3$ (See Figure 1(1)). We prove the case $d(u) = 3$, and $d(u) = 2$ can be proved in a similar way. Let $N(u) = \{v, u_{1}, u_{2}\}$, $G^{'} = G-uv$. By the minimality of $G$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Suppose that $c(uu_{i}) = i$ for $i = 1, 2$.

We consider the following two cases.

Case 3.1. $|C(u)\cap C(v)| = 0$.

Since $|C\setminus (C(u)\cup C(v))| = \Delta+1-3 = \Delta-2 > 0$, we can color $uv$ with $\alpha$ for $\alpha\in C\setminus (C(u)\cup C(v))$. Therefore, $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.2. $|C(u)\cap C(v)| = 1$.W.l.o.g., assume that $c(vw) = c(uu_{1}) = 1$. If there exists a color $\gamma\in\{3, \ldots, \Delta+1\}$ such that $G$ contains no $(1, \gamma)_{(u, v)}$-bichromatic path via $u_{1}$ and $w$, then we can color $uv$ with $\gamma$. In this way $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. Thus, there must exist a $(1, \alpha)_{(u, v)}$-bichromatic path via $u_{1}$ and $w$ for each $\alpha\in\{3, 4, \ldots, \Delta+1\}$. So $C(u_{1}) = C(w) = \{1, 3, 4, \ldots, \Delta+1\}$. Now we recolor $vw$ with 2. Similarly, there must exist a $(2, \alpha)_{(u, v)}$-bichromatic path via $u_{2}$ and $w$ for each $\alpha\in\{3, 4, \ldots, \Delta+1\}$. So $C(u_{2}) = \{2, 3, 4, \ldots, \Delta+1\}$. Now we exchange the colors between $uu_{1}$ and $uu_{2}$, color $uv$ with 3, color $vw$ with 1. Therefore, $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Next we discuss the degree sum of the neighbors of a particular vertex.

Lemma 3.3. Let $d(v) = k\in\{2, 3\}$ and $N(v) = \{v_{i}, 1\leq i\leq k\}$. Then $\sum_{i = 1}^{k}d(v_i)\geq \Delta+k+1$.

Proof. By contradiction, assume that $\sum_{i = 1}^{k}d(v_i)\leq \Delta+k$. Let $G^{'} = G-vv_{1}$, by the minimality of $G$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Since the neighbors of each 2-vertex are both $4^{+}$-vertices, we have $3\leq d(v_{i})\leq\Delta+k-6$ when $1\leq i\leq 3$ and $k = 3$. Suppose that $c(vv_{i}) = i-1$ for $i = 2, \ldots, k$. We consider the following three cases.

Case 3.3. $|C(v_{1})\cap C(v)| = 0$.

Since $|C\setminus (C(v_{1})\cup C(v))| = \Delta+1-(d(v_{1})-1)-(d(v)-1) = \Delta+3-d(v_{1})-d(v)\geq\Delta-d(v_{1}) > 0$, we can color $vv_{1}$ with $\alpha$ for $\alpha\in C\setminus (C(v_{1})\cup C(v))$. Therefore, $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.4. $|C(v_{1})\cap C(v)| = 1$. W.l.o.g., assume that $1\in C(v_{1})$.

(i) $k = 2$.

Since $|C\setminus (C(v_{1})\cup C(v_{2}))|\geq\Delta+1-(d(v_{1})-1)-(d(v_{2})-1) =$$\Delta+3-(d(v_{1})+d(v_{2}))\geq\Delta+3-(\Delta+2) = 1$, we can color $vv_{1}$ with $\beta$ for $\beta\in C\setminus (C(v_{1})\cup C(v_{2}))$.Therefore, $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

(ii) $k = 3$.

Since $|C\setminus (C(v_{1})\cup C(v)\cup C(v_{2}))|\geq\Delta+1-(d(v_{1})-1)-1-(d(v_{2})-1)$$= \Delta-(d(v_{1})+d(v_{2}))+2\geq\Delta-\Delta+2 = 2$, we can color $vv_{1}$ with $\alpha$ for $\alpha\in C\setminus(C(v_{1})\cup C(v)\cup C(v_{2}))$, $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.5. $|C(v_{1})\cap C(v)| = 2$. Namely, $d(v) = k = 3$.

Since $|C\setminus (C(v_{1})\cup C(v_{2})\cup C(v_{3}))|\geq$$\Delta+1-(d(v_{1})-1)-(d(v_{2})-1)-(d(v_{3})-1)$$= \Delta-(d(v_{1})+d(v_{2})+d(v_{3}))+4\geq1$, we can color $vv_{1}$ with $\alpha$ for $\alpha\in C\setminus(C(v_{1})\cup C(v_{2})\cup C(v_{3}))$, $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

For a 2-vertex, the number of $3^{-}$-vertex and $\Delta$-vertex of its neighbors is discussed below.

Lemma 3.4. For a 2-vertex $v$, let $N(v) = \{x, y\}$. Then (1) $n_{2}(x)\leq d(x)+d(y)-\Delta-2$; (2) $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-1$; (3) $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2$ if $d(x) < \Delta$.

Proof. Assume that $d(x) = s+1, \; d(y) = t+1, \; N(x) = \{v, x_{1}, x_{2}, \ldots, x_{s}\}, \; N(y) = \{v, y_{1}, y_{2}, \ldots, y_{t}\}$ (See Figure 1(2)). Let $G^{'} = G-vy$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Let $c(yy_{i}) = i$ for $1\leq i\leq t, \; T = C\setminus F_{x}^{c}(vx)$. It is clear that $|T| = \Delta+1-s\geq2$.

If $T\setminus F_{y}^{c}(vy)\neq\emptyset$, then we can recolor $vx$ with $\alpha$ for $\alpha\in T\setminus F_{y}^{c}(vy)$, color $vy$ with $\beta$ for $\beta\in \{t+1, \ldots, \Delta+1\}$($\beta\neq\alpha$). Now $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction. So $T\subseteq F_{y}^{c}(vy) = \{1, 2, \ldots, t\}$.

If there are $i_{0}\in T$ and $j_{0}\in\{t+1, \ldots, \Delta+1\}$, such that $G$ contains no $(i_{0}, j_{0})_{(v, y)}$-bichromatic path through $x$, then we can color $vx$ with $i_{0}$, color $vy$ with $j_{0}$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. So $G$ contains $(\alpha_{0}, j)_{(v, y)}$-bichromatic path for $c(vx) = \alpha_{0}, \alpha_{0}\in T$ and $j\in\{t+1, \ldots, \Delta+1\}$. This means that $\{t+1, \ldots, \Delta+1\}\subseteq F_{x}^{c}(vx)$. W.l.o.g., let $c(xx_{i}) = t+i$ for $1\leq i \leq \Delta+1-t$. Now recolor $c(vx) = i$ for any $i\in T$. Similarly, $G$ contains $(i, j)_{(v, y)}$-bichromatic path for any $j\in\{t+1, \ldots, \Delta+1\}$. So $T \subseteq F_{x_{l}}^{c}(xx_{l})$, which means that $d(x_{l})\geq |T|+1$ for $1\leq l \leq \Delta+1-t$.

(1) Since $d(x)\leq\Delta$, $|T| = \Delta+1-s = \Delta+1-(d(x)-1) = \Delta-d(x)+2\geq2$. This means that $d(x_{i})\geq3$ for $1\leq i \leq \Delta+1-t$. Therefore, $n_{2}(x)\leq d(x)-(\Delta+1-t) = d(x)-\Delta-1+d(y)-1 = d(x)+d(y)-\Delta-2$.

(2) If there are at least two 3-vertices in $\{x_{1}, \ldots, x_{\Delta+1-t}\}$, then assume that $d(x_{1}) = d(x_{2}) = 3$. Since $T \subseteq F_{x_{l}}^{c}(xx_{l})$($1\leq l \leq \Delta+1-t$), and $d(x_{1}) = d(x_{2}) = 3$, we have $T = \{1, 2\}$. So $F_{x_{1}}^{c}(xx_{1}) = F_{x_{2}}^{c}(xx_{2}) = \{1, 2\}$. Now we exchange the colors between $xx_{1}$ and $xx_{2}$, color $vx$ with 1, color $vy$ with $t+1$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. Therefore, $n_{2}(x)+n_{3}(x)\leq d(x)-(\Delta+1-t)+1 = d(x)+d(y)-\Delta-1$.

(3) If $d(x) < \Delta$, then $|T| = \Delta+1-s = \Delta+1-(d(x)-1) = \Delta-d(x)+2\geq3$. This implies that $d(x_{l})\geq|T|+1\geq4$ for $1\leq l \leq\Delta+1-t$. Therefore, $n_{2}(x)+n_{3}(x)\leq d(x)-(\Delta+1-t) = d(x)-\Delta-1+d(y)-1 = d(x)+d(y)-\Delta-2$.

Lemma 3.5. For 2-vertex $v$, let $N(v) = \{x, y\}$. If $n_{2}(x) = d(x)-2$, then $n_{\Delta}(x) = 2$, $n_{2}(y) = 1$, $n_{3}(y)\leq1$, $d(y) = \Delta$.

Proof. Let $N(x) = \{v, x_{1}, x_{2}, \ldots, x_{s}\}, N(y) = \{v, y_{1}, y_{2}, \ldots, y_{t}\}$, $d(x_{i}) = 2$, $N(x_{i}) = \{x, x_{i}^{'}\}$ for $3\leq i\leq s$ (See Figure 2(3)). Observe that $n_{2}(x)\leq d(x)+d(y)-\Delta-2$ by Lemma 3.4. If $n_{2}(x) = d(x)-2$, then $d(y) = \Delta$, which means that $t = \Delta-1$. Let $G^{'} = G-xv$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Suppose that $c(xx_{i}) = i$ for $1\leq i\leq s, \; T = C\setminus F_{y}^{c}(vy)$. It is clear that $|T| = \Delta+1-(d(y)-1) = 2$.

(1) $n_{\Delta}(x) = 2, n_{2}(y) = 1$.

We consider the following two cases.

Case 3.6. $T\setminus F_{x}^{c}(vx)\neq\emptyset$.

We can recolor $vy$ with $\alpha$ for $\alpha\in T\setminus F_{x}^{c}(vx)$, color $vx$ with $\beta$ for $\beta\in\{s+1, \ldots, \Delta+1\}$($\beta\neq\alpha$). Now $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.7. $T\setminus F_{x}^{c}(vx) = \emptyset$.

That is, $T\subseteq F_{x}^{c}(vx) = \{1, 2, \ldots, s\}$.

(i) $T\cap\{3, \ldots, s\}\neq\emptyset$.

Let $\alpha\in T\cap\{3, \ldots, s\}$. Since $|C\setminus(C(x)\cup C(x_{\alpha}))|\geq\Delta+1-(d(x)-1)-1 = \Delta+1-d(x)\geq1$, we can color $vy$ with $\alpha$, color $vx$ with $\beta$ for $\beta\in C\setminus(C(x)\cup C(x_{\alpha}))$, $c$ can be extended to be an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

(ii) $T\cap\{3, \ldots, s\} = \emptyset$.

That is, $T$ = $\{1, 2\}$ and $F_{y}^{c}(vy)$ = $\{3, 4, \ldots, \Delta+1\}$. Note that $c(vy)\in\{1, 2\}$, w.l.o.g., suppose that $c(vy)$ = $1$. If there is a color $\gamma\in\{s+1, \ldots, \Delta+1\}$ such that $G$ contains no $(1, \gamma)_{(x, v)}$-bichromatic path via $x_{1}$ and $y$, then we can color $vx$ with $\gamma$. In this way $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. So there must exist a $(1, j)_{(x, v)}$-bichromatic path via $x_{1}$ and $y$ for each $j(j\in\{s+1, \ldots, \Delta+1\}$), which implies that $\{s+1, \ldots, \Delta+1\}\subseteq C(x_{1})\cap C(y)$. Now we recolor $vy$ with 2, and don't change the colors of the other edges, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-xv$. As the same argument above, we have that $\{s+1, \ldots, \Delta+1\}\subseteq C(x_{2})$. If there is $i\in\{3, 4, \ldots, s\}$, such that $G$ contains no $(1, i)_{(x, v)}$-bichromatic path via $x_{1}$ and $y$, then we can color $vx$ with $i$. Don't change the colors of the other edges, and remove the color of $xx_{i}$, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-xx_{i}$, now we consider the color of $xx_{i}$. W.l.o.g., assume that $i = 3$.

If $c(x_{3}x_{3}^{'}) = j\geq s+1$, then $|C(x)\cup C(x_{3})|\leq s+1 = d(x)\leq\Delta$, we can color $xx_{3}$ with $\alpha$ for $\alpha\notin(C(x)\cup C(x_{3}))$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

If $c(x_{3}x_{3}^{'}) = j\in\{1, 2\}$, then it can be seen from the above argument that for each $\alpha\in\{s+1, \ldots, \Delta+1\}$, there are $(i, \alpha)_{(x, v)}$-bichromatic paths $(i = 1, 2)$. So $G-xx_{3}$ contains no $(i, \alpha)_{(x, x_{3})}$-bichromatic path $(i = 1, 2)$ for each $\alpha\in\{s+1, \ldots, \Delta+1\}$, we can color $xx_{3}$ with $\alpha$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

If $c(x_{3}x_{3}^{'}) = j = 3$, then we can color $xx_{3}$ with $\alpha$ for $\alpha\notin(C(x)\cup C(v))$ since $|C(x)\cup C(v)|\leq s+1 = d(x) < \Delta+1$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

If $c(x_{3}x_{3}^{'}) = j\in\{4, \ldots, s\}$, then we can recolor $xx_{3}$ with $\alpha$ for $\alpha\notin(C(x)\cup C(x_{j}))$ since $|C(x)\cup C(x_{j})|\leq s+1 = d(x) < \Delta+1$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. Hence, there are $(1, i)_{(x, v)}$-bichromatic paths via $x_{1}$ and $y$ for each $i\in\{3, 4, \ldots, s\}$, which implies that $\{1, 3, 4, \ldots, s\}\subseteq C(x_{1})$.

In conclusion, $C(x_{1}) = C(y) = \{1, 3, 4, \ldots, \Delta+1\}$. Now recolor $vy$ with 2, and don't change the colors of the other edges, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-xv$. As the same argument above, we have that $C(x_{2}) = \{2, 3, 4, \ldots, \Delta+1\}$. It follows that $F_{x_{1}}^{c}(xx_{1}) = F_{x_{2}}^{c}(xx_{2}) = F_{y}^{c}(vy) = \{3, 4, \ldots, \Delta+1\}$ and $\{1, 2\}\subseteq F_{y_{i}}^{c}(yy_{i})$ for $1\leq i\leq t$. Then $d(x_{1}) = d(x_{2}) = \Delta+1-2+1 = \Delta, \; n_{2}(y) = 1$.

(2) $n_{3}(y)\leq1$.

By contradiction, assume that $d(y_{1}) = d(y_{2}) = 3$. Now exchange the colors between $yy_{1}$ and $yy_{2}$, and don't change the colors of the other edges, $G-xv$ has a new acyclic $(\Delta+1)$-edge coloring $\phi$. Let $\phi(yy_{1}) = \alpha$.

If $\alpha\in\{s+1, \dots, \Delta+1\}$, then let $\phi(xv) = \alpha$. By symmetry, suppose that $\phi(vy) = 1$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

If $\alpha\in\{3, 4, \ldots, s\}$, assume that $\alpha = 3$, then let $\phi(xv) = 3$, remove the color of $xx_{3}$, $G-xx_{3}$ admits an acyclic $(\Delta+1)$-edge coloring $\phi^{'}$. Let $\phi^{'}(x_{3}x_{3}^{'}) = \beta$. It follows from the above argument that there is a $(1, \Delta)_{(x, v)}$-bichromatic path through $x_{1}$, so $G-xx_{3}$ contains no $(1, \Delta)_{(x, x_{3})}$-bichromatic path via $x_{1}$ and $\; x_{3}^{'}$. Similarly, $G-xx_{3}$ contains no $(2, \Delta)_{(x, x_{3})}$-bichromatic path via $x_{2}$ and $\; x_{3}^{'}$. If $\beta\in\{1, 2\}$, then let $\phi^{'}(xx_{3}) = \Delta$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. If $\beta\in\{4, \ldots, s\}$, then let $\phi^{'}(xx_{3}) = \gamma$ for $\gamma\notin(\phi^{'}(x) \cup \phi^{'}(x_{\beta}))$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. If $\beta\geq s+1$, then let $\phi^{'}(xx_{3}) = \gamma$ for $\gamma\notin(\phi^{'}(x) \cup \phi^{'}(x_{3}))$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. This implies that $n_{3}(y)\leq1$.

Lemma 3.6. For 2-vertex $v$, let $N(v) = \{x, y\}$. If $d(x) = 4$ and $n_{2}(x)+n_{3}(x) = 2$, then $n_{\Delta}(x) = 2$, $n_{2}(y) = 1, n_{3}(y)\leq1, d(y) = \Delta$.

Proof. Note that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2 = d(y)-\Delta+2$ by Lemma 3.4. It is clear that $d(y) = \Delta$ since $n_{2}(x)+n_{3}(x) = 2$. Let $N(x) = \{v, x_{1}, x_{2}, x_{3}\}, \; N(y) = \{v, y_{1}, y_{2}, \ldots, y_{\Delta-1}\}$ (See Figure 2(4)). If $n_{2}(x) = d(x)-2 = 2$, then $n_{\Delta}(x) = 2, n_{2}(y) = 1$ and $n_{3}(y)\leq1$ by Lemma 3.5. We prove the case $n_{2}(x) = 1$ and $n_{3}(x) = 1$. Suppose that $d(x_{3}) = 3$. Let $G^{'} = G-xv$, by the minimality of $G$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Assume that $c(xx_{i}) = i$ for $1\leq i\leq 3$, $T = C\setminus F_{y}^{c}(vy)$. Clearly, $|T| = \Delta+1-(\Delta-1) = 2$.

(1) $n_{\Delta}(x) = 2, n_{2}(y) = 1$.

We consider the following two cases.

Case 3.8. $T\setminus F_{x}^{c}(vx)\neq\emptyset$.

We can recolor $vy$ with $\alpha$ for $\alpha\in T\setminus F_{x}^{c}(vx)$, color $vx$ with $\beta$ for $\beta\in\{4, \ldots, \Delta+1\}$($\beta\neq\alpha$), $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.9. $T\setminus F_{x}^{c}(vx) = \emptyset$.

That is, $T\subseteq F_{x}^{c}(vx) = \{1, 2, 3\}$. Since $|T| = \Delta+1-(\Delta-1) = 2$, $\{1, 2, 3\}\setminus T\neq\emptyset$. As the same argument of Case 2 in Lemma 3.5, we have $n_{\Delta}(x) = 2, \; n_{2}(y) = 1$ by setting $s = 3$.

(2) $n_{3}(y)\leq1$.

By contradiction, suppose that $d(y_{1}) = d(y_{2}) = 3$. It follows from the above argument that $F_{y_{1}}^{c}(yy_{1}) = F_{y_{2}}^{c}(yy_{2}) = \{1, 2\}$. By the symmetry, assume that $c(vy) = 1$, exchange the colors between $yy_{1}$ and $yy_{2}$, $G-xv$ has a new acyclic $(\Delta+1)$-edge coloring $\phi$. Let $\phi(yy_{1}) = \alpha$.

If $\alpha\in\{4, \ldots, \Delta+1\}$, then let $\phi(vx) = \alpha$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

If $\alpha = 3$, then let $\phi(xv) = 3$, and remove the color of $xx_{3}$, $G-xx_{3}$ has an acyclic $(\Delta+1)$-edge coloring $\phi^{'}$. It follows from the above argument that there are $(i, \gamma)_{(x, v)}$-bichromatic paths under $c$ of $G-xv$ for $i = 1, 2$ and $\gamma\in\{4, 5, \ldots, \Delta+1\}$. So $G-xx_{3}$ contains no $(i, \gamma)_{(x, x_{3})}$-bichromatic path. If $|\phi^{'}(x)\cap \phi^{'}(x_{3})| = 0$, then $|\phi^{'}(x)\cup \phi^{'}(x_{3})|\leq3+2 = 5 < \Delta+1$. Let $\phi^{'}(xx_{3}) = \beta$ for $\beta\in C\setminus(\phi^{'}(x)\cup \phi^{'}(x_{3}))$, $\phi^{'}$ can be extended to $G$, a contradiction. If $|\phi^{'}(x)\cap \phi^{'}(x_{3})| = 1$, then suppose $1\in\phi^{'}(x_{3})$. Let $\phi^{'}(xx_{3}) = \beta$ for $\beta\in\{4, \ldots, \Delta+1\}\setminus \phi^{'}(x_{3})$, $\phi^{'}$ can be extended to $G$, a contradiction. If $|\phi^{'}(x)\cap \phi^{'}(x_{3})| = 2$, then $\phi^{'}(x)\cap \phi^{'}(x_{3}) = \{1, 2\}$, we can let $\phi^{'}(xx_{3}) = \beta$ for $\beta\in\{4, \ldots, \Delta+1\}$, $\phi^{'}$ can be extended to $G$, a contradiction. This implies that $n_{3}(y)\leq1$.

Next we discuss the number of $3^{-}$-vertex in the neighbors of $\Delta$-vertex.

Lemma 3.7. For $d(v) = \Delta$, if $n_{2}(v)\geq\Delta-3$, then $n_{2}(v)+n_{3}(v)\leq\Delta-2$.

Proof. Assume that $v_{4}\in N(v)$, $N(v_{4}) = \{v, v_{4}^{'}\}$. By Lemma 3.4, $n_{2}(v)\leq d(v)+d(v_{4}^{'})-\Delta-2 = d(v_{4}^{'})-2\leq\Delta-2$, $n_{2}(v)+n_{3}(v)\leq d(v)+d(v_{4}^{'})-\Delta-1 = d(v_{4}^{'})-1\leq\Delta-1$; if $n_{2}(v) = \Delta-2$, then $d(v_{4}^{'}) = \Delta$; if $n_{2}(v)+n_{3}(v) = \Delta-1$, then $d(v_{4}^{'}) = \Delta$. Note that $n_{\Delta}(v) = 2$ when $n_{2}(v) = \Delta-2$ by Lemma 3.5. Namely $n_{3}(v) = 0$, $n_{2}(v)+n_{3}(v) = \Delta-2+0 = \Delta-2$.

Otherwise $n_{2}(v) = \Delta-3$. By contradiction, suppose that $n_{2}(v)+n_{3}(v)\geq\Delta-1$. We have that $n_{2}(v)+n_{3}(v) = \Delta-1$ since $n_{2}(v)+n_{3}(v)\leq\Delta-1$. Let $N(v) = \{v_{1}, v_{2}, \ldots, v_{\Delta}\}, N(v_{i}) = \{v, x_{i}\}$ for $4\leq i\leq\Delta$. Assume that $d(v_{2}) = d(v_{3}) = 3$ (See Figure 3(5)). Let $G^{'} = G-vv_{\Delta}$, by the minimality of $G$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Let $c(vv_{i}) = i$ for $1\leq i\leq\Delta-1, T = C\setminus F_{x_{\Delta}}^{c}(v_{\Delta}x_{\Delta})$. Since $n_{2}(v)+n_{3}(v) = \Delta-1$, it follows from the above argument that $d(x_{\Delta}) = d(x_{\Delta-1}) = \ldots = d(x_{4}) = \Delta$, $|T| = \Delta+1-(\Delta-1) = 2$.

We consider the following two cases.

Case 3.10. $T\setminus C(v)\neq\emptyset$.

We can recolor $v_{\Delta}x_{\Delta}$ with $\alpha$ for $\alpha\in T\setminus C(v)$, color $vv_{\Delta}$ with $\beta$ for $\beta\in\{\Delta, \Delta+1\}$($\beta\neq\alpha$), $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.11. $T\setminus C(v) = \emptyset$. That is, $T\subseteq C(v) = \{1, 2, \ldots, \Delta-1\}$.

(i) $T\cap\{4, 5, \ldots, \Delta-1\}\neq\emptyset$.

We can color $v_{\Delta}x_{\Delta}$ with $i$ for $i\in T\cap\{4, 5, \ldots, \Delta-1\}$, color $vv_{\Delta}$ with $j$ for $j\in\{\Delta, \Delta+1\}\setminus\{c(v_{i}x_{i})\}$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

(ii) $T\cap\{4, 5, \ldots, \Delta-1\} = \emptyset$.

That is, $T\subseteq\{1, 2, 3\}$. Note that $c(v_{\Delta}x_{\Delta})\in T\subseteq\{1, 2, 3\}$. When $c(v_{\Delta}x_{\Delta}) = 1$, if there exists a color $\gamma\in\{\Delta, \Delta+1\}$, such that $G$ contains no $(1, \gamma)_{(v, v_{\Delta})}$-bichromatic path via $x_{\Delta}$ and $v_{1}$, then let $c(vv_{\Delta}) = \gamma$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. Hence, $G$ contains $(1, i)_{(v, v_{\Delta})}$-bichromatic paths via $x_{\Delta}$ and $v_{1}$ for each $i\in\{\Delta, \Delta+1\}$. This implies that $\{\Delta, \Delta+1\}\subseteq C(v_{1})\cap C(x_{\Delta})$. If $2\in T$, then we can recolor $v_{\Delta}x_{\Delta}$ with 2, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-vv_{\Delta}$, the same argument shows that $C(v_{2}) = \{2, \Delta, \Delta+1\}$. If $3\in T$, then we can recolor $v_{\Delta}x_{\Delta}$ with 3, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-vv_{\Delta}$, the same argument shows that $C(v_{3}) = \{3, \Delta, \Delta+1\}$.

(a) $1\notin T$. Namely, $T = \{2, 3\}$.

It follows from the above argument that $F_{v_{2}}^{c}(vv_{2}) = F_{v_{3}}^{c}(vv_{3}) = \{\Delta, \Delta+1\}$. Now exchange the colors between $vv_{2}$ and $vv_{3}$, we can color $v_{\Delta}x_{\Delta}$ with $\alpha$ for $\alpha\in T$, color $vv_{\Delta}$ with $\Delta$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

(b) $1\in T$. Suppose that $T = \{1, 2\}$.

It follows from the above argument that $\{\Delta, \Delta+1\}\subseteq C(v_{1})$ and $F_{v_{2}}^{c}(vv_{2}) = \{\Delta, \Delta+1\}$. Now let $c(v_{\Delta}x_{\Delta}) = 2, c(vv_{\Delta}) = 7$, remove the color of $vv_{7}$, $c$ is still an acyclic $(\Delta+1)$-edge coloring of $G-vv_{7}$. Let $T^{'} = C\setminus F_{x_{7}}^{c}(v_{7}x_{7})$, it is clear that $|T^{'}| = \Delta+1-(\Delta-1) = 2$. It follows from the above argument that $T^{'}\subseteq\{1, 2, 3\}$, and $1\in T^{'}$. Assume that $c(v_{7}x_{7}) = 1$. Since there is a $(1, \Delta)_{(v, v_{\Delta})}$-bichromatic path through $v_{1}$, $G-vv_{7}$ contains no $(1, \Delta)_{(v, v_{7})}$-bichromatic path via $v_{1}$ and $x_{7}$, we can color $vv_{7}$ with $\Delta$, $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction.

The following Lemma shows if a $k$-vertex($k\in\{4, 5, 6\}$) has no 2-neighbor, then $n_{3}(v) < k$.

Lemma 3.8. Let $v$ be a $k$-vertex, with $k\in\{4, 5, 6\}$. If $n_{2}(v) = 0$, then $n_{3}(v) < k$.

Proof. By contradiction, suppose that $n_{3}(v) = k$. Let $N(v) = \{x, v_{1}, v_{2}, v_{3}, v_{4}, v_{k-1}\}, \; N(x) = \{v, x_{1}, x_{2}\}$ and $N(v_{i}) = \{v, v_{i}^{'}, v_{i}^{''}\}\; (1\leq i\leq k-1$) (See Figure 3(8)). Let $G^{'} = G-xv$, by the minimality of $G$, $G^{'}$ admits an acyclic $(\Delta+1)$-edge coloring $c$. Let $c(vv_{i}) = i$ for $1\leq i\leq k-1$. We consider the following three cases.

Case 3.12. $|C(x)\cap C(v)| = 0$.

Note that $|C\setminus (C(x)\cup C(v))| = \Delta+1-2-(k-1) = \Delta-k > 0$, we can color $xv$ with $\alpha$ for $\alpha\in C\setminus (C(x)\cup C(v))$, $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

Case 3.13. $|C(x)\cap C(v)| = 1$.

W.l.o.g., assume that $c(xx_{1}) = c(vv_{1}) = 1, \; c(xx_{2}) = k$. If there exists a color $\gamma\in\{k+1, \ldots, \Delta+1\}$ such that $G$ contains no $(1, \gamma)_{(x, v)}$-bichromatic path, then we can color $xv$ with $\gamma$. In this way $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. So there must exist $(1, \alpha)_{(x, v)}$-bichromatic paths for each $\alpha\in\{k+1, \ldots, \Delta+1\}$, which implies that $\{k+1, \ldots, \Delta+1\}\subseteq C(x_{1})\cap C(v_{1})$. Thus, $d(v_{1})\geq\Delta+1-k+1\geq\Delta-4\geq4$, a contradiction.

Case 3.14. $|C(x)\cap C(v)| = 2$.

W.l.o.g., assume that $c(xx_{1}) = c(vv_{1}) = 1, \; c(xx_{2}) = c(vv_{2}) = 2$.

(i) $\Delta\geq9$.

Since $d(v_{1}) = d(v_{2}) = 3$ and $\Delta\geq9$, we have that $\{k, \ldots, \Delta+1\}\setminus (C(v_{1})\cup C(v_{2}))\neq\emptyset$. Let $\beta\in\{k, \ldots, \Delta+1\}\setminus (C(v_{1})\cup C(v_{2}))$. Note that $G$ contains no $(i, \beta)_{(x, v)}$-bichromatic path for $i = 1, 2$, we can color $xv$ with $\beta$, $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

(ii) $\Delta = 8$.

(a) $k\in\{4, 5\}$.

Since $d(v_{1}) = d(v_{2}) = 3$ and $\Delta\geq8$, we have that $\{k, \ldots, \Delta+1\}\setminus (C(v_{1})\cup C(v_{2}))\neq\emptyset$. Let $\beta\in\{k, \ldots, \Delta+1\}\setminus (C(v_{1})\cup C(v_{2}))$. Note that $G$ contains no $(i, \beta)_{(x, v)}$-bichromatic path for $i = 1, 2$, we can color $xv$ with $\beta$. In this way $c$ is an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

(b) $k = 6$.

If there exists a color $\gamma\in\{6, 7, 8, 9\}$ such that $G$ contains no $(i, \gamma)_{(x, v)}$-bichromatic path for $i = 1, 2$, then we can color $xv$ with $\gamma$. In this way $G$ is acyclically edge $(\Delta+1)$-colorable, a contradiction. So $\{6, 7, 8, 9\}\subseteq(C(v_{1})\cup C(v_{2}))$. Since $d(v_{1}) = d(v_{2}) = 3$, we have that $C(v_{1})\cup C(v_{2}) = \{1, 2, 6, 7, 8, 9\}$ and $c(v_{1}v_{1}^{'})\notin C(v_{2}), c(v_{1}v_{1}^{''})\notin C(v_{2})$. We can recolor $vv_{2}$ with $\alpha$ for $\alpha\in\{c(v_{1}v_{1}^{'}), c(v_{1}v_{1}^{''})\}$, don't change the colors of the other edges, $G^{'}$ has a new acyclic $(\Delta+1)$-edge coloring $c^{'}$, and $|C^{'}(x)\cap C^{'}(v)| = 1$. By the similar argument in case 2, we can get an acyclic $(\Delta+1)$-edge coloring of $G$, a contradiction.

3.2.   Discharging

Note that $G$ is a minimal counterexample to Theorem 1.1, and $G$ is a connected planar graph. By Euler$^{, }$s formula $|V|+|F|-|E| = 2$ and the relation $\sum\limits_{v\in V(G)}d(v) = \sum\limits_{f\in F(G)}d(f) = 2|E(G)|$, we can derive the identity

We define the initial charge function by $\omega(v) = d(v)-4$ for $v\in V(G)$ and $\omega(f) = d(f)-4$ for $f\in F(G)$. It follows from the identity that $\sum\limits_{x\in V(G)\cup F(G)}\omega(x) = -8$. According to the structures of $G$, we design some discharging rules and redistribute charge such that the total amount of charge has not changed. Once the discharging is finished, a new charge function $\omega^{'}(x)$ is produced. Next, we prove $\omega^{'}(x)\geq0$ for all $x\in V(G)\cup F(G)$. Therefore, we can get the following contradiction

Hence, we demonstrate that the counterexample can not exist and Theorem 1.1 is proved.

Discharging rules:

(R1) Every $5^{+}$-face $f$ sends $\frac{d(f)-4}{d(f)}$ to each incident vertex.

(R2) Every 4-vertex $v$ sends $\frac{1}{5}$ to each adjacent 3-vertex, and then distributes the remaining extra charge evenly among all adjacent 2-vertices.

(R3) Every 5-vertex $v$ sends $\frac{2}{5}$ to each adjacent 3-vertex, and then distributes the remaining extra charge evenly among all adjacent 2-vertices.

(R4) Every $6^{+}$-vertex $v$ sends $\frac{3}{5}$ to each adjacent 3-vertex, and then distributes the remaining extra charge evenly among all adjacent 2-vertices.

In the following, we will prove that $\omega'(v)\geq0$ for each $v\in V(G)$. Observe that $\delta(G)\geq 2$ by Lemma 3.1.

(1) $d(v) = 3$, $\omega(v) = -1$.

Let $N(v) = \{v_{1}, v_{2}, v_{3}\}$. We have that $d(v_{1})+d(v_{2})+d(v_{3})\geq\Delta+4\geq12$ by Lemma 3.3. Since the neighbors of 2-vertex are both $4^{+}$-vertices, then $n_{2}(v) = 0$, that is $d(v_{i})\geq3$ for $i = 1, 2, 3$, and $n_{3}(v)\leq2$.

If $n_{3}(v) = 2$, suppose that $d(v_{1}) = d(v_{2}) = 3$, then $d(v_{3})\geq6$. This implies that $\omega^{'}(v)\geq-1$+$2\times\frac{1}{5}$+$\frac{3}{5}$ = $0$ by $R1, R4$. If $n_{3}(v) = 1$, then either $n_{4}(v) = 1, \; n_{5^{+}}(v) = 1$ or $n_{4}(v) = 0, \; n_{5^{+}}(v) = 2$. By $R1, R2, R3, \; R4$, we have that $\omega^{'}(v)\geq-1+2\times\frac{1}{5}+\min\{\frac{1}{5}+\frac{2}{5}, 2\times\frac{2}{5}, \frac{2}{5}+\frac{3}{5}, 2\times\frac{3}{5}\} = 0$. If $n_{3}(v) = 0$, then $n_{4^{+}}(v) = 3$. By $R1, \; R4$, $\omega^{'}(v)\geq-1+2\times\frac{1}{5}+3\times\frac{1}{5} = 0$.

(2) $d(v) = 4$, $\omega(v) = 0$.

If $n_{2}(v)\neq0$, then $n_{2}(v)+n_{3}(v)\leq2$ by Lemma 3.4.

This means that $\omega^{'}(v)\geq0$+$3\times\frac{1}{5}-\frac{1}{5}n_{3}(v)-\frac{0+3\times\frac{1}{5}-\frac{1}{5}n_{3}(v)}{n_{2}(v)}\times n_{2}(v) = 0$ by $R1, R2$.

If $n_{2}(v) = 0$, then $n_{3}(v)\leq3$ by Lemma 3.8, which implies that $\omega^{'}(v)\geq0+3\times\frac{1}{5}-3\times\frac{1}{5} = 0$ by $R1, R4$.

(3) $d(v) = 5$, $\omega(v) = 1$.

If $n_{2}(v)\neq0$, then $\omega^{'}(v)\geq1+4\times\frac{1}{5}-\frac{2}{5}n_{3}(v)-\frac{1+4\times\frac{1}{5}-\frac{2}{5}n_{3}(v)}{n_{2}(v)}\times n_{2}(v) = 0$ by $R1, R3$.

If $n_{2}(v) = 0$, then $n_{3}(v)\leq4$ by Lemma 3.8. This implies that $\omega^{'}(v)\geq1+4\times\frac{1}{5}-4\times\frac{2}{5} = \frac{1}{5} > 0$ by $R1, R3$.

(4) $d(v) = 6$, $\omega(v) = 2$.

If $n_{2}(v)\neq0$, then $\omega^{'}(v)\geq2+5\times\frac{1}{5}-\frac{3}{5}n_{3}(v)-\frac{2+5\times\frac{1}{5}-\frac{3}{5}n_{3}(v)}{n_{2}(v)}\times n_{2}(v) = 0$ by $R1, R4$.

If $n_{2}(v) = 0$, then $n_{3}(v)\leq5$ by Lemma 3.8. This implies that $\omega^{'}(v)\geq2+5\times\frac{1}{5}-5\times\frac{3}{5} = 0$ by $R1, R4$.

(5) $d(v)\geq 7$, $\omega(v) = d(v)-4$.

If $n_{2}(v)\neq0$, then $\omega^{'}(v)\geq d(v)-4+\frac{1}{5}\times(d(v)-1)-\frac{3}{5}n_{3}(v)-\frac{d(v)-4+\frac{1}{5}\times(d(v)-1)-\frac{3}{5}n_{3}(v)}{n_{2}(v)}\times n_{2}(v) = 0$ by $R1, R4$.

If $n_{2}(v) = 0$, then $\omega^{'}(v)\geq d(v)-4+\frac{1}{5}\times(d(v)-1)-\frac{3}{5}n_{3}(v)\geq \frac{6}{5}d(v)-\frac{21}{5}-\frac{3}{5}d(v) = \frac{3}{5}d(v)-\frac{21}{5}\geq0$ by $R1, R4$.

(6) $d(v) = 2$, $\omega(v) = -2$.

For convenience, let $\tau(u\rightarrow v)$ denote the charge transferred out of $u$ into $v$ according to the above rules, $u, v\in V(G)$. Let $N(v) = \{x, y\}$, then $n_{2}(x)\leq d(x)-2, \; n_{2}(y)\leq d(y)-2$ by Lemma 3.4.

(6.1) If one of vertices in $\{x, y\}$, such as $x$, has $n_{2}(x)$ = $d(x)-2$, then $n_{\Delta}(x)$ = $2$, $n_{2}(y)$ = $1$, $n_{3}(y)\leq1$ and $d(y)$ = $\Delta$ by Lemma 3.5. By $R1$ and $R4$, we have that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}d(y)-\frac{1}{5}-1\times\frac{3}{5}}{1} = \frac{6}{5}d(y)-\frac{24}{5} = \frac{6}{5}\times(\Delta-4)\geq\frac{24}{5}$. This implies that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{24}{5} = 3 > 0$ by $R1$.

(6.2) $n_{2}(x)\leq d(x)-3, \; n_{2}(y)\leq d(y)-3$. Suppose that $d(x)\leq d(y)$.

(6.2.1) $d(x)\geq9$.

Observe that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-1$ by Lemma 3.4. Note that $\tau(x\rightarrow v)\geq\frac{\omega(x)+\frac{1}{5}\times(d(x)-1)-\frac{3}{5}n_{3}(x)}{n_{2}(x)}$$\geq\frac{d(x)-4+\frac{1}{5}d(x)-\frac{1}{5}-\frac{3}{5}\times(d(x)-1-n_{2}(x))}{n_{2}(x)}$$= \frac{\frac{3}{5}d(x)-\frac{18}{5}+\frac{3}{5}n_{2}(x)}{n_{2}(x)} = \frac{3}{5}\times(1+\frac{d(x)-6}{n_{2}(x)})\geq\frac{3}{5}\times(1+\frac{d(x)-6}{d(x)-3})$ = $\frac{3}{5}\times(2-\frac{3}{d(x)-3})$ by $R1, R4$.

Similarly, $\tau(y\rightarrow v)\geq\frac{3}{5}\times(2-\frac{3}{d(x)-3})$. Since $d(x)\geq9$, $d(x)\leq d(y)$, we have $\tau(x\rightarrow v)\geq\frac{9}{10}, \; \tau(y\rightarrow v)\geq\frac{9}{10}$. This implies that $\omega^{'}(v)\geq-2+\frac{1}{5}+2\times\frac{9}{10} = 0$ by $R1$.

(6.2.2) $d(x) = 8$, then $n_{2}(x)\leq d(x)-3 = 5$.

$(a)$ $\Delta\geq9$.

Observe that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2\leq d(x)-2$ by Lemma 3.4. Note that $\tau(x\rightarrow v)\geq\frac{\omega(x)+\frac{1}{5}\times(d(x)-1)-\frac{3}{5}n_{3}(x)}{n_{2}(x)}$$\geq\frac{d(x)-4+\frac{1}{5}\times(d(x)-1)-\frac{3}{5}\times(d(x)-2-n_{2}(x))}{n_{2}(x)}$$= \frac{3}{5}\times(1+\frac{d(x)-5}{n_{2}(x)})\geq\frac{3}{5}\times(1+\frac{d(x)-5}{d(x)-3}) = \frac{3}{5}\times(2-\frac{2}{d(x)-3}) = \frac{24}{25}$ by $R1, R4$.

If $d(y) = d(x) < \Delta$, then we have $\tau(y\rightarrow v)\geq\frac{3}{5}\times(1+\frac{3}{n_{2}(y)})\geq\frac{3}{5}\times(1+\frac{3}{5}) = \frac{24}{25}$ by the similar argument above. This implies that $\omega^{'}(v)\geq-2+\frac{1}{5}+2\times\frac{24}{25} = \frac{3}{25} > 0$ by $R4$.

If $d(y)\geq9$, then we have $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-1\leq d(y)-2$, $n_{2}(y)\leq d(y)-3$ by Lemma 3.4. This means that $\tau(y\rightarrow v)\geq\frac{3}{5}\times(1+\frac{d(y)-5}{n_{2}(y)})\geq\frac{3}{5}\times(2-\frac{2}{d(y)-3})$ by $R1$ and $R4$. $\tau(y\rightarrow v)\geq1$ since $d(y)\geq9$. So $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{24}{25}+1 = \frac{2}{25} > 0$ by $R4$.

$(b)$ $\Delta = 8$.

Now we have $d(x) = d(y) = \Delta = 8$. Observe that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-1\leq d(x)-1$ = $7$ by Lemma 3.4. If $n_{2}(x)\leq4$, then $\tau(x\rightarrow v)\geq\frac{3}{5}\times(1+\frac{2d(x)-14}{n_{2}(x)})\geq\frac{3}{5}\times(1+\frac{2}{4}) = \frac{9}{10}$ by $R1, \; R4$. Similarly, if $n_{2}(y)\leq4$, then $\tau(y\rightarrow v)\geq\frac{9}{10}$. If $n_{2}(x)\geq5$, then we have $n_{2}(x) = 5$ due to $n_{2}(x)\leq d(x)-3 = 5$. Observe that $n_{2}(x)+n_{3}(x)\leq\Delta-2 = 6$ by Lemma 3.7. This implies that $\tau(x\rightarrow v)\geq\frac{3}{5}\times(1+\frac{2d(x)-13}{n_{2}(x)}) = \frac{3}{5}\times(1+\frac{3}{5}) = \frac{24}{25}$ by $R1, \; R4$. Similarly, if $n_{2}(y)\leq5$, then $\tau(y\rightarrow v)\geq\frac{24}{25}$. Hence, $\omega^{'}(v)\geq-2+\frac{1}{5}+\min\{2\times\frac{9}{10}, \; 2\times\frac{24}{25}, \; \frac{9}{10}+\frac{24}{25}\} = 0$ by $R1$.

(6.2.3) $d(x) = 7$, then $n_{2}(x)\leq d(x)-3 = 4$.

Observe that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2\leq5$ by Lemma 3.4. Note that $\tau(x\rightarrow v)\geq\frac{3}{5}$ $\times(1+\frac{2d(x)-12}{n_{2}(x)})\geq\frac{9}{10}$ by $R1, R4$.

If $d(y) = 7$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 12-\Delta\leq4, \; n_{2}(y)\leq d(y)-3 = 4$ by Lemma 3.4. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)}\geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(4-n_{2}(y))}{n_{2}(y)} = \frac{3}{5}\times(1+\frac{2d(y)-11}{n_{2}(y)})\geq\frac{3}{5}$ $\times(1+\frac{3}{4}) = \frac{21}{20}$ by $R1, R4$. We have that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{9}{10}+\frac{21}{20} = \frac{3}{20} > 0$ by $R1$.

If $d(y)\geq8$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-1\leq d(y)-2, \; n_{2}(y)\leq d(y)-3$ by Lemma 3.4.

Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)}$$\geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(d(y)-2-n_{2}(y))}{n_{2}(y)}$$\geq\frac{3}{5}\times(1+\frac{d(y)-5}{n_{2}(y)})\geq\frac{3}{5}\times(2-\frac{2}{d(y)-3})$ by $R1, \; R4$. Since $d(y)\geq8$, $\tau(y\rightarrow v)\geq\frac{24}{25}$, we have that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{9}{10}+\frac{24}{25} = \frac{3}{50} > 0$ by $R1$.

(6.2.4) $d(x) = 6$, then $n_{2}(x)\leq d(x)-3 = 3$.

By Lemma 3.4, we have that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2\leq4$. Note that $\tau(x\rightarrow v)\geq\frac{3}{5}$ $\times(1+\frac{2d(x)-11}{n_{2}(x)})\geq\frac{4}{5}$ by $R1, R4$.

If $d(y) = 6$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 10-\Delta\leq2$ by Lemma 3.4. So $n_{2}(y)\leq2$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(2-n_{2}(y))}{n_{2}(y)} = \frac{3}{5}\times(1+\frac{2d(y)-9}{n_{2}(y)})\geq\frac{3}{5}$ $\times(1+\frac{3}{2}) = \frac{3}{2}$ by $R1, R4$. This means that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{4}{5}+\frac{3}{2} = \frac{1}{2} > 0$ by $R1$.

If $d(y) = 7$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 11-\Delta\leq3$ by Lemma 3.4. So $n_{2}(y)\leq3$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(3-n_{2}(y))}{n_{2}(y)} = \frac{3}{5}\times(1+\frac{2d(y)-10}{n_{2}(y)})\geq\frac{3}{5}$ $\times(1+\frac{4}{3}) = \frac{7}{5}$ by $R1, R4$. This means that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{4}{5}+\frac{7}{5} = \frac{2}{5} > 0$ by $R1$.

If $d(y)\geq8$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-1\leq d(y)-3, \; n_{2}(y)\leq d(y)-3$ by Lemma 3.4.

Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)}$$\geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(d(y)-3-n_{2}(y))}{n_{2}(y)}$$= \frac{3}{5}\times(1+\frac{d(y)-4}{n_{2}(y)})\geq\frac{3}{5}\times(2-\frac{1}{d(y)-3})$ by $R1, R4$. Since $d(y)\geq8$, $\tau(y\rightarrow v)\geq\frac{27}{25}$, we have that $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{4}{5}+\frac{27}{25} = \frac{2}{25} > 0$ by $R1$.

(6.2.5) $d(x) = 5$, then $n_{2}(x)\leq d(x)-3 = 2$.

By Lemma 3.4, we have that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2\leq3$. Note that $\tau(x\rightarrow v)\geq\frac{\omega(x)+\frac{1}{5}\times(d(x)-1)-\frac{2}{5}n_{3}(x)}{n_{2}(x)} \geq\frac{1+4\times\frac{1}{5}-\frac{2}{5}\times(3-n_{2}(x))}{n_{2}(x)} = \frac{2}{5}+\frac{3}{5}\times\frac{1}{n_{2}(x)}\geq\frac{2}{5}+\frac{3}{5}\times\frac{1}{2} = \frac{7}{10}$ by $R1, R3$. Observe that $d(x)+d(y)\geq\Delta+3$ by Lemma 3.3, so $d(y)\geq\Delta+3-d(x)\geq6$.

If $d(y) = 6$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 9-\Delta\leq1$ by Lemma 3.4, which means that $n_{2}(y) = 1, \; n_{3}(y) = 0$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} = \frac{2+5\times\frac{1}{5}-0\times\frac{3}{5}}{1} = 3$ by $R1, R4$. So $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{7}{10}+3 = \frac{19}{10} > 0$ by $R1$.

If $d(y) = 7$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 10-\Delta\leq2$ by Lemma 3.4. So $n_{2}(y)\leq2$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(2-n_{2}(y))}{n_{2}(y)} = \frac{3}{5}\times(1+\frac{5}{n_{2}(y)})\geq\frac{3}{5}$ $\times(1+\frac{5}{2}) = \frac{21}{10}$ by $R1, R4$. Hence, $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{7}{10}+\frac{21}{10} = 1 > 0$ by $R1$.

If $d(y)\geq8$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-1\leq d(y)-4$ by Lemma 3.4. So $n_{2}(y)\leq d(y)-4$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(d(y)-4-n_{2}(y))}{n_{2}(y)} = \frac{3}{5}\times(1+\frac{d(y)-3}{n_{2}(y)})\geq\frac{3}{5}$ $\times(2+\frac{1}{d(y)-4})$ by $R1, R4$. Observe that $\tau(y\rightarrow v) > \frac{6}{5}$ since $d(y)\geq8$. Then $\omega^{'}(v) > -2+\frac{1}{5}+\frac{7}{10}+\frac{6}{5} = \frac{1}{10} > 0$ by $R1$.

(6.2.6) $d(x) = 4$

By Lemma 3.4, we have that $n_{2}(x)+n_{3}(x)\leq d(x)+d(y)-\Delta-2\leq2$.

$(a)$ $n_{2}(x)+n_{3}(x) = 2$.

By Lemma 3.6, we have that $n_{\Delta}(x) = 2, \; n_{2}(y) = 1, \; n_{3}(y)\leq1$, and $d(y) = \Delta$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} \geq\frac{d(y)-4+\frac{1}{5}d(y)-\frac{1}{5}-1\times\frac{3}{5}}{1} = \frac{6}{5}d(y)-\frac{24}{5} = \frac{6}{5}(\Delta-4)\geq\frac{24}{5}$ by $R1, R4$. So $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{24}{5}$ = $3 > 0$ by $R1$.

$(b)$ $n_{2}(x)+n_{3}(x)\leq1$. That is $n_{2}(x) = 1, \; n_{3}(x) = 0$.

Note that $\tau(x\rightarrow v)\geq\frac{\omega(x)+\frac{1}{5}\times(d(x)-1)-\frac{1}{5}n_{3}(x)}{n_{2}(x)} \geq\frac{0+3\times\frac{1}{5}-0\times\frac{1}{5}}{1} = \frac{3}{5}$ by $R1, R2$. Observe that $d(x)+d(y)\geq\Delta+3$ by Lemma 3.3, so $d(y)\geq\Delta+3-d(x)\geq7$.

If $d(y) = 7$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-2 = 9-\Delta\leq1$ by Lemma 3.4, which means that $n_{2}(y) = 1, \; n_{3}(y) = 0$. Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)} = \frac{3+6\times\frac{1}{5}-0\times\frac{3}{5}}{1} = \frac{21}{5}$ by $R1, R4$. So $\omega^{'}(v)\geq-2+\frac{1}{5}+\frac{3}{5}+\frac{21}{5} = 3 > 0$ by $R1$.

If $d(y)\geq8$, then we have that $n_{2}(y)+n_{3}(y)\leq d(x)+d(y)-\Delta-1\leq d(y)-5$ by Lemma 3.4. Hence $n_{2}(y)\leq d(y)-5$.

Note that $\tau(y\rightarrow v)\geq\frac{\omega(y)+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}n_{3}(y)}{n_{2}(y)}$$\geq\frac{d(y)-4+\frac{1}{5}\times(d(y)-1)-\frac{3}{5}\times(d(y)-5-n_{2}(y))}{n_{2}(y)}$$= \frac{3}{5}\times(1+\frac{d(y)-2}{n_{2}(y)})\geq\frac{3}{5}\times(2+\frac{3}{d(y)-5})$ by $R1, R4$. We have that $\tau(y\rightarrow v) > \frac{6}{5}$ since $d(y)\geq8$. Hence, $\omega^{'}(v) > -2+\frac{1}{5}+\frac{3}{5}+\frac{6}{5} = 0$ by $R1$.

After $R1-R4$, we get $\omega^{'}(v)\geq0$, for all $v\in V(G)$. For all $f\in F(G)$, if $d(f) = 4$, then $\omega^{'}(f) = \omega(f) = d(f)-4 = 0$. If $d(f)\geq5$, then we have $\omega^{'}(f) = d(f)-4-\frac{d(f)-4}{d(f)}\times d(f) = 0$ by $R4$.

In summary, we get the following contradictory formula:

The above contradiction indicates that $G$ does not exist, so Theorem 1.1 is true.

4.   Conclusions

In this paper, we consider the acyclic chromatic index of planar graphs without 3-cycles and intersecting 4-cycles and proved that such graphs have $\chi_{a}^{'}(G)\leq\Delta+1$ if $\Delta(G)\geq8$. A natural problem in context of our main result is the following:

What is the optimal constant $c$ such that $\chi_{a}^{'}(G)\leq \Delta(G)+1$ for every planar graph $G$ with $g(G)\geq c$?

Acknowledgments

This work was supported by National Natural Science Foundations of China (Grant Nos. 11771403 and 11901243)

Conflict of interest

The authors declare no conflicts of interest.