Endomorphic GE-derivations

1.   Introduction

The coastal regions often face water scarcity despite the proximity to abundant seawater resources due to challenges in obtaining clean water ^[1]. Seawater, with an average salinity of 3.5% and a salinity measurement of around 35 psu, contains NaCl rendering and unsuitable for direct human consumption ^[2]. The salinity measurement and Total Dissolved Solids (TDS) ranging from 20.000 to 50.000 ppm in the Gulf of Prigi is needed for desalination processes ^[3,4,5]. Desalination offers a viable solution, often utilizing adsorption methods involving membrane technology, which efficiently reduce NaCl levels in seawater ^[6]. The demand for clean water remains a challenge, necessitating innovative solutions.

The exploration of calcium-based membranes for salt adsorption was aimed to optimize desalination efficiency ^[7]. The membranes synthesized from coral skeletons, predominantly composed of calcium carbonate (CaCO₃), are augmented with chitosan and sodium alginate, providing a cost-effective yet efficient solution for desalination ^[8,9]. The membrane synthesis process involves the crosslinking of sodium alginate and calcium, forming calcium alginate membranes capable of adsorbing NaCl from seawater ^[10,11].

Chitosan, a biopolymer with active NH₂ and OH- functional groups, holds potential for membrane manufacturing, specifically in adsorption applications ^[12]. Combination chitosan with alginate potentially enhances the membrane's properties, potentially forming pores and binding with metals ^[13,14]. The coral skeleton is a significant resource for calcium-based membrane production ^[9]. The extraction of calcium oxide (CaO) from coral skeletons through the calcination process further improves the membrane's functional properties ^[15]. Through future desalination, power material membranes aim to transform mineral-rich seawater into clean water in coastal areas where water supply remains insufficient ^[16].

Here, the synthesis of calcium alginate membranes involve the utilization of abundant coral skeletons, primarily composed of CaCO₃, and crosslinked with sodium alginate and calcium to form membranes capable of binding salt from seawater ^[17,18]. The combined coral skeletons and polymer materials like chitosan and sodium alginate in membrane synthesis provided a significant step toward creating efficient and cost-effective desalination methods ^[19]. We explored the addition of chitosan to calcium-alginate membranes for enhanced seawater salt adsorption, further advancing the development of viable desalination processes.

2.   Experimental detail

2.1.   Materials

The materials were coral skeletons, chitosan powder, sodium alginate, 37% HCl solution, NaCl solid, 1% K₂CrO₄ solution, AgNO₃ solid, distilled water, NaOH solution, and filter paper.

2.2.   Methods

2.2.1.   Sample coral preparation

Corals taken from Prigi Beach undergo a series of preparation stages, such as cleaning with demineralized water, drying at 60 ℃ until dryness, grinding and sieving (200 mesh) until a fine powder was obtained. The resulting coral powder was calcined at 800 ℃ for 2 hours to produce high purity CaCO₃ ^[20,21].

2.2.2.   Preparation of CaCl₂ solution from calcined coral

This CaCO₃ was processed into a homogeneous CaCl₂ solution, starting with diluting 83.3 mL of 37% HCl to obtain a 1 M HCl solution. Five grams of CaCO₃ was combined with 100 mL of 1 M HCl solution, producing a CaCl₂ solution after homogenization and filtration.

2.2.3.   Preparation of alginate and chitosan solutions

A total of 1 and 2 g of sodium alginate were individually weighed and each added to 100 mL of distilled water. The solutions were stirred using a hotplate magnetic stirrer at 300 rpm at 80 ℃ and left for 24 hours. Chitosan was prepared in concentrations of 1%, 2%, and 3%, respectively. A total of 1, 2, and 3 g of chitosan powder (w/v) were added to 100 mL of acetic acid solution with a concentration corresponding to the chitosan mass (1%, 2%, and 3% acetic acid). The solutions were then stirred using a hotplate magnetic stirrer at 300 rpm at 80 ℃ and left for 24 hours.

2.2.4.   Synthesis of calcium- alginate-chitosan membranes

The synthesis of Ca-alginate-chitosan membranes was carried out by mixing the polymer solutions (sodium alginate and chitosan) in a volume of 40 mL with a chitosan-to-alginate ratio of 1:2, resulting in a chitosan solution volume of 16.13 mL and a sodium alginate solution volume of 26.6 mL with the variation concentration ratio of chitosan to alginate (1:1, 1:2, 1:3, 1:4). After 24 hours, the alginate-chitosan mixture was added with 10 mL of 0.5 M CaCl₂ and left for 8 hours, followed by lifting and drying at room temperature for 24 hours. The resulting beads and transparent membranes were then characterized by measuring pH and washing with distilled water.

2.2.5.   Optimization of calcium- alginate-chitosan membrane synthesis

The process of optimizing the concentration of the alginate solution involved adsorption experiments with NaCl solutions using different chitosan-alginate compositions. This aims to determine the optimum alginate composition that produces the highest Cl^- adsorption concentration. Further optimization was focused on determining the ideal chitosan concentration for maximum Cl^- adsorption. The characterized membranes were applied by FT-IR analysis to identify functional groups and SEM analysis for microstructural observation.

2.2.6.   Characterization of calcium- alginate-chitosan membrane synthesis

The initial characterization of Calcium- Alginate-Chitosan Membrane Synthesis involved employing a Fourier transform infrared spectrometer (FT-IR, Shimadzu IR Prestige 21) to identify the compounds' functional groups. Subsequently, X-ray fluorescence (PANalytical) determined the elemental composition of a material/sample, while Scanning Electron Microscopy and Energy Dispersive X-ray (SEM EDX) can be used to characterize a material and its morphology.

2.2.7.   Adsorption experiments

In laboratory scale applications, the membrane was tested by stirring a 0.1 N NaCl solution with varying contact times. The resulting solution underwent Na⁺ concentration analysis using AAS (Thermo scientific ICE3000) after appropriate dilution. In addition, analysis of Cl^- concentration was carried out via Mohr's argentometric titration, which involves titration with a 0.1 N AgNO₃ standard solution.

After adsorption, the filtrate was analyzed for Na⁺ and Cl^- concentrations using specific techniques. The Na⁺ concentration was determined using AAS after adequate dilution, while the Cl^- concentration was determined via Mohr's argentometry titration involving titration with a 0.1 N AgNO₃ standard solution, both carried out in duplicate for accuracy. Blank titration was carried out as a reference for calculating Cl^- levels.

3.   Results and discussion

3.1.   Characterization of coral skeleton using XRF Test

The sieved coral skeleton was calcined at 800 ℃ to obtain high purity calcium oxide. Calcination functions remove CO₂, dirt, and minerals other than calcium. During this process, heat was applied to the surface of the coral particles, thereby encouraging the released CO₂ gas to migrate to the surface and disperse into the calcined sample. The resulting calcined coral as the natural sources for material CaCl₂ productions. XRF analysis of corals determines the content of calcium and various other elements. The elemental composition of coral, both before and after calcination is listed in Tables 1 and 2.

Table 1.  XRF Analyses of coral before alcination.

No	Elements	Wt (%)	Oxide	Wt (%)
1	Ca	90.82	CaO	90.86
2	Si	1.30	SiO2	2.30
3	Sr	4.40	SrO	3.42
4	Fe	1.70	Fe2O3	1.62
5	Ti	0.15	TiO2	0.16
6	Mo	0.89	MoO3	1.10
7	Cu	0.03	CuO	0.03
8	Mn	0.07	MnO	0.06
9	Ba	0.10	BaO	0.10
10	Yb	0.47	Yb2O3	0.35
11	Lu	0.09	Lu2O3	0.06

---

 | Show Table

DownLoad: CSV

Table 2.  XRF analyses of coral after calcination.

No	Elements	Wt (%)	Oxide	Wt (%)
1	Ca	92.58	CaO	93.41
2	Si	-	SiO2	-
3	Sr	4.54	SrO	3.56
4	Fe	-	Fe2O3	1.43
5	Ti	0.11	TiO2	0.12
6	Mo	1.10	MoO3	1.30
7	Cu	0.04	CuO	0.03
8	Mn	0.06	MnO	0.05
9	Ba	0.10	BaO	0.08
10	Yb	-	Yb2O3	-
11	Lu	-	Lu2O3	-

---

 | Show Table

DownLoad: CSV

The XRF measurements showed that the coral was composed mainly of calcium oxide, which has the potential to be used as a component of Ca²⁺ in the membrane. The percentage of CaO before and after calcination was 90.82 and 93.41%, respectively.

3.2.   Synthesis of calcium-alginate-chitosan

The process of dissolving sodium alginate in water using a hotplate magnetic stirrer is recommended at 80 ℃ with a speed of 300 rpm ^[22]. Chitosan powder was dissolved in high-concentration acetate acid or organic acid solvents with a pH range of 4–6 ^[22]. Furthermore, chitosan was dissolved at a relatively high temperature, around 80°–100℃. The solubility process of chitosan occurs through a protonation reaction, where the amine group (-NH₂) in chitosan accepts H⁺ released by acetic acid, resulting in a positive charge (-NH₃⁺). The addition of Ca²⁺ ion from CaCl₂ reacted as a cross-link with sodium alginate and chitosan. CaCl₂ functions as a crosslinking bound sodium alginate, with Ca²⁺ replacing Na⁺ to form calcium alginate. That cross link is essential for the formation of the gel structure. The formation of Ca-alginate-chitosan involves a drip technique, where a vacuum pump ensures a consistent drip frequency of the sodium alginate solution into the calcium chloride solution.

During Ca-alginate-chitosan beads production, the NaCl was removed through washing, achieved by soaking the beads in distilled water. The process requires a 300 mL sodium alginate solution and 150 mL of calcium chloride solution to release 100 grams of calcium alginate granules. This method is widely used in various scientific studies and industrial applications, and offers a controlled and efficient means of producing calcium alginate beads for diverse uses.

Figure 1.  Ca-alginate-chitosan beads.

DownLoad: Full-Size Img PowerPoint

3.3.   Characterization of Calcium-Based Alginate-Chitosan Membrane Using FTIR

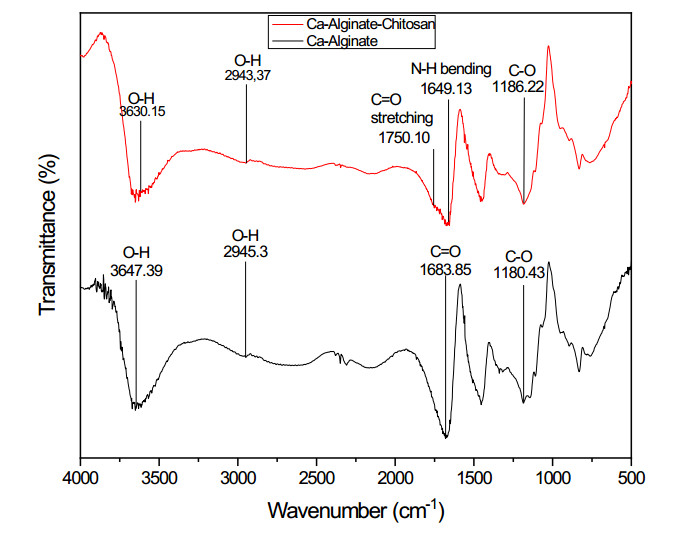
The calcium alginate-chitosan membrane was analyzed using FTIR to determine the functional group content present in the membrane. FTIR spectrum analysis was performed using the Origin application. The FTIR characterization is shown in Figure 2.

Figure 2.  FTIR Spectra of Calcium Alginate Membrane and Calcium Alginate-Chitosan Membrane.

DownLoad: Full-Size Img PowerPoint

The infrared (IR) spectrum shows characteristic features of calcium alginate and calcium alginate-chitosan membranes. In the calcium alginate spectrum, the prominent peak at 1683.85 cm^-1 indicates the characteristics of the carboxyl functional group (C = O). The range between 1594-1418 cm^-1 depicts the C-O symmetric stretch of the carboxyl group, and the presence of a C-O asymmetric stretch was identified at 1180.43 cm^{-1 [23]}. The peak at 2945.3 cm^-1 indicates intramolecular hydrogen bonds involving O-H and -COO- along with Ca²⁺ ions, while the peak at 3647.39 cm^-1 represents O-H stretching vibrations especially in calcium alginate ^[24].

In the alginate-chitosan spectrum, there was a shift and the emergence of new functional groups due to the addition of chitosan. An important shift occurs at 3630.15 cm^-1, which indicates O-H stretching vibrations and N-H stretching vibrations, consistent with previous research by Venkatesan et al. ^[25]. The wider band at 2943.37 cm^-1 indicates intramolecular bonds between O-H, -COO-, and Ca²⁺ ions together with the NH₂ group. The peak at 1186.22 and 1750.10 cm^-1 indicates asymmetric C-O and C = O stretching. The characteristic peak at 1649.13 cm^-1 represents the ketone C = O stretching vibration on primary NH₂, which indicates the presence of N-H bending which indicates interaction with the protonated amino group on chitosan. The wavenumber shift in the -OH group indicates an increase in energy level ^[26].

3.4.   Characterization of calcium-based alginate-chitosan membrane using SEM

The calcium-based alginate-chitosan membrane that has been formed is analyzed for its microstructure using SEM (Scanning Electron Microscope) to examine the surface and pore diameter of the membrane. The SEM results obtained under optimal conditions can be observed in Figure 3.

Figure 3.  SEM analysis of a calcium alginate membrane at (a) 1000x (b) 5000x magnification.

DownLoad: Full-Size Img PowerPoint

Under 5000x magnification, the surface of the calcium alginate particles shows a considerable surface area, displaying a particle diameter of 138 nm. Smaller particle size correlates with expanded surface area, leading to increase adsorption rates. These characteristics place calcium alginate in the classification of microporous materials, as indicated by its particle size and is described in detail in this study ^[27]. Figure 4 illustrates the comparative analysis between various calcium alginate membranes.

Figure 4.  SEM analysis of calcium alginate-chitosan membrane at (a) 1000x, (b) 5000x magnification.

DownLoad: Full-Size Img PowerPoint

SEM analysis findings at 5000x magnification show the inner surface structure of the membrane, which is characterized by roughness and porosity, with a diameter of 185.96 nm. This size classification aligns them with microporous membranes ^[27]. These membrane pores play an important role as adsorbents during NaCl adsorption, facilitating movement within the pore walls in the adsorption process.

3.5.   Adsorption of NaCl using calcium-based alginate-chitosan membrane synthesis

3.5.1.   Adsorption of NaCl using variation of alginate solution for optimization

Sodium alginate functions as the base material in gel formation along with Ca²⁺ from CaCl₂, which cross-links with sodium alginate and chitosan. The optimization process focuses on identifying the most effective concentration of sodium alginate for adsorption purposes. This optimization phase involves testing membrane configurations utilizing sodium alginate solutions at concentrations of 1 and 2% w/v, combined with 1% w/v of chitosan. The quantities utilized consist of 26.6 mL of Na-Alginate solution, 13.3 mL of chitosan solution, and 10 mL of 0.5 M CaCl₂. The optimized condition of ideal composition is shown in Table 3, as follows:

Table 3.  Optimized sodium alginate solution concentration form maximum adsorption.

Na-Alginate (ml; w/v)	Chitosan (vol; w/v)	Concentration (ppm)			%Adsorption
		[Cl-] Initial	[Cl-] Residue	[Cl-] Adsorbed
26.6; 1%	13.3; 1 %	3543	2290	1253	34.8
26.6; 2%	13.3; 1 %	3543	2130	1413	40.0
26.6; 3%	13.3; 1 %	3543	2330	1213	34.2
26.6; 4%	13.3; 1 %	3543	2370	1173	33.1

---

 | Show Table

DownLoad: CSV

As listed in Table, the membrane containing a 2%w/v alginate concentration demonstrates a higher capacity for adsorbing Cl^- ions compared to the 1% w/v alginate concentration membrane. The concentration of sodium alginate plays a crucial role in gel formation, influencing the density of particles within the solution. Higher concentrations lead to a denser presence of charges or particles, facilitating increased electrostatic interactions between more functional groups and the -NH₃⁺ groups in chitosan. Consequently, this interaction enhances the membrane's capacity for substance adsorption ^[28].

3.5.2.   Adsorption of NaCl using Variation of Chitosan for Optimized adsorption

The optimization of chitosan solution concentration is performed to determine the best membrane composition for further membrane application with contact time. The optimization data is listed in Table 4.

Table 4.  Optimized Chitosan Solution for adsorption maximum.

Na-Alginate (ml; w/v)	Chitosan (ml; w/v)	Concentration (ppm)			%Adsorption
		[Cl-] Initial	[Cl-]Residue	[Cl-] Adsorbed
26.6; 2%	13.3; 0 %	3542	2662	880	24.8
26.6; 2%	13.3; 1 %	3542	2130	1412	39.8
26.6; 2%	13.3; 2 %	3542	1846.0	1696	48.4
26.6; 2%	13.3; 3 %	3542	2378.5	1164	32.3

---

 | Show Table

DownLoad: CSV

Table 4 shows the membrane incorporating chitosan exhibits superior performance due to the incorporation of active cross-linking agents, which leads to an increase in membrane pore size, thereby enhancing its capacity for adsorption. The alginate-chitosan composite membrane was presumed to demonstrate superior absorption of chloride ions (Cl^-) up to 48.4%, and then decreasing of 32.3% with variation 2:3 between Na-Alginate and Chitosan composition.

The decrease in adsorption level at the 2:3 ratio of Na-alginate to chitosan may be due to the saturation of the chitosan solution, resulting in a decrease in the availability of active amino groups for cross-linking with alginate. This reduced the effective surface area for ion adsorption. Additionally, excess chitosan content possibly causes the formation of chitosan aggregates, which can hinder the formation of a uniform and stable membrane. The phenomenon of influenced chemical factors are related to the balance of ionic interactions between chitosan and alginate, as well as the availability of functional groups for cross-linking. An abundance of chitosan can disrupt this optimal interaction balance, resulting in a decrease in adsorption efficiency ^[29,30].

The process of combination between chitosan solution with alginate reveals in an interaction between the positively charged amino groups (-NH₃⁺) of chitosan and the -COO^- groups of alginates through ionic interactions, establishing cross-linking bonds.

3.5.3.   Adsorption of NaCl using the optimized condition

The utilization of the calcium alginate and chitosan as the membrane was assessed by adsorbing NaCl in the ranged from 10 to 50 minutes in the batch system. The outcomes of the membrane's work were measured in terms of the maximal percentage adsorption of Na⁺ and Cl^-. The data of adsorption test of calcium alginate with addition chitosan in the membrane for Na⁺ adsorption is presented in Table 5.

Table 5.  Analysis of the Na⁺ ion adsorption level by membrane using AAS.

Contact Time (Minutes)	Concentration (ppm)			%Adsorption
	[Na+] Initial	[Na+] Residue	[Na+] Adsorbed
10	1105	668	437	39.5
20	1105	693	411	37.2
30	1105	688	416	37.7
40	1105	657	447	40.5
50	1105	745	359	32.5

---

 | Show Table

DownLoad: CSV

As listed in Table 5, the optimal time analysis towards the maxima Na⁺ ion adsorption is 40 minutes. The particle aggregation on the membrane potentially affected the adsorption of Na⁺ ions. These ions are typically bound by -COO^- groups originating from alginate, crucial in the NaCl adsorption process. The presence of -NH₃⁺ groups from chitosan is suspected to contribute to this aggregation.

Figure 5 illustrates the correlation between contact time and the percentage of Na⁺ adsorption. This reveals a notable decline at the 50-minute. This implies a reduction in the membrane's adsorption capacity, potentially linked to a decrease in chitosan content or a decline in NH₂ groups within the membrane. Chitosan's efficacy in binding metals stems from its free amino groups and integral for ion exchange capabilities. The nitrogen content in chitosan with its high polymer chain correlates with its capacity to bind metals.

Figure 5.  Relationship between contact time and the percentage of Na⁺ and Cl^- ion adsorption.

DownLoad: Full-Size Img PowerPoint

As listed in Table 6, the ion Cl^- adsorption test was utilized using the Mohr method. As listed in the table, it becomes evident that the optimal duration for Cl^- ion adsorption is 40 minutes, the same with its pattern of Na⁺ ion. The contact time plays a vital role in the adsorption process, directly impacting the amount of adsorbed substance. The optimized contact allows for more solute molecules to be adsorbed, facilitating a well-functioning diffusion process ^[31]. It significantly influences adsorption until equilibrium is attained. Once equilibrium is reached, further contact time does not affect the process or possibly desorption.

Table 6.  Analysis of the Cl^- adsorption levels in the NaCl 0.1 N solution using the Mohr Method Argentometric titration.

Contact Time (Minute)	Concentration (ppm)
	[Cl-] Initial	[Cl-] Residue	[Cl-] Adsorbed	%Adsorption
10	3543	1988	1554	43.9
20	3543	1952	1590	44.9
30	3543	1864	1661	47.4
40	3543	1828	1696	48.4
50	3543	1881	1661	46.9

---

 | Show Table

DownLoad: CSV

Figure 5 indicates a substantial increase in the Na⁺ and Cl^- ions adsorption process at 40 minutes, revealing them as the optimal time for both ions. Conversely, there is a decline in observing them at 50 minutes. Prolonging the process beyond 60 minutes could potentially lead to desorption, releasing the adsorbate back into the solution. Figure 5 depicts the graphical representation of the relationship between contact time and the percentage of Na⁺ and Cl^- ions adsorption.

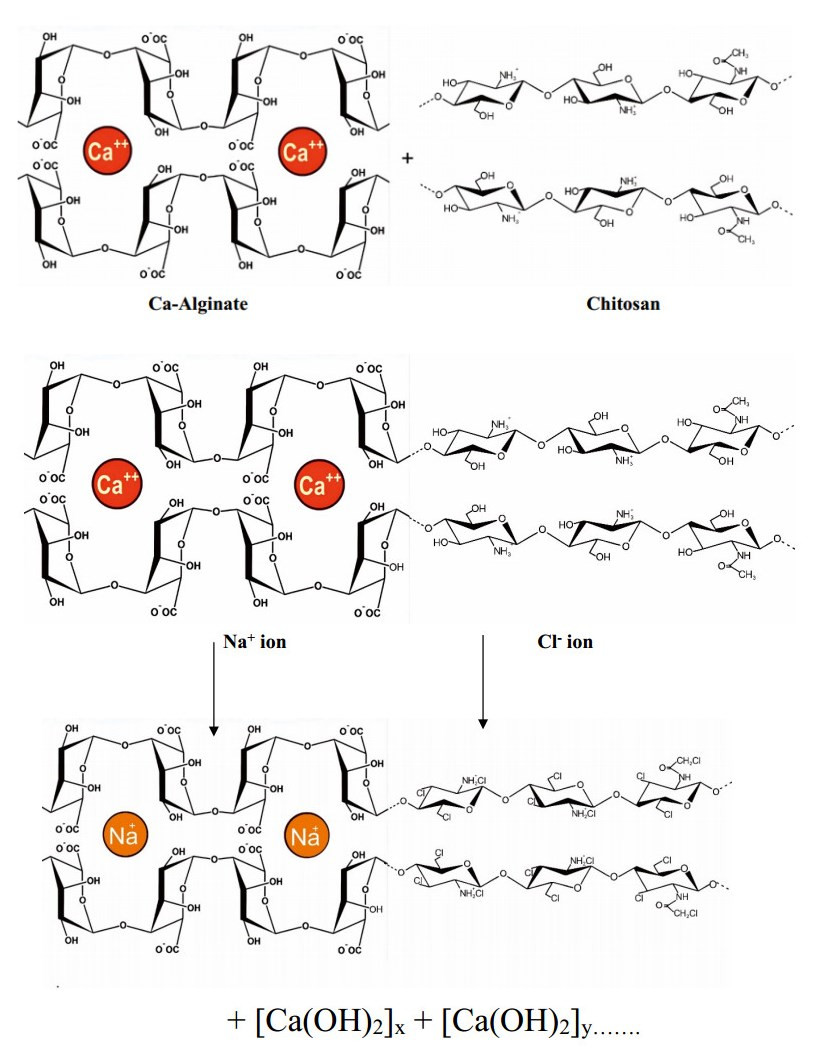
The possible mechanism reaction between Ca-alginate and chitosan during adsorption of Na⁺ and Cl^- as shown in Figure 6, as follows:

Figure 6.  The possible mechanism reaction between Ca-alginate chitosan with NaCl during the adsorption process.

DownLoad: Full-Size Img PowerPoint

The initial mechanism reaction started a reaction between Ca-alginate and chitosan to form a Ca-alginate-chitosan complex, causing the cross linking of the polymer to involve hydrogel formation for potentially adsorption application. During the adsorption, the first step involved the displacement of Ca²⁺ changing with Na⁺ ion due to the higher affinity of Na⁺ ion to alginate. The first product in the adsorption process was the dissolution of Ca complex and trapped Na-alginate chitosan in the membrane. In the second product, when the Cl^- ion was applied in the adsorption process, chitosan could possibly interact with Cl^- ions through electrostatic interactions, hydrogen bonding, and its positively charged amino groups attracted Cl^- ions. The residue of this process adsorption formed a Ca(OH)₂ complex. In the future prospect, the specific condition of pH and temperature between Ca-alginate chitosan and NaCl should be considered to determine the best capability membrane as adsorbent.

4.   Conclusions

The inclusion of chitosan in calcium alginate had an impact on membrane formation, which was reflected in FTIR characterization by observing shifts in the wave numbers of certain functional groups. On the calcium alginate membrane, the absorption of the O-H group at 3647.39 shifted to 3437 cm^-1, which indicated the existence of intramolecular bonds with the N-H group of chitosan. In addition, C = O, CO, and N-H groups were involved in NaCl binding. SEM analysis showed a particle size diameter of 185.96 nm, indicating rough and porous surface characteristics, indicating the micro-porous nature of the membrane, which is capable of absorbing NaCl. The calcium alginate-chitosan based membrane showed a Na⁺ and Cl^- adsorption peak of 40.5% and 48.4%, respectively. This maximum adsorption level was achieved using a membrane composition consisting of 13.3 mL of 2% chitosan (w/v) and 26.6 mL. The optimized contact time for this Ca-alginate addition with chitosan was detected at 40 minutes to adsorb of Na⁺ and Cl^- ions.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by Penelitian Dasar grant No. 0162/E5.4/DT.05.00/2023 on DRPM 2023

Conflict of Interests

The authors state that there are no conflicts of interest for this project.