Reliable analysis for obtaining exact soliton solutions of (2+1)-dimensional Chaffee-Infante equation

1.   Introduction

The intriguing quality of nonlinearity in nature has led many scientists to view nonlinear science as the most significant area of research for a fundamental understanding of nature. The study of a variety of classes of NODEs and nonlinear partial differential equations (NPDEs) is crucial to the mathematical modelling of complex processes that vary over time. These models come from a wide range of disciplines, including optical fibres, economics, solid state physics, plasma physics, infectious disease epidemiology, elasticity, neural networks, and population ecology. Due to such applications, the examination of soliton solutions of the before stated phenomena has been an exciting and extremely dynamic topic of research for the past several decades, with the related issue of the construction of closed-form wave solutions to a broad class of nonlinear differential equations, particularlyNPDEs. For such situations, closed-form soliton solutions offer improved internal information. Thus, a great deal of work has been done by mathematicians and physical scientists to obtain closed-form soliton solutions of such NPDEs. A number of effective and powerful methods have been developed, including the first integral method ^[1], Bäcklund transformation method ^[2], the modified simple equation method ^[3], the $(G' /G)$-expansion method ^[4,5,6], the exp-function method ^[7], the sine-cosine method ^[8], the homogeneous balance method ^[9], the modified Kudryashov method ^[10], the F-expansion method ^[11], the bilinear method ^[12], the tanh-function method ^[13], the projective Riccit equation method ^[14], and the $(G' /G, 1/G)$-expansion method ^[15] Riccati-Bernoulli Sub-ODE ^[16], Poincaré-Lighthill-Kuo method ^[17], sub-equation method ^[18], Khater method ^[19], Sardar sub-equation method ^[20], EDAM ^{[21,22,23,24,25]}, Hirota bilinear method ^[26], planar dynamic system method ^[27] and Bifurcation analysis method ^[28], among others ^[29,30]. The computation of complex standard eigenvalue problems for laminar-turbulent transition prediction, while the investigates dynamically controlling terahertz wavefronts. In the third reference, structural reliability analysis is performed using an improved wolf pack algorithm, while the fourth reference introduces a class of digital integrators based on trigonometric quadrature rules ^[31,32,33]. Lastly, the fifth reference focuses on opinion formation analysis in group decision-making systems. These references collectively showcase the breadth and depth of research across various domains, highlighting the importance of interdisciplinary approaches in addressing complex scientific and engineering challenges ^[34,35].

One of the most significant, straightforward, and efficient algebraic techniques in the aforementioned analytical methods for obtaining soliton solutions to NPDEs is the m-EDAM. The strategic m-EDAM comprises converting CIE into a NODE by variable transformation, which is then reduced to a set of nonlinear algebraic equations with the assumption of a closed-form solution ^[36,37,38]. Many soliton solutions in terms of exponential, rational, trigonometric, and hyperbolic functions are produced when the resultant system is solved using the Maple tool. A soliton is a single, self-reinforcing wave packet that moves across a medium without altering its shape or velocity. Since soliton solutions to nonlinear fractional partial differential equations (NFPDEs) provide a higher level of detail and coverage than traditional solutions, their study is still important from an academic standpoint ^[39,40,41]. Their resilience and fermion stability make them valuable in many areas of engineering and science. They make it possible for nonlinear systems to maintain long-distance coherence and convey information efficiently ^[42,43].

Numerous researchers have used the proposed m-EDAM to construct a new plethora of soliton solutions for many NPDEs andNFPDEs. For example, Saima et al. in ^[44] constructed soliton solutions for the (2+1)-dimensional Nizhnik-Novikov-Veselov model (NNVM) using a novel variant of m-EDAM called $r$+mEDAM. Ikram et al. employed the suggested mEDAM to analyse front events and solitons in the fractional Kolmogorov-Petrovskii-Piskunov equation ^[45]. Bilal et al. explored the soliton phenomena in the nonlinear spatiotemporal fractional Higgs system analytically, using an improved version of the ground-breaking analytical technique m-EDAM ^[46]. Lastly, Rashid et al. investigated soliton solutions in fractional quantum mechanical equations of nonlinear systems using the effective m-EDAM ^[47]. Overall, the m-EDAM research revealed that it is a reliable, practical, and easy-to-use tool that offers more general wave solutions for nonlinear models in mathematical physics and engineering.

Motivated by the ongoing research on soliton solutions, this research aims to extract and analyse soliton solutions for (2+1)-dimensional CIE using the m-EDAM. This model is articulated as ^[48]:

where $z = z(x, y, t)$, $\sigma$ is the degradation coefficient, while $\lambda$ is the diffusion coefficient. In a physical environment, the diffusion of a gas in a homogeneous medium is a significant phenomenon, and the CIE offers a helpful model to investigate such phenomena. One famous response to the Duffing equation in the physical sciences is the (2+1)-dimensional CIE ^[49].

Numerous scholars have addressed the CIE by employing various analytical approaches. Using the Hirota bilinear approach, for example, Sualiman et al. produced lump soliton solutions for CIE with variable coefficients ^[50]. To derive the kink and cuspon soliton solutions for CIE, Akbar et al. used the first integral equation in ^[48]. Similarly, a number of new generalised solitonary solutions for the CIE with unique physical structures have been constructed by Sakthivel and Chun ^[49] using the exp-function method. Lastly, Demiray and Bayrakci created soliton solutions for CIE in ^[51] by applying the sine-Gordon expansion approach. However, in this study, we aim to address CIE to construct soliton solutions for it using m-EDAM. Our study reveals that the soliton solutions obtained for CIE are either cuspon and kink soliton solutions, such as dark kink, bright kink, and bright-dark kink. A kink soliton is a kind of solitary wave that is distinguished by an abrupt change or discontinuity in the field or variable it represents. It is also referred to as a topological soliton or domain wall. Kink solitons usually occur in systems that experience a phase transition of a scalar field. Conversely, a cuspon soliton, also known as a cusped soliton, is a different kind of solitary wave that has a cusp, or sharp peak, at the crest. It is a solution to a specific class of nonlinear wave equations in which the propagating solitary wave keeps its shape.

The format of this article is as follows: Section 1 provides an introduction. Section 2 presents the operational methodology of m-EDAM. In Section 3, we build some new families of soliton solutions for CIE, and in Section 4, several illustrations and a graphical description are shown and analysed. Finally, Section 5 provides the conclusion.

2.   The operational procedure of m-EDAM

We describe the operating methods of the m-EDAM in this portion of the paper, focusing on addressing the subsequent general NPDE:

where $z = z(t, y_1, y_2, y_3, \ldots, y_j)$.

The strategy taken to solve Eq (2.1) is given as follows:

(1). Commencing with a variable transformation of the framework $z(t, y_1, y_2, y_3, \dots, y_j) = Z(\vartheta)$, where $\vartheta$ can be stated in a number of ways, Eq (2.1) proceeds through a transformation, resulting in the post-NODE:

where $Z' = \frac{d Z}{d\vartheta}$. On some occasions, the NODE becomes vulnerable to the homogeneous balancing principle due to the integration of Eq (2.2).

(2). Next, we suggest a series-based solution to the NODE in Eq (2.1) using the Riccati ODE, which is as follows:

In this context, $\rho_l (l = -N, ..., N)$ denotes the unknown parameters, and $\zeta(\vartheta)$ is the solution to the first-order Riccati ODE stated as:

where $Q, R$, and $P$ are invariables.

(3). Applying a homogeneous balancing strategy to Eq (2.2) that involves balancing the greatest nonlinear component and the highest-order derivative will yield the positive integer $N$ utilised in (2.3).

(4). Following that, we place (2.3) into (2.2) or the equation that arises from integrating (2.2), organising terms $\zeta(\vartheta)$ with identical orders. An expression in $\zeta(\vartheta)$ is produced by this process. A set of algebraic equations representing the variables $\rho_l$ (where $l = -N, \ldots, N$) and other pertinent parameters is then expressed after the coefficients in this expression are equated to zero.

(5). This system of algebraic equations is then solved using Maple tool.

(6). Then, by calculating and entering the unknown values into Eq (2.3) together with the $\zeta(\vartheta)$ (the solution to (2.4)), analytical soliton solutions for (2.2) are obtained. We can get the resulting families of soliton solutions by using the generic solution of Eq (2.4):

Family 1. For $\Phi < 0$ & $R\neq0$,

and

Family 2. For $\Phi > 0$ & $R\neq0$,

and

Family 3. For $QP > 0$ & $Q = 0$,

and

Family 4. For $RP < 0$ and $Q = 0$,

and

Family 5. For $P = R$ & $Q = 0$,

and

Family 6. For $R = -P$ & $Q = 0$,

and

Family 7. For $\Phi = 0$,

Family 8. For $Q = \mu$, $P = p\mu(p\neq0)$ & $R = 0$,

Family 9. For $Q = R = 0$,

Family 10. For $Q = P = 0$,

Family 11. For $P = 0$, $R\neq0$ & $Q\neq0$,

and

Family 12. For $Q = \mu$, $R = p\mu(p\neq0)$ & $P = 0$,

where $\Phi = Q^2-4RP$.

3.   The execution of m-EDAM

In this section of the study, soliton solutions for the CIE, as specified in Eq (1.1), are generated using the mEDAM approach. First, apply the following variable transformation as part of the method:

The following NODE is obtained by applying this transformation to (1.1):

The following outcome can be obtained from a single integration on (3.2) with a zero integration constant:

After creating a homogeneous balancing condition between $Z''$ and $Z^3$, it is determined that $N = 1$. Substituting $N = 1$ into Eq (2.3), we obtain the ensuing closed-form solution for (3.3):

We acquire an expression based on the terms $\zeta(\vartheta)$ via including (3.4) in (3.3) and bringing together terms with powers alike $\zeta(\vartheta)$. By setting the coefficients to zero, this expression can be reduced to a set of algebraic nonlinear equations. After using Maple to solve this system, the following two sets of solutions are obtained:

Case 1.

Case 2.

By considering Case 1 and using (3.1), (3.4), and the corresponding general solution to (2.4), we construct the ensuing families of soliton solutions for CIE given in (1.1):

Family 1.1. When $\Phi < 0, \quad R\neq0$,

and

Family 1.2. When $\Phi > 0, \quad R\neq0$,

and

Family 1.3. When $RP > 0$ and $Q = 0$,

and

Family 1.4. When $RP < 0$ and $Q = 0$,

and

Family 1.5. When $R = P$ and $Q = 0$,

and

Family 1.6. When $R = -P$ and $Q = 0$,

and

Family 1.7. When $P = 0$, $Q\neq0$ and $R\neq0$,

and

Family 1.8. When $Q = \mu$, $R = p\mu(p\neq0)$ and $P = 0$,

where $\vartheta = y+x-\sigma t.$

Now, by considering Case 2 and using (3.1), (3.4), and the corresponding general solution to (2.4), we construct the ensuing families of soliton solutions for CIE given in (1.1):

Family 2.1. When $\Phi < 0, \quad R\neq0$,

and

Family 2.2. When $\Phi > 0, \quad R\neq0$,

and

Family 2.3. When $RP > 0$ and $Q = 0$,

and

Family 2.4. When $RP < 0$ and $Q = 0$,

and

Family 2.5. When $R = P$ and $Q = 0$,

and

Family 2.6. When $R = -P$ and $Q = 0$,

and

Family 2.7. When $Q = \mu$, $P = p\mu(p\neq0)$ and $R = 0$,

where $\vartheta = y+x-(\sigma-3\, \sqrt {\Phi}) t.$

4.   Discussion and graphs

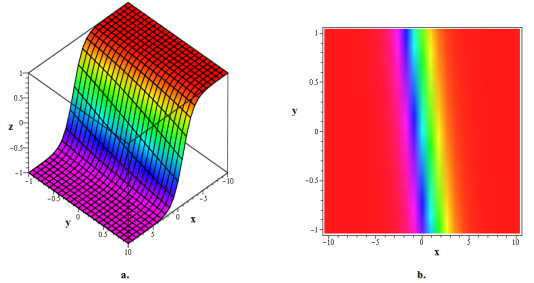
In this section, we show schematic illustrations of several wave configurations seen in the system that we are studying. Using m-EDAM, an improved version of EDAM, we discovered and visualised wave patterns in density and 3D graphs. These examples reveal that the soliton solutions generated primarily appear as cuspon or kink solitons. A kink soliton is the perfect example of a lone wave that has a sudden change or discontinuity in the variable or field it represents. It is also known as a domain wall or topological soliton. Kink solitons typically appear in systems that are going through a scalar field phase transition. On the other hand, a cuspon soliton, also called a cusped soliton, is a unique type of single wave with a cusp, or sharp peak, at the apex. It functions as a solution to a particular class of nonlinear wave equations in which the propagating single wave maintains its form.

Particular phenomena inherent to plasma physics account for the predominance of kink and cuspon solitons as principal soliton solutions to the CIE, a fundamental model of ion-acoustic waves to plasma. Particle interactions, magnetic fields, and nonlinear behaviours are all aspects of plasma dynamics that play a role in the creation and spread of single waves. The CIE, which records nonlinear phenomena in plasma, clarifies the creation of isolated waves with characteristic kinks and cusps. The CIE's mathematical foundations and plasma dynamics interact to produce cuspon solitons, which have sharp peaks, and kink solitons, which show sudden changes in fields as a result of phase transitions. As tracers of nonlinear interactions, these solitons provide information about the complex dynamics of ion-acoustic waves. Understanding these solitons helps to better understand plasma physics and provides insight into the wave behaviours of intricate plasma systems.

The m-EDAM has proven to be a reliable, practical, and easy-to-use tool that offers more general wave solutions for nonlinear models in mathematical physics and engineering. Moreover, our results, under some assumptions, agree with the results of other transformation-based methods such as the Riccati equation expansion method, $\left(\frac{G'}{G}\right)$-expansion method, sub-equation method, F-expansion method, and many more. For instance, all ten solutions by the modified F-expansion method in the study of Seadawy et al. ^[52] can be easily obtained from some of our 37 solutions produced by m-EDAM by assigning values to $P$, $Q$, and $R$ presented in our solutions. Our findings thus serve as a generalisation of the outcomes of the various approaches that were previously described. This adds an important new layer to the existing understanding of the CIE and demonstrates the adaptability and broader applicability of our research.

The graphical discussion presents the visualization of various soliton solutions derived from the mathematical models. Figure 1 illustrates the kink soliton solution $z_{1, 6}$ at $t = 0$ for specific parameter values. In Figure 2, the bright kink soliton solution $z_{1, 9}$ is depicted at $t = 1$, showcasing its behavior under different parameter settings. Figure 3 displays the bright kink soliton solution $z_{1, 18}$ at $t = 10$, highlighting its evolution over time. Meanwhile, Figures 4 and 5 focus on the imaginary part of cuspon soliton solutions $z_{1, 21}$ and $z_{1, 24}$ at different time instances, demonstrating their unique characteristics. In Figure 6, the kink soliton solution $z_{1, 32}$ is visualized at $t = 0$, revealing its structure under specific parameter conditions. Figures 7 and 8 showcase the dark kink soliton solutions $z_{2, 10}$ and $z_{2, 19}$ at different time points, emphasizing their behavior under varying parameters. Figure 9 presents the bright-dark soliton solution $z_{2, 23}$ at $t = 0$, while Figure 10 illustrates the kink soliton solution $z_{2, 31}$ at $t = 2$, providing insights into their dynamics under specific parameter configurations. Overall, these visualizations offer valuable insights into the behavior and characteristics of the soliton solutions under investigation.

5.   Conclusions

In conclusion, our study has thoroughly investigated the propagation of solitons in the CIE, a noteworthy model in plasma sciences, by employing the upgraded m-EDAM. By converting the CIE into a NODE and assuming a closed-form solution, numerous cuspon and kink soliton solutions have been identified, including hyperbolic, trigonometric, exponential, and rational functions. Density charts and 3D models that illustrate the propagating behaviour of specific soliton solutions provide important insights into the behaviour of soliton propagation processes, with direct applicability to domains related to the CIE. The results shown here are remarkable and demonstrate the novelty of using m-EDAM to the CIE, as they have not been covered in academic literature before. These discoveries advance our understanding of temporal evolution processes and nonlinear dynamics, which has significant implications for our comprehension of related physical phenomena. Moreover, the efficacy and uniformity of the employed techniques in this study underscore their broader significance for nonlinear problems across other scientific domains. While the utilisation of m-EDAM has significantly enhanced our understanding of soliton dynamics and their impact on the CIE, it is imperative to acknowledge the constraints of the methodology, particularly with the fair handling of the highest derivative and nonlinear variables. Despite this limitation, the work shows that our understanding of soliton behaviour and nonlinear dynamics will continue to expand and opens up new directions for future research in related fields. That is, the future scope of the current study lies in extending the proposed m-EDAM to study soliton events in nonlinear stochastic models, which will shed further light on how mechanistic and stochastic dynamics interact.

Author contributions

Naveed Iqbal: Conceptualization, Investigation and Writing-review & editing; Muhammad Bilal Riaz: Methodology, Conceptualization, Formal analysis and Administration and Funding acquisition; Meshari Alesemi: Methodology; Taher S. Hassan: Software and Investigation; Ali M. Mahnashi: Validation and Resources; Ahmad Shafee: Formal analysis and Resources. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This article has been produced with the financial support of the European Union under the REFRESH (Research Excellence For Region Sustainability and High-tech Industries) project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition.

The authors are thankful to the Deanship of Graduate Studies and Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program.

Conflict of interest

The authors declare that they have no conflicts of interest.