On the edge metric dimension of some classes of cacti

1.   Introduction

In graph theory, the metric dimension has become very popular nowadays and has sparked the interest of distinguished researchers to make more studies on it. This may be because of its applicability in real-life situations to diverse practical applications such as robot navigation, combinatorial optimization, processing of images, networks, tasks on coin-weighing and tricky games ^[1], pharmaceutical chemistry, pattern recognition ^[2], a tool for detecting network motifs ^[3], observers in detecting the source of a spread over a network ^[4], the basis of a method for embedding DNA sequences in real space ^[5], Sonar and coast guard Loran ^[6], etc. The idea of metric dimension was first introduced by Slater ^[6] who referred to it as a location number. He called the metric generator the locating set and the minimum metric generator the reference set. These ideas were also independently discovered by Harary and Melter ^[7], who used the term "metric dimension" for "location number". Nadeem et al. ^[38] worked on the locating number of biswapped interconnection networks. In this paper, we use the terms used by Harary and Melter. After discovering the metric dimension based on uniquely pinpointing distinct nodes, ^[8] went further on this idea, trying to think on the other side: What if the intruder is accessing the network through their connections (edges) between the nodes? Then, that intruder could not be pinpointed and, hence, the surveillance fails; this is where the idea of the edge metric dimension arises.

Since then, a significant number of results from different families of graphs have been published, such as ^{[9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]} to mention a few. In particular, the edge metric dimension of several graphs has been studied by different researchers. Iqbal et al. worked on the graphs $P_m \square P_n$, $P_m \square C_n$, and the generalized Petersen graph ^[9]; Filipović et al. ^[10] and Raza and Ji ^[11] studied the generalized Petersen graph; Iqbal et al. worked on double generalized Petersen graphs ^[12]; Geneson obtained a number of results about pattern avoidance in graphs with bounded edge metric dimension ^[13]; Goshi et al. ^[14] computed the fractional local edge dimension of a graph (FLED) of the Coxeter graph, Petersen graph, the families of cycle, complete, wheel, complete bipartite graphs, and grid; Geneson et al. ^[15] answered several open extremal problems on metric dimension and pattern avoidance in graphs posed by Geneson ^[13] and made the progress on a problem posed by Zubrilina ^[16]; Peterin and Yero studied the join, lexicographic, and corona product of graphs ^[17]; Zhang and Gao investigated some classes of plane graphs such as the web graph, convex polytope, and convex polytope antiprism and prism ^[18]; Siddiqui et al. determined the bounds of edge metric dimension of zero-divisor graphs ^[19]; Wei et al. ^[20] characterized all connected bipartite graphs with edge metric dimension $n-2$ and partially settled a problem from Zubrilina ^[16]; Zhu et al. ^[21] characterized the structure of topful graphs, and necessary and sufficient conditions for topful graphs were obtained; Zubrilina ^[16] settled two open problems posed by Kelenc et al. ^[8]; Adawiyah et al. studied some families of tree graph such as broom graph, star graph, banana tree graph, and double broom graph ^[22]; Deng et al. ^[23] worked on square, triangular and hexagonal Möbius ladder networks; Knor et al. ^[24] settled three open problems posed by Kelenc et al. ^[8]; Sedlar and Škrekovski worked on cacti where some results on edge metric dimension are obtained ^[25]; Ikhlaq et al. ^[26] studied dragon graph, paraline graph of dragon graph, line graph of dragon graph and line graph of dragon graph; Zhu et al. ^[27,28] studied unicyclic graphs; Knor et al. determined bounds on edge metric dimension of some simple 2-connected graphs ^[29]; Sedlar and Škrekovski showed the upper bound on leafless cacti and their characterization ^[30]; Sedlar and R. Škrekovski explored bounds on metric dimensions of graphs with edge disjoint cycles (cactus graphs) ^[31]; Rafiullah et al. studied some wheel related convex polytopes ^[32]; and Ahsan et al. worked on some classes of circulant graphs ^[33].

Graphs considered in this paper are undirected, finite, simple, and connected. Let $G =$ $(V, E)$ be a connected graph such that vertex $x \in V$ and edge $e = u v \in E$, then the distance between $x$ and $e$ is given by $d(x, e) = \min \{d(x, u), d(x, v)\}$. Two edges $e_1, e_2 \in E$ and $e_1 \neq e_2$ are said to be distinguished by a vertex $x \in V$ if $d\left(x, e_1\right) \neq d\left(x, e_2\right)$. A set $\mathcal{G}_e$ of vertices of a connected graph $G$ is an edge metric generator of $G$ if every two distinct edges of $G$ are distinguished by some vertex in $\mathcal{G}_e$. An edge metric generator with the smallest cardinality is called an edge metric basis of $G$, and the cardinality of the edge metric basis is called the edge metric dimension, which we denote by $\operatorname{edim}(G)$. The following approach might also be helpful for edge metric generators. Given an ordered set of vertices $\mathcal{G}_e = \left\{g_1, g_2, \ldots, g_k\right\}$ of a connected graph $G$, for any edge $e \in E$, we refer to the $k$ - vector (ordered $k$-tuple), $r\left(e \mid \mathcal{G}_e\right) =$ ($\left.d\left(e, g_1\right), d\left(e, g_2\right), \ldots, d\left(e, g_k\right)\right)$ as the edge metric representation of $e$ with respect to $\mathcal{G}_e$. In this regard, $\mathcal{G}_e$ is an edge metric generator for $G$ if, and only if, for every pair of distinct edges $e_1, e_2 \in$ $E$ implies $r\left(e_1 \mid \mathcal{G}_\epsilon\right) \neq r\left(e_2 \mid \mathcal{G}_e\right)$ or if $r\left(e_1 \mid \mathcal{G}_{\boldsymbol{\varepsilon}}\right) = r\left(e_2 \mid \mathcal{G}_{\boldsymbol{\varepsilon}}\right)$ implies $e_1 = e_2$.

Cactus graphs or cacti are connected graphs in which any two simple cycles have at most one vertex in common, or simply graphs with edge disjoint cycles. Some renowned researchers worked on these graphs. In ^[30], researchers studied leafless cacti, and the upper bound of edge metric dimension in terms of cyclomatic number is obtained; ^[25] worked on cacti using the configuration approach and obtained some significant results, including a simple upper bound on the edge metric dimension of cacti; ^[31] showed that metric dimension and edge metric dimension of cacti can differ by at most c, i.e., $|\operatorname{edim}(G)-\operatorname{dim}(G)| \leq c$, where $c$ is the number of cycles. In this paper, we investigate another class of cacti different from the cacti studied in ^[25,30,31]. The edge metric dimension of the following cacti: $\mathfrak{C}(n, c, r)$ and $\mathfrak{C}(n, m, c, r)$ will be explored in terms of the number of cycles (c) and the number of paths $(r)$.

2.   Preliminaries

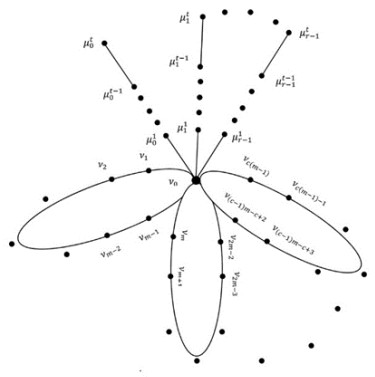
Cactus graphs or cacti are connected graphs in which any two simple cycles have at most one vertex in common. Let $\mathfrak{E}(n, c, r)$ be a cactus graph of order $n$ constructed by attaching $r$-paths in one common vertex of $c$-cycles of $C_m$ (see Figure 1); the respective lengths of each path and cycle are $t$ and $m$. For the sake of our proof, we will employ the following notations: $\mu_a^b$ as a vertex at $a^{\text {th}}$ path and distance $b$ from the common vertex $v_0, P_b^a$ as a path of length $b$ at $a^{\text {th}}$ position, $0 \leq$ $a \leq r-1, 1 \leq b \leq t$. Again, let $\mathfrak{E}(n, m, c, r)$ be a cactus graph of order $n$ constructed by attaching $c$-cycles of $C_3$ and $r$ - paths in one common vertex of $C_m$ (see Figure 2). Graphs explored in this study are expanded from the cactus graphs investigated in ^{[34,35,36,37]} on parameters different from edge metric dimension and worked on fixed cycles and pendant edges. In our study, we considered the graph with cycles of length $m$ and paths of length $t$, and the graph of any cycle of length $m$ with fixed cycles $\left(C_3\right)$ and paths of length $t$. We define: $V(\mathfrak{E}(n, c, r)) =$ $\left(\cup_{i = 1}^c V\left(C_i\right)\right) \cup\left(\cup_{j = 1}^r V\left(P_j\right)\right)$ and $E(\mathfrak{E}(n, c, r)) = \left(\cup_{i = 1}^c E\left(C_i\right)\right) \cup\left(\cup_{j = 1}^r E\left(P_j\right)\right)$, where $V\left(C_i\right) =$ $\left(\left\{v_0\right\}\right) \cup\left(\bigcup_{i = 1}^c\left(\left\{v_{(i-1) m-i+2}, v_{(i-1) m-i+3}, \ldots, v_{i(m-1)}\right\}\right)\right), V\left(P_j\right) = \bigcup_{j = 1}^r\left(\left\{\mu_{j-1}^1, \mu_{j-1}^2, \ldots, \mu_{j-1}^t\right\}\right)$ and $\quad E\left(C_i\right) = \cup_{i = 1}^c\left(\left\{v_0 v_{(i-1) m-i+2}, v_{(i-1) m-i+2} v_{(i-1) m-i+3}, \ldots, v_{i(m-1)} v_0\right\}\right), \quad E\left(P_j\right) =$ $U_{j = 1}^r\left(\left\{v_0 \mu_{j-1}^1, \mu_{j-1}^1 \mu_{j-1}^2, \ldots, \mu_{j-1}^{t-1} \mu_{j-1}^t\right\}\right)$, respectively. Again, $V(\mathfrak{E}(n, m, c, r)) = \left(V\left(C_m\right)\right) \cup$ $\left(\cup_{i = 1}^c V\left(C_i\right)\right) \cup\left(\cup_{j = 1}^r V\left(P_j\right)\right)$ and $E(\mathfrak{E}(n, m, c, r)) = \left(E\left(C_m\right)\right) \cup\left(\cup_{i = 1}^c E\left(C_i\right)\right) \cup\left(\cup_{j = 1}^r E\left(P_j\right)\right)$, where $\quad V\left(C_m\right) = \left(\left\{v_0\right\}\right) \cup \bigcup_{i = 1}^{m-1}\left(\left\{v_i\right\}\right), \quad V\left(C_i\right) = \bigcup_{i = 1}^c\left(\left\{v_0, \omega_{2 i-1}, \omega_{2 i}\right\}\right), V\left(P_j\right) =$ $\cup_{j = 1}^r\left(\left\{\mu_{j-1}^1, \mu_{j-1}^2, \ldots, \mu_{j-1}^t\right\}\right),$ and $\quad E\left(C_m\right) = \left\{v_0 v_1, v_1 v_2, \ldots, v_{m-1} v_0\right\}, \quad E\left(C_i\right) =$ $U_{i = 1}^c\left(\left\{v_0 \omega_{2 i-1}, \omega_{2 i-1} \omega_{2 i}, \omega_{2 i} v_0\right\}\right), \quad E\left(P_j\right) = \bigcup_{j = 1}^r\left(\left\{v_0 \mu_{j-1}^1, \mu_{j-1}^1 \mu_{j-1}^2, \ldots, \mu_{j-1}^{t-1} \mu_{j-1}^t\right\}\right)$, respectively.

Figure 1.  A cactus graph $\mathfrak{C}(n, c, r)$).

DownLoad: Full-Size Img PowerPoint

Figure 2.  A cactus graph $\mathfrak{C}(n, m, c, r)$).

DownLoad: Full-Size Img PowerPoint

Remark 2.1. ^[8] For any integer $n \geq 2, \operatorname{edim}\left(C_n\right) = \operatorname{dim}\left(C_n\right) = 2$.

3.   Results

Theorem 3.1. For any cactus graph $G = \mathfrak{C}(n, c, r)$ with $c$ number of $C_m$-cycles, such that every $C_m$ and $r$ paths have exactly one vertex in common, then $\operatorname{edim}(G) = 3 c-1$; moreover, if $r \neq c$, then $\operatorname{edim}(G) =$ $2 c+r-1$.

Proof. Let $\mathcal{G}_{e} = \left\{ \mu_{1}^{1}, \mu_{2}^{1}, \ldots, \mu_{r - 1}^{1}, \nu_{1}, \nu_{m - 1}, \nu_{m}, \nu_{2m - 2}, \ldots, \nu_{(c - 1)m - c + 2}, \nu_{c(m - 1)} \right\}$ be an edge metric generator (see Figure 1). We shall prove that $\mathcal{G}_{e}$ is an edge metric generator for any cactus graph $\mathfrak{C(}n, c, r)$, where $n$ is a total number of vertices of a cactus graph; to this end, we will employ the method of double inequality. For $edim\left(\mathfrak{C(}n, c, r) \right) \leq 3c - 1$, the following are the edge metric representations of all edges with respect to the edge metric generator $\mathcal{G}_{e}$.

$\begin{aligned} & r\left(\nu_{(\varphi - 1) + (m - 1)\omega}\nu_{\varphi + (m - 1)\omega} \middle| \mathcal{G}_{e} \right) \\ & = \left\{ \begin{array}{ccccc} \left(\varphi, \ldots, \varphi, \beta_{(c + 2\omega)^{th}position}, \varphi, \ldots, \varphi \right)_{(3c - 1\ tuple)}, & \omega = 0, & \varphi = \left\lfloor \frac{m}{2} \right\rfloor, & \beta = \varphi - 2, & m\ is\ odd, \\ \left(\varphi, \ldots, \varphi, \beta_{(c + 2\omega)^{th}position}, \varphi, \ldots, \varphi \right)_{(3c - 1\ tuple)}, & \omega = 1, & \varphi = \left\lfloor \frac{m}{2} \right\rfloor, & \beta = \varphi - 2, & m\ is\ odd, \\ \left(\varphi, \ldots, \varphi, \beta_{(c + 2\omega)^{th}position}, \varphi, \ldots, \varphi \right)_{(3c - 1\ tuple)}, & \omega = 2, & \varphi = \left\lfloor \frac{m}{2} \right\rfloor, & \beta = \varphi - 2, & m\ is\ odd, \\ \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ \left(\varphi, \ldots, \varphi, \beta_{(c + 2\omega)^{th}position}, \varphi \right)_{(3c - 1\ tuple)}, & \omega = c - 1, & \varphi = \left\lfloor \frac{m}{2} \right\rfloor, & \beta = \varphi - 2, & m\ is\ odd. \\ \end{array} \right. \end{aligned}$

Now, we need to show that no edges among these representations have the same representation. We shall show this by the contradiction approach. Suppose if possible, there are two distinct edges having the same representation, take edges $v_0 v_{1+(m-1) \varphi}$ and $v_{(m-1) \varphi} v_0$, then $r\left(v_0 v_{1+(m-1) \varphi} \mid \mathcal{G}_e\right) = r\left(v_{(m-1) \varphi} v_0 \mid \mathcal{G}_e\right)$, and, hence, $c+2 \varphi = c+2 \varphi-1$, a contradiction. Take edges $v_0 v_{1+(m-1) \varphi}$ and $v_\omega v_{\varphi}$, then $r\left(v_0 v_{1+(m-1) \varphi} \mid \mathcal{G}_e\right) = r\left(v_\omega v_{\varphi} \mid \mathcal{G}_e\right)$ implies $c+2 \varphi = \omega-1$, then $c+2 \varphi = \varphi-2$, and, hence, $c+\varphi+2 = 0$, a contradiction, since $c \geq 1$ and $\varphi \geq 1$. Take edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1}$ and $v_\omega v_{\varphi}$ where $\omega = \frac{m}{2}-1$ or $\left\lceil\frac{m}{2}\right\rceil-1$, then $r\left(v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1} \mid \mathcal{G}_e\right) = r\left(v_\omega v_{\varphi} \mid \mathcal{G}_e\right)$; implies $c = c+2 \omega$ and $c+1 = c+2 \omega+1$; both cases gives $\omega = 0$, a contradiction, since $\omega \geq 1$. Take edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1}$ and $v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega}$, and let $\lambda, \; \beta$ and $\lambda^{\prime}, \; \beta^{\prime}$ be parameters from edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1}$ and $v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega}$, respectively, then $\quad r\left(v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1} \mid \mathcal{G}_e\right) =$ $r\left(v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega} \mid \mathcal{G}_e\right)$ implies $\lambda = \beta^{\prime}$ and $\lambda^{\prime} = \beta$ if $m$ is even, then $\frac{m}{2}-1 = \frac{m}{2}-2$, a contradiction, and if $m$ is odd for the same edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1}$ and $v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega}$, let their parameters be $\beta$ and $\beta^{\prime}$, respectively, then $\varphi+1 = \varphi$ is a contradiction, and $\beta = \beta^{\prime}$ implies $\left\lfloor\frac{m}{2}\right\rfloor-1 = \left\lfloor\frac{m}{2}\right\rfloor-2$, a contradiction; again, $c+2 \omega = c+2 \omega+1$ is a contradiction. Take edges $v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega}$ and $v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1}$, then $r\left(v_{(\varphi-1)+(m-1) \omega} v_{\varphi+(m-1) \omega} \mid \mathcal{G}_e\right) = r\left(v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1} \mid \mathcal{G}_e\right)$ implies $c+2 \omega = c+2 \alpha-1$, and, hence, $2 c-2 = 2 c-1$, a contradiction.

Take edges $v_{(\alpha-1)(m-1)+\varphi} v_{(\alpha-1)(m-1)+\varphi+1}$ and $\quad v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1}$, then $r\left(v_{(\alpha-1)(m-1)+\varphi} v_{(\alpha-1)(m-1)+\varphi+1} \mid \mathcal{G}_e\right) = r\left(v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1} \mid \mathcal{G}_e\right)$ implies $c+2(\alpha-1) = c+2 \alpha-1$, and, hence, $2 \alpha-2 = 2 \alpha-1$, a contradiction. Take edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1} \quad$ and $\quad v_{(\alpha-1)(m-1)+\varphi} v_{(\alpha-1)(m-1)+\varphi+1}, \quad$ then $r\left(v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1} \mid \mathcal{G}_e\right) = r\left(v_{(\alpha-1)(m-1)+\varphi} v_{(\alpha-1)(m-1)+\varphi+1} \mid \mathcal{G}_e\right)$; implies $\beta = \omega$, and, hence, $\left\lfloor\frac{m}{2}\right\rfloor-1 = \left\lfloor\frac{m}{2}\right\rfloor-2$, a contradiction. Take edges $v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1}$ and $v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1}$, then $r\left(v_{\varphi+(m-1) \omega} v_{\varphi+(m-1) \omega+1} \mid \mathcal{G}_e\right) = r\left(v_{\alpha(m-1)-\varphi} v_{\alpha(m-1)-\varphi+1} \mid \mathcal{G}_e\right)$; implies $\beta = \omega$, and, hence, $\left\lfloor\frac{m}{2}\right\rfloor-1 = \left\lfloor\frac{m}{2}\right\rfloor-2$, a contradiction.

So, it clearly follows from the representations above that the edge metric representations of any two distinct edges of $\mathfrak{C}(n, c, r)$ are different. Thus, $\mathcal{G}_{e}$ is an edge metric generator and, therefore, $edim\left(\mathfrak{C}(n, c, r) \right) \leq 3c - 1.$

On the other hand, let us consider the converse part of double inequality. Assume that $\mathcal{G}_{e}$ is a set of vertices with at most $3c - 2$ distinct vertices, i.e., $edim\left(\mathfrak{C}(n, c, r) \right) \leq 3c - 2$. According to our graph, it suffices to show that $\mathcal{G}_{e}$ cannot be a set of vertices with $3c - 2$ distinct vertices, as any set of vertices less than $3c - 2$ distinct vertices also cannot be$\ \mathcal{G}_{e}$. Now, let us discuss the following cases.

Case 1: Let $\gamma \neq \gamma^{'}$, and take any two edge metric representations from edges $\nu_{0}\mu_{\gamma}^{1}$ and $\nu_{0}\mu_{\gamma'}^{1}$, where $\gamma, \gamma^{'} \in \omega$. First, let $\left| \mathcal{G}_{e}^{'} \right| = 3c - 1$ as the preceding part, before reducing at least one vertex from the vertices set $\mathcal{G}_{e}^{'},$ then $r\left(\nu_{0}\mu_{\gamma}^{1}|\mathcal{G}_{e}' \right) = \left(1, \ldots, 0_{\gamma^{th}position}, \ldots, 1 \right)_{(3c - 1\ tuple)}$ and $r\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e}' \right) = \left(1, \ldots, 0_{{\gamma^{'}}^{th}position}, \ldots, 1 \right)_{(3c - 1\ tuple)}$, since $\mu_{0}$ does not constitute to $\mathcal{G}_{e}'$ then $r\left(\nu_{0}\mu_{\gamma}^{1}|\mathcal{G}_{e}' \right) = (1, \ldots, 1)_{(3c - 1\ tuple)}$ for $\gamma = 0$ and $r\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e}' \right) = \left(1, \ldots, 0_{{\gamma^{'}}^{th}position}, \ldots, 1 \right)_{(3c - 1\ tuple)}$ for $2 \leq \gamma^{'} \leq r - 1$. Now, if any other vertex $\mu_{\gamma'}^{1}$ will be removed from $\mathcal{G}_{e}^{'}$ to form $\mathcal{G}_{e}$ with $\left| \mathcal{G}_{e} \right| = 3c - 2$, then we have; $r\left(\nu_{0}\mu_{\gamma}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ \gamma = 0$ and$\ r\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}$, $\ 2 \leq \gamma^{'} \leq r - 1$; similarly for $\gamma^{'} = 1$, we have $\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, {\ \ \gamma}^{'} = 1$, and, hence, $\mathcal{G}_{e}\ $ is not an edge metric generator, a contradiction.

Case 2: If vertex $\mu_{0}^{1}$ and one of the vertex $\nu_{i}, \ i = 1, m, 2m - 1, \ldots, (c - 1)m - c + 2$ from $C_{m}s$ does not constitute to$\mathcal{\ G}_{e}$, then we have; $r\left(\nu_{0}\nu_{i}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ i = 1, m, 2m - 1, \ldots, (c - 1)m - c + 2$, but then $r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}$, and, hence, $\mathcal{G}_{e}\ $ is not an edge metric generator, a contradiction.

Case 3: If vertex $\mu_{0}^{1}$ and one of the vertex $\nu_{j}, \ j = m - 1, 2m - 2, \ldots, c(m - 1)$ from $C_{m}s$ does not constitute to$\mathcal{\ G}_{e}$, then we have; $r\left(\nu_{0}\nu_{j}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ j = m - 1, 2m - 2, \ldots, c(m - 1)$, but then $r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}$, and, hence, $\mathcal{G}_{e}$ is not an edge metric generator, a contradiction.

Case 4: If vertex $\mu_{\gamma'}^{1}, \ 1 \leq \gamma^{'} \leq r - 1$ and one of the vertex $\nu_{i}\, \ i = 1, m, 2m - 1, \ldots, (c - 1)m - c + 2$ from $C_{m}s$ does not constitute to$\mathcal{\ G}_{e}$, then we have $r\left(\nu_{0}\nu_{i}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ \ i = 1, m, 2m - 1, \ldots, (c - 1)m - c + 2$, but then $r\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ 1 \leq \gamma^{'} \leq r - 1$, and, hence, $\mathcal{G}_{e}$ is not an edge metric generator, a contradiction.

Case 5: If vertex $\mu_{\gamma'}^{1}, \ 1 \leq \gamma^{'} \leq r - 1$ and one of the vertex $\nu_{j}, \ j = m - 1, 2m - 2, \ldots, c(m - 1)$ from $C_{m}s$ does not constitute to$\mathcal{\ G}_{e}$, then we have $r\left(\nu_{0}\nu_{j}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ j = m - 1, 2m - 2, \ldots, c(m - 1)$, but then $r\left(\nu_{0}\mu_{\gamma'}^{1}|\mathcal{G}_{e} \right) = (1, \ldots, 1)_{(3c - 2\ tuple)}, \ 1 \leq \gamma^{'} \leq r - 1$, and, hence, $\mathcal{G}_{e}$ is not an edge metric generator, a contradiction.

Case 6: If one of the vertex $\nu_{i}, \ i = 1, m, 2m - 1, \ldots, (c - 1)m - c + 2$ from $C_{m}s$ and one of the vertex $\nu_{j}, \ j = m - 1, 2m - 2, \ldots, c(m - 1)$ from $C_{m}s$ does not constitute to$\mathcal{\ G}_{e}$, then we have $r\left(\nu_{0}\nu_{i}|\mathcal{G}_{e} \right) = r\left(\nu_{0}\nu_{j}|\mathcal{G}_{e} \right)$, and, hence, $\mathcal{G}_{e}$ is not an edge metric generator, a contradiction.

Now, from our discussion above it is clearly observed that $\mathcal{G}_{e}$ with $3c - 2$ distinct vertices or less than $3c - 2$ distinct vertices cannot be an edge metric generator, hence $edim\left(\mathfrak{C}(n, c, r) \right) \geq 3c - 1$; this proves double inequality, that is, $edim\left(\mathfrak{C}(n, c, r) \right) = 3c - 1$. Now, for $r \neq c$, we have to consider the number of paths $(r)$ and the number of cycles $(c)$ independently, since $\mathcal{G}_{e}$ contains at least two vertices from each cycle and one vertex from each path except one path, then $\left| \mathcal{G}_{e} \right| = 2c + r - 1$. The proof is analogous to the preceding proof with slight changes. Replace $3c - 1\ tuple$ with $2c + r - 1\ tuple$ and $3c - 2\ tuple$ with $2c + r - 2\ tuple$, hence, $edim(G) = 2c + r - 1$. □

Theorem 3.2. For any cactus graph $G\mathfrak{ = C}(n, m, c, r)$ $\textrm{with}$ $r -$ paths, $c -$ number of $C_{3}$ cycles, and one $C_{m}$ cycle at one common vertex of $C_{m}$, then$\ edim(G) = 2c + r + 1$; moreover, if $c = r$, then $edim(G) = 3c + 1$.

Proof. We shall prove our result by the double inequality approach, and now we prove that the upper bound of edge metric dimension of $G$ is $2c + r + 1$, that is, $edim(G) \leq 2c + r + 1$. Let $\mathcal{G}_{e}$ be a set of vertices consisting of two vertices from $C_{m}$, two vertices from each $C_{3}$, and one vertex from each $(r - 1)$ paths (see Figure 2), then $\mathcal{G}_{e}$ is an edge metric generator with cardinality $2c + r + 1$; if each $C_{3}$ and path has exactly one vertex in common, thus $\mathcal{G}_{e}$ has cardinality $3c + 1$. So, the metric representations of all edges of $G$ with respect to $\mathcal{G}_{e}$ are discussed hereunder.

Let $P_{t}^{0}$ be the path of length $t$ from vertex $\nu_{0}$ to vertex $\mu_{0}^{t}$ where $\nu_{0}$ is the common vertex for $C_{3}$, r-paths, and $C_{m}$, $\mu_{0}^{i}$, $1 \leq i \leq t$ is the vertex on the path that does not constitute any vertex to $\mathcal{G}_{e}$, and edges on this path are $e_{1} = \left\{ \nu_{0}, \mu_{0}^{1} \right\}, \ e_{i} = \left\{ \mu_{0}^{i - 1}, \mu_{0}^{i} \right\}, \ 2 \leq i \leq t$. Now, if we let $e_{i}$ and $e_{i + \alpha}, \ 2 \leq i \leq t, \ 1 \leq \alpha \leq t - 2$ be any two distinct edges on this path, then $r\left(e_{1}|\mathcal{G}_{e} \right) = {(1, \ldots, 1)\ }_{(2c + r + 1\ tuple)}$, $r\left(e_{i}|\mathcal{G}_{e} \right) = {(i, \ldots, i)\ }_{(2c + r + 1\ tuple)}, \ \ r\left(e_{i + \alpha}|\mathcal{G}_{e} \right) = {(i + \alpha, \ldots, i + \alpha)\ }_{(2c + r + 1\ tuple)}$. Clearly, $\mathcal{G}_{e}$ distinguishes all edges of $P_{i}^{0}$. Take one edge from $P_{i}^{0}, \ 1 \leq i \leq t$ and one edge from any of the path $P_{j}^{k}, \ 1 \leq j \leq t, \ \ 1 \leq k \leq r$ that constitute one vertex to $\mathcal{G}_{e}$, edges of $P_{j}^{k}$ are $e_{1} = \left\{ \nu_{0}, \mu_{k}^{1} \right\}, \ e_{j} = \left\{ \mu_{k}^{j - 1}, \mu_{k}^{j} \right\}, \ 2 \leq j \leq t, \ 1 \leq k \leq r$, then $r\left(e_{1}|\mathcal{G}_{e} \right) = {(0, 1, \ldots, 1)\ }_{(2c + r + 1\ tuple)},$ for $k = 1$, $r\left(e_{1}|\mathcal{G}_{e} \right) = {\left(1, \ldots, 0_{k^{th}Position}, \ldots, 1 \right)\ }_{(2c + r + 1\ tuple)}$ for $k \geq 2$, $r\left(e_{j}|\mathcal{G}_{e} \right) = {(j - 2, j, \ldots, j)\ }_{(2c + r + 1\ tuple)}$ for $k = 1$, $r\left(e_{j}|\mathcal{G}_{e} \right) = {\left(j, \ldots, (j - 2)_{k^{th}position}, \ldots, j \right)\ }_{(2c + r + 1\ tuple)}$ for $k \geq 2$, $i \neq j$. If $i = j$, let $e_{j} = e_{i}'$ to distinguish from edges of $P_{i}^{0}$, $r\left(e_{i}'|\mathcal{G}_{e} \right) = {(i - 2, i, \ldots, i)\ }_{(2c + r + 1\ tuple)}$ for $k = 1$, $r\left(e_{i}'|\mathcal{G}_{e} \right) = {\left(i, \ldots, (i - 2)_{k^{th}position}, \ldots, i \right)\ }_{(2c + r + 1\ tuple)}$ for $k \geq 2$, Clearly, $\mathcal{G}_{e}$ distinguishes any edge of $P_{i}^{0}$ from any edge of $P_{j}^{k}$. Take two distinct edges in path $P_{j}^{k}$, say $e_{j} = \left\{ \mu_{k}^{j - 1}, \mu_{k}^{j} \right\}, \ 2 \leq j \leq t, \ 1 \leq k \leq r$, and $e_{j + \alpha} = \left\{ \mu_{k}^{j + \alpha - 1}, \mu_{k}^{j + \alpha} \right\}, \ 1 \leq \alpha \leq t - 2$, then $r\left(e_{j + \alpha}|\mathcal{G}_{e} \right) = {(j + \alpha - 2, j + \alpha, \ldots, j + \alpha)\ }_{(2c + r + 1\ tuple)}$for $k = 1$, $r\left(e_{j + \alpha}|\mathcal{G}_{e} \right) = {\left(j + \alpha, \ldots, (j + \alpha - 2)_{k^{th}position}, \ldots, j + \alpha \right)\ }_{(2c + r + 1\ tuple)}$ for $k \geq 2$, $\mathcal{G}_{e}$ distinguishes all edges of $P_{j}^{k}$. Take one edge from $P_{i}^{0}$ and one edge incident to $\nu_{0}$ from $C_{3}$. Let edges incident to $\nu_{0}$ from $C_{3}$ be $\nu_{0}\omega_{\gamma}\, 0 \leq \gamma \leq 2c - 1$, their representation is ${r(\nu}_{0}\omega_{\gamma}\left| \mathcal{G}_{e} \right) = \left(1, \ldots, 0_{(r + \gamma + 2)^{th}position}, \ldots, 1 \right)_{(2c + r + 1\ tuple)}, 0 \leq \gamma < 2c - 1, \ {\ \ r(\nu}_{0}\omega_{\gamma}\left| \mathcal{G}_{e} \right) = \left(1, \ldots, 1, 0_{(2c - 1)^{th}position} \right)_{(2c + r + 1\ tuple)}$, and $\ \mathcal{G}_{e}$ distinguishes edges of $P_{i}^{0}$ from edges incident to $\nu_{0}$ of $C_{3}$. Take one edge from $P_{i}^{0}$ and one edge which is not incident to $\nu_{0}$ from $C_{3}$, let edges which are not incident to $\nu_{0}$ from $C_{3}$ be $\omega_{2\gamma}\omega_{2\gamma + 1}, \ 0 \leq \gamma \leq c - 1$, their representation is $r\left(\omega_{2\gamma}\omega_{2\gamma + 1} \middle| \mathcal{G}_{e} \right) = \left(2, \ldots, 0_{(r + 2\gamma + 2)^{th}position}, 0_{(r + 2\gamma + 3)^{th}position}\ldots, 2 \right)_{(2c + r + 1\ tuple)}, \ 0 \leq \gamma \leq c - 1$, and $\ \mathcal{G}_{e}$ distinguishes edges of $P_{i}^{0}$ from edges which are not incident to $\nu_{0}$ of $C_{3}$. Take one edge from $P_{j}^{k}$ and one edge incident to $\nu_{0}$ from $C_{3}$; and refer their representation; clearly, $\mathcal{G}_{e}$ distinguishes edges of $P_{j}^{k}$ from edges incident to $\nu_{0}$ of $C_{3}$. Similarly, edges of $P_{j}^{k}$ and edges which are not incident to $\nu_{0}$ of $C_{3}$ are distinguished by $\mathcal{G}_{e}$. Now, we show that $\mathcal{G}_{e}$distinguishes all edges of $C_{m}$, and the following are representation of all edges in $C_{m}$.

${r(\nu}_{0}\nu_{1}\left| \mathcal{G}_{e} \right) = \left(1, \ldots, 0_{r^{th}position}, \ldots, 1 \right)_{(2c + r + 1\ tuple)}$,

${r(\nu}_{m - 1}\nu_{0}\left| \mathcal{G}_{e} \right) = \left(1, \ldots, 0_{{r + 1}^{th}position}, \ldots, 1 \right)_{(2c + r + 1\ tuple)}$,

If $m$ is even then,

${r(\nu}_{\varphi}\omega_{\varphi + 1}\left| \mathcal{G}_{e} \right) = \left(\varphi + 1, \ldots, (\varphi - 1)_{r^{th}position}, \ldots, \varphi + 1 \right)_{(2c + r + 1\ tuple)},$ $1 \leq \varphi \leq \frac{m}{2} - 2$,

${r(\nu}_{\frac{m}{2} - 1}\nu_{\frac{m}{2}}\left| \mathcal{G}_{e} \right) = \left(\frac{m}{2}, \ldots, \left(\frac{m}{2} - 2 \right)_{r^{th}position}, \left(\frac{m}{2} - 1 \right)_{(r + 1)^{th}position}, \ldots, \frac{m}{2} \right)_{(2c + r + 1\ tuple)}$,

${r(\nu}_{\frac{m}{2}}\nu_{\frac{m}{2} + 1}\left| \mathcal{G}_{e} \right) = \left(\frac{m}{2}, \ldots, \left(\frac{m}{2} - 1 \right)_{r^{th}position}, {\left(\frac{m}{2} - 2 \right)\ }_{(r + 1)^{th}position}, \ldots, \frac{m}{2} \right)_{(2c + r + 1\ tuple)}$,

${\ r(\nu}_{\frac{m}{2} + \varphi}\nu_{\frac{m}{2} + \varphi + 1}\left| \mathcal{G}_{e} \right) = \left(\frac{m}{2} - \varphi, \ldots, \left(\frac{m}{2} - \varphi - 2 \right)_{(r + 1)^{th}position}, \ldots, \frac{m}{2} - \varphi \right)_{(2c + r + 1\ tuple)}$, $1 \leq \varphi \leq \frac{m}{2} - 2$.

If $m\ $ is odd then,

${r(\nu}_{\varphi}\omega_{\varphi + 1}\left| \mathcal{G}_{e} \right) = \left(\varphi + 1, \ldots, (\varphi - 1)_{r^{th}position}, \ldots, \varphi + 1 \right)_{(2c + r + 1\ tuple)}, \ 1 \leq \varphi \leq \left\lfloor \frac{m}{2} \right\rfloor - 1$,

${\ r(\nu}_{\left\lfloor \frac{m}{2} \right\rfloor}\nu_{\left\lfloor \frac{m}{2} \right\rfloor + 1}\left| \mathcal{G}_{e} \right) = \left(\left\lfloor \frac{m}{2} \right\rfloor + 1, \ldots, \left(\left\lfloor \frac{m}{2} \right\rfloor - 1 \right)_{r^{th}position}, \left(\left\lfloor \frac{m}{2} \right\rfloor - 1 \right)_{(r + 1)^{th}position}, \ldots, \left\lfloor \frac{m}{2} \right\rfloor + 1 \right)_{(2c + r + 1\ tuple)}$,

${r(\nu}_{\left\lfloor \frac{m}{2} \right\rfloor + \varphi}\nu_{\left\lfloor \frac{m}{2} \right\rfloor + \varphi + 1}\left| \mathcal{G}_{e} \right) = \left(\left\lfloor \frac{m}{2} \right\rfloor - \varphi + 1, \ldots, \left(\left\lfloor \frac{m}{2} \right\rfloor - \varphi - 1 \right)_{r^{th}position}, \ldots, \left\lfloor \frac{m}{2} \right\rfloor - \varphi + 1 \right)_{(2c + r + 1\ tuple)}$, $1 \leq \varphi \leq \left\lfloor \frac{m}{2} \right\rfloor - 1$.

Clearly, $\mathcal{G}_{e}$ distinguishes all edges of $C_{m}$. Furthermore, by referring their representation of edges of $P_{i}^{0}$, $\ P_{j}^{k}$, $\ C_{3}$, and $C_{m}$, one can easily see that $\mathcal{G}_{e}$ distinguishes all their edges. This shows that $\mathcal{G}_{e}$ is an edge metric generator for the graph $G$, which implies that$\ edim(G) \leq 2c + r + 1$.

On the other hand, we have to prove that the lower bound of edge metric dimension of $G$ is $2c + r + 1$, that is, $edim(G) \geq 2c + r + 1$. To this end, we have to show that there is no edge metric generator with cardinality$\ 2c + r$. Contrary, we suppose that there is $\mathcal{G}_{e}'$ with cardinality $2c + r$ such that $\mathcal{G}_{e}' \subset \mathcal{G}_{e} = \left\{ g_{1}, \ldots, g_{l} \right\}, \ 1 \leq l \leq 2c + r + 1$. Let $\mu_{0}^{1}$ be a vertex of $P_{i}^{0}$ that does not constitute to $\mathcal{G}_{e}$. Now, let us consider the following cases.

Case 1: Let $\mathcal{G}_{e}^{'} \subset \mathcal{G}_{e}$ be an edge metric generator obtained by removing one $g_{l}$ vertex of the path $P_{j}^{k}$ from $\mathcal{G}_{e}$, say $x \in \left\{ g_{1}, \ldots, g_{l} \right\}$, then $r\left(\nu_{0}x|\mathcal{G}_{e}' \right) = r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e}' \right)$, a contradiction.

Case 2: Let $\mathcal{G}_{e}^{'} \subset \mathcal{G}_{e}$ be an edge metric generator obtained by removing one $g_{l}$ vertex of the $C_{3}$ from $\mathcal{G}_{e}$, say $y \in \left\{ g_{1}, \ldots, g_{l} \right\}$ then $r\left(\nu_{0}y|\mathcal{G}_{e}' \right) = r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e}' \right)$, a contradiction.

Case 3: Let $\mathcal{G}_{e}^{'} \subset \mathcal{G}_{e}$ be an edge metric generator obtained by removing one $g_{l}$ vertex of the $C_{m}$ from $\mathcal{G}_{e}$, either $\nu_{1}$ or $\nu_{m - 1}$, since $\nu_{1}, \nu_{m - 1} \in \left\{ g_{1}, \ldots, g_{l} \right\}$; are the only vertices that constitute to $\mathcal{G}_{e}$ from $C_{m}$. Now say $\nu_{1}$ is removed from $\mathcal{G}_{e}$, then $r\left(\nu_{0}\nu_{1}|\mathcal{G}_{e}' \right) = r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e}' \right)$, a contradiction; if $\nu_{m - 1}$ is removed instead of $\nu_{1}$, then$\ r\left(\nu_{0}\nu_{m - 1}|\mathcal{G}_{e}' \right) = r\left(\nu_{0}\mu_{0}^{1}|\mathcal{G}_{e}' \right)$, a contradiction.

So, in either case, if we reduce the number of vertices from $\mathcal{G}_{e}$ by at least one, we arrive to contradiction. This shows that $\mathcal{G}_{e}'$ with cardinality $2c + r$ cannot be an edge metric generator, which implies that $edim(G) \geq 2c + r + 1$. □

4.   Conclusions

The exploration of the edge metric dimension across various classes of cacti has revealed an interesting feature of graph theory. In this paper, we investigated the edge metric dimension of cactus graphs, namely, $\mathfrak{\ C(}n, c, r)$ and $\mathfrak{C}(n, m, c, r)$. The investigation has demonstrated that the number of cycles and paths determines the edge metric dimension of this class of cacti rather than their respective lengths, emphasizing the importance of structural features in understanding graph metric properties. This observation not only broadens our understanding of the relationship between graph topology and metric dimension in these classes of cacti, but also extends to the wide range of graph families that have been studied in this area, from ^[9] through ^[33] where edge metric dimension was determined in different ways. For instance, just to mention a few, in ^[25] edge metric dimension was determined in terms of the number of leaves and number of cycles, constant edge metric dimension was determined in ^[12,23], etc. Moreover, in $\mathfrak{C(}n, c, r)$, if one $C_{m}$ cycle is fixed and the rest are replaced by $C_{3}$, then the resulting graph is $\mathfrak{C}(n, m, c, r)$, however, the proof for each graph is given independently and purposefully. Their edge metric dimensions differ by 2, and this difference is due to the fixed $C_{m}$ cycle; by Remark 2.1.

Author contributions

Lyimo Sygbert Mhagama: Conceptualization, Methodology and Formal Analysis, Investigation, Writing-original draf; Muhammad Faisal Nadeem: Conceptualization, Validation, Writing-review & editing; Mohamad Nazri Husin: Conceptualization, Validation, Investigation, Writing-review & editing. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors acknowledge the support of the Universiti Malaysia Terengganu and the Higher Education for Economic Transformation (HEET) project of the government of the United Republic of Tanzania for their financial support while doing this research.

Conflict of interest

There is no conflict of interest declared by the authors.