Model averaging with causal effects for partially linear models

1.   Introduction

Causal effects are fundamental to project evaluation across various fields, such as economics, finance, and biomedicine. It is well known that the central issue in project evaluation in these fields is to identify the "causal relationships" that exist between project treatments and project outcomes and to quantify the "causal effects". For example, pharmaceutical companies are interested in the effect of a new drug or device developed to treat a disease, and investment banks are concerned with the profitability of companies that have received significant capital investment. These research questions rely on estimating treatment effects; thus, studying the identification, estimation, and empirical application of treatment effects is crucial and meaningful. Causal effects are also referred to as treatment effects in the literature.

It is essential, in some cases, to accurately capture heterogeneous treatment effects. For example, a new medicine could be more beneficial for children than for adults; an advertising strategy for sanitary napkins may be more persuasive for women than for men. These results indicate that using knowledge of heterogeneous treatment effects can maximize the value and effectiveness of treatment programs ^[15]. A commonly used heterogeneous treatment effects measurement is the conditional average treatment effect (CATE), to which much recent attention has been given.

In several studies, CATE has been estimated by fitting a parametric model to the relationship between observations and baseline covariates, in conjunction with treatment assignment. Alternatively, CATE can be estimated by modeling the conditional mean of potential outcomes using a parametric model based on the baseline covariates for each treatment group. Examples include ^[2,9,19,22]. However, in practice, practitioners generally have datasets in which not all covariates show a linear relationship with each other. Instead, the data may be nonparametric. In this context, partially linear models (PLMs) are more applicable to such datasets, which combine the interpretability of linear models with the flexibility of nonparametric models.

Therefore, we consider a partially linear regression framework ^[3] in which the distribution of the response $Y_i$ may depend on a binary treatment assignment indicator $\delta_i\in\{0, 1\}$ and the baseline covariates $(X_i, U_i)$. To segregate the treatment differences of the primary interest, we assume for the observations that

where $\{Y_{t, i}, Y_{c, i}\}$ denote the $Y_i$ associated pair of potential outcomes and $\delta_i$ represents the treatment indicator variable, taking $\delta_i = 1$ if the individual belongs to the treatment group and $\delta_i = 0$ otherwise. $X_i = (x_{i1}, x_{i2}, \dots)^{\rm{T}}$ is covariate and $U_i$ is univariate covariate. ${\boldsymbol{\beta}}$ is an unknown coefficient vector associated with $X_i$, $g(\cdot)$ is an unknown smooth nonlinear function, and $e_1, \dots, e_n$ are unobservable heteroscedastic random errors independent of $\{X_i, U_i\}_{i = 1}^n$ with conditional mean $E(e_i|X_i, U_i) = 0$ and conditional variance $E(e_i^2|X_i, U_i) = \sigma_{i}^2$. A fundamental problem in statistics and causal inference is to improve predictive accuracy based on observable datasets $\{Y_i, X_i, U_i, \delta_i\}_{i = 1}^n$.

Researchers, however, usually have multiple candidate models assumed based on various understandings of the observed data. Thus, Polling and Yang ^[15] proposed the treatment effect across-validation (TECV) method. It is a model selection method for studying CATE, which is able to identify a model that is most suitable for estimating CATE among multiple candidate models. However, there is a risk of model uncertainty, and it is impossible to know whether the model is the most suitable for the dataset. If researchers cannot select the optimal model, they will face missing useful information, leading to unstable estimation. The model averaging method can reduce the risk of regression estimation and the bias introduced by selecting a single model, avoid ignoring the useful information contained in the remaining candidate models, and thereby improve prediction accuracy.

Model averaging methods have been applied to handle causal inference problems. For example, Gao et al., ^[5] developed a model averaging method based on the JMA of ^[7] to estimate the average treatment effect (ATE). ^[11] proposed a data-driven approach to averaging the estimators over candidate specifications to address the specification uncertainty in the weighted estimation of propensity scores for the average treatment effect on treated (ATT). Rolling et al., ^[16] introduced a model combination technique, treatment effect estimation by mixing (TEEM), which was designed to amalgamate estimators from various programs. This approach is used to generate more accurate CATE estimations. Although TEEM is compatible with parametric, nonparametric, or semiparametric statistical models, as well as nonstatistical machine learning processes and even subjective expert judgment, the approach proposed by ^[16] may encounter difficulties in finding treatment-control pairs in each cell after partitioning. This is especially true when dealing with a large or even moderate number of covariates. Thus, we discussed a model averaging estimation for the CATE with multiple candidate partially linear regression models.

To the best of our knowledge, no optimal model averaging estimation has been developed for PLMs based on the jackknife-type criterion to address causal inference problems. Motivated by this, under heteroscedastic error, the primary goal of the current article is to develop a model averaging estimation for the conditional average treatment effect with PLMs based on a jackknife-type criterion called the CPLJMA method, where C, PL, and JMA represent causal effects, partially linear, and jackknife model averaging, respectively. However, it is difficult to directly extend the available results to our idea for the following reasons: For existing optimal model averaging estimations for PLMs, important examples include ^[27], who proposed optimal model averaging estimation for PLMs with the Mallows-type criterion based on kernel estimation (MAPLM). Zeng et al., ^[25] proposed focused information criteria and frequentist model averaging estimators for semiparametric partially linear models with missing responses and established their theoretical properties. We utilize a different jackknife-type weight choice criterion from theirs, and, additionally, we add an extra theorem of weight convergence. Our main contributions to these challenges are as follows: (ⅰ) On a theoretical basis, the proposed estimator is asymptotically optimal in terms of minimizing the squared error loss. (ⅱ) The convergence property of the weights is investigated, and we prove that the sum of the weights assigned to the correct candidate model is one as the sample size increases to infinity. This is true, provided that there is at least one correctly specified candidate model. In the simulation section, numerical simulations and empirical analysis are applied to verify the validity of the proposed model averaging approach and the analytical framework; this proves theoretical support for the wide application of such model averaging methods.

The remainder of this paper is organized as follows. In Section 2, we describe the estimation procedure of the jackknife criterion for CATE based on PLMs, and we study its theoretical properties in Section 3. Section 4 illustrates the performance of our proposal via simulations and data examples. Concluding remarks are made in Section 5. Technical proofs are deferred to the Supplementary.

2.   Model and estimation procedure

2.1.   Preliminaries

First, we use the potential outcomes framework ^[8,18] to define the CATE as the expectation of the random variable conditional on the observed value of the baseline covariates $(X_i, U_i)$, that is

where $Y_{t, i}-Y_{c, i}$ indicates the treatment effect for the $i$th individual; this is also labeled the "fundamental problem of causal inference" because $Y_{t, i}$ and $Y_{c, i}$ are infeasible to observe simultaneously. The main goal of this study is to estimate $\mu_i$ based on the model averaging method.

Under the causal inference framework, we make the following identifiability assumptions ^[1]:

Assumption 1. Consistency: $Y_i = \delta_iY_{t, i}+(1-\delta_i)Y_{c, i}$;

Assumption 2. Unconfoundedness: $\{Y_{t, i}, Y_{c, i}\}\perp \delta_i\mid \{X_i, U_i\}$;

Assumption 3. Positivity: $0 < c_{\pi}\leq \pi(X_i, U_i)\leq 1-c_{\pi} < 1$ almost surely, where $\pi(X_i, U_i) = P(\delta_i = 1|Y_{t, i}, Y_{c, i}, X_i, U_i) = P(\delta_i = 1|X_i, U_i)$ denotes the propensity score and $c_{\pi}$ is a positive constant.

Assumption 1 links potential outcomes to observed outcomes and requires the potential outcomes to be well defined. Assumption 2 is conditional independence, which implies that the treatment assignment indicator $\delta_i$ is independent of the potential outcome $\{Y_{t, i}, Y_{c, i}\}$ given covariates $X_i$ and $U_i$, and it requires that all potential confounding information on the relationship between treatments and potential outcomes is observed in the covariates; it precludes potential confounding between treatment assignments and outcomes. Assumption 3 implies that treatment assignments are not deterministic, which is crucial for controlling confounding bias and systematic differences between the treatment and control groups. This assumption also guarantees $\pi(X_i, U_i)$ and $1-\pi(X_i, U_i)$ are invertible with probability one. ^[17] referred to the combination of Assumptions 2 and 3 as a "strongly ignorable treatment assignment".

Inverse probability weighting (IPW) based on the potential outcome framework is a powerful tool for correcting confounding bias. The IPW approach utilizes the inverse of the propensity scores to construct weights for observed outcomes to balance baseline covariates between groups ^[10]. Under the strongly ignorable treatment assignment assumption, suppose

to construct the unbiased estimator of $\mu_i$ given the conditions $X_i$, $U_i$. Then, after careful calculation, we have

The unreasonable model selected to estimate the CATE may yield uncertain estimations. To provide a more reasonable and robust CATE estimator, we develop a model averaging estimation for CATE with multiple candidate PLMs.

2.2.   Estimation procedure

As discussed earlier, we can obtain computationally feasible PLMs of heterogeneous causal effects based on treatment-control pairs. In accordance with Eq (2.1) and model (1.1), we let $e_{\pi, i} = Z_{\pi, i}-\mu_{i}$. Then, we have

where $\mu_i$ denotes the CATE for the $i$th individual, $E(e_{\pi, i}|X_i, U_i) = 0$, and $E(e^2_{\pi, i}|X_i, U_i) = \sigma_{\pi, i}^2$. Let us note that $\{Z_{\pi, i}, X_i, U_i\}^n_{i = 1}$ is fully observed when $\pi(X_i, U_i)$ is known.

Specifically, we consider multiple candidate models for model (2.2) of the form

used for evaluating $\mu_i$, where $x_{ij}^{(m)}$ is the $j$th entry of $X_i^{(m)}$, $X_i^{(m)}$ is an $k_m$-dimensional subvector of $X_i$, $\beta_j^{(m)}$ is the corresponding regression coefficient vector, $g(\cdot)$ is an unknown function in the nonparametric part, and $M_n$ denotes the total number of candidate models allowed to go to infinity.

Define ${{\mathbf Z}}_{\pi} = (Z_{\pi, 1}, \ldots, Z_{\pi, n})^{\rm{T}}\in\mathbb{R}^{n}$, ${{\mathbf X}}^{(m)} = (X_1^{(m)}, \dots, X_n^{(m)})^{\rm{T}}\in\mathbb{R}^{n\times k_m}$, where $\{x_{ij}^{(m)^{\rm{T}}}\}_{i = 1}^n$ is an $1\times k_m$ column vector, ${{\mathbf g}}({{\mathbf U}}) = (g(U_1), \dots, g(U_n))^{\rm{T}}\in\mathbb{R}^{n}$, and ${{\mathbf e}}_{\pi} = (e_{\pi, 1}, \dots, e_{\pi, n})^{\rm{T}}\in\mathbb{R}^{n}$. Then, the $m$th candidate model in matrix form is

To estimate the nonparametric function, we use the B-spline regression method. Let $\mathcal{S}_{n}$ be the space of polynomial splines of degree $l\ge 1$, and let $\{\psi_{k}, k = 1, \ldots, d_{n}\}$ denote a normalized B-spline basis. For any $g_{n}\in\mathcal{S}_{n}$, we have

for some coefficients $\{\alpha_{k}\}_{k = 1}^{d_{n}}$, where $\Psi({{\mathbf U}}) = (\psi_1({{\mathbf U}}), \dots, \psi_{d_n}({{\mathbf U}}))^{\rm{T}}$, ${\boldsymbol{\alpha}} = (\alpha_1, \dots, \alpha_{d_n})^{\rm{T}}$. Here, $d_{n}$ increases with $n$. We define the $n\times d_n$ matrix ${{\mathbf K}} = (\Psi(U_1), \dots, \Psi(U_n))^{\rm{T}}$. Then, we assume that the $n\times (p+d_n)$ matrix ${{\mathbf X}}^{(m)^*} = ({{\mathbf X}}^{(m)}, {{\mathbf K}})$ is nonsingular and associated with the unknown $(p+d_n)$-dimensional parameter vector ${\boldsymbol{\gamma}}^{(m)} = ({\boldsymbol{\beta}}^{(m)^{\rm{T}}}, {\boldsymbol{\alpha}}^{\rm{T}})^{\rm{T}}$. Thus, we have

By regressing ${{\mathbf Z}}_{\pi}$ on ${{\mathbf X}}^{(m)^*}$, the least squares estimator of ${\boldsymbol{\beta}}^{(m)}$ and $\alpha$ can be obtained as

and

where ${{\mathbf Q}} = {{\mathbf K}}({{\mathbf K}}^{\rm{T}}{{\mathbf K}})^{-1}{{\mathbf K}}^{\rm{T}}$ is a symmetric idempotent matrix. Then

where $\tilde{{{\mathbf X}}}^{(m)} = ({{\mathbf I}}-{{\mathbf Q}}){{\mathbf X}}^{(m)}$ is a symmetric idempotent matrix and ${{\mathbf P}}^{(m)} = {{\mathbf Q}}+\tilde{{{\mathbf X}}}^{(m)}(\tilde{{{\mathbf X}}}^{(m)^{\rm{T}}}\tilde{{{\mathbf X}}}^{(m)})^{-1}\tilde{{{\mathbf X}}}^{(m)^{\rm{T}}}$. Then the corresponding model averaging estimator of ${\boldsymbol{\mu}}$ can be formulated as

where ${{\mathbf P}}({\boldsymbol{\omega}}) = \sum_{m = 1}^{M_n}\omega_m {{\mathbf P}}^{(m)}$ and ${\boldsymbol{\omega}} = (\omega_1, \dots, \omega_{M_n})^{\rm{T}}$ is a weight vector belonging to the continuous set ${\mathcal{H}}_n = \left\{{\boldsymbol{\omega}}\in[0, 1]^{M_n}:\sum_{m = 1}^{M_n}\omega_m = 1\right\}$.

Notably, the choice of weight vector is crucial in the model averaging method. Thus, we consider the jackknife-type criterion to choose the weight vector ${\boldsymbol{\omega}}$ for (2.4) in the PLMs framework. Specifically, leave-one-out cross-validation (LOO-CV) is used to estimate ${\boldsymbol{\mu}}$, and then the estimator in the $m$th candidate model is given by

where ${{\mathbf D}}^{(m)} = {\rm{diag}}(D_{11}^{(m)}, \dots, D_{nn}^{(m)})\in\mathbb{R}^{n\times n}$ with the $i$th diagonal element $D_{ii}^{(m)} = h_{m, ii}/(1-h_{m, ii})$, ${{\mathbf A}}^{(m)} = {{\mathbf I}}_n-{{\mathbf P}}^{(m)}$, and $h_{m, ii}$ is the $i$th diagonal entry of ${{\mathbf P}}^{(m)}$. Thus, the jackknife-type model averaging estimator is

where $\tilde{{{\mathbf P}}} = \sum_{m = 1}^{M_n}\omega_m\tilde{{{\mathbf P}}}^{(m)}$. Then, the weight choice criterion is

The optimal weight vector is obtained by minimizing the criterion in (2.5) over the space ${\mathcal{H}}_n$. However, such a minimization process in real-world data analysis is computationally infeasible because $\pi(X_i, U_i)$ is generally unknown. In our modeling framework, we estimate it by adopting the logistic partially linear models (LPLMs) in ^[24],

which relies on generalized partially linear models (GPLMs) in ^[14], where the coefficients $\theta$ for the linear part and the nonparametric part $\kappa(\cdot)$ are estimated using B-spline basis estimation. This method is facilitated by the "sgplm1" function within the R package "gplm", with the degrees of freedom set to "$df = 3$". Further elucidation of this choice is provided in the subseqent numerical simulations. Then, $\hat{\pi}(X_i, U_i)$ is substituted for $\pi(X_i, U_i)$ with ${{\mathbf Z}}_{\pi}$ to obtain ${{\mathbf Z}}_{\hat{\pi}}$. Then, a feasible counterpart of $\mbox{CV}_{\pi}({\boldsymbol{\omega}})$ in (2.5) becomes

The optimal weights $\hat{{\boldsymbol{\omega}}}_{cv}$ are obtained by selecting ${\boldsymbol{\omega}}\in {\mathcal{H}}_n$ to minimize the jackknife-type criterion in

Given $\tilde{{\boldsymbol{\omega}}}_{cv}$, substituting it into (2.4) yields the optimal model averaging estimator of ${\boldsymbol{\mu}}$ as $\hat{{\boldsymbol{\mu}}}_{\hat\pi}(\hat{{\boldsymbol{\omega}}}_{cv})$ in the case where $\hat{\pi}(X_i, U_i)$. $\mbox{CV}_{\hat\pi}({\boldsymbol{\omega}})$ is a quadratic programming problem with respect to ${\boldsymbol{\omega}}$, that is, $\mbox{CV}_{\hat\pi}({\boldsymbol{\omega}}) = {\boldsymbol{\omega}}^{\rm{T}}{{\mathbf H}}_{\hat\pi}^{\rm{T}}{{\mathbf H}}_{\hat\pi}{\boldsymbol{\omega}}$, where ${{\mathbf H}}_{\pi} = ({{\mathbf Z}}_{\hat\pi}-\tilde{{{\mathbf P}}}_{(1)}{{\mathbf Z}}_{\hat\pi}, \dots, {{\mathbf Z}}_{\hat\pi}-\tilde{{{\mathbf P}}}_{(M_n)}{{\mathbf Z}}_{\hat\pi})$.

3.   Theoretical properties

In this section, we focus on some theoretical properties of our proposed model averaging method. In Subsection 3.1, we prove the asymptotic optimality of the model averaging estimator $\hat{{\boldsymbol{\mu}}}(\hat{{\boldsymbol{\omega}}}_{cv})$ by illustrating that the selected weight vector $\hat{{\boldsymbol{\omega}}}_{cv}$ yields a squared error that is asymptotically identical to that of the infeasible optimal weight vector. Subsection 3.2 concerns the convergence property of the optimal weight vector $\hat{{\boldsymbol{\omega}}}_{cv}$. When the sample size tends to infinity, the sum of the weights assigned to the correct model by the optimal weight vector obtained by the proposed method converges to one in probability.

3.1.   Asymptotic optimality

Before introducing the theoretical properties, we first define some notations. Let $\mu_{t, i} = E(Y_{t, i}|X_i, U_i)$ and $e_{t, i} = Y_{t, i}-\mu_{t, i}$ denote the conditional expectation and the random error of the treatment group, respectively, in which $\sigma^2_{t, i} = E(e_{t, i}^2|X_i, U_i)$. The loss function and the corresponding risk function of $\hat{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})$ are defined as

respectively, where $\|\cdot\|$ is the Euclidean norm. Let $\xi_{\pi} = \inf_{\omega\in\mathcal{H}_n}R_{\pi}({\boldsymbol{\omega}})$, $\bar{k} = \max_{1\leq m\leq M_n} k_m$, and $\bar{h} = \max_{1\leq m\leq M_n}\max_{1\leq i\leq n}h_{m, ii}$. The following conditions are assumed with respect to $n\rightarrow \infty$.

(C1) $\sqrt{n}\|\hat{\theta}_n-\theta_0\| = O_p(1)$ and $\|\hat{\kappa}_{\hat{\theta}_n}-\kappa_0\| = o_p(n^{-1/4})$, in which $\theta_0$ and $\kappa_0$ are the true values of $\theta$ and $\kappa$, respectively, and the first derivatives of $\hat{\pi}(X_i, U_i; \theta, \kappa)$ with respect to $\theta$ and $\kappa$ are continuous and bounded.

(C2) For some integers $G\geq 1$,

where $i = 1, \dots, n$, and $\bar{C}$ is a positive constant.

(C3) For some integers $1\leq G\leq \infty$,

(C4) $\bar{h} \quad \stackrel{a.s.}\rightarrow 0$ and $(\bar{d}+\bar k)\xi_{\pi}^{-2} \quad \stackrel{a.s.}{\rightarrow }0$.

(C5) The functions $\{g_j(U)\}_{j = 1}^{n}$ belong to a class of functions $\mathcal{F}$, whose $r$th derivative $g_j^{(r)}$ exists and is Lipschitz of order $\eta$,

for some positive constant $G$, where $r$ is a nonnegative integer and $\eta\in(0, 1]$, such that $\upsilon = r+\eta > 0.5$.

Condition (C1), a commonly used restriction for GPLMs, requires $\sqrt{n}$-consistent estimates for the parametric component $\hat{\theta}_n$. The nonparametric component $\hat{\kappa}_{\hat{\theta}_n}$ is viewed as a function of the parametric component to achieve consistency. This restriction is reasonable ^[20]. Condition (C2) is a moment condition concerning random errors, and it is satisfied by $\{\mu_i, \mu_{t, i}\}_{i = 1}^n$, which are bounded. Condition (C3) is a convergence condition that imposes certain restrictions on the circumstances for applying our asymptotic outcome. A prerequisite for Condition (C3) to hold is $\xi_{\pi}\rightarrow \infty$, which requires that no finite-dimensional correct model exists in the class of candidate models ^[6]. It also requires that $M_n$ and $\max_{1\leq m\leq M_n}R_{\pi}(\omega_m^o)$ go to infinity slowly enough. Condition (C4), an assumption that excludes the case of extremely unbalanced design matrices as candidate models, is widely imposed in studies of optimal model averaging based on cross-validation, such as ^[7,12], among others. The B-spline approximation in PLMs requires Condition (C5) with references to ^[4,21], which is a regularity condition that necessitates the nonparametric coefficient function to be sufficiently smooth.

Theorem 1. If Conditions (C1)–(C5) are satisfied, then

Theorem 1 demonstrates its asymptotic optimality by minimizing the approximate risk with squared error loss. This theorem illustrates that the square error with selected model weights $\hat{{\boldsymbol{\omega}}}_{cv}$ minimized by the LOO-CV criterion is asymptotically equal to that of the infeasible optimal weight vector.

3.2.   Weight convergence

In this subsection, we concentrate on the convergence properties of the optimal weights in model averaging. It should be noted that, in this article, the $m$th candidate model in (2.3) is deemed correctly specified or a correct model if there exists ${\boldsymbol{\beta}}^{(m)^*}$ such that $\mu = {{\mathbf X}}^{(m)}{\boldsymbol{\beta}}^{(m)^*}+{{\mathbf g}}({{\mathbf U}})$; otherwise, model (2.3) is said to be mispecified or an incorrect model.

We first introduce some notation. $\hat{s}_{cv}$ is defined as the sum of the weights assigned to the correct candidate models using our proposed method, which can be denoted as $\hat{s}_{cv} = \sum_{m = 1}^{m_0}\hat{{\boldsymbol{\omega}}}_{cv, m}$ in mathematical notation, where $m_0$ indicates that the first $m_0$ candidate models are all correctly specified. Let ${\mathcal{H}}_{F} = \{{\boldsymbol{\omega}}\in[0, 1]^{M_n}:\sum_{m = m_0+1}^{M_n}\omega_m = 1\}$ be the weight set of all incorrect candidate models and $\xi_{\pi, F} = \inf_{{\boldsymbol{\omega}}\in{\mathcal{H}}_F}R_{\pi}({\boldsymbol{\omega}})$ is the optimal risk when the weights are assigned to all the mispecified candidate models. We specify some necessary conditions for further analysis based on $n\rightarrow \infty$.

$({\rm{C6}})$ For some integers $1\leq G\leq \infty$,

$({\rm{C7}})$ $\bar{h} = O(n^{-1/2})$.

Condition (C6) requires $\xi_{\pi, F}^{-2G}$ to grow at a rate no slower than $m_0(\bar{d}+\bar{k})^{2G}$ and $(M_n-m_0)\sum_{m = m_0}^{M_n-m_0}\{R_{\pi}(\omega_m^o)\}^G$. It is worth noting that if $(M_n-m_0)\sum_{m = m_0}^{M_n-m_0}\{R_{\pi}(\omega_m^o)\}^G$ is larger than $m_0(\bar{d}+\bar{k})^{2G}$, then Condition (C6) is identical to $(M_n-m_0)\xi_{\pi, F}^{-2G}\sum_{m = m_0}^{M_n-m_0}\{R_{\pi}(\omega_m^o)\}^G \quad \stackrel{a.s.}\rightarrow 0$ and is thus analogous to Condition (C3). Condition (C7), excluding the case of peculiar models as candidate models, is from ^[13].

Theorem 2. If Conditions (C1)–(C7) are satisfied, then

Theorem 2 indicates that the model averaging estimator $\hat{{\boldsymbol{\mu}}}(\hat{{\boldsymbol{\omega}}}_{cv})$ of our proposal is sufficient for the sum of the weights assigned to the correct models to converge to one in probability as the sample size goes to infinity and automatically excludes the incorrect models.

4.   Numerical studies

To demonstrate the theoretical properties of Section 3, in this section we conduct two Monte Carlo experiments on the finite-sample performance, where Case 1 verifies the asymptotic optimality of Theorem 1 with the candidate models all misspecified, and Case 2 justifies the weight convergence property of Theorem 2 with at least one correct model specified. In addition, the superiority of our method is illustrated by applying it to the Diabetes dataset. For a better analysis, we also consider several relevant existing methods as competitors to our CPLJMA approach, including the model selection methods for AIC, BIC, and treatment effect cross-validation (TECV) proposed by ^[15]; Information criterion-based model averaging methods such as SAIC and SBIC; the equal weight method (EW); and treatment effect estimation by mixing (TEEM) and the Mallows averaging of partially linear models (MAPLM). We calculate the mean squared error (MSE) to assess the performances of the estimators, defined as $\mbox{MSE} = \frac{1}{nD}\sum_{d = 1}^{D}\|\{\hat{{\boldsymbol{\mu}}}({\boldsymbol{\omega}})\}^{(d)}-{\boldsymbol{\mu}}^{(d)}\|^2$, where ${\boldsymbol{\mu}}^{(d)}$ and $\{\hat{{\boldsymbol{\mu}}}({\boldsymbol{\omega}})\}^{(d)}$ are the CATE and model averaging estimator in the $d$th replicate, respectively. $D$ denotes the number of replicates of the simulation. Additionally, we calculated $\mbox{MSE}_{median}$ in the empirical analysis, defined as $\mbox{MSE}_{median} = \mbox{median}_{d = 1, \dots, D}\mbox{MSE}^{(d)}$, and the optimal rate, which is the percentage of the smallest MSE value. In complement to the rigorous numerical investigations detailed earlier, we embark on the task of determining the number of (interior) knots. Like the pivotal role of bandwidth in kernel smoothing, these knots, akin to tuning parameters, have a remarkable influence on the smoothness and adaptability of our spline models. The details of the numerical study and its results are described in the following subsections.

4.1.   Monte Carlo study

Case 1: Without correct candidate models

The data-generating process (DGP) is as follows:

where $X_{i1} = 1$. $\{X_{ij}\}_{j = 2}^J$, the covariates of the linear part, are generated from a multivariate normal distribution with mean 0 and covariance $0.5^{|j_1-j_2|}$ between $x_{ij_1}$ and $x_{ij_2}$. The associated coefficients in the linear component are taken as $\beta_j = 1/j$. The coefficient function $g(U_i) = \sin(2\pi U_i)$, where $U_i \sim \mbox{Uniform}[0, 1]$. $\{e_{t, i}, e_{c, i}\}$ are independent random errors distributed from $N(0, \sigma^2X_{i2}^2)$, where the parameter $\sigma^2$ is chosen by $R^2 = var(\mu_i)/var(Y_{t, i}-Y_{c, i})$, which varies on a grid between 0.1 and 0.9. Then

We rescaled $\mu_i$ to have unit variance so that the expected $R^2$ equals $\frac{1}{1+\sigma^2}$ for the unknown model. It is clear from (4.1) that the class of candidate models considered in this case is misspecified. In addition, to obtain $\{\delta\}^n_{i = 1}$, the propensity score is taken as

Thus, we obtain $\{Y_i\}^n_{i = 1}$. For $\hat{\pi}(X_i, U_i)$, we use the GPLMs in (2.6) to approximate the coefficients of the linear part and the form of the nonparametric part.

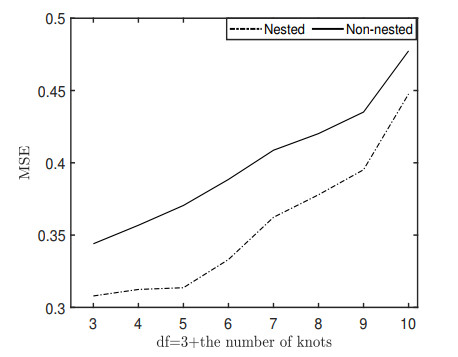
First, we delve into the influence of interior knots within the B-spline basis on the performance of our proposed CPLJMA approach. By employing the "$bs(\cdot, df)$" function from the R package "$splines$", we generate an appropriate B-spline basis matrix. Here, the degree of freedom parameter, denoted as $df$, is a crucial factor, determined by "$df = 3 + the\; number\; of\; knots$".

Figure 1 shows the variation in MSE as the number of interior knots varies, considering a sample size of $n = 300$ and $R^2 = 0.5$, and for both nested and nonnested setting scenarios. In the nested setting, the $m$th candidate model comprises the first $m$ linear variables in $\{X_{ij}\}_{j = 1}^{500}$. The number of candidate models $M_n$ is determined as the nearest integer from $3n^{1/3}$, resulting in $M_n = 20$. In the nonnested setting, the linear components of all candidate models are a subset of $\{X_{i1}, \dots, X_{i5}\}$, disregarding the remaining $X_i$ variables, thereby yielding a total of $2^5-1 = 31$ candidate models. As depicted in the figure, the MSE increases with an increase in the number of knots, potentially exacerbating the phenomenon of overfitting. Consequently, we opt for "$df = 3$" as the degree of freedom for the CPLJMA method, ensuring a balance between model flexibility and susceptibility to overfitting.

The greater the number of covariates, the more tedious the computation. Therefore, in substantiating the theoretical properties outlined in Theorem 1 through numerical simulations, we adopt a nested setting. Accordingly, when the sample sizes are $n = 75,150,300$, and $600$, then $M_n = 12, 15, 20$, and $25$, respectively.

Figure 2 illustrates a numerical inspection for the asymptotic optimality of $\hat{\mu}_{\hat{\pi}}(\hat{\omega}_{cv})$ in Theorem 1 by showing the mean of LR, defined as $LR = L_{\hat\pi}(\hat{{\boldsymbol{\omega}}}_{cv})/\inf_{{\boldsymbol{\omega}}\in\mathcal{H}_n}L_{\hat\pi}({\boldsymbol{\omega}})$, for different samples and various $R$. In a simulation trial based on 100 replications, we observe that the mean curve of LR decreases and converges to one as $n$ increases. This intuitively demonstrates the asymptotic optimality of CPLJMA.

Figure 3 shows the MSE ratio curves for the seven CATE ${\boldsymbol{\mu}}$ estimators we considered, where we used the AIC as the denominator to yield the MSE ratio with an entry of 1.00. Generally, our proposed CPLJMA outperforms its competitors on the MSE ratios when $R^2$ or $n$ is small or moderate, particularly because it is difficult to identify the optimal model when there is considerable noise in the model. The advantage of model averaging without relying on a single model is that it provides protection against poor model selection. As expected, SAIC and SBIC invariably yielded more accurate results than did their respective model selection rivals. In short, to some extent, CPLJMA is superior to its competitors.

Case 2: With correct candidate models

The DGP is generated from

where the vector of covariates $X_i = (X_{i1}, \dots, X_{i5})^{\rm{T}}$ is from an independent standard normal distribution $N(0, 1)$, $U_i$ is distributed as $U[-1, 1]$, and the corresponding coefficient and nonparametric function are $\beta_j = 1/j$ and $1.2U_i$, respectively. The settings for $\{e_{t, i}, e_{c, i}\}$, $\sigma$, $R^2$, and $bf$ are the same as those in Case 1. Thus, we can obtain

The propensity score is taken as

Based on the LPLMs in (2.6), we can obtain $\{\hat{\pi}(X_i, U_i)\}_{i = 1}^n$ and thus $\{Z_{\pi, i}\}_{i = 1}^n$. In this case, we consider the nonnested models. The linear parts of all candidate models are constructed by varying combinations of $\{X_{i1}, X_{i2}, X_{i3}, X_{i4}, X_{i5}\}$; thus, $M_n = 2^5-1$. The sample size is taken as $n = 75,150,300,600$. The results for the convergence of the model weights $\hat{{\boldsymbol{\omega}}}_{cv}$ and the MSE ratio of the above methods are given in Figures 4 and 5, respectively, based on 100 replications.

Figure 4 clearly shows that the sum of the weights corresponding to the correct candidate models tends to one as the sample sizes $n$ and $R^2$ increase. This intuitively confirms the convergence of $\hat{\omega}_{cv}$ presented in Theorem 2 via numerical inspection.

As shown in Figure 5, we still derive the MSE ratio using AIC as the denominator. In most cases, the results of the MSE ratio demonstrate the merits of our approach over its competitors. Obviously, as $R^2$ increases progressively, the MSE ratio for all scenarios tends to decrease, as expected. Increasing the sample size also improved the performance for all approaches. Overall, CPLJMA still outperforms several existing methods.

4.2.   Empirical analysis

Our proposed method is applied to the Diabetes dataset from Dr. John Schorling, Department of Medicine, University of Virginia School of Medicine. The original data consisted of 19 covariates on 403 subjects from 1046 subjects interviewed in a study. However, due to the availability of missing data, we selected 16 covariates and 366 respondents as the dataset for the current case study, 175 of whom respondents resided in Buckingham and 191 of whom did not.

Our analysis considers the outcome variable ${{\mathbf Y}}$ to be stabilized glucose. The treatment indicator variable $\delta$ takes the value of 1 if people reside in Buckingham, and 0 otherwise. We calculated the Pearson correlation coefficients of the 14 baseline covariates ${{\mathbf X}}$ and ${{\mathbf U}}$ with ${{\mathbf Y}}$ and ranked them in descending order of correlation strength. Let us note that all continuous covariates ${{\mathbf X}}$ and ${{\mathbf Y}}$ are standardized to have a mean of zero and a variance of one, and ${{\mathbf U}}$ is scaled to $[0, 1]$. See Table 1 for details.

We assume that the candidate models consist of nested models constructed from the covariates in $\{X_1, \dots, X_{13}, {{\mathbf U}}\}$ with intercept terms, where the baseline covariates are ${{\mathbf X}}$ for the linear part, and we consider that age is a covariate ${{\mathbf U}}$ for the nonparametric part. Accordingly, there are 13 well-prepared candidate models. To implement our proposal, the propensity score $\pi(X_i, U_i)$ is still solved by LPLMs.

We conduct a "guided simulation experiment" to evaluate the performance of our proposal and that of its competitors. In particular, we use the largest candidate model containing all covariates as a guided model, and $m^*$ denotes the index of that model in the class of candidate models. Based on the $m^*$th candidate model and the original dataset $\{Y_i, X_i, U_i, \delta_i\}_{i = 1}^n$, we can obtain a simulation dataset $\{Y_{i}^{(m^*)}, X_i, \delta_i, U_i\}_{i = 1}^n$. Thus,

where $\hat{\rho}^{(m^*)}$ and $\hat{\eta}^{(m^*)}$ are the regression coefficient estimators for the linear part, $f^{(m^*)}(U_i^{(m^*)})$ and $h^{(m^*)}(U_i^{(m^*)})$ are the estimators for the nonparametric part, and $\{e_{t, i}^{(m^*)}, e_{c, i}^{(m^*)}\}_{i = 1}^n$ is from $N(0, 1)$. Therefore, the "true" $\mu_i$, CATE, is known in this analysis dataset, namely,

We randomly selected samples from $20\%, 40\%, 60\%, 80\%$, and $100\%$ of the dataset to describe the performance of the proposed CPLJMA and its competitors by MSE, $MSE_{median}$, and the optimal rate based on 100 replications.

The results are displayed in Table 2. Our approach produced a lower MSE and median and a higher optimal rate than those of its competitors across all sample sizes considered. As expected, the average methods based on the information criterion perform better than the model selection methods. To some extent, our proposal has a clear advantage over its competitors in solving practical problems.

5.   Conclusions

Considering the heterogeneity and heteroskedasticity information embedded in the dataset, the problem of model uncertainty, and the flexibility and interpretability of PLMs, a jackknife-type method based on the weight selection criterion and its feasible form, called the CPLJMA method, are proposed for estimating the CATE. Within this context, we consider the optimal model weights chosen by minimizing the LOO-CV criterion, in which the B-splines approximate the nonparametric function, and we demonstrate its asymptotic optimality in accordance with a minimization of the approximate risk with squared error loss. In addition, since the choice of weights is crucial to the model averaging method, we considered the convergence properties of the weights, that is, when the sample size goes to infinity and at least one candidate model is correctly specified, the sum of weights obtained by our approach for the correct candidate models converges to one in probability. In the simulation section, we examine the finite-sample performance of our estimator and compare it with several other model selection and averaging methods. We illustrate our method by using a real-world dataset. The simulation results indicated that our method possessed some advantages relative to its competitors.

There are still many issues worthy of further discussion. First, our proposed CPLJMA method is valid only for one-dimensional covariates with respect to the nonparametric part, and it can be further refined and extended to multiple dimensions. Second, the least squares loss used as the loss function in our analysis is more sensitive to outliers. Thus, quantile regression, which is less sensitive to outliers, is considered as a loss function because developing the model averaging process and establishing its asymptotic properties remains challenging; this area deserves future research.

Author contributions

X. Zhang: Writing—original draft; X. Zhang and J. Li: Writing—review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the editors and reviewers for their valuable and insightful comments. The authors also thank Professor Guangren Yang for his advice for revising the paper.

Conflict of interest

The authors declare no conflict of interest.

Supplementary

This Supplementary provides detailed proofs of the main theorems stated in the above.

Lemmas and their proofs

We introduce some lemmas and their proofs before proving the Theorems in Section 3.

Lemma 1. Provided that Conditions (C1)-(C2) hold, we have $\|Z_{\hat{\pi}}-Z_{\pi}\|^2 = O_p(1)$.

Proof. According to the monotonicity of the $L_r$-norm and the Holder inequality, we have

almost surely, where the second inequality and the last inequality are attributed to the Holder inequality and Condition (C2), respectively. Thus, we know that for any $\epsilon > 0$, there exists an integer $N_{\epsilon}$ such that $P(\max_{1\leq i\leq n}\sigma_i^2 > \bar{C})\leq\epsilon/2$ for all $n\geq N_{\epsilon}$. Let $M_{\epsilon} = 2\bar{C}/\epsilon$. Then we have

Thus, we have

Similarly, it can be obtained that

By the Cauchy-Schwarz inequality, we obtain

where the last equation is due to Condition (C2), (5.2) and (5.3). Lemma 1 holds, if we can prove that

By the Taylor expansion, one has

where $\theta_i^*$ is a vector between $\hat{\theta}_n$ and $\theta_0$, and $\kappa_i^*$ is a vector between $\kappa_{\hat{\theta}_n}$ and $\kappa_0$. Expanding $\hat{\pi}(X_i, U_i; \theta_i^*, \kappa_i^*)$ in a Taylor series and considering the property of $\pi(X_i, U_i)$, we have

where $\theta_i^{**}$ is a vector between $\hat{\theta}_i^{*}$ and $\theta_0$, and $\kappa_i^{**}$ is a vector between $\hat{\kappa}_i^{*}$ and $\kappa_0$. Together with Condition (C2), this shows that (5.4) is valid. Likewise, we determine that (5.5) is valid. Therefore, the proof of Lemma 1 is completed. □

Lemma 2. By Condition (10) of Theorem 2.1 in ^[26], we have

With Assumption 3, for some integer $1\leq G\leq \infty$, there exists

Lemma 3. Let $\widetilde{{\boldsymbol{\omega}}} = \mathit{\mbox{argmin}}_{{\boldsymbol{\omega}}\in {\mathcal{H}}_n} \{L_n({\boldsymbol{\omega}})+a_n({\boldsymbol{\omega}})+b_n\}$, where $a_n({\boldsymbol{\omega}})$ is a term related to ${\boldsymbol{\omega}}$ and $b_n$ is a term unrelated to ${\boldsymbol{\omega}}$. Let $R_n({\boldsymbol{\omega}}) = E\{L_n({\boldsymbol{\omega}})|X, U\}$. If

and there exists a constant $c$ and a positive integer $N^*$ so that when $n\geq N^*$, $\inf_{{\boldsymbol{\omega}}\in {\mathcal{H}}_n} R_n({\boldsymbol{\omega}})\geq c > 0$ almost surely, then $L_n(\tilde{{\boldsymbol{\omega}}})/\inf_{{\boldsymbol{\omega}}\in {\mathcal{H}}_n}L_n({\boldsymbol{\omega}})\rightarrow 1$ in probability. $

Lemma 4. For any $n_1\times n_2$ matrices ${\mathbf B}_1$ and ${\mathbf B}_2$,

Theorems and theirs proofs

Proof of Theorem 1:

$\lambda_{\max}(\cdot)$ is denoted as the largest singular value of a matrix. From Condition (C2), we have

By the definition of $R_{\pi}({\boldsymbol{\omega}})$, it can be shown that

where ${{\mathbf A}}({\boldsymbol{\omega}}) = {{\mathbf I}}_{n}-{{\mathbf P}}({\boldsymbol{\omega}})$. Define the loss function of $\tilde{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})$ as $\tilde{L}_{\pi}({\boldsymbol{\omega}}) = \|{\boldsymbol{\mu}}-\tilde{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})\|^2$ and its corresponding risk function as $\tilde{R}_{\pi}({\boldsymbol{\omega}}) = E\{\tilde{L}_{\pi}({\boldsymbol{\omega}})|X, U\}$. Similarly, we have $\tilde{R}_{\pi}({\boldsymbol{\omega}}) = \|\tilde{{{\mathbf A}}}({\boldsymbol{\omega}}){\boldsymbol{\mu}}\|^2+{\rm{tr}}\{\tilde{{{\mathbf P}}}({\boldsymbol{\omega}}){\boldsymbol{\Omega}}_{\pi} \tilde{{{\mathbf P}}}({\boldsymbol{\omega}})^{\rm{T}}\}$ in which $\tilde{{{\mathbf A}}}({\boldsymbol{\omega}}) = {{\mathbf I}}_{n}-\tilde{{{\mathbf P}}}({\boldsymbol{\omega}})$. Define

Then we have

Thus, to prove Theorem 1, it suffices to hold that

We can obtain (5.12) in Lemma 2, which implies that (5.12) is valid.

For (5.13), it is noted that

Hence, for (5.13) to hold, it suffices to show that

In addition, according to Lemma 4 and the property of ${{\mathbf P}}_{(m)}$, we have

Note that

which, along with (5.18) and the first term of Condition (C4), leads us to

To prove (5.16), it is necessary only to verify that, for any $\delta > 0$,

where $C_1$ is a positive constant. The third inequality, fourth inequality, and fifth inequality are derived from the triangle inequality, Markov's inequality and (7) of Theorem 2 of ^[23], respectively. The sixth line follows from inequality ${\rm{tr}}({{\mathbf B}}_1{{\mathbf B}}_2)\leq \lambda_{\max}({{\mathbf B}}_1){\rm{tr}}({{\mathbf B}}_2)$, and the last inequality is contributed to ${\rm{tr}}\left\{\tilde{{{\mathbf P}}}(\omega_m^o)^{\rm{T}}{\boldsymbol{\Omega}}_{\pi}\tilde{{{\mathbf P}}}(\omega_m^o)\right\}\leq \tilde{R}_{\pi}(\omega_m^o)$. The last inequality is guaranteed by Lemma 2, (5.10), and (5.20). Thus, (5.16) is valid.

By similar arguments, for (5.17), we obtain that

where $C_2$ is a positive constant, and the last inequality is due to the fact that $\left\|\tilde{{{\mathbf A}}}(\omega_m^o){\boldsymbol{\mu}}\right\|^2\leq\tilde{R}_{\pi}(\omega_m^o)$, which is implied by (5.11). Thus, (5.17) is valid. This completes the proof of (5.13).

By the Cauchy-Schwarz inequality, it can be shown that

Thus, to prove (5.14), it suffices to show that

Similarly, using the technique used in deriving (5.13), it can be shown that (5.21) is valid. By Lemma 1, Lemma 4, Condition (C3), and (5.18), we have

As a result, (5.21) and (5.22) are valid, and thus (5.14) is valid.

By the jackknife criterion in (2.2), straightforward and careful calculation yields

where the term $\|{{\mathbf Z}}_{\hat{\pi}}-{\boldsymbol{\mu}}\|^2$ is independent of ${\boldsymbol{\omega}}$, and

Thus, for (2.5) to hold, it only needs to verify that, as $n\to\infty$,

Using the Cauchy-Schwarz inequality, Lemma 4 and (5.20), we obtain that

where

Therefore, for (5.24) to hold, it suffices to prove that

Likewise, the technique is applied to derive (5.17). For any $\delta > 0$, we have

where $C_3$ is a positive constant. By Conditions (C2) and (C3) and (5.10), we know that (5.26) is valid.

It can be observed that

Therefore, (5.27) holds if we can prove that

Similar to (5.26), it can be shown that

where $C_4$ is a positive constant. As a result, (5.29) is valid.

By (5.10), Condition (C4), and the fact that all the diagonal elements of $\tilde{{{\mathbf P}}}^{(m)}$ are zeros, it is observed that

Thus, (5.30) is valid.

Similarly, for (5.28), we have that

Then, for (5.28) to hold, we only need to prove

By the proof of (5.16), it can be shown that (5.31) is valid. Letting ${{\mathbf S}}^{(m)} = {{\mathbf D}}^{(m)}+{{\mathbf I}}_n$, this together with (5.19) generates

where

Under Lemma 2 and the second part of Condition (C4), we have

where $\tilde{\xi}_{\pi} = \inf_{{\boldsymbol{\omega}}\in{\mathcal{H}}_n}\tilde{R}({\boldsymbol{\omega}})$. Which, along with (5.10) and (5.33), implies that

and thus (5.32) is valid. In conclusion, the proof of Theorem 1 is completed. □

Proof of Theorem 2:

Define ${\boldsymbol{\psi}}_n({\boldsymbol{\omega}}) = {{\mathbf Z}}_{\hat{\pi}}-{{\mathbf Z}}_{\pi}+\hat{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})-\tilde{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})+\tilde{{\boldsymbol{\mu}}}_{\pi}({\boldsymbol{\omega}})-\tilde{{\boldsymbol{\mu}}}_{\hat{\pi}}({\boldsymbol{\omega}})$. A simple calculation yields

where $\hat{{\boldsymbol{\omega}}}_C = (\hat{\omega}_{cv, 1}, \dots, \hat{\omega}_{cv, m_0}, 0, \dots, 0)/\hat{s}_{cv}\in {\mathcal{H}}_n$ and $\hat{{\boldsymbol{\omega}}}_F = (0, \dots, 0, \hat{\omega}_{cv, m_0+1}, \dots, \hat{\omega}_{cv, M_n})/(1-\hat{s}_{cv})\in {\mathcal{H}}_n$. Likewise, we obtain that

We know that $CV_{\hat{\pi}}(\hat{{\boldsymbol{\omega}}}_{cv})\leq CV_{\hat{\pi}}(\hat{{\boldsymbol{\omega}}}_{C})$, which with (5.34), (5.35), and the Cauchy-Schwarz inequality, implies that

Condition (C6) indicates that to prove Theorem 2, it suffices to show

For the correct model with $m = 1, 2, \dots, m_0$, we have

where ${{\mathbf Q}}\tilde{{{\mathbf X}}}^{(m)} = {{\mathbf Q}}({{\mathbf I}}-{{\mathbf Q}}){{\mathbf X}}^{(m)} = 0$. This implies that

Thus, for (5.36) to hold, we need to make

By Markov's inequality, for any $\delta > 0$, we have

which is $o_p(1)$ under Condition (C6), implying that (5.43) is valid and thus guarantees that (5.36) is valid.

Indeed, (5.37) is further simplified to the following form:

Thus, by the proof of (5.43), it can be shown that (5.37) is valid.

For (5.38), one can obtain that

where the third step is derived from the Cauchy-Schwarz inequality and (5.25), and the last step is obtained from Lemma 2 and Condition (C7). Therefore, (5.44) holds if we can prove that

By (5.19), Lemma 4, and the Cauchy-Shwarz inequality, we have

where $\lambda_{\max}({{\mathbf A}}) = -1$. This, along with Condition (C2), Condition (C4), and (5.46), implies that, to prove (5.44), it only suffices to prove

Likewise, we use the same technique used in Lemma 1 in deriving (5.48). Thus, it is valid and obtaining (5.38) is valid. Based on (5.48) and Condition (3), we know that (5.39) is valid.

Under Conditions (C6) and (C7), it is observed that

This result implies that Conditions (C3) and (C4) are satisfied for $\{Z_{\pi, i}, X_{i}, U_i\}^{n}_{i = 1}$ with $\omega\in{\mathcal{H}}_{F}$. Therefore, it is analogous to (5.13), and we directly obtain that (5.40)–(5.42) are valid. Above all, this completes the proof of Theorem 2. □