Event-triggered impulsive control for second-order nonlinear multi-agent systems under DoS attacks

1.   Introduction

In recent years, the issue of multi-agent consensus has garnered considerable attention and research across various disciplines, including computer science, control theory, communication, and related fields. Multi-agent systems comprise numerous interacting intelligent agents collaborating to accomplish predefined objectives. Many researchers have studied the issue of achieving consensus in multi-agent systems under different conditions. There are several effective methods for achieving consensus, such as distributed control ^[1,2], sliding mode control ^[3], fault-tolerant control ^[4,5], and impulsive control ^[6,7,8,9].

Compared to the continuous control methods mentioned above, the use of impulsive control protocols significantly reduces information transmission. Impulsive control involves only information transfer at discrete impulsive moments. This helps to reduce the risk of communication losses. In recent decades, impulsive control has widespread applications in fields such as signal processing, communication, and medical devices. In ^[10], researchers investigated bounded consensus in heterogeneous multi-agent systems using impulsive control. Additionally, some multi-agent systems with heterogeneous delays were discussed and studied in ^[11,12]. In ^[13], two different impulsive control were proposed: Partial state constraint and full state constraint. They delved into the consensus problem of nonlinear MASs featuring grouping through state constraint impulsive protocols. They examined two scenarios: One involving a leader agent and another without, each analyzed using distinct two kinds of protocol. Considering that the network communication topology is not always constant, in ^[14], scholars employed algebraic graph theory and impulsive stability theory to explore the consensus problem in fixed-topology systems using impulsive control. In ^[15], the flexible handling of communication interruptions and topology switches was achieved using the T-S fuzzy model and impulsive control. It is important to note that the above-mentioned impulsive control methods are all time-triggered, which may result in additional communication and control overhead during information transmission. Therefore, it is necessary to study a new impulsive control method to address this issue. In ^[16], a distributed ETIC strategy was proposed to achieve consensus of MASs. Considering the evident benefits of ETIC, in recent years, numerous scholars have conducted research on ETIC and reported their corresponding results ^[17]. In ^[18], a distributed ETIC protocol was proposed to achieve consensus in MASs. Furthermore, in ^[19], an innovative dynamic event-triggered impulsive control protocol has been introduced, offering a more efficient means to reduce controller updates and minimize the waste of communication resources.

In practice, complex network systems or MAS tend to be more complex and vulnerable to cyber attacks by malicious actors. In recent years, scholars have gradually turned their attention to nonlinear multi-agent systems. In ^[20] scholars proposed an improved prescribed performance approach for human-in-the-loop consensus tracking control in unmanned aerial vehicle (UAV) systems. Their research underscores the importance of establishing effective interactions between humans and machines to achieve efficient control of UAV systems. In ^[21], scholars explored a privacy preservation mechanism for multi-agent systems and introduced a gain iterative disturbance observer. Their research focuses on safeguarding information privacy within systems while maintaining stability and reliability of system performance. In ^[22], scholars proposed an improved predefined-time adaptive neural control approach for addressing control issues in nonlinear multi-agent systems. Their research aims to overcome limitations of traditional control methods in complex systems, presenting a control solution with enhanced adaptability and robustness. In ^[23], scholars investigated quantized guaranteed cost memory consensus for nonlinear multi-agent systems with switching topology and actuator faults. Their study addresses uncertainties and faults within the system, introducing a novel guaranteed cost memory consensus method. Furthermore, cyber attacks have also been a hot research direction in recent years. Cyber attacks are typically categorized into two types: deception attacks ^[24,25] and DoS attacks ^{[26,27,28,29,30,31,32,33]}. Deception attacks focus on tampering with the data in the communication network, while DoS attacks typically overload the resources of the target system, rendering it unable to provide services and thus disrupting the information transmission channel. In ^[24], the impulsive consensus of nonlinear leader-follower MASs under DoS attacks was studied. The authors in ^[25] considered cases where sensor data transmission involves packet loss, with the objective of maximizing the terminal state covariance as the attack target, and presents optimal energy-constrained DoS attack scheduling schemes. In ^[26], the scholars developed a resilient cooperative ETIC scheme of linear MASs with DoS attacks. In ^[27], the guided bounded consensus of MASs with ETIC was studied in the presence of DoS attacks. In ^[28], the adaptive fault-tolerant control was investigated by designing an adaptive scheme and state feedback control gain. In ^[29], the scholars investigated positive impulsive effects and negative impulsive effects, and by employing the concept of "average impulsive interval, " they have unified the quasi-synchronization criteria for systems with two types of impulsive effects.

Inspired by the aforementioned research, this paper studies event-triggered impulsive consensus in second-order nonlinear MASs under DoS attacks. The system suffered DoS attacks, communication links are disrupted, and the communication topology of the system undergoes changes. The proposed ETIC can achieve consensus of second-order MASs under DoS attacks. The key contributions of this study are summarized as follows:

(1) We investigate a second-order nonlinear multi-agent system that experiences DoS attacks, resulting in communication interruption. The considered attack model is more general, and the paper provides sufficient conditions for the asymptotic convergence of the system.

(2) Compared with ^[34], we introduce an event-triggered mechanism within the impulsive control framework to investigate the security consensus of multi-agent systems with switching topology. The proposed mechanism efficiently reduces communication resource wastage and avoiding Zeno behavior.

Notation. $\mathbb{R}$ and $\mathbb{R}^{N\times N}$ denote the set of real numbers and the set of $N\times N$ real matrix, $\left \| \cdot \right \|$ denotes the Euclidean norm of a vector or the spectral norm of a matrix. The superscripts $T$ represent transpose of a matrix, and $\lambda _{max}(\cdot)$ and $\lambda _{min}(\cdot)$ represent the maximum and minimum eigenvalues of a matrix, $\bigotimes$ denote the Kronecker product.

2.   Problem statement

2.1.   Communication graphs

Consider a MAS, the digraph $\mathcal{G}$ is $\left (\mathcal{V}, \mathcal{E}\right)$, where $\mathcal{V} = \left \{1, 2, \cdots, N\right \}$ is the set of nodes and $\mathcal{E}\subseteq \mathcal{V} \times \mathcal{V}$ represents the edge set of followers. The information exchange between each node can be described by adjacency matrix $A$ and Laplacian matrix $L$. $A = \left [a_{ij}\right]\in \mathbb{R}^{N\times N}$ if agents $i$ and $j$ communicate with one another, $a_{ij} = 1$, otherwise $a_{ij} = 0$ and $L = \left [l_{ij}\right]\in \mathbb{R}^{n\times n}$ where $L = D-A$. The degree matrix $D = diag(d_{i})$ with $d_{i} = \sum_{i = 1}^{N}a_{ij}$.

2.2.   The system model

We consider a second-order MASs with a leader, where the dynamics equation of the leader is described as

and the $i$th follower's dynamics equation can be defined as

where $x_{0}\in \mathbb{R}^{n}, v_{0}\in \mathbb{R}^{n}$ are the positions and velocities of the leader, $x_{i}\in \mathbb{R}^{n}, v_{i}\in \mathbb{R}^{n}$ are the positions and velocities of the $i$th follower agent, $f(x, v)$ is a nonlinear function, $u_{i}(t) \in \mathbb{R}^{n}$ is the control input.

Then, the state error is defined as

In this paper, we consider a second-order leader system under DoS attacks, so the impulsive control input can be designed as

where $c$ denotes the coupling strength, $m$ defines the topology under DoS attacks, the local neighborhood consensus error is $p_{i}(t) = \sum_{j\in N_{i}}a_{ij}(x_{j}(t)-x_{i}(t))$+$b_{i}(x_{0}-x_{i})+\sum_{j\in N_{i}}a_{ij}(v_{j}(t)-v_{i}(t))+b_{i}(v_{0}-v_{i})$, $\delta (\cdot)$ is the Dirac function, $\left \{t_{k}\right \}$ is the impulse sequence, it satisfies $\lim_{k\to\infty }t_{k} = \infty, k\in \mathbb{N}_{+}$.

From (1) and (2), the state error system are as follows

where $f(e_{p}, e_{v}) = f(x_{i}(t), v_{i}(t))-f(x_{0}(t), v_{0}(t))$.

From the (3)–(5), we can get

where $p_{i}(t_{k})(m) = \sum_{j\in N_{i}}a_{ij}(m)(x_{j}(t)-x_{i}(t))+b_{i}(m)(x_{0}-x_{i})$+$\sum_{j\in N_{i}}a_{ij}(m)(v_{j}(t)-v_{i}(t))+b_{i}(m)(v_{0}-v_{i})$, $\Delta e_{vi}(t_{k}) = e_{vi}(t_{k})-e_{vi}(t^{-}_{k})$, $e_{vi}(t_{k}) = e_{vi}(t^{+}_{k}) = \lim_{h\to 0^{+}}e_{vi}(t_{k}+h)$, $e_{vi}(t^{-}_{k}) = \lim_{h\to 0^{-}}e_{vi}(t_{k}+h)$, and $e(t)$ is right-hand continuous at $t = t_{k}$.

The system (6) can be rewritten as:

where $e_{p} = [e_{p1}, e_{p2}, \cdots, e_{pN}]^{T}$, $e_{v} = [e_{v1}, e_{v2}, \cdots, e_{vN}]^{T}$, $F(e_{p}, e_{v}) = [f(e_{p1}, e_{v1}), f(e_{p2}, e_{v2}), \cdots, f(e_{pN}, e_{vN})]^{T}$, $B = diag\left \{ b_{i}\right \}\in \mathbb{R}^{N\times N}$.

Lemma 1. (^[35] Differential Mean Value Theorem) Let $f(\cdot)$ is a continuously differentiable nonlinear function, for any $x_{1}, x_{2} \in \mathbb{R}$, the following formula is satisfied:

where $f(z_{i}) = f(x_{i}(t_{0})+\Delta (x_{i}(t)-x_{i}(t_{0})), v_{i}(t_{0}+\Delta (v_{i}(t)-v_{i}(t_{0})))$, $0 < \Delta < 1$.

Definition 1. ^[28] The second-order MASs (1) and (2) with an impulsive controller $u_i(t)$ is said to be global exponential consensus, if there exist a scalar $\theta$ and a decay rate $\varepsilon$ such that for any $x_{1}(t_{0}), x_{0}(t_{0}) \in\; \mathbb{R}$.

2.3.   DoS attack model

When MASs are targeted by DoS attacks, the attacks focus on disrupting the communication network, causing varying degrees of damage to the communication connections among system nodes. Consequently, leading to a disconnection of the communication channel, the network communication topology undergoes changes. It is noted that the MASs incorporates a recovery mechanism that allows the communication topology to be restored once the attack concludes. We assume that DoS attacks are not continuous and that the attacks needs time to recover energy after one attack. Thus, there is a minimum interval between attacks.

We assume that the time interval of an attack cycle is divided into three periods.

(1) Normal control period($N_{n}$): The multi-agent system is normal working. The DoS attack has not arrived yet.

(2) Attack period($N_{a}$): DoS attacks and switching topologies occur in this interval.

(3) Recovery period($N_{r}$): The period during which the system recovers from a DoS attack. (minimum interval between attacks)

Definition 2. ^[28] Define the average impulsive interval as $\phi > 0$ in the time interval $[t_{0}, t]$. If there exist positive integer $N_{0}$, such that

where $N(t_{0}, t)$ is the number of impulsive times in $[t_{0}, t]$.

Definition 3. ^[28] According to the DoS attack model, suppose that $N_{n}(t_{0}, t)$, $N_{a}(t_{0}, t)$ and $N_{r}(t_{0}, t)$ denote the number of impulse instants in the normal control period, attack period and recovery period. The total time of an attack cycle is $N(T_{0}, T) = N_{n}(t_{0}, t)+N_{a}(t_{0}, t)+N_{r}(t_{0}, t)$. Then the impulsive attack ratio $\eta_{a}$ can be defined as

Assumption 1. The graph $\mathcal{G}$ contains a spanning tree which the root node is the leader.

3.   Main results

In this section, by designing an appropriate Lyapunov function and utilizing linear matrix inequalities, the system errors can be driven towards a bounded set, resulting in successful synchronization. Next, we designed the event trigger condition to be

where $a, \xi > 0$ are event trigger parameters.

Theorem 1. Under that Assumption 1, the MASs (1) and (2) are said to be globally exponentially synchronized, if there exist a symmetric matrix $P > 0$, system parameters $\alpha, \phi, \xi > 0$, $0 < \mu_{1}, \mu_{m} < 1$, such that

where we denote

The definition of $R$ and $R(m)$ are given later.

Proof. Let $e(t) = [e_{p}(t), e_{v}(t)]^{T}$, according to Lemma 1 and Assumption 1, we can get

where $\bar{A} = \begin{bmatrix} 0 & I_{N}\\ I_{N}+\frac{\partial \boldsymbol{f}(\boldsymbol{z_{i}})}{\partial \boldsymbol{x}} & \frac{\partial \boldsymbol{f}(\boldsymbol{z_{i}})}{\partial \boldsymbol{v}} \end{bmatrix}$, $\frac{\partial \boldsymbol{f}(\boldsymbol{z_{i}})}{\partial \boldsymbol{x}} = diag^{N}_{i = 1}[\frac{\partial {f}(z_{i})}{\partial x_{i}}]$, $\frac{\partial \boldsymbol{f}(\boldsymbol{z_{i}})}{\partial \boldsymbol{v}} = diag^{N}_{i = 1}[\frac{\partial {f}(z_{i})}{\partial v_{i}}]$.

Then, choose a Lyapunov function as

For $t\in[t_{k-1}, t_{k})$, differentiating $V(t)$ with respect to time $t$,

Based on (10), one has

which leads to

On the another hand, when $t = t_{k}, k = 1, 2, \cdots, n$,

where

Let $t\in[t_{0}, t_{1})$, from (17),

For $t\in[t_{1}, t_{2})$, from (17), (19) and (20)

By induction, for $t\in[t_{k}, t_{k+1})$,

According to the Definitions 2 and 3, it is easy to get

In a similar way, $N_{n}$ and $N_{r}$ is similar to $N_{a}$.

According to Assumption 2, the multi-agent system is not attacked $(N(t_{0}, t) = N_{n}(t_{0}, t)+N_{r}(t_{0}, t))$, one has

Based on trigger condition, for any $t\in [t_{k}, t_{k+1})$, we have

During the second pulse control time, there are three possible event triggering conditions: Event triggering zero times, event triggering one time, and event triggering multiple times.

(1) Event triggering zero times: $V(t)\leq e^{a+\xi (t_{0}-t_{1})}V(t_{0})$.

(2) Event triggering one times: $V(t)\leq\mu _{1} e^{2a+\xi (t_{0}-t_{2})}V(t_{0})$.

(3) Event triggering $k$ times: $V(t)\leq\mu _{1}^{k} e^{ka+\xi (t_{0}-t_{k+1})}V(t_{0})$.

In general, we have $V(t)\leq e^{k(\ln \mu _{1}+a)} e^{-\xi (t-t_{0})}V(t_{0})$, when $t\in[t_{0}, t]$, $k = 0, 1, 2, \cdot\cdot\cdot, n$

According to the condition,

On the another hand, when there are attacks$(N(t_{0}, t) = N_{n}(t_{0}, t)+N_{a}(t_{0}, t)+N_{r}(t_{0}, t))$.

where $\theta = \mu _{1}^{-N_{0}\frac{N_{n}(t_{0}, t)+N_{r}(t_{0}, t)}{N(t_{0}, t)}}\mu _{m}^{-N_{0}\frac{N_{a}(t_{0}, t)}{N(t_{0}, t)}}$, $\varepsilon = -(\frac{\ln \mu_{1}}{\phi }\frac{N_{n}(t_{0}, t)+N_{r}(t_{0}, t)}{N(t_{0}, t)}+\frac{\ln \mu_{m}}{\phi }\frac{N_{a}(t_{0}, t)}{N(t_{0}, t)}+\alpha)$ =$-(\frac{\ln \mu_{1}}{\phi }(1-\eta _{a})+\frac{\ln \mu_{m}}{\phi }\eta _{a}+\alpha)$. According to the condition and Definition 1, the proof is completed.

Next, it is proved that there is no Zeno behavior. Assume that $t_{1} < t_{2} < ... < t_{k}$ are the trigger instants, and based on (26), it holds that

which implies that $t_{1}-t_{0}\geq \frac{\phi (a+N_{0}\ln \mu_{1})}{\phi \alpha +\phi \varepsilon +\ln \mu_{1}}$. It means that event-triggered time interval $\begin{Bmatrix} t_{k+1}-t_{k} \end{Bmatrix}_{k\in \mathbb{N}}$ are lower bounded by $\tau$ ($\tau = \frac{\phi (a+N_{0}\ln \mu_{1})}{\phi \alpha +\phi \varepsilon +\ln \mu_{1}}$). The conditions in Theorem 1 prove that $\tau > 0$. Therefore, the system does not exhibit Zeno behavior.

Remark 1. We analyze the time upper bound and attack intensity that can sustain the DoS attack cycle of the system in Theorem 1. In this paper, an attack cycle is divided into three periods to be analyzed, and it is worth noting that the system will not be attacked during the adjustment period. In addition, different from the general event-triggered control strategy, in the control protocol proposed in this paper, the controller works only when the system state meets the trigger condition, and the controller does not perform pulse control in the rest time. This effectively reduces the number of information transmission and avoids the congestion of information transmission channels.

Remark 2. Compared with literature ^[36], literature ^[36] introduced an event trigger interval parameter and a mandatory immediate sequence. The event trigger mechanism in this paper only needs the system information of the previous event trigger time to determine the departure time of the next event, which makes the proposed algorithm easy to implement.

4.   Simulation examples

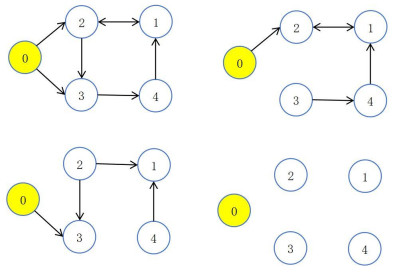
Consider MASs with nonlinear dynamics (1), where the network topology is shown in Figure 1. 0 is the leader, and the rest are the followers. Control input matrix $A$, and the Laplace matrix of the switching topology are described as

Take the initial values of the leader as $X_{0} = [0.2356 0.5688 0.6325]$, nonlinear function $f(x_{ij}(t)) = 0.5\times (\left | x_{ij}+1\right |-\left | x_{ij}-1\right |)$, and other system parameters $c = 0.4$, $a = 0.05$, $\xi = 0.1$.

Figures 2 and 3 describe the position error and velocity error images. It is evident from these graphs that the system error gradually diminishes over time. Figure 4 describes the motion position trajectory of multi-agent i (0, 1, 2, 3, 4). It is easy to see that the followers' states converge towards those of the leader as time progresses. In addition, the system was attacked in 8–10 seconds, 15–18 seconds, 23–29 seconds. The network topology is changed due to a DoS attack. The trigger time of each agent is shown in Figure 5. In the initial 10 seconds, the system state error is large and the trigger is more frequent. When t = 10s, the position of multiple agents gradually tends to be consistent, the trigger times decrease, and the event trigger pulse control does not trigger after reaching an agreement, which indicates that the event trigger pulse control can effectively solve the problem of limited bandwidth. Moreover, comparing the proposed event-triggered mechanism in this paper with the one in ^[35] under similar consensus performance, one can conclude from Table 1 that the communication burden can be reduced greatly by adopting the mechanism in this paper. The design of event triggering function in literature ^[35] is as follows

where $\rho = 1.2$.

5.   Conclusions

We investigate event-triggered impulsive consensus in second-order nonlinear MASs under DoS attacks. By employing Lyapunov functions, matrix graph theory, and inequality techniques, the conditions for asymptotic convergence of the global synchronization error system are studied. The influence of DoS attacks is solved by the design of a appropriate event-triggered impulsive controller. An example simulation substantiates the efficiency of the control schema. Furthermore, in future research, we will consider other control strategies to alleviate the impact of diverse network attacks.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded in part by National Natural Science Foundation of China under Grant 62273109, in part by the Guangdong Basic and Applied Basic Research Foundation under Grant 2023A1515010168, Grant 2019A1515010830, in part by the Key Special Foundation for General Universities in Guangdong Province under Grant 2022ZDZX1018, and in part by the Maoming Science and Technology Plan Foundation under Grant 2022S043.

Conflict of interest

The author declares no conflicts of interest in this paper.