Finite-time synchronization of fractional-order heterogeneous dynamical networks with impulsive interference via aperiodical intermittent control

1.   Introduction

Complex dynamical networks (CDNs), composed of numerous interconnected nodes, have been extensively used to model various large-scale real-world systems, such as social networks, the internet, multiagent networks, power grids, and communication networks ^[1,2,3]. It is important to note that most existing research results on the dynamics of CDNs are concentrated on integer-order systems. In fact, many real-world systems are often modeled as fractional-order systems, such as heat conduction ^[4], biological systems ^[5], viscoelastic systems ^[6], electromagnetic wave systems ^[7], and quantitative finance ^[8], etc. Thus, incorporating fractional-order calculus into CDNs can better characterize and reveal the properties of real-world complex systems.

Impulse is ubiquitous in real life and is widely used in nanoscale electronic circuits, secure communications, population dynamics ^[9,10,11], etc. It describes the phenomenon that the state of system changes suddenly at certain specific moments and has attracted widespread attention. Although impulses have a positive effect on the synchronization of fractional-order dynamical networks (FODNs) ^{[12,13,14,15]}, they may interfere with data transmission and cause oscillations as a negative effect in the dynamical process of the system, which are some common phenomena in physics ^[14,15]. In other words, impulsive effects can either strengthen or weaken network synchronization, and they can even destroy it. Since FODNs may experience transient perturbations or sudden changes under certain circumstances, considering the impulsive effect in FODNs can make the model more meaningful in practical application.

Synchronization, as a representative collective behavior, is the most important dynamic behavior of FODNs. Since many FODNs cannot achieve synchronization by themselves, appropriate control strategies are required to achieve the goal ^[16,17,18]. Intermittent control is a discontinuous control strategy that has garnered increasing attention since it was first proposed. In practical applications such as aircraft control, spacecraft orbit adjustments, wind power management, and windshield wiper control, continuous system control is often unnecessary, which makes intermittent control particularly important ^[19,20,21]. In fact, intermittent control consists of alternating periods of "working time" (when the controller is active) and "rest time" (when the controller is inactive). During each working time, the controller is operational, while it remains off during the rest time. This method allows control signals to be input into the system at fixed time intervals, thereby reducing control cost and extending the service life of the control equipment ^{[22,23,24,25,26]}. Furthermore, intermittent control can be categorized into periodic intermittent control (PIC) ^{[19,21,25,26]} and aperiodic intermittent control (APIC) ^{[20,22,23,24,27,28]} based on whether the control instants and periods are fixed. In ^[26], different from the traditional Mittag-Leffler function repeated iteration method, the authors proposed a novel fractional-order exponent differential inequality. Additionally, by designing a set of intermittent control strategies, sufficient conditions were established to ensure that the FODNs can achieve finite-time synchronization (FTS). However, the control interval and rest interval are fixed in periodic intermittent control, which may lead to conservative conditions. Therefore, in practical engineering applications, such as vehicle control and wind power generation, strict requirements for periodicity may be unreasonable. With regards to this, APIC is introduced to improve flexibility and applicability. The APIC enables the versatile development of control strategies with variable control periods and widths, demonstrating remarkable stability even in the presence of parameter uncertainties. In ^[24], the problem of quasi-synchronization for fractional-order dynamical networks with aperiodic intermittent pinning control was considered and the exponential convergence rate and error bound of quasi-synchronization were estimated. In ^[27,28], the stabilization problem of nonlinear systems subjected to impulsive disturbance is investigated via aperiodic intermittent control.

Time-triggered control (TTC) is a traditional control strategy used in engineering and control systems. It relies on predetermined time intervals for sampling and control updates. This method has excellent control accuracy in the steady-state stage, but lacks flexibility and intelligent monitoring capabilities. It cannot adjust the sampling frequency and control signals according to the actual operating conditions of the system, resulting in excessive resource consumption and communication burden ^[29,30,31]. For example, in a drone operating system, continuous time-triggered sampling can lead to excessive and unnecessary data transmission, resulting in inefficient use of power resources. To solve these problems, event-triggered control (ETC) has emerged as an innovative discontinuous control strategy. ETC means that the control signal is updated only at discrete moments triggered by specific events, which offers substantial advantages in reducing communication load and saving energy ^{[32,33,34,35]}. However, since the control signal still needs to be input into the system at the time of event triggering, it may still lead to a certain waste of resources. To further optimize resource utilization, event-triggered intermittent control (ETIC) combines the advantages of ETC and intermittent control. The ETIC strategy activates the control signal only during the necessary time period under specific conditions, reducing unnecessary control overhead. ETIC has demonstrated its effectiveness in stabilization and synchronization problems of complex dynamical networks. In ^[33], the authors improved the constraints on control width and minimum average control width in ETIC, and proposed an ETIC based on state control width.

Within the finite-time framework, researchers have begun focusing on different forms of stability problems. On one hand, some studies are dedicated to exploring special asymptotic stability and synchronization, where the system's trajectory gradually converges to an equilibrium point, as seen in the works of ^[36,37]. On the other hand, some studies have focused on finite time stability and synchronization, which requires that the system trajectory does not exceed a predefined threshold greater than an initial threshold in a finite-time. Up to now, there have been many distinguished theoretical results for finite-time stability in ^[27,28,32]. In fact, the finite-time synchronization study of fractional-order heterogeneous dynamic networks (FOHDNs), especially those subjected to impulsive disturbance, faces many difficulties and challenges. First, extensive research has been conducted on FTS in complex dynamic network models where the coupled nodes have identical intrinsic dynamics, as referenced in ^[38,39]. However, the heterogeneity in the topology of coupled nodes disrupts the overall state of the system, making finite-time synchronization in heterogeneous neural networks more challenging.

FTS of heterogeneous dynamical networks is a challenging problem because the heterogeneity of the topological structures of the coupled nodes can corrupt the state of the system ^[16,27,40]. Second, under the framework of a time-triggered and event-triggered mechanism, how to establish the potential relationship between aperiodic control periods, aperiodic control widths, and control parameters is crucial for increasing the freedom of the designed control periods and control widths. Finally, considering the beginning stage of each control period as an impulsive instant, and how to restrain the influence of impulsive interference by designing aperiodic intermittent control (AIC) also have theoretical and practical significance.

Motivated by the discussion above, the main contributions of this paper can be summarized as follows:

$\bullet$ Different from the synchronization of isomorphic complex dynamic networks discussed in ^{[16,23,26,38]}, this paper discusses the synchronization of heterogeneous dynamic networks in finite time, and this network model has a wider application in reality.

$\bullet$ The relationship between impulsive intensity, aperiod control widths, and control parameters is established on the premise of ensuring the synchronization in finite time between the heterogeneous dynamical networks with impulsive disturbance and the target node, which is conducive to adjusting the width of each control period and control parameters according to the impulsive intensity.

$\bullet$ Combining the advantages of event-triggered and intermittent control in saving resources and reducing communication burden, an ETIC is designed to ensure the finite-time synchronization of the system.

The rest of this paper is organized as follows. Section 2 provides an introduction to useful lemmas, definitions, and the system model. In Section 3, the main results of this paper are obtained. Section 4 provides two numerical examples to verify the theoretical results above. Finally, some conclusions are drawn in Section 5.

To facilitate understanding, see Table 1 for the symbols used in this article.

2.   Preliminaries and model description

This section introduces the notations, essential lemmas, fundamental concepts of the Caputo fractional derivative, and the model for FOHDNs.

2.1.   Notation

See Table 1.

2.2.   Preliminaries

Definition 1. ^[4] Let $\mathrm{H}(t)\in \mathcal{C}^{n}([t_0, t], \mathbb{R})$, $\eta > 0$, and $\Gamma(\cdot)$ be the gamma function. The Riemann-Liouville fractional-order integral is defined as

Definition 2. ^[4] The Caputo fractional derivative of order $\eta$ for a function $\mathrm{H}(t)$ is defined by

where $t \geq t_{0}$ and $n$ is a positive integer such that $n-1 < \eta < n$. Particularly, when $0 < \eta < 1$,

It is widely recognized that fractional-order systems with Caputo derivatives have initial conditions similar to those of integer-order systems, making them more suitable for engineering applications. Thus, this paper focuses on the analysis of Caputo derivatives. For simplicity, we can replace ${ }_{t_{0}}^{c} D_{t}^{\eta}$ with $D^{\eta}$.

Assumption 1. For the nonlinear function $f(\cdot)$, there exist a positive constant $l_{ij}$ such that

where $u = {\left(u_{1}, u_{2}, \ldots, u_{n}\right)}^{\top}$, $v = {\left(v_{1}, v_{2}, \ldots, v_{n}\right)}^{\top}$, $i\in \mathbb{N}_{1}^{n}$. The means that $\|f(u)-f(v)\|\le L_{f}\|u-v\|$ with $L_{f} = \|\bar{L}\|$, $\bar{L} = {(l_{ij})}_{n\times n}$, see ^[23,24,26] and the references therein.

Assumption 2. Suppose Assumption 1 holds, and there exist constants $\beta_{i} > 0$, $i\in\mathbb{N}_{1}^{N}$, such that

Lemma 1. ^[30] Suppose that $\mathcal{V}(t)\in \mathcal{C}^{1}([t_0, t], \mathbb{R})$ is a continuously differentiable function, and satisfies

where $\beta$ and $\gamma$ are constants. Then,

Lemma 2. ^[28] For matrix $\mathcal{E}$, which is symmetric and positive, it is assumed that there exist constant $\xi > 0$ such that

Lemma 3. ^[24] Let $\mathrm{H}(t)\in \mathcal{C}^{n}([t_0, t], \mathbb{R})$ and $\mathrm{P}\in \mathbb{R}^{n\times n}$ be a positive definite matrix. Then,

Lemma 4. ^[24] Consider the following matrix inequality:

where \(\mathbf{A}(\mathbf{z}) = \mathbf{A}^{\top}(\mathbf{z})\) and \(\mathbf{C}(\mathbf{z}) = \mathbf{C}^{\top}(\mathbf{z})\). This inequality is equivalent to either of the following two conditions:

2.3.   Model description

Consider the following class of fractional-order dynamical networks (FODNs), which is composed of $N$ nonidentical nodes:

where $0 < \eta < 1$, $x_{i}(t) = {\left(x_{i1}(t), \ldots, x_{in}\right)}^{\top}\in \mathbb{R}^{n}$ is the $i$th node-state vector, $u_{i}(t)$ delegates the control input, $f(x_{i}(t)) = {\left(f_{1}\left(x_{i}(t)\right), f_{2}\left(x_{i}(t)\right), \ldots, f_{n}\left(x_{i}(t)\right)\right)}^{\top} \in \mathbb{R}^{n}$ signifies a nonlinear continuous vector-valued function, $A_{i}$ and $B_{i}$ are constant matrix, $\sigma > 0$ delegates the coupling strength, and $\varGamma = \operatorname{diag}\left(\gamma_{1}, \gamma_{2}, \ldots, \gamma_{n}\right) > 0$ represents the inner coupling matrices. $x_{i}(0) = x_{i}^{0}\in\mathbb{R}^{n}$ is the initial values of the $i$th node. $C = {\left(c_{i j}\right)}_{N \times N}$ is the outer coupling matrices of the network topology. If the $j$th node and then $i$th node have a connection ($j\neq i$), the $c_{ij} > 0$ and otherwise $c_{ij} = 0$. Specially, $c_{ii} = -\sum_{j = 1, j\geq i}^{N}c_{ij}$.

Let $s(t) \in \mathbb{R}^{n}$ be the target trajectory, whose dynamics are given as follows:

where $A\neq A_{i}$ and $B\neq B_{i}$ are heterogeneous constant matrices, i.e., isolated node (2.2) has different system parameters from each coupled node in the FODN (2.1). In other words, there are parameter mismatches between FODN (2.1) and system (2.2). In this paper, we assume that the target trajectory $s(t)$ is bounded. That is, for any initial conditions $s(0)\in \mathbb{R}^{n}$, there exist a positive scalar $\widehat{M}$ and a time instant $T$, such that $\|s (t)\|\le\widehat{M}$ for all $t\geq T$.

Let $e_{i}(t) = x_{i}(t)-s(t)$. The error system can be derive as

where $\bar{e}(t) = {\left(e_{1}(t), \ldots, e_{N}(t)\right)}^{\top}$, $e_{i}(t) = \left(e_{i1}(t), \ldots, e_{in}(t)\right)^{\top}$, $\tilde{f}(e_{i}(t)) = f(x_{i}(t))-f(s(t))$, $i\in \mathbb{N}_{1}^{N}$, and $\Upsilon_{i}(s(t)) = (A_{i}-A)s(t)+(B_{i}-B)f(s(t))$. The initial condition is given as $\bar{e}(0) = \phi_{e}$, $\phi_{e}\in \mathbb{R}^{N\times n}$.

Due to the presence of parameter mismatches between the systems, achieving stabilization in finite time of error system (2.3) becomes challenging. Therefore, the objective of this paper is to develop the effective control schemes that ensure finite-time stabilization of (2.3). The definition of FTS is provided as follows.

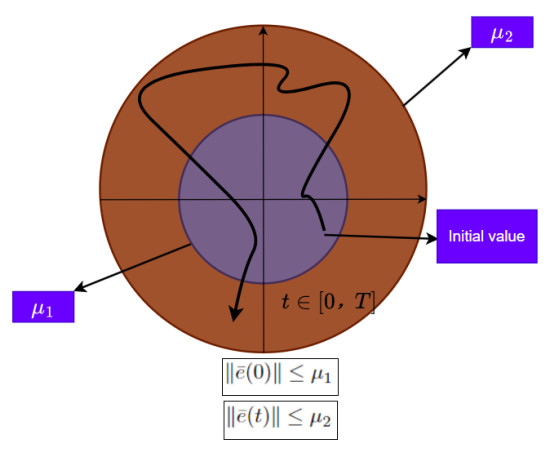
Definition 3. We are given three positive constants $T$, $\mu_{1}$, and $\mu_{2}$ with $0 < \mu_{1} < \mu_{2}$. System (2.3) is said to be finite-time stabilization with respect to $(w.r.t.)(T, \mu_{1}, \mu_{2})$. If $\|\phi_{e}\|\le \mu_{1}$, this implies that $\|\bar{e}(t)\|\le \mu_{2}$, for all $t\in [0, T]$.

Remark 1. It is important to highlight that $\mu_{1}$, $\mu_{2}$, and $T$ are all predetermined for the respective problems. Finite-time stabilization delegates the scenario where the system's initial state is confined within a predefined bound and will eventually reach a specified bound within a finite time, which depicts the boundedness of the system. The trajectory of finite-time stabilization is depicted in Figure 1.

Design AIC as:

where $\mathrm{K}_{i}$, $i\in\mathbb{N}_{1}^{N}$ represents the control gain matrix, $t_{k}$ is the $k$th instant of the impulsive instant, and $t_{k+1}$ is the next event impulsive instant. $\delta_{k}$ signifies the width of each control interval and satisfies $0 < \delta_{k}\le t_{k+1}-t_{k}$, $k\in \mathbb{N}^{+}$.

Then, under AIC (2.4), system (2.3) can be converted into the following form:

It can be observed that the controller operates only within the control intervals, with no input information being transmitted during the remaining intervals. This implies that system (2.5) alternates between closed loop and open loop control. Additionally, considering that the state of system (2.5) may suddenly change at certain instants due to input noise, measurement errors, and uncertainties, resulting in an impulsive phenomenon, we regard this as impulsive disturbance. Therefore, the system (2.5) under impulsive disturbance can be described as follows:

where $\mathcal{J}$ delegates the impulsive gain matrix and the state variable $e_{i}(t)$ of system (2.6) is supposed to be right continuous. The sequence $\{t_k\}_{k = 1}^\infty$ satisfies $0 = t_0 < t_1 < \cdots < t_k < \cdots$ and $\lim_{k\to\infty}t_{k} = \infty$.

3.   Main results

In this section, we explore the sufficient conditions required to ensure that systems (2.1) and (2.2) achieve finite-time synchronization. We primarily introduce two types of aperiodical intermittent control strategies: one is time-triggered, and the other is event-triggered.

3.1.   Finite-time synchronization via time-triggered intermittent control

For convenience, we denote the following notations. For $i, j\in \mathbb{N}_{1}^{N}$, let $\mathcal{A} = \text{diag}\left(A_{1}, A_{2}, \ldots, A_{N}\right)$, $\mathcal{B} = \text{diag}\left(B_{1}, B_{2}, \ldots, B_{N}\right)$, $\mathcal{C} = \left(\tilde{c}_{i j}\right)_{N \times N}$, $\tilde{c}_{i j} = \left\{\begin{array}{cc}c_{i j}\|\Gamma\|, & i \neq j \\ c_{i i} \lambda_{\min }(\Gamma), & i = j\end{array}\right.$. In addition, denote $\mathcal{K} = \text{diag}(k_{1}, k_{2}\ldots, k_{N}, )$, $\hat{\mathcal{A}} = \mathcal{A}+\mathcal{A}^{\top}$, $\hat{\mathcal{B}} = \mathcal{B}\mathcal{B}^{\top}$, $\hat{\mathcal{C}} = \mathcal{C}+\mathcal{C}^{\top}$.

Theorem 1. Suppose that Assumptions 1 and 2 hold and the positive constants $\rho_{1}$, $\rho_{2}$, $\varrho_{1}$, $\varrho_{2}$, $\mu_{1}$, $\mu_{2}$, $\xi_{1}$, $\xi_{2}$ with $\frac{\varrho_{1}}{\rho_{1}} < \mu_{1} < \mu_{2}$, $\varrho_{1} = \varrho_{2}$, and $\alpha\geq1$ satisfy

where

In addition, $L_{f} = \|\bar{L}\|$ with $\bar{L} = (l_{ij})_{N\times N}$, $\alpha = \lambda_{\max }\left(\mathcal{J}^{\top}\mathcal{J}\right)$, $\varrho_{1} = \varrho_{2} = \xi_{2}^{-1}\tilde{\beta}$, $\tilde{\beta} = \sum_{i = 1}^{N}\beta_{i}$. $k$ delegates the number of control periods on $(0, T], T \neq t_{k}$. Then, systems (2.6) is finite-time stabilization $w.r.t \left(T, \mu_{1}, \mu_{2}\right)$, that is, system (2.1) and (2.2) can achieve finite-time synchronization under aperiodic time-triggered intermittent control and impulsive disturbance $w.r.t \left(T, \mu_{1}, \mu_{2}\right)$.

Proof. Let $\bar{e}(t) = \bar{e}(t, 0, \phi_{e})$, $\phi_{e}\in \mathbb{R}^{N\times n}$, be the solution of (2.6). For $0 < \|\bar{e}(0)\|\le\mu_{1}$, consider the Lyapunov candidate function:

For $t = t_{k}$, we have

For $t\neq t_{k}$, when $t\in[t_{k}, t_{k}+\delta_{k})$, we have

According to Lemma 2 and Assumption 1, there exists $\xi_{1} > 0$ which satisfies,

From Lemma 2 and Assumption 2, there exists $\xi_{2} > 0$ such that

Since $c_{ij}\geq 0\:(i\neq j)$ and $c_{ii} = -\sum_{j = 1, j\neq i}^{N} c_{ij}$, $i, j\in \mathbb{N}_{1}^{N}$, we have

Recalling the definition of $\mathcal{K}$ yields

Then, combining (3.5)–(3.7), there exist constants $\rho_{1} > 0$ and $\varrho_{1} > 0$ such that

From Lemma 1 and (3.9), we have

Similarly, for $t\in [t_{k}+\delta_{k}, t_{k+1})$, there exist constants $\rho_{2} > 0$ and $\varrho_{2} > 0$ such that

In accordance with Lemma 1 and (3.11), when $t\in [t_{k}+\delta_{k}, t_{k+1})$, one has

From (3.10), when $t\in [0, \delta_{0})$, we have

and

For $t\in [\delta_{0}, t_{1})$, we have

and

For $t\in [t_{1}, t_{1}+\delta_{1})$ and $\alpha\geq 1$, we have

and

For convenience, we define the following notations: $\inf_{k \in \mathbb{N}^{+}} \left(\delta_{k}\right) = \tilde{\Theta} \quad\text{and}\quad \delta_{k} \text{ is the width of each control interval.}$ $\sup_{k \in \mathbb{N}^{+}} \left(t_{k+1}-t_{k}- \delta_{k}\right) = \hat{\Theta} \quad\text{and}\quad t_{k+1}-t_{k}- \delta_{k} \text{ is the width of each non-control interval.}$ In addition, $T_{k}$ = $t_{k+1}-t_{k}$, $\widehat{T} = \max_{k\in \mathbb{N}^{+}} T_{k}$, $\widetilde{T} = \min_{k\in \mathbb{N}^{+}} T_{k}$.

For $t\in [t_{1}+\delta_{1}, t_{2})$, we have

and

Let

It follows from (3.17) and (3.18) that

For $t\in [t_{k}, t_{k}+\delta_{k})$, we have

and

For $t\in [t_{k}+\delta_{k}, t_{k+1})$, one obtains

and

For $t\in [t_{k}+\delta_{k}, t_{k+1})$, we have

Then, from $\mathcal{V}(\bar{e}(0)) > \frac{\varrho_{1}}{\rho_{1}}$ and conditions $(c)$ and $(d)$, we have

which means $\|\bar{e}(t)\|\le \mu_{2}$, and thus, $\|\bar{e}(t)\|\le \mu_{2}$ holds on $[0, T]$. Therefore, systems (2.1) and (2.2) has FTS, that is, systems (2.1) and (2.2) can attain FTS under time-triggered AIC and impulsive disturbance. The proof is complete.

Remark 2. The authors analyzed the synchronization problem of fractional-order systems based on the following fractional-order differential inequalities in ^[21,24]:

However, the two intermittent differential inequalities mentioned above cannot guarantee finite-time synchronization. Theorem 1 of this paper provides a differential inequality that ensures finite-time synchronization. In addition, literatures ^[21,24] employ the function iteration method to address the periodic intermittent control problem in fractional-order network systems. Compared to traditional periodic intermittent control results, which use fixed control periods and control widths, Theorem 1 introduces a synchronization criterion based on non-fixed control periods and control widths. This approach is more versatile and flexible.

Remark 3. Let $\hat{T} = \max_{k\in\mathbb{N}^{+}}T_{k}$ and

$0 < \tilde{\Theta} < 1$. We can conclude that $\mathfrak{V}(\tilde{\Theta})$ is a monotonically nonincreasing continuous derivative function of $\tilde{\Theta}$, since $\mathfrak{V}(0) = \exp\left(k\ln\alpha+\frac{(k+1)\rho_{2}}{\Gamma(1+\eta)}\right) > 1$ and

Based on the intermediate value theorem, there exist $0 < \tilde{\Theta}^{*} < 1$ such that $\mathfrak{V}(\tilde{\Theta}^{*}) = 1$, where $v^{*} = \sup\left\{0 < \tilde{\Theta}^{*} < 1|\mathfrak{V}(\tilde{\Theta}^{*}) = 1\right\}$. Consequently, the condition $(c)$ in (3.1) can be satisfied for any $\widetilde{\Theta}\in (\tilde{\Theta}^{*}, 1)$.

Remark 4. It is important to note that if the target trajectory $s(t)$ is bounded and the function $f(\cdot)$ satisfies the Lipschitz condition, we can always find a positive scalar $\beta_{i}$ such that Assumption 2 holds. Especially, when $f(0) = 0$, one can simply choose $\beta_{i} = \left(\left\|A_{i}-A\right\|+L_{f}\left\|B_{i}-B\right\|\right)\widehat{M}$ to make Assumption 2 hold for all $t \geq T(s(0))$ because $\|f(s(t))\| = \| f(s(t))-f(0)\|\leq L_{f}\|s(t)\|$ and $\|s(t)\| \leq \widehat{M}$ for all $t \geq T(s(0))$. While in the case of $f(0) \neq 0$, $\beta_{i}$ can be set to $\left(\left\|A_{i}-A\right\|+L_{f}\left\|B_{i}-B\right\|\right) \widehat{M} +\left\|B_{i}-B\right\|\|f(0)\|$ due to the fact that $\|f(s(t))\| = \| f(s(t))-f(0)+ f(0)\|\leq L_{f}\| s(t)\|+\| f(0) \|$.

Remark 5. It is worth noting that conditions $(a)$ and $(b)$ in Theorem 1 make Eqs (3.10) and (3.12) true, where $\rho_{1}$ and $\rho_{2}$ are presented to depict the possible rate of change of system (2.6). Obviously, when control input is present, system (2.6) exhibits a decreasing trend. However, in the absence of control input, system (2.6) shows a divergent trend. In summary, stability occurs during the controlled intervals.

3.2.   Finite-time synchronization via event-triggered intermittent control

In this section, to avoid certain resource consumption and reduce the frequency of events triggered, the aperiodic event-triggered intermittent mechanism is adopted to realize the objective of the FTS.

Let $t_{k}$ be the triggering instant of the state, and the $t_{k+1}$ is next event triggering instant. The event-triggered mechanism is defined as follows:

where $\Xi_{k}(t_{k}+\delta_{k}, t] = \{t:t > t_{k}+\delta_{k}, \mathcal{V}(\bar{e}(t))\geq \vartheta V(\bar{e}(t_{k}+\delta_{k}))\}$, $\delta_{k} > 0$, $\vartheta > 1$, $k\in\mathbb{N}^{+}$. $\vartheta$ delegates threshold value and $\varsigma > 0$ represent the check-period, which is constant and and usually designed to be sufficiently large.

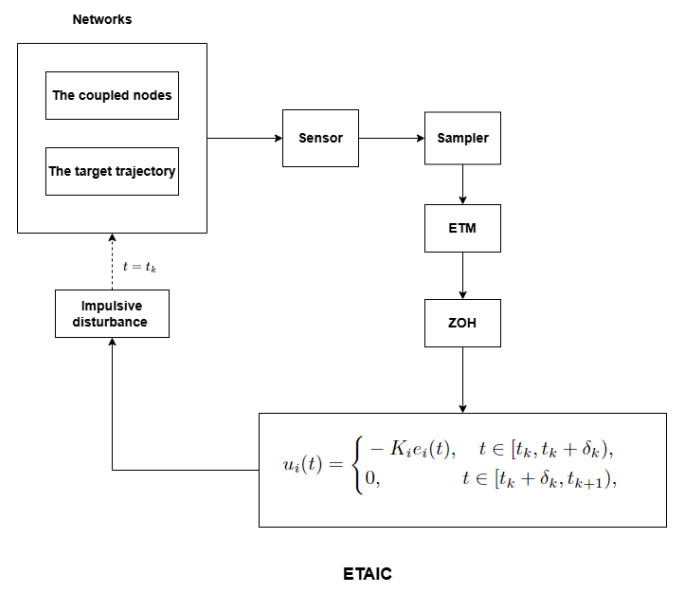
The general framework of the event-triggered aperiodic intermittent mechanism is shown in Figure 2, where ZOH represents a zero-order hold. When $t\in t\in[ t_{k}, t_{k}+\delta_{k})$, the event-triggered controller $u_{i}(t) = -\mathrm{K}_{i}e_{i}(t)$ is activated. When $t\in[ t_{k}+\delta_{k}, t_{k+1})$, the event-triggered controller $u_{i}(t) = 0$ is activated.

Remark 6. In event-triggered mechanism (3.23), $\varsigma$ represents the check-period, which is applied when $\Xi_{k}(t_{k}+\delta_{k}, t_{k}+\varsigma] = \emptyset$, indicating that the event condition does not occur within the check-period. When the check-period ends, the event-triggered mechanism (3.23) ensures that the control input remains at the end of the check-period, thus preventing the situation where the event condition cannot be triggered.

Theorem 2. Suppose Assumptions 1 and 2 are established, conditions $(a)$ and $(b)$ in Theorem 1 are satisfied and there exist positive constant $\rho_{1}$, $\rho_{2}$, $\varrho_{1}$, $\varrho_{2}$, $\xi_{1}$, $\xi_{2}$, $\mu_{1}$, $\mu_{2}$ with $\frac{\varrho_{1}}{\rho_{1}} < \mu_{1} < \mu_{2}$, $\vartheta > 1$ and $\alpha\geq 1$. If the following conditions are satisfied

Thus, the Zeno phenomenon can be avoided, and system (2.1) can achieve synchronization with system (2.2) within finite time under the event-triggered mechanism (3.23) and in the presence of impulsive disturbances.

Proof. For $0\le \|\bar{e}(0)\|\le \mu_{1}$, assume $\bar{e}(t) = \bar{e}(t, 0, \phi)$ is the solution of system (2.6). According to Theorem 1, for $t = t_{k}$, we have

For $t\neq t_{k}$, one obtains

Then

According to (3.23), then $\delta_{k} < t_{k+1}-t_{k}\leq\varsigma$ and the next event will not be triggered until the event generator function crosses zero, that is

Therefore, combining (3.27) an (3.28), we get

From $e$ in (3.24), let $\Lambda(k) = \left[\left(\frac{\Gamma(\eta+1)}{\rho_{2}}\right)\ln\left(\frac{\vartheta\mathcal{V}(\bar{e}(t_{k}+\delta))+\frac{\varrho_{2}}{\rho_{1}}}{\mathcal{V}(\bar{e}(t_{k}+\delta))+\frac{\varrho_{2}}{\rho_{1}}}\right)\right]^{\frac{1}{\eta}}$ with $\vartheta > 1$, and we have

Thus, the Zeno phenomenon can be excluded.

For $t\in [t_{k}+\delta, t_{k+1})$, from event-triggered mechanism (3.23), one obtains

For $t\in [t_{k}, t_{k}+\delta)$, we have

Then, for $t\in [0, \delta_{0})$, one has

and

For $t\in [\delta_{0}, t_{1})$, we have

and

For $t\in [t_{1}, t_{1}+\delta_{1})$, we have

and

For $t\in [t_{1}+\delta_{1}, t_{2})$, we have

and

By mathematical induction, for $t\in [t_{k}+\delta_{k}, t_{k+1})$, we have

which implies

Then, in line with $(f)$ in Theorem 2, we have

which signifies $\|\bar{e}(t)\|\le \mu_{2}$, and thus, $\|\bar{e}(t)\|\le \mu_{2}$ holds on $[0, T]$. As a result, systems (2.1) and (2.2) have synchronization in finite time, that is, systems (2.1) and (2.2) can attain finite-time synchronization under event-triggered intermittent control and impulsive disturbance. The proof is complete.

Remark 7. In Theorems 1 and 2, the general sufficient conditions are established to ensure the finite-time synchronization between the network (2.1) and system (2.2) can be achieved under the control strategy (2.4). However, it is still unclear how to choose the appropriate control gain matrix $\mathcal{K}$, and the configuration parameters $\rho_{1}$ and $\rho_{2}$ to satisfy conditions $(a)$ and $(b)$ in Theorem 1. We can choose the following inequalities to be equivalent to $(a)$ and $(b)$.

4.   Numerical simulations

This section presents some simulations to illustrate the effectiveness of the proposed theoretical results.

Consider the target trajectory $s(t)$, which is described by the following fractional-order system:

where $s(t) = \left(s_{1}(t), s_{2}(t), s_{3}(t)\right)^{\top}\in \mathbb{R}^{3}$. $f(s(t)) = \left(\tanh(s_{1}(t)), \tanh(s_{2}(t)), \tanh(s_{3}(t))\right)^{\top}$, $\eta = 0.98$, and

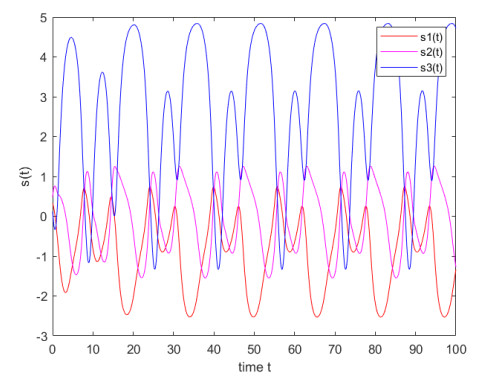
Figure 3 indicates the chaotic behavior of system (4.1), and one can observe that the target trajectory $s(t)$ is bounded by $\widehat{M} = 5$. Additionally, it is obvious that $l_{ii} = 1$ and $l_{ij}(i\geq j)$, $i, j \in\mathbb{N}_{1}^{3}$, and therefore the Lipschitz constant is $L_{f} = 1$.

Consider a directed network consisting of 5 nonidentical fractional-order dynamical networks described by (4.1), which is depicted as following:

where $x_{i}(t) = \left(x_{i1}(t), x_{i2}(t), x_{i3}(t)\right)^{\top}$, $\sigma = 2$, $\Gamma = \text{diag}\left(1, 1, 1\right)$, and the network structure is shown in Figure 3. The outer coupling matrix $\mathcal{C}$ can be expressed as

Let $e_{i}(t) = x_{i}(t)-s(t)$, $i\in \mathbb{N}_{1}^{5}$. If considering the aperiodic intermittent control and impulsive disturbances, the error system can be expressed as follows:

where

For brevity, the matrices $A_{i}$, $B_{i}$, $i\in\mathbb{N}_{1}^{10}$, are given as $A_{i} = A-0.0002(i-5.5)I_{3}$, $B_{i} = B+0.0001(i-5.5)I_{3}$, $i\in \mathbb{N}_{1}^{10}$. Simple calculations show that

Example 1: Synchronization via time-triggered APIC

Think about system (4.3) with $t_{0} = 0$, $T = 5$, $\sigma = 2$, $\beta_{i} = 0.0006|i-5.5|$, $\xi_{1} = 0.25$, $\xi_{2} = 2$, and

According to $(i)$–$(iii)$ of Remark 7, we get $\xi_{1}^{-1} = 4$, $\xi_{2}^{-1} = 0.5$, $\rho_{1}\geq -8.5472$, $\rho_{2}\geq 14.0028$, and control gain $\mathrm{K}_{i} > 2.7543$. By calculating $\mathcal{J}^{\top}\mathcal{J}$, one has $\alpha = 19.0981$, $\varrho_{1} = \varrho_{2} = \xi_{2}^{-1}\sum_{i = 1}^{N}\beta_{i}^{2} = 0.0123$.

In this example, we use time-triggered mechanisms to divide the control intervals. For convenience, the select periods $\overline{\mathrm{T}}_{k} = t_{k+1}-t_{k}, k\in \mathbb{Z}^{+}$, are considered to have the following form ^[24]:

where $k \in \mathbb{Z}^{+}, \hbar_{0}$ and $T_{0}$ are positive scalars satisfying $\hbar_{0} < T_{0}$, and $\varpi_{0}$ is a positive integer. $\sup _{l \in \mathbb{Z}^{+}}\left\{t_{l+1}-t_{l}\right\} = \widehat{\mathrm{T}} = \varpi_{0}\left(T_{0}-\hbar_{0}\right)+\hbar_{0} \quad$ and $\quad \inf _{l \in \mathbb{Z}^{+}}\left\{t_{l+1}-\right. \left.t_{l}\right\} = \widetilde{T} = \hbar_{0}$. In the numerical simulations, we let the control periods $\overline{\mathrm{T}}_{l} = t_{l+1}-t_{l}, l \in \mathbb{Z}^{+}$, satisfy (4.5) with $T_{0} = 0.35$, $\hbar_{0} = 0.2$, and $\varpi_{0} = 2$, and then we have $\widehat{\mathrm{T}} = 0.5$, and $\widetilde{\mathrm{T}} = 0.2$. Then, combining with Remark 3 and condition $(c)$ in Theorem 1, we have $\tilde{\Theta} \in (0.843, 1)$.

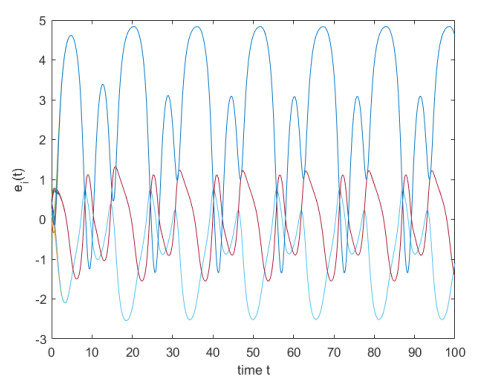
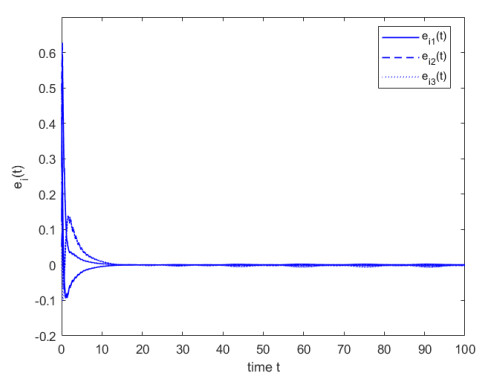
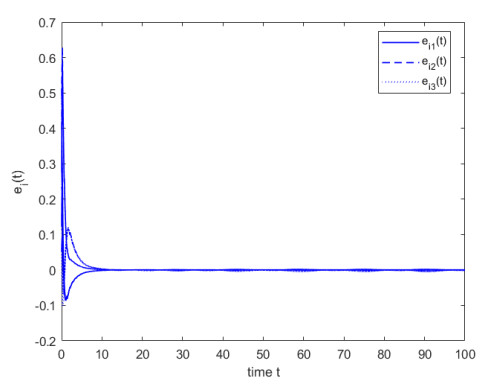
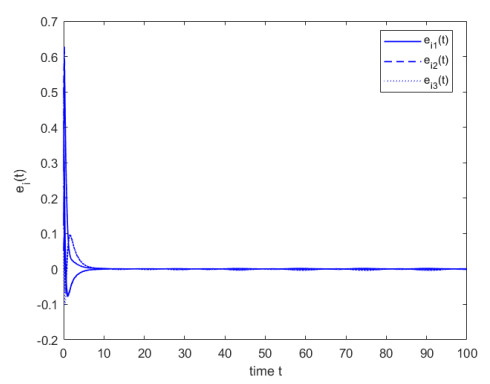
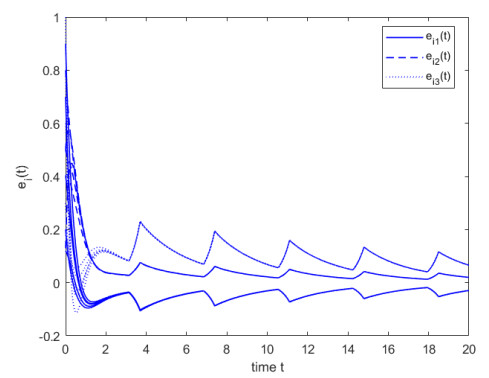
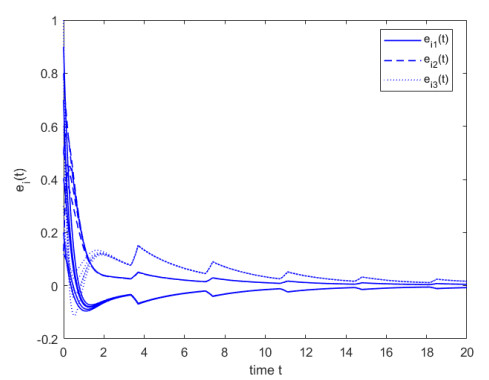
Select the control gains $\mathrm{K}_{i} = 3$, $i\in \mathbb{N}_{1}^{5}$, $\rho_{1} = 7.2675$, $\rho_{2} = 15.2354$, $\mu_{1} = 0.5$, $\mu_{2} = 1$, and $\tilde{\Theta} = 0.85$, then all conditions of Theorem 1 are ture. That is, the finite-time synchronization between the system (4.1) and FOHDN (4.2) could be implemented under the controller (4.5). The state trajectory of system (4.3) is depicted in Figures 5. For comparison, Figures 6 and 7 are presented to represent the state trajectories of the system when $\tilde{\Theta} = 0.9$ and $\tilde{\Theta} = 0.95$, respectively.

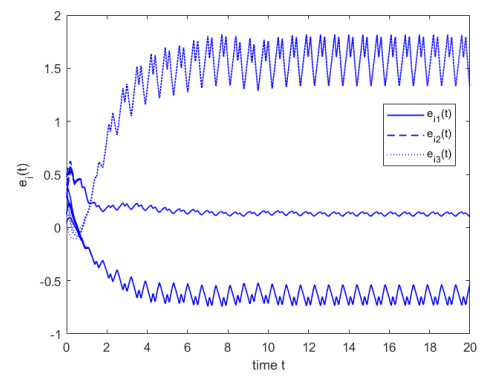
Remark 8. When Theorem 1 is satisfied, the error system achieves finite-time synchronization. At the same time, the corresponding control period and control width can be obtained through condition $(c)$ in Theorem 1. If the control width is changed to $\tilde{\Theta} = 0.4474$ on the basis of the same impulsive sequence $\left\{t_{k}\right\}$, the condition is no longer established, and the state trajectory of system (4.3) will exceed the range of $\mu_{2} = 1$, although the initial condition $\|\phi_{e}\|\le \mu_{1} = 0.5$ still holds, see Figure 8, i.e., system (4.3) cannot achieve FTS $w.r.t\:(10, 0.5, 1)$.

Remark 9. The novelty of this paper lies in its consideration of finite-time synchronization in heterogeneous dynamic networks, which has broader practical applications than the isomorphic networks explored in previous works ^[16,23,26]. Additionally, the paper introduces a model that accounts for impulsive interference, a factor that may disrupt synchronization, making it more universally applicable compared to systems without impulsive effects ^[30,31,36]. Unlike previous continuous control strategies for fractional-order dynamic networks ^[16,38], this paper proposes a discontinuous control approach, reducing control costs while offering more flexibility with an adjustable control period, unlike the fixed control periods in ^[21,24]. Finally, the adoption of event-triggered intermittent control, with a lower update frequency compared to traditional time-triggered methods ^[26,27,28], contributes to a more efficient and adaptable control scheme.

Example 2: Synchronization via event-triggered APIC

Let $t_{0}$, $T$, $\sigma$, $\alpha$, $\xi_{1}$, $\xi_{2}$, $\mu_{1}$, $\mu_{2}$, and other predefined parameters have the same value as in Example 1. Assume $\varsigma = 5$, $\vartheta = e$, and $\delta_{k} = 2.1$. By simply calculating condition $(f)$ in Theorem 2, we have $\tilde{\Theta} = 0.8452$ and then the sequence of impulsive instants ${t_{k}}$ is determined by

where $\Xi_{k}(t_{k}+\delta_{k}, t] = \{t:t > t_{k}+\delta_{k}, \mathcal{V}(\bar{e}(t))\geq \vartheta V(\bar{e}(t_{k}+\delta_{k}))\}$. Then the state trajectory of system (4.3) under APIC (4.4) are exhibited in Figure 9. For comparison, Figures 10 and 11 are presented to represent the state trajectories of the system when $\tilde{\Theta} = 0.9$ and $\tilde{\Theta} = 0.95$, respectively.

5.   Conclusions

This paper investigates the intermittent control problem of fractional-order heterogeneous dynamical networks subject to impulsive disturbances. First, a non-periodic time-triggered controller is proposed, and a sufficient condition is provided to ensure that finite-time synchronization between the fractional-order heterogeneous dynamical network and the target trajectory can be achieved. Additionally, the relationships between control period width, impulsive disturbances, and controller parameters are established. Furthermore, within the framework of event-triggered control, a class of event-triggered controllers is designed, and the connections between impulsive disturbances, event-triggering conditions, and control period width are derived. Finally, two numerical examples are presented to verify the effectiveness of the theoretical results. It is important to note that due to limitations in signal transmission and processing speeds between network nodes, time delays are inevitable in complex dynamical networks ^[14,20,34]. Therefore, time delays must be considered in the realistic modeling of fractional-order dynamical networks. Moreover, although this paper ensures finite-time synchronization, it does not calculate the system's settling time. In practical engineering applications, estimating the settling time helps to predict and control the system's dynamic behavior. At present, to the best of our knowledge, there is a lack of effective methods to address these critical issues, which will be the focus of our future research.

Author contributions

T. Xie: Data curation, resources, funding acquisition, visualization; X. Xiong: Software, formal analysis, validation, investigation, writing-original draft; T. Xie, X. Xiong: Conceptualization, supervision, methodology, project administration, writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.