1.
Introduction
The emergence of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in late 2019 has caused unprecedented problems in health around the globe. The infection of the novel coronavirus has led to a devastating loss of lives and the production of a substantial burden on healthcare systems around the worldwide. Due to its urgency, the scientific community wants to comprehend the complexity of the disease and has hence investigated the spreading of SARS-CoV-2 not only by symptomatic individuals, but also by those who exhibited no apparent signs of illness but still transmitted the disease to others, i.e., asymptomatic individuals [1]. Symptomatic individuals experience cough, fever, and other respiratory symptoms which are recognized as the primary sources of disease transmission. The role of asymptomatic individuals has been gaining increasing amounts of attention because these individuals with no symptoms can transmit the disease to others making it difficult to control the spread of the novel coronavirus. Scholars have previously noted that 47% and 38% of newly infected cases are reported to be due to the contact with asymptomatic and symptomatic individuals, respectively [2]. Therefore, the existence of a small number of asymptomatic populations can produce a major disaster. The identification and understanding of the dynamics of both asymptomatic and symptomatic individuals can help to control the novel infection with the aid of effective control mechanisms.
Modeling the epidemiological process is a useful tool and has been vastly utilized to test various theories related to the dynamics and control of communicable diseases [3,4,5,6]. Different researchers have used these models to investigate the temporal dynamics of infectious diseases [7,8,9,10,11,12,13]. Dynamical systems representing the SARS-CoV-2 virus transmission are also abundant in literature, and numerous epidemiological models have been frequently exercised to investigate the predictability of the disease spread; see for instance [14,15,16,17]. Indeed, the models reported to represent the temporal dynamics of the novel coronavirus yielded interesting results; however, the authors mostly used a deterministic approach to model the interacting components of the novel model of coronavirus spread. Disease transmission is different everywhere due to the environment of the area and the immune system of the individual as well as the death rate and implementation of the vaccination program varying from place to place. Thus, due to the complex nature of SARS-CoV-2, it is observed that the novel disease has a stochastic nature. Recently, a model utilizing a stochastic approach has been studied to investigate the dynamics of coronavirus 2, as detailed in [18], where the authors did not consider various important factors that greatly influence the disease dynamics, e.g., the classification of infected individuals as a symptomatic and asymptomatic individuals has not been considered. However, models with an appropriate structure provide accurate dynamics and forecast the long-term spread for the disease which is very helpful for public health officials. Thus, we have formulated an epidemiological model by taking the extended version of the model reported in [18] to represent the accurate dynamics of the novel coronavirus and realize the following contributions:
● Infected individuals are included as asymptomatic and symptomatic individuals because they are very important in the pandemic trend of the SARS-CoV-2 virus transmission. In fact, the existence of asymptomatic individuals with a small amount of the virus can create a major outbreak because without experiencing any symptoms, they produce environmental reservoirs and transmit the disease to others.
● We have investigated the multi-infection pattern of the novel of coronavirus by applying various phases of asymptomatic and symptomatic, and we show that successful interaction between the susceptible population and infected individuals either leads to symptomatic or asymptomatic individuals; therefore, have applied probability-based transmission while applying the outflow of the susceptible population to either infected group of individuals.
● The randomness is taken in each group of the model compartments because every parameter involved in the epidemic process of the novel coronavirus disease has a stochastic nature.
● We have developed an algorithm for the model simulations by using Milstein's higher order procedure to check the validity of the analytical work and represent the long-term with the aid of numerical simulations.
Thus, the goal of this study was to explore the dynamics of novel coronavirus transmission by including the above features and enhancing the model by taking an extended version of the model studied in [18]. To this end, we chose to classify the various infected sources of disease transmission as symptomatic, asymptomatic, and environmental reservoirs, and to take the randomness in every group of individuals by using different Brownian motions according to the disease characteristics. Keeping in view these hypotheses, we chose to first formulate the model and discuss its feasibility in the form of existence analysis and positivity. For this, we will use a combination of the Itô formula and the Lyapunov function. We then calculate the various stochastic reproductive parameters to discuss the conditions for the persistence and extinction of the novel coronavirus. In addition, we discuss the detailed extinction and persistence analysis of the model and derived sufficient conditions for it in terms of the stochastic reproductive parameters. Finally, to interpret the obtained results based on graphical visualization, we chose to develop an algorithm by using the Milstein higher-order method and present the large-scale numerical simulations of the model.
To provide a comprehensive and systematic analysis of the paper, we present the organization of the paper as follows. Following the introduction and recent literature, we formulate the model with a complete description in Section 2. To show the feasibility of the epidemic problem, we provide some basic concepts and notations and discuss the model analysis in Section 3. Subsequently, to examine the model extinction and persistence, and to derive sufficient conditions for it, we investigate the extinction and persistence analysis in Section 4. In addition, to perform the large-scale numerical simulations of the model, we have developed the algorithm by using of Milstein's Higher Order method, as presented in Section 5. Particularly, the discretization of the model is reported in Section 5.1, while the numerical experiments are presented in Section 5.2. Lastly, we conclude the summary of our work with the main findings in Section 6.
2.
The model structure
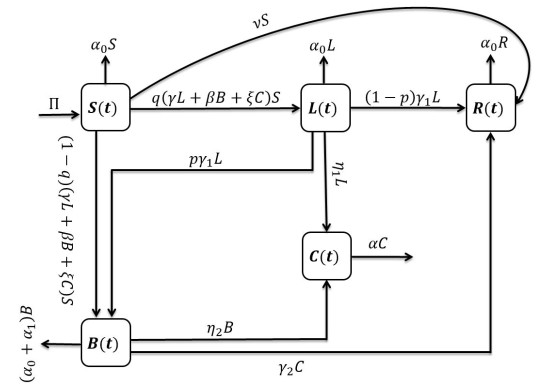
In this part, we formulated the model for the dynamics of the novel coronavirus transmission keeping in view the characteristics of latent/asymptomatic and symptomatic individuals, as well as the environmental reservoirs. We assume that (Θ,QT,(Qt)t∈[0,T],P) is a space of filtered probability that includes a 5D-Brownian motion W:=(W(t))t≥0, where W(t):=(W1(t),W2(t),W3(t),W4(t),W5(t)). The novel disease transmits via environmental reservoirs and human interaction, differing everywhere. We, therefore, assume that groups of the model population will have a stochastic nature that is driven by different randomness sources i.e., Wi(t), i=1,…,5. The proposed epidemiological model incorporates the variations in all groups of individuals associated with various sources of information denoted by Q=(Qt)t≥0, where Qt:=σ(W(t)) represents the σ−algebra derived from W(t); thus, the fluctuations are considered to be taken in all groups of individuals in the model. Further, the groups of humans are categorized into susceptible, latent or asymptomatic, symptomatic, and recovered groups, which are respectively denoted by S(t), L(t), B(t), and R(t), while the concentration of environmental reservoirs is symbolized by C(t). In addition, we provided the flow diagram that represents the transfer mechanism for the model population in Figure 1.
Thus, the below dynamical system represents the novel coronavirus dynamics:
In the model (2.1), the rate of births is denoted by Π, while the parameters γ, β, and ξ are used to represent the disease transmission from various sources. Vaccination for the novel coronavirus plays a significant role and it denoted by v, while α0 denotes the natural death rate. Moreover, the death rate attributable to the novel disease is described by α1, and p is the probability of direct recovery of latent/asymptomatic individuals, as some individuals directly recover without producing any symptoms. We also use q as the probability at which the susceptible individuals enter the asymptomatic/latent population, and γ1 and γ2 are the portions of individuals who recover from the contagious infection of the novel coronavirus disease. In addition, Wi(t) and ϑi, i=1,…,5 are the standard Brownian motions and white noise intensities, respectively, satisfying that Wi(0)=0 and ϑ2i>0 for all i=1,2,3,4,5.
3.
The analysis of the model
In this part, we show the model feasibility to prove the well-posedness of the proposed epidemic model. Particularly, we discuss the existence analysis of the model and its positivity. However, before presenting the results, first, we briefly recall some basic concepts that are helpful for deriving our conclusion.
Lemma 3.1. [19] Let u=(u1,u2,…,uk) and v=(v1,v2,…,vk) represent two square-integrable adopted processes with k-dimensions. We assume the process Y=(y1,y2,…,yk) for n∈{1,2,3,…,k}; then, Yn is expressed as the following differential equation:
If a function G from Rk to R is twice continuously differentiable, then
where ⟨,⟩ represents the quadratic variation; therefore, ⟨dW(t),dW(t)⟩=dt and ⟨dt,dW(t)⟩=⟨dW(t),dt⟩=⟨dt,dt⟩=0.
In addition, to examine the extinction and persistence with the aid of the proposed model, we first describe the definitions that will be used in the model extinction and persistence analysis. Let
Then, the disease persists if lim(inf⟨L(t)⟩), lim(inf⟨B(t)⟩) and lim(inf⟨C(t)⟩) are positive whenever t increases without bound or equivalently, we can say that the epidemiological model (2.1) persists if
are positive.
Moreover, we assume that RSa, RSb, RSc, and RSd are the components of the stochastic reproductive parameter, and they are respectively defined by
Then, the stochastic reproductive parameter for the epidemiological model (2.1) becomes RS0=RSa+RSb+RSc+RSd.
In order to show the model existence analysis, we use a combination of the Itô formula and Lyapunov theory. Define
Thus, regarding the model existence the result will be shown in the following theorem.
Theorem 3.2. For the initial conditions (S(0),L(0),B(0),R(0),C(0)) contained in R5+, there exists a solution (S(t),L(t),B(t),R(t),C(t)) of the epidemiological model (2.1) which is unique and remains in R5+ such that
Proof. Noted that for the model that is under consideration, the local Lipschitz continuity condition holds by following the methodology as adopted by Lei and Yang in [20]. Let X=(S,L,B,R,C) be the model solution for all t in [0,te) (where te is the explosion time), while X0 symbolizes the initial values (S(0),L(0),B(0),R(0),C(0)) for the model contained in R5+; then, the property of Lipschitz continuity implies that the solution of the model (2.1) is unique and local. To demonstrate that the solution is global, it is enough to show that te=∞. To proceed further, we assume a constant ϱ0≥0 that is sufficiently large apply 1ϱ0<X0<ϱ0 and define the stopping time as follows:
Note that infφ=∞, where φ represents the null set; also, since tρ varies with changing ϱ, that is if ϱ increases without bound, tϱ also increases. For t→∞, we set lim=t∞ and t∞=∞. Thus, we need to prove that te=∞ only. Let 0<ζ<1, T>0, and
For ϱ1≥ϱ0
Let H contained in C2 such that H:R5+→R+ be defined by
Note that H≥0; thus, for ϱ0≤ϱ and T≥0, the implementation of the Itô formula yields
where
Applying some algebraic manipulation and simplification, we arrive at
Let K1=max{γ+γ1+η1,β+γ2+η2,ξ}; then, by following S+L+B+R+C≤1 from Eq (3.6), the last inequality appears as follows:
Plugging Eq (3.14) into Eq (3.11), we obtain
Applying the integration on both sides gives
The implementation of expectation yields that
which implies that
Let Φϱ=T≥tϱ for all ϱ≥ϱ1; then, P(Φϱ)≥ζ. For every ϵ∈Φϱ there exists at least one S(ϵ,tϱ), L(ϵ,tϱ), B(ϵ,tϱ), R(ϵ,tϱ) or C(ϵ,tϱ) that is either equal to ϱ or 1/ϱ, thus,
Following Eqs (3.8) and (3.16), we may write
This gives that
In the above equation 1Φϱ(ϵ) represents the indicator function for Φϱ(ϵ). For an increase in n without bound, ∞>H(X0)+ΦT=∞ yields a contradiction; so, t∞=∞.
□
Remark 1. The existence analysis for the considered model reveals that there exists a unique global solution X∈R5+ for any initial groups of population X(0)∈R5+.
Theorem 3.3. The proposed epidemiological model (2.1) possesses positive solutions for all initial groups of populations in R5+.
Proof. To begin the proof, we follow the work investigated in [21], and assume that [0,+∞) is the interval of solution. Since every differential equation in the model (2.1) corresponds to a geometric Brownian motion, we assume the 5 processes to be (ηS(t))t∈R+, (ηL(t))t∈R+, (ηB(t))t∈R+, (ηR(t))t∈R+ and (ηC(t))t∈R+, respectively denoted
By applying the Itô formula to the function lnη., the solution of the above system can be easily derived, as follows:
The solutions of the model process are derived based on the assumption that each solution can be expressed as a product of the stochastic process and associated geometric Brownian motion, i.e., S(t)=ηS(t)YS(t), and YS(t), respectively [21]. So, the stochastic integration based on the implementation of the integral to S(t)η−1S(t) gives the assertion for YS(t). Hence, the model solutions can be represented as follows:
Clearly, all the solutions are positive because η. and η−1. are in exponential form while the initial data and all other epidemic parameters of the epidemiological model have non-negative values.
□
4.
Extinction and persistence of the model
In this section, we discuss the disease extinction and persistence to derive the conditions for it, which will be in the form of an expression containing white noise intensities and model epidemic parameters. Thus, the extinction of the epidemiological model (2.1) is illustrated by giving the subsequent result.
Theorem 4.1. If
a. RSa<1 and RSb<1,
b. (1−q)(γ+β+ξ)(α0+α1+γ2)≥p(v+α0),
then the infection of the novel coronavirus will decay exponentially, that is
and
In addition
Proof. To begin, we integrate both sides of the system (2.1), which gives the integral system as follows
Considering the above integral system with some algebraic manipulation, we have
The addition of the 1st three equations gives
which implies that
where
Obviously Υ(t)=0 as t increases without bounds to ∞
By the application of the Itô lemma to the model (2.1), the second equation yields
Integrating the above equation and then dividing both sides by t, we get the following assertion:
Since, ⟨S(t)B(t)L(t)⟩≤⟨S(t)B(t)⟩≤⟨S(t)⟩ and ⟨S(t)C(t)L(t)⟩≤⟨S(t)C(t)⟩≤⟨S(t)⟩, the above equation can be re-expressed follows
Plugging Eq (4.2) into last equation, we arrive at
Using the stochastic reproductive parameters and following the Strong Law of Large Numbers [22], the final inequality may take the form given by
Thus, limL(t)=0 as t increases without bound and RS1<1.
To proceed further by once again using the Itô lemma, the third equation of the epidemiological model (2.1) appears as follows:
or equivalently, we can write
In a similar fashion as above, once again using stochastic integration, we arrive at
Using the same steps as performed for the previous case, the last inequality can be re-casted as follows:
Plugging in the value of ⟨S(t)⟩, Eq (4.12) can be transformed to obtain
If (1−q)(γ+β+ξ)(α0+α1+γ2)≥pγ1(α0+v), then, through the use of the stochastic reproductive parameters and the implementation of the strong law of large numbers with little rearrangement and simplification, the last inequality is given by
Hence, limB(t)=0 as t approaches ∞ whenever RSb<1. In addition, we take the limiting system of the first, fourth, and fifth equations of the proposed model, whose solution yields that limS(t)=Π/(α0+v), limR(t)=vΠα0(v+α0) and limC(t)=0 if t increases without bound. Thus, the extinction is subject to the values of the stochastic reproductive parameters RSa and RSb, and if they are less than unity, the disease will go extinct. □
Theorem 4.2. For the initial groups of the population (S(0),L(0),B(0),R(0),C(0)) in Φ, the solutions of the epidemiological model (2.1) satisfy
and
where
Proof. The direct use of Eq (4.8) ultimately gives that
which implies that
Using the sup property and applying lim as t approaches ∞, we derive the following:
Similar to Eq (4.6), we can write
Applying some algebraic manipulation with liminf yields
Similarly, the direct use of Eq (4.13) gives that
Re-arrangement with some algebraic manipulation yields
Through the implementation of lim with sup for an increasing t without bound, the last inequality may take the following form:
Likewise, from Eq (4.10), we obtain that
As t approaches ∞, taking lim and inf, we can obtain the following assertion from the last inequality
In addition, from the last equation of the integral system of the model (2.1), we can write
By taking lim as t increases without bound and applying sup and inf respectively to the above equation, we obtain the following assertions
and
Thus, Eqs (4.16)–(4.21) imply that L2≤liminf⟨L(t)⟩≤limsup⟨L(t)⟩≤L1, B2≤liminf⟨B(t)⟩≤limsup⟨B(t)⟩≤B1 and C2≤liminf⟨C(t)⟩≤limsup⟨C(t)⟩≤C1, if t tends to ∞ and RSa>1, RSb>1, RSc>1 and RSd>1, which proves the conclusion. □
5.
Discretization of the model and numerical experiments
To perform the numerical assessment of the stochastic epidemiological model (2.1), we chose to use the numerical Milstein higher-order method; for details, see [23]. Here, we will first demonstrate the model discretization that is used for the numerical investigation.
5.1. Discretization of the model
For, this, we assume that if K≥0 and the interval of time is [0,T] with the time step Δt=T/K, then li=iΔt is the point of the discretized interval. We also use (Si,Li,Bi,Ri,Ci) while writing (S(li),L(li),B(li),R(li),C(li)) and Wj(li)=Wji,j=1,2,3,4,5 for simplicity. Thus, the truncation of the Itˆo-Taylor expansion gives the procedure of Milstein's scheme for the reported model (2.1):
To calculate the discretized Brownian paths that will be applied for Wj(li)−Wj(li−1) for the model (2.1) discretization, we assume the step size Δt to be an integral multiple of R≥1 of the increment δt. So the increments Wj(li)−Wj(li−1) becomes
Thus, the implementation of Milstein's higher order method for the considered model can be concluded with the following steps.
(1) Interval descretization of [0,T] into subintervals δt=TK>0: 0=l0<l1<⋯<lK=T in K with equal width with ln=nδt.
(2) Defining the proper initial data for the compartmental population groups of the model (S0,L0,B0,R0,C0).
(3) Defining the recursive formulas (Sj,Lj,Bj,Rj,Cj) for 1≤i≤K as described through the procedure of Milstein's scheme.
(4) Discretizing the Brownian paths to be used in the calculation of Wj(li)−Wj(li−1) while using the constant R≥1 and increment Δt.
(5) Finding of Wj(li)−Wj(li−1)=Wj(iRδt)−Wj((i−1)Rδt)=∑iRk=iR−R+1dWk.
5.2. Numerical experiments
We shall present the numerical experiment of the model with the aid of Milstein's Higher Order method as concluded in the above algorithm. According to Milstein's higher order method, we can assume two different sets of parameter values based on the sufficient analysis and calculations of the conditions that satisfy the derived analytical results in Theorems 4.1 and 4.2. We also assume some feasible biological initial sizes of the groups of the compartmental populations while implementing the algorithm. More precisely, the set of values of the epidemiological parameters for extinction analysis is assumed to be A1={Π,γ,β,ξ,α0,v,γ1,α1,γ2,p,q,η1,η2,α,ϑ1,ϑ2,ϑ3,ϑ4,ϑ5}, where the values are assigned as Π=0.9, γ=0.68, β=0.03, ξ=0.1, v=0.40, α=0.34, ϑ1=0.32, ϑ2=0.31, ϑ3=0.451, ϑ4=0.731, ϑ5=0.64, α=0.6, q=0.51, γ1=0.35, p=0.022, γ2=0.06, α1=0.65, η1=0.43 and η2=0.87, while the densities for the initial data were adjusted to be S(0)=0.50, L(0)=0.40, B(0)=0.30, R(0)=0.20, C(0)=0.10. Using these parametric values and initial data, we chose to implement Milstein's higher order scheme for the proposed epidemiological model (2.1) in Matlab and produce the output as depicted in Figures 2–6, which respectively demonstrate the temporal dynamics of susceptible, latent or asymptomatic and symptomatic, recovered individuals, as well as the amount of reservoir in the long term. This investigates the model extinction, which reveals that in the case of extinction analysis, the calculation of the stochastic reproductive parameters implies that RSa=0.68, RSb=0.96, RSc=0.57, and RSd=0.041, while the infected population, as well as the amount of reservoirs, goes to zero (vanishes) in the long term, as shown in Figures 3, 4 and 6. However, there will be always a non-infected population in the case of model extinction as shown in Figures 2 and 10.
On the other hand, the set A2 is assumed to be the set of parameters whose values for the model persistence have been adjusted to be γ=0.68, β=0.3, ξ=0.1, v=0.40, Π=0.9, α=0.14, ϑ1=0.31, ϑ2=0.41, ϑ3=0.251, ϑ4=0.731, ϑ5=0.64, α=0.6, q=0.51, γ1=0.35, p=0.022, γ2=0.06, α1=0.65, η1=0.43 and η2=0.87, while the initial data are same as that taken in the case of model extinction. We accordingly calculated the values of the reproductive parameters to be RSa=1.59, RSb=3.80, RSc=1.00 and RSd=1.05. With these parametric values and initial data, the implementation of Milstein's higher order algorithm generates the outputs shown in Figures 7–11, which depict the temporal dynamics of the model population whenever RSa>1, RSb>1, RSc>1 and RSd>1. We observed that in the case that the values of the reproductive numbers are greater than unity, there will always be infected individuals and an amount of reservoir in the community as shown in Figures 8, 9, and 11 respectively. Accordingly, the disease will persist and reach an endemic level. In addition, we also observed a strong impact of noise in coronavirus 2 transmission, where increasing noise intensity leads to the extinction; however, there is an inverse relation between the persistence and noise intensity.
6.
Conclusions
In this work, we investigated the dynamics of SARS-CoV-2 virus transmission under the effects of asymptomatic and symptomatic infection phases, and various sources of randomness by assuming variation in all groups of the model compartmental populations. Keeping in view the asymptotic behavior of the disease, we categorized the infected group of individuals into two subcategories namely, asymptomatic and symptomatic populations, as both are responsible for the transmission of the disease. More precisely, we classified the total populations, into four epidemiological groups of susceptible, asymptomatically infected, symptomatically infected, and recovered individuals, and we assumed that both the asymptomatic and symptomatic individuals are causes of diseases transmission and the production of environmental reservoirs. We also used the probability-based disease transmission coefficient because susceptible individuals either become asymptomatic or symptomatic after getting infected. The model has been developed and studied in terms of its biological and mathematical feasibility to prove that the considered problem is well-possed. We then calculated the threshold quantities and derived the conditions for the model extinction and persistence. Finally, on the basis of theoretical results, we developed the algorithm with the aid of Milstein's higher order procedure to verify the model and show the validity of the results that have been obtained in the theoretical investigation of the model. We observed that the asymptotic behavior of the infected individuals and the white noise intensity are very influential in the analysis of the dynamics of SARS-CoV-2 virus transmission. The extinction of the disease is directly related to the intensity of noise while there is an inverse relationship between persistence and the intensity of white noise.
In the future, we will incorporate suitable time dependent control measures into the proposed model by using optimal control theory to design a mechanism that leads to elimination of the infection from the community. We will also study the fractional version of the model with the aid of fractional calculus. Further, we will use the Euler-Maruyama scheme and exponential Euler-Maruyama method for simulation purposes.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to extend their appreciation to the Deanship of Scientific Research at King Khalid University for supporting this work through a research group program under grant no. R.G.P2/202/44. Further, the author Muhammad Bilal Riaz is thankful to the Ministry of Education, Youth and Sports of the Czech Republic for their support through the e-INFRA CZ (ID: 90254).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:













