Analysis of a Holling-type IV stochastic prey-predator system with anti-predatory behavior and Lévy noise

1.   Introduction

In recent years, there has been increasing interest in population dynamics models of prey-predator interactions within both the fields of biology and mathematics ^[1]. The Volterra prey-predator model has received criticism for its unrealistic assumptions. However, theoretical results have shown that the prey-predator interaction is a crucial relationship in an ecosystem. To model this interaction, the functional response function is used. This mathematical model describes the predation rates of predators at varying prey densities and their response to changes in prey density. C. S. Holling ^[2] proposed Holling-type functional response functions, which have received significant attention in the academic community. Holling classified functional response functions into three types: Holling-type I, Holling-type II, and Holling-type III. Holling-type I ($m(x) = bx$, linear) is commonly used to describe the rate at which predators feed on a population of unresisting prey without a saturation point, such as herbivores feeding on grass. ^[3,4] has conducted further studies on this topic. On the other hand, Holling-type II ($m(x) = \frac{bx}{a+x}$, concave increasing) is used to describe low-level predators that are sensitive to prey selection and have saturation limits. ^[5,6,7,8] has explored this type of predator. Finally, Holling-type III ($m(x) = \frac{bx^{2}}{a+x^{2}}$, sigmoid increasing) is an extension of Holling-type II and is used to describe more complex predatory predators like predatory birds. This type of predator has been studied by ^[9,10,11,12].

An improved Holling-type function, known as the Holling-type IV functional response function, has been proposed ^[13]. This function $m(x) = \frac{bx}{a+x^{2}}$ suggests a non-monotonic response at higher levels of nutrient concentration, meaning that there may be an inhibitory effect on specific growth rates, as noted in previous research ^[14]. Specifically, when prey densities are low, predation rates increase with prey abundance. However, when prey concentrations reach a threshold, prey collectively defend themselves, causing predator intake rates to decrease ^[15]. The Holling-type IV functional response function has been studied by many scholars, see ^{[16,17,18,19]}. A differential equation model with Holling-type IV is obtained:

where $x(t)$ and $y(t)$ represent the population density of prey and predator at time $t$, respectively. $r_{1}$ denotes the intrinsic growth rate of prey. $r_{2}$ represents the natural birth rate of the predator. $K$ denotes the environmental holding capacity of the population, $b$ denotes the capture rate of the predator. $\mu$ denotes the prey-to-predator conversion rate. $c$ denotes the natural mortality rate of the predator population.

The following model, which take into account the predation resistance, intraspecific competition for predators, and prey gestation time delays, were developed as follows:

The size of the population is significantly impacted by the existence of intraspecific competition. The specifics are in ^{[20,21,22,23]}. Let $d$ stand for the intra-species competition rate. ^[24] added the knowledge that adult prey can kill young predators in addition to intraspecific rivalry. It actually affects the ecosystem. Reports from Africa ^[25] suggest that elephants may exhibit anti-predatory behavior by turning on lion cubs and killing them, especially if the lions pose a threat to young elephants. The impact of such behavior on population size remains uncertain and requires further research. ^[26] said that although African hunting dogs will defend themselves when confronted by powerful predators, the effect on their population size is negligible. On the other hand, ^[27] indicated that seals' anti-predatory behavior can aid in boosting their population growth when faced with challenges. We propose the parameter $\eta$, which represents the rate of adult prey resistance to predation on juvenile predators, based on the reasoning from above.

Furthermore, the authors ^[28] emphasized that time delays must be taken into account because a model's evolution frequently involves the past till present states in addition to the current one. In ^[29], a model with gestation time delay was investigated, where the delay exceeding a predetermined threshold and the significant effects on population growth were discovered. The authors of ^[30] examined how harvest rates and time delays affected generalized Gaussian-type prey-predator models and discovered that time delays could change stability or perhaps make it more unstable. C. J. Xu et al. ^[31] conducted a study on the impact of time delay on the stability of integer-order and fractional-order delayed BAM neural networks exhibiting Hopf bifurcation. The study found that by adjusting the value of the time delay, the stability region of fractional-order BAM neural networks can be expanded and the onset of Hopf bifurcation can be delayed. The significance of time delays is also illustrated in ^[32]. Based on the aforementioned research, we consider the prey's delayed gestational time in this study. $\tau$ indicates the delayed gestation of the prey.

On the other hand, populations are disturbed by various kinds of random noise as shown in ^[33]. Among them, let us first consider white noise. Assuming that $r_{i}$ $(i = 1, 2)$ is affected by white noise, we have $r_{i}\to r_{i}+\sigma_i dW_i(t)$, where $W_i(t)$ is a standard Wiener process defined on the complete probability space $(\Omega, \left\{\mathcal{F}_{t}\right\}_{t \geq 0}, \mathbb{P})$; $\sigma_{i}^{2}$ is the intensity of white noise, $i = 1, 2$. The authors ^[33] mathematically demonstrated that white noise increased the risk of species extinction. In ^[34], the problem of optimal harvesting of delayed logic models with white noise was investigated by Liu et al. It once again validated this view. ^[35] studied the effects of white noise on the persistence, extinction and stability of biological populations. It revealed that the effects of white noise on different species are not uniform for all populations. In summary, there is a need to study the effect of white noise on the system dynamics. Thus, the following stochastic biomathematical model with white noise is given:

In addition, the growth of populations affected by environmental fluctuations is usually a stochastic process. In reality, the process of population growth is inevitably exposed to natural disasters such as floods, earthquakes and tsunamis. However, these phenomena can not be explained by white noise ^[36,37]. Some scholars (e.g., ^{[38,39,40,41]}) have suggested that such sudden random perturbations can be represented by Lévy noise which plays a key role in the persistence and extinction of populations. Zhao et al. ^[21] studied a two-species Lotka-Volterra model in a stochastic environment and found that Lévy noise can have the opposite effect on the population growth. Zhou et al. ^[42] studied models of infectious diseases with Lévy noise and found that Lévy noise can be effective in controlling outbreaks of infectious diseases. It is necessary to consider the effect of Lévy noise on the population size of organisms, so we include Lévy noise as a stochastic environmental factor in the system for our study:

Here $x_{i}\left(t^{-}\right) = \lim _{s \uparrow t} x_{i}(s), \mathbb{Y} \subseteq(0, +\infty), \tilde {N}(d t, d u) = N(d t, d u)-\lambda(d u) d t, N(d t, d u)$ represents a Poisson counting measure with characteristic measure $\lambda$ and $\lambda(\mathbb{Y}) < \infty, \gamma_{i}(u) > -1, u \in \mathbb{Y}, i = 1, 2$. Further details can be found in ^[21].

Combining the above analysis, this paper investigates a stochastic prey-predator model with Holling-type IV functional responses, anti-predatory behavior, gestation time delay of prey and Lévy noise. We discuss the dynamical properties of model (1.4) in subsequent sections. The theoretical knowledge and model assumptions used in the proofs are presented in Section 2. Section 3 covers the existence and limitations of a global positive solution to system (1.4) and provides sufficient conditions for the persistence and extinction of both species. The stable distribution is discussed in Section 4. In Section 5, we use MATLAB R2021b to carry out simulations of the results. The conclusions of this paper are given in Section 6.

2.   Preliminaries

In this section, we give the theoretical knowledge needed for the subsequent proofs and make reasonable assumptions about the model (1.4).

First, we introduce the form of Itô's formula with Lévy noise. The following stochastic differential equation with Lévy noise is given:

where $F_{1}, F_{2}$ and $F_{3}$ denote measurable functions mapped onto $\mathbb{R}^{n}$. Let $x(t)\in \mathbb{R}^{n}$ be the solution of Eq (2.1) and set $V \in C^{2, 1}\left(\mathbb{R}^{n} \times \mathbb{R}_{+}; \mathbb{R}\right)$. We define the operator function by:

We obtain the following Itô's formula with Lévy noise:

where $V_{t}(x, t) = \frac{\partial V(x, t)}{\partial t}, V_{x}(x, t) = \frac{\partial V(x, t)}{\partial x}, V_{xx}(x, t) = \frac{\partial ^{2} V(x, t)}{\partial x_{i} \partial x_{j}}$. See ^[43] for more details on stochastic differential equations with Lévy noise.

Next, for further calculations, it is assumed that the model (1.4) satisfies the following assumptions.

($\mathcal{A}_{1}$) We let the initial values $\left (x(\varrho), y(\varrho)\right)$ be positive and belong to the Banach space $C_{g}$. The definition is as follows

where $g > 0$, there exists a probability measure $\pi$ on $(-\infty, 0]$ such that

If $\theta \le 0$ in the above equation, it is obvious that the assumption holds when $\pi _{i}(\theta) = e^{mr\theta } (m > 2)$. Then, there are many such probability measures.

($\mathcal{A}_{2}$) In this paper, we assume that there exist constants $c_{i} > 0, i = 1, 2$ such that

For each $h > 0$, there exists $\omega_{h}$ such that

($\mathcal{A}_{3}$) All parameters are positive values. The stochastic perturbations $N$, $W_{1}$ and $W_{2}$ are all independent of each other.

3.   Extinction and persistence

In this section, we begin with the existence and uniqueness of a global positive solution to model (1.4), then give some sufficient conditions for the extinction and persistence of the solution for population $x(t)$ and $y(t)$.

For the sake of subsequent proofs and calculations, we define the following notations:

Theorem 3.1. Supposing ($\mathcal{A}_{1}$) and ($\mathcal{A}_{2}$) hold. For any given positive initial value $\left (x(\varrho), y(\varrho) \right) \in C_{g}$, the system (1.4) has a unique global solution $\left (x(t), y(t) \right) \in \mathbb{R}_{+}^{2}$ for all $t\ge -\tau$ and the solution will remain in $\mathbb{R}_{+}^{2}$ with probability 1, that is

Proof. All coefficients of the model (1.4) are locally Lipschitz continuous, so for initial values $\left (x(\varrho), y(\varrho) \right)$ in the space $\mathbb{R}_{+}^{2}$, there exists a unique local solution $\left (x(t), y(t) \right)$ for all $t\in \left [-\tau, \tau _{e} \right]$, where the concept $\tau _{e}$ represents the duration of the explosion. To prove that this solution is also global, it suffices to show that $\tau _{e} = \infty$ almost surely. To prove this, we consider a sufficiently large positive integer $k_{0}$ such that $\left (x(\varrho), y(\varrho) \right)$ belong to interval $\left [\frac{1}{k_{0}}, k_{0} \right]$. Furthermore, for any $k\ge k_{0}$, we define the stopping time as

In this paper, we set $\inf \emptyset = \infty \left (\emptyset \text{ denotes the empty set} \right)$. Let $\tau_{\infty} = \lim _{k \rightarrow \infty} \tau_{k}$. Since $\tau_{k}$ is non-decreasing, then $\tau_{\infty}\le \tau _{e}$. We only need to verify that $\tau_{\infty} = \infty$. Otherwise, there exists $T > 0$ and $\varepsilon \in \left (0, 1 \right)$ such that $\mathbb{P}\left\{\tau_{\infty} \leq T\right\} > \varepsilon$. Thus, by indicating $\Psi _{k} = \left\{\tau_{k} \leq T\right\}$, there exists $k_{1} \geq k_{0}$ such that

To further prove this, we define a $C^{2} \text {-function } V$ from the space $\mathbb{R}_{+}^{2}$ to $\mathbb{R}_{+}^{2}$:

When $(x(t), y(t)) \in \mathbb{R}_{+}^{2},$ by using Itô's formula

where

where $\Xi$ is a positive constant. The following proof is similar to Theorem 3.1 in Xue and Shao ^[44], so we omit it here. So far, Theorem 3.1 is proved. □

Lemma 3.1. (See Lemma 2.2 in ^[45]) Let $A(t) \in C\left(\Omega \times[0, \infty), \mathbb{R}_{+}\right)$ and assumption ($\mathcal{A}_{2}$) holds.

$(1)$ If there exist positive values $\delta, \delta _{0}, \tilde{\delta} _{i}(i = 1, 2)$ and some positive moment $T$, for any $t \ge T$, there exists the following equation

then we have

$(2)$ If there exist positive values $\delta, \delta _{0}, \tilde{\delta} _{i}(i = 1, 2)$ and some positive moment $T$, for any $t \ge T$, there exists the following equation

then we have

Theorem 3.2. Supposing ($\mathcal{A}_{1}$) and ($\mathcal{A}_{2}$) hold. For the model (1.4), we have

$(1)$ if $\delta _{1} < 0,$ $\delta _{2} < 0,$ then both $x(t)$ and $y(t)$ tend to extinction:

$(2)$ if $\delta _{1} < 0,$ $\delta _{2} > 0,$ $x(t)$ tends to extinction, but $y(t)$ is persistent in time average:

$(3)$ if $\delta _{1} > 0,$ $\delta _{2} < 0,$ $y(t)$ tends to extinction, but $x(t)$ is persistent in time average:

Proof. By Itô's formula, from the model (1.4), we obtain the following equation

Integrating both sides of the above Eq (3.3) simultaneously yields

and

First, we prove $(1)$. From Eqs (3.4) and (3.5), we have

and

According to the law of large numbers, it yields that

According to Lemma 3.1, we have $\lim_{t \to +\infty}x(t) = \lim_{t \to +\infty}y(t) = 0 \quad a.s.$

Second, we prove $(2).$ The following formula can be obtained from Eq (3.5)

If $\delta _{1} < 0$, then it follows from $(1)$ that $\lim_{t \to +\infty}x(t) = 0, a.s.$ Further computations show that

$(i)$ It is clear that

When assumption ($\mathcal{A}_{2}$) holds, we can easily obtain $\lim_{t \to +\infty} \frac{\sigma _{2}W_{2}(t)+\int_{0}^{t} \int _{\mathbb{Y} }ln(1+\gamma _{2}(u))\tilde{N} (ds, du)}{t} = 0 \quad a.s.$ By utilizing Lemma 3.1, it derives that

Letting $\varepsilon \to 0,$ by further calculation, we can obtain

$(ii)$ Similarly,

By the same token, we can obtain

Letting $\varepsilon \to 0,$ by further calculation, we can obtain

Summarizing $(i)$ and $(ii)$, when $\delta _{1} < 0, \delta _{2} > 0,$ it can be concluded that

Third, we prove $(3)$. The proof of $(3)$ is very similar to the proof of $(2)$. From synthesis of the above analysis, when $\delta _{1} > 0, \delta _{2} < 0,$ it can be concluded that

□

Definition 3.1. (See in ^[46]) The system (1.4) is permanent in time average if there exist positive constants $\mathcal{L} _{i}$ and $\mathcal{C} _{i},$ for any solution $(x(t), y(t))$ under initial conditions $(x(\varrho), y(\varrho)) \in C_{g}$, satisfies the following equation

Theorem 3.3. Under the conditions $\delta_{1}-\frac{b\delta_{2}}{ad} > 0, \delta_{2}-\frac{k\eta\delta_{1}}{r_{1}} > 0$ and assumptions $(\mathcal{A}_{1})$ and $(\mathcal{A}_{2})$ hold, for any initial data $(x(\varrho), y(\varrho)) \in C_{g}$, the solutions $(x(t), y(t))$ of the system have the following properties

where

That is, the model (1.4) will be permanent in time average.

Proof. Due to (3.4), it yields that

Letting $\varepsilon \to 0,$ i.e.,

Further calculations are performed to get

From Theorem 3.2, it follows that

Making use of the condition $\delta_{1}-\frac{b\delta_{2}}{ad} > 0$, we obtain

Similarly,

Making use of the condition $\delta_{2}-\frac{k\eta\delta_{1}}{r_{1}} > 0$, we obtain

Meanwhile,

Making use of the condition $\delta_{2}-\frac{k\eta\delta_{1}}{r_{1}} > 0$, we obtain

The proof is complete. □

4.   Stability in distribution

In this section, we establish the sufficient criteria for stability in distribution of the system (1.4). First, we give the following important lemma.

Lemma 4.1. Assuming $(x(t), y(t))$ is a component of the solution of the system (1.4) with any initial value, then there exists a positive constant $K(\rho) > 0$ for any $\rho > 0$ such that

Proof. Since the proof procedure for this lemma is very similar to the method of ^[38,47], we omit it here. □

Definition 4.1. Let $(x(t; \phi), y(t; \phi))$ and $(x(t; \psi), y(t; \psi))$ be two solutions of the model (1.4) and the initial values satisfy $\phi (\theta), \psi (\theta)\in C_{g}$. We call a system globally attractive or globally asymptotically stable if the following equation is satisfied.

Theorem 4.1. If assumption $(\mathcal{A}_{3})$ holds, then system (1.4) is asymptotically stable in distribution. That is, as $t \to + \infty$, there exists a unique probability measure $\mu(\cdot)$ such that, for any given initial value $(x(\varrho), y(\varrho))\in \mathbb{R}_{+}^{2}$, the transition probability density $p(t, \phi, \cdot)$ of solution $(x(t), y(t))$ converges weakly to $\mu(\cdot)$.

Proof. Let $(x(t; \phi), y(t; \phi))$ and $(x(t; \psi), y(t; \psi))$ be two solutions of the model (1.4) and the initial values satisfy $\phi (\theta), \psi (\theta)\in C_{g}$. Define

Using Itô's formula to find the right differentiation of the above Eq (4.1) yields

Thus,

Obviously $V(0)\ge 0$, and we can obtain

Under assumption $(\mathcal{A}_{3})$, as well as $\frac{r_{1}}{K}+\eta -\frac{\mu b}{a} > 0$ and $\frac{b}{a}+d > 0$, we can obtain

In addition, the following equation can be obtained from the model (1.4)

From Lemma 4.1, we have

where $G_{x}^{\ast }$ and $G_{y}^{\ast }$ are both positive constants. By using Barbalat's Lemma ^[33], we yield that

Next, let $p(t, (\phi, \psi), d\varsigma)$ denote the transfer probability density of the process $(x(t), y(t))\in \mathcal{B}$. $\mathcal{B}$ is a Borel measurable set on $\mathbb{R}_{+}^{2}$. Let $\mathcal{P}(\mathbb{R}_{+}^{2})$ denote the probability measures on $\mathbb{R}_{+}^{2}$. For any given measures $\mathcal{P}_{1}, \mathcal{P}_{2} \in \mathcal{P}(\mathbb{R}_{+}^{2})$, the metric $d_{\mathcal{BL} }$ is defined as follows,

where

We first prove $p(t, (\phi, \psi), d\varsigma)$ is Cauchy in the space $\mathcal{P}(\mathbb{R}_{+}^{2})$ with $d_{\mathcal{BL} }$. According to Chebyshev's inequality ^[48] and Lemma 4.1, we can get $\mathcal{P}(\mathbb{R}_{+}^{2})$ to be tight. For arbitrary $u\in \mathcal{BL}, t > 0, s > 0,$ we can obtain

From equation above, there exists a constant $T > 0$ such that

Similarly,

Combining the above analyses, we can obtain

We have proved $p(t, (\phi, \psi), d\varsigma)$ is Cauchy in the space $\mathcal{P}(\mathbb{R}_{+}^{2})$ with $d_{\mathcal{BL} }$, so there is a unique probability measure $\mu(\cdot) \in \mathbb{R}_{+}^{2}$ such that

By further calculation, combining with (4.6) and (4.8), then

That is

This completes the proof. □

5.   Numerical simulations

In this section, we perform simulations using MATLAB R2021b to confirm the accuracy of our previous conclusions. Therefore, we set each parameter in the model (1.4) as follows.

In addition, $\mathbb{Y} = (0, +\infty), \lambda(\mathbb{Y}) = 1,$ and we set the initial value to $(x(\varrho), y(\varrho)) = (10, 10).$

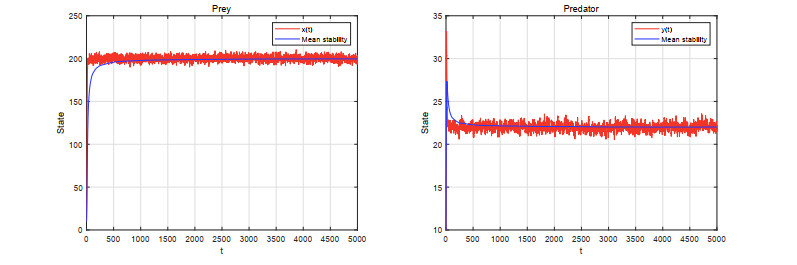
First, we set $\sigma_{1} = \sigma_{2} = 0.01.$ In the above setup, we calculate that $\delta_{1} = 0.29995 > 0, \delta_{2} = 0.41995 > 0.$ Both conditions are consistent with the setting of the stable persistence condition for prey and predators in Theorem 3.2. It follows that both prey and predator numbers fluctuate up and down along the mean. The results of this simulation are shown in Figure 1.

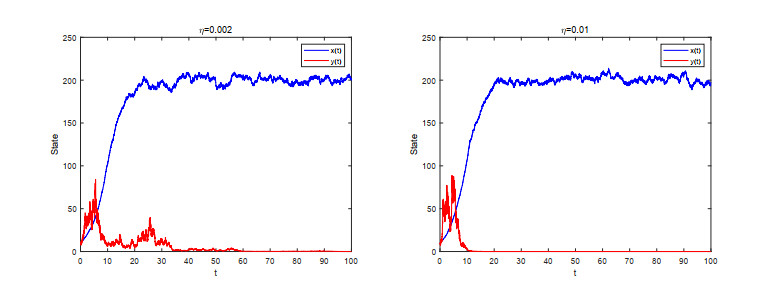
Second, we analyze the anti-predation behavior rate $\eta$ for adult prey attacking young predators, taking $\eta = 0.002$ and $\eta = 0.01$, respectively, and the simulation results can be seen in Figure 2. Compared to Figure 1, the anti-predation behavior rate has a greater effect on the population size of predators. It indicates that smaller anti-predation rate can easily cause fluctuations in predator populations, while the anti-predation rate is larger, and the predator populations face extinction.

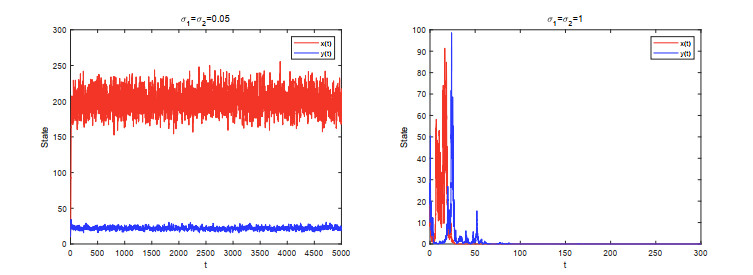
Third, by contrast to Figure 1, we now consider adjusting the strength of the random term to investigate changes in prey and predator population size for different white noise intensities. We set the random term parameter to $\sigma_{1} = \sigma_{2} = 0.05,$ which satisfy $\delta _{1} = 0.29875 > 0, \delta _{2} = 0.295 > 0$ at this point, and the population is persistent. We set $\sigma_{1} = \sigma_{2} = 1,$ then by calculation, $\delta _{1} = -0.2 < 0, \delta _{2} = -0.08 < 0$. Through the simulation results shown in Figure 3, we find that the population size fluctuates significantly as the random term parameter increases, and the population size tends to become extinct when the random term parameter is large enough. This is consistent with our conclusion.

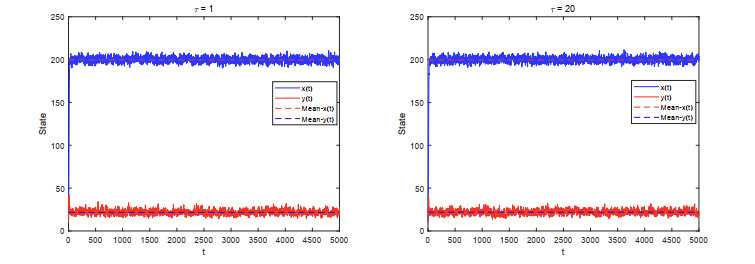
Fourth, we investigate how the delay in gestation time of prey affects the population size. We keep the model parameters unchanged but set parameters $\sigma_{1} = 0.01, \sigma_{2} = 0.07,$ and $\tau_{1} = 1, \tau _{2} = 20$. It is clear that both populations are consistently stable. The comparison of two plots in Figure 4 shows that different sizes of gestational delay have minimal effects on either population, which is consistent with our findings in this paper.

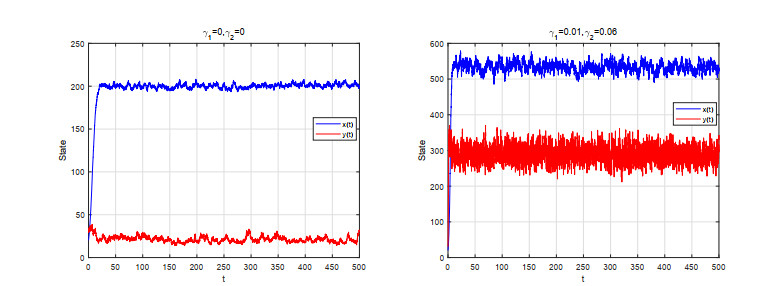
Finally, we investigate the effect of Lévy noise on the prey and predator populations in the model (1.4). We use the same parameter settings as before, but adjust the parameters $\gamma_{1} = 0, \gamma_{2} = 0$ to $\gamma_{1} = 0.01, \gamma_{2} = 0.06$. We conclude that, without Lévy noise, the number of predators remains low and fluctuates less, and that Lévy noise with appropriate intensity can increase the number of prey and predators to some extent. This is consistent with our research, as seen in Figure 5.

6.   Conclusions

This paper examines the existence and stability of a delayed prey-predator system with anti-predatory behavior and Lévy noise. Building on previous work, we involve the Holling-type IV functional response into the prey-predator model and establish sufficient conditions that ensure the stability of the solutions. The previous conclusions are verified through numerical simulations, and the effects of anti-predatory behavior, time lag, and stochastic parameters are analyzed.

The simulation results indicate that anti-predation behavior brings a significant effect on the population stability. Increasing the rate of anti-predation behavior leads to the acceleration of population extinction. While the intensity of white noise has a minimal impact on the global stability of the model (1.4), but when the intensity of white noise is increased, the system stability is lost and both populations become extinct. According to numerical simulations, anti-predation behavior and white noise play crucial roles in maintaining population stability, while time delay has almost no effect. If the effect of Lévy noise is absent, then both prey and predators remain at a low fluctuation level. Increasing the intensity of Lévy noise leads to a moderate increase in the population of both prey and predators.

This paper focuses on a Holling-type IV functional response in the model setting, but there are other functional responses related to ratios that require further study. Additionally, only the prey's gestation delay is examined in the time delay setting, leaving room for future research on different types of time delays. C. J. Xu et al. ^[49,50] investigated a category of fractional-order predator models that incorporated both distributed and discrete delays. They were able to establish a stability and bifurcation criterion that was independent of delay, and used time delay as a bifurcation parameter. This research offers valuable insights that can inform our future investigations. We leave these to future investigations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors express their gratitude towards the reviewers for their insightful suggestions and valuable comments. These inputs have significantly contributed to improving the quality of this paper's presentation.

This article is financially supported by NSF of China (11861027).

Conflict of interest

The authors declare that they have no competing interests in this article.