Dynamics of a stochastic epidemic model with quarantine and non-monotone incidence

1.   Introduction

The Weighted Complementarity Problem (WCP), which is to find a pair of $\left( {x, s, y} \right) \in {R^n} \times {R^n} \times {R^m}$ such that

where, $F:{R^{2n + m}} \to {R^{n + m}}$ is a continuously differentiable function, $w \in R_ + ^n$ is the given weight vector, $xs: = x \circ s$ is the componentwise product of the vectors $x$ and $s$. When $w = 0$, WCP (1.1) reduces to the classical Nonlinear Complementarity Problem (NCP). At present, there are many effective algorithms ^[1,2,3,4,5] that can solve NCP. For examples, Newton method ^[1], Quasi-Newton method ^[2], L-M method ^[3,4], Neural-Networks method ^[5] etc. If

problem (1.1) is the Linear Weighted Complementarity Problem (LWCP) studied in this paper, which is to find a pair of $\left( {x, s, y} \right) \in {R^n} \times {R^n} \times {R^m}$ such that

where, $P \in {R^{\left( {n + m} \right) \times n}}, Q \in {R^{\left( {n + m} \right) \times n}}, R \in {R^{\left( {n + m} \right) \times m}}, a \in {R^{n + m}},$ are given matrices and vector. In addition, when

problem (1.1) is the perturbed Karush-Kuhn-Tucker(KKT) condition for the following Nonlinear Programming(NLP)

Problem(1.3) was introduced by Potra ^[6] in 2012 and has been widely studied for its important applications in management, market equilibrium, etc. Many equilibrium problems can also be transformed into LWCP to solve, such as the famous Fisher market equilibrium problem ^[7], and the quadratic programming and weighted center problem ^[6].

In recent years, many effective algorithms have been proposed to solve problem (1.1) or (1.3) ^{[8,9,10,11,12,13]}. For examples, Chi et al. ^[9] proposed the full-Newton step infeasible interior-point method for solving LWCP. Zhang et al. ^[12] proposed the smoothing Newton type method for solving LWCP. Tang et al. ^[13] proposed the nonmonotone L-M method for NWCP. The interior point method depends on the choice of initial value. The classical Newton method needs the positive definite of Hessian matrix, otherwise, it is difficult to guarantee that the Newton direction is descending. The L-M method does not depend on the choice of initial values, nor does it require the positive definiteness of the Hessian matrix. Therefore, this paper mainly considers using L-M method to solve problem (1.3). Motivated by ^[13], we consider using a nonmonotone L-M method to solve LWCP.

LWCP is a more general complementary model. For the solution of this model, we hope to use the WCP functions obtained by the extension of NCP functions. However, due to the existence of weighting term, not all NCP functions can be directly extended to WCP functions. For NCP function in the form of FB function, many scholars have extended it to WCP function. In this paper, motivated by the smoothed penalty function for ^[14], we construct a smoothng function for WCP. And then use L-M method to approximate the equivalent reconstruction equations of problem (1.3). The comparison experiment of random generation shows the feasibility and effectiveness of our algorithm.

The following notations will be used throughout this paper. The superscript T denotes transpose. R denotes real numbers, ${R^n}$ represents the set of all n dimensional real column vectors. The matrix I denotes the identity matrix, and $\left\| \cdot \right\|$ denotes 2-norm. All vectors in this article are column vectors.

2.   Weighted complementary function and its properties

In this section, we study a class of complementary functions with participation weights and discuss its properties. Based on this weighted complementary function, the equivalent reconstruction equations of problem (1.3) are given.

Definition 2.1. For a fixed $c \geqslant 0$, a function $\phi :{R^2} \to R$ is called a weighted complementarity function ^[13], if it satisfies

When $c = 0$, ${\phi ^c}(a, b)$ reduces to the NCP function.

In this paper, to solve the LWCP (1.3), we hope to use the WCP functions obtained by the extension of NCP functions. However, due to the existence of weighting term, not all NCP functions can be directly generalized to WCP functions. For example, the two piecewise NCP functions given in ^[2]:

For FB function, many scholars have extended it to WCP function. For example, Liu et al. ^[11] based on the symmetric disturbance FB function in ^[15] constructed:

where, $c$ is a given nonnegative vector.

Zhang^[12] proposed:

where, $\theta \in \left( { - 1, 1} \right],$$c$ is a given nonnegative vector.

In addition, ^[13] provides another smooth function:

where, $c$ is a given nonnegative vector, $\tau \in \left[ {0, 4} \right)$ is a constant, $q > 1$ is an odd integer. Compared with (2.4) and (2.5), (2.6) does not need to introduce the smoothing factor $\mu$. By controlling the value of $q$, smoothing can be achieved. This smoothing method will be used to smooth the new WCP function given below.

where, $c$ is a given nonnegative vector, $\tau \in \left[ {0, 1} \right]$ is a constant.

Since Eq (2.7) is not smooth, we make the following smoothing treatment:

where, $c$ is a given nonnegative vector, $\tau \in \left[ {0, 1} \right]$ is a constant, $q > 1$ is an odd integer.

Theorem 2.1. Let $\phi _{\tau , q}^c$ be defined by (2.8) with $\tau \in \left[ {0, 1} \right]$ and $q > 1$ being a positive odd interger. Then $\phi _\tau ^q$ is a family of WCP functions, i.e.,

Proof. Since for any $\alpha , \beta \in R$ and any positive odd interger $q$, there is ${\alpha ^q} = {\beta ^q} \Leftrightarrow \alpha = \beta .$ So we have

That is to say, we only need to prove that $\phi _\tau ^c(a, b)$ is a family of WCP functions. On the one hand, we fist suppose that $\forall a, b \in R$ satisfy, $\phi _\tau ^c(a, b) = 0$ i.e.,

By squaring the two sides of (2.11), we have $2(1 + \tau )ab = 2(1 + \tau )c,$ which together with $\tau \in [0, 1]$. yields $ab = c.$ By substituing $ab = c$ into (2.2), we have $\sqrt {{a^2} + {b^2} + 2ab} = a + b \geqslant 0.$ Since $c = ab \geqslant 0,$ it follows that $a \geqslant 0, b \geqslant 0.$ On the other hand, we suppose that $a \geqslant 0, b \geqslant 0, ab = c,$ then $a + b \geqslant 0$ and

Which implies that $\phi _\tau ^c(a, b) = 0.$

Lemma 2.1. Let $\phi _{\tau , q}^c$ be defined by (2.8) with $\tau \in [0, 1]$ and $q > 1$ being a positive odd interger. Let

Then

(ⅰ)When $q > 1$, $\phi _{\tau , q}^c$ is continuously differentiable at any $\left( {a, b} \right) \in {R^2}$ with

where

(ⅱ)When $q > 3$, $\phi _{\tau , q}^c$ is twice continuously differentiable at any $\left( {a, b} \right) \in {R^2}$ with

where

Lemma 2.2. Let $\phi _{\tau , q}^c$ be defined by (2.8) with $\tau \in [0, 1]$ and $q > 1$ being a positive odd interger. Defining the closed and convex set $\Omega \left( u \right): = \left\{ {u \in {R^2}\left| {\left\| u \right\|} \right. \leqslant \theta } \right\}$, where $\theta$ is a positive constant. Then:

(ⅰ)When $q > 1$, $\phi _{\tau , q}^c$ is Lipschitz continuous on $\Omega \left( u \right)$ for any $\theta > 0$.

(ⅱ)When $q > 3$, $\nabla \phi _{\tau , q}^c$ is Lipschitz continuous on $\Omega \left( u \right)$ for any $\theta > 0$.

Since $\phi _{\tau , q}^c$ and $\nabla \phi _{\tau , q}^c$ are bounded on the set $\Omega \left( u \right)$, therefore the conclusion (ⅰ) and (ⅱ) can be obtained from the Mean-Value-Theorem.

Given weight vector $w \in R_ + ^n$, let $z: = (x, s, y) \in {R^{2n + m}}$ and

where

Then the solution of LWCP (1.3) is equivalent to the approximate solution of the system of equations $H(z) = 0$.

Lemma2.3. Let $H\left( z \right):{R^{2n + m}} \to {R^{2n + m}}, \Phi _{\tau , q}^w:{R^{2n}} \to {R^n}$ be defined by (2.16) and (2.17), respectively. Then:

(ⅰ)$\Phi _{\tau , q}^w\left( {x, s} \right)$ is continuously differentiable at any $z = \left( {x, s, y} \right) \in {R^{2n + m}}$.

(ⅱ)$H\left( z \right)$ is continuously differentiable at any $z = \left( {x, s, y} \right) \in {R^{2n + m}}$ with its Jacobian

where

Let $H(z)$ be defined by (2.16), then its value function $M:{R^{2n + m}} \to {R_ + }$ can be defined as:

Obviously, the solution of LWCP (1.3) is also equivalent to the approximate solution of the system of equations $M(z) = 0.$ In addition, the following conclusion can be obtained from the Lemma 2.3.

Lemma 2.4. Let $M:{R^{2n + m}} \to {R_ + }$ be defined by (2.19), then $M(z)$ is continuously differentiable at any $z \in {R^{2n + m}}$, and $\nabla M(z) = H'{\left( z \right)^T}H\left( z \right).$

3.   Algorithm and convergence analysis

In this section, based on the WCP function in Section 2, we will give the smooth L-M type algorithm and its convergence.

Algorithm3.1 (A smooth L-M method)

Step 0: Choose $\theta , \sigma , \gamma , \delta \in \left( {0, 1} \right)$ and ${z^0}: = \left( {{x^0}, {s^0}, {y^0}} \right) \in {R^{2n + m}}$, let $0 \leqslant \varepsilon \leqslant 1$, and ${C_0} = M\left( {{z^0}} \right)$. Choose a sequence $\left\{ {{\eta _k}\left| {\forall k \geqslant 0, } \right.{\eta _k} \in \left( {0, 1} \right)} \right\}$, set $k: = 0.$

Step 1: Compute $H({z^k})$. If $\left\| {H({z^k})} \right\| \leqslant \varepsilon$ then stop.

Step 2: Let ${\mu _k}: = \theta {\left\| {H\left( {{z^k}} \right)} \right\|^2}$. Compute the search direction ${d_k} \in {R^{2n + m}}$ by

Step 3: If ${d_k}$ satisfies

Then let ${\alpha _k}: = 1$, and go to step 5. Otherwise, go to step 4.

Step 4: Set ${j_k}$ be the smallest nonnegative integer $j$ satisfying

let ${\alpha _k}: = {\delta ^{{j_k}}}$, and go to step 5.

Step 5: Set ${z^{k + 1}}: = {z^k} + {\alpha _k}{d_k}$ and

Step 6: Let $k: = k + 1$, and go to step 1.

Existing L-M type methods ^[16,17,18] are usually designed based on the Armijo line search. While algorithm 3.1 adopts a nonmonotone derivate free line search. The choice of ${\eta _k}$ controls the degree of nonmonotoicity. If ${\eta _k} \equiv 0$, then the line search is monotone.

Theorem3.1. Let $\left\{ {{z^k}} \right\}$ be the sequence generated by Algorithm 3.1. Then, $\left\{ {{z^k}} \right\}$ satisfying $M({z^k}) \leqslant {C_k}$ for all $k \geqslant 0$.

Proof. By Algorithm 3.1 ${C_0} = M\left( {{z^0}} \right).$ We first assume that $M\left( {{z^k}} \right) \leqslant {C_k}$. If $\nabla M\left( {{z^k}} \right) = 0,$ then Algorithm 3.1 terminates. Otherwise $\nabla M\left( {{z^k}} \right) \ne 0$ which implies that $H\left( {{z^k}} \right) \ne 0$, hence ${\mu _k} = \theta {\left\| {H\left( {{z^k}} \right)} \right\|^2} > 0$. So the matrix $H'{\left( {{z^k}} \right)^T}H'\left( {{z^k}} \right) + {\mu _k}I$ is positive definite. Thus the search direction ${d_k}$ in step 3 is well-defined and ${d_k} \ne 0$. Since $\nabla M\left( {{z^k}} \right) \ne 0$, we have

This implies that ${d_k}$ is a descent direction of $M\left( {{z^k}} \right)$ at the point ${z^k}$. Next we will prove that at least one step size is obtained by step 4. Inversely, we assume that for any $j$, $M\left( {{z^k} + {\delta ^j}{d_k}} \right) > {C_k} - \gamma {\left\| {{\delta ^j}{d_k}} \right\|^2}$, then

thereby

By letting $j \to \infty$ in (3.7), we have $\nabla M{\left( {{z^k}} \right)^T}{d_k} \geqslant 0$, which contradicts (3.5). Therefore, we can always get ${z^{k + 1}}$ by Step 3 or Step 4. If ${z^{k + 1}}$ is generated by step 3, i.e., $\left\| {H\left( {{z^k} + {d_k}} \right)} \right\| \leqslant \sigma \left\| {H\left( {{z^k}} \right)} \right\|$, then $\frac{1}{2}{\left\| {H\left( {{z^k} + {d_k}} \right)} \right\|^2} \leqslant \frac{1}{2}{\sigma ^2}{\left\| {H\left( {{z^k}} \right)} \right\|^2}$, so $M\left( {{z^{k + 1}}} \right) \leqslant {\sigma ^2}M\left( {{z^k}} \right)$. And because, $\sigma \in \left( {0, 1} \right)$, therefore, we have $M\left( {{z^{k + 1}}} \right) \leqslant {\sigma ^2}M\left( {{z^k}} \right) < M\left( {{z^k}} \right) \leqslant {C_k}$. If ${z^{k + 1}}$ is generated by step 4, we can get $M\left( {{z^{k + 1}}} \right) \leqslant {C_k}$ directly. So, from(3.4), we can get that ${C_k} \geqslant \frac{{{\eta _k}{Q_k}M\left( {{z^{k + 1}}} \right) + M\left( {{z^{k + 1}}} \right)}}{{{Q_{k + 1}}}} = M\left( {{z^{k + 1}}} \right)$. Hence, we conclude that $M({z^k}) \leqslant {C_k}$ for all $k \geqslant 0$.

Next, we first suppose that $\nabla M\left( {{z^k}} \right) \ne 0$ for all $k \geqslant 0$. In order to discuss the convergence of algorithm 3.1, we need the following lemma.

Lemma 3.1. Let $\left\{ {{z^k}} \right\}$ be the sequence generated by Algorithm 3.1, then there exists a nonnegative constant ${C^ * }$ such that

Proof. By Theorem3.1, we can get $0 \leqslant M\left( {{z^k}} \right) \leqslant {C_k}$ for all $k \geqslant 0$ and ${C_{k + 1}} \leqslant \frac{{{\eta _k}{Q_k}{C_k} + {C_k}}}{{{Q_{k + 1}}}} = {C_k}.$ Hence, by The Monotone Bounded Theorem, there exists a nonnegative constant ${C^ * }$ such that $\mathop {\lim }\limits_{k \to \infty } {C_k} = {C^ * }$. By the definition of ${Q_k}$, we have

Hence, we conclude that ${\eta _k}{Q_k} \leqslant \frac{{{\eta _{\max }}}}{{1 - {\eta _{\max }}}}$ is bounded, which together with $\mathop {\lim }\limits_{k \to \infty } {C_k} = {C^ * }$ yields $\mathop {\lim }\limits_{k \to \infty } {\eta _{k - 1}}{Q_{k - 1}}\left( {{C_k} - {C_{k - 1}}} \right) = 0.$ So, it follows from (3.4) that

Hence

We complete the proof.

Theorem3.2. Let $\left\{ {{z^k}} \right\}$ be the sequence generated by Algorithm 3.1. Then any accumulation point ${z^ * }$ of $\left\{ {{z^k}} \right\}$ is a stationary point of $M\left( z \right)$.

Proof. By Lemma 3.1, we have $\mathop {\lim }\limits_{k \to \infty } M\left( {{z^k}} \right) = \mathop {\lim }\limits_{k \to \infty } {C_k} = {C^ * }, {C^ * } \geqslant 0$. If ${C^ * } = 0$, then $\mathop {\lim }\limits_{k \to \infty } H\left( {{z^k}} \right) = 0$ which together with Lemma 2.4 yields $\nabla M\left( {{z^ * }} \right) = 0$. In the following, we discuss the case of ${C^ * } > 0$. Set $N: = \left\{ {k\left| {\left\| {H\left( {{z^k} + {d_k}} \right)} \right\| \leqslant \sigma \left\| {H\left( {{z^k}} \right)} \right\|} \right.} \right\}$. Then $N$ must be a finite set, otherwise $M\left( {{z^{k + 1}}} \right) \leqslant {\sigma ^2}M\left( {{z^k}} \right)$ holds for infinitely many $k$. By letting $k \to \infty$ with $k \in N$, we can have ${C^ * } \leqslant {\sigma ^2}{C^ * }$ and $1 \leqslant {\sigma ^2}$ which contradicts $\sigma \in \left( {0, 1} \right)$. Therefore, we can suppose that there exists an index $\bar k > 0$ such that $\left\| {H\left( {{z^k} + {d_k}} \right)} \right\| > \sigma \left\| {H\left( {{z^k}} \right)} \right\|$ for all $k \geqslant \bar k$. Thereby, there exists a ${j_k}$ such that $M\left( {{z^{k + 1}}} \right) \leqslant {C_k} - \gamma {\left\| {{\delta ^{{j_k}}}{d_k}} \right\|^2}$, i.e.,

Next, we suppose that ${z^ * }$ is the limit of the subsequence ${\left\{ {{z^k}} \right\}_{k \in K}} \subset \left\{ {{z^k}} \right\}$ where $K \in \left\{ {0, 1, 2, \cdots } \right\}$, i.e., $\mathop {\lim }\limits_{k\left( { \in K} \right) \to \infty } {z^k} = {z^ * }$. Hence, by the continuity, we have ${C^ * } = M\left( {{z^ * }} \right) = \frac{1}{2}{\left\| {H\left( {{z^ * }} \right)} \right\|^2}$. By $\mathop {\lim }\limits_{k \to \infty } {\mu _k} = \mathop {\lim }\limits_{k \to \infty } \theta {\left\| {H\left( {{z^k}} \right)} \right\|^2} = \mathop {\lim }\limits_{k \to \infty } 2\theta M\left( {{z^k}} \right) = 2\theta {C^ * }$, we can get that

According to the proof process of theorem 3.1, the matrix $H'{\left( {{z^k}} \right)^T}H'\left( {{z^k}} \right) + {\mu _k}I$ is a symmetric positive definite matrix. In addition, because of ${C^ * } > 0$, the matrix $H'{\left( {{z^ * }} \right)^T}H'\left( {{z^ * }} \right) + 2\theta {C^ * }I$ is also symmetric positive definite matrix. Hence, we have

and

By (3.5), we can get

By letting $k \to \infty$ with $k \in N$ in (3.12), we have $\mathop {\lim }\limits_{k\left( { \in K} \right) \to \infty } \left\| {{\delta ^{{j_k}}}{d_k}} \right\| = 0$. If ${\delta ^{{j_k}}} > 0$, then $\mathop {\lim }\limits_{k\left( { \in K} \right) \to \infty } {d_k} = {d^ * } = 0$ which together with (3.15) yields $\nabla M\left( {{z^ * }} \right) = 0$. Otherwise, $\mathop {\lim }\limits_{k\left( { \in K} \right) \to \infty } {\delta ^{{j_k}}} = 0$. From step 4 and Theorem 3.1

i.e.,

Now that $M\left( z \right)$ is continuously differentiable at ${z^ * }$, so we have

Then, from (3.16), we can get $\nabla M{\left( {{z^ * }} \right)^T}{d^ * } = 0$ and

Since the matrix $H'{\left( {{z^ * }} \right)^T}H'\left( {{z^ * }} \right) + 2\theta {C^ * }I$ is a positive matrix, so we have

Now that the matrix ${\left[ {H'{{\left( {{z^ * }} \right)}^T}H'\left( {{z^ * }} \right) + 2\theta {C^ * }I} \right]^{ - 1}}$ is also positive matrix, we can get $\nabla M\left( {{z^ * }} \right) = 0.$

4.   Numerical experiments

In this section, we carry out some numerical experiments on the LWCP by Algorithm 3.1. All experiments were conducted on a ThinkPad480 with a 1.8GHz CPU and 8.0GB RAM. The codes are run in MATLAB R2018b under Win10.

We first generate the matrices $P, Q, R$ and vector $a$ by following way:

where $A \in {R^{m \times n}}$ is a full row rank matrix with $m < n$, the matrix $M$ is an $n \times n$ symmetric semidefinite matrix, $b \in {R^m}, f \in {R^n}.$ In our algorithm we set:$\gamma = 0.01, \sigma = 0.5, \delta = 0.8, \theta = {10^{ - 4}}.$ The initial points are choosing as :${x^0} = \left( {1, \cdots , 1} \right), {s^0} = \left( {1, \cdots , 1} \right), {y^0} = \left( {0, \cdots , 0} \right).$

In the course of experiments, we generate LWCP (1.3) by the following two ways.

(ⅰ) We take $A = randn\left( {m, n} \right)$ with $rank\left( A \right) = m$, and $M = \frac{{B{B^T}}}{{\left\| {B{B^T}} \right\|}}$ with $B = rand\left( {n, n} \right)$. we first generate $\hat x = rand\left( {n, 1} \right), f = rand\left( {n, 1} \right)$, then we set $\hat b: = A\hat x, \hat s = M\hat x + f, w = \hat x\hat s$.

(ⅱ) We choose $a = \left( {\begin{array}{*{20}{c}} b \\ { - f} \end{array}} \right) - \xi$ where $\xi \in {R^{n + m}}$ is a noise. We choose $M = diag(v)$ with $v = rand\left( {n, 1} \right)$. The matrix $A$ and vectors $b, f$ are generated in the same way as (ⅰ). In the course of experiments, we take $\xi = {10^{ - 4}}rand(1, 1)p$ with $p: = {\left( {1, 1, 0, \cdots , 0} \right)^T} \in {R^{n + m}}$.

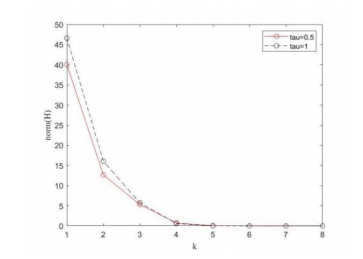
First, in order to observe the local convergence of algorithm 3.1, we conducted two sets of random test experiments on LWCP (ⅰ) with $n = 1000, m = 500$. Figure 1 gives the convergence curve of $\left\| {H\left( {{z^k}} \right)} \right\|$ at the $k$-th iteration. We can clearly see that algorithm 3.1 is locally fast, or at least locally superlinear.

Next, we conducted comparative experiments with ^[13]. In the course of experiments, the parameters in the WCP functions $\phi _{\tau , q}^w$ are respectively taken as $\tau = 0.5, q = 3, \tau = 1, q = 3$ and $\tau = 0.3, q = 3, \tau = 0.8, q = 3$. The numerical results are presented in Tables 1, 2, Figures 2 and 3 respectively. Where AIT, ACPU, ANH are respectively the average number of iterations, the average CPU time (unit seconds), and the average number $\left\| {H\left( {{z^k}} \right)} \right\|$ of iterations at the end of 10 random experiments. LM represents our experimental result, TLM is the experimental result of ^[13].

Tables 1 and 2 show the numerical results for LWCP (ⅰ). Where, the parameters are taken as $\tau = 0.5, q = 3;\tau = 1, q = 3$ respectively. It can be seen from the table that no matter what value $\tau$ takes, our algorithm 3.1 has less iteration time or higher accuracy than algorithm 1 in ^[13].

Figures 2 and 3 show the numerical results for solving LWCP (ⅱ). Where, the parameters are respectively taken as $\tau = 0.3, q = 3, m = \frac{n}{2};\tau = 0.8, q = 3, m = \frac{n}{2}$. It can be seen from the figure that with the increase of dimension, the AIT of algorithm 3.1 fluctuates slightly, but it is always smaller than the AIT in ^[13]. The ACPU increases steadily and always smaller than the ACPU in ^[13].

When $\tau = 0.6, q = 3, m = \frac{n}{2}$, Figure 4 shows the ACPU and AIT comparison line graphs for LWCP (ⅰ) and LWCP (ⅱ) solved by algorithms 3.1 and ^[13] respectively. It can be seen from the figure that after adding noise to LWCP (ⅰ), the solution speed of both algorithms decreases, but our algorithm still has certain advantages.

In general, the problems generated by numerical experiments converge in a few iterations. The number of iterations varies slightly with the dimension of the problem. Our algorithm is effective for the linear weighted complementarity problem LWCP (1.3), because each problem can be successfully solved in a very short time with a small number of iterations. Numerical results show the feasibility and effectiveness of the algorithm 3.1.

5.   Conclusions

Based on the idea of L-M method, with the help of a new class of WCP functions ${\varphi }_{\tau , q}^{c}(a, b),$ we give the algorithm 3.1 for solving the LWCP (1.3). Under certain conditions, our algorithm can obtain the approximate solution of LWCP (1.3). Numerical experiments show the feasibility and effectiveness of the algorithm 3.1.

Conflict of interest

The authors declare no conflicts of interest.