Study of quantum calculus for a new subclass of $q$-starlike bi-univalent functions connected with vertical strip domain

1.   Introduction and definitions

Let $\mathcal{A}$ be the class of analytic functions in the open unit disk $\mathcal{U} = \{z\in \mathbb{C} :\left \vert z\right \vert < 1\}$ and have the series of the form

and normalized by the conditions

Consider $\mathcal{S}$ as the class of functions in $\mathcal{A}$ that are univalent in $\mathcal{U}$. Let a function $h\in \mathcal{S}$ of the form (1.1) have an inverse $h^{-1}$ defined by

and

where

Let the class $\mathcal{P}$ be defined as

A function $h\in \mathcal{A}$ is said to be bi-univalent in $\mathcal{U}$ if both $h$ and $h^{-1}$ are univalent in $\mathcal{U}$. Let the symbol $\Sigma$ denote the class of bi-univalent functions in the open unit disk $\mathcal{ U}$. Several scholars have recently examined the bounds of the coefficients of analytic and bi-univalent functions. We recommend ^{[1,2,3,4,5,6,7,8,9,10,11]} for more current research on this subject.

When Bieberbach ^[12] examined the coefficient hypothesis in 1916, scholars first started studying the theory of functions, which was first recognized as a promising field of study in 1851. De Branges ^[13] confirmed the Bieberbach theory in 1985, despite the fact that a huge number of well-known researchers attempted to either confirm or disprove it between 1916 and 1985. Understanding the theory of analytic and univalent functions, as well as how these ideas assess the expansion of functions within their designated domains, is essential. This is made up of an arrangement of the Taylor series, function coefficients, and associated functional inequalities. Fekete and Szegö ^[14] made the important and useful discovery of the Fekete-Szegö inequality in 1933. The Fekete and Szeg ö inequality, connected to the Bieberbach conjecture, is a mathematical inequality that deals with the coefficients of univalent analytic functions. The maximizing of the nonlinear functional $\left \vert a_{3}-\mu a_{2}^{2}\right \vert$ has been proven to have a number of impacts. This kind of problem, known as a sharp Fekete-Szegö problem, is presented as follows:

The subordination form of two analytic functions $h_{1}$ and $h_{2}$ is

If a Schwarz function $\omega$ that is analytic in $\mathcal{U}$ exists and satisfies the requirements $\omega (0) = 0$ and $\left \vert \omega (z)\right \vert < 1$, then $h_{1}(z) = h_{2}(\omega (z))$, $z\in \mathcal{U}$. If $h_{2}$ is univalent in $\mathcal{U}$, then (see ^[15])

Remark 1.1. Let $h_{1}(z)$ and $h_{2}(z)$ be analytic in $\mathcal{U}$. If $h_{2}$ is univalent in $\mathcal{U}$, then the subordination (1.3) is equivalent to the condition (1.4).

The well-known class of starlike $(\mathcal{S}^{\ast })$ functions is defined as

and it can be written in terms of subordination as

For $0\leq \delta < 1$, a function $h\in \mathcal{A}$ is said to be starlike of order $\delta$ if it satisfies the condition

and it is denoted by $\mathcal{S}^{\ast }\left(\delta \right)$. Additionally, we define $M(\sigma)$ as the subclass of $\mathcal{A}$ of functions $h(z)$ that satisfies the following inequality:

Moreover, the subclass $\mathcal{S}^{\ast }\left(\delta, \sigma \right) \subset \mathcal{A}$ consists of functions, that satisfy the following inequality:

We note that Kuroki and Owa ^[15] and Uralegaddi et al. ^[16] were the first to explore the functional classes $M(\sigma)$ and $\mathcal{S}^{\ast }\left(\delta, \sigma \right)$, respectively.

The class of normalized analytic functions $\mathcal{K}\left(\lambda, \delta, \sigma \right)$ satisfying the two-sided inequality

was studied by Sun et al. ^[17] in 2015.

Recently, Sun et al. ^[18] studied the applications of the vertical strip domain for the class of starlike functions and investigated integral representations, convolutions, and coefficient inequalities for functions belonging to this class. Furthermore, they considered radius problems and inclusion relations involving certain classes of strongly starlike functions, parabolic starlike functions, and other types of starlike functions. Later on, Bulut ^[19] studied the uses of the vertical strip domain for the class of close-to-convex functions.

Several analytic function subclasses have been developed using the concept of subordination based on the geometrical interpretation of their image domains, including the right half plane, circular disc, oval and petal type domains, conic domain, leaf-like domain, and generalized conic domains, which have all been defined and studied (see, for details, ^{[20,21,22,23,24,25]}). In this article, we define two new subclasses of $q$-satrlike functions associated with the vertical strip domain.

In ^[15], Kuroki and Owa defined an analytic function $f_{\delta, \sigma }:\mathcal{U}\rightarrow \mathbb{C}$ as

with

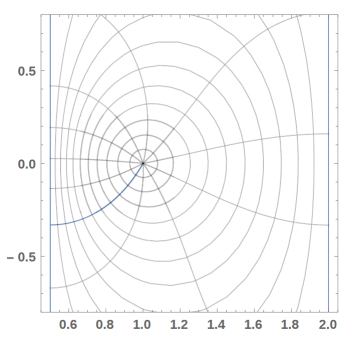
They proved that $f_{\delta, \sigma }$ maps $\mathcal{U}$ onto the vertical strip domain (see Figure 1):

conformally and the function $f_{\delta, \sigma }$ is a convex univalent function in $\mathcal{U}$ having the form

where

and

A great number of scholars have been attracted and motivated by the exploration of $q$-calculus (or quantum calculus) because of its use in a variety of quantitative sciences. The research on the $q$-derivative has inspired scholars to use it in geometric function theory and other fields of mathematics and mathematical sciences. Jackson ^[26,27] was one of the main contributors to the introduction and development of the $q$ -calculus theory. Just as $q$-calculus was applied in other mathematical sciences, its formulations are frequently used to investigate the existence of different function theory structures. Ismail et al. ^[28] was the first who established a connection between the geometric nature of the analytic functions and the $q$-derivative operator. The first characteristics of the $q$-difference operator are described by Kanas and Răducanu ^[29]. They used the $q$-difference operator, applied the idea of convolution, and defined the $q$-analogue of the Ruscheweyh differential operator, while the authors of ^[30] present the class of $q$-starlike functions associated with the $q$-analogue of the Ruscheweyh differential operator. Zang et al. ^[31] used the idea of $q$-calculus notations and the technique of subordinations to define a generalized conic domain, then considered this domain to investigate the class of $q$-starlike functions. A number of authors recently published research on the classes of $q$-starlike functions; see ^{[32,33,34,35,36,37,38]}. For studying a new subclasses of analytic and bi-univalent functions, we first need the definition of the $q$-difference operator.

Definition 1.1. ^[26,27] For $h\in \mathcal{A}$, the $q$-difference operator can be defined as follows:

Combining (1.1) and (1.10), we have

and

where

We consider the above $q$-difference operator and define a new subclass of the $q$-starlike functions related to the vertical strip domain.

Definition 1.2. An analytic function for $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$, if $h$ satisfies the following inequality:

where $q\in \left(0, 1\right)$, $0\leq \delta < 1 < \sigma$.

Remark 1.2. For $q\rightarrow 1-$, in Definition 1.2, then $\mathcal{S}^{\ast }\left(\delta, \sigma, q\right) = \mathcal{S}^{\ast }\left(\delta, \sigma \right)$ are investigated in ^[15].

Definition 1.3. For $q\in \left(0, 1\right)$, $0\leq \delta < 1 < \sigma$, we denote by $\mathcal{S}_{\Sigma }^{\ast }\left(\delta, \sigma, q\right)$ the class of bi-univalent functions consisting of the functions such that

where $h^{-1}$ is the inverse function of $h$.

The study of $q$-calculus is among the most challenging subjects in mathematics. It has been studied for 300 years since Euler. Today, research in the subject of $q$-calculus advances quickly because of its use in many fields, including physics and mathematics. There are several applications in combinatorics for the working history of $q$-analysis, quantum physics, theta functions, hypergeometric functions, analytic number theory, finite difference theory, mock theta functions, Bernoulli and Euler polynomials, and gamma function theory. In addition, thermodynamics makes use of the $q$ -difference operator. It has been shown that the thermodynamics of the $q$ -deformed algebra may be realized via the formalization of the $q$-calculus. It has been discovered that the complete structure of thermodynamics is preserved if an appropriate Jackson derivative ^[26,27] is employed in place of the standard thermodynamic derivative ^[39]. In this article, we use $q$-calculus notations associated with the vertical strip domain, define two new subclasses of $q$-starlike functions, and investigate some useful properties of the functions $h$ belonging to these classes.

2.   A set of lemmas

To demonstrate our findings, we shall employ the following lemmas:

Lemma 2.1. Let $h\in \mathcal{A}$ and $0\leq \delta < 1 < \sigma$, then $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$ if and only if

where $f_{\delta, \sigma }(z)$ is given by (1.7).

Proof. Let us consider the function $f_{\delta, \sigma }(z)$ by

with $0\leq \delta < 1 < \sigma$. The function $f_{\delta, \sigma }(z)$ is, therefore, clearly analytic and univalent in $\mathcal{U}$ with $f_{\delta, \sigma }(0) = 1$. Moreover, we have

We can see that $f_{\delta, \sigma }(z)$ maps $\mathcal{U}$ onto the strip domain $\omega$ with $\delta < {Re}\left(\omega \right) < \sigma$. As a result, it follows from Remark 1.1 that the subordination (2.1) is equivalent to the inequality (1.11), which proves the assertion of Lemma 2.1.

Lemma 2.2. ^[40] Let

be analytic and univalent in $\mathcal{U}$ and suppose that $p(z)$ maps $\mathcal{U}$ onto a convex domain. Let

be analytic in $\mathcal{U}$ and satisfy the subordination

then

Lemma 2.3. ^[41] Let $p(z) = 1+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}$ be a function with a positive real part in $\mathcal{U}$, then,

3.   Main results

The following theorem provides sharp coefficient estimates for the function $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$.

Theorem 3.1. Let $h$ be of the form (1.1) and $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$, then,

where $T_{1}$ and $T_{2}$ are given by (1.9). The results are sharp for the functions given in (3.8) and (3.9).

Proof. Let $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$, and let $\omega (z) = \frac{zD_{q}h(z)}{h(z)}$, then the subordination (2.1) can be written as follows:

Note that the function $f_{\delta, \sigma }(z)$ defined by (1.5) is convex in $\mathcal{U}$ and of the form

where $T_{n}$ is given by (1.8).

Let

or

Using $\omega (z) = \frac{zD_{q}h(z)}{h(z)}$, we have

We know that

Taking the right hand side of (3.2), we get

Taking the left hand side of (3.2), we get

Equating the coefficients from (3.3) and (3.4), we get

Applying modulus, and using $\left \vert c_{n}\right \vert \leq 2$, we have

Equating the coefficients from (3.3) and (3.4), after some simple calculation, we get

Taking a modulus on both sides, we have

Applying Lemma 2.3, we get

For sharpness, consider the function $h_{1}:\mathcal{U\rightarrow } \mathbb{C}$ such that

where

For sharpness, consider the function $h_{2}:\mathcal{U\rightarrow } \mathbb{C}$ such that

where

Theorem 3.2. Let an analytic function $h$ be of the form (1.1) belonging to the class $\mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$, then,

where $\mu \in \mathbb{C}$, $T_{1}$ and $T_{2}$ are given by (1.9). The result is sharp for the function $h_{2}$ given by (3.9).

Proof. Using (3.5) and (3.7) in $\left \vert a_{3}-\mu a_{2}^{2}\right \vert$ and after some simple calculation, we get

where

Using Lemma 2.3, we have

Hence, the result is proved.

Initial bounds for inverse functions:

Theorem 3.3. Let $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$ and $h^{-1}$ be the inverse function of $h$. If

then,

and

where $T_{1}$ and $T_{2}$ are given by (1.9). The results are sharp for the function given in (3.11) and (3.12).

Proof. The relations (1.2) and (3.10) yield

Thus, in view of (3.6) and the identity $\left \vert b_{2}\right \vert = \left \vert a_{2}\right \vert \leq \frac{T_{1}}{\left[ 2\right] _{q}-1}$. Hence,

Furthermore, for $b_{3}$, we apply Theorem 3.1 with $\mu = 2$ and we get

Results are sharp for the functions

and

Theorem 3.4. Let $h\in \mathcal{A}$, be defined in (1.1). If $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$, then,

and

where $T_{1}$ is given in (1.9).

Proof. Let

and the function $f_{\delta, \sigma }(z)$ be given by (1.7), then, the subordination (2.1) can be written as follows:

Note that the function $f_{\delta, \sigma }(z)$ defined by (1.7) is convex in $\mathcal{U}$ and has the form

where $T_{n}$ is given by (1.8). If we let

then from Lemma 2.2, we see that the subordination (3.15) implies

where $T_{1}$ is given by (1.9). Now, (3.14) implies that

Then, by comparing the coefficients of $z^{n}$ on both sides, we see that

After some simple calculation and using the inequality (3.16) yields that

where $T_{1}$ is given in (1.9) and $\left \vert T_{1}\right \vert = \frac{ 2\left(\sigma -\delta \right) }{\pi }\sin \frac{\pi \left(1-\delta \right) }{\sigma -\delta }$. Hence, we have

To prove the remaining part of the theorem, we need to show that

for $n = 3, 4, 5, ...$ We use induction to prove (3.17). The case $n = 3$ is clear. Next, assume that the inequality (3.17) holds for $n = t$, then a straightforward calculation gives

which implies that the inequality (3.17) holds for $n = t+1$. Hence, the desired estimate for $\left \vert a_{t}\right \vert$ $(n = 3, 4, 5, ...)$ follows, as asserted in (3.13).

This completes the proof of Theorem 3.4.

Taking $q\rightarrow 1-$ in Theorem 3.4, we get the known Corollary 3.2, proved in ^[17].

Corollary 3.1. ^[17] For an analytic function $h$ defined by (1.1) and $h\in \mathcal{S}^{\ast }\left(\delta, \sigma \right)$, we have

where $T_{1}$ is given by (1.9).

Theorem 3.5. Let $h\in \mathcal{S}_{\Sigma }^{\ast }\left(\delta, \sigma, q\right)$, then,

and

Proof. If $h\in \mathcal{S}_{\Sigma }^{\ast }\left(\delta, \sigma, q\right)$, then $h\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$ and $g = h^{-1}\in \mathcal{S}^{\ast }\left(\delta, \sigma, q\right)$. Hence,

and

where $f_{\delta, \sigma }(z)$ is given by (1.7). Let

and

Thus, $t$ and $k$ are analytic, have a positive real part in $\mathcal{U}$, and satisfy the well-known estimates

Therefore, we have

and

By comparing the coefficients, we get

where $T_{1}$ and $T_{2}$ are given by (1.9). From (3.21) and (3.23), we obtain

Adding (3.22) and (3.24), and using (3.21) and (3.25), we get

Subtracting (3.22), (3.24) and (3.25), we get

These equations, together with (3.20), give the bounds on $\left \vert a_{2}\right \vert$ and $\left \vert a_{3}\right \vert$ as asserted in (3.18) and $\left(3.19\right)$. This completes the proof of Theorem 3.5.

We get the known corollary proved in ^[17] by setting $q\rightarrow 1-$.

Corollary 3.2. ^[17] Let $h\in \mathcal{S}_{\Sigma }^{\ast }\left(\delta, \sigma \right)$, then,

and

where $T_{1}$ and $T_{2}$ are given by (1.9).

4.   Conclusions

In this research, we studied and explored a novel family of normalized holomorphic and bi-univalent functions associated with the vertical strip domain and quantum calculus. This article is divided into three sections. Section 1 provided a brief overview and common terminology. This part also introduced two new subclasses of analytic and bi-univalent functions related to the $q$-calculus operator theory. In Section 2, a number of common lemmas are provided. In Section 3, we investigated some interesting problems involving function $h$ that belong to the subclasses of analytic and bi-univalent functions. These included the first two initial coefficient bounds, estimates for the Fekete-Szego type functional, and results for a class of bi-univalent functions. Similar findings were obtained from further investigation of the inverse functions. The Fekete-Szegö problem and the initial bounds have been shown to be sharp in this article. We hope that this study will inspire future scholars to expand on this concept for a different subclass of analytic functions, such as bi-univalent, multivalent, meromorphic, and others.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

The authors extend their appreciation to the Arab Open University for funding this work through AOU research fund no. (AOUKSA-524008).

Conflict of interest

The authors declare that they have no competing interests.