N-dimension for dynamic generalized inequalities of Hölder and Minkowski type on diamond alpha time scales

Elkhateeb S. Aly; Ali M. Mahnashi; Abdullah A. Zaagan; I. Ibedou; A. I. Saied; Wael W. Mohammed; Elkhateeb S. Aly; Ali M. Mahnashi; Abdullah A. Zaagan; I. Ibedou; A. I. Saied; Wael W. Mohammed

doi:10.3934/math.2024454

AIMS Mathematics

2024, Volume 9, Issue 4: 9329-9347. doi: 10.3934/math.2024454

Previous Article Next Article

Research article Special Issues

N-dimension for dynamic generalized inequalities of Hölder and Minkowski type on diamond alpha time scales

1.
Department of Mathematics, College of Science, Jazan University, P. O. Box 114, Jazan 45142, Kingdom of Saudi Arabia
2.
Nanotechnology Research Unit, College of Science, Jazan University, P. O. Box 114, Jazan 45142, Saudi Arabia
3.
Department of Mathematics, Faculty of Science, Benha university, Benha, Egypt
4.
Department of Mathematics, College of Science, University of Ha'il, Ha'il 2440, Saudi Arabia
5.
Department of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt

Received: 20 January 2023 Revised: 19 February 2024 Accepted: 01 March 2024 Published: 06 March 2024
MSC : 26D10, 26D15, 34N05, 39A12, 47B38

Expanding on our research, this paper introduced novel generalizations of H ölder's and Minkowski's dynamic inequalities on diamond alpha time scales. Specifically, as particular instances of our findings, we replicated the discrete inequalities established when $\mathbb{T = N}$ . Furthermore, our investigation extended to the continuous case with $\mathbb{ T = R}$ , revealing additional inequalities that are both new and valuable for readers seeking a comprehensive understanding of the topic.

Keywords:

Citation: Elkhateeb S. Aly, Ali M. Mahnashi, Abdullah A. Zaagan, I. Ibedou, A. I. Saied, Wael W. Mohammed. N-dimension for dynamic generalized inequalities of Hölder and Minkowski type on diamond alpha time scales[J]. AIMS Mathematics, 2024, 9(4): 9329-9347. doi: 10.3934/math.2024454

Related Papers:

[1]	Can Kızılateş, Halit Öztürk . On parametric types of Apostol Bernoulli-Fibonacci, Apostol Euler-Fibonacci, and Apostol Genocchi-Fibonacci polynomials via Golden calculus. AIMS Mathematics, 2023, 8(4): 8386-8402. doi: 10.3934/math.2023423
[2]	William Ramírez, Can Kızılateş, Daniel Bedoya, Clemente Cesarano, Cheon Seoung Ryoo . On certain properties of three parametric kinds of Apostol-type unified Bernoulli-Euler polynomials. AIMS Mathematics, 2025, 10(1): 137-158. doi: 10.3934/math.2025008
[3]	Mohra Zayed, Shahid Ahmad Wani, Georgia Irina Oros, William Ramŕez . A study on extended form of multivariable Hermite-Apostol type Frobenius-Euler polynomials via fractional operators. AIMS Mathematics, 2024, 9(6): 16297-16312. doi: 10.3934/math.2024789
[4]	Mohra Zayed, Shahid Ahmad Wani, Georgia Irina Oros, William Ramírez . Unraveling multivariable Hermite-Apostol-type Frobenius-Genocchi polynomials via fractional operators. AIMS Mathematics, 2024, 9(7): 17291-17304. doi: 10.3934/math.2024840
[5]	Tabinda Nahid, Mohd Saif, Serkan Araci . A new class of Appell-type Changhee-Euler polynomials and related properties. AIMS Mathematics, 2021, 6(12): 13566-13579. doi: 10.3934/math.2021788
[6]	Mohra Zayed, Shahid Ahmad Wani . Properties and applications of generalized 1-parameter 3-variable Hermite-based Appell polynomials. AIMS Mathematics, 2024, 9(9): 25145-25165. doi: 10.3934/math.20241226
[7]	Awatif Muflih Alqahtani, Shahid Ahmad Wani, William Ramírez . Exploring differential equations and fundamental properties of Generalized Hermite-Frobenius-Genocchi polynomials. AIMS Mathematics, 2025, 10(2): 2668-2683. doi: 10.3934/math.2025125
[8]	Li Chen, Dmitry V. Dolgy, Taekyun Kim, Dae San Kim . Probabilistic type 2 Bernoulli and Euler polynomials. AIMS Mathematics, 2024, 9(6): 14312-14324. doi: 10.3934/math.2024696
[9]	Jung Yoog Kang, Cheon Seoung Ryoo . Exploring variable-sensitive $q$ -difference equations for $q$ -SINE Euler polynomials and $q$ -COSINE-Euler polynomials. AIMS Mathematics, 2024, 9(6): 16753-16772. doi: 10.3934/math.2024812
[10]	Rabab Alyusof, Mdi Begum Jeelani . Some families of differential equations associated with the Gould-Hopper-Frobenius-Genocchi polynomials. AIMS Mathematics, 2022, 7(3): 4851-4860. doi: 10.3934/math.2022270

Abstract

1. Introduction

For $\kappa\in \mathbb{N}_0, u \in \mathbb{C}$ , with $u \neq 1$ , the Frobenius–Euler polynomials $\mathcal{H}_{r}^{(\kappa)}(x; u)$ of order $\kappa$ , are defined by the generating function as follows (by (see e.g., ^[4,14] and the references therein):

$\begin{equation*} \left( \dfrac{1-u}{e^{z}-u}\right) ^{\kappa}e^{x z} = \sum\limits_{r = 0}^{\infty}\mathcal{H}_{r}^{(\kappa)}(x;u)\frac{z^{r}}{r!}, \quad |z| < |\log (u)|. \end{equation*}$

When $\kappa = 1$ , $\mathcal{H}_{r}^{(1)}(x; u): = \mathcal{H}_{r}(x; u)$ is called the $r$ -th Frobenius–Euler polynomials. In the special case where $\kappa = 1$ and $u = -1$ , $\mathcal{H}_{r}(x; -1): = E_{r}(x)$ denotes Euler polynomials (see ^[17] and the references therein).

A remarkable amount of research has been done on polynomial families and their various extensions (see, for example, ^{[6,8,18,21,22]}). The introduction of new generalizations has been accompanied by the establishment of several fundamental properties, recurrence formulas, differential equations, and relationships between these polynomials and other families of numbers and polynomials.

The polynomials ${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]}(x; u;\gamma)$ represent an intriguing blend of two classes of special functions: the hypergeometric Euler polynomials and the Frobenius–Euler polynomials. The notable presence of these polynomial families across diverse fields, including physical mathematics, information theory, combinatorics, approximation theory, number theory, numerical analysis, and partial differential equations, is well-documented and widely recognized. The significance of investigating the properties of the polynomials ${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]}(x; u;\gamma)$ lies in their fundamental role in mathematical analysis, number theory, and applied sciences. These polynomials generalize various well-known polynomial families, providing deeper insights into their structural properties, recurrence relations, and differential equations. Here are some key aspects of their significance:

Unification and generalization. The study connects the generalized Apostol-type Frobenius–Euler polynomials with well-established families, such as the Stirling numbers, Apostol–Bernoulli, Apostol–Euler, Apostol–Genocchi polynomials, and classical polynomials like Fubini, Bernstein, and Hermite polynomials. This broader framework allows for new interpretations and extensions of known results.

Structural properties and recurrence relations. Establishing recurrence relations and differential equations associated with these polynomials is crucial for their computational efficiency and theoretical applications. These relations provide a foundation for deriving explicit formulas and generating functions, which are instrumental in various mathematical fields.

Connection with other special functions and polynomials. The exploration of connection formulas highlights the interplay between different polynomial families. Such connections often lead to new combinatorial identities, algebraic properties, and functional equations, which can be applied in diverse mathematical and engineering problems.

Zero distribution and graphical applications. The graphical representation and analysis of the zeros of these polynomials offer insights into their asymptotic behavior and structural patterns. Understanding the distribution of zeros is crucial in approximation theory, spectral analysis, and numerical methods.

Applications in mathematical and applied fields. The study of these polynomials can have implications in combinatorial mathematics, quantum physics, and numerical analysis. Their recurrence relations and differential properties may lead to new results in solving differential equations, signal processing, and optimization problems.

Thus, the investigation of these polynomials enriches the theory of special functions, providing new tools and results that contribute to both theoretical mathematics and practical applications.

The objective of this study is to investigate a number of properties of the polynomials ${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]}(x; u;\gamma)$ , including their connection formulas and the distribution of their zeros. The organization of this paper is as follows: In Section 2, we provide definitions and review previous results concerning Stirling numbers of the second kind, as well as generalized Apostol–Bernoulli, Apostol–Euler, Apostol–Genocchi polynomials of level $m$ , and the Fubini, Bernstein, and Hermite polynomials. Section 3 delves into several properties of the generalized Apostol-type Frobenius–Euler polynomials, their recurrence relations, and differential equations. Section 4 presents various formulas establishing connections with other families of numbers and polynomials. Finally, Section 5 presents the graphical application for the polynomials so that the zeros of the function and how the nets are formed for different n can be studied.

2. Background and previous results

Throughout this paper, adherence is observed to the following standard conventions: The set of natural numbers is denoted by $\mathbb{N} = 1, 2, 3, \ldots$ The set of non-negative integers is denoted by $\mathbb{N}_0 = 0, 1, 2, \ldots$ represents the set of non-negative integers; $\mathbb{Z}$ refers to the set of integers; $\mathbb{R}$ denotes the set of real numbers, and $\mathbb{C}$ stands for the set of complex numbers. When referring to the complex logarithm, we adopt the principal branch, and for expressions of the form $w = z^\kappa$ , we denote the single branch of the multi-valued function $w = z^\kappa$ such that $1^\kappa = 1$ .

The Stirling numbers ${S}(r, s)$ of the second kind are defined by (see [19, p. 78]):

$\begin{align} \dfrac{\left(e^{z}-1 \right)^{s} }{s!}& = \sum\limits_{r = s}^{\infty}{S}(r,s)\frac{z^{r}}{r!}, \\ z^{r}& = \sum\limits_{s = 0}^{r}{S}(r,s)z(z-1) \cdots(z-s+1), \end{align}$

(2.1)

so that

$\begin{equation*} {S}(r,1) = {S}(r,r) = 1, \quad {S}(r,r-1) = \binom{r}{2}. \end{equation*}$

On the other hand, Açíkgöz et al. [, Eq (2.12)] defined the generalized $(p, q)$ –Stirling numbers ${S}_{p, q}^{[m-1]}(r; k;\gamma)$ of the second kind by means of the generating function

$\begin{equation*} \label{stirling2} \dfrac{\left( \gamma e_{p,q}^{z}- \sum\nolimits_{h = 0}^{m-1}\frac{z^{h}}{[h]_{p,q}!}\right)^{\upsilon} }{[\upsilon]_{p,q}!} = \sum\limits_{r = 0}^{\infty}{S}_{p,q}^{[m-1]}(r;\upsilon;\gamma)\frac{z^{r}}{[r]_{p,q}!}, \end{equation*}$

when $q \longrightarrow p = 1$ , we obtain

$\begin{equation} \dfrac{\left( \gamma e^{z}- \sum\nolimits_{h = 0}^{m-1}\frac{z^{h}}{h!}\right)^{\upsilon} }{\upsilon!} = \sum\limits_{r = 0}^{\infty}{S}^{[m-1]}(r;\upsilon;\gamma)\frac{z^{r}}{r!}. \end{equation}$

(2.2)

Note that, when $m = \gamma = 1$ , the above expression reduces to Eq (2.1).

The generating function of the two-variable Fubini polynomials is given by (see ^[13]):

$\begin{equation*} \dfrac{e^{x z}}{1-y\left( e^{z}-1\right) } = \sum\limits_{r = 0}^{\infty}{F}_{r}(x;y)\dfrac{z^{r}}{r!}. \end{equation*}$

Note that ${F}_{r}(0;y): = {F}_{r}(y)$ and ${F}_{r}(0;1): = {F}_{r}.$

The Bernstein polynomials ${B}_{s, r}(x),$ of degree $r$ , are defined by employing the following generating function (see ^[1,3]):

$\begin{equation} \dfrac{(zx)^{s}}{s!}e^{(1-x)z} = \sum\limits_{r = s}^{\infty}{B}_{s,r}(x)\frac{z^{r}}{r!},\quad s \in \mathbb{N}_{0}, \end{equation}$

(2.3)

where

$\begin{equation*} {B}_{s,r}(x) = \binom{r}{s}x^{s}\left( 1-x \right)^{r-s}. \end{equation*}$

For mathematical convention, we usually set ${B}_{s, r}(x) = 0$ if $s > r$ .

The generating function of the ordinary Hermite polynomials is defined by (see ^[10]):

$\begin{equation*} e^{2x z-z^{2}} = \sum\limits_{r = 0}^{\infty}{H}_{r}(x)\frac{z^{r}}{r!}, \end{equation*}$

so that

${H}_{r}(x) = r!\sum\limits_{s = 0}^{[\frac{r}{2}]}\dfrac{(-1)^{s}(2x)^{r-2s}}{(r-2s)!s!},$

where $\left[ \frac{r}{2}\right]$ is the truncated part of $\frac{r}{2}.$

Let $\gamma \in \mathbb{C}, \kappa\in \mathbb{N}_0$ , $a, c \in \mathbb{R^{+}}$ the generalized Apostol–Euler $\mathfrak{E}_{r}^{[m-1, \kappa]}(x; c, a;\gamma)$ polynomials of order $\kappa$ , are defined respectively (cf. ^[5,7,15]):

$\begin{equation} \sum\limits_{r = 0}^{\infty}\mathfrak{E}_{r}^{[m-1,\kappa]}(x;c,a;\gamma)\dfrac{z^{r}}{r!} = \left( \dfrac{2^{m}}{\gamma c^{z}+\sum\nolimits_{h = 0}^{m-1}\frac{(z ln a)^{h}}{h!}}\right)^{\kappa}c^{x z}. \end{equation}$

(2.4)

When $c = a = e$ , we arrive at the following:

$\begin{align*} \mathfrak{E}_{r}^{[m-1,\kappa]}(x;e,e;\gamma): = \mathfrak{E}_{r}^{[m-1,\kappa]}(x;\gamma). \end{align*}$

Recently, Quintana et al. ^[9] introduced some properties and recurrence formula of generalized Euler polynomials ${E}_{r}^{[m-1]}(x)$ of level $m$ . Also, they provided the following expression:

$\begin{equation*} e^{z}+ \sum\limits_{h = 0}^{m-1}\frac{z^{h}}{h!} = \sum\limits_{n = 0}^{\infty}\left(1+ a_{r,m} \right)\frac{z^{r}}{r!}, \end{equation*}$

where

$\begin{equation*} a_{r,m} = \begin{cases} 1,\quad &\text{if } 0\leq r < m ,\\ 0,\quad &\text{if } r\geq m . \end{cases} \end{equation*}$

Motivated by these papers, we define the generalized Apostol-type Frobenius–Euler polynomials of order $\kappa$ and level $m$ .

3. The generalized Apostol-type Frobenius–Euler polynomials and their properties

Definition 3.1. For a fixed $m \in \mathbb{N}$ , $\kappa, r \in \mathbb{N}_{0}$ , $\gamma \in \mathbb{C}, u \in \mathbb{C}\setminus\left\lbrace 1 \right\rbrace$ , the generalized Apostol-type Forbenius–Euler polynomials of order $\kappa$ and level $m$ are defined by the following generating function, in a suitable neighborhood of $z = 0$ :

$\begin{equation} \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{x z} = \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^r}{r!}. \end{equation}$

(3.1)

Upon setting $x = 0$ in (3.1), we have

$\begin{equation*} \label{numfrobeuler} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(0;u;\gamma): = {{}_{F}\mathcal{E}_r}^{[m-1,\kappa]}(u;\gamma), \end{equation*}$

called the generalized Apostol-type Frobenius–Euler numbers of order $\kappa$ and level $m$ .

Taking $u = -1$ in (3.1), we obtain the generalized Apostol–Euler polynomials $\mathfrak{E}_{r}^{[m-1, \kappa]}(x; c, a;\gamma)$ ; when $c = a = e.$ Compare [15, p. 55],

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;-1;\gamma)& = \mathfrak{E}_r^{[m-1,\kappa]}(x;e,e;\gamma): = \mathfrak{E}_r^{[m-1,\kappa]}(x;\gamma). \end{align*}$

According to Definition 3.1, we remark that

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{[m-1,1]}(x;u;\gamma)&: = {{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;u;\gamma),\\ {{}_{F}\mathcal{E}_{r}}^{[0,\kappa]}(x;u;\gamma)&: = {{}_{F}\mathcal{E}_{r}}^{(\kappa)}(x;u;\gamma): = \mathcal{H}_{r}^{(\kappa)}(x;u;\gamma),\\ {{}_{F}\mathcal{E}_{r}}^{[0,1]}(x;u;\gamma)&: = {{}_{F}\mathcal{E}_{r}}(x;u;\gamma): = \mathcal{H}_{r}(x;u;\gamma). \end{align*}$

For example, the first four generalized Apostol-type Frobenius–Euler polynomials of order $\kappa$ and level $m = 3$ are:

$\begin{align*} {{}_{F}\mathcal{E}_{0}}^{[2,\kappa]}(x;u;\gamma)& = \frac{\left( 1-u \right)^{3\kappa}}{\left( \gamma -u \right)^{\kappa}},\\ {{}_{F}\mathcal{E}_{1}}^{[2,\kappa]}(x;u;\gamma)& = \dfrac{\left( x-\kappa \right)\left( 1-u\right)^{3\kappa}}{\left(\gamma-u \right)^{\kappa}},\\ {{}_{F}\mathcal{E}_{2}}^{[2,\kappa]}(x;u;\gamma)& = \dfrac{\left(x-\kappa \right)^{2}\left( 1-u\right)^{3\kappa} }{\left(\gamma -u \right)^{\kappa}},\\ {{}_{F}\mathcal{E}_{3}}^{[2,\kappa]}(x;u;\gamma)& = \dfrac{\left[\left(u\kappa^{3}-\gamma\kappa^{3}-u\kappa \right)+\left(3\kappa^{2}\gamma-3\kappa^{2}u \right)x+\left(3\kappa u-3\kappa \gamma\right)x^{2}+\left(\gamma -u \right)x^{3}\right]\left(1-u\right)^{3\kappa}}{\left(\gamma-u \right)^{\kappa+1}}. \end{align*}$

Upon setting $\kappa = \gamma = 1$ and $u = -1$ above, we obtain the first four generalized Euler polynomials of level $m = 3$ (see [9, p. 47]).

Performing some manipulations on the generating function (3.1), we have

$\begin{equation*} \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{x z} = \left( \dfrac{(1-u)^{m}}{2^{m}(-u)}\right)^{\kappa}\left( \frac{2^{m}}{\left(\frac{-\gamma}{u} \right) e^z+ \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{x z}, \end{equation*}$

and thus,

$\begin{equation*} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma) = \left( \dfrac{(1-u)^{m}}{2^{m}(-u)}\right)^{\kappa}\mathfrak{E}_{r}^{[m-1,\kappa]}\left( x,\frac{-\gamma}{u}\right). \end{equation*}$

The proposition 3.1 provides some properties of the generalized Apostol-type Frobenius–Euler polynomials ${{}_{F}\mathcal{E}_r}^{[m-1, \kappa]}(x; u;\gamma)$ without proofs since they can easily be proved through Definition 3.1.

Proposition 3.1. For a fixed $m \in \mathbb{N}$ , let $\left\lbrace {{}_{F}\mathcal{E}_{r}}^{\left[ m-1, \kappa\right] }(x; u;\gamma)\right\rbrace_{r = 0}^{\infty}$ be the sequence of the generalized Apostol-type Frobenius–Euler polynomials, of order $\kappa$ and level $m$ . Then the following identities hold true:

(1) Special value. For every $r \in \mathbb{N}_{0}$

$\begin{align} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,0\right] }(x;u;\gamma)& = x^{r}. \end{align}$

(3.2)

(2) Summation formula. For every $r \in \mathbb{N}_{0}$

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa\right] }(x;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1,\kappa\right] }(u;\gamma)x^{k}. \end{align*}$

(3) Differential relation. For a fixed $m \in \mathbb{N},$ $\kappa, \gamma \in \mathbb{C}$ and $r, j \in \mathbb{N}_{0}$ with $0\leq j\leq r,$ we have

$\begin{align*} D_{x}{{}_{F}\mathcal{E}_{r+1}}^{\left[ m-1,\kappa \right]}(x;u;\gamma)& = \left( r+1\right) {{}_{F}\mathcal{E}_{r}}^{\left[m-1,\kappa \right]}(x;u;\gamma), \end{align*}$

$\begin{align} D_{x}^{(j)}{{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa \right]}(x;u;\gamma)& = \dfrac{r!}{(r-j)!}{{}_{F}\mathcal{E}_{r-j}}^{\left[ m-1,\kappa \right]}(x;u;\gamma). \end{align}$

(3.3)

(4) Integral formula. For a fixed $m \in \mathbb{N},$ $\kappa, \gamma \in \mathbb{C}$ , we have

$\begin{align*} \int_{x_{0}}^{x_{1}}{{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa \right]}(x;u;\gamma)dx & = \dfrac{{{}_{F}\mathcal{E}_{r+1}}^{\left[ m-1,\kappa \right]}(x_{1};u;\gamma)-{{}_{F}\mathcal{E}_{r+1}}^{\left[ m-1,\kappa \right]}(x_{0};u;\gamma)}{\left( r+1\right) }. \end{align*}$

(5) Addition theorems.

$\begin{align} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa \right]}(x+y;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1,\kappa \right]}(x;u;\gamma)y^{s}, \end{align}$

(3.4)

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa \right]}(x+y;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{s}}^{\left[ m-1,\kappa \right]}(u;\gamma)\left( x+y\right) ^{r-s}. \end{align*}$

Setting $y = 1$ in (3.4), we have

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa \right]}(x+1;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1,\kappa \right]}(x;u;\gamma). \end{align*}$

(6) Addition theorems of the argument.

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{\left[ m-1,\kappa\pm\beta \right]}(x+y;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1,\kappa \right]}(x;u;\gamma){{}_{F}\mathcal{E}_{s}}^{\left[ m-1,\pm\beta\right]}(y;u;\gamma). \end{align*}$

(7) We have

$\begin{align*} \mathfrak{E}_{r}^{\left[m-1 \right] }(x;\gamma)& = \dfrac{2^{m}\gamma^{m-1}}{\left( \gamma+1\right) ^{m}}{{}_{F}\mathcal{E}_{r}}^{\left[ m-1\right] }(x;-\gamma^{-1};1). \end{align*}$

Proposition 3.2. The generalized Apostol-type Frobenius–Euler polynomials satisfy the following inversion formula:

$\begin{align} x^{r}& = \dfrac{1}{\left( 1-u\right)^{m} }\sum\limits_{s = 0}^{r}\binom{r}{s}\left(\gamma -ua_{s,m} \right){{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1\right] }(x;u;\gamma), \end{align}$

(3.5)

where

$\begin{equation*} a_{s,m} = \begin{cases} 1,\quad &{if}\; 0\leq s < m ,\\ 0,\quad &{if}\; s\geq m . \end{cases} \end{equation*}$

Proof. Setting $\kappa = 1$ in (3.1), we have

$\begin{align*} (1-u)^{m}e^{x z} & = \left( \gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}\right) \left( \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_r}^{[m-1]}(x;u;\gamma)\frac{z^r}{r!}\right) \\ & = \left( \sum\limits_{r = 0}^{\infty}\left(\gamma -ua_{r,m} \right)\frac{z^{r}}{r!}\right)\left( \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_r}^{[m-1]}(x;u;\gamma)\frac{z^r}{r!}\right) , \end{align*}$

therefore,

$\begin{equation*} (1-u)^{m}\sum\limits_{r = 0}^{\infty}x^{r}\frac{z^{r}}{r!} = \sum\limits_{r = 0}^{\infty}\sum\limits_{s = 0}^{r}\binom{r}{s}\left(\gamma -ua_{s,m} \right){{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1\right] }(x;u;\gamma)\frac{z^{r}}{r!}. \end{equation*}$

By comparing the coefficients of $\dfrac{z^{r}}{r!}$ on both sides, we obtain the result. □

Proposition 3.3. The generalized Apostol-type Frobenius–Euler polynomials satisfy the following relations:

$\begin{align} \gamma{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma) -u\sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1,\kappa]}(x;u;\gamma) = \left( 1-u\right)^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa-1]}(x;u;\gamma), \end{align}$

(3.6)

$\begin{align} \gamma{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma) -u\sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1,\kappa]}(x-1;u;\gamma) = \left( 1-u\right)^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa-1]}(x-1;u;\gamma). \end{align}$

(3.7)

Upon setting $\kappa = 1$ , in (3.6), we give the following corollary.

Corollary 3.1.

$\begin{align*} x^{r}& = \dfrac{1}{\left(1-u\right)^{m} }\left[ \gamma \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{k}}^{\left[ m-1\right] }(x;u;\gamma)- u \sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1\right] }(x;u;\gamma) \right]. \end{align*}$

Proof. (3.6). We have

$\begin{align*} &\sum\limits_{r = 0}^{\infty}\left( \gamma{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma) -u\sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1,\kappa]}(x;u;\gamma)\right)\frac{z^{r}}{r!}\\ = &\gamma\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma)\frac{z^{r}}{r!} -u\sum\limits_{r = 0}^{\infty}\sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!}\\ = &\gamma\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma)\frac{z^{r}}{r!} -u\sum\limits_{l = 0}^{m-1}\frac{z^{l}}{l!}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!}. \end{align*}$

Now, using (3.1), we obtain

$\begin{align*} &\gamma\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma)\frac{z^{r}}{r!} -u\sum\limits_{l = 0}^{m-1}\frac{z^{l}}{l!}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!}\\ = &\gamma \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{\left(x+1\right)z}- u\sum\limits_{l = 0}^{m-1}\frac{z^{l}}{l!} \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{x z}\\ = &\left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{x z} \left( \gamma e^{z}-u\sum\limits_{l = 0}^{m-1}\frac{z^{l}}{l!}\right) = \left(1-u\right)^{m}\left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa-1} e^{x z}, \end{align*}$

thus

$\begin{align*} \left(1-u\right)^{m}\left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa-1} e^{x z} = \left(1-u\right)^{m}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa-1]}(x;u;\gamma)\dfrac{z^{r}}{r!}. \end{align*}$

Comparing the coefficients of $\dfrac{z^{r}}{r!}$ , we obtain (3.6). □

Proof. For the proof of (3.7), a similar scheme to the previous one is used. □

Theorem 3.1. The generalized Apostol-type Frobenius–Euler polynomials satisfy the following relation, with $u\neq 1$ :

$\begin{eqnarray*} \frac{\gamma{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma) -u{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)}{\left( 1-u\right)}& = & \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{k}}^{[m-1,\kappa]}(x;u;\gamma){{}_{F}\mathcal{E}_{r-s}}^{(-1)}(u;\gamma). \end{eqnarray*}$

Proof.

$\begin{align*} &\sum\limits_{r = 0}^{\infty}\left( \gamma{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+1;u;\gamma) -u{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\right) \dfrac{z^{r}}{r!}\\ = &\gamma e^{z}\sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\dfrac{z^{r}}{r!} -u\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\dfrac{z^{r}}{r!}\\ = &\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\dfrac{z^{r}}{r!}\left( \gamma e^{z}-u\right)\\ = &\left(1-u \right) \sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\dfrac{z^{r}}{r!}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[0,-1]}(u;\gamma)\dfrac{z^{r}}{r!}. \end{align*}$

Applying the Cauchy product in the above equation and comparing the coefficients of $\frac{z^{r}}{r!}$ on both sides, we obtain the proof. □

Theorem 3.2. The generalized Apostol-type Frobenius–Euler polynomials satisfy the following identity:

$\begin{eqnarray} \label{rel7} \gamma{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x+1;u;\gamma) -u\sum\limits_{s = 0}^{\min (r,m-1)}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1]}(x;u;\gamma) = \sum\limits_{s = 0}^{r}\binom{r}{s}\left(\gamma -ua_{s,m} \right) \times{{}_{F}\mathcal{E}_{r-s}}^{\left[ m-1\right] }(x;u;\gamma), \end{eqnarray}$

where

$\begin{equation*} a_{s,m} = \begin{cases} 1,\quad &\mathit{\text{if $0\leq s < m $}},\\ 0,\quad &\mathit{\text{if $ s\geq m $}}. \end{cases} \end{equation*}$

Proof. To prove Theorem 3.2, it is enough to use Definition 3.1 and perform the necessary mathematical calculations, which lead directly to the desired result. □

Theorem 3.3. The following implicit summation formula for the generalized Apostol-type Frobenius–Euler polynomials holds true:

$\begin{equation} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(w+y;u;\gamma) = \sum\limits_{r,n = 0}^{s,l}\binom{s}{r}\binom{l}{n}\left(w-x \right)^{r+n}{{}_{F}\mathcal{E}_{s+l-r-n}}^{[m-1,\kappa]}(x+y;u;\gamma). \end{equation}$

(3.8)

Proof. From (3.1), we have

$\begin{align} \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\kappa} e^{(x+y)z} & = \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^r}{r!}, \end{align}$

substituting $z$ by $z+a$ in the above equation, we obtain

$\begin{align*} \left( \frac{(1-u)^{m}}{\gamma e^{(z+a)}-u \sum\limits_{l = 0}^{m-1}\frac{(z+a)^l}{l!}}\right)^{\kappa} e^{x(z+a)}e^{y(z+a)} & = \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{(z+a)^r}{r!}. \end{align*}$

Now, using the following formula [20, p. 52]:

$\begin{align} \sum\limits_{N = 0}^{\infty}f(N)\frac{\left(x+y \right)^{N} }{N!}& = \sum\limits_{s,l}^{\infty}f(s+l)\frac{x^{s}y^{l}}{s!l!}, \end{align}$

(3.9)

we obtain

$\begin{align*} \left( \frac{(1-u)^{m}}{\gamma e^{(z+a)}-u \sum\limits_{l = 0}^{m-1}\frac{(z+a)^l}{l!}}\right)^{\kappa} e^{y(z+a)} & = e^{-x(z+a)}\sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}. \end{align*}$

Replacing $x$ by $w$ in the above equation and equating the resultant equation to the above equation, we obtain

$\begin{align} e^{(w-x)(z+a)}\sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}& = \sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(w+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!},\\ \sum\limits_{N = 0}^{\infty}\left( w-x\right)^{N}\frac{\left( z+a\right)^{N} }{N!} \sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}& = \sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(w+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!} . \end{align}$

(3.10)

Recalling (3.9), the left-hand side of (3.10) becomes

$\begin{align*} &\sum\limits_{N = 0}^{\infty}\left( w-x\right)^{N}\frac{\left( z+a\right)^{N} }{N!} \sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}\\ = &\sum\limits_{r,n = 0}^{\infty}\left(w-x \right)^{r+n}\frac{z^{r}a^{n}}{r!n!}\sum\limits_{s,l = 0}^{\infty} {{}_{F}\mathcal{E}_{s+l}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}\\ = &\sum\limits_{s,l = 0}^{\infty}\sum\limits_{r,n = 0}^{s,l}\frac{\left(w-x \right)^{r+n}}{r!n!} {{}_{F}\mathcal{E}_{s-r+l-n}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{(s-r)!(l-n)!}\\ = &\sum\limits_{s,l = 0}^{\infty}\sum\limits_{r,n = 0}^{s,l}\binom{s}{r}\binom{l}{n}\left(w-x \right)^{r+n} {{}_{F}\mathcal{E}_{s+l-r-n}}^{[m-1,\kappa]}(x+y;u;\gamma)\frac{z^{s}a^{l}}{s!l!}. \end{align*}$

Comparing coefficients, we get the assertion (3.8). □

Theorem 3.4. The following relation for the generalized Apostol-type Frobenius–Euler polynomials holds true:

$\begin{align} &(2u-1)\sum\limits_{j = 0}^{r}\sum\limits_{s = 0}^{\min(j,m-1)}\binom{r}{j}\binom{j}{s}{{}_{F}\mathcal{E}_{r-j}}^{[m-1]}(u;\gamma){{}_{F}\mathcal{E}_{j-s}}^{[m-1]}(x;1-u;\gamma) \\ = & u^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;u;\gamma) -(1-u)^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x,1-u;\gamma). \end{align}$

(3.11)

Proof. We set

$\begin{align} & \dfrac{\left( 2u-1\right)\left( 1-u\right)^{m}u^{m}e^{x z}\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}}{\left(\gamma e^{z}-u\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)\left( \gamma e^{z}-(1-u)\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}\right)} = \dfrac{\left( 1-u\right)^{m}u^{m}e^{x z}}{\left(\gamma e^{z}-u\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)} -\dfrac{\left( 1-u\right)^{m}u^{m}e^{x z}}{\left(\gamma e^{z}-(1-u)\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)}. \end{align}$

(3.12)

On the left-hand side of (3.12), we deduce

$\begin{eqnarray*} & & \dfrac{\left( 2u-1\right)\left( 1-u\right)^{m}u^{m}e^{x z}\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}}{\left(\gamma e^{z}-u\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)\left( \gamma e^{z}-(1-u)\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}\right)}\\ & = &\left( 2u-1\right)\dfrac{\left( 1-u\right)^{m}\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}}{\left(\gamma e^{z}-u\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)} \dfrac{\left( 1-(1-u)\right)^{m}e^{x z} }{\left( \gamma e^{z}-(1-u)\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!}\right)}\\ & = &\left( 2u-1\right) \sum\limits_{r = 0}^{\infty}\sum\limits_{j = 0}^{r}\binom{r}{j}{{}_{F}\mathcal{E}_{r-j}}^{[m-1]}(u;\gamma) \sum\limits_{s = 0}^{\min(j,m-1)}\binom{j}{s}{{}_{F}\mathcal{E}_{j-s}}^{[m-1]}(x;1-u;\gamma)\frac{z^{r}}{r!}. \end{eqnarray*}$

On the right-hand side of (3.12), we obtain

$\begin{eqnarray*} & & \dfrac{\left( 1-u\right)^{m}u^{m}e^{x z}}{\left(\gamma e^{z}-u\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)}-\dfrac{\left( 1-u\right)^{m}u^{m}e^{x z}}{\left(\gamma e^{z}-(1-u)\sum\nolimits_{l = 0}^{m-1}\frac{z^{l}}{l!} \right)} \\ & = &u^{m}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;u;\gamma)\frac{z^{r}}{r!} -\left(1-u \right) ^{m}\sum\limits_{r = 0}^{\infty}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;1-u;\gamma)\frac{z^{r}}{r!}\\ & = &\sum\limits_{r = 0}^{\infty}\left( u^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;u;\gamma) \right. \left.-\left(1-u \right) ^{m}{{}_{F}\mathcal{E}_{r}}^{[m-1]}(x;1-u;\gamma)\right) \frac{z^{r}}{r!}.\\ \end{eqnarray*}$

Comparing coefficients yields (3.11). □

Theorem 3.5. For the generalized Apostol-type Frobenius–Euler polynomials, we have the following recurrence relation:

$\begin{eqnarray} {{}_{F}\mathcal{E}_{r+1}}^{[m-1,\kappa]}(x;u;\gamma)& = &\left( x-\kappa\right){{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)-\dfrac{u \kappa r!}{\left( 1-u\right)^{m}\left(m-1 \right)!\left( r+1-m\right)!}\\ & & \times{{}_{F}\mathcal{E}_{r+1-m}}^{[m-1,\kappa+1]}(x;u;\gamma). \end{eqnarray}$

(3.13)

Upon setting $m = \gamma = 1$ and $u = -1$ in (3.13), we obtain:

$\begin{align*} {E}_{r+1}^{(\kappa)}(x) = \left( x-\kappa \right){E}_{r}^{(\kappa)}(x) +\dfrac{\kappa}{2}{E}_{r}^{(\kappa+1)}(x), \end{align*}$

where ${E}_{r+1}^{(\kappa)}(x)$ , is the Euler polynomial of order $\kappa$ and degree $r+1$ (see [11, p. 3258]).

Proof. Let us consider the following generating function

$G^{[m-1,\kappa]}(x;z;u;\gamma) = \left(\dfrac{\left( 1-u\right)^{m} }{\gamma e^{z}-u\sum\nolimits_{h = 0}^{m-1}\frac{z^{h}}{h!}} \right)^{\kappa}e^{x z}.$

Then, the differentiation of both sides of the above equation

$\begin{eqnarray*} \frac{\partial}{\partial z}G^{[m-1,\kappa]}(x;z;u;\gamma)& = &\kappa \left(\dfrac{\left( 1-u\right)^{m} }{\gamma e^{z}-u\sum\nolimits_{k = 0}^{m-1}\frac{z^{h}}{h!}} \right)^{\kappa-1}\left[ \dfrac{-(1-u)^{m}\left( \gamma e^{z}-u\sum\nolimits_{k = 0}^{m-2}\frac{z^{h}}{h!} \right) }{\left( \gamma e^{z}-u\sum\nolimits_{h = 0}^{m-1}\frac{z^{h}}{h!}\right)^{2} }\right]e^{x z}\\ & & + x \left(\dfrac{\left( 1-u\right)^{m} }{\gamma e^{z}-u\sum\nolimits_{h = 0}^{m-1}\frac{z^{h}}{h!}} \right)^{\kappa}e^{x z}\\ & = &(x-\kappa)G^{[m-1,\kappa]}(x;z;u;\gamma)-\dfrac{u\kappa z^{m}G^{[m-1,\kappa]}(x;z;u;\gamma)G^{[m-1]}(0;z;u;\gamma)}{\left(1-u \right)^{m}\left(m-1 \right)!z }, \end{eqnarray*}$

and consequently

$\begin{eqnarray} & & \left( 1-u \right)^{m}\left(m-1 \right)!z \frac{\partial}{\partial z}G^{[m-1,\kappa]}(x;z;u;\gamma) \\ & = &\left(1-u\right)^{m}\left(m-1 \right)!z (x-\kappa)G^{[m-1,\kappa]}(x;z;u;\gamma) -u\kappa z^{m}G^{[m-1,\kappa]}(x;z;u;\gamma)G^{[m-1]}(0;z;u;\gamma). \end{eqnarray}$

(3.14)

Now, differentiating with respect to $z$ on the right-hand side of (3.1) and using (3.14), we obtain

$\begin{align} \left( 1-u \right)^{m}\left(m-1 \right)!z \frac{\partial}{\partial z}G^{[m-1,\kappa]}(x;z;u;\gamma) = \left( 1-u \right)^{m}\left(m-1 \right)!\sum\limits_{r = 0}^{\infty}r{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!}. \end{align}$

(3.15)

On the other hand, we have

$\begin{align} & \left( 1-u \right)^{m}\left(m-1 \right)!z (x-\kappa)G^{[m-1,\kappa]}(x;z;u;\gamma) \\ = &\left( 1-u \right)^{m}\left(m-1 \right)! (x-\kappa) \times \sum\limits_{r = 0}^{\infty}r{{}_{F}\mathcal{E}_{r-1}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!} \end{align}$

(3.16)

and

$\begin{align} &u\kappa z^{m}G^{[m-1,\kappa]}(x;z;u;\gamma)G^{[m-1]}(0;z;u;\gamma) \\ = & u\kappa\sum\limits_{r = m}^{\infty}\dfrac{r!}{(r-m)! }\sum\limits_{s = 0}^{r-m}\binom{r-m}{s} {{}_{F}\mathcal{E}_{r-m-s}}^{[m-1]}(u;\gamma){{}_{F}\mathcal{E}_{s}}^{[m-1,\kappa]}(x;u;\gamma)\frac{z^{r}}{r!}. \end{align}$

(3.17)

Substitution of (3.15)–(3.17) into (3.14) and equating coefficients of power series on both sides, the proof is complete.□

Theorem 3.6. For the generalized Apostol-type Frobenius–Euler polynomials, we have the following differential equation:

$\begin{eqnarray} \left[ \left( x-\kappa\right){D}_{x} -\dfrac{u \kappa}{\left( 1-u\right)^{m}\left( m-1\right)!}\sum\limits_{s = 0}^{r+1-m}\dfrac{{{}_{F}\mathcal{E}_{r+1-m-s}}^{[m-1]}(u;\gamma)}{\left( r+1-m-s\right)! }{D}_{x}^{r-s+1}-r\right] \times{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma) = 0. \end{eqnarray}$

(3.18)

Proof. Applying the factorization method (see ^[12,16]) and using (3.3), we can rewrite (3.13) as follows:

$\begin{align} &{{}_{F}\mathcal{E}_{r+1}}^{[m-1,\kappa]}(x;u;\gamma) \\ = &\left[ \left( x-\kappa\right) -\dfrac{u \kappa}{\left( 1-u\right)^{m}\left( m-1\right)!}\sum\limits_{s = 0}^{r+1-m}\dfrac{{{}_{F}\mathcal{E}_{r+1-m-s}}^{[m-1]}(u;\gamma)}{\left( r+1-m-s\right)! }{D}_{x}^{n-k}\right] \times{{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma). \end{align}$

(3.19)

Therefore, the operator

$\begin{equation*} {L}_{r,m}^{+} = \left[ \left( x-\kappa\right) -\dfrac{u \kappa}{\left( 1-u\right)^{m}\left( m-1\right)!}\sum\limits_{s = 0}^{r+1-m}\dfrac{{{}_{F}\mathcal{E}_{r+1-m-s}}^{[m-1]}(u;\gamma)}{\left( r+1-m-s\right)! }{D}_{x}^{r-s}\right], \end{equation*}$

where

${D}_{x}^{r-s} : = \dfrac{d^{r-s}}{dx^{r-s}}.$

Now, applying the operator ${L}_{r+1}^{-}: = \dfrac{1}{r+1}{D}_{x}$ on both sides of (3.19), we have

$( {L}_{r+1}^{-} {L}_{r,m}^{+}){{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma) = {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma).$

Finally, after some rearrangements of terms, we achieve the desired result. □

4. Some connection formulas for the generalized Apostol-type Frobenius–Euler polynomials

In this section, we present some formulas connecting the generalized Apostol-type Frobenius–Euler polynomials with generalized Stirling numbers of the second kind, the two-variable Fubini polynomials, Bernstein polynomials, and Hermite polynomials.

Theorem 4.1. Let $m \in \mathbb{N}$ , $\upsilon, j \in \mathbb{N}_{0}$ . The following relations are demonstrated between the generalized Frobenius with Euler polynomials of the Apostol type and the generalized Stirling numbers of the second kind:

$\begin{align} x^{n}& = \upsilon!\left( \dfrac{u}{(1-u)^{m}}\right)^{\upsilon}\sum\limits_{j = 0}^{r}\binom{r}{j}{{}_{F}\mathcal{E}_{j}}^{[m-1,\upsilon]}(x;u;\gamma){S}^{[m-1]}\left(r-j,\upsilon,\frac{\gamma}{u}\right), \end{align}$

(4.1)

$\begin{align} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa-\upsilon]}(x;u;\gamma)& = \upsilon! \left( \dfrac{u}{(1-u)^{m}}\right)^{\upsilon}\sum\limits_{j = 0}^{r}\binom{r}{j}{{}_{F}\mathcal{E}_{j}}^{[m-1,\kappa]}(x;u;\gamma){S}^{[m-1]}\left(r-j,\upsilon,\frac{\gamma}{u}\right). \end{align}$

(4.2)

Proof. (4.1). Indeed,

$\begin{align*} \left( \frac{(1-u)^{m}}{\gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!}}\right)^{\upsilon} e^{x z} & = \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\upsilon]}(x;u;\gamma)\frac{z^r}{r!}, \end{align*}$

$\begin{align*} e^{x z}& = \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\upsilon]}(x;u;\gamma)\frac{z^r}{r!}\left( \gamma e^z-u \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!} \right)^{\upsilon}\left( \dfrac{\upsilon!}{\upsilon !(1-u)^{m\upsilon}} \right)\\ & = \upsilon! \sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\upsilon]}(x;u;\gamma)\frac{z^r}{r!}\dfrac{\left(\frac{\gamma}{u} e^z- \sum\limits_{l = 0}^{m-1}\frac{z^l}{l!} \right)^{\upsilon}}{\upsilon!}\left( \dfrac{u}{(1-u)^{m}} \right)^{\upsilon}. \end{align*}$

Now, using (2.2), we have

$\begin{align*} \sum\limits_{r = 0}^{\infty}x^{r}\frac{z^{r}}{r!}& = \upsilon! \left( \dfrac{u}{(1-u)^{m}} \right)^{\upsilon}\sum\limits_{r = 0}^{\infty} {{}_{F}\mathcal{E}_{r}}^{[m-1,\upsilon]}(x;u;\gamma)\frac{z^r}{r!} \sum\limits_{r = 0}^{\infty}{S}^{[m-1]}\left(r;\upsilon;\frac{\gamma}{u}\right)\frac{z^{r}}{r!}\\ & = \upsilon! \left( \dfrac{u}{(1-u)^{m}} \right)^{\upsilon}\sum\limits_{r = 0}^{\infty}\sum\limits_{j = 0}^{r}\binom{r}{j} {{}_{F}\mathcal{E}_{j}}^{[m-1,\upsilon]}(x;u;\gamma) {S}^{[m-1]}\left(r-j;\upsilon;\frac{\gamma}{u}\right)\frac{z^{r}}{r!}. \end{align*}$

Finally, comparing the coefficients, we obtain the assertion (4.1). □

Corollary 4.1. We have

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{[m-1,-\upsilon]}(x;u;\gamma)& = \upsilon! \left( \dfrac{u}{(1-u)^{m}}\right)^{\upsilon}\sum\limits_{j = 0}^{r}\binom{r}{j}{S}^{[m-1]}\left(r-j,\upsilon,\frac{\gamma}{u}\right)x^{j}. \end{align*}$

Proof. If we set $\kappa = 0$ in (4.2) and use Eq (3.2), we complete the proof of the corollary. □

Proposition 4.1. Let $m \in \mathbb{N}$ and $r \in \mathbb{N}_{0}$ . The following relationships have been established between the generalized Apostol-type Frobenius–Euler polynomials and the two-variable Fubini polynomials, the Bernstein polynomials, the Stirling polynomials of the second kind of level $m$ , and the Hermite polynomials:

$\begin{align*} {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)& = \sum\limits_{s = 0}^{r}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s}}^{[m-1,\kappa]}(u;\gamma)\left[(1+w){F}_{s}(x,w)-w{F}_{s}(x+1,w) \right], \\ {B}_{s,r}(x)& = x^{s}\sum\limits_{n = 0}^{r-s}\binom{r-s}{n}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s-n}}^{[m-1,-\upsilon]}(u;\gamma){{}_{F}\mathcal{E}_{n}}^{[m-1,\upsilon]}(1-x;u;\gamma),\\ {B}_{r,s}(x)& = x^{s}\upsilon!\left(\dfrac{u}{(1-u)^{m}} \right)^{\upsilon}\sum\limits_{j = 0}^{r-s}\binom{r-s}{j}\binom{r}{s}{{}_{F}\mathcal{E}_{r-s-j}}^{[m-1,\kappa]}(1-x;u;\gamma){S}^{[m-1]}\left(j;\upsilon,\frac{\gamma}{u}\right),\\ {{}_{F}\mathcal{E}_{r}}^{[m-1,\kappa]}(x;u;\gamma)& = \sum\limits_{s = 0}^{[\frac{r}{2}]}\sum\limits_{j = 0}^{r-2s}\binom{r-2s}{j}\binom{r}{2s}\frac{(2s)!}{s!}{{}_{F}\mathcal{E}_{j}}^{[m-1,\kappa]}(u;\gamma){H}_{r-2s-j}\left( \frac{x}{2}\right). \end{align*}$

5. Apostol–type Frobenius–Euler polynomials and their applications

This section presents an application due to the zero distributions of this new class of generalized Apostol-type Frobenius–Euler polynomials.

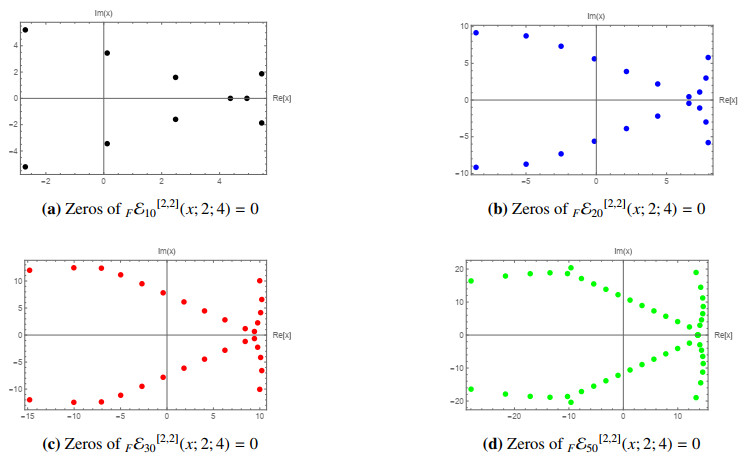
To study the zero distributions using (3.1) and Mathematica Wolfram, we show the zero patterns. We show plots of zero distributions; to plot these, we give values to the coefficients of the Apostol-type Frobenius–Euler polynomials $\{m \to 3, u \to 2, \kappa \to 2, \gamma \to 4\}$ , and the equation used is:

$\begin{equation} \frac{e^{x z}}{\left(4 e^z - 2 \left(1 + z + \frac{z^2}{2}\right)\right)^2}. \end{equation}$

(5.1)

We give values for $n$ (10, 20, 30, 50), and we have the plots.

In Figure 1 the plots are organized as 1(a) black dots for 10 points, in 1(b) blue dots for 20 points, in 1(c) red dots for 30 points, and 1(d) green dots for 50 points, the shape of these plots seems like a fish. At the same time, as we increase the dots, we can see a more defined shape, and in the plot 1(d), here we see two dots around (-10, -20) and (-10, 20).

Figure 1. Roots of Apostol-type Frobenius–Euler generalized polynomials, plotted considering 10, 20, 30, and 50 points.

DownLoad: Full-Size Img PowerPoint

Another interesting application is the induced mesh of generalized Apostol-type Frobenius–Euler polynomials for different numbers of n (3.1) ${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]} = 0.$

In Figure 2, we show four graphs representing the mesh distribution by z-coefficient equal to 10, 20, 30 and 50, respectively. As we increase the z-value, we notice that it forms a cone shaped. In Figure 2(a), there are black dots for 10 points, and in Figure 2(d) green dots for 50 points, we see a more defined mesh shape.

Figure 2. Mesh distribution of Apostol-type Frobenius–Euler generalized polynomials, plotted considering 10, 20, 30 and 50 points.

DownLoad: Full-Size Img PowerPoint

Then, based on the Apostol-type Frobenius–Euler polynomials. We computed an approximate solution that satisfies them, ${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]}$ for $n = 2, 3, ..., 10$ . The results are presented in Table 1.

Table 1. Approximate solutions for

${{}_{F}\mathcal{E}_{r}}^{[m-1, \kappa]} = 0$ .

n	x
1	0.817219
2	0.820808 - 0.817211 i, 0.820808 + 0.817211 i
3	0.585556 - 1.48212 i, 0.585556 + 1.48212 i, 1.31145
4	0.239933 - 2.06742 i, 0.239933 + 2.06742 i, 1.42216 - 0.730256 i, 1.42216 + 0.730256 i
5	-0.181558 - 2.59823 i, -0.181558 + 2.59823 i, 1.3582 - 1.38743 i, 1.3582 + 1.38743 i, 1.79663
6	-0.762338 - 3.3425 i, -0.762338 + 3.3425 i, -0.567434, 1.92081 - 2.62112 i,
	1.92081 + 2.62112 i, 3.28321
7	-1.27326 - 3.64882 i, -1.27326 + 3.64882 i, -0.567429, 1.26675 - 3.3269 i,
	1.26675 + 3.3269 i, 3.28321 + 1.43895 i, 3.29972 + 1.43895 i
8	-1.73694 - 4.00473 i, -1.73694 + 4.00473 i, -0.567428, 0.608126 - 3.82671 i,
	0.608126 + 3.82671 i, 2.90345 + -2.584355 i, 2.90345 + 2.58435 i, 3.91179
9	-2.23827 - 4.43454 i, -2.23827 + 4.43454 i, -0.567428, -0.0245166 - 4.13057 i,
	-0.0245166 + 4.13057 i, 2.34366 + -3.41153 i, 2.34366 + 3.41153 i,
	3.99888 - 1.34432 i, 3.99888 + 1.34432 i
10	-2.70965 - 5.20815 i, -2.70965 + 5.20815 i, 0.117982 - 3.44461 i,
	0.117982 + 3.44461 i, 2.47995 + -1.59536 i, 2.47995 + 1.59536 i,
	4.37324, 4.94372, 5.45324 -1.86857 i, 5.45324 + 1.86857 i

| Show Table

DownLoad: CSV

6. Conclusions

This paper introduces a novel category of generalized Apostol-type Frobenius with Euler polynomials and investigates their intricate mathematical properties in detail using generating function techniques. A significant contribution of this study is the establishment of their associated differential equation through the factorization method, complemented by the formulation of a recurrence relation for these polynomials. Furthermore, the study derives several correlation formulas that establish a connection between these generalized polynomials and classical special functions, including the Bernstein, Fubini, and Hermite polynomials.

Moreover, graphical representations are provided by analysing the behavior of polynomial zeros and visualising their networks for specific values of $n$ . These graphs offer insights into the structure and behavior of the polynomials and demonstrate their practical utility in modeling and numerical computations.

The results presented in this paper establish a solid foundation for future explorations. In the field of approximation theory, these generalized polynomials have the potential to enhance the efficacy of techniques such as spectral methods, orthogonal expansions, and the approximation of complex functions. Similarly, their associations with special polynomials demonstrate fascinating avenues for the advancement of number theory, particularly concerning modular forms, integer sequences, and combinatorial identities. Finally, the factorization and recurrence approaches adopted here could inspire new developments in classical analysis and symbolic computation, rendering these polynomials a promising tool for further interdisciplinary research.

Author contributions

Letelier Castilla: Conceptualization, Data curation, Investigation, Resources, Validation, Writing original draft; William Ramírez: Conceptualization, Investigation, Methodology, Project administration, Software, Supervision, Writing original draft; Clemente Cesarano: Conceptualization, Data curation, Formal analysis, Funding, Supervision; Shahid Ahmad Wani: Conceptualization, Investigation, Project administration, Supervision, Writing the final version; Maria-Fernanda Heredia-Moyano: Conceptualization, Investigation, Methodology, Project administration, Software, Supervision. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

Prof. Clemente Cesarano is the Guest Editor of Special Issue "Special functions and related applications" for AIMS Mathematics. Prof. Clemente Cesarano was not involved in the editorial review and the decision to publish this article.

The authors declare no competing interests.

References

[1]	O. Hölder, Uber einen mittelwerthssatz, Nachr. Ges. Wiss. Gottingen, 1889 (1889), 38–47.
[2]	W. T. Sulaiman, Reverses of Minkowski's, Hölder's, and Hardy's integral inequalities, Int. J. Mod. Math. Sci., 1 (2012), 14–24.
[3]	B. Sroysang, More on reverses of Minkowski's integral inequality, Math. Aeterna, 3 (2013), 597–600.
[4]	U. S. Kirmaci, On generalizations of Hölder's and Minkowski's inequalities, Math. Sci. Appl. E Notes, 11 (2023), 213–225. https://doi.org/10.36753/mathenot.1150375 doi: 10.36753/mathenot.1150375
[5]	S. Hilger, Analysis on measure chains-a unified approach to continuous and discrete calculus, Results Math., 18 (1990), 18–56. https://doi.org/10.1007/BF03323153 doi: 10.1007/BF03323153
[6]	R. P. Agarwal, D. O'Regan, S. Saker, Dynamic inequalities on time scales, New York: Springer, 2014. https://doi.org/10.1007/978-3-319-11002-8
[7]	G. AlNemer, A. I. Saied, M. Zakarya, H. A. A. El-Hamid, O. Bazighifan, H. M. Rezk, Some new reverse Hilbert's inequalities on time scales, Symmetry, 13 (2021), 2431. https://doi.org/10.3390/sym13122431 doi: 10.3390/sym13122431
[8]	E. Awwad, A. I. Saied, Some new multidimensional Hardy-type inequalities with general kernels on time scales, J. Math. Inequal., 16 (2022), 393–412. https://doi.org/10.7153/jmi-2022-16-29 doi: 10.7153/jmi-2022-16-29
[9]	R. Bibi, M. Bohner, J. Pečarić, S. Varošanec, Minkowski and Beckenbach-Dresher inequalities and functionals on time scales, J. Math. Inequal., 7 (2013), 299–312. https://doi.org/10.7153/jmi-07-28 doi: 10.7153/jmi-07-28
[10]	M. Bohner, S. G. Georgiev, Multivariable dynamic calculus on time scales, Springer, 2016,449–515. https://doi.org/10.1007/978-3-319-47620-9
[11]	P. Řehák, Hardy inequality on time scales and its application to half-linear dynamic equations, J. Inequal. Appl., 2005 (2005), 942973. https://doi.org/10.1155/JIA.2005.495 doi: 10.1155/JIA.2005.495
[12]	H. M. Rezk, W. Albalawi, H. A. A. El-Hamid, A. I. Saied, O. Bazighifan, M. S. Mohamed, et al., Hardy-Leindler-type inequalities via conformable Delta fractional calculus, J. Funct. Spaces, 2022 (2022), 2399182. https://doi.org/10.1155/2022/2399182 doi: 10.1155/2022/2399182
[13]	S. H. Saker, A. I. Saied, M. Krnić, Some new dynamic Hardy-type inequalities with kernels involving monotone functions, Rev. Real Acad. Cienc. Exactas Fis. Nat., 114 (2020), 142. https://doi.org/10.1007/s13398-020-00876-6 doi: 10.1007/s13398-020-00876-6
[14]	S. H. Saker, A. I. Saied, M. Krnić, Some new weighted dynamic inequalities for monotone functions involving kernels, Mediterr. J. Math., 17 (2020), 39. https://doi.org/10.1007/s00009-020-1473-0 doi: 10.1007/s00009-020-1473-0
[15]	S. H. Saker, J. Alzabut, A. I. Saied, D. O'Regan, New characterizations of weights on dynamic inequalities involving a Hardy operator, J. Inequal. Appl., 2021 (2021), 73. https://doi.org/10.1186/s13660-021-02606-x doi: 10.1186/s13660-021-02606-x
[16]	S. H. Saker, A. I. Saied, D. R. Anderson, Some new characterizations of weights in dynamic inequalities involving monotonic functions, Qual. Theory Dyn. Syst., 20 (2021), 49. https://doi.org/10.1007/s12346-021-00489-3 doi: 10.1007/s12346-021-00489-3
[17]	M. Zakarya, G. AlNemer, A. I. Saied, R. Butush, O. Bazighifan, H. M. Rezk, Generalized inequalities of Hilbert-type on time scales nabla calculus, Symmetry, 14 (2022), 1512. https://doi.org/10.3390/sym14081512 doi: 10.3390/sym14081512
[18]	M. Zakarya, A. I. Saied, G. AlNemer, H. A. A. El-Hamid, H. M. Rezk, A study on some new generalizations of reversed dynamic inequalities of Hilbert-type via supermultiplicative functions, J. Funct. Spaces, 2022 (2022), 8720702. https://doi.org/10.1155/2022/8720702 doi: 10.1155/2022/8720702
[19]	M. Zakarya, A. I. Saied, G. AlNemer, H. M. Rezk, A study on some new reverse Hilbert-type inequalities and its generalizations on time scales, J. Math., 2022 (2022), 6285367. https://doi.org/10.1155/2022/6285367 doi: 10.1155/2022/6285367
[20]	E. S. Aly, Y. A. Madani, F. Gassem, A. I. Saied, H. M. Rezk, W. W. Mohammed, Some dynamic Hardy-type inequalities with negative parameters on time scales nabla calculus, AIMS Math., 9 (2024), 5147–5170. https://doi.org/10.3934/math.2024250 doi: 10.3934/math.2024250
[21]	W. W. Mohammed, F. M. Al-Askar, C. Cesarano, On the dynamical behavior of solitary waves for coupled stochastic Korteweg-de vries equations, Mathematics, 11 (2023), 3506. https://doi.org/10.3390/math11163506 doi: 10.3390/math11163506
[22]	M. Alshammari, N. Iqbal, W. W. Mohammed, T. Botmart, The solution of fractional-order system of KdV equations with exponential-decay kernel, Results Phys., 38 (2022), 105615. https://doi.org/10.1016/j.rinp.2022.105615 doi: 10.1016/j.rinp.2022.105615
[23]	W. W. Mohammed, F. M. Al-Askar, C. Cesarano, E. S. Aly, The soliton solutions of the stochastic shallow water wave equations in the sense of Beta-derivative, Mathematics, 11 (2023), 1338. https://doi.org/10.3390/math11061338 doi: 10.3390/math11061338
[24]	F. M. Al-Askar, C. Cesarano, W. W. Mohammed, The influence of white noise and the Beta derivative on the solutions of the BBM equation, Axioms, 12 (2023), 447. https://doi.org/10.3390/axioms12050447 doi: 10.3390/axioms12050447
[25]	M. J. Huntul, I. Tekin, Simultaneous determination of the time-dependent potential and force terms in a fourth-order Rayleigh-Love equation, Math. Methods Appl. Sci., 46 (2022), 6949–6971. https://doi.org/10.1002/mma.8949 doi: 10.1002/mma.8949
[26]	M. J. Huntul, I. Tekin, Inverse coefficient problem for differential equation in partial derivatives of a fourth order in time with integral over-determination, Bull. Karaganda Univ. Math. Ser., 4 (2022), 51–59. https://doi.org/10.31489/2022M4/51-59 doi: 10.31489/2022M4/51-59
[27]	M. J. Huntul, I. Tekin, An inverse problem of identifying the time-dependent potential and source terms in a two-dimensional parabolic equation, Hacet. J. Math. Stat., 52 (2023), 1578–1599. https://doi.org/10.15672/hujms.1118138 doi: 10.15672/hujms.1118138
[28]	M. Bohner, A. Peterson, Dynamic equations on time scales: an introduction with applications, Birkhäuser, 2001. https://doi.org/10.1007/978-1-4612-0201-1
[29]	D. Anderson, J. Bullock, L. Erbe, A. Peterson, H. Tran, Nabla dynamic equations on time scales, Panam. Math. J., 13 (2003), 1–47.
[30]	N. Atasever, B. Kaymakçalan, G. Lešaja, K. Taş, Generalized diamond- $\alpha$ dynamic opial inequalities, Adv. Differ. Equations, 2012 (2012), 109. https://doi.org/10.1186/1687-1847-2012-109 doi: 10.1186/1687-1847-2012-109
[31]	U. S. Kirmaci, M. K. Bakula, M. E. Özdemir, J. E. Pecaric, On some inequalities for $p$ -norms, J. Inequal. Pure Appl. Math., 9 (2008), 27.

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1333) PDF downloads(64) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

N-dimension for dynamic generalized inequalities of Hölder and Minkowski type on diamond alpha time scales

Related Papers:

Abstract

1. Introduction

2. Background and previous results

3. The generalized Apostol-type Frobenius–Euler polynomials and their properties

4. Some connection formulas for the generalized Apostol-type Frobenius–Euler polynomials

5. Apostol–type Frobenius–Euler polynomials and their applications

6. Conclusions

Author contributions

Use of Generative-AI tools declaration

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Mathematics

N-dimension for dynamic generalized inequalities of Hölder and Minkowski type on diamond alpha time scales

Related Papers:

Abstract

1. Introduction

2. Background and previous results

3. The generalized Apostol-type Frobenius–Euler polynomials and their properties

4. Some connection formulas for the generalized Apostol-type Frobenius–Euler polynomials

5. Apostol–type Frobenius–Euler polynomials and their applications

6. Conclusions

Author contributions

Use of Generative-AI tools declaration

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog